Open Access Article
Open Access ArticleStrong interfacial interactions induced a large reduction in lateral thermal conductivity of transition-metal dichalcogenide superlattices
Wenjie Zhang,
Jia-Yue Yang * and
Linhua Liu*
* and
Linhua Liu*
School of Energy and Power Engineering, Shandong University, Qingdao 266237, China. E-mail: jy_yang@sdu.edu.cn; liulinhua@sdu.edu.cn
First published on 10th January 2019
Abstract
van der Waals heterostructures formed by vertically stacking two-dimensional (2D) crystals can not only harness the already fascinating properties of their constituent monolayers but also extend them due to the coupled interlayer interactions. With their emerged interlayer and intralayer excitons, 2D transition metal dichalcogenides (TDMC) crystals and their heterostructures have drawn growing attention for the applications of nanoelectronics, optoelectronics and nanophotonics. Yet, there are few studies on how interlayer and interfacial interactions influence the thermal transport in TDMC heterostructures which is critical for heat management. In this work, we investigate the lateral and out-of-the-plane thermal conductivity (κ) of four prototype TDMC heterostructures (bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2) by solving the phonon Boltzmann transport equation from first-principles. The calculated room-temperature lateral κ of bilayer MoS2 and WS2 are 61.13 W m−1 K−1 and 87.52 W m−1 K−1, respectively, in reasonable agreement with literature experiments. The weak interlayer interactions in the heterobilayer MoS2/WS2 help preserve the high lateral thermal transport (70.01 W m−1 K−1) of its constituent monolayer. In the superlattice MoS2/WS2, there exist strong interlayer and interfacial interactions between the alternating MoS2 and WS2 monolayer which reduce the lateral κ to be 7.22 W m−1 K−1 by a factor of 10. The greatly reduced lateral κ of the superlattice mainly arises from the low phonon relaxation time, which indicates the existence of strong interfacial anharmonic phonon scattering. This work aims at uncovering the physics of emerged thermal transport properties in TDMC heterostructures and helps advance their applications in heat management among nanoelectronics and optoelectronics.
I. Introduction
With their unique combination of direct bandgaps, atomic-scale thickness, strong light-matter interactions and spin-orbital coupling, and favorable mechanical properties, two-dimensional (2D) transition metal dichalcogenides (TMDC) have become the emerging class of materials for applications in next-generation nanoelectronics, spintronics and nanophotonics.1–7 Considerable efforts have enabled the robust growth of heterostructures and superlattices from 2D TDMCs with predetermined attributes and functionalities.8–12 Held together by van der Waals forces, different TDMC layers with diverse properties vertically stack on each other and their quantum states interact and couple to one another, which could generate fascinating electrical, optical and thermal properties in 2D heterostructures and superlattices.13–16Among those properties, exploring thermal transport in the 2D TDMC heterostructures and superlattices is not only of fundamental physics interest but also crucial to advance heat management for their applications in nanoelectronics and optoelectronics. Using a refined optothermal Raman technique, Zhang and co-workers17 measured the lateral thermal conductivity (κ) and interfacial thermal conductance of suspended single and bilayer MoS2 and MoSe2 at room temperature. By analyzing the temperature and excitation dependences of active Raman modes, Peimyoo et al.18 determined the lateral κ of suspended single and bilayer WS2. Using classical molecular dynamics, Zhang and co-workers19 calculated the lateral κ of heterobilayer MoS2/MoSe2 and showed that it preserved the high thermal conductivity of most 2D TDMC materials. Moreover, the interfacial interactions had little influence on the lateral thermal performance. Those studies greatly advance the understanding of thermal transport in 2D TDMC and the related heterostructures. Yet to modulate and engineer thermal transport in the 2D TDMC heterostructures with a higher precision, it requires a sound knowledge on phonon transport in 2D TDMCs and how the vertically stacking TDMCs layers influence the quantum behaviors of phonons.
In this work, we choose four prototype TDMCs, bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2, and investigate their lateral and out-of-the-plane κ using first-principles calculations without empirical parameters. By analyzing anharmonic lattice dynamics coupled with the Boltzmann transport theory, the calculated lateral κ of bilayer MoS2 and WS2 agree with previous experiments. In comparison, the lateral κ of heterobilayer MoS2/WS2 preserves the high values of bilayer MoS2 and WS2, and the interlayer van der Waals forces has little influence on it. By comparing heterobilayer and superlattice MoS2/WS2, it shows that the strong interfacial interactions in the superlattice greatly affect the lateral κ of heterobilayer and reduce it by a factor of 10.
II. Computational methodology
The 2D TDMC semiconductors exhibit 2H symmetry with the general formula MX2, where M = Mo, W; X = S, Se and Te. In Fig. 1, the lattice structures of bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2 are presented. After structure optimization, the thickness of bilayer MoS2 and WS2 and heterobilayer MoS2/WS2 is 0.9605 nm, 0.9633 nm and 0.9622 nm, respectively. To avoid the interlayer van der Waals interaction, one 1 nm-thick vacuum layer was introduced. The relaxed lattice parameter for the superlattice MoS2/WS2 was a (b) = 0.3281 nm and c = 1.2986 nm. After performing the phonon dispersion relation calculations, the nonexistence of imaginary phonon modes indicates the dynamic stability of those TDMCs structures.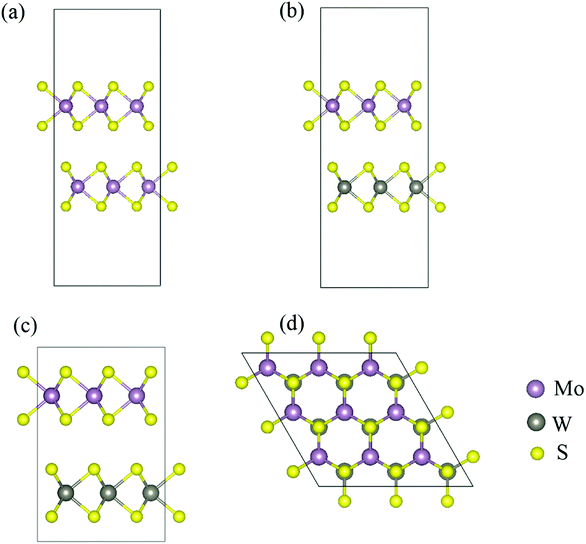 | ||
| Fig. 1 The side view of bilayer (a) MoS2, (b) heterobilayer MoS2/WS2, (c) superlattice MoS2/WS2 and (d) top view of TDMC heterostructures. | ||
In 2D TDMC semiconductors, the thermal transport is dominated by the free carriers of phonons whose transport capacities are mainly limited by the intrinsic phonon–phonon interaction.20–22 According to Boltzmann transport theory, κ is determined by23,24
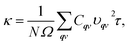 | (1) |
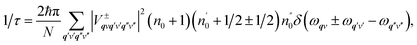 | (2) |
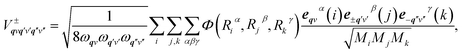 | (3) |
To calculate the harmonic and third-order IFCs, we employed the Vienna ab initio simulation package (VASP)28 which uses the projector augmented wave (PAW) method.29 The Perdew–Burke–Ernzerhof (PBE)30,31 exchange-correlation functional was adopted and the vdW-DF2 functional32 was included to calculate the van der Waals forces. The Brillouin-zone integration was computed with the 12 × 12 × 1 (12 × 12 × 12 for superlattice) Monkhorst–Pack k-mesh33 and the cutoff energy was 600 eV. For the structural relaxation, the force convergence threshold was set as 0.1 μeV Å−1. After collecting the harmonic and third-order IFCs, the phonon relaxation time and thermal conductivity were computed with the ShengBTE package.25 The automatically generated 20 × 20 × 1 (20 × 20 × 20 for the superlattice) q grid was employed and the Gaussian smearing with breadth of 1 was applied.
III. Results and discussions
Phonon dispersion relation
Prior to computing thermal conductivity of TDMC heterostructures, it is essential to understand their quantum behaviors of phonons. In Fig. 2, the phonon dispersion relations and projected density of states (PDOS) of bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2 are presented and compared. Since van der Waals (vdW) forces hold the TDMC layers together in the above heterostructures, the inclusion of vdW functional for the force calculations helps stabilize the bilayer, heterobilayer and superlattice heterostructures and eliminate the imaginary phonon modes. Due to the same 2H symmetry in lattice structure, there exists large similarity in the phonon dispersion relation of bilayer MoS2 and WS2 except that bilayer MoS2 has relatively higher phonon frequencies. That is because the mass of Mo (95.94 amu, 1 amu = 1.660539 × 10−27 kg) is much lighter than that of W (183.84 amu). By vertically stacking one MoS2 layer on top of one WS2 layer, the newly formed MoS2/WS2 heterobilayer still keeps the 2H symmetry and its phonon dispersion keeps the similar shape of bilayer MoS2 and WS2. However, the phonon degeneracy is decreased and more phonon modes are generated, which is mainly caused by the coupled quantum states between MoS2 layer and WS2 layer. By periodically alternating the MoS2 and WS2 layer, the superlattice MoS2/WS2 is built. By comparing the heterobilayer and superlattice MoS2/WS2, it finds that their phonon dispersion relations along the lateral direction are the same and interlayer van der Waals forces don't affect the lateral phonon dispersions.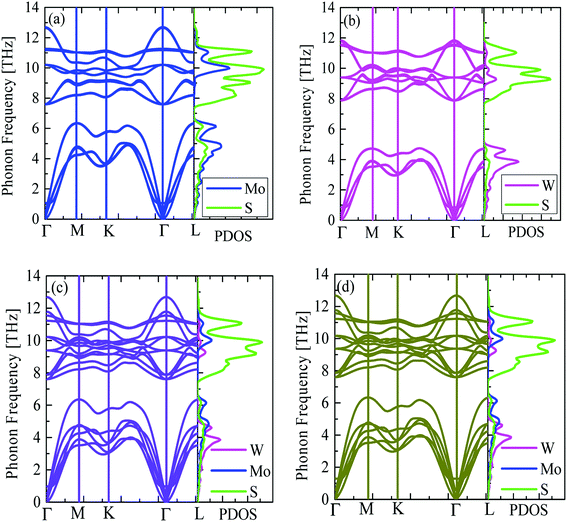 | ||
| Fig. 2 Phonon dispersion relation and projected phonon density of states (PDOS) of bilayer (a) MoS2, (b) WS2, (c) heterobilayer MoS2/WS2 and (d) superlattice MoS2/WS2. | ||
Lateral thermal conductivity
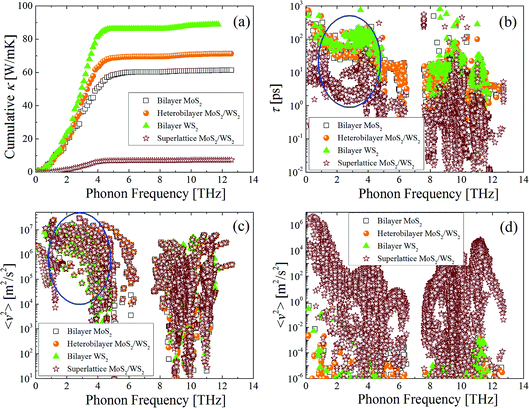
In Fig. 3(a), the calculated lateral κ of bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2 are presented and compared with literature experimental data, in order to study the influence of interlayer interactions on lateral thermal transport. By only considering the phonon–phonon interaction, the calculated lateral κ of bilayer MoS2 at 300 K and 500 K is 61.13 W m−1 K−1 and 36.77 W m−1 K−1, respectively, in good agreement with the measured value of 77 ± 25 W m−1 K−1 and 29 ± 10 W m−1 K−1.17 For the bilayer WS2, the calculated lateral κ at 300 K is 87.52 W m−1 K−1, relatively higher than the measured value of 53 W m−1 K−1.18 This difference may be caused by the neglect of electron–phonon interaction (EPI) which shows strong effect in the few-layer WX2 (X = S, Se and Te) crystals.34–36 Yet the neglect of EPI calculations which require heavy computing resources does not affect our conclusion about the influence of interlayer interactions on lateral κ. By comparing the bilayer MoS2 and WS2, heterobilayer MoS2/WS2, it shows that the lateral κ lies between that of bilayer MoS2 and WS2 and preserves the high thermal performance, indicating that the interlayer van der Waals force in the heterobilayer MoS2/WS2 does not affect the lateral κ. However, in the superlattice MoS2/WS2 with alternating MoS2 and WS2 monolayer, the interlayer van der Waals forces has a strong effect and reduces the room-temperature lateral κ of heterobilayer MoS2/WS2 from 70.01 W m−1 K−1 to 7.22 W m−1 K−1 by a factor of 10.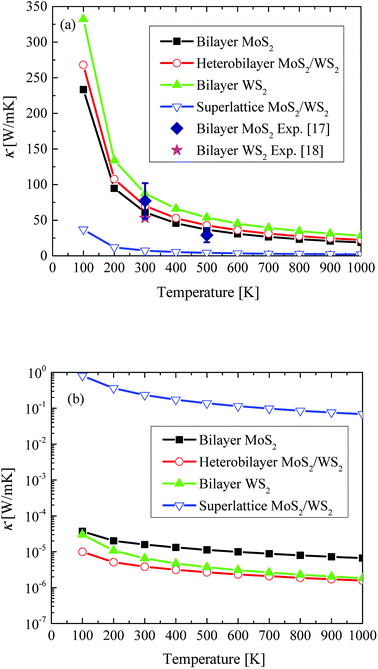 | ||
| Fig. 3 The calculated (a) lateral and (b) out-of-the-plane κ of bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2, in comparison with literature data of ref. 17 and 18. | ||
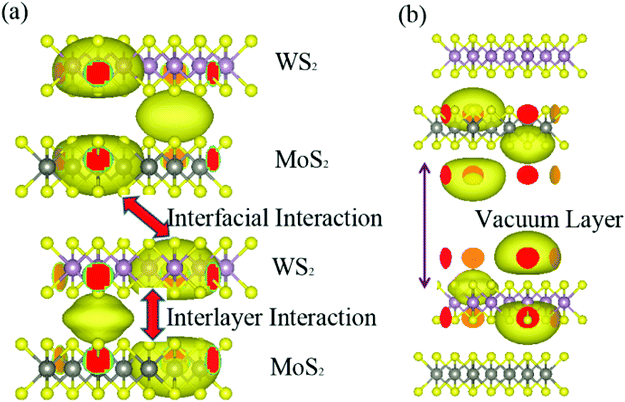
To interpret such large reduction in lateral κ, we further compare the calculated τ and averaged square group velocity (〈v2〉) which are the two relevant parameters dominating lateral thermal transport. In Fig. 4(a), by analyzing the cumulative lateral κ with phonon frequency, it shows that the propagating phonons mainly (more than 90%) contributing to the lateral thermal transport lie in the energy range of 1–5 THz. In Fig. 4(b), by comparing τ in the energy range of 1–5 THz, it observes that the calculated value of superlattice MoS2/WS2 is one order of magnitude lower than that of bilayer MoS2 and WS2 and heterobilayer MoS2/WS2. On the other hand, there is little difference in the calculated 〈v2〉 along the lateral direction in the energy range of 1–5 THz, as shown in Fig. 4(c). Therefore, it can conclude that the low τ leads to the greatly reduced lateral κ of the superlattice MoS2/WS2, compared with the heterobilayer. The low τ means the existence of strong phonon–phonon interaction in the superlattice. To explain it, we first analyze the lattice structures. The structural difference between superlattice and heterobilayer MoS2/WS2 is that there exists periodically alternating MoS2 and WS2 monolayer in the superlattice, while in the heterobilayer there is a large vacuum layer on top of MoS2/WS2. The periodically alternating MoS2 and WS2 monolayer introduce large van der Waals forces and induce strong interactions. This will bring large restoring forces for atoms and lead to large group velocity. In Fig. 4(d), the calculated 〈v2〉 of superlattice MoS2/WS2 along the out-of-the-plane direction is eight orders of magnitude larger than that of heterobilayer, which justifies the existence of strong interlayer interactions in the superlattice. Furthermore, the analysis of charge density distribution in Fig. 5 shows that there is a relatively large interlayer charge density along the out-of-the plane direction in the superlattice, while in the heterobilayer there is no interlayer charge density due to the existence of vacuum layer. The existence of interlayer charge density in the superlattice can help explain the strong interlayer interactions. On the other hand, in the alternating MoS2 and WS2 layer of neighboring unit cell in the superlattice, there exists large charge density around Mo and W atoms, respectively, which would induce the strong interfacial interactions as shown in Fig. 5. The interfacial interactions can enhance the anharmonic scattering among propagating phonons along the plane direction and thus reduce the lateral κ. To peer more microscopic insights on the interfacial interactions of superlattice MoS2/WS2, one can analyze the kinetic diffusion and collision process among lateral and flexural phonon modes using the phonon wave-packet dynamics method.37 It would require the separation of lateral and flexural phonons but it is beyond the capability of present method.
Out-of-the-plane thermal conductivity
For the 2D TDMC heterostructures, the interfacial (out-of-the plane) thermal conductance is of great importance for the heat management. In Fig. 3(b), the out-of-the-plane κ of bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2 are presented. With its nanometer thickness, the room-temperature out-of-the-plane κ of bilayer MoS2 and WS2 and heterobilayer MoS2/WS2 is limited to be 1.58 × 10−5 W m−1 K−1, 6.52 × 10−6 W m−1 K−1 and 3.86 × 10−6 W m−1 K−1, respectively. It shows that the vertically stacking MoS2 and WS2 monolayer do not influence the interfacial thermal conductance. By periodically alternating MoS2 and WS2 monolayer with strong interlayer interactions, the room-temperature out-of-the-plane κ of superlattice MoS2/WS2 is increased to be 0.23 W m−1 K−1 and 5 orders of magnitude larger than that of heterobilayer.IV. Conclusions
In summary, we have calculated four prototype TDMC heterostructures (bilayer MoS2 and WS2, heterobilayer MoS2/WS2 and superlattice MoS2/WS2) and investigated their lateral and out-of-the-plane κ from first-principles. By analyzing the anharmonic lattice dynamics coupled with solving the phonon Boltzmann transport equation, the calculated lateral κ of bilayer MoS2 and WS2 at 300 K is 61.13 W m−1 K−1 and 87.52 W m−1 K−1, respectively, in reasonable agreement with experimental data of 77 ± 25 W m−1 K−1 and 53W m−1 K−1. By vertically stacking the MoS2 and WS2 monolayer together and applying a nanometer-sized vacuum layer on its top, the heterobilayer MoS2/WS2 forms and it preserves the high lateral κ of 70.01 W m−1 K−1 at 300 K, which indicates that the weak interlayer interactions do not affect the lateral thermal transport. Moreover, the coupled quantum states of vertically stacking MoS2 and WS2 monolayer do not influence the out-of-the-plane κ. For the superlattice composed of periodically alternating MoS2 and WS2 monolayer, the charge density distribution analysis shows that there exist strong interlayer and interfacial interactions. Consequently, the interfacial anharmonic phonon scattering is enhanced and phonon relaxation time is greatly decreased for the propagating phonons, leading to a significant reduction of lateral κ from 70.01 W m−1 K−1 to 7.22 W m−1 K−1 almost by a factor of 10. This work shows that the strong interfacial interactions indeed influence the lateral thermal transport in the superlattice MoS2/WS2. The physical insights obtained from this work can help predict the thermal transport in other TDMC heterostructures and advance the thermal management in their applications in nanoelectronics and optoelectronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J.-Y. Y. is grateful for the financial support by the Excellence Initiative of the German Federal and State Governments (Project No. StUpPD_268-17) and W. Zhang thanks the support by the Shandong Provincial Natural Science Foundation, China (No. ZR2017BEE051). We gratefully acknowledge the computing time granted by the John von Neumann Institute for Computing (NIC) and provided on the supercomputer JURECA at Forschungszentrum Jülich, Germany (Project ID: JHPC51).References
- P. Rivera, H. Yu, K. L. Seyler, N. P. Wilson, W. Yao and X. Xu, Nat. Nanotechnol., 2018, 13, 1004–1015 CrossRef CAS PubMed.
- C. Jin, E. Y. Ma, O. Karni, E. C. Regan, F. Wang and T. F. Heinz, Nat. Nanotechnol., 2018, 13, 994–1003 CrossRef CAS PubMed.
- H. Yu, X. Cui, X. Xu and W. Yao, Natl. Sci. Rev., 2015, 2, 57–70 CrossRef CAS.
- A. M. Jones, H. Yu, N. J. Ghimire, S. Wu, G. Aivazian, J. S. Ross, B. Zhao, J. Yan, D. G. Mandrus, D. Xiao, W. Yao and X. Xu, Nat. Nanotechnol., 2013, 8, 634 CrossRef CAS PubMed.
- D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed.
- W. Zhao, Z. Ghorannevis, K. K. Amara, J. R. Pang, M. Toh, X. Zhang, C. Kloc, P. H. Tan and G. Eda, Nanoscale, 2013, 5, 9677–9683 RSC.
- L. Yuan and L. Huang, Nanoscale, 2015, 7, 7402–7408 RSC.
- B. Hunt, J. D. Sanchez-Yamagishi, A. F. Young, M. Yankowitz, B. J. LeRoy, K. Watanabe, T. Taniguchi, P. Moon, M. Koshino, P. Jarillo-Herrero and R. C. Ashoori, Science, 2013, 340, 1427–1430 CrossRef CAS PubMed.
- C. R. Dean, L. Wang, P. Maher, C. Forsythe, F. Ghahari, Y. Gao, J. Katoch, M. Ishigami, P. Moon, M. Koshino, T. Taniguchi, K. Watanabe, K. L. Shepard, J. Hone and P. Kim, Nature, 2013, 497, 598 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed.
- Z. Zhang, P. Chen, X. Duan, K. Zang, J. Luo and X. Duan, Science, 2017, 357, 788–792 CrossRef CAS PubMed.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033 CrossRef CAS.
- K. Chen, X. Wan, J. Wen, W. Xie, Z. Kang, X. Zeng, H. Chen and J.-B. Xu, ACS Nano, 2015, 9, 9868–9876 CrossRef CAS PubMed.
- W. Aggoune, C. Cocchi, D. Nabok, K. Rezouali, M. Akli Belkhir and C. Draxl, J. Phys. Chem. Lett., 2017, 8, 1464–1471 CrossRef CAS PubMed.
- C. Chen, J. Avila, S. Wang, Y. Wang, M. Mucha-Kruczyński, C. Shen, R. Yang, B. Nosarzewski, T. P. Devereaux, G. Zhang and M. C. Asensio, Nano Lett., 2018, 18, 1082–1087 CrossRef CAS PubMed.
- X. Zhang, D. Sun, Y. Li, G.-H. Lee, X. Cui, D. Chenet, Y. You, T. F. Heinz and J. C. Hone, ACS Appl. Mater. Interfaces, 2015, 7, 25923–25929 CrossRef CAS PubMed.
- N. Peimyoo, J. Shang, W. Yang, Y. Wang, C. Cong and T. Yu, Nano Res., 2015, 8, 1210–1221 CrossRef CAS.
- J. Zhang, Y. Hong, X. Wang, Y. Yue, D. Xie, J. Jiang, Y. Xiong and P. Li, J. Phys. Chem. C, 2017, 121, 10336–10344 CrossRef CAS.
- J.-Y. Yang, L. Cheng and M. Hu, Appl. Phys. Lett., 2017, 111, 242101 CrossRef.
- J.-Y. Yang, S.-Y. Yue and M. Hu, Phys. Rev. B, 2016, 94, 235153 CrossRef.
- J. M. Ziman, Electrons and phonons: the theory of transport phenomena in solids, Oxford University Press, 1960 Search PubMed.
- D. A. Broido, A. Ward and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014308 CrossRef.
- K. Esfarjani, G. Chen and H. T. Stokes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085204 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- L. Lindsay, D. A. Broido and T. L. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165201 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- N. F. Hinsche, A. S. Ngankeu, K. Guilloy, S. K. Mahatha, A. Grubišić Čabo, M. Bianchi, M. Dendzik, C. E. Sanders, J. A. Miwa, H. Bana, E. Travaglia, P. Lacovig, L. Bignardi, R. Larciprete, A. Baraldi, S. Lizzit, K. S. Thygesen and P. Hofmann, Phys. Rev. B, 2017, 96, 121402 CrossRef.
- A. P. S. Gaur, S. Sahoo, J. F. Scott and R. S. Katiyar, J. Phys. Chem. C, 2015, 119, 5146–5151 CrossRef CAS.
- I. Niehues, R. Schmidt, M. Drüppel, P. Marauhn, D. Christiansen, M. Selig, G. Berghäuser, D. Wigger, R. Schneider, L. Braasch, R. Koch, A. Castellanos-Gomez, T. Kuhn, A. Knorr, E. Malic, M. Rohlfing, S. Michaelis de Vasconcellos and R. Bratschitsch, Nano Lett., 2018, 18, 1751–1757 CrossRef CAS PubMed.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Appl. Phys. Lett., 2002, 80, 2484–2486 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |