Intermediate crystalline structures of colloids in shape space
Abstract
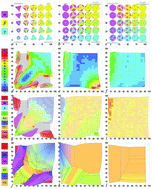
We computationally study the thermodynamic assembly of more than 40 000 hard, convex polyhedra belonging to three families of shapes associated with the triangle groups 323, 423, and 523. Each family is defined by vertex and/or edge truncation of symmetric polyhedra with equal edge length, producing shapes for which the majority are intermediates of more symmetric polyhedra found among the Platonic, Archimedean, and Catalan solids. In addition to the complex crystals cI16 lithium, BC8 silicon, γ-brass, β-manganese, and a dodecagonal quasicrystal, we find that most intermediate shapes assemble distorted variants of four basic cubic crystals: face-centered cubic, body-centered cubic, simple cubic, and diamond. To quantify the degree of distortion, we developed an algorithm that extracts lattice vectors from particle positions and then evaluates closeness to the four reference cubic crystals. This analysis allows us to group together in shape space related intermediate structures that would otherwise be placed in different lattice systems had we followed the lattice systems' strict definitions for angles and lengths of lattice vectors. The resulting landscapes show, as a function of shape, regions where ordered structures assemble, what is assembled and at what density, locations of transitions between regions of ordered structures, and regions of disorder. Our results provide a guide to self-assembling a host of related colloidal crystals through systematic design, by careful tweaking of the particle shape.


 Please wait while we load your content...
Please wait while we load your content...