Continuum percolation-based tortuosity and thermal conductivity of soft superball systems: shape dependence from octahedra via spheres to cubes

Abstract

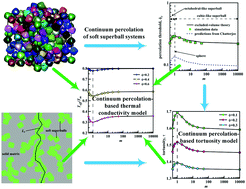
Understanding the effect of particle shape on the percolation threshold, tortuosity and thermal conductivity of soft (geometrical overlapping) particle systems is very crucial for the design and optimization of such materials, including colloids, polymers, and porous and fracture media. In this work, we first combine the excluded-volume theory with the Monte Carlo simulations to determine the percolation threshold for a family of soft superballs, the shape of which interpolates between octahedra and cubes via spheres. Then, we propose two continuum percolation-based models to respectively obtain the tortuosity and effective thermal conductivity of soft superball systems considering their percolation behavior, where monodisperse overlapping superballs are uniformly distributed in a homogeneous solid matrix. Specifically, both models cover the whole feasible range of superball volume fractions, including near the percolation threshold. Comparison with extensive experimental, numerical and theoretical results confirms that the present models are capable of precisely predicting the percolation threshold, tortuosity and thermal conductivity of such systems. Furthermore, we apply the proposed models to probe the influence of particle shape on these important parameters. Our results show that the decreasing percolation threshold and tortuosity as soft particles become more anisotropic is consistent with increasing conductivity. It suggests that the anisotropic-shaped inclusion phase is more conducting than the spherical inclusion phase. The present theoretical strategies and conclusions may provide sound guidance for the synthesis of colloidal and polymer superballs.