Open Access Article
Open Access ArticleFirst-principles investigations of manganese oxide (MnOx) complex-sandwiched bilayer graphene systems
Rafique Muhammad ab,
Yong Shuai*a,
Ahmed Irfanb and
Tan He-Pinga
ab,
Yong Shuai*a,
Ahmed Irfanb and
Tan He-Pinga
aSchool of Energy Science and Engineering, Harbin Institute of Technology, 92 West Dazhi Street, Harbin 150001, PR China. E-mail: shuaiyong@hit.edu.cn
bMehran University of Engineering and Technology, SZAB Campus, Khairpur Mirs’, Pakistan
First published on 28th June 2018
Abstract
In this paper, we calculate the structural, electronic, magnetic and optical parameters of MnOx (x = 0–4), cluster-sandwiched bilayer graphene (Gr) systems, utilizing first-principles calculations with van der Waals corrections implemented with density functional theory (DFT). Charge transfer is observed from the graphene layers to the MnOx clusters, thus producing a hole doping phenomenon in the graphene layers. The MnOx clusters’ electronegative nature greatly modifies the electronic structure of bilayer graphene. It is observed that the MnOx clusters’ incorporation in bilayer graphene converts zero band gap semimetal bilayer graphene to a half metallic or dilute magnetic semiconducting material. Interestingly, the Gr/MnO3/Gr complex structure displays indirect band gap semiconductor behavior for both spin channels, and has a ∼20 meV band gap value. The band gap during spin up and spin down band channels increases as the size of MnOx is increased in between the graphene layers. Through spin density diagrams, it is revealed that the MnOx clusters’ incorporation in the graphene layers converts nonmagnetic bilayer graphene to a magnetic substrate. The obtained magnetic moments for Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr, sandwiched bilayer graphene systems were found to be 3.53 μB, 3.03 μB, 2.46 μB, 1.03 μB and 0.00 μB, respectively. Through density of states (DOS) plots, it is inferred that the d orbitals of the Mn atoms are mainly responsible for the generation of magnetic moments in the given bilayer graphene systems. The optical parameters, specifically absorption, reflectivity and refractive coefficients, were obtained for all given systems. The absorption spectrum of bilayer graphene is improved in the visible range when MnOx clusters are sandwiched between the graphene layers. It is revealed that MnOx clusters’ incorporation in bilayer graphene improves these optical parameters in the low lying energy region. The results obtained during this study provide the basis for future experimental extrapolations to make multilayer graphene systems functional for optoelectronic and spintronic applications.
1. Introduction
Two dimensional (2D) monatomic graphene synthesized in 2004![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with impressive electrical, electronic and thermal properties,2–5 has acquired lots of attention from the research community throughout the last decade. The linear dispersion relation near the Fermi energy (EF) level makes graphene charge carriers act like massless Dirac fermions.6 It has been widely established that graphene-based magnetic substrates are more stable and efficient than traditional transition metal based magnets.7 Hence, 2D graphene materials have prospective applications for spintronic devices. Magnetism in graphene can be induced through intrinsic defects,8 doping nonmetal9,10 as well as transition metal impurities.11–14 However, the graphene charge carriers’ mobility is reduced when individual impurities are added in its lattice, subjecting it to stronger interactions between the doped impurities and constituent carbon (C) atoms of graphene.15 Ideal doping impurities can be those which not only produce stable structures but also maintain the intrinsic behavior of graphene. Superhalogens can be regarded as ideal dopants, since these clusters possess higher electronegativity, with electron affinity values exceeding those of the halogen atoms.16,17 Attributed to their strong oxidation nature and high electronegativity,18 3d metal tri and tetraoxide superhalogen complex-based doped graphene,19,20 h-BN layer21 and MoS2 layer22 structures present higher stability compared to that of individual TM atom doped graphene, h-BN and MoS2 monolayer structures. Recently, multilayered graphene structures have also attracted lots of interest, due to the possibility of producing a well-defined band gap by breaking the symmetry between constituent graphene layers.23,24 Different techniques such as external electrical field applications,25,26 and molecular doping in bilayer graphene,27,28 have been adopted to produce a well-defined band gap in the bilayer graphene structures. In addition, some experimental studies have also been carried out on the intercalation of FeCl3 clusters in graphite and few layer graphene (FLG) systems.29–31
1 with impressive electrical, electronic and thermal properties,2–5 has acquired lots of attention from the research community throughout the last decade. The linear dispersion relation near the Fermi energy (EF) level makes graphene charge carriers act like massless Dirac fermions.6 It has been widely established that graphene-based magnetic substrates are more stable and efficient than traditional transition metal based magnets.7 Hence, 2D graphene materials have prospective applications for spintronic devices. Magnetism in graphene can be induced through intrinsic defects,8 doping nonmetal9,10 as well as transition metal impurities.11–14 However, the graphene charge carriers’ mobility is reduced when individual impurities are added in its lattice, subjecting it to stronger interactions between the doped impurities and constituent carbon (C) atoms of graphene.15 Ideal doping impurities can be those which not only produce stable structures but also maintain the intrinsic behavior of graphene. Superhalogens can be regarded as ideal dopants, since these clusters possess higher electronegativity, with electron affinity values exceeding those of the halogen atoms.16,17 Attributed to their strong oxidation nature and high electronegativity,18 3d metal tri and tetraoxide superhalogen complex-based doped graphene,19,20 h-BN layer21 and MoS2 layer22 structures present higher stability compared to that of individual TM atom doped graphene, h-BN and MoS2 monolayer structures. Recently, multilayered graphene structures have also attracted lots of interest, due to the possibility of producing a well-defined band gap by breaking the symmetry between constituent graphene layers.23,24 Different techniques such as external electrical field applications,25,26 and molecular doping in bilayer graphene,27,28 have been adopted to produce a well-defined band gap in the bilayer graphene structures. In addition, some experimental studies have also been carried out on the intercalation of FeCl3 clusters in graphite and few layer graphene (FLG) systems.29–31
As mentioned earlier, substituting tri and tetraoxide superhalogen clusters in monolayer graphene produces stable structures. Keeping this in mind we extend this concept by incorporating MnOx clusters in a bilayer graphene system. These MnOx clusters were sandwiched in between two graphene layers. Recently, X. Zhang et al.32 performed first-principles calculations on MnF3(4) cluster-sandwiched bilayer graphene systems. The authors reported that these structures display ferromagnetic behavior and that the MnF3(4) clusters greatly improve the electronic properties of the bilayer graphene systems without affecting the intrinsic nature of graphene. Since these systems are based on only magnetic superhalogen clusters, in this work we provide a detailed study on individual the Mn atom and different MnOx cluster (i.e. MnO, MnO2, MnO3, MnO4) sandwiched bilayer graphene systems. The MnOx clusters’ substitution in bilayer graphene serves two purposes, (i) these clusters significantly modify the electronic and magnetic parameters, attributed to the hole doping phenomenon induced in both graphene layers by the MnOx clusters, (ii) weaker interaction between the MnOx clusters and graphene layers maintain the intrinsic behavior of graphene. These Gr/MnOx/Gr structures can be regarded as being suitable for spintronic devices such as spin field-effect transistors (FET) or vertical (FET) devices.
Since, MnOx cluster substitution in bilayer graphene modifies its electronic structure, it also modifies the interband and intraband transitions, which in turn can alter the optical parameters. Hence, in addition to the electronic and magnetic parameters, we also investigated the optical properties – specifically the absorption coefficient, reflectivity and refractive coefficient of MnOx cluster-incorporated bilayer graphene systems. The optical parameters of monolayer graphene and h-BN systems have been widely investigated.33–35 However, no complete account for the optical parameters of bilayer graphene systems is available. Hence, this study provides a substantial contribution towards tuning the optical parameters of bilayer graphene systems through incorporation of foreign clusters.
This work presents the structural, electronic, magnetic and optical parameters of MnOx cluster-sandwiched bilayer graphene systems through first-principles DFT calculations. This paper is arranged as follows; computational details are produced in Section 2, the obtained results and their general discussion are elaborated in Section 3 and this work is finally concluded in Section 4. It can be presumed that the structural, electronic, magnetic and optical characteristics of such a system has not been defined comprehensively. The results provided in this paper can provide a new approach for tuning the above-mentioned properties, in order to make multilayered graphene systems which are applicable for nanoelectronic and spintronic devices, distinctive to single layered graphene systems.
2. Computational details
First-principles calculations based on DFT were utilized to investigate the structural, electronic, magnetic and optical parameters of MnOx cluster-sandwiched bilayer graphene systems using the generalized-gradient approximation (GGA) implemented in the Vienna Ab-initio simulation package (VASP).36,37 VASP adopts projector augmented wave (PAW) potentials38 with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional39. All the calculations were performed in spin-polarized mode. The Grimme (DFT-D2)40 method was employed for van der Waals (vdW) corrections due to its appropriate account of long-range vdW interactions.41–43 A 500 eV cutoff energy was applied for the wave function to be expanded in plane waves. A 4 × 4 bilayer graphene supercell was adopted in which a vacuum layer thickness of 20 Å in the Z-direction was added to remove the interference between neighboring layers. A 9 × 9 × 1 Γ-centered k-point mesh for Brillouin zone (BZ) sampling was employed to achieve good convergence parameters. Hellmann–Feynman forces of less than 0.01 eV Å−1 and a total change in energy of less than 10−6 eV were selected for the geometry optimization process. The Gaussian smearing method was utilized to avoid the problems related to partial occupancies. To remove the inaccuracies generated from electrostatic potential, atomic forces and the total energy caused by periodic boundary conditions, the dipole correction technique was also adopted.443. Results and discussion
3.1 Structural and magnetic properties of MnOx cluster-sandwiched bilayer graphene
Bilayer graphene structures were incorporated with an individual Mn atom and different MnOx (i.e. MnO, MnO2, MnO3 and MnO4) clusters, as described in Fig. 1(a)–(e), respectively. In this section, the structural and magnetic parameters of these systems were investigated using the first-principles method.The bond distances of the C–C atoms, Mn–O atoms and the distance of the MnOx clusters from both graphene layers is also shown in Fig. 1(a)–(e), respectively. After performing the geometry relaxation process on these systems, it is established that the C atoms lying above and below the MnOx clusters drift away from the graphene 2D plane, and thus a change in the C–C atoms’ bond lengths occurs. After incorporation of the MnOx clusters in bilayer graphene, the distance between the graphene layers also increases. It is interesting to observe that the 2D planar structure of both graphene layers is maintained, which suggests that the intrinsic behavior of the graphene layer will remain unaltered. From the structures given in Fig. 1(a)–(e), it is observed that the sandwiched Mn atom of the MnOx cluster tries to maintain its position just below the C atoms of the graphene layer. Moreover, these MnOx clusters try to reduce their distance from a single graphene layer (either the upper or lower layer) as evident by the bond lengths of Mn–C atoms described in Fig. 1(a)–(e), respectively.32,45
The total magnetization of MnOx cluster-sandwiched bilayer graphene supercells, magnetic moments of individual the Mn atom and the average equatorial bond lengths of the Mn–C, Mn–O and C–C atoms for all the MnOx cluster-sandwiched bilayer graphene systems are presented in Table 1. After MnOx cluster incorporation in bilayer graphene, the Mn–C bond lengths were in between 1.93 and 2.1 Å, the C–C bond lengths were in the range of 1.44–1.47 Å and the obtained variation for the C–C bond lengths was in between 0.2 and 0.5 Å. The obtained total magnetic moments of different Gr/MnOx/Gr systems listed in Table 1, clearly indicate that MnOx cluster incorporation into bilayer graphene significantly improves its ferromagnetic behavior as demonstrated by the larger magnetic moment values for each given system. Only the MnO4 cluster-sandwiched bilayer graphene carries a 0.00 μB magnetic moment. This non-magnetic behavior of the Gr/MnO4/Gr system, can be attributed to quenching of the magnetic moment of the Mn atom by the four O atoms present around the Mn atom. The negative magnetic moment of the O atoms nullifies the magnetic moments of the Mn atoms thus producing a 0.00 μB net magnetic moment for Gr/MnO4/Gr system.20,46
| Impurity | μtot, in μB | μMN, in μB | dMn–C (Å) | dC–C (Å) | dMn–O (Å) | Eb (eV) |
|---|---|---|---|---|---|---|
| Mn | 3.53 | 3.054 | 1.94 | 1.44 | — | 2.52 |
| MnO | 3.03 | 3.026 | 1.96 | 1.46 | 2.01 | 2.91 |
| MnO2 | 2.46 | 2.5 | 2.1 | 1.45 | 1.98 | 3.08 |
| MnO3 | 1.03 | 1.5 | 2.01 | 1.45 | 1.89 | 3.85 |
| MnO4 | 0.00 | 0.00 | 1.96 | 1.47 | 1.88 | 4.31 |
In order to determine whether the given Gr/MnOx/Gr systems are thermodynamically stable enough or not, we calculated the binding energy for each system using the following expression32 and the obtained binding energies are presented in Table 1,
| Eb = E(gp+MnOx) − (2E(gp) + EMnOx) | (1) |
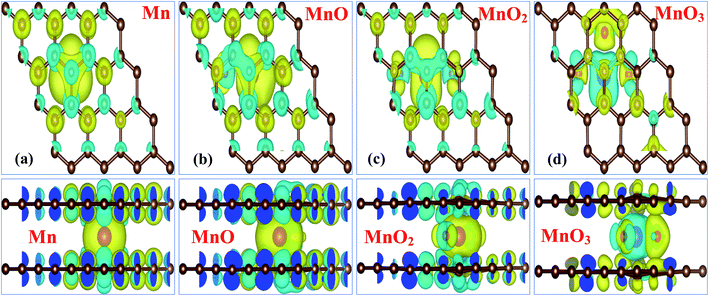
The obtained total magnetic moments μtot and individual Mn atom magnetic moments μMn provided in Table 1, clearly demonstrate that incorporation of the MnOx cluster in bilayer graphene is a suitable way to make it a magnetic material. Only the MnO4 cluster-sandwiched graphene system displays non-magnetic behavior. To further support our predictions of the magnetic properties of MnOx cluster-sandwiched bilayer graphene systems, we elaborated on the magnetic coupling nature of the Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr and Gr/MnO3/Gr bilayer graphene systems and the resulting diagrams are presented in Fig. 2(a)–(d), respectively. The Gr/MnO4/Gr system was omitted due to its 0.00 μB magnetic moment. Fig. 2(a)–(d) describes the top and side views of the spin densities (ρ↑ − ρ↓) of the different MnOx cluster-sandwiched bilayer graphene systems.
The spin density diagrams provided in Fig. 2(a)–(d) suggest that, the sandwiched MnOx clusters induce magnetic moments on the C atoms of the graphene layer lying above or below the impurity clusters. A parallel spin polarization direction is achieved between the MnOx clusters and C atoms of bilayer graphene. Moreover, the unfilled d-orbitals of Mn atoms carry clockwise spin direction as shown by the yellow isosurface (0.002 e Å−3), for all the given MnOx clusters except for the MnO3 cluster. The direction of spin polarization between Mn and O atoms was antiparallel for the MnO and MnO2 clusters, while it was parallel for the MnO3 cluster as shown in Fig. 2(b)–(d). From the spin density diagrams it can be further presumed that despite having weaker interactions between the MnOx clusters and graphene layers, the distortion in the spin density observed in both graphene layers was not localized at the periphery of the MnOx clusters. Rather, the spin density was distributed on both the graphene layers.32,48,50
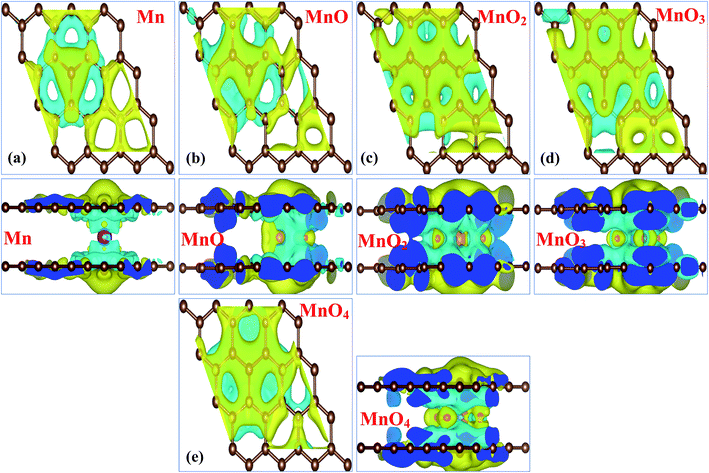
The charge density differences and charge transfer phenomena for all MnOx cluster-sandwiched bilayer graphene systems were investigated through Bader analysis,51,52 in order to further understand the behaviors of MnOx clusters incorporated in bilayer graphene systems. The charge density difference can be described by Δρ = ρMnOx-BL/graphene − ρBL/graphene − ρMnOx. Where ρMnOx-BL/graphene, ρBL/graphene and ρMnOx represent the charge density of the MnOx cluster-sandwiched bilayer graphene systems, the charge density of the graphene layers and the charge density of the MnOx clusters respectively. The resulting charge density difference diagrams for all MnOx cluster-sandwiched bilayer graphene systems are shown in Fig. 3(a)–(e). Electron gain and loss configurations are presented by the yellow (0.0003 e Å−3) and cyan (0.0003 e Å−3) isosurfaces, respectively. The charge density difference diagrams of Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr cluster-sandwiched bilayer graphene systems presented in Fig. 3(a)–(e) describe a similar nature of charge difference between the graphene layers and MnOx clusters. A charge depletion pattern (i.e. the cyan isosurface 0.0003 e Å−3) is observed around the MnOx clusters, while individual the Mn and O atoms are filled with yellow isosurface (0.0003 e Å−3), suggesting electron gain behavior of the impurity clusters. This partial distribution of the cyan and yellow isosurfaces in between bilayer graphene, as visible in Fig. 3(a)–(e), suggests that the interaction between graphene layers and the MnOx clusters is covalent in nature. Moreover, it can be suggested that the direction of charge transfer is from the graphene layers to the MnOx clusters. As the bilayer graphene transfers its charge carriers to the impurity clusters, it can also be presumed that the hole doping process is initiated in both the graphene layers. These results are consistent with previously reported results.21,53–55
3.2 Electronic structures of MnOx cluster-sandwiched bilayer graphene systems
Here, we investigate the electronic structures of MnOx cluster-sandwiched bilayer graphene systems through first-principles calculations. Spin polarized band structures and projected DOS plots are determined for all MnOx cluster-sandwiched bilayer graphene systems. A thirty K-points grid is adopted along the path Γ–M–K–Γ in the IBZ in order to obtain the band structure diagrams with fine quality. 9 × 9 × 1 Γ-centered BZ sampling is applied for calculating the spin polarized projected (PDOS) plots for all the Gr/MnOx/Gr sandwiched bilayer graphene systems. A Gaussian width of 0.02 eV was utilized for smearing the energy eigenvalues.Spin polarized electronic structures of MnOx cluster-sandwiched bilayer graphene systems are provided in Fig. 4(a)–(e). For comparison, the electronic structure of pure bilayer graphene is also shown in Fig. 4, named ‘pure bilayer (BL) graphene’. The well recognized quadratic dispersion of energy near the high symmetric K-points and the straddling of valence and conduction bands at the Fermi energy level (EF) is visible in the electronic structure of bilayer graphene shown in Fig. 4. The electronic structure of pure bilayer graphene calculated during this work is in consensus with previous studies.56–58 Significant change in the electronic structure of bilayer graphene is predicted after MnOx cluster incorporation. The Dirac cone appearing at the high symmetric K-point shifts down to the valence band by ∼0.9 eV and ∼1 eV during spin up and spin down channels, respectively for the Gr/Mn/Gr sandwiched bilayer graphene systems as shown in Fig. 4(a). For the Gr/MnO/Gr system, the Dirac cone also creeps down to the valence band by ∼0.5 eV and ∼0.8 eV during spin up and spin down channels, respectively. During this, a band gap of ∼0.02 eV and ∼0.04 eV appears at the high symmetric K-point during spin up and spin down channels, respectively as is evident in Fig. 4(b). For the Gr/MnO2/Gr system, the Dirac cone shifts into the valence band by ∼0.2 eV for both spin up and spin down channels and a band gap of ∼0.03 eV is produced at the high symmetric K-point for both channels as shown in Fig. 4(c). Interestingly, the Gr/MnO3/Gr bilayer graphene system displays indirect band gap semiconductor behavior for both spin up and spin down band channels. The band gap achieved during spin up and spin down band channels for this system was found to be ∼1.1 eV and ∼0.6 eV as shown in Fig. 4(d). As listed in Table 1, the Gr/MnO4/Gr bilayer system possesses a 0.00 μB magnetic moment; hence its bands appear at the same energy level without having any polarization. From Fig. 4(e), it can be maintained that Gr/MnO4/Gr exhibits half metallic properties as some impurity states are observed at the (EF) level. The obtained band gap values for different Gr/MnOx/Gr bilayer graphene systems have to be considered carefully, since the DFT method slightly underestimates the electronic band gap. Results provided in Fig. 4 are consistent with previous reports.32,57,58
 | ||
| Fig. 4 Spin polarized band structures for MnOx cluster-sandwiched bilayer graphene (4 × 4) supercell structures. | ||
We also investigated the spin polarized total and projected PDOS plots for all the Gr/MnOx/Gr cluster-sandwiched bilayer graphene systems, in order to determine the origins of the magnetic moments and the electronic hybridization between the MnOx clusters and graphene layers. The TDOS and PDOS on the d orbitals of the Mn atom, the p orbitals of the O atoms and the orbitals of the C atoms of the graphene layers were calculated and are presented in Fig. 5(a)–(e), respectively. In these plots, the EF level is described by a solid grey line drawn at 0 eV energy in the respective PDOS plots. It is assumed that some surface states will be induced by the MnOx clusters in between the valence and conduction bands, as can be observed in Fig. 5(a)–(e). When covalent bonding occurs between the graphene layers and MnOx clusters, it produces a robust hybridization which, in turn, induces some surface states at the EF level. As the Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr cluster-sandwiched bilayer graphene systems carried 3.53 μB, 3.03 μB, 2.46 μB, 1.03 μB and 0.00 μB magnetic moments, respectively, the C and O atom p orbitals and Mn atom d orbitals of the Gr/MnOx/Gr structures which contain finite magnetic moments, displayed spin polarization. Only the Gr/MnO4/Gr cluster-sandwiched bilayer graphene system does not contain any spin polarization in its orbitals since it possesses a 0.00 magnetic moment. The above statements can be verified through the PDOS plots presented in Fig. 5(a)–(e). The PDOS plots of Fig. 5(a)–(e) support the prediction that the magnetic moments of the MnOx cluster-sandwiched bilayer graphene systems are induced by five different orbitals (dxy, dyz, dz2, dxz and dx2−y2) of the Mn atom. For all the MnOx cluster-sandwiched bilayer graphene systems, the dz2, dxy and dx2−y2 orbitals of the Mn atoms do not hybridize with the O atom p orbitals, while the dxy and dyz orbitals of the Mn atom produce soft hybridization with the O atom p orbitals as described in Fig. 5(a)–(e). These plots further support the predictions that the opening of the band gap at a high symmetric K-point occurs at different energy levels during both the spin up and spin down band channels as is evident in Fig. 4(a)–(e) as well. From the electronic structure and PDOS plots it can be concluded that 2D magnetic substrates can be synthesized by incorporating superhalogen MnOx clusters in bilayer graphene systems.
 | ||
| Fig. 5 Total and projected DOS plots for Gr/MnOx/Gr cluster-sandwiched bilayer graphene systems. The solid grey line appearing at 0 eV energy level depicts the Fermi energy level. | ||
3.3 Optical properties of MnOx cluster-sandwiched bilayer graphene
Finally, we determine the effects of MnOx cluster incorporation on the optical characteristics of bilayer graphene through the Random Phase Approximation (RPA)59 approach implemented in DFT. Local field effects are not included, while interband transitions are considered in this technique, hence some inaccuracies can be observed in the dielectric constant parameter in the lower energy range. For the optical parameters calculations, we adopted 11 × 11 × 1 Γ-centered BZ sampling, thus our obtained optical parameters contain some distortions in their profiles. If the number of K-points is increased, the profile can easily be smoothed, but a lack of available computational power limited our K-point mesh to smaller values.Optical parameters, specifically absorption coefficient ‘α’, reflectivity ‘R’, refraction index ‘n’ and extinction coefficient ‘k’ were calculated during this study. These parameters can easily be extracted from the dielectric constant values. The summation of real and imaginary parts i.e. ε = ε′ + iε′′ together provides the dielectric constant parameter. The imaginary dielectric tensor can be determined through the summation of empty states as provided in the following expression,
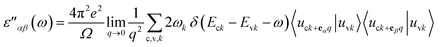 | (2) |
Using the Kramers–Kronig transformation, the real dielectric tensor can be obtained as
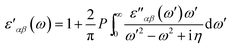 | (3) |
Through these dielectric tensor values, the absorption coefficient ‘α’, reflectivity ‘R’, refraction index ‘n’ and extinction coefficient ‘k’ can easily be determined. This is explained in detail in ref. 33.
The refractive index ‘n’ and extinction coefficient ‘k’ plots for the pure and MnOx cluster-sandwiched bilayer graphene systems are presented in Fig. 6(a) and (b). These plots are generated in a single plot to demonstrate the comparison between the pure and MnOx cluster-sandwiched bilayer graphene systems. The static refraction ‘n’ and extinction ‘k’ (i.e. the ‘n’ and ‘k’ values observed at 0 eV energy) values were found to be 2.7 and 0 for pure bilayer graphene. When MnOx clusters were sandwiched in bilayer graphene, the static refraction values were increased but the static extinction coefficient value remained same, as shown in Fig. 6(a) and (b). The static refractive index values for Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr cluster-sandwiched bilayer graphene systems were found to be 4.8, 4.75, 5.01, 6.5 and 3.6 respectively, as shown in Fig. 6(a).
 | ||
| Fig. 6 (a) Refractive index ‘n’ and (b) extinction coefficient ‘k’ values of pure and different Gr/MnOx/Gr cluster-sandwiched bilayer graphene systems. | ||
Furthermore, the first extinction peak intensity for pure bilayer graphene is observed at 2 eV with a peak intensity of 2.4 as shown in Fig. 6(b), but this peak is shifted to lower energy values after MnOx cluster incorporation in bilayer graphene. This indicates a red shift in the extinction coefficient of bilayer graphene. The value of first extinction peak maintains its intensity in the range of 1.8–2.8 and in energy interval of 0–1.7 eV, depending upon the type of MnOx cluster-sandwiched in between bilayer graphene as evident in Fig. 6(b).60,61 Since the extinction coefficient is also linked to the absorption coefficient parameter, the red shift produced in the extinction coefficient will reflect a red shift in the absorption coefficient as well, and this is also demonstrated in the upcoming section.
Fig. 7(a) demonstrates the absorption coefficient ‘α’ parameter of pure and different MnOx cluster-sandwiched bilayer graphene systems. The pure bilayer graphene absorption coefficient, shown in navy, depicts a value of zero in between the 0 and 1 eV energy interval as shown in Fig. 7(a). The absorption coefficient was described in the energy range of a 0–12 eV energy interval, in order to determine the modification in the absorption spectrum in the visible range. The first main absorption peak induced by low energy π → π* transitions is observed at ∼4 eV energy with ∼5000 peak intensity. After MnOx cluster incorporation, the absorption spectrum of bilayer graphene starts to increase in value from 0 eV energy, indicating a rise in the absorption coefficient in the lower energy range. As observed with the extinction coefficient, a red shift in the absorption coefficient quantity is also observed, as shown in Fig. 7(a). Moreover, the first minimum peak observed at ∼4 eV energy reduces in intensity when MnOx clusters are sandwiched in bilayer graphene. It is worth noting that the absorption coefficient quantity also increases in value in the 6–11 eV energy range after the incorporation of MnOx clusters in bilayer graphene as shown in Fig. 7(a). It can be concluded that the incorporation of MnOx clusters significantly improves the absorption coefficient of bilayer graphene in the visible range of the spectrum.62,63
 | ||
| Fig. 7 (a) Absorption coefficient ‘α’ and (b) reflectivity ‘R’ parameters of pure and different Gr/MnOx/Gr cluster-sandwiched bilayer graphene systems. | ||
Similarly, the reflectivity parameters of pure and different MnOx cluster-sandwiched bilayer graphene systems are presented in Fig. 7(b). The static reflectivity of pure bilayer graphene is found to be 0.2, while MnOx cluster incorporation increases this parameter to 0.41, 0.4, 0.44, 0.6 and 0.31 for Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr cluster-sandwiched bilayer graphene systems, respectively. Overall, it is observed that the static reflectivity is improved while the reflectivity parameter decreases in value over a higher energy range as demonstrated in Fig. 7(b).64,65
4. Conclusion
Different Gr/MnOx/Gr cluster-sandwiched bilayer graphene systems were examined by first-principles DFT calculations. The high electronegative nature of the MnOx clusters supports the stability of bilayer graphene as shown by the calculated binding energies. Spin densities of Gr/MnOx/Gr cluster-sandwiched systems suggest that the electron rich nature of MnOx clusters induces positive spin electrons into the graphene layers and significant magnetic behavior can be expected from these complex structures. Even with weaker electronic interactions between C and MnOx clusters, stronger magnetic coupling can be achieved for the MnOx sandwiched systems. The obtained magnetic moments for Gr/Mn/Gr, Gr/MnO/Gr, Gr/MnO2/Gr, Gr/MnO3/Gr and Gr/MnO4/Gr complexes were found to be 3.53 μB, 3.03 μB, 2.46 μB, 1.03 μB and 0.00 μB respectively. The direction of charge transfer is from bilayer graphene to the MnOx clusters, thus inducing a hole doping process in bilayer graphene.Through spin polarized electronic structures, it is revealed that the MnOx clusters’ incorporation greatly modifies the band structure of graphene; firstly by moving the Dirac cone up/down the EF level along with inducing a finite band gap at the high symmetric K-point. Interestingly, Gr/MnO3/Gr sandwiched bilayer graphene depicts an indirect band gap semiconducting property with a band gap of ∼1.1 eV and ∼0.6 eV during spin up and spin down band channels, respectively. The obtained PDOS plots further reveal that the sandwiched systems with finite magnetic moments display orbital polarization, along with a finite band gap at different energy levels during spin up and spin down bands for given systems. Moreover, it is predicted that five different orbitals (i.e. dxy, dyz, dz2, dxz and dx2−y2) of the Mn atom are mainly responsible for the induction of magnetic moments in bilayer graphene. This spin-polarized electronic behavior of the Gr/MnOx/Gr sandwiched systems suggests that the given systems can be utilized for spintronic device applications.
The optical parameters of MnOx cluster-sandwiched bilayer graphene systems reveal that, the static ‘n’ and ‘R’ parameters of MnOx sandwiched systems attain larger values in comparison to the static ‘n’ and ‘R’ parameters of pure bilayer graphene. Similarly, the ‘α’ and ‘k’ parameters of the MnOx sandwiched systems demonstrate a red shift and these two parameters are improved in the visible range. A combination of the electronic, magnetic and optical parameters of MnOx cluster-sandwiched bilayer graphene systems revealed that these Gr/MnOx/Gr cluster-sandwiched structures display significant potential for applications in novel spintronic and optoelectronic device applications, which are distinctive to pure bilayer graphene structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51522601, 51421063) and the Higher Education Commission, Pakistan under SRGP (No. 21-1778/SRGP/R&D/HEC/2017). In addition, we would like to acknowledge the support that NVIDIA provided us through the GPU Grant Program.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef PubMed
.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef PubMed
.
- F. Guinea, N. Peres, K. Novoselov, A. Geim and A. C. Neto, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef
.
- Z. Jiang, Y. Zhang, Y.-W. Tan, H. Stormer and P. Kim, Solid State Commun., 2007, 143, 14–19 CrossRef
.
- S. D. Sarma, S. Adam, E. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407 CrossRef
.
- K. Novoselov, A. K. Geim, S. Morozov, D. Jiang, M. Katsnelson, I. Grigorieva, S. Dubonos and A. Firsov, nature, 2005, 438, 197–200 CrossRef PubMed
.
- T. Alonso-Lanza, A. Ayuela and F. Aguilera-Granja, arXiv preprint arXiv:1606.00165, 2016.
- X. Cui, R. Zheng, Z. Liu, L. Li, B. Delley, C. Stampfl and S. P. Ringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125410 CrossRef
.
- D. Soriano, N. Leconte, P. Ordejón, J.-C. Charlier, J.-J. Palacios and S. Roche, Phys. Rev. Lett., 2011, 107, 016602 CrossRef PubMed
.
- K. M. McCreary, A. G. Swartz, W. Han, J. Fabian and R. K. Kawakami, Phys. Rev. Lett., 2012, 109, 186604 CrossRef PubMed
.
- K. T. Chan, J. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430 CrossRef
.
- Z. Qiao, S. A. Yang, W. Feng, W.-K. Tse, J. Ding, Y. Yao, J. Wang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161414 CrossRef
.
- J. Ding, Z. Qiao, W. Feng, Y. Yao and Q. Niu, arXiv preprint arXiv:1108.6235, 2011.
- H. Zhang, C. Lazo, S. Blügel, S. Heinze and Y. Mokrousov, Phys. Rev. Lett., 2012, 108, 056802 CrossRef PubMed
.
- A. Krasheninnikov, P. Lehtinen, A. S. Foster, P. Pyykkö and R. M. Nieminen, Phys. Rev. Lett., 2009, 102, 126807 CrossRef PubMed
.
- G. Gutsev and A. Boldyrev, Adv. Chem. Phys., 1985, 61, 169–221 Search PubMed
.
- G. Gutsev and A. Boldyrev, Chem. Phys., 1981, 56, 277–283 CrossRef
.
- K. Pradhan, G. L. Gutsev, C. A. Weatherford and P. Jena, J. Chem. Phys., 2011, 134, 144305 CrossRef PubMed
.
- M. Rafique, Y. Shuai, H.-P. Tan and H. Muhammad, Appl. Surf. Sci., 2017, 399, 20–31 CrossRef
.
- M. Rafique, Y. Shuai, H.-P. Tan and H. Muhammad, Appl. Surf. Sci., 2017, 408, 21–33 CrossRef
.
- J. Meng, D. Li, Y. Niu, H. Zhao, C. Liang and Z. He, Phys. Lett. A, 2016, 380, 2300–2306 CrossRef
.
- D. Li, Y. Niu, H. Zhao, C. Liang and Z. He, Phys. Lett. A, 2014, 378, 1651–1656 CrossRef
.
- E. V. Castro, K. Novoselov, S. Morozov, N. Peres, J. L. Dos Santos, J. Nilsson, F. Guinea, A. Geim and A. C. Neto, Phys. Rev. Lett., 2007, 99, 216802 CrossRef PubMed
.
- H. Min, B. Sahu, S. K. Banerjee and A. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155115 CrossRef
.
- Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2009, 459, 820–823 CrossRef PubMed
.
- H. Miyazaki, K. Tsukagoshi, A. Kanda, M. Otani and S. Okada, Nano Lett., 2010, 10, 3888–3892 CrossRef PubMed
.
- J. Park, S. B. Jo, Y. J. Yu, Y. Kim, J. W. Yang, W. H. Lee, H. H. Kim, B. H. Hong, P. Kim and K. Cho, Adv. Mater., 2012, 24, 407–411 CrossRef PubMed
.
- D. L. Duong, S. M. Lee, S. H. Chae, Q. H. Ta, S. Y. Lee, G. H. Han, J. J. Bae and Y. H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205413 CrossRef
.
- N. Kim, K. S. Kim, N. Jung, L. Brus and P. Kim, Nano Lett., 2011, 11, 860–865 CrossRef PubMed
.
- M. Dresselhaus and G. Dresselhaus, Adv. Phys., 1981, 30, 139–326 CrossRef
.
- K. Ohhashi and I. Tsujikawa, J. Phys. Soc. Jpn., 1974, 36, 422–430 CrossRef
.
- X. Zhang, D. Li, J. Meng, R. Yan, Y. Niu, H. Zhao, C. Liang and Z. He, Comput. Mater. Sci., 2016, 124, 316–322 CrossRef
.
- A. Marinopoulos, L. Reining, A. Rubio and V. Olevano, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 245419 CrossRef
.
- O. Sedelnikova, L. Bulusheva and A. Okotrub, J. Chem. Phys., 2011, 134, 244707 CrossRef PubMed
.
- T. Eberlein, U. Bangert, R. Nair, R. Jones, M. Gass, A. Bleloch, K. Novoselov, A. Geim and P. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 233406 CrossRef
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef PubMed
.
- S. Grimme, C. Mück-Lichtenfeld and J. Antony, J. Phys. Chem. C, 2007, 111, 11199–11207 CrossRef
.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2008, 10, 2722–2729 RSC
.
- N. Kharche and S. K. Nayak, Nano Lett., 2011, 11, 5274–5278 CrossRef PubMed
.
- G. Makov and M. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014 CrossRef
.
- T. Rasheed, S. A. Siddiqui and N. Bouarissa, J. Fluorine Chem., 2013, 146, 59–65 CrossRef
.
- M. Rafique, Y. Shuai, M. Xu, G. Zhang and Y. Guo, Phys. E, 2017, 93, 26–38 CrossRef
.
- K. S. Kim, A. L. Walter, L. Moreschini, T. Seyller, K. Horn, E. Rotenberg and A. Bostwick, Nat. Mater., 2013, 12, 887 CrossRef PubMed
.
- J. Lin, W. Fang, W. Zhou, A. R. Lupini, J. C. Idrobo, J. Kong, S. J. Pennycook and S. T. Pantelides, Nano Lett., 2013, 13, 3262–3268 CrossRef PubMed
.
- J. Han, D. Kang and J. Dai, RSC Adv., 2018, 8, 19732–19738 RSC
.
- S. D. Chakarova-Käck, E. Schröder, B. I. Lundqvist and D. C. Langreth, Phys. Rev. Lett., 2006, 96, 146107 CrossRef PubMed
.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef PubMed
.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
.
- M. Wu, C. Cao and J. Jiang, New J. Phys., 2010, 12, 063020 CrossRef
.
- D. Li, C. Wang, Y. Niu, H. Zhao and C. Liang, Chem. Phys. Lett., 2014, 601, 16–20 CrossRef
.
- Z. Chen, I. Santoso, R. Wang, L. F. Xie, H. Y. Mao, H. Huang, Y. Z. Wang, X. Y. Gao, Z. K. Chen and D. Ma, Appl. Phys. Lett., 2010, 96, 213104 CrossRef
.
- S.-O. Guillaume, B. Zheng, J.-C. Charlier and L. Henrard, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035444 CrossRef
.
- S. Latil and L. Henrard, Phys. Rev. Lett., 2006, 97, 036803 CrossRef PubMed
.
- S. Latil, V. Meunier and L. Henrard, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 201402 CrossRef
.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef
.
- S. Chopra, ChemPhysChem, 2015, 16, 1948–1953 CrossRef PubMed
.
- C. Shen, C. Tseng, C. Lin, L. Li and H. L. Liu, Thin Solid Films, 2014, 571, 675–679 CrossRef
.
- K. F. Mak, L. Ju, F. Wang and T. F. Heinz, Solid State Commun., 2012, 152, 1341–1349 CrossRef
.
- C. Yelgel, Doctoral degree thesis, University of Exeter, 2013
.
- F. Nelson, V. Kamineni, T. Zhang, E. Comfort, J. Lee and A. Diebold, Appl. Phys. Lett., 2010, 97, 253110 CrossRef
.
- L. Yang, J. Deslippe, C.-H. Park, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2009, 103, 186802 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2018 |