Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced photoelectrochemical performance of anatase TiO2 for water splitting via surface codoping
Jiajun Wanga,
Jing Huang*bc,
Jie Mengb,
Qunxiang Li *b and
Jinlong Yang
*b and
Jinlong Yang b
b
aTianjin Key Laboratory of Structure and Performance for Functional Molecules, Key Laboratory of Inorganic-Organic Hybrid Functional Materials Chemistry, Ministry of Education, College of Chemistry, Tianjin Normal University, Tianjin 300387, China
bHefei National Laboratory for Physical Sciences at the Microscale, Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: liqun@ustc.edu.cn
cSchool of Materials and Chemical Engineering, Anhui Jianzhu University, Hefei, Anhui 230601, China. E-mail: jhuang@ustc.edu.cn
First published on 16th August 2017
Abstract
Codoping can effectively engineer the band structures of photocatalysts (e.g. TiO2) to enhance their photoelectrochemical performance, however, previous investigations mainly focused on codoped bulk materials. In this work, we explore the (Rh + F) surface codoping effect on anatase TiO2 (101) and (001) facets for solar water splitting by performing extensive density functional theory calculations. According to the calculated defect formation energies, we find that the noble metal (Rh) atoms can be stably doped at the anatase TiO2 (101) surface with the aid of the codoped F atoms, thus can act as active sites for photocatalytic H2 evolution, which also provides the possibility of single-atom Rh catalysis on the (Rh + F) codoped anatase TiO2 (101) surface. The band gap of the codoped system is narrowed to about 2.14 eV through introducing several occupied and delocalized intermediate states which prevent the recombination of photogenerated carriers. Remarkably, the valence band maximum and conduction band minimum of the (Rh + F) codoped anatase TiO2 (101) surface match well with the water redox potentials and the visible light absorption is significantly enhanced. These findings imply that this kind of surface codoping is an effective approach to obtain visible light photocatalysts for water splitting.
1 Introduction
Since the pioneering work by Fujishima and Honda,1 anatase titanium dioxide (TiO2) has been used widely as a promising photocatalyst for water splitting due to its high photocatalytic activity, cost effectiveness, environmental friendliness, availability, and long-term stability against photo- and chemical corrosion.2–4 Unfortunately, because of the wide band gap (3.2 eV) possessed by anatase TiO2, its practical application for the photocatalytic water splitting for hydrogen production is limited by the narrow range of irradiation from a light source, which falls in the ultraviolet (UV) region.5–7 Therefore, band gap engineering of TiO2 to enhance solar energy utilization has been an important issue in photocatalyst studies. To improve the visible-light photocatalytic performance, doping TiO2 with foreign elements including non-metals (such as N, B, C, F, S, etc.) and transition metals (such as Fe, Cr, Co, Mo, V, etc.) has been used widely.8–11 However, experimental and theoretical studies show that substituting oxygen with non-metal elements needs to overcome a larger energy barrier and non-metal dopants prefer to be in interstitial sites near to the oxygen lattice and that transition-metal dopants can introduce localized states into the band gap and lead to a relatively high recombination rate of photo-generated electron–hole pairs.12–14 Consequently, the photoelectrochemical efficiency of monodoped TiO2 is usually very low. Fortunately, charge compensated donor–acceptor codoping can improve the solubility of the alloying elements and more effectively narrow the band gap than monodoping, enhancing the photocatalytic activity of TiO2.15,16 Since the codoping concept was proposed, it has attracted intense research interest in the field of photocatalytic water splitting.17–24 Note that these reported studies of doped-TiO2 are focused on the bulk material. Since the photoreactive properties of materials are mainly determined by the exposed facets, and the reactions occur on substrate surfaces, theoretical investigation of the surface codoping effect is urgently needed.In addition, a bare photocatalyst without loading a cocatalyst would exhibit a poor photocatalytic hydrogen evolution activity. In order to guarantee hydrogen evolution, noble metals (such as Pt, Pd, Ru, Rh and Au) are usually needed to be loaded as a cocatalyst, which not only provides a large number of active sites, but also promotes charge separation.25,26 Unfortunately, the application of noble metals in photocatalytic materials is greatly restricted due to the high cost and low abundance.27,28 Alternatively, surface doping with noble metals would be a sensible way to decrease the noble metal loading and to increase the activity. Recently, Okamoto et al.29 have reported that Rh-doped Ca–Nb–O nanosheets exhibit a high photocatalytic activity for hydrogen production from a water/methanol system. In addition, Xing et al.30 have also proven that doping TiO2 with isolated noble metal atoms (Pt, Pd, Rh or Ru) leads to a 6–13-fold increase in photocatalytic activity over metal clusters loaded on TiO2 by the traditional method. Clearly, the surface doped noble metals can be expected to be directly involved in the catalytic reaction, and act as reaction sites for hydrogen evolution, thus causing a significant improvement in photocatalytic performance.
Based on these experimental findings, to develop photocatalytic materials with visible light response and high activity, more attention should be paid to surface doping with noble metals. However, theoretical investigation of the effect of surface codoping on the surface electronic structure and catalytic activity of TiO2 is rare so far.31 Here, we focus on the anatase TiO2 (101) surface for the following two reasons: (i) the activity of anatase in photocatalytic processes is found to be much higher than that of rutile32 and (ii) the (101) termination is the most thermodynamically stable low-index surface of anatase TiO2.33 By performing extensive density functional theory (DFT) calculations, the effect of surface (Rh + F) codoping on the electronic structure and photocatalytic activities of the anatase TiO2 (101) surfaces is carefully examined. We find that a single Rh atom can be stably anchored to the anatase TiO2 (101) surface by codoping with a F atom. The (Rh + F) codoping can not only effectively narrow the band gap by introducing occupied and delocalized intermediate states, but can also create the ideal band edge alignment for solar water splitting.
2 Computational model and methods
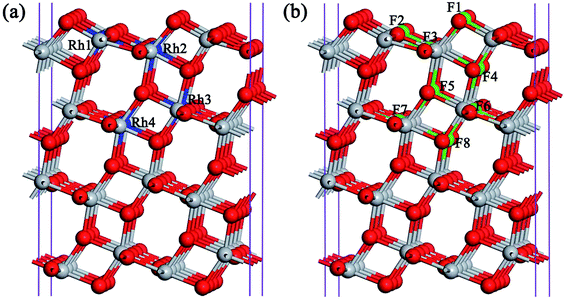
Our DFT calculations are performed using the Vienna ab initio simulation package (VASP).34,35 The interaction between the core and valence electrons is described using the frozen-core projector augmented wave approach (PAW).36 The PAW potentials with the 4s and 3d valence states for the Ti atoms, 2s and 2p for the O and F atoms, and 4d and 5s for the Rh atom are employed. The exchange and correlation effects are described by the Perdew–Burke–Ernzerhof (PBE) functional.37 The Monkhorst–Pack mesh of k-points38 (2 × 2 × 1 points) is used to sample the Brillouin zone. A plane-wave cutoff energy of 520 eV is used, all atomic positions in the selected top layers are relaxed at the PBE level until the atomic forces are smaller than 0.02 eV Å−1, and the tolerance for energy convergence is set to 10−5 eV.Firstly we optimize the pure anatase TiO2 structure, and obtain bulk lattice parameters (a = 3.82 Å and c = 9.69 Å) which are in good agreement with previous experimental and theoretical results.21,39 Then, the TiO2 (101) surface is simulated by a 2 × 3 periodic-slab model that contains eight O–Ti–O trilayers, as shown in Fig. 1. The slab model is separated by a 15 Å-thick vacuum gap and the total number of atoms is 144. The lengths along the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] and [010] directions of the surface model are 10.42 and 11.46 Å, which are long enough, and the self-interactions among the impurities could be ignored. In the examined surface models, the top four trilayers are fully relaxed, while the bottom four trilayers are fixed to mimic the bulk region. To visit the surface codoping effect, one Ti and/or O atom is replaced by one Rh and/or F atom, respectively. This means that the atomic impurity concentrations (Rh or F) are 0.69%.
] and [010] directions of the surface model are 10.42 and 11.46 Å, which are long enough, and the self-interactions among the impurities could be ignored. In the examined surface models, the top four trilayers are fully relaxed, while the bottom four trilayers are fixed to mimic the bulk region. To visit the surface codoping effect, one Ti and/or O atom is replaced by one Rh and/or F atom, respectively. This means that the atomic impurity concentrations (Rh or F) are 0.69%.
In order to predict the correct electronic structures and defect levels of transition metal oxides,40,41 the more time consuming hybrid density functional as prescribed by Heyd–Scuseria–Ernzerhof (HSE06)42,43 has been adopted. The exchange–correlation contribution employed in the HSE06 functional is divided into short- and long-range parts. The 25% Hartree–Fock (HF) exchange is mixed with PBE exchange in the short-range part, and the expression for exchange–correlation in HSE06 is given by
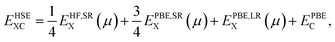 | (1) |
In order to determine the relative stabilities of different doping configurations and find the optimal synthetic condition, we calculate the defect formation energy (Eform) according to the following equations,
| Eform = ERhTi − Epure + μTi − μRh | (2) |
| Eform = EFO − Epure + μO − μF | (3) |
| Eform = ERhTi+FO − Epure + μTi + μO − μRh − μF | (4) |
To examine the coupling strength between the dopants in the codoped system, we calculate the defect pair binding energy (Eb), which is defined as
| Eb = ERhTi + EFO − ERhTi+FO − Epure | (5) |
3 Results and discussion
3.1 Defect formation energy
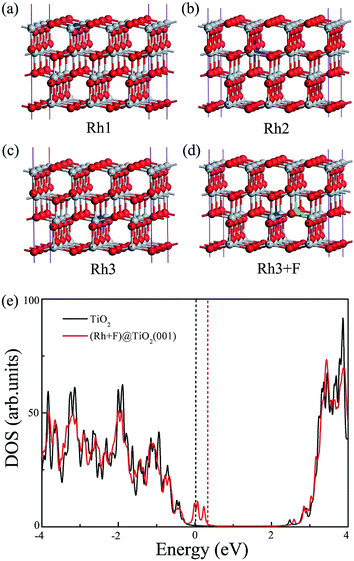
To be a reaction site for H2 evolution, as mentioned above, the anchoring of the single noble metal atom to the catalyst surface is highly desirable to maximize its photocatalytic efficiency. Thus, we firstly investigate the possibility of anchoring the Rh atom on the TiO2 (101) surface. To confirm whether Rh substitution at the uppermost surface is favored with respect to subsurface substitution, various possible nonequivalent surface and subsurface Rh doping configurations are examined, as shown in Fig. 1(a). The formation energies of four kinds of Rh monodoping under the O-rich and Ti-rich conditions are summarized in Table 1. Under the O-rich growth condition, the calculated formation energies for the substitutions of Ti by Rh atoms are negative, while these values are positive under the Ti-rich growth condition. This observation indicates that it is relatively easier to incorporate Rh atoms into the anatase TiO2 lattice by replacing Ti sites under the O-rich condition. However, the most stable substitutional site of the Rh atom, labeled as Rh3 in Fig. 1(a), is the sixfold coordinated Ti site in the second trilayer. The Rh dopant is located about 4.4 Å below the surface. That is to say, the doped Rh atom cannot act as a direct reaction site in photocatalytic H2 evolution.| Dopants | EO-richform (in eV) | ETi-richform (in eV) | Eb (in eV) |
|---|---|---|---|
| Rh1 | −0.82 | 8.06 | — |
| Rh2 | −0.93 | 7.95 | — |
| Rh3 | −1.10 | 7.78 | — |
| Rh4 | −0.78 | 8.10 | — |
| F1 | −0.85 | −5.29 | — |
| F2 | −0.43 | −4.87 | — |
| F3 | −0.64 | −5.08 | — |
| F4 | −0.11 | −4.55 | — |
| F5 | −0.83 | −5.27 | — |
| F6 | −0.60 | −5.04 | — |
| F7 | −0.73 | −5.17 | — |
| F8 | −0.34 | −4.78 | — |
| (Rh1 + F) | −2.15 | 2.29 | 1.25 |
| (Rh2 + F) | −2.87 | 1.57 | 1.89 |
| (Rh3 + F) | −2.57 | 1.87 | 1.77 |
| (Rh4 + F) | −2.23 | 2.21 | 1.51 |
In contrast to Rh monodoping, F atoms prefer to substitute at O sites in the uppermost surface layer whether under O-rich or Ti-rich growth conditions, as shown in Table 1. The most stable substitutional site for F monodoping is the twofold coordinated bridging O site in the top trilayer, labeled as F1 in Fig. 1(b). Moreover, the minimum formation energies for one F atom substituting an O atom in the anatase TiO2 (101) surface under Ti-rich and O-rich conditions are −5.29 and −0.85 eV, respectively. The negative value of the formation energy indicates that F monodoping is relatively easy to achieve in experiments.
Since the coulombic attraction between the anion and cation dopants can enhance the solubility of the dopants in TiO2 and the crystallinity of the doped systems,15 we turn to examine the anatase TiO2 (101) surfaces with the (Rh + F) codoping pair, in which the O atom connected to the Rh atom is substituted by a F atom to introduce a charge compensated donor–acceptor pair. Four different (Rh + F) codoping configurations are considered, and the corresponding dopant pair formation energies are listed in Table 1. Similarly to the anion–cation codoping in the bulk phase, the calculated binding energies of the (Rh + F) codoped TiO2 surface are all positive, indicating that the two dopants tend to bind with each other on the TiO2 (101) surface due to the strong Coulomb interaction between the Rh and F dopants. This relatively large defect pair binding energy also indicates that the (Rh + F) codoping pair is more stable than the isolated Rh and F monodoped anatase TiO2 (101) surfaces. Interestingly, the most stable structure of the (Rh + F) codoping configuration is that in which the Rh atom occupies the surface sixfold coordinated Ti site (Rh2 in Fig. 1(a)) while the F atom occupies the nearby twofold coordinated bridging O site (F1 in Fig. 1(b)). Moreover, the formation energy of the most stable (Rh + F) codoping structure is less than that with Rh monodoping whether under O-rich or Ti-rich conditions, indicating that codoping with F atoms makes Rh doping easier. These novel observations show the possibility of single-atom Rh catalysis on the anatase TiO2 (101) surface. Of course, these Rh atoms in the (Rh + F) codoped anatase TiO2 (101) surface can act as active sites for photocatalytic H2 production.
3.2 Electronic structure
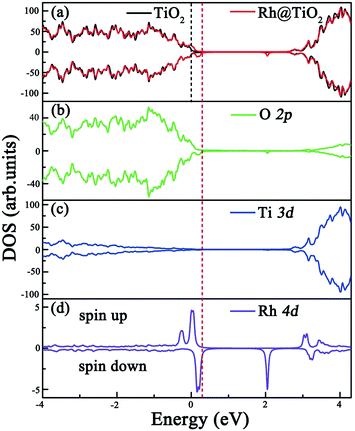
Before exploring the effect of codoping on the electronic structure of the anatase TiO2 (101) surface, we calculate the total density of states (DOS) and projected DOS of the pure anatase TiO2 (101) surface and show them in Fig. 2. The HSE06 calculated band gap of the pure TiO2 surface is predicted to be 2.74 eV, which is very close to the experimental value.44 Similarly to in bulk anatase TiO2,6 the valence band maximum (VBM) is mainly contributed to by O 2p orbitals, while the conduction band minimum (CBM) has predominantly Ti 3d character. As for the anatase TiO2 (101) surface with Rh monodoping, we find that the main features of these calculated electronic structures of the Rh-doped TiO2 surface with different nonequivalent surface and subsurface doping sites are similar. For clarity, we focus on the most stable Rh-doped configuration. Due to the unpaired 3d electron from the Rh dopant, the ground state of the Rh-doped TiO2 surface is spin-polarized. The magnetic moment is predicted to be 1.0 μB per supercell, which mainly originates from the Rh atom (the atomic magnetic moment is about 0.74 μB). The spin-resolved total DOS of the Rh-doped anatase TiO2 (101) surface and the partial DOS for the O 2p, Ti 3d and Rh 4d electrons are plotted in Fig. 3(a), (b), (c) and (d), respectively. In comparison with the pure TiO2 surface, the Rh dopant creates some unoccupied and localized empty states above the Fermi level as well as several fully occupied impurity states at the VB tails. These impurity states originate from the hybridization of the Rh 4d and O 2p orbitals, as shown in Fig. 3(b) and (d). As a result, they lead to band gap narrowing. The reduced band gap value is about 1.01 eV. To understand the nature of these impurity states, we further consider the valence electron configurations of Rh and Ti. Upon substitution of Ti with a Rh atom, the Rh dopant should be in a formal +4 state (Rh4+), and the corresponding valence electron configuration changes from 4d85s1 to 4d55s0. Note that to reach a stable oxidation state (Rh3+), the Rh dopant needs to transfer an electron from a neighboring O atom to itself (Rh4+).45 Moreover, the unoccupied impurity states located at 1.73 eV above the VBM can act as deep acceptor energy levels. Additionally, these acceptor states are rather localized, thus would have an adverse influence on the photocatalytic performance since the carrier mobility drastically reduces and the photogenerated carrier recombination increases.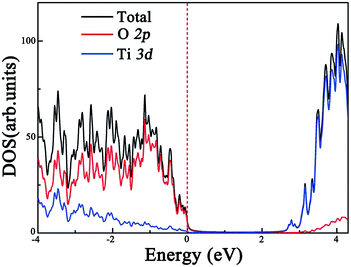 | ||
| Fig. 2 Calculated total and partial DOS of the pure anatase TiO2 (101) surface at the HSE06 level. The vertical dashed line indicates the Fermi level. | ||
To solve these problems and then enhance the photocatalytic performance, the unoccupied and localized impurity states should be passivated. Since an F atom contains one more valence electron than an O atom, the substitution of F on the O site will introduce one extra electron into the system. Once a (Rh + F) codoping pair is incorporated into the anatase TiO2 (101) surface, an extra electron from the F atom will transfer to the Rh dopant, thus, the Rh dopant will be in the stable +3 oxidation state. In this sense, the anion–cation surface codoping pair suppresses the formation of the Rh4+ state, and passivates the unoccupied and localized states through charge compensation.
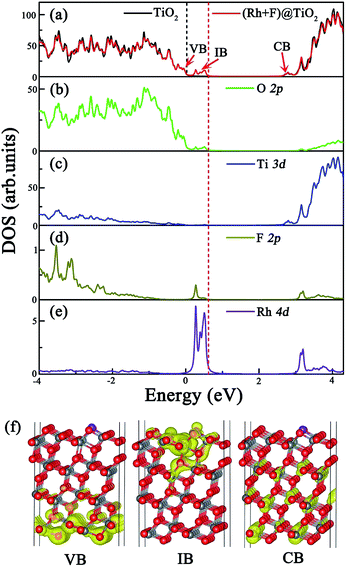
To assess the surface codoping effect, we calculate the total DOS of the (Rh + F) doped anatase TiO2 (101) surface and the partial DOS of the O 2p, Ti 3d, F 2p and Rh 4d orbitals, and compare them with the corresponding results for the pure TiO2 surface. The results are plotted in Fig. 4. In contrast to the Rh monodoping case, the ground state of the (Rh + F) doped TiO2 surface is spin-restricted, and the magnetic moment is zero, indicating the absence of an unpaired electron in the codoped system. Fig. 4(a) clearly demonstrates that the (Rh + F) codoping pair just slightly perturbs the VBM and CBM positions compared to the pure anatase TiO2 surface. Intermediate bands (IBs) located below the Fermi level appear within the band gap. The effective band gap of the (Rh + F) codoped TiO2 surface is significantly narrowed to about 2.14 eV. According to the calculated partial DOS, as shown in Fig. 4(b), (d) and (e), the occupied IBs are mainly contributed to by O 2p orbitals, Rh 4d orbitals and F 2p orbitals. In comparison with the Rh monodoping case, the width of the IBs are substantially broadened due to the strong hybridization. These substantially broad, delocalized, and occupied IBs induced by the (Rh + F) codoping pair can not only effectively reduce the band gap, but can also prevent the recombination of photogenerated carriers. Moreover, no acceptor states appear above the Fermi level, which indicates that the recombination centers will be greatly reduced compared with the Rh or F monodoping case.
It is well known that there are three processes in the photocatalytic generation of H2: (1) the photocatalyst absorbs sunlight and generates excited electrons and holes, (2) the excited electrons and holes separate and migrate to the surface of the photocatalyst separately, and (3) molecules are reduced and oxidized by the photogenerated electrons and holes (i.e. water is split into H2 and O2), respectively.3 In the second step, whether the photogenerated electrons can jump from the VB to the CB via the IBs depends on their localized or delocalized nature.46 Therefore, we plot the electron density distributions of the VBM, IB and CBM of the (Rh + F) codoped anatase TiO2 (101) surface in Fig. 4(f). Clearly, both the VB and CB near the band edges are highly delocalized, indicating that (Rh + F) codoping just slightly affects the VB and CB of the pure TiO2 surface. Whereas the IBs, mainly composed of Rh 4d and O 2p orbitals with a slight contribution from F 2p orbitals, can be deemed somewhat delocalized. As stated by Zhang et al.,46,47 the delocalized nature is of significance if the IB acts as a stepping stone to bridge the VBM and the CBM. This nature will ensure migration of the electrons excited by photon energies in the visible region to jump from the CB to the IB.
3.3 Photocatalytic activity
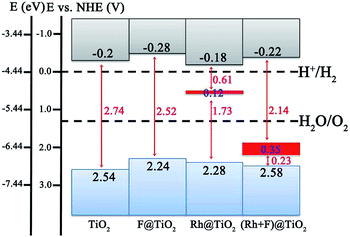
Although the band structure of the anatase TiO2 (101) surface is effectively modified by the (Rh + F) codoping pair, one should be aware of the band edge positions with respect to the redox potentials of the adsorbates on the surface.48–50 If the CBM of the photocatalyst is above (more negative than) the potential level of the acceptor species, while the VBM of the photocatalyst is below (more positive than) the potential level of the donor species, the photocatalytic water splitting is able to proceed to produce H2 and O2 simultaneously.51–53 To evaluate the effect of surface doping on the photocatalytic performance, we plot the band edge alignment of the pure and doped anatase TiO2 (101) surface compared with the water reduction and oxidation potentials in Fig. 5. Here, the CBM position for the pure anatase TiO2 (101) surface with respect to the normal hydrogen electrode (NHE) potential is taken from experiment.44 The VBM position is deduced from the energy gaps calculated using HSE06. As for the Rh-doped, F-doped, and (Rh + F) codoped anatase TiO2 (101) surfaces, the CB and VB edge positions are determined according to the calculated DOS results (see Fig. 3 and 4), which have been aligned on one diagram using the 2s core levels of the O atoms farthest away from the dopants.As shown in Fig. 5, the CBM of the pure anatase TiO2 (101) surface is higher (by about 0.2 eV) than the reduction potential of H+/H2 (located at −4.44 eV), while its VBM is more positive (by about 1.31 eV) than the oxidation potential of O2/H2O (−5.67 eV). This observation implies that the pure TiO2 surface has a strong reduction/oxidation ability, but it cannot effectively harvest solar light. As for the F-doped anatase TiO2 (101) surface, the CBM and VBM both shift upward with respect to the pure TiO2 surface by 0.08 and 0.3 eV, respectively. Clearly, the photoreduction capacity is improved, however, the reduction of the band gap is too small (less than 0.3 eV). Actually, the strong reduction ability of the pure TiO2 surface is well preserved in the Rh monodoping case since the CBM does not significantly change. Unfortunately, the position of the VBM moves upward by about 0.26 eV, thus the driving force for water photooxidation may decline. In addition, Rh monodoping leads to unoccupied and localized IBs within the band gap, which are detrimental for water splitting. In the (Rh + F) codoped system, the VBM and CBM positions are just slightly perturbed, suggesting that the strong oxidizing and reducing abilities of the anatase TiO2 (101) surface remain. The occupied and delocalized IBs with a band width of 0.35 eV appear in the band gap, which reduces the band gap to 2.14 eV. Among all the examined systems, the anatase TiO2 (101) surface with (Rh + F) codoping is a potential candidate for photoelectrochemical water splitting since it has a suitable band gap and a nice band edge alignment with the water reduction and oxidation potentials.
3.4 Optical properties
An important index of the photocatalytic performance of the modified anatase TiO2 (101) surface is its optical absorption. Here, the frequency-dependent dielectric function, which is defined as ε(ω) = ε1(ω) + iε2(ω), is further calculated. The imaginary part ε2(ω) of the dielectric function ε(ω) is calculated by summing all possible transitions from the unoccupied to the occupied wave functions within the selection rules, while the real part ε1(ω) can be derived from ε2(ω) using the Kramer–Kronig relationship. The optical absorption coefficient αabs is calculated from the dielectric components ε1(ω) and ε2(ω) according to the following relation,54
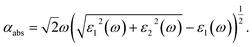 | (6) |
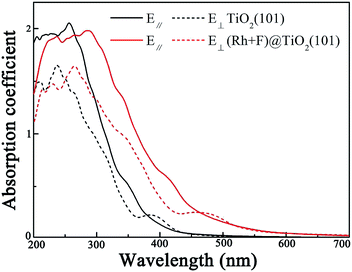
The calculated optical absorption spectra of the pure and (Rh + F) codoped anatase TiO2 (101) surfaces are shown in Fig. 6. In our calculations, ε2(ω) and ε1(ω) along parallel and vertical directions relative to the anatase TiO2 (101) surfaces are evaluated. It is clear that the absorption spectrum of the pure anatase TiO2 (101) surface depends on the polarization direction of the incoming light, whether in parallel or perpendicular to the anatase TiO2 (101) surface. As for the (Rh + F) codoped anatase TiO2 (101) surface, there is a significant redshift of the absorption edge due to the significant reduction of the band gap of the pure anatase TiO2 (101) surface by the (Rh + F) codoping pair. Clearly, the (Rh + F) codoped anatase TiO2 (101) surface should be a promising visible light photocatalyst, since it can effectively harvest the visible light spectrum.
3.5 The anatase TiO2 (001) surface
Finally, to explore the influence of (Rh + F) codoping toward other TiO2 surfaces, we examine the anatase TiO2 (001) surface as an example since it is often seen as a high activity facet. For Rh monodoping and (Rh + F) codoping, we consider various possible nonequivalent surface and subsurface doping sites, as shown in Fig. 7. The formation energies of three kinds of surface doping under O-rich and Ti-rich conditions are summarized in Table 2. Fig. 7(b) show the most stable substitutional site of the Rh atom (the sixfold coordinated Ti site in the second trilayer), which is similar to the Rh monodoping case in the (101) surface in which the doped Rh atom also locates below the surface. This implies that the Rh dopant cannot act as a direct reaction site in photocatalytic H2 evolution. If the O atom connected to the Rh atom is further substituted by a F atom, the most stable structure of the (Rh + F) codoping configuration is that in which the Rh atom occupies the sixfold coordinated Ti site of the third trilayer while the F atom occupies the nearby threefold coordinated O site, as shown in Fig. 7(d). It is clear that the Rh atom in the (Rh + F) codoped anatase TiO2 (001) surface still locates below the surface, which is different to the (Rh + F) codoped anatase TiO2 (101) surface.| Dopants | EO-richform (in eV) | ETi-richform (in eV) |
|---|---|---|
| Rh1 | −0.72 | 8.16 |
| Rh2 | −0.93 | 7.95 |
| Rh3 | −0.27 | 8.61 |
| (Rh1 + F) | −1.78 | 2.66 |
| (Rh2 + F) | −2.34 | 2.10 |
| (Rh3 + F) | −2.62 | 1.82 |
At the HSE06 level, we calculate the total DOS of the (Rh + F) doped anatase TiO2 (001) surface, and plot them in Fig. 7(e). Clearly, the (Rh + F) codoping pair slightly perturbs the VBM and CBM positions compared to the pure (001) surface. Similarly to the codoping in the (101) surface, there are some fully occupied and delocalized intermediate bands within the band gap. Thus the effective band gap of the (Rh + F) codoped TiO2 (001) surface is narrowed to about 2.05 eV.
4 Conclusions
By performing extensive DFT calculations, we examine the effect of (Rh + F) codoping on the electronic structures and photocatalytic activities of anatase TiO2 (101) and (001) surfaces. Our simulated results clearly reveal that single Rh atoms can be stably anchored on the anatase TiO2 (101) surface through introducing the codoped F atom, which shows the possibility of single-atom Rh catalysis on the (Rh + F) codoped anatase TiO2 (101) surface. The (Rh + F) codoping can not only effectively reduce the band gap by forming occupied and delocalized intermediate bands within the band gap, but can also lead to nice band edge alignment. Moreover, the (Rh + F) codoping pair significantly enhances the optical absorption. These theoretical findings suggest that this kind of surface codoping is a promising approach to design visible-light photocatalysts for water splitting.Acknowledgements
This work was partially supported by the State Key Research & Development Program of China (No. 2016YFA0200600), by the National Key Basic Research Program (No. 2014CB921101), by the NSFC (No. 21503149, 21473168 and 11634011), and by the Doctoral Program Foundation of Tianjin Normal University (No. 52XB1408) (J. W. and Q. L.). J. H. thanks the Natural Science Foundation of the Anhui Higher Education Institutions (No. KJ2016A144) and the Natural Science Foundation of Anhui Province (No. 1408085QB26). Computational resources have been provided by CAS, Shanghai and USTC Supercomputer Centers.References
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed.
- H. Xu, S. Ouyang, L. Liu, P. Reunchan, N. Umezawa and J. Ye, J. Mater. Chem. A, 2014, 2, 12642–12661 CAS.
- H. Tang, F. Levy, H. Berger and P. E. Schmid, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 7771–7774 CrossRef CAS.
- J. Wang, Q. Meng, J. Huang, Q. Li and J. Yang, J. Chem. Phys., 2014, 140, 174705 CrossRef PubMed.
- R. Asahi, T. Morikawa, H. Irie and T. Ohwaki, Chem. Rev., 2014, 114, 9824–9852 CrossRef CAS PubMed.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271 CrossRef CAS PubMed.
- S. U. M. Khan, M. Al-Shahry and J. W. B. Ingler, Science, 2002, 297, 2243–2245 CrossRef CAS PubMed.
- T. Umebayashi, T. Yamaki, H. Itoh and K. Asai, Appl. Phys. Lett., 2002, 81, 454–456 CrossRef CAS.
- W. Y. Choi, A. Termin and M. R. Hoffmann, J. Phys. Chem., 1994, 98, 13669–13679 CrossRef.
- J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891 CrossRef CAS PubMed.
- J. Zhang, Y. Wu, M. Xing, S. A. K. Leghari and S. Sajjad, Energy Environ. Sci., 2010, 3, 715–726 CAS.
- J. Wang, S. Chen, Q. Li and J. Yang, Int. J. Hydrogen Energy, 2016, 41, 13050–13057 CrossRef CAS.
- Y. Gai, J. Li, S.-S. Li, J.-B. Xia and S.-H. Wei, Phys. Rev. Lett., 2009, 102, 036402 CrossRef PubMed.
- W.-J. Yin, H. Tang, S.-H. Wei, M. M. Al-Jassim, J. Turner and Y. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045106 CrossRef.
- M. Niu, W. Xu, X. Shao and D. Cheng, Appl. Phys. Lett., 2011, 99, 203111 CrossRef.
- Y.-F. Li, D. Xu, J. I. Oh, W. Shen, X. Li and Y. Yu, ACS Catal., 2012, 2, 391–398 CrossRef CAS.
- N. Feng, Q. Wang, A. Zheng, Z. Zhang, J. Fan, S.-B. Liu, J.-P. Amoureux and F. Deng, J. Am. Chem. Soc., 2013, 135, 1607–1616 CrossRef CAS PubMed.
- G. Wang, H. Chen, Y. Li, A. Kuang, H. Yuan and G. Wu, Phys. Chem. Chem. Phys., 2015, 17, 28743–28753 RSC.
- J. Wang, H. Sun, J. Huang, Q. Li and J. Yang, J. Phys. Chem. C, 2014, 118, 7451–7457 CAS.
- B. Modak, P. Modak and S. K. Ghosh, RSC Adv., 2016, 6, 90188–90196 RSC.
- H. Zhuang, Y. Zhang, Z. Chu, J. Long, X. An, H. Zhang, H. Lin, Z. Zhang and X. Wang, Phys. Chem. Chem. Phys., 2016, 18, 9636–9644 RSC.
- S. N. Phattalung, S. Limpijumnong and J. Yu, Appl. Catal., B, 2017, 200, 1–9 CrossRef.
- J. Yang, D. Wang, H. Han and C. Li, Acc. Chem. Res., 2013, 46, 1900–1909 CrossRef CAS PubMed.
- J. Ran, J. Zhang, J. Yu, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2014, 43, 7787–7812 RSC.
- Y.-J. Yuan, H.-W. Lu, Z.-T. Yu and Z.-G. Zou, ChemSusChem, 2015, 8, 4113–4127 CrossRef CAS PubMed.
- J. Wang, Z. Guan, J. Huang, Q. Li and J. Yang, J. Mater. Chem. A, 2014, 2, 7960–7966 CAS.
- Y. Okamoto, S. Ida, J. Hyodo, H. Hagiwara and T. Ishihara, J. Am. Chem. Soc., 2011, 133, 18034–18037 CrossRef CAS PubMed.
- J. Xing, J. F. Chen, Y. H. Li, W. T. Yuan, Y. Zhou, L. R. Zheng, H. F. Wang, P. Hu, Y. Wang, H. J. Zhao, Y. Wang and H. G. Yang, Chem.–Eur. J., 2014, 20, 2138–2144 CrossRef CAS PubMed.
- Z. Zhao, Z. Li and Z. Zou, ChemPhysChem, 2012, 13, 3836–3847 CrossRef CAS PubMed.
- K. K. Hashimoto, H. Irie and A. Fujishima, Jpn. J. Appl. Phys., 2005, 44, 8269 CrossRef CAS.
- A. S. M. Lazzeri and A. Vittadini, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409 CrossRef.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- J. K. Burdett, T. Hughbanks, G. J. Miller, J. W. Richardson and J. V. Smith, J. Am. Chem. Soc., 1987, 109, 3639–3646 CrossRef CAS.
- J. Wang, J. Huang, J. Meng, Q. Li and J. Yang, Phys. Chem. Chem. Phys., 2016, 18, 17517–17524 RSC.
- B. Modak and S. K. Ghosh, J. Phys. Chem. C, 2016, 120, 6920–6929 CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Pan, G. Liu, G. Q. Lu and H.-M. Cheng, Angew. Chem., Int. Ed., 2011, 50, 2133–2137 CrossRef CAS PubMed.
- B. Modak and S. K. Ghosh, J. Phys. Chem. C, 2015, 119, 7215–7224 CAS.
- H. Pan, B. Gu, G. Eres and Z. Zhang, J. Chem. Phys., 2010, 132, 104501 CrossRef PubMed.
- W. Zhu, X. Qiu, V. Iancu, X.-Q. Chen, H. Pan, W. Wang, N. M. Dimitrijevic, T. Rajh, H. M. Meyer, M. P. Paranthaman, G. M. Stocks, H. H. Weitering, B. Gu, G. Eres and Z. Zhang, Phys. Rev. Lett., 2009, 103, 226401 CrossRef PubMed.
- Y. Qu and X. Duan, Chem. Soc. Rev., 2013, 42, 2568–2580 RSC.
- P. Liao and E. A. Carter, Chem. Soc. Rev., 2013, 42, 2401–2422 RSC.
- Y. Liu, W. Zhou, Y. Liang, W. Cui and P. Wu, J. Phys. Chem. C, 2015, 119, 11557–11562 CAS.
- A. L. Linsebigler, G. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735–758 CrossRef CAS.
- B. Ohtani, Phys. Chem. Chem. Phys., 2014, 16, 1788–1797 RSC.
- J. Wang, J. Meng, Q. Li and J. Yang, Phys. Chem. Chem. Phys., 2016, 18, 17029–17036 RSC.
- M. Gajdos, K. Hummer, G. Kresse, J. Furthmuller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |