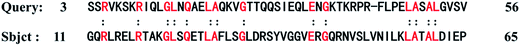Open Access Article
Open Access ArticleA database assisted protein structure prediction method via a swarm intelligence algorithm
Pengyue Gao a,
Sheng Wanga,
Jian Lvb,
Yanchao Wang*a and
Yanming Ma*a
a,
Sheng Wanga,
Jian Lvb,
Yanchao Wang*a and
Yanming Ma*a
aState Key Laboratory of Superhard Materials, Jilin University, Changchun 130012, China. E-mail: wyc@calypso.cn; mym@jlu.edu.cn
bCollege of Materials Science and Engineering, Jilin University, Changchun 130012, China
First published on 16th August 2017
Abstract
The complex and rugged potential energy landscape has made protein structure prediction a challenging task in computational biology. Here, we propose an efficient protein structure prediction method combining both template-based and template-free methods. Specifically, the initial protein conformations can be built by a non-redundant protein database and random sampling method with constraints of the secondary structure of the proteins. Three different structure evolution methods including improved particle swarm optimization (PSO) algorithm, random perturbation and fragment substitution are employed to update the protein structures while keeping the secondary structures the same. The present method is benchmarked on several known protein structures with distinct folding patterns, including α proteins, β proteins and αβ proteins. The high success rate and the accuracy of the results demonstrate the reliability of this method.
I. Introduction
The function of a protein is determined by its three-dimensional (3D) structure, and this plays a crucial role in governing certain life processes.1 The rapid development of sequencing technologies has resulted in an exponential increase in the number of known protein sequences. However, the experimental determination of protein structure (e.g., by X-ray crystallography and nuclear magnetic resonance spectroscopy) is limited in part by the labor-intensive, lengthy process of protein structure resolution. For example, although more than 70 million known protein sequences have been deposited in the UniProtKB/TrEMBL protein database,2 less than 1% of these protein structures (about 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 protein structures) have been determined experimentally at the atomic level in the Protein Data Bank (PDB).3 This reflects the large gap between identifying the sequence of a protein and determining its structure. Therefore, the development of low-cost and efficient computer-aided methods for predicting protein 3D structures is highly desirable.
000 protein structures) have been determined experimentally at the atomic level in the Protein Data Bank (PDB).3 This reflects the large gap between identifying the sequence of a protein and determining its structure. Therefore, the development of low-cost and efficient computer-aided methods for predicting protein 3D structures is highly desirable.
Currently, protein structure prediction methods are classified into two categories based on the extent to which they exploit the known experimental structures in the PDB database: template-based method and template-free method. Template-based method, including comparative modeling4 and fold recognition modeling,5,6 builds protein models by aligning query sequences on solved protein structures to identify structure templates. Comparative modeling identifies templates by sequence or sequence profile comparison, since similar sequences adopt similar protein structures. Fold recognition identifies templates by matching the query sequence directly onto known protein structures. Template-based method has been proven more accurate than template-free methods. However, it's only successful when templates are available in the PDB library. On the contrary, template-free method, also called ab initio modelling,7–9 doesn't rely on any protein structure template and conducts a conformational search under guidance of the energy function to determine the protein structure. According to the thermodynamic hypothesis proposed by Anfinsen,10 the native conformation lies at the global free energy minimum. Several ab initio methods8,9,11–18 have been developed and used to determine various protein structures.8,11,14 However, with increasing protein sizes, the conformational phase space of sampling sharply increases, which makes the ab initio modeling extremely difficult. In practice, the current trends are pointing to approaches, which can extensively combine both methods. Template-based method always includes exploring template independent conformational space. Similarly, the ab initio modeling builds up models by using fragments of known structures.19–22
Here, we develop a general protein structure prediction method enabling the determination of the three-dimensional structure of a protein based on its sequence. The protein sequence is divided into two regions: template-dependent region and template-independent region. The former is constructed by template-based method and the latter is constructed by ab initio method (e.g., random sampling using the secondary structure information). It is also noteworthy that ab initio method is employed for structure evolution. Specifically, all the structures will be updated by improved PSO algorithm, fragment substitution method and random perturbation. Due to employment of combination of the template-based and ab initio methods, our method can achieve an adequate trade-off between two opposite terms: exploration and exploitation. The method is applied to several proteins with distinct folding patterns and system sizes. The high success rate and accuracy support the reliability of the method for protein structure prediction.
II. Method and implementation
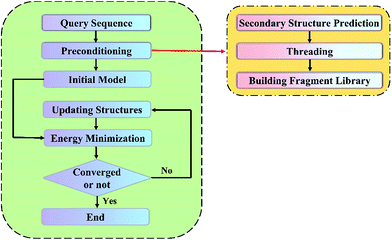
A flow chart for the proposed protein structure prediction method is shown in Fig. 1. It consists of four main steps: (a) preconditioning; (b) construction of initial conformation with the all-atom model of a protein; (c) energy minimization and evaluation of the static energy of the protein 3D structure with the all-atom force field parameters; and (d) generation of evolutionary related structures with the improved PSO algorithm, random perturbation and fragment substitution.a. Preconditioning
The aim of preconditioning is selecting the template protein and building a fragment library on basis of the given protein sequence. It's divided into three main steps: secondary structure prediction, threading and building the fragment library.The secondary structure of proteins is the 3D form of local segments of proteins. Once the secondary structure is determined, there will be a considerable reduction of the computational cost of structure prediction. Here, one of the widely used secondary structure prediction method: PSIPRED23 is adopted in our method.
Threading, as a template-based protein structure prediction method, aims to select template proteins, which share the similar structural motifs with the target protein, from known protein structure databases. The process details are as follows:
First, the query sequence is matched against a non-redundant sequence database (downloaded from http://zhanglab.ccmb.med.umich.edu/library/) by position-specific iterated BLAST (PSI-BLAST),24 to identify sequence similarity. Note that a critical parameter (E-value) is used in the PSI-BLAST search to estimate the probability of sequence similarity and exclude the similar sequences or homologous proteins. In this manuscript, the templates with an E-value < 0.05 are usually excluded to prove the robustness of the method. For a given protein sequence, a large number of target-template alignments can be found by the PSI-BLAST search. In order to select the potential template to construct the initial conformation, all the target-template alignments are evaluated by a score function related to both sequence and structure, borrowed from a profile–profile aligning approach: PPA approach25 and ranked according to their scores. Only the structures with the high-score can be selected as the potential templates.
To validate the threading method used in our studies, the protein 1r69_ (61 residues) is employed as the benchmark. The sequence of protein 1r69_ as the query sequence is matched against the non-redundant sequence database by PSI-BLAST method and all the target-template alignments are evaluated by PPA approach. A protein alignment (1y7yA) with the highest score of 2.82 is shown in Fig. 2. The Cα-RMSD between the structures of the native protein 1r69_ (3rd–56th residue) and protein 1y7yA (11th–65th residue) is only 1.4 Å. Obviously, both of structures share the similar sequence and structural motif, validating the threading method.
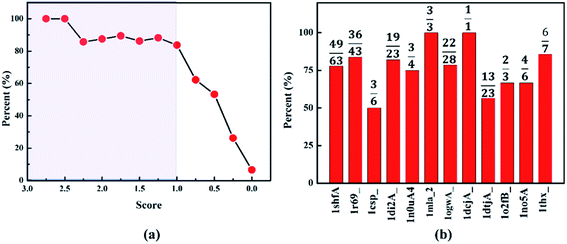
It should be emphasized that two key criteria should be suggested for the potential templates to construct the initial protein model: structural similarity and alignment length. To evaluate the structural similarity, the Cα-RMSD of all target-template alignments should be calculated. It is accepted that the template with Cα-RMSD of template less than 3.0 Å and alignment length more than half of the target sequence usually leads to high success ratio to predict the native-like protein. Therefore, two conditions should be satisfied for a potential template: the Cα-RMSD in the alignment region from template structure to native protein is less than 3.0 Å and the alignment length is larger than half of the target sequence. The score is well established to quantify the alignment length and structural similarity of template, while one of the central challenges is deciding an appropriate and acceptable the cutoff of score to find the potential template protein. To obtain well-defined cutoff of the score, we use the protein 1r69_ as an example to calculate the success rate of finding a potential template with different cutoff. It can be noted that the success rate for the target-template alignments as potential templates dependence on the score is shown in Fig. 3a. The success rate is greater than 80%, when the cutoff is set as 1. While it drops to 62% with cutoff as 0.75. Therefore, the cutoff of score is suggested to be 1. In order to further test the cutoff setting, we calculate the success rate for other proteins. Just as shown in Fig. 3b, the success rates for all the protein are not lower than 50%. Particularly, seven proteins are greater than 70%. The high success rates reveal that it is reasonable to set 1.0 as the truncation of score for identifying a potential template among all the target-template alignments.
As mentioned before, there usually are a large number of target-template alignments, which share similar structures or structure motifs. To use these information, we try to build a fragment library on the basis of these templates. The fragment library can be used to update protein models to improve the success rate of structure prediction. The process is as followed: we list all amino acid sequence fragments (seen as segments) with length of 9 residues26 in the query sequence sequentially, until the last letter of the query sequence is included. All the templates can be divided into several protein fragments in the same way (no gap is permitted in any fragment). The fragments can be ranked by the alignment score25 and 25 fragments with high score for each segment are used to build fragment library. The protein fragment containing 9 residues associates with protein database, while the segment is the amino acid sequence fragment with length of 9 residues in the query sequence. In practice, a segment can be replaced by the protein fragment, which can be randomly selected from 25 fragments in the fragment library.
b. Construction of initial conformation with the all-atom model of a protein
The all-atom model is used to determine the 3D structure of the protein in the present method. In the model, the 3D structure of a protein consists of the main backbone and the side chains. The main backbone can be constructed by varying the dihedral angles (ϕ and ψ) and by fixing bond lengths and angles within idealized geometries. The fixed bond lengths are set at 1.47 Å (N–Cα), 1.53 Å (Cα–C), 1.32 Å (C–N), and 1.24 Å (C–O), and the fixed bond angles are set at 110° (N–Cα–C), 114° (Cα–C–N), 123° (C–N–Cα), and 121° (Cα–C–O).27 Peptide bonds are considered to be in an all-trans conformation, and thus the dihedral angles (ω) are set at 180°. The side chains are added by using the SCWRL28 program for a given backbone structure, relying on a backbone-dependent rotamer library to select the most favorable rotamers.After the PSI-BLAST search, the query sequence is divided into two regions: template-dependent region and template-independent region. For the template-dependent region, the dihedral angles of the template are copied to construct the initial conformation. For the template-independent region, the initial conformation is constructed based on results of the secondary structure prediction. The two common secondary structures are α-helix and β-sheet, in which the dihedral angle ϕ/ψ values are fixed: −57° and −47° for α-helix and −139° and 135° for β-sheet, respectively.29 Other dihedral angles are randomly generated.
c. Energy minimization and evaluation of the static energy of the protein 3D structure with the all-atom force field parameters
One common step for protein structure prediction is to sample a large number of possible conformations based on a sequence, followed by energy evaluation of each conformation. Therefore, an efficient, reliable scoring function to evaluate the energies of an ensemble of structures and to rank the structures accordingly is valuable for improving the accuracy of a structure prediction program. To reduce the noise of energy surfaces and generate physically justified structures, energy minimization with an all-atom molecular mechanics force field is one of the most important processes in protein structure prediction for deriving the local minima from a pool of initial structures. Several molecular force fields have been developed for model quality assessment, including AMBER,30–32 CHARMM,33–35 and GROMOS96,36 which are derived from the laws of physics. In the present study, energy minimization is performed with the GROMACS software package,37 in which the OPLS force field38 is used to describe the interactions between the atoms of a protein by using a GB/SA model39,40 for implicit solvation. Additionally, the knowledge-based potential, RWplus,41 which has good transferability, is used to calculate the static energy of the protein as the fitness function to guide the evolution processes.d. Generation of evolutionary related structures with the improved PSO algorithm, random perturbation and fragment substitution
Efficient sampling of the complex and rugged potential energy surface of protein systems requires multi-dimensional global optimization algorithms. Particle swarm optimization (PSO) algorithm, as an efficient global optimization method, has been successfully applied to predict the structures of clusters,42,43 crystals,44,45 two-dimensional layers46 and surfaces,47 and other systems,48 which are related to sampling of complex potential energy surface.In the PSO scheme, a structure (an individual) in the search space is regarded as a particle. A set of individual particles is called a population or a generation. Each particle is initialized at a random position in the search space. During the evolution process, eqn (1) is used to update the positions of particles as
| xi,jt+1 = xi,jt + νi,jt+1. | (1) |
The new velocity (νi,jt+1) of the ith individual at the jth dimension is calculated based on its previous location xi,jt, previous velocity νi,jt, current location pbesti,jt with an achieved best fitness for this individual, and the population global location to date, gbestt, with the best fitness value for the entire population according to eqn (2)
| νi,jt+1 = K × (νi,jt + n1 × r1 × (pbesti,jt − xi,jt) + n2 × r2 × (gbestt − xi,jt)) | (2) |
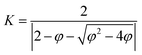 | (3) |
Fragment substitution method uses the structural fragments from the built fragment library to replace the existing part of protein conformations for structure evolution. The position for replacing the protein conformation is randomly selected and the fragment is randomly selected from the 25 fragments. Dihedral angles from the selected fragment replace the dihedral angles in the protein conformation. Fragment substitution can lead to rapid convergence on collapsed structures of plausible topology. Random perturbation method tries to perturb the current dihedral angles, which are randomly selected. In our method, the upper limit of the perturbation is 30°. Random perturbation method can effectively increase the structure diversity.
Note that the secondary structures and bond lengths are frozen, only dihedral angles of coil regions are updated during the structure evolution. Each operated structure is rejected or accepted on the basis of energy criteria. If the energy of the operated structure is lower than the energy of previous structure, the operation is accepted. Otherwise, it is rejected.
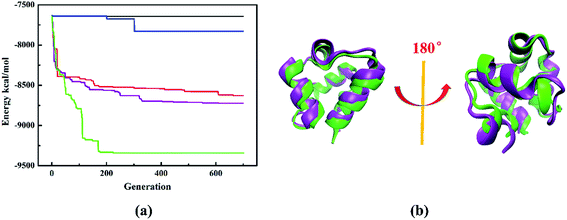
To evaluate the performance of different structure evolution strategies, we take protein 1r69_ as an illustrative example. The evolution histories with different structure evolution strategies are shown in Fig. 4a. First, we compare three structure evolution strategies: the traditional PSO algorithm (back line), random perturbation (blue line) and the improved PSO algorithm (red line). During the structure evolution by the traditional PSO algorithm or random perturbation, the system soon stagnates and one or more local minima dominate the search, while the improved PSO algorithm can achieve a fine exploration of potential energy surface and further predict the protein model with lower energy. Therefore, it is more efficient than traditional PSO algorithm or random perturbation. Furthermore, we also consider combination of different structure operations, including the improved PSO algorithm combined with random perturbation (purple line), random perturbation and fragment substitution (green line). The combination of two operations (purple line) can obtain the model with lower energy and it demonstrates that the combination is superior to single one. Especially, the energy decreases fast and the model with lowest-energy is successfully predicted at 225th generation, when the combination of three structure operations is used to perform structure evolution. The model with lowest-energy is proved to be a native-like structure and the Cα-RMSD of lowest energy model relative to native protein is only 1.9 Å. Furthermore, the superposition of lowest-energy model onto the native structure is shown in the Fig. 4b. A subtle difference between the lowest energy model and native structure is insignificant. Obviously, the structure evolution strategy of composite structure operations is the most powerful method to update protein structure.
III. Results and discussion
Generally, the protein structure prediction methods under the guide of homologous proteins will lead to high success rate and accuracy. Therefore, it is less persuasive to prove the robustness of protein prediction method using the template of homologous proteins. So it usually excludes homologous proteins from the structure database when evaluating the performance of protein prediction method. In our studies, we only focus on the results excluding homologous proteins from the database and the criterion for excluding homologous proteins is E-value = 0.05 of the PSI-BLAST search.The three categories of proteins with distinct folding patterns, including α proteins, β proteins and αβ proteins, are used to evaluate the performance of our approach. The modelling results of several known proteins, with length from 47 residues to 118 residues, are predicted by our approach and shown in Table 1. It is obvious that the Cα-RMSDs of most targets are less than 10 Å, which can be useful for biological application.50 Particularly, the Cα-RMSD of seven targets of 1shfA, 1r69_, 1di2A, 1ogwA, 1o2fB_, 2f3nA and T0716-D1 predicted by our method are less than 2.5 Å (the generally accepted criterion of high-resolution model50). Thus it can be seen that our method can successfully predict native-like models with different systems sizes and folding patterns, demonstrating the robustness and accuracy of our method.
| PDB code | N | Secondary structure | REmin | ROSETTA | I-TASSER |
|---|---|---|---|---|---|
| a Ref. 25.b Website: http://zhanglab.ccmb.med.umich.edu/decoys/decoy3.html.c Website: http://predictioncenter.org/casp10/index.cgi. | |||||
| 1shfAa | 59 | β | 2.1 (0.71) | 10.8 | 1.7 (0.75) |
| 1r69_a | 61 | α | 1.9 (0.71) | 1.2 | 1.9 (0.75) |
| 1csp_a | 67 | β | 5.3 (0.61) | 4.7 | 2.1 (0.76) |
| 1di2A_a | 69 | αβ | 1.6 (0.81) | 2.6 | 2.3 (0.78) |
| 1n0uA4a | 69 | αβ | 5.1 (0.42) | 10.2 | 4.4 (0.48) |
| 1mla_2a | 70 | αβ | 3.8 (0.59) | 8.7 | 2.8 (0.66) |
| 1ogwA_a | 72 | αβ | 1.5 (0.82) | 1.0 | 1.1 (0.88) |
| 1dcjA_a | 73 | αβ | 8.9 (0.37) | 2.5 | 10.5 (0.39) |
| 1dtjA_a | 74 | αβ | 4.8 (0.61) | 1.2 | 1.9 (0.80) |
| 1mkyA3a | 81 | αβ | 5.1 (0.51) | 6.3 | 5.2 (0.40) |
| 1tfi_a | 47 | β | 5.0 (0.46) | — | 4.6 (0.56) |
| 1ah9a | 63 | β | 4.1 (0.45) | — | 4.3 (0.56) |
| 2f3nAa | 65 | α | 1.7 (0.75) | — | 1.8 (0.74) |
| 1kviAa | 68 | αβ | 3.1 (0.56) | — | 2.0 (0.72) |
| 1itpAa | 68 | αβ | 4.5 (0.44) | — | 10.9 (0.33) |
| 1o2fB_a | 77 | αβ | 2.0 (0.76) | — | 7.1 (0.41) |
| 1sro_a | 71 | β | 6.3 (0.33) | — | 3.4 (0.66) |
| 1of9Aa | 77 | α | 4.1 (0.47) | — | 3.6 (0.53) |
| 1gixAa | 77 | β | 5.2 (0.56) | — | 6.9 (0.44) |
| 1ten_a | 87 | β | 2.7 (0.69) | — | 1.6 (0.85) |
| 1npsAa | 88 | αβ | 3.6 (0.63) | — | 2.1 (0.79) |
| 1no5Aa | 93 | αβ | 9.0 (0.35) | — | 10.6 (0.43) |
| 1thx_a | 108 | αβ | 5.9 (0.56) | — | 2.1 (0.83) |
| 1jnuAa | 104 | αβ | 5.1 (0.54) | — | 2.7 (0.75) |
| 1orgAa | 118 | α | 5.2 (0.53) | — | 2.4 (0.78) |
| 2czsAb | 70 | α | 10.9 (0.24) | — | — |
| 1i27Ab | 73 | αβ | 8.2 (0.43) | — | — |
| 1w53Ab | 84 | α | 11.0 (0.40) | — | — |
| 2ip6Ab | 87 | α | 11.5 (0.33) | — | — |
| T0716-D1c | 51 | α | 2.1 (0.73) | — | — |
| T0662-D1c | 79 | α | 2.9 (0.69) | — | — |
| T0726-D2c | 81 | αβ | 4.3 (0.57) | — | — |
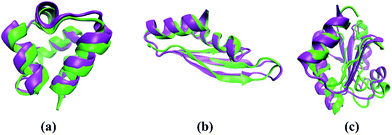
The accuracy of our method is demonstrated through comparison with the all-atomic ROSETTA53 and I-TASSER25 methods. Here we take three typical proteins, including α protein (1r69_) and αβ protein (1di2A_ and 1thx_) as examples. The protein 1r69_ has a topology of four α-helices with 61 amino acid residues. The Cα-RMSD of the lowest energy model predicted by our method is 1.9 Å, which is comparable to the values determined by the ROSETTA (1.2 Å) and I-TASSER (1.9 Å) method. The superposition of the lowest model predicted by our method onto the corresponding native structure is shown in Fig. 5a. A subtle difference observed between the two models demonstrates the accuracy of our method. Furthermore, protein 1di2A_ contains three stands and two helices. The superposition of the lowest-energy model predicted by our method onto the corresponding native structure is shown in the Fig. 5b. The difference between the two models is negligible. Particularly, the model predicted by our method has the Cα-RMSD of 1.6 Å, which is superior to that obtained by the ROSETTA (2.6 Å) and I-TASSER (2.3 Å). We also test a complex protein 1thx_ with more than 100 amino acid residues. The Cα-RMSD of the lowest energy model predicted by our method is 5.9 Å. A native-like structure of target 1thx_ is successfully generated and the difference between the predicted structure and native structure is the relative position of the secondary structures (Fig. 5c). Although the model is not good as that obtained with the I-TASSER method (2.1 Å), the model has approximately correct topology and is still useful for biological application.50 Therefore, the present method is comparable or superior to previously described protein structure search method and can be used to efficiently predict protein structures.
It is well-known that the conformational phase space of sampling sharply increases with protein sizes increasing, which makes the ab initio modeling of proteins with large sizes extremely difficult. Our calculations indicate the accuracy of the models obtained by our method decreases with increasing protein sizes. Just as illustrated in Table 1, the Cα-RMSD of proteins with length > 100 residues (1thx_, 1jnuA and 1orgA) predicted by our method are more than 5 Å. It is obvious that only the coarse models can be obtained by our method for the proteins, whose lengths are more than 100 residues.
To explore the reasons for the success of our developed method, we perform the structure prediction of two typical proteins of 1shfA and 1n0uA4. The 1shfA is a typical β protein, containing 59 amino acid residues. The Cα-RMSD of the lowest-energy model predicted by our method is 2.1 Å, which is superior to that obtained by ROSETTA method (10.8 Å). In-depth study shows that a high-resolution initial model with the Cα-RMSD of 2.5 Å is obtained from the known protein structure databases plays a critical role in successfully predicting the native-like protein. It demonstrates the process of determining the template is very effective for our protein structure prediction. To illustrate the effectiveness of ab initio structure evolution method, we take the protein 1n0uA4 as an example. Protein 1n0uA4 has the length of 69 amino acid residues with four stands and two helices. The initial model is constructed by selected potential template with the Cα-RMSD of 6.8 Å. The lowest-energy model is predicted at 833th generation with the Cα-RMSD of 5.1 Å, which is superior to the initial model. The superposition of the native and the lowest-energy structures showed in the Fig. 6a indicates that a native-like structure of target 1n0uA4 is successfully generated. These results indicate that the structure evolution algorithm adopted in our method can effectively improve the modelling accuracy.
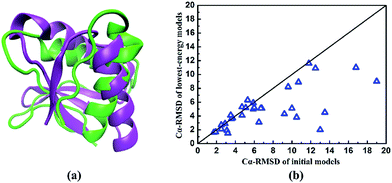 | ||
| Fig. 6 (a) The superposition of the native and the lowest-energy structures of protein 1n0uA4. The purple represents the native structure and the green represents the predicted lowest-energy model. (b) The comparison of Cα-RMSD between initial models and predicted lowest-energy models of the studied proteins listed in Table 1. | ||
In order to further evaluate the performance of our method, we compare the Cα-RMSD of the initial models with the lowest-energy models for all proteins in Table 1. Just as shown in Fig. 6b, it can be clearly seen that most Cα-RMSDs of predicted models are reduced. In other words, the predicted protein conformations become closer to the native proteins than initial ones. These results further demonstrate that our structure evolution algorithm has a powerful ability to improve the modelling accuracy.
IV. Conclusions
In the manuscript, we propose a protein structure prediction method by combining the templated-based method and ab initio search. Several information including ideal bond lengths and angles, secondary structure constraints and fragment library obtained by known protein database are implemented to substantially reduce the search space. Furthermore, the designed structure operations including an improved PSO algorithm, random perturbation, fragment substitution and their combinations are developed to perform structure evolution. Our method has been implemented in the CALYPSO software package and benchmarked by several known proteins with distinct folding patterns. The native-like structures of these proteins are successfully predicted. The high success rate and accuracy demonstrate the reliability and robustness of this method, which holds promise for narrowing the sequence-structure gap.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the funding support from the National Natural Science Foundation of China under Grant No. 11274136, 11404128, and 11534003, the National Key Research and Development Program of China under Grants No. 2016YFB0201200, the 2012 Changjiang Scholar of the Ministry of Education, the National Key Laboratory of Shock Wave and Detonation Physics and the China Postdoctoral Science Foundations (No. 2015T80294 and No. 2014M551181). Parts of the calculations are performed in the high performance computing center of Jilin University and at Tianhe2-JK in the Beijing Computational Science Research Center.References
- H. Rangwala and G. Karypis, Introduction to protein structure prediction: methods and algorithms, John Wiley & Sons, Inc, Hoboken, New Jersey, 2010 Search PubMed.
- The UniProt Consortium, Nucleic Acids Res., 2007, 36, D190–D195 CrossRef PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- N. Guex and M. C. Peitsch, Electrophoresis, 1997, 18, 2714–2723 CrossRef CAS PubMed.
- Y. Xu and D. Xu, Proteins: Struct., Funct., Genet., 2000, 40, 343–354 CrossRef CAS.
- J. Skolnick, D. Kihara and Y. Zhang, Proteins: Struct., Funct., Genet., 2004, 56, 502–518 CrossRef CAS PubMed.
- A. Liwo, M. Khalili and H. A. Scheraga, Proc. Natl. Acad. Sci., 2005, 202, 2362–2367 CrossRef PubMed.
- J. L. Klepeis, Y. Wei, M. H. Hecht and C. A. Floudas, Proteins: Struct., Funct., Genet., 2005, 58, 560–570 CrossRef CAS PubMed.
- J. Klepeis and C. Floudas, Biophys. J., 2003, 85, 2119–2146 CrossRef CAS PubMed.
- C. B. Anfinsen, Science, 1973, 181, 223–230 CAS.
- R. Das, B. Qian, S. Raman, R. Vernon, J. Thompson, P. Bradley, S. Khare, M. D. Tyka, D. Bhat, D. Chivian, D. E. Kim, W. H. Sheffler, L. Malmström, A. M. Wollacott, C. Wang, I. Andre and D. Baker, in Proteins: Structure, Function and Genetics, 2007, vol. 69, pp. 118–128 Search PubMed.
- Y. Zhang and J. Skolnick, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7594–7599 CrossRef CAS PubMed.
- H. Zhou and J. Skolnick, Biophys. J., 2007, 93, 1510–1518 CrossRef CAS PubMed.
- Y. Zhang, Proteins, 2007, 69, 108–117 CrossRef CAS PubMed.
- A. Liwo, J. Lee, D. R. Ripoll, J. Pillardy and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 5482–5485 CrossRef CAS.
- F. L. Custódio, H. J. C. Barbosa and L. E. Dardenne, Appl. Soft Comput. J., 2014, 15, 88–99 CrossRef.
- A. Verma, A. Schug, K. H. Lee and W. Wenzel, J. Chem. Phys., 2006, 124, 044515 CrossRef CAS PubMed.
- S. Roy, S. Goedecker, M. J. Field and E. Penev, J. Phys. Chem. B, 2009, 113, 7315–7321 Search PubMed.
- D. Xu and Y. Zhang, Proteins: Struct., Funct., Bioinf., 2012, 80, 1715–1735 CrossRef CAS PubMed.
- D. Xu and Y. Zhang, Proteins: Struct., Funct., Bioinf., 2013, 81, 229–239 CrossRef CAS PubMed.
- I. Kalev and M. Habeck, Bioinformatics, 2011, 27, 3110–3116 CrossRef CAS PubMed.
- D. T. Jones, Proteins: Struct., Funct., Genet., 2001, 45, 127–132 CrossRef PubMed.
- D. T. Jones, J. Mol. Biol., 1999, 292, 195–202 CrossRef CAS PubMed.
- S. F. Altschul, T. L. Madden, A. A. Schäffer, J. Zhang, Z. Zhang, W. Miller and D. J. Lipman, Nucleic Acids Res., 1997, 25, 3389–3402 CrossRef CAS PubMed.
- S. Wu, J. Skolnick and Y. Zhang, BMC Biol., 2007, 5, 17 CrossRef PubMed.
- C. A. Rohl, C. E. M. Strauss, K. M. S. Misura and D. Baker, Methods Enzymol., 2004, 383, 66–93 CAS.
- M. J. Zaki, C. Bystroff and J. Mohammed, Protein structure prediction, Humana Press, New York, USA, 2008 Search PubMed.
- M. J. Bower, F. E. Cohen and R. L. Dunbrack, J. Mol. Biol., 1997, 267, 1268–1282 CrossRef CAS PubMed.
- A. Kukol, Molecular Modeling of Proteins, Humana Press, Hatfield, Hertfordshire, UK, 2015, vol. 1215 Search PubMed.
- S. J. Weiner, P. A. Kollman, D. A. Case, U. C. Singh, C. Ghio, G. Alagona, S. Profeta and P. Weinerl, J. Am. Chem. Soc., 1984, 106, 765–784 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- Y. Duan and P. A. Kollman, Science, 1998, 282, 740–744 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- E. Neria, S. Fischer and M. Karplus, J. Chem. Phys., 1996, 105, 1902–1921 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- L. D. Schuler, X. Daura and W. F. Van Gunsteren, J. Comput. Chem., 2001, 22, 1205–1218 CrossRef CAS.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- G. a. Kaminski, R. a. Friesner, J. Tirado-rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- W. C. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129 CrossRef CAS.
- D. Qiu, P. S. Shenkin, F. P. Hollinger and W. C. Still, J. Phys. Chem. A, 1997, 101, 3005–3014 CrossRef CAS.
- J. Zhang and Y. Zhang, PLoS One, 2010, 5, e15386 Search PubMed.
- C. Steffen, K. Thomas, U. Huniar, A. Hellweg, O. Rubner and A. Schroer, J. Comput. Chem., 2010, 31, 2967–2970 CAS.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–8 Search PubMed.
- Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- S. Lu, Y. Wang, H. Liu, M.-S. Miao and Y. Ma, Nat. Commun., 2014, 5, 3666 CAS.
- B. Gao, X. Shao, J. Lv, Y. Wang and Y. Ma, J. Phys. Chem. C, 2015, 119, 20111–20118 CAS.
- A. Carlisle and G. Dozier, Proceeding Work. Part. Swarm Optim., 2001, vol. 1, pp. 1–6 Search PubMed.
- Y. Zhang, Curr. Opin. Struct. Biol., 2009, 19, 145–155 CrossRef CAS PubMed.
- Y. Zhang and J. Skolnick, Proteins: Struct., Funct., Genet., 2004, 57, 702–710 CrossRef CAS PubMed.
- J. Xu and Y. Zhang, Bioinformatics, 2010, 26, 889–895 CrossRef CAS PubMed.
- P. Bradley, Science, 2005, 309, 1868–1871 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |