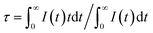Cation–anion substitution induced spectral tuning and thermal stability optimization in Sr₂SiO₄:Eu phosphors

Abstract

Spectral tuning and thermal stability are important for the optimization and modification of phosphor materials. Herein we report a solid solution of Sr₂Si_1−xAl_xO_4−2xN_x:Eu phosphors in which cation–anion substitution (Al³⁺–N³⁻ replacing Si⁴⁺–O²⁻) leads to the co-existence of Eu²⁺ and Eu³⁺ activators even under a reducing atmosphere. X-ray diffraction, FT-IR, photoluminescence analysis, UV-vis absorption and fluorescence lifetime studies indicated that the structure reconstruction contributes to tunable emission colors and better thermal quenching behavior, which are valuable for pc-WLED applications.

---

1 Introduction

Due to its high energy efficiency, long lifetime, short response time, huge energy savings and environmental friendliness, nowadays phosphor-converted white light-emitting diodes (pc-WLEDs) have gained a broad consensus to act as the next-generation solid state lighting (SSL) source after incandescent and fluorescent lamps. This profound achievement benefits from continual research of technologies and materials related to LEDs, which show great prospects in visual signals, common lighting, communication, sensors, light matter interactions and so on.^1–3 At present, a typical pc-WLED is assembled through a blue InGaN LED chip and a yellow cerium(III)-doped yttrium aluminium garnet (YAG:Ce³⁺) phosphor. However, with long-wavelength spectral emission lacked, this solution to generate white light suffers from a high correlated color temperature (CCT > 4000 K) and a poor color rendering index (CRI < 80). To improve the CRI and tune the CCT value, LED chips (blue-emitting or n-UV) coated with red-, yellow-/green- and blue-emitting multi-phased phosphors have attracted considerable attentions. But this multi-phased phosphors method frequently results in increasing manufacture cost, and strong reabsorption owing to spectral mismatch.^4,5 Plainly, the phosphors play a key role in producing high-quality white lighting. Therefore, in addition to luminescence efficiency and chemical/thermal stability, spectral tuning and matching must be considered for light-conversion luminescent materials in WLEDs.

Given the unavoidably spectral mismatching problem of multi-phased phosphor solution, the realization of multi-color luminescence in a single phase offers a promising possibility to generate white light with superior CRI and lower CCT, which also reconcile spectra adjustment and energy loss simultaneously. The most common and easiest way for multi-color emitting is the combination of several luminescence centers in one host, like Eu²⁺/Mn²⁺ codoping phosphors.^6,7 However, this multi-color luminescence depends on the energy transfer from sensitizer to activator in the co-doping system, implying the relatively low luminescence efficiency.

Recently, the focus on the tunable luminescence of phosphors has become a research hotspot, especially based on the modification of local crystal structure including doping level control, cation substitution, anion substitution and cation–anion substitution etc.^8–10 For instance, Sato et al. realized the tailoring of deep-red luminescence in Ca₂SiO₄:Eu²⁺ on the basis of the Eu²⁺ ions tending to occupy another cation site (corresponding to long-wavelength emitting) with the increasing doping level.¹¹ Xia described the strategy of “chemical unit cosubstitution” to tune luminescent properties in Ca₂(Al_1−xMg_x)(Al_1−xSi_1+x)O₇:Eu²⁺ and Lu₃(Al,Mg)₂(Al,Si)₃O₁₂:Ce³⁺ with the substitution of Al³⁺–Al³⁺ couple by Mg²⁺–Si⁴⁺ pair.^12,13 Generally, all these variations in host composition usually alter the symmetry, coordination environment, crystal field strength, covalence, and the energy transfer, thus influencing luminescence properties. In particular, the approach of cation–anion substitution can result in tunable valences of the activators in some special cases, for example, Huang et al. reported a tuneable valence of Eu in Ca₁₂Al₁₄O₃₂F₂ by controlling the activator sites through the replacement of Si–O by Al–F.¹⁴ Xia et al. also achieved coexistence of Eu²⁺ and Eu³⁺ ions in the Ca_2+xLa_8−x(SiO₄)_6−x(PO₄)_xO₂ host lattice via the preferential site occupancy and charge balance of cation co-substitution.¹⁵ This creative discovery, obtaining the emissions of Eu²⁺ and Eu³⁺ ions in a single phase simultaneously, performs great benefits in pc-WLEDs due to their abundant emission colors of 5d–4f or 4f–4f transitions. Though the cation–anion substitution method gets the natural advantage to obtain white light emitting in pc-WLEDs with superior CRI and lower CCT, published literatures and alternative hosts are relative few until now. On the other hand, this approach commonly needs a high level of doping or substitution, which easily sacrifices the emission intensity and thermal stability of phosphor.^9,14,16

(Ca,Sr,Ba)₂SiO₄:Eu²⁺ is a widely used class of phosphor with interesting thermal quenching behavior. These compounds exhibit efficient excitation under near-UV and blue light, with emissions ranging from green for Ba₂SiO₄:Eu²⁺ to yellow for Sr₂SiO₄:Eu²⁺.^17–19 The cation substitution (e.g., (Ca/Sr/Ba)₂SiO₄:Eu²⁺) and anion substitution (e.g., α′-Sr₂Si_3x/4O₂N_x:Eu²⁺, Sr₂SiN_zO_4−1.5z:Eu²⁺ and Sr₂Si(O_1−xN_x)₄:Eu²⁺) performed to optimize the emission peak and thermal stability.^20–23 However, no report about the effects of cation–anion cosubstitution on the luminescence property in Sr₂SiO₄:Eu²⁺ has been previously noted in the literature. In this study, the cation–anion cosubstitution of Si⁴⁺–O²⁺ by Al³⁺–N³⁻ in Sr₂SiO₄:Eu²⁺ was investigated in detail, including the variation of structure and luminescence property. The disordered solid-solution Sr₂Si_1−xAl_xO_4−2xN_x:Eu resulted in the mixed Eu valences, continuous spectral tuning and thermal stability optimization, which are valuable for high-quality pc-WLEDs applications.

2 Experimental section

2.1 Materials and synthesis

Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu phosphors were prepared from appropriate stoichiometric mixture of SrCO₃ (A. R.), SiO₂ (A. R.), AlN (A. R.), and Eu₂O₃ (A. R.) by traditional high temperature solid-state reaction method. All raw materials were purchased commercially without further treatment. In a typical process, the starting materials were weighted and mixed thoroughly in an agate mortar according to different values of x. Then the powder mixtures were annealed at 1250 °C for 4 h in a corundum crucible under the reducing atmosphere (N₂/H₂ = 95 : 5%). The as-prepared samples were cooled to room temperature naturally, and after discarding the top layer of the nongrinded products, the interior of uniform samples was ground into powder for next characterization. For comparison, sample Sr_1.98SiO₄:0.02Eu³⁺, synthesized in air was also obtained under same sintered procedure.

2.2 Characterization

Crystal structure of the samples was analyzed by X-ray powder diffractometer (SHIMADZU, XRD-6000, Cu Kα radiation, λ = 0.15406 Å). The data were collected in a 2θ range from 20° to 80° with a scanning step of 0.02° and a scanning rate of 4° min⁻¹. Room-temperature photoluminescence and photoluminescence excitation (PLE) spectra were measured with a Hitachi F-7000 (Tokyo, Japan) spectrophotometer equipped with a 150 W xenon arc lamp. The digital pictures of the samples are photographed using a digital camera (Canon EOS 40D, Tokyo, Japan). Temperature-dependent (300–460 K) photoluminescence spectra were conducted using a heating apparatus (OXFORD instrument, Oxon, UK) in combination with the above Hitachi 7000 spectrophotometer. Decay curves were measured using a FSP920 Time Resolved and Steady State Fluorescence Spectrometers (Edinburgh Instruments) equipped with a 450 W Xe lamp, a 150 W nF900 flash lamp, TM300 excitation monochromator and double TM300 emission monochromators and thermo-electric cooled red-sensitive PMT. Fourier-transform infrared (FT-IR) spectra were measured on a BRUKER TENSOR 27 spectrophotometer in the range of 400–4000 cm⁻¹ using the KBr pellet (∼2 wt%) method. UV-vis spectra were measured on a Shimadzu UV-2550 spectrophotometer.

3 Results and discussion

The phase purities of the Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.1) compounds were confirmed using X-ray powder diffraction (XRD), as shown in Fig. 1. Sr₂SiO₄ has two crystallographic phases: the high temperature α′-Sr₂SiO₄ (orthorhombic, Pmab) phase and the low temperature β-Sr₂SiO₄ (monoclinic, P2₁/c) phase. The low temperature (∼358 K) of α′ ↔ β phase transition results in frequently co-existence of the two phases through a short-range rearrangement of the coordination structure without breaking any bonds.^24,25 When sintered at 1250 °C, it shows that all the diffraction peaks matched well with the α′-Sr₂SiO₄ phase, except for small amounts impurity of β-Sr₂SiO₄ phase (marked as β symbol) peaking at 27.6° and 32.3° (2θ) with x values of 0 and 0.01. These suggest that the introduction of europium and AlN cannot affect the main crystal structure through partial replacement. After the incorporation of AlN into Sr₂SiO₄ host, the diffraction peaks also show small shifts toward larger 2θ value, indicating the formation of solid solutions. When x value exceeds 0.1, unknown phases were detected and the crystallinity degree of the obtained production was lower, as signposted in Fig. S1 in ESI.† The FT-IR spectra of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0 and 0.1) phosphors also support the successful incorporation of AlN into host compounds, in which the peak of Sr/Eu–N bond vibration appears in sample of x = 0.1, while the sample with x = 0 does not show such peak (see Fig. S2 in ESI†).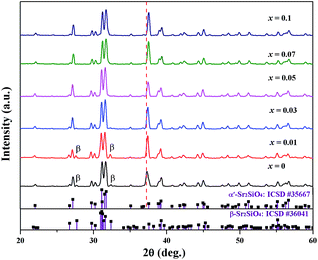

Fig. 1 XRD patterns of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.1), together with the standard data for α′/β-Sr₂SiO₄ (ICSD #35667 and ICSD #36041) as reference.

Both in α′-Sr₂SiO₄ and β-Sr₂SiO₄, Sr²⁺ ion occupies two kind of inequivalent sites: the ten-coordinated Sr(1) and the nine-coordinated Sr(2) sites, while Sr(1) and Sr(2) occur in the same amount. Given the change of O atom position and occupation, the α′-Sr₂SiO₄ phase further exist disordered (isotropic) and ordered (anisotropic) structure models.²¹ In the disordered α′-Sr₂SiO₄, each atom lying on the mirror plane was split into two, in very close positions equivalent by symmetry; and four kind of oxygen atoms can be observed, as shown in Fig. 2. After careful analysis the cases Sr₂SiN_zO_4−1.5z:Eu²⁺ and Sr₂Si(O_1−xN_x)₄:Eu²⁺, it is not hard to find that the obtained Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.1) phosphors also possess the disordered α′-Sr₂SiO₄ phase in consideration of the inhomogeneous substitutions (Al³⁺–N³⁻ → Si⁴⁺–O²⁻), resulting in local coordination environment changes.

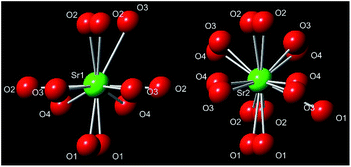Fig. 2 Coordination spheres of the two different Sr²⁺ sites in the disordered α′-Sr₂Si_1−xAl_xO_4−2xN_x.

Fig. 3 gives the excitation and emission spectra of samples Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.07 and 0.1). As seen in Fig. 3a, the emission spectrum of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0), namely, Sr_1.98SiO₄:0.02Eu²⁺, reveals two obviously broad emission bands under 320 nm excitation. Due to the similar ion radii of Sr²⁺ (1.31 Å, 9CN; 1.36 Å, 10CN) and Eu²⁺ (1.30 Å, 9CN; 1.35 Å, 10CN), the doped Eu²⁺ ions will occupy the Sr²⁺ sites in Sr₂SiO₄ host lattice.²⁶ Eu(1) and Eu(2) emissions, originating from the Eu²⁺ ions incorporation at Sr(1) and Sr(2) sites respectively, are seriously affected by local crystal field. Accordingly, the broad emission bands can be fitted to two subbands centered at 490 nm and 550 nm by using Gaussian functions, related to the parity allowed 4f⁶5d → 4f⁷ transitions of Eu²⁺ ions. The higher-energy emission peak (490 nm) corresponds to the Eu(1) emission owning to its loose environment (10-coordination), while the lower-energy emission peak (550 nm) originates form Eu(2) emission for the tighter environment (9-coordination).²⁷ On the other hand, the excitation spectrum (λ_em = 550 nm) of Sr_1.98SiO₄:0.02Eu²⁺ shows a broad band ranging from 250 nm to 450 nm, which is attributable to the 4f⁶5d multiplets of Eu²⁺ excited states. However, the excitation spectrum (λ_em = 490 nm) exhibits a narrower excitation band centered at 320 nm.

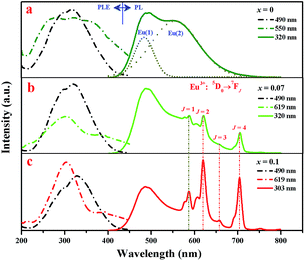Fig. 3 Room-temperature PLE and PL spectra of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.07 and 0.1) phosphors.

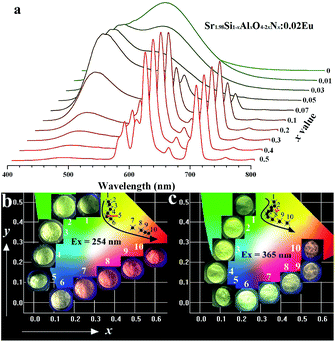
The introduction of AlN into Sr₂SiO₄:Eu was supposed to replace Si⁴⁺–O²⁻, resulting in Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu phosphors under the reducing atmosphere. Note that sharp red emission appeared as the doping amount of cation–anion substitution exceeds 0.07 (see in Fig. 3b and c). Furthermore, with doping content level of AlN increases, the sharp red emission intensity increases while the luminescence (∼490 nm) originating from Eu²⁺ decreases to intuitively disappearing at x = 0.5, as shown in Fig. 4a. Given the well-known characteristic 4f–4f electron transitions of Eu³⁺, we concluded these sharp emissions comes from Eu³⁺ emission, which means that two activators of Eu³⁺ and Eu²⁺ co-exists in Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu phosphors (0.07 ≤ x < 0.5). To confirm this, sample Sr_1.98SiO₄:0.02Eu³⁺ was synthesized in air, and its PL and PLE spectra were given in Fig. S3 in ESI.† The strongest line emission peak at 614 nm (⁵D₀ → ⁷F₂) and other characteristic peaks are consistent with the sharp red emissions in Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu. However, obvious difference occurs between the charge transfer bands (CTB) of O²⁻ → Eu: the CTBs of Sr_1.98SiO₄:0.02Eu³⁺ and Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu phosphors locate at 254 nm and 303 nm respectively, indicating the different band transitions and successful reconstruction through cation–anion substitution in host lattices. Besides, Fig. S4† shows the UV-vis absorption spectra of Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0 and 0.1) phosphors. A strong absorption band in the range 200–320 nm of sample x = 0.1 was mainly ascribed to the intra configurational 4f–4f transition from the ground 4F₀ level of Eu³⁺, while the broad band in the range 250–500 nm of sample x = 0 are contributed to the 5d–4f transitions of Eu²⁺, which corresponds to corresponding excitation spectra. These results are in good agreement with those reported in the literature.²⁸ Fig. 4b further lists the photographs and Commission International de I'Eclairage (CIE) coordinates of all samples (x = 0–0.5). As shown, the luminescence colors can be tuned from green to red, corresponding CIE coordinates of these samples are regularly shifted from (0.38, 0.465) to (0.569, 0.346), (0.368, 0.498) to (0.432, 0.396) under 254 nm and 365 nm excitation respectively.

Fig. 4 (a) PL spectra (λ_ex = 320 nm) of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.5). (b & c) Dependence of CIE chromaticity coordinates and digital photos on various x values upon 254 and 365 nm excitation, respectively. The numbers 1–10 corresponds to the x values from 0 to 0.5.

Fig. 5 depicts the normalized lifetime decay curves for samples Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0 and 0.1) by monitoring at 619 nm and 490 nm under 320 nm excitation. It turns out that the decay curve (x = 0, λ_em = 619 nm; x = 0.1, λ_em = 490 nm) can be well fitted by a second order exponential equation:

I(t) = I₀ + A₁ exp(−t/τ₁) + A₂ exp(−t/τ₂)

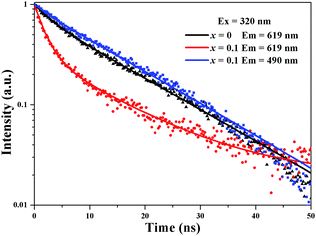Fig. 5 Decay curves of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0 and 0.1), the solid line was obtained by fitting.

While the decay curve (x = 0.1, λ_em = 619 nm) can be well fitted by the nonexponential equation:^29,30

where I(t) represents the luminescent intensity at time t, A₁ and A₂ are constants while τ₁ and τ₂ are the decay times for the exponential components. These results further confirm the structure reconstruction and the coexistence of Eu²⁺ and Eu³⁺ activators after AlN incorporation. With the combination of crystal sites and the characteristic emissions of Eu²⁺ and Eu³⁺ ions, the double exponential components τ₁ and τ₂ corresponds to the lifetime of two Eu(1)²⁺ and Eu(2)²⁺ emissions, and the lifetime τ (x = 0.1, λ_em = 619 nm) reflects the comprehensive results of Eu³⁺ and Eu²⁺ emissions. The average lifetimes for above decay curves were calculated to be 13.40 ns, 10.21 ns and 13.66 ns, respectively.

From the point view of applied physics, multiple factors, such as coordination environment, crystal site size and band gap of the compound, are the reasons for valance stability of lanthanide. Partial substitution commonly results in the variations of local crystal structure. Based on the ions radius: r(Si⁴⁺) = 0.26 Å (4CN), r(Al³⁺) = 0.39 Å (4CN), r(N³⁻) = 1.46 Å (4CN) and r(O²⁻) = 1.38 Å (4CN),²⁶ the cation–anion substitution of Si⁴⁺–O²⁻ by Al³⁺–O³⁻ leads to the expansion of (Si/Al)(O/N)₄ tetrahedron, which will shrink the position of Sr²⁺ sites. Fig. S4† shows the excitation spectra (λ_em = 490 nm) of samples Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.2). The strongest excitation band trends to redshift from 318 nm to 350 nm with increasing x value, which results from the suppress of Eu²⁺ vibration after cation–anion substitution. In the cases of Ca₁₂Al_14−zSi_zO₃₂F_2−z:Eu, and Ca_1+xY_1−xAl_1−xSi_xO₄:Eu, the occupation sites of Eu³⁺ in CaO₆F and CaO₉ get to expand after corresponding substitutions, which could favor the reduction Eu³⁺ to Eu²⁺.^14,31 On the contrary, the shrinkage of (Sr/Eu)O₉ in Sr₂Si_1−xAl_xO_4−2xN_x:Eu gets the ability to fix the activators as trivalent valence.³² Therefore, here the cation–anion substitution contributes to the emerge of Eu³⁺ in Sr₂Si_1−xAl_xO_4−2xN_x:Eu even under the reducing atmosphere.

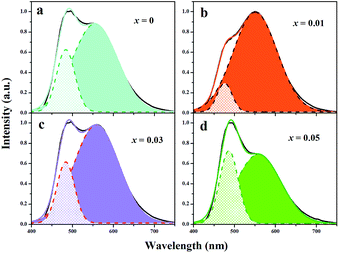
It is vulnerable to overlook the fact that the activator Eu³⁺ emerges at Sr(2) site initially, not just because the peak position of Eu³⁺ emission locates at the longer-wavelength side. Careful analysis was conducted below. As mentioned before, there are no obvious sharp emissions of Eu³⁺ activator in the emission spectra of samples 0 ≤ x ≤ 0.05 (see Fig. 4a). Specifically, the emission intensity of Eu²⁺ at Sr(2) site decreases with the doping content of AlN increases, but the emission intensity of Eu²⁺ at Sr(1) site increases in the range of 0 ≤ x ≤ 0.07. On the other hand, the Eu³⁺ ions have smaller ion radius than that of Eu²⁺ ions, indicating that Eu³⁺ prefer to occupy at the compact site. Fig. 6 further represents the emission spectra fitted with two Gaussian functions of samples Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.01, 0.03 and 0.05), which shows the contribution of Eu(1) and Eu(2) emissions in two distinct crystallographic sites to the total emission spectra. The proportion of Eu(1) emission to total emission varies from 25.2%, 12.2%, 11.2% to 16.2% with x values of 0, 0.01, 0.03 and 0.05, respectively, which that of Eu(2) emissions are 79.2%, 91.4%, 40.9% and 35.6%. The results show that the integrated area of Eu(2) emission to total emission increase when x value rises from 0 to 0.01. This may contribute to the energy transfer between Eu²⁺ ions at Sr sites because the large band overlap of excitation spectrum of Eu²⁺ in Sr(2) site and emission spectrum of Eu²⁺ in Sr(1) site. When x value exceeds 0.03, the proportion of Eu(1) emission increases due to part of Eu activators at Sr(2) site fixing as Eu³⁺ ions with the amount of cation–anion substitution increases.

Fig. 6 Emission spectra fit to two Gaussian functions show the contribution to the emission spectra from Eu²⁺ in two distinct crystallographic sites. Dashed lines represent the individual Gaussian functions and the solid line represents the total fit.

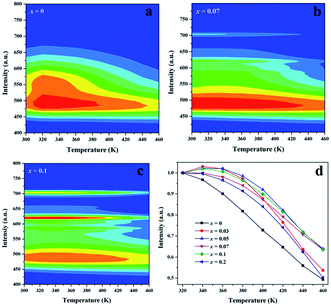
For applications in high power LEDs, the thermal stability of phosphors must be taken into consideration due to high operating temperature. Fig. 7 gives the temperature-dependent emission spectra of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.07 and 0.1), plotted in a two-dimensional wavelength-temperature contour map. For all emissions at different temperatures (300–460 K), the 5d–4f transitions of Eu²⁺ at Sr(1) site (x = 0, 0.07 and 0.1) show the same peak positions at 490 nm, while the emission of Eu²⁺ in Sr(2) site (x = 0) exhibit strong temperature quenching. Of course, the contour map also shows obvious emission of Eu³⁺ ions. With respect to the integrated PL intensity at different temperature, detail information was represented in Fig. 7d. As seen, the PL intensity shows a constant decreasing with the temperature increasing from 300 K to 460 K due to the nonradiative energy transfer. The decreasing integrated PL intensity can be well fitted by Arrhenius equation³³

I(T) = I₀/(1 + C exp(−E_A/kT))

where I₀ and I(T) are the intensity at temperature T, respectively. k is the Boltzmann constant while C is a rate constant for the thermally activated escape. E_A is the activation energy for the thermal quenching process. Thus, the corresponding E_A of Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.03, 0.05, 0.07, 0.1 and 0.2) are calculated to be 0.25 eV, 0.46 eV, 0.43 eV, 0.35 eV, 0.40 eV and 0.42 eV, respectively. Compared to sample Sr_1.98SiO₄:0.02Eu²⁺ (x = 0), the thermal quenching optimization was attributed to two factors, partly for the incorporation of nitrogen into the host and partly because the emission of Eu(2) possessing poor thermal stability tends to disappear with cation–anion substitution.

Fig. 7 (a–c) Temperature-dependent (300–460 K) PL spectra contour plots for Sr_1.98Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0, 0.07 and 0.1) excited at 320 nm; (d) dependence of integrated PL intensities on measured temperature for samples Sr₂Si_1−xAl_xO_4−2xN_x:0.02Eu (x = 0–0.2).

4 Conclusions

The Sr₂Si_1−xAl_xO_4−2xN_x:Eu (0 ≤ x ≤ 0.5) phosphors were prepared by a conventional solid state reaction method. The XRD analysis results indicated that cation–anion substitution of Si⁴⁺–O²⁻ by Al³⁺–N³⁻ incorporated into α′-Sr₂SiO₄ successfully and form substitutional solid solution. The replacement could achieve the co-existence of Eu²⁺ and Eu³⁺ activators. While the Eu³⁺ ions preferred to occupy at the Sr(2) site and its characteristic emissions emerged around a doping content level of 0.07. The Sr₂Si_1−xAl_xO_4−2xN_x:Eu phosphor exhibited broad excitation bands and both green emission (∼490 nm and ∼550 nm) and red emission (∼619 nm), corresponding luminescence colors can be tuned from green to red with CIE coordinates shifting from (0.38, 0.465) to (0.569, 0.346), (0.368, 0.498) to (0.432, 0.396) under 254 nm and 365 nm excitation respectively. Furthermore, the cation–anion substitution could improve the thermal stability of the Sr₂SiO₄:Eu²⁺ phosphor. Based on the adjustable emission properties from green to red and the optimized thermal stability, Sr₂Si_1−xAl_xO_4−2xN_x:Eu phosphor could be a good candidate for use in white light emitting diodes.

Acknowledgements

The present work was supported by the National Natural Science Foundations of China (Grant No. 21371062, 21671070), the Teamwork Projects funded by the Guangdong Natural Science Foundation (Grant No. S2013030012842), the Project for Construction of High-level University in Guangdong Province, the Provincial Science and Technology Project of Guangdong Province (No. 2016A050502043, 2015B090903074), the Guangzhou Science & Technology Project (No. 201605120833193) funded for Bingfu LEI, the Spectral Funds for the Cultivation of Guangdong College Student Scientific and Technological Innovation (“Climbing Program” Special Funds), and the Student Innovative Project (Grant No. 201610564354).

Notes and references

1. H. A. Höppe, Angew. Chem., Int. Ed., 2009, 48, 3572–3582.
2. H. K. Park, J. H. Oh, H. Kang, J. Zhang and Y. R. Do, ACS Appl. Mater. Interfaces, 2015, 7, 4549–4559.
3. S. P. Liu, J. A. Mares, X. Q. Feng, A. Vedda, M. Fasoli, Y. Shi, H. M. Kou, A. Beitlerova, L. X. Wu, C. D. Ambrosio, Y. B. Pan and M. Nikl, Adv. Opt. Mater., 2016, 4, 731–739.
4. C. H. Huang, W. R. Liu, T. S. Chan and Y. T. Lai, Dalton Trans., 2014, 43, 7917–7923.
5. H. Daicho, T. Lwasaki, K. Enomoto, Y. Sasaki, Y. Maeno, Y. Shinomiya, S. Aoyagi, E. Nishibori, M. Sakata, H. Sawa, S. Matsuishi and H. Hosono, Nat. Commun., 2012, 3, 1132.
6. J. Chen, Y. G. Liu, L. F. Mei, Z. Y. Wang, M. H. Fang and Z. H. Huang, J. Mater. Chem. C, 2015, 3, 5516–5523.
7. K. Li, M. G. Xu, J. Fan, M. M. Shang, H. Z. Lian and J. Lin, J. Mater. Chem. C, 2015, 3, 11618–11628.
8. M. M. Shang, C. X. Li and J. Lin, Chem. Soc. Rev., 2014, 43, 1372–1386.
9. G. G. Li, Y. Tian, Y. Zhao and J. Lin, Chem. Soc. Rev., 2015, 44, 8688–8713.
10. Z. G. Xia and Q. L. Liu, Prog. Mater. Sci., 2016, 84, 59–117.
11. Y. Sato, H. Kato, M. Kobayashi, T. Masaki, D.-H. Yoon and M. Kakihana, Angew. Chem., Int. Ed., 2014, 53, 7756–7759.
12. Z. G. Xia, C. G. Ma, M. S. Molokeev, Q. L. Liu, K. Rickert and K. R. Poeppelmeier, J. Am. Chem. Soc., 2015, 137, 12494–12497.
13. H. P. Ji, L. Wang, M. S. Molokeev, N. Hirosaki, R. J. Xie, Z. H. Huang, Z. G. Xia, O. M. ten Kate, L. H. Liu and V. V. Atuchin, J. Mater. Chem. C, 2016, 4, 6855–6863.
14. K. W. Huang, W. T. Chen, C. I. Chu, S. F. Hu, H. S. Sheu, B. M. Cheng, J. M. Chen and R. S. Liu, Chem. Mater., 2012, 24, 2220–2227.
15. Y. Xia, J. Chen, Y. G. Liu, M. S. Molokeev, M. Guan, Z. Huang and M. Fang, Dalton Trans., 2016, 45, 1007–1015.
16. L. Shi and H. J. Seo, Opt. Express, 2011, 19, 7147–7152.
17. H. He, R. L. Fu, X. F. Song, D. L. Wang and J. K. Chen, J. Lumin., 2008, 128, 489–493.
18. K. A. Denault, J. Brgoch, M. W. Gaultois, A. Mikhailovsky, R. Petry, H. Winkler, S. P. DenBaars and R. Seshadri, Chem. Mater., 2014, 26, 2275–2285.
19. C. F. Guo, Y. Xu, F. Lv and X. Ding, J. Alloys Compd., 2010, 497, L21–L24.
20. Z. G. Pan, H. He, R. L. Fu, S. Agathopoulos and X. F. Song, J. Lumin., 2009, 129, 1105–1108.
21. X. J. Li, Y. J. Hua, H. P. Ma, D. G. Deng, G. H. Jia and S. Q. Xu, RSC Adv., 2015, 5, 62659–62669.
22. Z. Y. Zhao, Z. G. Yang, Y. R. Shi, C. Wang, B. T. Liu, G. Zhu and Y. H. Wang, J. Mater. Chem. C, 2013, 1, 1407–1412.
23. J. Park, S. J. Lee and Y. J. Kim, Cryst. Growth Des., 2013, 13, 5204–5210.
24. J. Barzowska, K. Szczodrowski, M. Grinberg, S. Mahlik, K. Anders, R. Piramidowicz and Y. Zorenko, J. Phys.: Condens. Matter, 2013, 25, 425501.
25. L. C. Ju, X. Xu, L. Y. Hao, Y. Lin and M. H. Lee, J. Mater. Chem. C, 2015, 3, 1567–1575.
26. R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767.
27. X. J. Li, Y. J. Hua, H. P. Ma, D. G. Deng and S. Q. Xu, CrystEngComm, 2015, 17, 9123–9134.
28. H. Nagabhushana, D. V. Sunitha, S. C. Sharma, B. D. Prasad, B. M. Nagabhushana and R. P. S. Chakradhar, J. Alloys Compd., 2014, 595, 192–199.
29. Z. G. Xia, M. S. Molokeev, A. S. Oreshonkov, V. V. Atuchin, R. S. Liu and C. Dong, Phys. Chem. Chem. Phys., 2014, 16, 5952–5957.
30. J. Wang, H. R. Zhang, B. F. Lei, H. W. Dong, H. M. Zhang, Y. L. Liu, M. T. Zheng and Y. Xiao, J. Am. Ceram. Soc., 2015, 98, 1823–1828.
31. Y. Zhang, X. J. Li, K. Li, H. Z. Lian, M. M. Shang and J. Lin, ACS Appl. Mater. Interfaces, 2015, 7, 2715–2725.
32. W. Li, J. Wang, H. R. Zhang, Y. L. Liu, B. F. Lei, J. L. Zhuang, J. H. Cui, M. Y. Peng and Y. Zhu, RSC Adv., 2016, 6, 33076–33082.
33. J. Wang, H. R. Zhang, Y. L. Liu, H. W. Dong, B. F. Lei, M. T. Zheng, Y. Xiao, M. Y. Peng and J. Wang, J. Mater. Chem. C, 2015, 3, 9572–9579.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28209a

---