Open Access Article
Open Access ArticleMolecular dynamics study of microscopic structures, phase transitions and dynamic crystallization in Ni nanoparticles
Trong Dung Nguyena,
Chinh Cuong Nguyenb and
Vinh Hung Tran *c
*c
aFaculty of Physics, Hanoi National University of Education, 136 Xuan Thuy Street, Cau Giay District, Hanoi, Vietnam. E-mail: dungntsphn@gmail.com
bFaculty of Physics, Hanoi National University of Education, 136 Xuan Thuy Street, Cau Giay District, Hanoi, Vietnam. E-mail: cuongnc@hnue.edu.vn
cInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, 50-422 Wrocław, Poland. E-mail: V.H.Tran@int.pan.wroc.pl
First published on 11th May 2017
Abstract
Using molecular dynamics simulations in conjunction with the quantum-corrected Sutton–Chen potential, we studied the influence of the heating and cooling rates, number of particles, temperature and relaxation time on the microscopic structure, phase transitions and dynamics of crystallization in four model systems containing N = 4000, 5324, 6912 and 8788 nickel atoms. The simulation results of a representative ensemble of 5324 Ni atoms have shown that the glass transition temperature, Tg, crystallization temperature, Tc, and melting temperature, Tm, are observed with heating and cooling rates in the range of ΔT/Δt = 2 × 1012 K s−1 to 4 × 1013 K s−1, but Tg or Tc increases while Tm decreases with decreasing ΔT/Δt. By applying ΔT/Δt = 4 × 1012 K s−1 we found that after cooling from 2000 K down to 300 K the Ni atoms form nanoparticles for which the grain size follows the relation d ∝ N−1/3, and simultaneously the total potential energy of the investigated systems decreases linearly with the number of Ni atoms. With the help of common neighbor analysis, we detected the coexistence of amorphous and crystalline phases during the whole crystallization process. In the solid state, the dominant crystalline phase is characterized by the FCC and HCP structures, although a very small fraction of the BCC structure may occur at 300 K. It was established that the formation of the FCC structure is favored over the HCP one. In particular, lowering the temperature and increasing the relaxation time favour crystallization of the FCC lattice.
1 Introduction
Metallic nanoparticles have received considerable attention throughout recent decades due to their unique physical, chemical and optical properties associated with quantum mechanical and topological effects.1,2 The materials are of great importance not only for basic research, but also primarily for a wide variety of applications in fields like medicine and biology,3,4 microelectronics and optoelectronics,5–8 and so on. Among metal nanomaterials, nickel nanoparticles are useful systems for various applications, e.g. in catalysis,9,10 the power industry as fuel cells,11 or for solar energy techniques,12 just to mention a few.As a matter of fact, the physical properties of nanomaterials depend strongly on their structural and morphological properties, which as a consequence are intimately related to crystallization aging. This process essentially relies on applied synthesis methods, typically realized by chemical reactions, i.e. with a chemistry route,13–15 or with physical methods.16,17 It turns out that despite the large amount of experimental data and numerous theoretical investigations, the final physical properties of nanomaterials are not always desirable. As far as we know, the basic reason behind the problem is that there are still various unsolved issues, for instance, the dynamic aspects of phase transitions and instability of surfaces and grain sizes during crystallization/solidification.
To get a better understanding of the factors predisposing the dynamics of the crystallization process, and to elucidate the factors responsible for the change of structure and phase instabilities in the systems, atomistic simulation methods have often been employed as a complementary tool to experimental studies. These studies are important because they may allow us to follow the evolution of physical properties from the atomic scale to the bulk system. In fact, molecular dynamics (MD) simulations have been performed for the metal clusters Ni,18–24 Fe,25,26 Cu,27,28 Pt29,30 and Au,31,32 and the binary alloy clusters Cu–Ag and Cu–Ni,33 Cu–Zr,34 Ni–Ag,35 Pt–Pd36,37 and Pd–Ag.38
In the present work, we use molecular dynamics simulations to investigate the microscopic structure, phase transitions and dynamics of crystallization during the heating and cooling of four model clusters, which contain N = 4000, 5324, 6912 and 8778 Ni atoms. Hereafter, we denote these ensembles as Ni4000, …, Ni8778. Where possible, our results are compared with those reported in the literature. Most notably, the previous MD studies of Ni-based systems showed that the glass transition in the 4000 atom system occurs at 800 K,21 whereas the melting temperature, Tm, follows a power law for the number of atoms, N, as Tm ∝ N−1/3, i.e. Tm increases from 980 K in an ensemble with 336 atoms to 1380 K in a system with 8007 atoms.19 It was also reported that the melting temperatures of the metal nanoclusters are dependent not only on the cluster size but also upon other related factors such as shape and dimensionality.24 As an example, Wen et al. showed that the melting temperature, Tm, of Ni nanowires is inversely proportional to their diameter, D, i.e. Tm ∝ D−1.20 Here, we paid particular attention to the effects of both the cooling rates on crystallization and the cluster sizes on grain size and microscopic structures. Moreover, we establish that the crystal structure of the solid Ni nanoparticles is of the multi-domain type, involving mainly face-centered-cubic (FCC) and hexagonal-close-packed (HCP) structures, coexisting with a minor proportion of body-centered-cubic (BCC) structure and amorphous phases.
2 Calculation method
In molecular dynamics simulations, in order to predict the crystal structures and physical properties of materials one needs to define realistically the interactions between atoms or molecules. One of the approaches, which has been used confidently on many-body interactions in metallic systems, is the so-called embedded atom method.39,40 Originally, the energy of system is defined as the sum of the electrostatic repulsive potentials from the charged particles and the embedded energy accounting for electron local density. In this work we used the electronic charge and the pair interaction functions as given by Sutton–Chen (SC):41
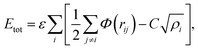 | (1) |
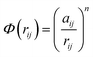 | (2) |
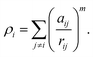 | (3) |
The investigated ensembles of nickel atoms were initially arranged in the FCC lattice. Instead of periodic boundary conditions, we used in the calculations a cut-off distance of the interatomic potential, rc = 1.996 nm, assuming that beyond rc interaction may be safely ignored. We carried out MD simulations in a series of increasing temperatures from 0 to 2000 K. After equilibrating the energy in the liquid phase, we cooled the system from 2000 K down to T = 0, 300, 500, 700, 800, 900 and 1100 K. The numeric temperature of the system was controlled using a Nosé–Hoover thermostat.44,45 We used four different heating and cooling rates, ΔT/Δt = 2 × 1012 K s−1, 4 × 1012 K s−1, 2 × 1013 K s−1 and 4 × 1013 K s−1. The time step in the simulation was 2 fs. The dynamics of the supercooled liquid and crystallization were considered by simulations with time steps up to 4 × 105, corresponding to a relaxation time of t = 800 ps. To characterize the microscopic structures of the investigated ensembles, we used common neighbor analysis.46,47 The calculations presented here were performed using software developed in the Center for Computational Science of Hanoi National University of Education.
3 Results and discussion
3.1 Effects of heating and cooling rates on melting and crystalline state and glass formation
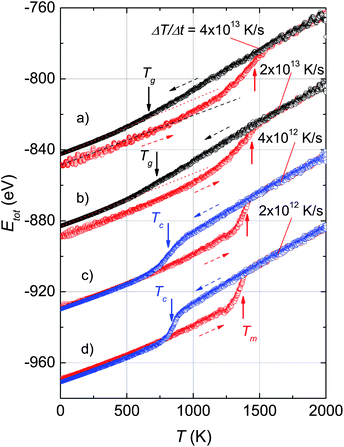
Fig. 1 shows the variation of total potential energy during heating, Ehtot, and cooling, Ectot, for the model system, Ni5324, as a representative of the studied ensembles. Apparently the phase transition/crossover from the solid to the liquid phase, and the reverse, can be evidenced by an anomaly in the Etot vs. T curves. We assume that the prominent jump in the Ehtot curves is due to melting. The value of the melting temperature, Tm, is defined as the temperature where the derivative of the energy has a maximum dEtot/dT|max. Our studies reveal that Tm decreases with decreasing ΔT/Δt and locates in the temperature range 1460–1375 K for the applied ΔT/Δt. It was noticed that the observed value Tm = 1375 K agrees well with the value of 1350 K predicted using the Tm ∝ N−1/3 rule.19 It is clear that our study and also the studies by Qi et al.19 and by Wen et al.20 provide significantly lower values of extrapolated Tm than expected for bulk Ni (∼1590 K), compared to the experimental value of 1728 K.48 This suggests that the physics of the nanosystems is not applicable for the bulk system.In the cooling process, a pronounced drop in Ectot is observed, and the heating and cooling curves approach each other when the heating/cooling rates were applied in the range 2 × 1012 to 4 × 1012 K s−1. Such behaviour of the energy vs. T implies a liquid-crystalline phase transition. Following this, the cooled system changed into the crystalline state below the transition denoted as the crystallization temperature, Tc. Our data indicate that Tc has values of ∼810–830 K for the cooling rates below 1 × 1013 K s−1. It seems that Tc increases with the number of atoms since the observed Tc value for Ni5324 is much larger than Tc = 750 K for 1004 atoms.19 In contrast to the low rates of cooling, a fast quenching, i.e. cooling rates higher than 1 × 1013 K s−1, causes the potential energy to decrease smoothly with decreasing temperature. Nevertheless, a transformation from the liquid to solid state can be recognized. By close examination of the slope of the Ectot(T) curves we see a noticeable deviation of the Ectot(T) curves from a straight line (see dotted lines in Fig. 1). However, because of the lack of a melting-crystallization hysteresis (i.e. without an abrupt drop in energy at Tc and the absence of overlapping Ectot(T) and Ehtot(T) values), we may ascribe the anomaly to a phase crossover, more likely corresponding to the glass temperature, Tg. We would expect that after solidification, the system has an amorphous phase. From our calculations, Tg ranges from 660 K to 720 K, being lower than the value of 800 K previously reported for the 4000 atom system.21
The effect of different rates of heating and cooling on phase transitions and crossover in Ni5324 is collated and evaluated in Fig. 2. It can be seen that not only the values of Tm, Tc and Tg are vulnerable to ΔT/Δt as discussed above, but there is also a change of width of the phase transitions (ΔTc and ΔTm) with ΔT/Δt upon changing ΔT/Δt: namely, the transition gets sharper and the width of the phase transitions becomes narrower with decreasing ΔT/Δt. As a result, with heating and cooling rates of 4 × 1012 K s−1, ΔTm and ΔTc are as low as about 150 K and 80 K, respectively. It would be interesting to see the behaviour of a system with lower ΔT/Δt rates. Unfortunately, such a study would be carried out in the future, because at present the necessary computing power is not available to us.
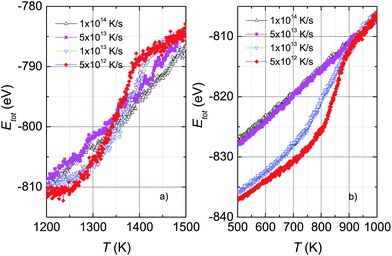 | ||
| Fig. 2 (a) Dependence of the melting temperature on heating rates and (b) dependence of the crystallization and glass temperatures on cooling rates for Ni5324. | ||
By applying ΔT/Δt rates higher than 1 × 1013 K s−1, we observe broader transitions, thus inhomogeneous melting and imperfect crystallization are anticipated. In particular, for fast quenching the crystallization is no longer observed by us. The experimental rapid quenching of metallic alloys usually led to the formation of an amorphous phase, for instance, cooling rates of about 104 to 106 K s−1 provide a metallic glass.49
Apparently, the studied ensemble does exhibit two distinct types of behaviour depending upon whether slow cooling or fast quenching occurs. This property can be explained assuming the existence of manifold minimum-energy structures. In the case of slow enough cooling, there will be a slow relaxation process and the system will accomplish an equilibrium state with its lowest minimum energy. This process is accompanied by the structural ordering of atoms. Conversely, fast quenching causes the system to fluctuate between different energy structures. In this case, the system does not achieve the lowest energy yet, but rather falls into numerous states with a local minimum energy. The actual solidification is either an imperfect crystallization process or glass state formation.
3.2 Effects of cluster size on grain size and microscopic structure of the crystalline phases
To examine the impact of the number of atoms on the grain size and microscopic structures of the crystalline phases, we considered only the case with a heating and cooling rate of 2 × 1012 K s−1. The most important results obtained after cooling from 2000 K down to 300 K are summarized in Table 1 and plotted in Fig. 3 and 4. As shown in Table 1, the grain size, d, gradually increases with the number of Ni atoms, from 13.93 nm to 18.11 nm for ensembles with N increasing from 4000 to 8788 respectively. In light of the fact that the melting temperature, Tm, scales with the number of atoms as Tm ∝ N−1/3,19 we are interested to check whether there is a reasonable relationship between grain size, d, and N. Actually, a plot of d versus N−1/3 for the investigated ensembles, shown in Fig. 3a, yields a linear dependence, which can be described by the mean of the function, d [nm] = 31.72 − 282.85N−1/3. Therefore, we are convinced that the linear relationship of both Tm vs. N−1/3,19 and d vs. N−1/3 (presented in this study) emphasizes the suggestion that the mechanisms underlying melting and grain growth in Ni nanoclusters have the same origin.| N | Grain size d (nm) | Etot (eV) | r(1) (nm) | r(2) (nm) |
|---|---|---|---|---|
| 4000 | 13.93 | −630.16 | 0.245 | 0.34, 0.347 |
| 5324 | 15.53 | −841.61 | 0.245 | 0.34, 0.348 |
| 6912 | 16.72 | −1094.17 | 0.245 | 0.34, 0.352 |
| 8788 | 18.11 | −1399.20 | 0.245 | 0.34, 0.349 |
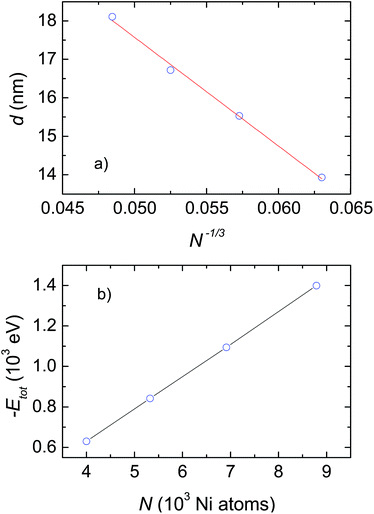 | ||
| Fig. 3 (a) Dependence of grain size on the cluster size. The solid line shows the fit of d to a linear function of N−1/3. (b) Potential energy, Etot, as a function of the number of Ni atoms, N. | ||
In light of the fact that the four studied ensembles do not have the same grain size, but their grain size is contingent on N, one should make further comparison between them regarding the change in their potential energy. Accordingly, we plot the obtained energy, Etot, as a function of the number of Ni atoms, N, in Fig. 3b. Evidently, the energy, Etot, systematically decreases with increasing N. The observation conceptualizes, first of all, that clusters with bigger sizes will be more stable than ones with smaller sizes. As a consequence, as the temperature increases the smaller ensemble will melt before the bigger ensemble. This result explicitly explains the reliance of Tm on N, that was documented previously by Qi et al.19
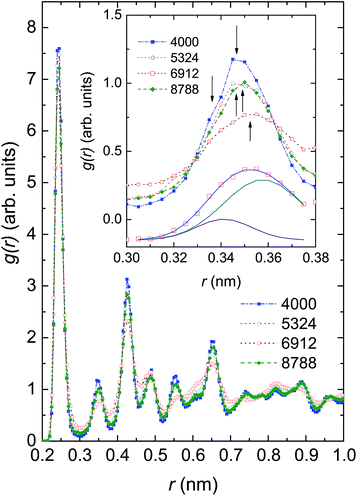
In Fig. 4 we compare the radial distribution function (RDF), g(r), of the investigated ensembles at 300 K. For each of these systems the highest peak is found at r = 0.245 nm, corresponding to the nearest-neighbour (NN) distance between Ni atoms, dNN. Because the observed dNN value is approximately twice the covalent radius of 0.121 nm or metallic radius of 0.124 nm,50 we may conjecture that the Ni–Ni bonding is of a covalent-metallic type. Considering the change of the height of the first peak in response to the number of Ni atoms, we see that there is no monotonic relationship between g(r) and N; the largest g(r) value of 7.59 (arb. units) is observed in Ni4000, whereas the smallest g(r) value of 6.82 (arb. units) is observed in Ni6912. The finding reflects the existence of some microscopic structures, of which the local orders compete against one another. The non-homogeneity of the microscopic structures in the ensembles can be strongly supported by the multi-peaked structure of the second peak of g(r). In the inset of Fig. 4 we show g(r) around the second peak. It can be seen that the second peak involves at least two overlapping maxima located at approximately 0.34 nm and 0.35 nm. As a representative peak analysis, we show the least-squares fit of a double peak Gaussian function to the g(r) of Ni6912 atoms (see the solid lines in the bottom of the inset of Fig. 4).
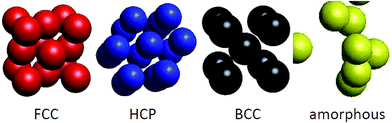
Before considering the microscopic structures of Ni nanoparticles, we would like to recall that nickel metal can undergo transformations between several crystal structures. Normally, Ni metal crystallizes in the FCC structure, but nanosize Ni can adopt the HCP structure,51,52 can exist in both FCC and HCP structures,53 and can even form the BCC lattice.54 The illustration of crystal structures potentially adopted by Ni ensembles, i.e., FCC, HCP, BCC and amorphous structures, is shown in Fig. 5. However, a remark has to be made for the BCC structure. Brewer showed that the crystal structure of 3d-electron metals depends on the electron configuration of the outermost shell,55 and accordingly, the FCC structure is stable for electron configurations in the range sp1.5–sp2, HCP is stable in the range sp0.7–sp1.1 and BCC is stable for configurations in the range sp–sp0.5. The considerable difference between sp2 of metallic Ni, and sp–sp0.5 expected for the BCC structure, makes the appearance of the BCC structure for nanosize Ni very astonishing.
The results of structural analysis based on the CNA method are shown in Table 2. We state the coexistence of amorphous and crystalline phases. In addition, the amorphous phase plays a minor role, representing about 7 at.% of the crystalline phase, compared to the major fraction of almost 93 at.%. Remarkably, in the latter phase the formation of the face-centered-cubic lattice seems to be favoured over the hexagonal-close-packed structure. At this stage, we must admit that the presence of a dozen or so Ni atoms composing a BCC structure in Ni5324 is arguable. We think that future calculations based on other methods, notably the centrosymmetry parameter,56,57 bond angle analysis,58 bond order analysis,59 and so on, should be helpful to solve this conundrum.
| N | FCC | HCP | BCC | Amorphous |
|---|---|---|---|---|
| 4000 | 2606 | 1174 | 0 | 220 |
| 5324 | 3345 | 1583 | 13 | 383 |
| 6912 | 3876 | 2024 | 0 | 1012 |
| 8788 | 6039 | 2136 | 0 | 613 |
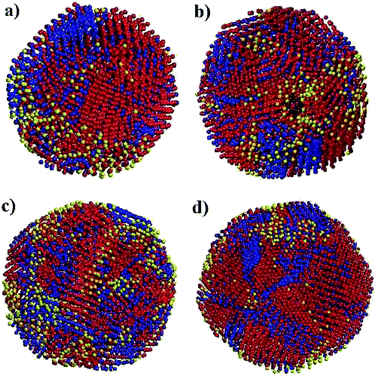
Fig. 6 shows snapshots of solid nanoparticles of Ni with (a) 4000, (b) 5324, (c) 6912 and (d) 8799 atoms at 300 K. The visualized ensembles are characterized by a mixture of several microscopic structures. The atoms are coloured according to their crystal structures: red for FCC, blue for HCP, black for BCC and yellow for amorphous as obtained by CNA. It can be seen that there is no even distribution of structures and instead the Ni atoms huddle together to form clusters of defined structures. This observation points to two messages: (i) a new state of Ni ensemble has been formed after cooling from 2000 K to 300 K, and (ii) there are competing local orders between FCC, HCP and amorphous structures.
3.3 Structural transformations in Ni nanoparticles during cooling
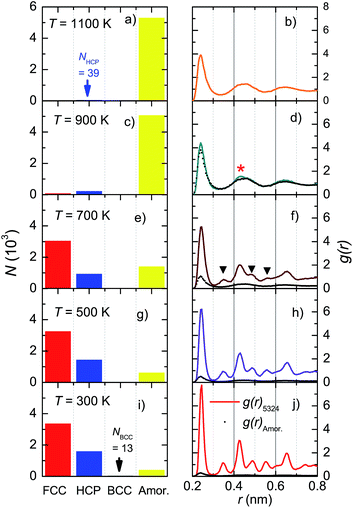
To examine the formation process of microscopic structures, we studied the Ni5324 ensemble during cooling from 2000 K to 1100, 900, 700, 500 and 300 K, applying a cooling rate of 4 × 1012 K s−1. Fig. 7 shows the evolution of microscopic structures through the crystallization temperature, Tc, between 700 and 900 K. At 1100 K (Fig. 7a), the fraction of atoms with an amorphous structure dominates, while small clusters of 39 Ni atoms with an HCP structure are created. Approaching Tc, in addition to the crystalline HCP phase, a FCC kernel also settles (Fig. 7c). When the ensemble crosses Tc, the number of atoms with FCC and HCP structures increases sharply (Fig. 7e). The fraction of formed structures becomes larger and larger on further decreasing the temperature (Fig. 7g and j). It is also worth noting that at 300 K a very small fraction consisting of 13 Ni atoms appears only in the BCC structure, indicating an enhanced entropy. This finding may imply that low energy is not sufficient but entropy must be high enough to enable the equilibrium of the system.The radial distribution functions corresponding to the structural transformations are shown in the right panels of Fig. 7. In the supercooled liquid region (Fig. 7b and d), the RDF has only the first peak at r(1) = 0.239 nm, which is strong and distinguishable. This peak represents the average nearest-neighbour Ni–Ni distance. The remaining peaks are very broad due to the overlapping of individual peaks and their merging into the broad ones. The shape of the RDF demonstrates an oscillating character, thus indicating an amorphous atomic packing. Nonetheless, a comparison of g(r) between the amorphous phase and the total g(r) in Fig. 7d features the presence of a small crystal peak at r = 0.43 nm (denoted by *). This behaviour signalizes a nucleation, in agreement with the data shown in Fig. 7c, where a small fraction of Ni atoms forms local microscopic structures of the HCP and FCC lattices. Obviously, the existence of new, additional peaks in g(r) at 700 K (denoted by ▼ in Fig. 7f) marks the growth of the crystalline FCC and HCP phases. Sharper peaks and their higher intensities seen in Fig. 7j, compared to those in Fig. 7h, indicate a higher degree of crystallinity in the ensemble at 300 K.
3.4 Dynamic crystallization process
The total energy of the Ni5324 ensemble at several temperatures as a function of relaxation time, t, is shown in Fig. 8. At 1100 K, Etot is constant during the relaxation. Lowering the temperature to 900 K causes crystallization, which is evidenced by a sudden drop in the total energy after the incubation time, ti = 50 ps. With decreasing temperature, ti goes down, i.e. at 800 K, ti amounts to 25 ps. Interestingly, at this temperature, Etot(t) does exhibit a conspicuous, second drop at ti = 275 ps. This feature can be considered the result of a noticeable change in the relative fractions of the existing phases. Finally, as the temperature decreases to 300 K, the Etot value decreases by a very small amount vs. t, indicating that the crystalline and amorphous phases are close to equilibrium.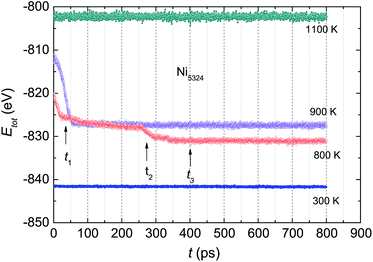 | ||
| Fig. 8 The total energy Etot of the Ni5324 ensemble at various temperatures as a function of relaxation time t. | ||
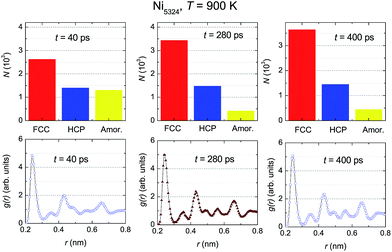
To examine the dynamic crystallization of the Ni5324 ensemble in detail, we considered the relaxation time dependencies of the crystalline and amorphous fractions, and also the t-dependence of the respective radial distribution functions for three relaxation times, t1 = 40 ps, t2 = 280 ps and t3 = 400 ps (marked by arrows in Fig. 8) at two temperatures, 900 K and 800 K. The fact that the nucleus for crystallization at 900 K appears before 50 ps (shown in Fig. 8) is now strengthened by the presence of crystalline phases with FCC and HCP structures at t = 40 ps (Fig. 9). Furthermore, we see that whilst the fraction of the FCC structure increases firmly, the fraction of the HCP structure slightly rises with an increasing relaxation time. As expected, at the expense of increasing the crystalline quantity, the amorphous fraction strongly reduces. The radial distribution functions shown in the bottom panels of Fig. 9 confirm the structural fraction change. Note the difference between the data for 40 ps and 400 ps – it can be observed that the peaks of g(r) sharpen, and the scission of the third and fourth peaks (and likewise, the pair of fifth and sixth peaks) takes place as t increases.
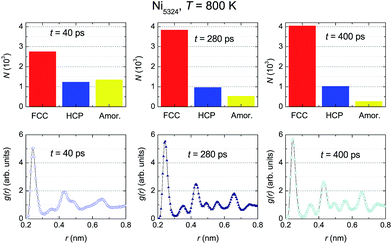
The evolution of the structural fractions at 800 K upon relaxation time variation is displayed in Fig. 10. For t = 40 ps, in a similar manner as at 900 K, in addition to the dominant FCC fraction, there are plentiful fractions of the HCP and amorphous phases. The content of the latter phases in the ensemble is comparable. Further microstructural analysis allows us to infer that as the relaxation time increases, only the FCC structure fraction enhances whereas the contribution of both the HCP and amorphous phases declines. The change in the HCP content certainly accounts for the anomaly of g(r) around t2. A comparison between g(r) at two temperatures (Fig. 9 vs. 10) indicates that the developments of the peaks with t, in general, are similar. For small relaxation times, the third and fourth peaks and also the fifth and sixth peaks overlap significantly, giving important information regarding the fraction of the amorphous phase. The increase in height and decrease in width of the peaks when extending the relaxation time assists with the augmentation of the fraction with the FCC lattice, and simultaneously overthrows the amorphous structure. The higher peaks of g(r) observed at 800 K compared to those at 900 K points to a larger degree of crystallinity in the ensemble at the lower temperature.
4 Summary
We have performed molecular dynamics simulations for ensembles containing 4000, 5324, 6912 and 8788 Ni atoms. It is found that the melting temperature increases with heating rate. The effect of the cooling rate on crystallization/solidification is strong. A slow cooling rate favours the formation of crystalline phases, while a fast cooling rate favours the formation of an amorphous structure. This can be understood by assuming the existence of manifold minimum energy structures.We have established the effects of cluster size on the grain size and microscopic structure of the crystalline phases. We observe that the Ni atoms bound together to form nanoscale grains with sizes, d, between 14 nm and 18 nm. In particular, d follows a power law for the number of Ni atoms, as d vs. N−1/3. We ascertained a linear relationship between the total energy and the number of Ni atoms, which confirms that a bigger ensemble is more stable than a smaller one. Below the crystallization temperature, all studied ensembles have a new state as compared to the initial FCC arrangement. The new state is a mixture of amorphous and crystalline phases with FCC, HCP and BCC lattices. Among the crystalline structures, the FCC structure is dominant. It is noted that a very small amount of Ni atoms crystallize in the BCC structure. Presumably, the appearance of the BCC lattice enhances the entropy, which is indispensable for the equilibrium of the system.
From the CNA results, the Ni5324 ensemble is proven to have coexisting FCC, HCP and amorphous structures during crystallization. However, the dynamics of crystal growth of the FCC and HCP phases is different. Remarkably, increasing the relaxation time always assists with the formation of the FCC lattice, and the relaxation time at 900 K and 800 K has opposite effects on crystallization to form the HCP lattice. Finally, the underlying physics of the BCC structure, coexisting with the FCC, HCP and amorphous ones, is not clear yet, and this issue will encourage further study.
References
- C. I. Contescu and K. Putyera, Dekker Encyclopedia of Nanoscience and Nanotechnology, CRC Press, 2nd edn, 2008 Search PubMed
.
- G. Cao and Y. Wang, Nanostructures & nanomaterials: synthesis, properties, and applications, in World Scientific Series in Nanoscience and Nanotechnology, ed. F. Spaepen, World Scientific Publishing Co Pte Ltd, 2nd edn, 2004, vol. 2 Search PubMed
.
- T. K. Jain, M. A. Morales, S. K. Sahoo, D. L. Leslie-Pelecky and V. Labhasetwar, Mol. Pharm., 2005, 2, 194–205 CrossRef CAS PubMed
.
- S. Y. Shim, D. K. Lim and J. M. Nam, Nanomedicine, 2008, 3, 215–232 CrossRef CAS PubMed
.
- S. Karmakar, S. Kumar, R. Rinaldi and G. Maruccio, J. Phys.: Conf. Ser., 2011, 292, 012002 CrossRef
.
- D. Weller and M. F. Doerner, Annu. Rev. Mater. Sci., 2000, 30, 611–644 CrossRef CAS
.
- L. D. Sio, T. Placido, R. Comparelli, M. L. Curri, M. Striccoli, N. Tabiryan and T. J. Bunning, Prog. Quantum Electron., 2015, 41, 23–70 CrossRef
.
- M. A. H. Muhammed, M. Döblinger and J. Rodríguez-Fernández, J. Am. Chem. Soc., 2015, 137, 11666–11677 CrossRef CAS PubMed
.
- A. Wang, H. Yin, M. Ren, H. Lu, J. Xue and T. Jiang, New J. Chem., 2010, 34, 708–713 RSC
.
- Y. G. Morozov, O. V. Belousova and M. V. Kuznetsov, Inorg. Mater., 2011, 47, 36–40 CrossRef CAS
.
- Y. Ruan, C. Wang and J. Jiang, J. Mater. Chem. A, 2016, 4, 14509–14538 CAS
.
- L. Gaouyat, Z. He, J.-F. Colomer, D. Schryvers, F. Mirabella and O. Deparis, in Linking Optical Properties and Nanostructure of NiCrOx Cermet Nanocomposite for Solar Thermal Application, ed. B. Di Bartolo, J. Collins and L. Silvestri, Springer Netherlands, Dordrecht, 2015, pp. 497–497 Search PubMed
.
- H. Schmidt, Appl. Organomet. Chem., 2001, 15, 331–343 CrossRef CAS
.
- K.-C. Huang and S. H. Ehrman, Langmuir, 2007, 23, 1419–1426 CrossRef CAS PubMed
.
- D. V. Goia, J. Mater. Chem., 2004, 14, 451–458 RSC
.
- N. S. Tabrizi, Q. Xu, N. M. van der Pers, U. Lafont and A. Schmidt-Ott, J. Nanopart. Res., 2008, 11, 1209 CrossRef
.
- H. Förster, C. Wolfrum and W. Peukert, J. Nanopart. Res., 2012, 14, 926 CrossRef
.
- J. Lu and J. A. Szpunar, Philos. Mag. A, 1997, 75, 1057–1066 CAS
.
- Y. Qi, T. Çağin, W. L. Johnson and W. A. Goddard III, J. Chem. Phys., 2001, 115, 385–394 CrossRef CAS
.
- Y.-H. Wen, Z.-Z. Zhu, R. Zhu and G.-F. Shao, Phys. E, 2004, 25, 47–54 CrossRef CAS
.
- Y. Zhang, L. Wang and W. Wang, J. Phys.: Condens. Matter, 2007, 19, 196106 CrossRef
.
- P. H. Kien, ISRN Mater. Sci., 2014, 2014, 253627 Search PubMed
.
- A. N. Andriotis, Z. G. Fthenakis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 073413 CrossRef
.
- H. M. Lu, P. Y. Li, Z. H. Cao and X. K. Meng, J. Phys. Chem. C, 2009, 113, 7598–7602 CAS
.
- L. J. Lewis, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 12954–12956 CrossRef CAS
.
- N. H. Nguyen, R. Henning and J. Z. Wen, J. Nanopart. Res., 2011, 13, 803–815 CrossRef CAS
.
- H. Pang, Z. H. Jin and K. Lu, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094113 CrossRef
.
- C. Gang, W. Chuanjie and Z. Peng, Phys. Chem. Liq., 2015, 53, 518–528 CrossRef
.
- S. H. Lee, S. S. Han, J. K. Kang, J. H. Ryu and H. M. Lee, Surf. Sci., 2008, 602, 1433–1439 CrossRef CAS
.
- H. Akbarzadeh and G. A. Parsafar, Fluid Phase Equilib., 2009, 280, 16–21 CrossRef CAS
.
- H.-S. Nam, N. M. Hwang, B. D. Yu and J.-K. Yoon, Phys. Rev. Lett., 2002, 89, 275502 CrossRef PubMed
.
- Z. Qiao, H. Feng and J. Zhou, Phase Transitions, 2014, 87, 59–70 CrossRef CAS
.
- Y. Qi, T. Çağin, Y. Kimura and W. A. Goddard III, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3527–3533 CrossRef CAS
.
- G. Duan, D. Xu, Q. Zhang, G. Zhang, T. Cagin, W. L. Johnson and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224208 CrossRef
.
- A. Y. Pryadilshchikov, A. T. Kosilov, A. V. Evteev and E. V. Levchenko, J. Exp. Theor. Phys., 2007, 105, 1184–1189 CrossRef CAS
.
- S. K. R. S. Sankaranarayanan, V. R. Bhethanabotla and B. Joseph, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 195415 CrossRef
.
- C. Fernández-Navarro and S. Mejía-Rosales, Adv. Nanopart., 2013, 2, 323–328 CrossRef
.
- H. H. Kart, M. Uludoǧan, T. Çağin and M. Tomak, Simulation of crystallization and glass formation for binary Pd–Ag metal alloys in: Nanoengineered Nanofibrous materials, Kluwer Academic Publishers, Dordrecht, Boston, London, 2004, pp. 487–493 Search PubMed
.
- M. S. Daw and M. I. Baskes, Phys. Rev. Lett., 1983, 50, 1285–1288 CrossRef CAS
.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS
.
- A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146 CrossRef
.
- T. Çağin, Y. Qi, H. Li, Y. Kimura, H. Ikeda, W. L. Johnson and W. A. Goddard III, MRS Symp. Ser., 1999, 554, 43–48 CrossRef
.
- Y. Kimura, Y. Qi, T. Çağin and W. A. Goddard III, Technical Report, Pasadena: Caltech ASCI, 1998, vol. 3, pp. 1–29 Search PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef
.
- J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963 CrossRef CAS
.
- H. Tsuzuki, P. S. Branicio and J. P. Rino, Comput. Phys. Commun., 2007, 177, 518–523 CrossRef CAS
.
- C. Kittel, Introduction to Solid State Physics, John-Wiley & Sons, Inc, 8th edn, 2005 Search PubMed.
- W. Wang, C. Dong and C. Shek, Mater. Sci. Eng., R, 2004, 44, 45–89 CrossRef
.
- Atomic Radii of the Elements, data Page, Wikipedia, 10 November, 2016.
- S. Zharkov, V. Zhigalov and G. Frolov, Phys. Met. Metallogr., 1996, 81, 328–330 Search PubMed
.
- Y. Mi, D. Yuan, Y. Liu, J. Zhang and Y. Xiao, Mater. Chem. Phys., 2005, 89, 359–361 CrossRef CAS
.
- R.-T. Chiang, R.-K. Chiang and F.-S. Shieu, RSC Adv., 2014, 4, 19488–19494 RSC
.
- C. S. Tian, D. Qian, D. Wu, R. H. He, Y. Z. Wu, W. X. Tang, L. F. Yin, Y. S. Shi, G. S. Dong, X. F. Jin, X. M. Jiang, F. Q. Liu, H. J. Qian, K. Sun, L. M. Wang, G. Rossi, Z. Q. Qiu and J. Shi, Phys. Rev. Lett., 2005, 94, 137210 CrossRef CAS PubMed
.
- L. Brewer, Science, 1968, 161, 115–122 CAS
.
- C. L. Kelchner, S. J. Plimpton and J. C. Hamilton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11085–11088 CrossRef CAS
.
- J. Li, Modell. Simul. Mater. Sci. Eng., 2003, 11, 173 CrossRef
.
- G. J. Ackland and A. P. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 054104 CrossRef
.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2017 |