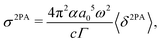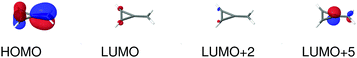Open-ended formulation of self-consistent field response theory with the polarizable continuum model for solvation†
Received
5th October 2016
, Accepted 15th November 2016
First published on 15th November 2016
Abstract
The study of high-order absorption properties of molecules is a field of growing importance. Quantum-chemical studies can help design chromophores with desirable characteristics. Given that most experiments are performed in solution, it is important to devise a cost-effective strategy to include solvation effects in quantum-chemical studies of these properties. We here present an open-ended formulation of self-consistent field (SCF) response theory for a molecular solute coupled to a polarizable continuum model (PCM) description of the solvent. Our formulation relies on the open-ended, density matrix-based quasienergy formulation of SCF response theory of Thorvaldsen, et al., [J. Chem. Phys., 2008, 129, 214108] and the variational formulation of the PCM, as presented by Lipparini et al., [J. Chem. Phys., 2010, 133, 014106]. Within the PCM approach to solvation, the mutual solute–solvent polarization is represented by means of an apparent surface charge (ASC) spread over the molecular cavity defining the solute–solvent boundary. In the variational formulation, the ASC is an independent, variational degree of freedom. This allows us to formulate response theory for molecular solutes in the fixed-cavity approximation up to arbitrary order and with arbitrary perturbation operators. For electric dipole perturbations, pole and residue analyses of the response functions naturally lead to the identification of excitation energies and transition moments. We document the implementation of this approach in the Dalton program package using a recently developed open-ended response code and the PCMSolver libraries and present results for one-, two-, three-, four- and five-photon absorption processes of three small molecules in solution.
1 Introduction
An important challenge in molecular sciences is the study at the quantum molecular mechanical level of systems of growing complexity. The behavior of simple, isolated molecules is in general well understood, but large systems that include multiple constituents pose additional problems, both due to their sheer size and the interaction of the different components. On the experimental side, the best tools to address such systems are provided by spectroscopic techniques, in which photons interact with the system and the response of the system to these perturbations is monitored. Simultaneously, technological improvements both in the intensity of the photon source and the sensitivity of detectors allow new experimental techniques to be developed and applied to complex systems. As a result, methods that used to be proof-of-principle concepts are today routinely employed to study increasingly complex systems.
An example of such a class of experiments is multiphoton absorption (MPA): the simultaneous absorption of several photons. The effect, originally predicted for two-photon absorption (2PA) by Göppert-Mayer in 1931,1 is too weak to be detected unless laser sources are employed. As a consequence, the first measurement was only made possible in 1961.2 2PA is still not as widespread as one-photon absorption (1PA), but its use is increasing. In part, this is due to its different symmetry selection rules that allow exploring excited states that are dark in 1PA. In addition, 2PA experiments afford a greater focality than in 1PA, due to their quadratic dependence on the intensity of the incident radiation. More recently, higher-order methods such as three-,3 four-4 and five-photon5 absorption have emerged, although their use is in no way as widespread as 1PA and 2PA.
The growth in available spectroscopic techniques and their application to systems of ever increasing complexity calls for a corresponding effort on the theoretical side to describe correctly the underlying molecular phenomena and to tackle the complexity of the system in a manageable way.
Olsen and Jørgensen have shown how transition moments between ground and excited states can be calculated from residues of response functions of a molecule in its ground state.6 The residues of the linear response function can thus be used to calculate the strength of transitions in UV/Vis spectroscopy (1PA). 2PA and three-photon absorption (3PA) can in turn be calculated from the residues of the quadratic and cubic response functions, respectively.6–8 Similarly, four- and five-photon absorption cross sections (4PA and 5PA) can be calculated from the corresponding higher-order response functions. The higher the order of the response functions needed, the more complex the working equations become, in particular if attention is given to computational efficiency.
Our group has in the last few years developed an open-ended formulation of response theory9 and implemented it using recursive programming techniques,10 enabling the calculation of response properties to any order at the Hartree–Fock (HF) and density-functional theory (DFT) levels and limited only by the degree of generality in connected modules for perturbed one- and two-electron integrals and exchange-correlation (XC) contributions.9–11 The approach has recently been extended to include single residues of response functions.11 Single residues of these high-order response functions have already been used by our group to calculate 4PA11 and 5PA12 absorption cross sections. Arbitrary higher-order processes are also accessible from this open-ended approach. The open-ended response formalism is therefore able to address the challenge of the ever-growing variety of spectroscopic methods available, significantly reducing the development effort and the time required to model new spectroscopic processes for relevant applications.
Several approaches have been developed to tackle large and complex systems, such as solutions and proteins, in the presence of external fields. When the phenomenon studied is localized to a single molecule and its immediate surroundings—as is often the case for MPA where the majority of the response arises from a chromophore in the complex—an efficient strategy is to use focused models that only treat a small portion of the system (e.g. the chromophore molecule) using quantum mechanical (QM) methods, whereas the rest (the environment) is treated classically. A distinction can be drawn between methods keeping atomistic detail in the classical environment, and those which disregard it. The former are commonly known as molecular mechanics (MM) methods, whereas the latter are referred to as dielectric continuum (DC) methods. Both models have strengths and weaknesses: MM methods are better suited to describe specific intermolecular interactions but require configurational sampling.
In contrast, DC methods are more effective at addressing long-range interactions.13–15 and are easier to parametrize, requiring only a handful of macroscopic solvent parameters (dielectric constant ε, refractive index n), and the cavity specification (atom-specific radii). Both methods can be augmented with a supermolecular approach (including one or more solvent molecules in the QM system) to address specific quantum effects. A three-layer model which combines a description of the specific effects near the chromophore by an MM part with pre-averaged long-range effects described by the DC part has also been reported.16 For details we refer to the relevant literature.16–19
The above mentioned open-ended approach to response theory has recently been extended to include molecular environment effects for electric dipole properties through a polarizable embedding (PE) QM/MM approach.20 In this work, we will present an open-ended response formalism for the PCM,21 in its integral equation formalism (IEF) formulation,22 which is the most versatile DC method available. For details about the PCM, the reader is referred to two authoritative reviews.13,23 The model features a molecule-shaped cavity made of interlocking spheres,24,25 is able to describe a wide variety of environments due to the generality of the IEF formalism,22,26,27 and can treat dynamical processes thanks to the nonequilibrium formalism.28,29 All such features are available in the PCMSolver module, an application programming interface (API) for the PCM.30 Additional features not yet available in PCMSolver are the treatment of non-electrostatic terms in the solvation energy,31,32 and the state-specific formalism.33–36
Crucial aspects of our work are the variational formulation of the PCM equations37 and the modular approach employed in the implementation. Both PCMSolver and the open-ended response code10 are two independent modules which can be interfaced to any quantum chemistry software. This approach has several advantages over a non-modular code: modules can be developed and tested separately, new features can be made available to several programs at once, avoiding lengthy, tedious and error-prone multiple implementations, and the master program can be chosen freely, for instance based on the availability of different functionality.
The rest of the paper is organized as follows: in Section 2 we present the theory for the quasienergy formalism in the context of the PCM. In Section 3 we discuss the details of our modular implementation. After briefly discussing the computational details (Section 4), we will present our results on the MPA processes (up to 5PA) on para-nitroaniline (PNA), para-dinitrobenzene (PDNB) and methylenecyclopropene (MCP) in Section 5. In Section 6 we summarize the main conclusions and future implications of our work.
2 Theory
2.1 Variational formulation of the polarizable continuum model
The variational formulation of the PCM was first presented by Lipparini et al. in ref. 37 and is based on the weak approach to boundary integral equations (BIEs).38 The weak formulation of partial differential equations (PDEs), boundary value problems (BVPs) associated BIEs is a well-known tool in mathematics.38–40 Given a partition of Euclidean space ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 into a closed subdomain C, the cavity, with a sufficiently regular boundary Γ = ∂C, we want to solve the following transmission problem for a solvent with a homogeneous, isotropic relative permittivity ε:
3 into a closed subdomain C, the cavity, with a sufficiently regular boundary Γ = ∂C, we want to solve the following transmission problem for a solvent with a homogeneous, isotropic relative permittivity ε:| | | ∇2u(r) = −4πρ(r) ∀r ∈ C | (1a) |
| | 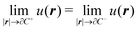 | (1c) |
| | 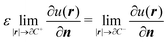 | (1d) |
| | | |u| ≤ C ‖x‖−1 for ‖x‖ → ∞ | (1e) |
where n is the outward-pointing normal vector to the cavity boundary Γ. The electrostatic potential u(r) in space is sought, given the jump conditions for its traces and conormal derivatives across the boundary, eqn (1c) and (1d), respectively, and the appropriate radiation condition at infinity, eqn (1e). This can be recast in terms of an integral equation:| | 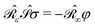 | (2) |
with σ(s), the apparent surface charge (ASC), representing the reaction potential arising from solvent polarization and φ(s) the molecular electrostatic potential (MEP). The integral operators 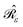 and
and 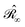 are given in terms of the components of the Calderón projector,
are given in terms of the components of the Calderón projector, 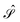 and
and 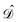 ,38,41 and the identity operator
,38,41 and the identity operator 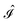 :
:| | 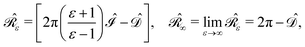 | (3) |
such that the operator 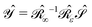 is self-adjoint and positive definite. The
is self-adjoint and positive definite. The 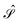 and
and 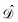 boundary integral operators are mappings between Sobolev spaces of fractional order, which thus are the natural mathematical setting for integral formulations of BVPs.38–40 These are normed spaces, equipped with the scalar product:
boundary integral operators are mappings between Sobolev spaces of fractional order, which thus are the natural mathematical setting for integral formulations of BVPs.38–40 These are normed spaces, equipped with the scalar product:| | 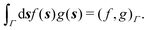 | (4) |
The polarization energy functional:
| | 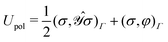 | (5) |
is strictly convex and has a unique minimum,
σ0. This is the unique solution to the IEF-PCM
eqn (2):
37,42| | 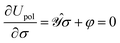 | (6) |
This allows us to treat the ASC as an additional, independent, variational density to be optimized. This offers distinct advantages from a theoretical point of view:
• there is no need to invoke a nonlinear coupling in the Hamiltonian to introduce the classical solute–solvent interaction,13,43
• the functional clearly describes a charge distribution interacting (unfavorably) with itself and (favorably) with its inducing external field and constitutes the polarization energy of the medium,37
• a classical analogue of the Hellmann–Feynman theorem naturally holds for the variational ASC:44
| | 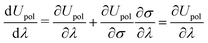 | (7) |
Simultaneous optimization algorithms can also be successfully employed in practical implementations,
45 but this is not the main topic of this work. Finally, let us note that the use of the term weak formulation of PDEs and BVPs originates from the weaker regularity requirements that can be imposed on the solution, while still handling a well-posed problem (in the sense of Hadamard). The terms “weak” and “variational” formulation are here used interchangeably, given that the weak formulation of the PCM satisfies the hypotheses of both the Lax–Milgram lemma and its variational corollary.
39
2.2 PCM-SCF open-ended response theory
Notation.
The PCM equations will be written in the “complete basis”: we will introduce the usual boundary-element method (BEM) discretization at the very end of the derivation. In other words, we will be working with the exact integral equation and not with its discretized counterpart. As a consequence, the apparent surface charge σ and the electrostatic potential φ will have a continuous dependence on a “cavity surface” index s. Whenever a charge-potential product is present, it is to be interpreted as the surface integral, i.e. the scalar product in the suitable, infinite-dimensional vector space on the cavity boundary Γ. The following shorthand notation will be adopted: σφ = (σ, φ)
Γ
. We use lowercase Latin letters (a, b, c…) as a composite index for the perturbation operator and the frequency index (cf. eqn (7)–(16) in ref. 9). The perturbation strength for a given perturbing one-electron operator A associated with a frequency ω
a
will thus be written as ε
a
. Perturbation-strength derivatives will be denoted by lowercase Latin superscripts (a, b, c…) to the differentiated quantities. Finally, a tilde will be used for quantities that are considered at general field strengths and thus, in general, are time dependent. As an example, the overlap matrix and its derivative with respect to ε
a
at general perturbation strength will be ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) and
and ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) a
, respectively. Equivalently, S and S
a
denote the overlap matrix and its perturbation-strength derivative at zero field strength, respectively.
a
, respectively. Equivalently, S and S
a
denote the overlap matrix and its perturbation-strength derivative at zero field strength, respectively. 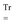 will denote that the trace of the expression to follow should be taken.
will denote that the trace of the expression to follow should be taken. 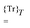 will additionally denote that the tracing is followed by time-averaging over a period T of the collected perturbations.
will additionally denote that the tracing is followed by time-averaging over a period T of the collected perturbations.
Our derivation follows closely the one in ref. 9 and the subsequent developments in ref. 10. The original expressions were developed for a system considered to be in vacuo, and in order to incorporate the effects of the PCM, any energy-like term that appears in these expressions will be augmented by the appropriate solvent term. The solvent term will be derived according to the polarization energy functional given in eqn (5) and the classical Hellmann–Feynman theorem it satisfies, namely eqn (7).
Response functions can be expressed as perturbation-strength derivatives of the perturbation-strength-differentiated time-averaged quasienergy Lagrangian evaluated at zero perturbation strengths. For example, the linear response function can be written as
| | 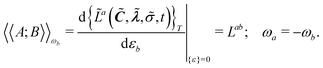 | (8) |
In an atomic orbital-based density matrix parametrization, the time-averaged quasienergy derivative needed to evaluate response functions is given as
| | 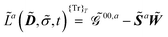 | (9) |
where an element of the overlap matrix
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif)
is given by
and where the generalized, energy-weighted density matrix
![[W with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0057_0303.gif)
was introduced and is given by
| | 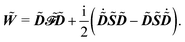 | (11) |
This expression for W involves the density matrix ![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) , its time-differentiated analogue
, its time-differentiated analogue 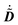 and the generalized Kohn–Sham (KS) matrix
and the generalized Kohn–Sham (KS) matrix 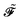 given by
given by
| | 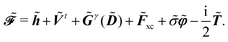 | (12) |
The expression for
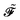
includes both vacuum-like and PCM contributions. The vacuum-like contributions are expressed in terms of the one-electron matrices
![[h with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0068_0303.gif)
and
Ṽt, and the two-electron matrix
![[G with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0047_0303.gif) γ
γ(
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif)
), which are, respectively, defined in the following way:
| | 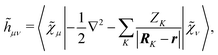 | (13a) |
| | 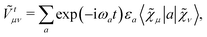 | (13b) |
| | 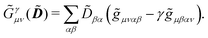 | (13c) |
Another part of the vacuum-like contribution is the functional derivative matrix
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) xc,μν
xc,μν of the XC potential, whose elements are given by
| | 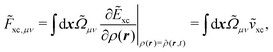 | (14) |
where the integration involves the overlap distribution
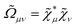
and the functional derivative of the XC functional in the adiabatic approximation. The
x variable refers to both spatial and spin coordinates. The last vacuum-like contribution in
eqn (12) is the anti-Hermitian, time-differentiated overlap matrix
![[T with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0054_0303.gif)
whose elements are given by
| | 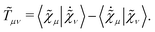 | (15) |
Finally, the PCM contribution ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e12c.gif) involves the electrostatic potential integrals
involves the electrostatic potential integrals
| | 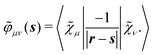 | (16) |
The first term in eqn (9), 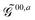 , involves the generalized KS energy
, involves the generalized KS energy 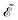 as shown in eqn (97) in ref. 9. The free energy term
as shown in eqn (97) in ref. 9. The free energy term 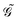 including PCM effects is produced by additionally considering solute–solvent interaction terms, so that
including PCM effects is produced by additionally considering solute–solvent interaction terms, so that
| | 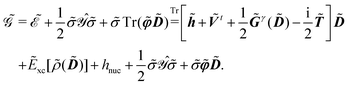 | (17) |
Due to the implicit time dependence of ![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) and
and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , higher-order derivatives of the KS generalized energy will require application of the chain rule. The mn, abc… superscript describes how and to what extent the chain rule was applied for a given term, i.e. the number of explicit differentiations with respect to the variational densities, so that
, higher-order derivatives of the KS generalized energy will require application of the chain rule. The mn, abc… superscript describes how and to what extent the chain rule was applied for a given term, i.e. the number of explicit differentiations with respect to the variational densities, so that
| | 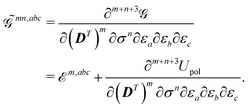 | (18) |
In this notation, the index
m denotes the order of differentiation with respect to the density matrix
D, while the index
n symbolizes the order of differentiation with respect to the ASC density
σ. Differentiation with respect to the density matrix will result in a 2
m-rank tensor, while differentiation with respect to the ASC density will result in a function of the continuous cavity index
s. For higher-order properties, mixed terms involving both density matrix and ASC density differentiation may generally occur. In the fixed-cavity approximation, the cavity is kept frozen at a given molecular geometry.
46 Under this simplifying assumption, only the linear interaction term in the polarization functional
eqn (5) will be affected by the movements of the nuclei
via the dependence of basis functions on the molecular geometry. Its perturbation-strength derivative will then be
| | 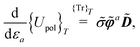 | (19) |
where the second term only involves derivatives of the electrostatic potential integrals. We remark that, under the fixed-cavity approximation, both the density matrix –
m – and ASC density –
n – differentiation indices in
eqn (18) can only assume the values 0 or 1 in order for the
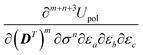
term not to be zero. By construction, the density matrix dependence in the polarization functional is at most linear, while, by virtue of the classical Hellmann–Feynman theorem,
eqn (7), the ASC variational density will also appear at most linearly in
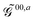
.
The free energy term perturbation strength derivative is given as
| | 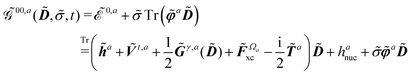 | (20) |
where the matrix
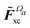
denotes the functional derivative matrix defined in terms of the perturbed overlap distributions
![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) a
a, so that
| | 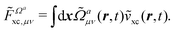 | (21) |
Response functions can then be obtained by straightforward differentiation with respect to additional perturbations and subsequent evaluation at zero perturbation strength, so that
| | 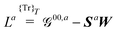 | (22a) |
| | 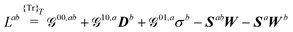 | (22b) |
| | 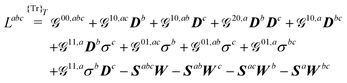 | (22c) |
and similarly for higher-order response functions. More detailed expressions for the derivatives of the generalized KS free energy are shown in Appendix A. The expressions
(22a)–(22c) adhere to the
n + 1 formulation, whereby perturbation-strength derivatives of the variational densities up to order
n are required in order to assemble response functions of order
n + 1. It is possible to make other formulations of response theory for which truncation rules for perturbed arguments between and including the
n + 1 and 2
n + 1 rules are possible.
9,10,47 This entails the introduction of Lagrange multipliers
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0df.gif) a
a and
![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e126.gif) a
a to take into consideration the idempotency of the density matrix and the time-dependent SCF (TD-SCF) equations, respectively, so that the idempotency condition is expressed with the matrix
Ỹ and the TD-SCF condition with the matrix
![[Z with combining tilde]](https://www.rsc.org/images/entities/b_i_char_005a_0303.gif)
, where
and
| | 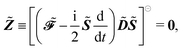 | (24) |
and where the Lagrange multiplier terms are given by
and
| | 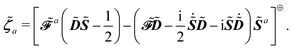 | (26) |
The operators [
M]
⊖ and [
M]
⊕ used in the above expressions were defined in
ref. 9. Response properties including PCM effects can then be calculated from the expression
| | 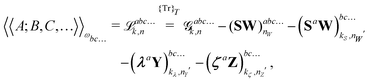 | (27) |
where the subscript integers
k and
n in the various forms shown in this expression denote a given choice of truncation rule. The original expression for systems considered
in vacuo contains an energy term
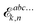
instead of the free energy term
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) abck,n
abck,n but is otherwise unchanged upon solvation, and we will therefore omit further details here about the derivation leading up to
eqn (27), referring instead to previous work for more information and for details about the (
k,
n) truncation rules that can be chosen and applied.
9,10 We note that the task of evaluating
eqn (27) and obtaining terms needed for this evaluation can be cast in recursive form, as shown in
ref. 10, and we further remark that these routines can be augmented to enable the calculation of single residues of response functions.
11 However, the methodological and algorithmic development needed for residues calculations is not changed by the inclusion of PCM effects, and we will therefore again refer to previous work
9,11 for details.
2.3 Parametrization of the perturbed densities and response equations
In order to compute response properties from eqn (27), the various perturbed D, F and S matrices and the derivatives of the ASC density σ that enter into this expression must be obtained. The perturbed overlap matrices can be directly assembled from the relevant one-electron integral derivatives, while the perturbed density and Fock matrices can be obtained from a procedure that involves solving the appropriate response equations. The first step in this procedure is to take perturbation-strength derivatives of the idempotency and TD-SCF conditions of eqn (23) and (24) and evaluating them at zero perturbation strength.9,10 The evaluation of the perturbation-strength-differentiated ASC density introduces an additional response equation, which is constructed by differentiating the equation governing the ASC:| | 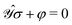 | (28) |
Differentiating eqn (23) and introducing a decomposition of the density matrix into frequency components leads to
| | 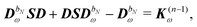 | (29) |
where
bN is the tuple of applied perturbations and
ω is the sum of the associated frequencies. The RHS matrix
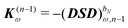
contains all terms that contain derivatives of the density matrix up to order
n − 1.
The perturbed density matrix is partitioned into a particular 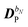 and a homogenous
and a homogenous 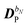 term (H/P partition) as
term (H/P partition) as
| | 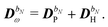 | (30) |
The former may be evaluated in terms of
K(n−1)ω,
i.e. lower-order density matrices and differentiated overlap integrals, so that
| | 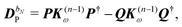 | (31) |
where the projectors
P =
DS,
Q = 1 −
P were used. The homogeneous component is parametrized in terms of the
n-th order response parameters
XbN as
| | 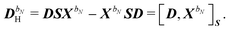 | (32) |
The governing equations for the perturbed ASC densities are obtained in analogy with the handling of perturbed density matrices outlined above. We introduce a decomposition of the ASC density into frequency components into the perturbation-strength derivative of eqn (28), so that
| | 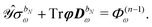 | (33) |
The symbol Φ(n−1)ω has been introduced in analogy to the K(n−1)ω matrix, where
| | 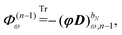 | (34) |
and it contains all terms that depend on lower-order density matrices and differentiated electrostatic potential integrals, for which the latter acts as the metric matrix
S in the definition of
K(n−1)ω. The term
Φ(n−1)ω always contains at least a first derivative of the electrostatic potential integrals and is thus zero if the basis set is independent of the perturbation tuple being considered. We now introduce the H/P partitioning of
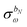
, so that
| | 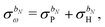 | (35) |
and apply
eqn (30), which leads to a separation of the response integral equation into the following system of equations:
| | 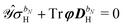 | (36a) |
| | 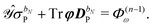 | (36b) |
We note that the particular ASC is nonzero if and only if the basis set depends on the external perturbation.
We finally turn our attention to the TDSCF equation. The perturbation-strength differentiated generalized KS matrix is first separated into its frequency components 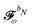 . The H/P partition introduced for the variational densities will induce a similar partition into these frequency components:
. The H/P partition introduced for the variational densities will induce a similar partition into these frequency components:
| | 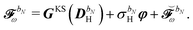 | (37) |
The two-electron and XC contributions depending on the homogeneous perturbed density matrix have been collected in the
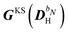
matrix, while all other contributions are collected in
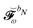
. A more detailed discussion of these aspects can be found in
ref. 9 and 10. The parametrization of the homogeneous part of the perturbed density matrix can be exploited to conveniently reformulate the perturbed TDSCF equation, so that
| | 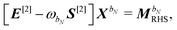 | (38) |
where the generalized Hessian
E[2] and metric
S[2] matrices were introduced and are defined by their transformations on the response parameters
XbN:
48,49| | 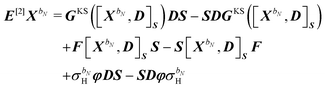 | (39) |
| | | S[2]XbN = S[XbN, D]SS. | (40) |
The generalized Hessian matrix E[2] includes two types of solvent contributions: implicit terms included in the zeroth-order Fock matrix, F, and explicit terms, involving the N-th order homogenous ASC variational density. The latter are the last two terms in eqn (39). The theoretical treatment of frequency-dependent properties in solution within the PCM requires adoption of a nonequilibrium response framework.13,50 The explicit PCM terms in eqn (39) are then evaluated using the optical permittivity, defined as the square of the refractive index of the solvent ε∞ = n2, instead of the static permittivity εs, which is employed to compute the implicit contributions. In contrast to E[2], the generalized metric matrix S[2] is unchanged. The right-hand side (RHS) in the response equation only includes terms that depend on particular contributions up to the desired order or lower-order perturbed density matrices:
| | 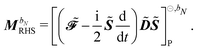 | (41) |
2.4 PCM-SCF linear response: comparison with previous formulations
Derivations of the linear50,51 and nonlinear response functions52,53 for the PCM-SCF model have previously appeared in the literature. All previous derivations exploit the definition of a solute Hamiltonian which is nonlinearly coupled to the classical dielectric continuum.13,43 In such a framework, the solvent polarization is not treated as an independent, variational degree of freedom. Solvent contributions to the Hamiltonian are partitioned based on their order dependence on the density matrix: zeroth, first (linear) or second (quadratic) order. We remark that one- and two-electron contributions to the energy are also linearly and quadratically dependent, respectively, on the density matrix. Solvent contributions will thus enter into response theory expressions in much the same way as the proper one- and two-electron terms do.
A derivation of open-ended response theory for an SCF solute coupled with a classical description of the solute has already been presented in the context of the PE MM model.20 There, the abovementioned order dependence on the density matrix of solvent contributions, which arises when a nonlinear Hamiltonian is invoked, was used to facilitate the identification of the polarization terms to be included in the open-ended formulation of electric response properties. That derivation can also be used when the classical solvent model is implicit, such as the PCM considered in the present work, and will in this case lead to a specific implementation strategy, vide infra. However, the converse is also true. As shown by Lipparini et al.,54 a variational formulation can also be used for classical polarizable explicit solvation models.
To the best of our knowledge, the first derivation of the linear response function exploiting the variational formulation for a quantum/classical polarizable Hamiltonian was presented by Lipparini et al. in ref. 19. Our derivation naturally includes general perturbations, if the fixed-cavity approximation is assumed, and avoids the use of nonlinear Hamiltonians, representing a clear theoretical advantage.
An explicit example: first-order, electric response properties.
We here report explicit expressions for the first-order response equations. The differentiated TDSCF condition of eqn (24) evaluated at zero perturbation strength is| | 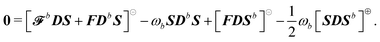 | (42) |
Decomposing into frequency components and introducing the H/P partition for the variational densities yields:| | 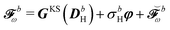 | (43) |
where all the contributions not depending on H-type terms are collected into 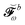 , so that
, so that| | 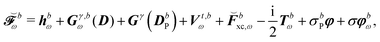 | (44) |
where 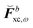 contains derivative terms of the XC matrix that are independent of the response parameters. We refer to eqn (A26) of the original paper for its explicit expression.9 Reorganizing eqn (43) to have all terms dependent on Xb on the left-hand side (LHS) yields
contains derivative terms of the XC matrix that are independent of the response parameters. We refer to eqn (A26) of the original paper for its explicit expression.9 Reorganizing eqn (43) to have all terms dependent on Xb on the left-hand side (LHS) yields| | | GKS([Xb,D]S)DS − SDGKS([Xb,D]S) + F[Xb,D]SS − S[Xb,D]SF + σbHφDS − SDφσbH − ωbS[Xb,D]SS = [E[2] − ωbS[2]]Xb, | (45) |
where we recognize the action of the propagator [E[2] − ωbS[2]] on the response vector Xb. Finally, the right-hand side MbRHS becomes| |  | (46) |
letting us cast the first-order response equations in the usual form| | | [E[2] − ωbS[2]]Xb = MbRHS. | (47) |
Since perturbation-independent basis sets are usually employed in the calculation of electric response properties, considerable simplifications arise in all expressions. As an example, we will illustrate how the equations look when only electric dipole perturbations are considered, and we will use the symbol f for such perturbations. First of all, the particular perturbed variational densities are identically zero:
| | | DfP = PK(0)ωP† − QK(0)ωQ† = 0 | (48) |
since
K(0)ω = −
DSfωD =
0. Moreover, since
Φ(0)ω = −Tr
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φfωD
φfωD = 0, one also has
σfP = 0. Therefore, only terms including
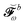
will enter the RHS and among these, only those involving
Vt,bω will be nonzero, so that
| | | [E[2] − ωbS[2]]Xb = [Vt,bω]⊖. | (49) |
3 Implementation
The algorithmic realization of the open-ended PCM-SCF response theory presented requires the solution of the coupled response equations for the homogeneous density matrix, eqn (38), and ASC, eqn (36a). Hence, one can envision two possible strategies for a computer implementation of the open-ended scheme:
Strategy 1
eqn (36a) and (38) are simultaneously solved, in much the same way as described by Lipparini et al. for the SCF equations.45 A suitable initial guess is provided for both densities and the appropriate iterative linear equation solvers are employed.55,56 A convergence acceleration scheme might also be exploited.57,58
Strategy 2 given the initial guess for the response parameters, the homogenous density matrix is formed and the perturbed MEP calculated. Eqn (36a) is solved, eventually allowing the computation of the linear transformation in eqn (39) and the solution of eqn (38).
The two strategies are of course expected to lead to identical results. Strategy 1 could be advantageous when large molecular solutes are considered and might show better convergence properties, at the expense of a nontrivial extension to both the quasienergy derivative Lagrangian framework for the efficient elimination of response parameters9,47 and to the corresponding recursive implementation.10,11 The implementation we present in this work follows Strategy 2. This avoids excessive modifications to the recursive core of the open-ended response code and allows a straightforward use of efficient response parameter elimination schemes.47 The resulting computer code exploits interfaces between the Dalton program package,59 the PCMSolver library,30 the implementation of the open-ended, recursive approach to atomic orbital-based density matrix response theory10 and the subsequent development of the latter for the calculation of single residues of response functions.11 The interface to PCMSolver provides an alternative implementation of PCM capabilities at the SCF level of theory to the one presented by Cammi et al.60 To test the linear transformations of the generalized Hessian and metric matrices of eqn (39) and (40), a non-recursive PCM-SCF linear response code was implemented exploiting the PCMSolver library.30 Further testing for the linear, quadratic and cubic response functions and corresponding single residues for electric dipole perturbations was achieved by comparing to previously published, non-recursive implementations available in Dalton.50–53
4 Computational details
4.1 Molecular structures
The molecules investigated in this work are PNA, PDNB and MCP, shown in Fig. 1.
 |
| | Fig. 1 Molecules investigated in this work: para-nitroaniline (PNA), para-dinitrobenzene (PDNB) and methylenecyclopropene (MCP). | |
The geometries were optimized in vacuo using Gaussian 09,61 the B3LYP XC functional62–65 and the cc-pVQZ basis set.66 No constraints were used on the symmetry during the geometry optimization, yielding point groups Cs, D2h and C2v for PNA, PDNB and MCP, respectively. The structures of PDNB (identical to the one used in ref. 12) and MCP are planar, whereas the structure of PNA (identical to the one used in ref. 11) is non-planar with a H–N–C–C dihedral angle of 21°. All PCM calculations are done on the vacuum geometry so that all differences arise from direct solvent effects rather than from indirect (geometrical) effects. The ESI† contains the molecular structures used in the calculations, in Dalton input format.
4.2 MPA calculations
The calculations were performed in a development version of the Dalton program using the open-ended response code of Ringholm et al.10 One-electron property integrals and their arbitrary-order derivatives were provided by the Gen1Int library.67 The XC functionals library XCFun68 and the integrator library XCint were used for the evaluation of the XC terms and their derivatives. Finally, the PCM functionality was provided by the PCMSolver library.30 The ESI† contains details about software versions and build toolchain used in this work. Vertical excitation energies were calculated for the 7 lowest excited states of the molecules in Fig. 1. MPA transition moments S were calculated for the same excitations from the residues of the response functions using the implementation described in ref. 11. The CAM-B3LYP XC functional69 and the aug-cc-pVDZ basis set66 were chosen based on previous results in ref. 11.
Rotationally averaged transition strengths 〈δMPA〉 were calculated from the transition moments S and their complex conjugates ![[S with combining macron]](https://www.rsc.org/images/entities/b_char_0053_0304.gif) as70
as70
| | 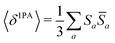 | (50) |
| | 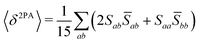 | (51) |
| | 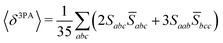 | (52) |
| | 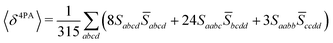 | (53) |
| | 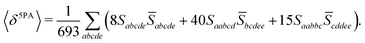 | (54) |
The dimensionality, in atomic units, of the MPA strengths is systematically given by11
| | | [〈δMPA〉] = a02M·Eh2(M−1) | (55) |
where
a0 and
Eh are the atomic units for length and energy, respectively, and
M is the number of photons involved. MPA strengths in atomic units are used throughout unless otherwise stated.
4.3 PCM details
The calculations of the transition moments were performed in a range of solvents with different static (εs) and dynamic (ε∞) relative permittivities: vacuum (εs = 1.0, ε∞ = 1.0), n-heptane (εs = 1.92, ε∞ = 1.918), cyclohexane (εs = 2.023, ε∞ = 2.028), tetrachloromethane (εs = 2.228, ε∞ = 2.129), benzene (εs = 2.247, ε∞ = 2.244), 1,4-dioxane (εs = 2.250, ε∞ = 2.023), toluene (εs = 2.379, ε∞ = 2.232), chloroform (εs = 4.90, ε∞ = 2.085), chlorobenzene (εs = 5.621, ε∞ = 2.320), aniline (εs = 6.89, ε∞ = 2.506), tetrahydrofurane (εs = 7.58, ε∞ = 1.971), dichloromethane (εs = 8.93, ε∞ = 2.020), dichloroethane (εs = 10.36, ε∞ = 2.085), acetone (εs = 20.7, ε∞ = 1.841), ethanol (εs = 24.55, ε∞ = 1.847), methanol (εs = 32.63, ε∞ = 1.758), acetonitrile (εs = 36.64, ε∞ = 1.806), nitromethane (εs = 38.20, ε∞ = 1.904), dimethylsulfoxide (εs = 46.7, ε∞ = 2.179), propylene carbonate (εs = 64.96, ε∞ = 2.019) and water (εs = 78.39, ε∞ = 1.776). No local field effects were included in this study.71–76
The molecular cavities were generated from the van der Waals surface, i.e. from a set of atom-centered, interlocking spheres. For every molecule this was computed from the Bondi–Mantina set of van der Waals radii:77,78 1.20 Å for hydrogen, 1.70 Å for carbon, 1.55 Å for nitrogen and 1.52 Å for oxygen. All radii were scaled by a factor of 1.2. Cavity generation and discretization was performed according to the one-point centroid collocation GePol scheme, deactivating the addition of non-atom-centered spheres.24,25 Since vacuum geometries are used in all calculations, the cavity is the same across all solvents.
5 Results
The excitation energies of the lowest electronic excitations in PNA, PDNB and MCP are shown in Fig. 2 as a function of the Onsager factor 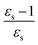 , where εs is the static relative permittivity.79
, where εs is the static relative permittivity.79
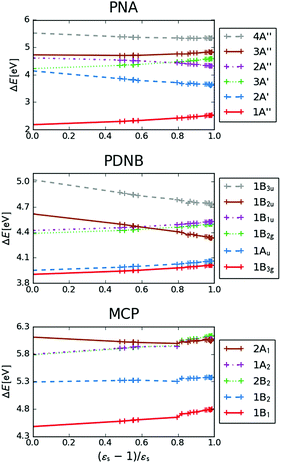 |
| | Fig. 2 Selected excitation energies ΔE [eV] as a function of the Onsager factor ((εs − 1)/εs, where εs is the static permittivity) for PNA, PDNB and MCP. See the ESI† for the plot containing all states included in this study. | |
For some states, the excitation energy increases (e.g. 3A′ in PNA) or decreases (e.g. 1B2u in PDNB) considerably with solvent polarity, leading to a change in the ordering of the different excited states. The non-monotonic behavior of the excitation energy when going from chloroform (εs = 4.90, 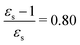 , ε∞ = 2.085) to chlorobenzene (εs = 5.621,
, ε∞ = 2.085) to chlorobenzene (εs = 5.621, 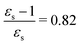 , ε∞ = 2.320) and aniline (εs = 6.89,
, ε∞ = 2.320) and aniline (εs = 6.89, 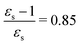 , ε∞ = 2.506) can be explained by the increase in the optical dielectric constant (ε∞) in the latter two solvents. Thus, the occurrence of these discontinuities is an effect of the non-equilibrium formulation of PCM that we employ. The calculated solvatochromic shifts are smaller than the experimental ones (see Appendix B), which is likely related to the (deliberate) omission of indirect solvent effects.
, ε∞ = 2.506) can be explained by the increase in the optical dielectric constant (ε∞) in the latter two solvents. Thus, the occurrence of these discontinuities is an effect of the non-equilibrium formulation of PCM that we employ. The calculated solvatochromic shifts are smaller than the experimental ones (see Appendix B), which is likely related to the (deliberate) omission of indirect solvent effects.
MPA strengths and dominating orbitals for selected excitations in PNA are shown in Fig. 3 and 4. Among the first five excitations of PNA (thus excluding the 4A′′ state), the 2A′ excitation is the strongest excitation in vacuo for 1PA up to 5PA, as has been observed for 1PA–4PA before.11 This state is also the brightest in 1PA and 2PA for all solvents examined. The sixth excitation (4A′′), however, is one of the excitations that has a higher strength for 3PA–5PA in the more polar solvents. This illustrates that even qualitative results are poorly transferable from vacuum to solvent and from 1PA to MPA.
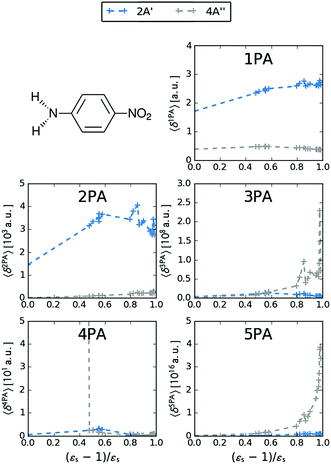 |
| | Fig. 3 MPA strengths 〈δMPA〉 [a.u.] (see eqn (55)) for increasing solvent polarity for two selected electronic excitations in PNA. See the ESI† for the plot containing all states included in this study. | |
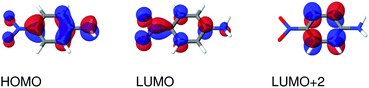 |
| | Fig. 4 Molecular orbitals involved in the electronic excitations of para-nitroaniline (PNA) discussed in this work. The 2A′ excitation is dominated by a HOMO → LUMO transition and the 4A′′ excitation is dominated by a HOMO → LUMO+2 transition. An isosurface value of 0.05 was used to make the plots. | |
The discontinuities in the MPA strengths when increasing the solvent polarity can again be related to the use of the non-equilibrium formulation of PCM. Whereas the static permittivity (εs) increases monotonously from left to right due to the choice of the x-axis, the dynamic permittivity (ε∞) does not. The discontinuities thus reflect the variation in ε∞ with non-monotonous behaviours observed for aniline 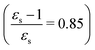 and dimethylsulfoxide
and dimethylsulfoxide 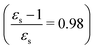 . This effect is hardly observable for 1PA, but is pronounced for the higher-order MPA strengths, and for 3PA and 5PA in particular (Fig. 3).
. This effect is hardly observable for 1PA, but is pronounced for the higher-order MPA strengths, and for 3PA and 5PA in particular (Fig. 3).
MPA strengths can be selectively enhanced by an intermediate state at a defined fraction of the energy of the state in question.12 The 2PA strength of a state with energy ω can be enhanced if another state has an energy of 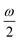 . In the same way, the 3PA strength can be enhanced if another state has an energy of
. In the same way, the 3PA strength can be enhanced if another state has an energy of 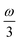 or
or 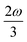 . When another state has an energy of
. When another state has an energy of 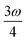 , the 4PA strength (but not the 2PA strength) is selectively enhanced. For 5PA, the most likely resonance condition is another state at
, the 4PA strength (but not the 2PA strength) is selectively enhanced. For 5PA, the most likely resonance condition is another state at 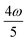 .
.
This resonance enhancement explains the dramatic increase of the 4PA strength of the 4A′′ state in the vacuum calculation. The excitation energy of the 2A′ excitation happens to be at 0.749 times the excitation energy of the 4A′′ excitation (Fig. 2), giving rise to a resonance condition and enhancement of the 4PA strength. Resonance enhancement also contributes to the high 3PA strength of the 4A′′ in dimethylsulfoxide (εs = 46.7, 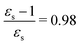 ), where the excitation energy of the 2A′ excitation is 0.678 times the excitation energy of the 4A′′ excitation. It is important to note that our response theory approach breaks down close to such resonance and the results cannot be considered quantitatively accurate. To circumvent this divergence in the MPA strengths, damped response theory should be used,80,81 as reported for 2PA by Kristensen et al.82
), where the excitation energy of the 2A′ excitation is 0.678 times the excitation energy of the 4A′′ excitation. It is important to note that our response theory approach breaks down close to such resonance and the results cannot be considered quantitatively accurate. To circumvent this divergence in the MPA strengths, damped response theory should be used,80,81 as reported for 2PA by Kristensen et al.82
The variation of the MPA strengths with solvent polarity clearly increases with the number of photons. This has also been observed experimentally, comparing 1PA and 2PA for the same excitation in PNA.83 The inclusion of solvent effects thus becomes increasingly important for quantitative MPA calculations with increasing number of photons. Comparison with experimental cross sections83 indicates that the absolute value of the 2PA cross section is underestimated by up to a factor of 2 in the calculations, while the relative strengths across different solvents are not reproduced in the calculations (Appendix B). The underestimation of the 2PA cross sections may be partially caused by the use of TDDFT and can be related to underestimated difference dipole moments.84,85 Indeed, TDDFT/CAM-B3LYP has been shown to underestimate difference dipole moments in PNA.84,86,87
We now turn our attention to the centrosymmetric molecule PDNB. MPA strengths and dominating orbitals for selected excitations in PDNB are shown in Fig. 5 and 6. The high point group symmetry determines whether the different excited states will be allowed for the different one- and multiphoton absorption processes. The 1B3u excitation is the brightest excitation for 1PA, 3PA and 5PA among the first seven excitations, while the B2g excitation is the brightest for 2PA and 4PA. We note that the intensities of the different odd- or even-order photon excitation processes follow each other both in vacuum and in the different solvents. This is due to the fact that the intensity of odd- and even-order multiphoton absorption processes can be shown to be proportional to the one- or two-photon absorption cross section, respectively,12 with exceptions arising due to near-resonances.
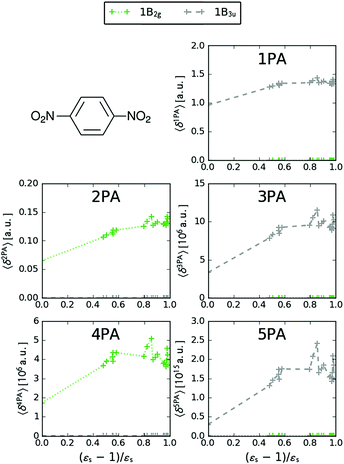 |
| | Fig. 5 MPA strengths 〈δMPA〉 [a.u.] (see eqn (55)) for increasing solvent polarity for two selected electronic excitations in PDNB. See the ESI† for the plot containing all states included in this study. | |
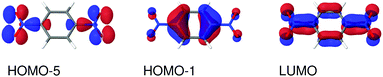 |
| | Fig. 6 Molecular orbitals involved in the electronic excitations of para-dinitrobenzene (PDNB) discussed in this work. The 1B2g excitation is dominated by a HOMO−5 → LUMO transition and the 1B3u excitation is dominated by a HOMO−1 → LUMO transition. An isosurface value of 0.05 was used to make the plots. | |
As a final example, we have considered MCP: some of its excited states undergo a sign change in dipole moment across the solvent polarity scale chosen in this study. The MPA strengths and dominating orbitals for selected excitations in MCP are shown in Fig. 7 and 8. The π → π* 2A1 transition has significant orbital overlap between the occupied and the virtual orbitals (Fig. 8) and is the only strong transition in 1PA. The 1B2 and 2B2 states, however, are accessible via multi-step processes and are indeed the strongest states in 2PA/4PA and 3PA/5PA, respectively. The maximum in the 4PA strength for the 2A1 excitation is due to a resonance with the 1B1 state which is located at 0.759 times the excitation energy of the 2A1 state for n-heptane (εs = 1.920, 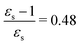 ).
).
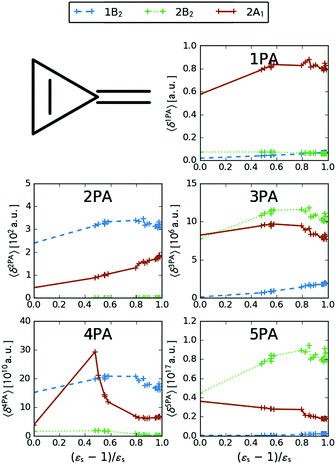 |
| | Fig. 7 MPA strengths 〈δMPA〉 [a.u.] (see eqn (55)) for increasing solvent polarity for three selected electronic excitations in MCP. See the ESI† for the plot containing all states included in this study. | |
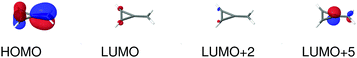 |
| | Fig. 8 Molecular orbitals involved in the electronic excitations of methylenecyclopropene (MCP) discussed in this work. The 1B2 excitation is dominated by a HOMO → LUMO transition, the 2B2 excitation is dominated by a HOMO → LUMO+2 transition and the 2A1 excitation is dominated by a HOMO → LUMO+5 transition. An isosurface value of 0.05 was used to make the plots. | |
The kink in the 1PA strength of the 2A1 state between 1,4-dioxane (εs = 2.250, 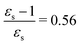 ), toluene (εs = 2.379,
), toluene (εs = 2.379, 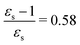 ) and chloroform (εs = 4.90,
) and chloroform (εs = 4.90, 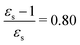 ) can be related to the excited-state dipole moment, which changes sign between 1,4-dioxane and toluene. The excited-state dipole moment of the 1B2 state also has a different direction in vacuum than in solvent. We report the relevant plots of the difference between ground- and excited-state dipole moments in the ESI.†
) can be related to the excited-state dipole moment, which changes sign between 1,4-dioxane and toluene. The excited-state dipole moment of the 1B2 state also has a different direction in vacuum than in solvent. We report the relevant plots of the difference between ground- and excited-state dipole moments in the ESI.†
The results presented serve as an illustration of the applicability of our implementation. When interpreting the results, one should bear in mind the limitations of our methodology. First of all, we have calculated vertical excitation energies and neglected vibronic effects, which have been demonstrated to play a role in 2PA.88,89 Secondly, we have not taken into account the indirect effect of the solvent on the geometry of the chromophore. Indirect solvent effects can be taken into account by using PCM also in the geometry optimization, which has however not been done here, to allow for a comparison of the direct contribution of the various solvents on the MPA strength. Thirdly, the implementation of the solvent model used here does not include explicit local field effects in the molecular cavity71–76 nor non-electrostatic effects.31,32,90,91 Explicit solute–solvent interactions are also not included, but can in principle be recovered using a QM cluster model of the system. Finally, DFT is not likely to give MPA strengths (and, in general, excited-state properties) of high accuracy, as shown for 2PA using a coupled-cluster benchmark.85 There is a clear need for benchmarking DFT MPA strengths against methods of higher accuracy also beyond 2PA.85,92 All these factors are important if a realistic comparison with experiment is to be attempted. The recent coupling of our open-ended response code to a PE QM/MM framework is able to take into account indirect solvent effects, local field effects and explicit solute–solvent interactions, albeit by necessity introducing configurational sampling in the computational protocol.20
6 Conclusion
We have presented the theory and implementation for calculating molecular response properties to arbitrary order in solution within the framework of the polarizable continuum model. The theoretical derivation is based on an energy functional where both the density matrix and the electrostatic polarization in the medium are treated as variational degrees of freedom. Contrary to previous work, the quantum/classical polarizable coupling is not achieved by assuming a nonlinear interaction potential in the Hamiltonian. We have shown that, in the fixed-cavity approximation, molecular response functions to arbitrary order are straightforwardly obtained as higher-order derivatives of the proposed functional. Moreover, differentiation of the stationarity conditions naturally leads to the appropriate response equations determining higher-order perturbed wave function and polarization parameters. Our implementation relies on modular components encapsulating the different tasks required to carry out a response calculation, in line with previous work by some of us.10,11 In particular, we added the PCM terms to the workflow by means of the PCMSolver library,30 in the spirit of the PE implementation recently presented by Steindal et al.20 We have illustrated the implementation by calculating MPA strengths for three small organic molecules. The enhancement of the MPA strength from vacuum to different solvents increases with the number of photons involved in the excitation, clearly emphasizing the importance of including solvent effects in MPA calculations. Relative intensities between features corresponding to different electronic excitations in one- or multiphoton absorption spectra are not necessarily preserved between phenomena involving different numbers of photons absorbed, which is partially related to molecular symmetry. We have also described resonance enhancements in our MPA calculations.
Appendix
A Derivatives of the generalized KS free energy
The generalized KS energy derivatives are given by:| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,a = 00,a = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,a + {σ 0,a + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T Tr(φaD)}T | (56a) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,ab = 00,ab = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,ab + {σ 0,ab + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabD)}T Tr(φabD)}T | (56b) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,abc = 00,abc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,abc + {σ 0,abc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabcD)}T Tr(φabcD)}T | (56c) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,aDb = 10,aDb = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,aDb + {σ 1,aDb + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDb)}T Tr(φaDb)}T | (56d) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,aσb = {σb 01,aσb = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T Tr(φaD)}T | (56e) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,acDb = 10,acDb = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,acDb + {σ 1,acDb + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φacDb)}T Tr(φacDb)}T | (56f) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,abDc = 10,abDc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,abDc + {σ 1,abDc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabDc)}T Tr(φabDc)}T | (56g) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 20,aDbDc = 20,aDbDc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2,aDbDc 2,aDbDc | (56h) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,aDbc = 10,aDbc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,aDbc + {σ 1,aDbc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDbc)}T Tr(φaDbc)}T | (56i) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 11,aσcDb= {σc 11,aσcDb= {σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDb)}T Tr(φaDb)}T | (56j) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,acσb = {σb 01,acσb = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φacD)}T Tr(φacD)}T | (56k) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,abσc = {σc 01,abσc = {σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabD)}T Tr(φabD)}T | (56l) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,aσbc = {σbc 01,aσbc = {σbc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T Tr(φaD)}T | (56m) |
| | ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 11,aσbDc = {σb 11,aσbDc = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDc)}T Tr(φaDc)}T | (56n) |
B Comparison with experimental data
Although the paper is essentially methodological, we provide a short comparison of our results with available experimental data. A detailed study of the solvatochromic shift of PNA including 2PA spectra has been presented recently by Wielgus et al.83 For PDNB, maximum absorption has been observed at 4.75 eV in ethanol.93 For MCP, two values have been reported in the literature: 4.01 eV in n-pentane and 4.49 eV in methanol.94 In Table 1, we report our vertical excitation energies (VEEs) together with available experimental results, when the same solvent was available (our calculated values in n-heptane are however compared to experimental data obtained in n-hexane for PNA and in n-pentane for MCP).
Table 1 Calculated vertical excitation energy (VEE) in different solvents for PNA, PDNB and MCP compared with the available experimental absorption maxima. All values are in eV
| Substrate |
Solvent |
Abs max (exp.) |
VEEa (calc.) |
|
This work.
Experimental values from ref. 83.
Calculated values using n-heptane as solvent.
Experimental values from ref. 93.
Experimental values from ref. 94.
|
| PNAb |
n-Hexanec |
3.87 |
3.86 |
| Toluene |
3.59 |
3.79 |
| 1,4-Dioxane |
3.51 |
3.82 |
| THF |
3.42 |
3.69 |
| Methanol |
3.35 |
3.66 |
| Ethanol |
3.32 |
3.65 |
| Water |
3.25 |
3.65 |
| DMSO |
3.19 |
3.61 |
|
|
| PDNBd |
Ethanol |
4.75 |
4.75 |
|
|
| MCPe |
n-Pentanec |
4.01 |
4.57 |
| Methanol |
4.49 |
4.79 |
For PNA, our results are overall qualitatively well correlated with the experimental absorption maxima. However, the calculations are more compressed (an overall variation of 0.25 eV compared to 0.68 eV for the experiments) and water and 1,4-dioxane are slight outliers. A possible explanation for the range compression is the lack of indirect solvent effects (vacuum geometries have been employed throughout, a conscious choice to isolate the direct effects on the MPA cross sections), whereas specific solvent effects might explain why water is an outlier.
For MCP, the computed solvent shift (0.22 eV) is also less pronounced than for the experimental value (0.48 eV) but in good agreement with previous state-specific multiconfigurational calculations (0.18 eV) reported in ref. 60. For PDNB, we cannot draw any conclusions from one isolated number and the observed agreement with experiment is likely to be fortuitous.
2PA strengths for PNA in three solvents were converted to cross sections for comparison with available experimental data83 using85
| | 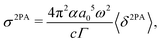 | (57) |
where
α is the fine structure constant,
a0 is the bohr radius,
c is the velocity of light,
ω is the photon energy (
i.e. half the excitation energy) and
Γ is the half-width half-maximum (HWHM) of the (Lorentzian) broadening function describing homogeneous broadening. The HWHM for 1,4-dioxane, propylene carbonate and dimethyl sulfoxide were taken from reported experimental work (FWHW 4672 cm
−1, 4490 cm
−1, 4014 cm
−1),
83 giving
Γ = 0.2897 eV, 0.2783 eV and 0.2488 eV, respectively. The dimensionality of the 2PA cross section is cm
4 s photon
−1 with 1 × 10
−50 cm
4 s photon
−1 commonly referred to as 1 GM (
Table 2).
Table 2 Calculated excitation energies ΔE [eV], 2PA strengths 〈δ2PA〉 [a04·Eh2] and MPA cross sections σ2PA [GM] and experimental83σ2PAexp [GM] for the 2A′ excitation in para-nitroaniline (PNA) in various solvents
| Solvent |
ΔE |
〈δ2PA〉 |
σ
2PA
|
σ
2PAexp
|
| 1,4-Dioxane |
3.82 |
3334 |
6.1 |
8.04 |
| Dimethyl sulfoxide |
3.61 |
3438 |
5.9 |
12.17 |
| Propylene carbonate |
3.62 |
3171 |
6.1 |
9.52 |
Acknowledgements
The authors thank Daniel H. Friese and Radovan Bast (University of Tromsø—The Arctic University of Norway) for discussion and technical help. R. D. R. thanks Filippo Lipparini (Johannes Gutenberg Universität, Mainz) for discussions on the weak formulation of the PCM and Jógvan Magnus Haugaard Olsen (University of Southern Denmark) for helping with the implementation and testing of the open-ended response scheme within Dalton. The authors acknowledge support from the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30), from the European Research Council through a Starting Grant (Grant No. 279619) and from the Norwegian Supercomputer Program through a grant for computer time (Grant No. NN4654K). A. H. S. acknowledges financial support from Tromsø Forskningsstiftelse (SurfInt grant).
References
- M. Göppert-Mayer, Ann. Phys., 1931, 401, 273–294 Search PubMed.
- W. Kaiser and C. G. B. Garrett, Phys. Rev. Lett., 1961, 7, 229–231 Search PubMed.
- G. S. He, P. P. Markowicz, T. C. Lin and P. N. Prasad, Nature, 2002, 415, 767–770 Search PubMed.
- P. P. Markowicz, G. S. He and P. N. Prasad, Opt. Lett., 2005, 30, 1369–1371 Search PubMed.
- Q. Zheng, H. Zhu, S.-C. Chen, C. Tang, E. Ma and X. Chen, Nat. Photonics, 2013, 7, 234–239 Search PubMed.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235–3264 Search PubMed.
- H. Hettema, H. J. Aa. Jensen, P. Jørgensen and J. Olsen, J. Chem. Phys., 1988, 97, 1174–1190 Search PubMed.
- D. Jonsson, P. Norman and H. Ågren, J. Chem. Phys., 1996, 105, 6401–6419 Search PubMed.
- A. J. Thorvaldsen, K. Ruud, K. Kristensen, P. Jørgensen and S. Coriani, J. Chem. Phys., 2008, 129, 214108 Search PubMed.
- M. Ringholm, D. Jonsson and K. Ruud, J. Comput. Chem., 2014, 35, 622–633 Search PubMed.
- D. H. Friese, M. T. P. Beerepoot, M. Ringholm and K. Ruud, J. Chem. Theory Comput., 2015, 11, 1129–1144 Search PubMed.
- D. H. Friese, R. Bast and K. Ruud, ACS Photonics, 2015, 2, 572–577 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 Search PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed. Engl., 2009, 48, 1198–1229 Search PubMed.
-
J. M. H. Olsen and J. Kongsted, Advances in Quantum Chemistry, Academic Press, 2011, vol. 61, pp. 107–143 Search PubMed.
- A. H. Steindal, K. Ruud, L. Frediani, K. Aidas and J. Kongsted, J. Phys. Chem. B, 2011, 115, 3027–3037 Search PubMed.
- C. Curutchet, A. Muñoz-Losa, S. Monti, J. Kongsted, G. D. Scholes and B. Mennucci, J. Chem. Theory Comput., 2009, 5, 1838–1848 Search PubMed.
- S. Caprasecca, C. Curutchet and B. Mennucci, J. Chem. Theory Comput., 2012, 8, 4462–4473 Search PubMed.
- F. Lipparini, C. Cappelli and V. Barone, J. Chem. Theory Comput., 2012, 8, 4153–4165 Search PubMed.
- A. H. Steindal, M. T. P. Beerepoot, M. Ringholm, N. H. List, K. Ruud, J. Kongsted and J. M. H. Olsen, Phys. Chem. Chem. Phys., 2016, 18, 28339–28352 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 Search PubMed.
- E. Cancès and B. Mennucci, J. Math. Chem., 1998, 23, 309–326 CrossRef.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 Search PubMed.
- J. L. Pascual-Ahuir, E. Silla, J. Tomasi and R. Bonaccorsi, J. Comput. Chem., 1987, 8, 778–787 Search PubMed.
-
C. S. Pomelli, Continuum Solvation Models in Chemical Physics, John Wiley & Sons, Ltd, 2007, pp. 49–63 Search PubMed.
- L. Frediani, R. Cammi, S. Corni and J. Tomasi, J. Chem. Phys., 2004, 120, 3893–3907 Search PubMed.
- R. Di Remigio, K. Mozgawa, H. Cao, V. Weijo and L. Frediani, J. Chem. Phys., 2016, 144, 124103 Search PubMed.
- M. A. Aguilar, F. J. Olivares del Valle and J. Tomasi, J. Chem. Phys., 1993, 98, 7375–7384 Search PubMed.
- R. Cammi and J. Tomasi, Int. J. Quantum Chem., 1995, 56, 465–474 Search PubMed.
- PCMSolver, an Application Programming Interface for the Polarizable Continuum Model electrostatic problem, written by R. Di Remigio, L. Frediani and K. Mozgawa, (see http://pcmsolver.readthedocs.io/).
- C. Amovilli and B. Mennucci, J. Phys. Chem. B, 1997, 101, 1051–1057 Search PubMed.
- V. Weijo, B. Mennucci and L. Frediani, J. Chem. Theory Comput., 2010, 6, 3358–3364 Search PubMed.
- R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513 Search PubMed.
- S. Corni, R. Cammi, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 123, 134512 Search PubMed.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 Search PubMed.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504 CrossRef PubMed.
- F. Lipparini, G. Scalmani, B. Mennucci, E. Cancès, M. Caricato and M. J. Frisch, J. Chem. Phys., 2010, 133, 014106 Search PubMed.
-
G. C. Hsiao and W. L. Wendland, Boundary Integral Equations, Springer, 2008 Search PubMed.
-
A. Ern and J.-L. Guermond, Theory and Practice of Finite Elements, Springer, 2004 Search PubMed.
-
S. A. Sauter and C. Schwab, Boundary Element Methods, Springer, 2011 Search PubMed.
-
W. Hackbusch, Integral Equations: Theory and Numerical Treatment, Birkhäuser, 1995 Search PubMed.
- E. Cancès and B. Mennucci, J. Chem. Phys., 1998, 109, 249–259 Search PubMed.
- J. E. Sanhueza, O. Tapia, W. G. Laidlaw and M. Trsic, J. Chem. Phys., 1979, 70, 3096–3098 Search PubMed.
- F. Lipparini, C. Cappelli, G. Scalmani, N. De Mitri and V. Barone, J. Chem. Theory Comput., 2012, 8, 4270–4278 Search PubMed.
- F. Lipparini, G. Scalmani, B. Mennucci and M. J. Frisch, J. Chem. Theory Comput., 2011, 7, 610–617 Search PubMed.
- R. Cammi and J. Tomasi, J. Chem. Phys., 1994, 101, 3888–3897 Search PubMed.
- K. Kristensen, P. Jørgensen, A. J. Thorvaldsen and T. Helgaker, J. Chem. Phys., 2008, 129, 214103 Search PubMed.
- H. Larsen, P. Jørgensen, J. Olsen and T. Helgaker, J. Chem. Phys., 2000, 113, 8908–8917 Search PubMed.
- T. Kjærgaard, P. Jørgensen, J. Olsen, S. Coriani and T. Helgaker, J. Chem. Phys., 2008, 129, 054106 Search PubMed.
- R. Cammi and B. Mennucci, J. Chem. Phys., 1999, 110, 9877–9886 Search PubMed.
- R. Cammi, L. Frediani, B. Mennucci and K. Ruud, J. Chem. Phys., 2003, 119, 5818–5827 Search PubMed.
- L. Frediani, H. Ågren, L. Ferrighi and K. Ruud, J. Chem. Phys., 2005, 123, 144117 Search PubMed.
- L. Ferrighi, L. Frediani and K. Ruud, J. Chem. Phys., 2010, 132, 024107 Search PubMed.
- F. Lipparini, L. Lagardère, B. Stamm, E. Cancès, M. Schnieders, P. Ren, Y. Maday and J. P. Piquemal, J. Chem. Theory Comput., 2014, 10, 1638–1651 Search PubMed.
- J. Kauczor, P. Jørgensen and P. Norman, J. Chem. Theory Comput., 2011, 7, 1610–1630 Search PubMed.
-
Y. Saad, Iterative Methods for Sparse Linear Systems, Society for Industrial and Applied Mathematics, 2003 Search PubMed.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 Search PubMed.
- R. J. Harrison, J. Comput. Chem., 2004, 25, 328–334 Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 Search PubMed.
- R. Cammi, L. Frediani, B. Mennucci, J. Tomasi, K. Ruud and K. V. Mikkelsen, J. Chem. Phys., 2002, 117, 13–26 Search PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 Search PubMed.
- B. Gao, A. J. Thorvaldsen and K. Ruud, Int. J. Quantum Chem., 2011, 111, 858–872 Search PubMed.
- U. Ekström, L. Visscher, R. Bast, A. J. Thorvaldsen and K. Ruud, J. Chem. Theory Comput., 2010, 6, 1971–1980 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 Search PubMed.
- D. H. Friese, M. T. P. Beerepoot and K. Ruud, J. Chem. Phys., 2014, 141, 204103 Search PubMed.
- R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 1998, 102, 870–875 Search PubMed.
- P. Macak, P. Norman, Y. Luo and H. Ågren, J. Chem. Phys., 2000, 112, 1868–1875 Search PubMed.
- R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2000, 104, 4690–4698 Search PubMed.
- R. Cammi, L. Frediani, B. Mennucci and J. Tomasi, THEOCHEM, 2003, 633, 209–216 Search PubMed.
- L. Ferrighi, L. Frediani, C. Cappelli, P. Sałek, H. Ågren, T. Helgaker and K. Ruud, Chem. Phys. Lett., 2006, 425, 267–272 Search PubMed.
- S. Pipolo, S. Corni and R. Cammi, J. Chem. Phys., 2014, 140, 164114 Search PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 Search PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 Search PubMed.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 Search PubMed.
- P. Norman, D. M. Bishop, H. J. Aa. Jensen and J. Oddershede, J. Chem. Phys., 2001, 115, 10323–10334 Search PubMed.
- P. Norman, D. M. Bishop, H. J. Aa. Jensen and J. Oddershede, J. Chem. Phys., 2005, 123, 194103 Search PubMed.
- K. Kristensen, J. Kauczor, A. J. Thorvaldsen, P. Jørgensen, T. Kjærgaard and A. Rizzo, J. Chem. Phys., 2011, 134, 214104 Search PubMed.
- M. Wielgus, J. Michalska, M. Samoc and W. Bartkowiak, Dyes Pigm., 2015, 113, 426–434 Search PubMed.
- R. Zaleśny, G. Tian, C. Hättig, W. Bartkowiak and H. Ågren, J. Comput. Chem., 2015, 36, 1124–1131 Search PubMed.
- M. T. P. Beerepoot, D. H. Friese, N. H. List, J. Kongsted and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 19306–19314 Search PubMed.
- M. Ehara, R. Fukuda, C. Adamo and I. Ciofini, J. Comput. Chem., 2013, 34, 2498–2501 Search PubMed.
- J. J. Eriksen, S. P. A. Sauer, K. V. Mikkelsen, O. Christiansen, H. J. Aa. Jensen and J. Kongsted, Mol. Phys., 2013, 111, 1235–1248 Search PubMed.
- E. Kamarchik and A. I. Krylov, J. Phys. Chem. Lett., 2011, 2, 488–492 Search PubMed.
-
A. Rizzo, S. Coriani and K. Ruud, Computational Strategies for Spectroscopy. From Small Molecules to Nano Systems, John Wiley and Sons, 2012, pp. 77–135 Search PubMed.
- K. Mozgawa, B. Mennucci and L. Frediani, J. Phys. Chem. C, 2014, 118, 4715–4725 Search PubMed.
- K. Mozgawa and L. Frediani, J. Phys. Chem. C, 2016, 120, 17501–17513 Search PubMed.
- M. J. Paterson, O. Christiansen, F. Pawłowski, P. Jørgensen, C. Hättig, T. Helgaker and P. Sałek, J. Chem. Phys., 2006, 124, 054322 Search PubMed.
- T. Abe, BCSJ, 1960, 33, 220–222 Search PubMed.
- S. W. Staley and T. D. Norden, J. Am. Chem. Soc., 1984, 106, 3699–3700 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Contains code and build toolchain details, input and output files, data harvesting scripts, collected data and plotting scripts. See DOI: 10.1039/c6cp06814f and https://dx.doi.org/10.6084/m9.figshare.3971661.v2 |
| ‡ Present address: Laboratoire de Mathématiques et de Physique, Université de Perpignan Via Domitia, 52 Avenue Paul Alduy, 66860 Perpignan cedex 9, France. |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Maarten T. P.
Beerepoot
*,
Maarten T. P.
Beerepoot
 ,
Yann
Cornaton‡
,
Magnus
Ringholm
,
Arnfinn Hykkerud
Steindal
,
Kenneth
Ruud
and
Luca
Frediani
,
Yann
Cornaton‡
,
Magnus
Ringholm
,
Arnfinn Hykkerud
Steindal
,
Kenneth
Ruud
and
Luca
Frediani
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 into a closed subdomain C, the cavity, with a sufficiently regular boundary Γ = ∂C, we want to solve the following transmission problem for a solvent with a homogeneous, isotropic relative permittivity ε:
3 into a closed subdomain C, the cavity, with a sufficiently regular boundary Γ = ∂C, we want to solve the following transmission problem for a solvent with a homogeneous, isotropic relative permittivity ε: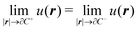
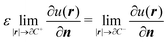
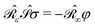
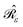 and
and 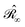 are given in terms of the components of the Calderón projector,
are given in terms of the components of the Calderón projector, 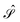 and
and 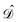 ,38,41 and the identity operator
,38,41 and the identity operator 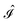 :
: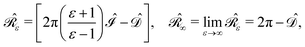
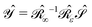 is self-adjoint and positive definite. The
is self-adjoint and positive definite. The 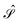 and
and 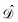 boundary integral operators are mappings between Sobolev spaces of fractional order, which thus are the natural mathematical setting for integral formulations of BVPs.38–40 These are normed spaces, equipped with the scalar product:
boundary integral operators are mappings between Sobolev spaces of fractional order, which thus are the natural mathematical setting for integral formulations of BVPs.38–40 These are normed spaces, equipped with the scalar product: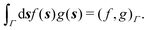
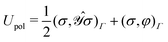
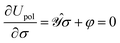
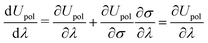
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) and
and ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) a
, respectively. Equivalently, S and S
a
denote the overlap matrix and its perturbation-strength derivative at zero field strength, respectively.
a
, respectively. Equivalently, S and S
a
denote the overlap matrix and its perturbation-strength derivative at zero field strength, respectively.  will denote that the trace of the expression to follow should be taken.
will denote that the trace of the expression to follow should be taken.  will additionally denote that the tracing is followed by time-averaging over a period T of the collected perturbations.
will additionally denote that the tracing is followed by time-averaging over a period T of the collected perturbations.
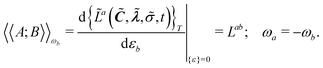
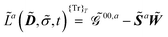
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) is given by
is given by![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) μν = 〈
μν = 〈![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) μ|
μ|![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) ν〉,
ν〉,![[W with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0057_0303.gif) was introduced and is given by
was introduced and is given by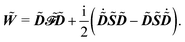
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) , its time-differentiated analogue
, its time-differentiated analogue  and the generalized Kohn–Sham (KS) matrix
and the generalized Kohn–Sham (KS) matrix  given by
given by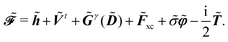
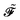 includes both vacuum-like and PCM contributions. The vacuum-like contributions are expressed in terms of the one-electron matrices
includes both vacuum-like and PCM contributions. The vacuum-like contributions are expressed in terms of the one-electron matrices ![[h with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0068_0303.gif) and Ṽt, and the two-electron matrix
and Ṽt, and the two-electron matrix ![[G with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0047_0303.gif) γ(
γ(![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) ), which are, respectively, defined in the following way:
), which are, respectively, defined in the following way: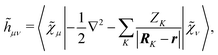
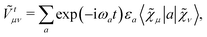
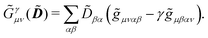
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) xc,μν of the XC potential, whose elements are given by
xc,μν of the XC potential, whose elements are given by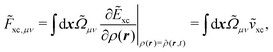
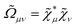 and the functional derivative of the XC functional in the adiabatic approximation. The x variable refers to both spatial and spin coordinates. The last vacuum-like contribution in eqn (12) is the anti-Hermitian, time-differentiated overlap matrix
and the functional derivative of the XC functional in the adiabatic approximation. The x variable refers to both spatial and spin coordinates. The last vacuum-like contribution in eqn (12) is the anti-Hermitian, time-differentiated overlap matrix ![[T with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0054_0303.gif) whose elements are given by
whose elements are given by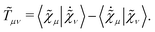
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif)
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e12c.gif) involves the electrostatic potential integrals
involves the electrostatic potential integrals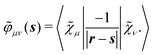
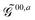 , involves the generalized KS energy
, involves the generalized KS energy  as shown in eqn (97) in ref. 9. The free energy term
as shown in eqn (97) in ref. 9. The free energy term  including PCM effects is produced by additionally considering solute–solvent interaction terms, so that
including PCM effects is produced by additionally considering solute–solvent interaction terms, so that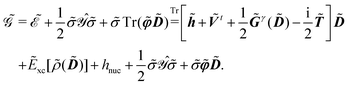
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) and
and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , higher-order derivatives of the KS generalized energy will require application of the chain rule. The mn, abc… superscript describes how and to what extent the chain rule was applied for a given term, i.e. the number of explicit differentiations with respect to the variational densities, so that
, higher-order derivatives of the KS generalized energy will require application of the chain rule. The mn, abc… superscript describes how and to what extent the chain rule was applied for a given term, i.e. the number of explicit differentiations with respect to the variational densities, so that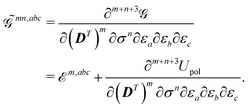
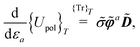
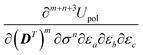 term not to be zero. By construction, the density matrix dependence in the polarization functional is at most linear, while, by virtue of the classical Hellmann–Feynman theorem, eqn (7), the ASC variational density will also appear at most linearly in
term not to be zero. By construction, the density matrix dependence in the polarization functional is at most linear, while, by virtue of the classical Hellmann–Feynman theorem, eqn (7), the ASC variational density will also appear at most linearly in 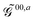 .
.
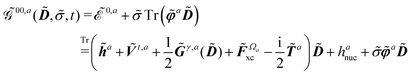
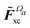 denotes the functional derivative matrix defined in terms of the perturbed overlap distributions
denotes the functional derivative matrix defined in terms of the perturbed overlap distributions ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) a, so that
a, so that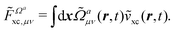
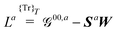
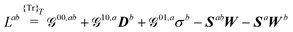
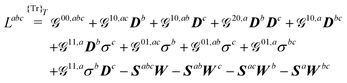
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0df.gif) a and
a and ![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e126.gif) a to take into consideration the idempotency of the density matrix and the time-dependent SCF (TD-SCF) equations, respectively, so that the idempotency condition is expressed with the matrix Ỹ and the TD-SCF condition with the matrix
a to take into consideration the idempotency of the density matrix and the time-dependent SCF (TD-SCF) equations, respectively, so that the idempotency condition is expressed with the matrix Ỹ and the TD-SCF condition with the matrix ![[Z with combining tilde]](https://www.rsc.org/images/entities/b_i_char_005a_0303.gif) , where
, where![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif)
![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif)
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) −
− ![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) = 0
= 0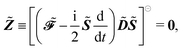
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e0df.gif) a = [Da
a = [Da![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif)
![[D with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0044_0303.gif) ]⊖,
]⊖,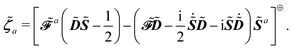
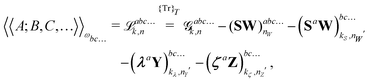
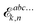 instead of the free energy term
instead of the free energy term ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) abck,n but is otherwise unchanged upon solvation, and we will therefore omit further details here about the derivation leading up to eqn (27), referring instead to previous work for more information and for details about the (k, n) truncation rules that can be chosen and applied.9,10 We note that the task of evaluating eqn (27) and obtaining terms needed for this evaluation can be cast in recursive form, as shown in ref. 10, and we further remark that these routines can be augmented to enable the calculation of single residues of response functions.11 However, the methodological and algorithmic development needed for residues calculations is not changed by the inclusion of PCM effects, and we will therefore again refer to previous work9,11 for details.
abck,n but is otherwise unchanged upon solvation, and we will therefore omit further details here about the derivation leading up to eqn (27), referring instead to previous work for more information and for details about the (k, n) truncation rules that can be chosen and applied.9,10 We note that the task of evaluating eqn (27) and obtaining terms needed for this evaluation can be cast in recursive form, as shown in ref. 10, and we further remark that these routines can be augmented to enable the calculation of single residues of response functions.11 However, the methodological and algorithmic development needed for residues calculations is not changed by the inclusion of PCM effects, and we will therefore again refer to previous work9,11 for details.
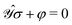
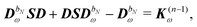
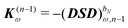 contains all terms that contain derivatives of the density matrix up to order n − 1.
contains all terms that contain derivatives of the density matrix up to order n − 1.
 and a homogenous
and a homogenous  term (H/P partition) as
term (H/P partition) as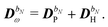
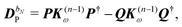
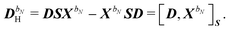
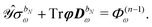
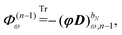
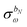 , so that
, so that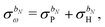
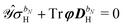
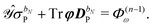
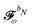 . The H/P partition introduced for the variational densities will induce a similar partition into these frequency components:
. The H/P partition introduced for the variational densities will induce a similar partition into these frequency components: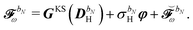
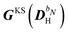 matrix, while all other contributions are collected in
matrix, while all other contributions are collected in 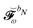 . A more detailed discussion of these aspects can be found in ref. 9 and 10. The parametrization of the homogeneous part of the perturbed density matrix can be exploited to conveniently reformulate the perturbed TDSCF equation, so that
. A more detailed discussion of these aspects can be found in ref. 9 and 10. The parametrization of the homogeneous part of the perturbed density matrix can be exploited to conveniently reformulate the perturbed TDSCF equation, so that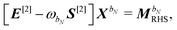
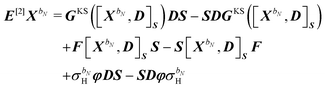
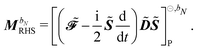
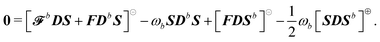
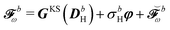
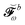 , so that
, so that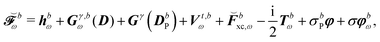
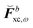 contains derivative terms of the XC matrix that are independent of the response parameters. We refer to eqn (A26) of the original paper for its explicit expression.9 Reorganizing eqn (43) to have all terms dependent on Xb on the left-hand side (LHS) yields
contains derivative terms of the XC matrix that are independent of the response parameters. We refer to eqn (A26) of the original paper for its explicit expression.9 Reorganizing eqn (43) to have all terms dependent on Xb on the left-hand side (LHS) yields
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φfωD = 0, one also has σfP = 0. Therefore, only terms including
φfωD = 0, one also has σfP = 0. Therefore, only terms including 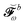 will enter the RHS and among these, only those involving Vt,bω will be nonzero, so that
will enter the RHS and among these, only those involving Vt,bω will be nonzero, so that
![[S with combining macron]](https://www.rsc.org/images/entities/b_char_0053_0304.gif) as70
as70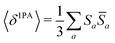
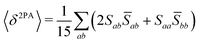
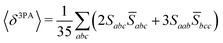
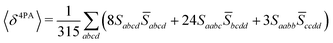
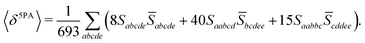
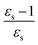 , where εs is the static relative permittivity.79
, where εs is the static relative permittivity.79

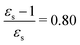 , ε∞ = 2.085) to chlorobenzene (εs = 5.621,
, ε∞ = 2.085) to chlorobenzene (εs = 5.621, 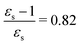 , ε∞ = 2.320) and aniline (εs = 6.89,
, ε∞ = 2.320) and aniline (εs = 6.89, 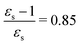 , ε∞ = 2.506) can be explained by the increase in the optical dielectric constant (ε∞) in the latter two solvents. Thus, the occurrence of these discontinuities is an effect of the non-equilibrium formulation of PCM that we employ. The calculated solvatochromic shifts are smaller than the experimental ones (see Appendix B), which is likely related to the (deliberate) omission of indirect solvent effects.
, ε∞ = 2.506) can be explained by the increase in the optical dielectric constant (ε∞) in the latter two solvents. Thus, the occurrence of these discontinuities is an effect of the non-equilibrium formulation of PCM that we employ. The calculated solvatochromic shifts are smaller than the experimental ones (see Appendix B), which is likely related to the (deliberate) omission of indirect solvent effects.
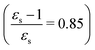 and dimethylsulfoxide
and dimethylsulfoxide 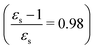 . This effect is hardly observable for 1PA, but is pronounced for the higher-order MPA strengths, and for 3PA and 5PA in particular (Fig. 3).
. This effect is hardly observable for 1PA, but is pronounced for the higher-order MPA strengths, and for 3PA and 5PA in particular (Fig. 3).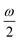 . In the same way, the 3PA strength can be enhanced if another state has an energy of
. In the same way, the 3PA strength can be enhanced if another state has an energy of 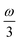 or
or 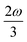 . When another state has an energy of
. When another state has an energy of 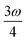 , the 4PA strength (but not the 2PA strength) is selectively enhanced. For 5PA, the most likely resonance condition is another state at
, the 4PA strength (but not the 2PA strength) is selectively enhanced. For 5PA, the most likely resonance condition is another state at 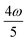 .
.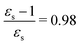 ), where the excitation energy of the 2A′ excitation is 0.678 times the excitation energy of the 4A′′ excitation. It is important to note that our response theory approach breaks down close to such resonance and the results cannot be considered quantitatively accurate. To circumvent this divergence in the MPA strengths, damped response theory should be used,80,81 as reported for 2PA by Kristensen et al.82
), where the excitation energy of the 2A′ excitation is 0.678 times the excitation energy of the 4A′′ excitation. It is important to note that our response theory approach breaks down close to such resonance and the results cannot be considered quantitatively accurate. To circumvent this divergence in the MPA strengths, damped response theory should be used,80,81 as reported for 2PA by Kristensen et al.82
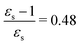 ).
).
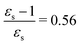 ), toluene (εs = 2.379,
), toluene (εs = 2.379, 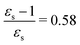 ) and chloroform (εs = 4.90,
) and chloroform (εs = 4.90, 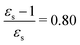 ) can be related to the excited-state dipole moment, which changes sign between 1,4-dioxane and toluene. The excited-state dipole moment of the 1B2 state also has a different direction in vacuum than in solvent. We report the relevant plots of the difference between ground- and excited-state dipole moments in the ESI.†
) can be related to the excited-state dipole moment, which changes sign between 1,4-dioxane and toluene. The excited-state dipole moment of the 1B2 state also has a different direction in vacuum than in solvent. We report the relevant plots of the difference between ground- and excited-state dipole moments in the ESI.†![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,a =
00,a = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,a + {σ
0,a + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T
Tr(φaD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,ab =
00,ab = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,ab + {σ
0,ab + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabD)}T
Tr(φabD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 00,abc =
00,abc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 0,abc + {σ
0,abc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabcD)}T
Tr(φabcD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,aDb =
10,aDb = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,aDb + {σ
1,aDb + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDb)}T
Tr(φaDb)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,aσb = {σb
01,aσb = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T
Tr(φaD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,acDb =
10,acDb = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,acDb + {σ
1,acDb + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φacDb)}T
Tr(φacDb)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,abDc =
10,abDc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,abDc + {σ
1,abDc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabDc)}T
Tr(φabDc)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 20,aDbDc =
20,aDbDc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 2,aDbDc
2,aDbDc![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 10,aDbc =
10,aDbc = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) 1,aDbc + {σ
1,aDbc + {σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDbc)}T
Tr(φaDbc)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 11,aσcDb= {σc
11,aσcDb= {σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDb)}T
Tr(φaDb)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,acσb = {σb
01,acσb = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φacD)}T
Tr(φacD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,abσc = {σc
01,abσc = {σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φabD)}T
Tr(φabD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 01,aσbc = {σbc
01,aσbc = {σbc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaD)}T
Tr(φaD)}T![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 11,aσbDc = {σb
11,aσbDc = {σb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tr(φaDc)}T
Tr(φaDc)}T