Diffusive dynamics of polymer chains in an array of nanoposts
Yi
Ye
ab,
Zhongjie
Du
b,
Ming
Tian
*ab,
Liqun
Zhang
ab and
Jianguo
Mi
*a
aState Key Laboratory of Organic-Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, China. E-mail: tianm@mail.buct.edu.cn; mijg@mail.buct.edu.cn
bKey Laboratory of Beijing City on Preparation and Processing of Novel Polymer Materials, Beijing University of Chemical Technology, Beijing, China
First published on 16th November 2016
Abstract
We present a dynamic density functional approach to study polymer chain diffusion in a good solvent in the confinement of a nanopost array. Three key results emerge from our study. First, we show different scaling laws of the chains moving toward, close to, and around the posts. Second, in the flux process of polymer chains, the head, side, and middle segments display different scaling laws. As the chains come in contact with the posts, an enlarged motion discrepancy emerges between the head and middle segments perpendicular to the posts. For instance, the motion of head segments transforms from Zimm to reputation type, whereas the middle segments almost retain the Zimm motion. Third, as the spacing crack between two posts narrows down, a climbing effect along the posts can be clearly observed in the polymer motion.
Introduction
Diffusion of polymer chains plays a significant role in polymer science and engineering because of its extensive applications, such as in surface coating, polymer separation, thin-film formation processes and biomedical technologies.1–6 Diffusion is a ubiquitous transport process, which executes a three-dimensional random movement in fluid systems. In contrast to small molecules, polymer diffusion displays a rich and unusual viscoelastic behavior over time and distance scales.7 Even in a bulk system, the self-diffusion coefficient is no longer a constant, since polymer chains have to move in specific ways which are limited by the fact that they are connected to other beads and cannot cut through each other. In the confined systems, such as the porous materials, polymer films, and cells, chain dynamics additionally depends sensitively on the emergence of topological constraints that hinder the overall chain motion,8 resulting in different physical mechanisms that generate a wide variety of transport properties.9–11In the past decades, polymer science has developed a rather mature understanding of the mechanisms and timescales of polymer diffusion in solution or melt.12–14 It seems that the dynamic behavior at the level of an individual polymer molecule, usually exhibited by the scaling index, underpins the macroscopic properties, such as viscoelasticity, glass-transition and rheology.15,16 In recent years, polymer chain diffusion under confinement with the same length scale as polymer molecules has stimulated interest in polymer physics, and dramatic advances have been achieved in understanding the single-chain dynamics of dilute polymer solution during flow—at least in a simple unidirectional flow.17,18 It has been clearly realized that the dynamic properties of confined chains are a function of the coupling between chain conformation and solvent flow, both of which depend on the size of the cross-sectional dimension of the channel.19 However, the transport of polymers in complex confined geometries which substantially distort the motions of polymer and solvent remains poorly understood. Unfortunately, there has been no experiment up to now to exploit the microscopic origin of the confinement effects.
Molecular simulation has been proven to be a powerful tool to provide molecular level insights into polymer diffusion under confinement. Direct simulations of flexible polymers in dilute solution can efficiently incorporate the confinement effect on flow, predicting the existence of hydrodynamic depletion layers that can be much larger than the equilibrium molecular sizes. The predictions of chain dynamics in moderately confined geometries are in semiquantitative agreement with experimental results. In a dense solution, however, simulation methods encounter many difficulties, such as how the migration and diffusive scaling depend on the concentration, particularly in complex geometries, and to what extent the solvent-flow-mediated interactions can lead to qualitatively different behavior of merely considering the stochastic Brownian motion of polymer chains.20,21 Even though the coarse-grained models have been widely used for high efficiency computation and allow the simulation of experimentally relevant molecular weights with a small number of beads, the complicate movement of polymer chains under hydrodynamic interactions needs sufficiently long time,22 making such simulation infeasible. As a consequence, the current simulations of polymer diffusion in confinement systems are constrained to one or two dimensions, such as in simple channels23 or near walls.24
Kinetic theory provides an alternative tool for interpreting polymer flux in confined cases. Theoretical treatments of simple polymer patterns have led to analytically tractable models, including the bead-spring chain model,25 self-consistent field theory,26 and cell dynamics computation,27 which qualitatively encompass the key phenomena. These theoretical expressions provide analytical solutions for concentration distributions, but cannot describe the diffusion details, let alone the effect of hydrodynamic interactions. Consequently, the Zimm scaling cannot be obeyed presumably in the diffusivity of a flexible chain in solutions.28 In this regard, it is necessary to develop a more reliable theoretical method to clarify the physical rules governing the polymer dynamics in nanoconfinement.
Density functional theory (DFT) is one of the efficient theoretical tools employed for the prediction of the microscopic structure and macroscopic properties of inhomogeneous fluids under external forces, both atomic and polymeric.29 In view of the success of DFT,30 a few dynamic DFT (DDFT) versions have been developed to describe the diffusion of fluids under non-equilibrium conditions. Recently, more attempts have been made to account for the hydrodynamic interactions among the particles in the presence of a viscous solvent.31,32 A key feature of these proposed DDFT models is that, even for the simple case of non-interacting Brownian particles suspended in a fluid, the resulting equations appear to be different from Fick's law, in contrast to the case of independent Brownian walkers.33 For polymer systems, the situations are more complicated. Although a polymer chain can be envisioned as a set of Brownian particles connected by harmonic springs in a short length, the movements of different segments are not the same due to the topological constraints.34 Integrative consideration of the shifts of connected segments is the essential task during the time-dependent density evolution.35–37
Here we formulate a three-dimensional DDFT model for polymer chain diffusion in the presence of an array of nanoposts to make a quantitative assessment of the contribution of nanostructures to chain diffusion. In fact, the natural porous media are extremely heterogeneous with variations in pore size and connectivity. In a theoretical model, however, it is necessary to formulate a relatively simple structure to approximately represent the porous characteristics. As such, we choose the specific array to reduce heterogeneity and enable microscopic studies that isolate the effects of confinement on the diffusion of polymer chains. Our model is explicitly worked out for far-field hydrodynamic interactions on the Rotne–Prager level.38,39 In the initial step, we optimize the structure of polymer chains by a multi-point-density-based DFT.29 Subsequently, we study the diffusive dynamics of polymer chains or segments in nanoscale confinements through the spatial density distribution, mean square displacement, and the scaling index for general inhomogeneous non-equilibrium situations. These situations can in principle be realized by the fact that confining micrometer-sized polymer chains change its transport properties. As such, we try to present some new insights of how the diffusion behaviors are influenced by polymer conformation under the confinement effect.
Theoretical model
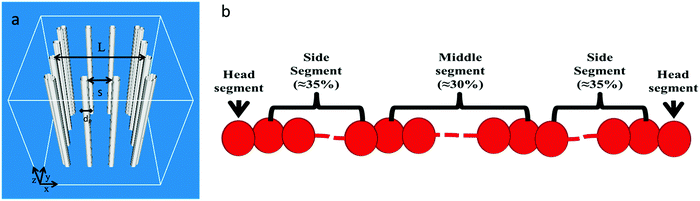
We consider polymer diffusion in a good solvent confined in nanoposts. The polymer chains are flexible or semiflexible linear chains with 25, 50 and 100 numbers of beads. For many flexible polymers, the bead diameter corresponds to the statistical segment length on the order of 1.0 nm. An array of nanoposts is formed with a diameter of dP = 1.0σbead arranged on a square lattice with the length of L = 15.0σbead and the spacing crack of S (as shown in Fig. 1a). Each chain is divided into five different segments (as shown in Fig. 1b), and the beads in the same segment have the same dynamics, which allows us to efficiently describe the different dynamic characteristics of chain topology. Meanwhile, the spacing crack is set to 1.5σbead and 2.0σbead to evaluate the confinement effect on chain diffusion. Since we focus on the effects of polymer conformation and spacing crack on polymer diffusion, the interactions of nanoposts with polymer chains are overlooked.Initially, a droplet of polymer solution with a diameter of 8.0σbead is put in the center of a post array, and the packing fraction of the polymer is set to η = 0.4, corresponding to an ordinary dense polymer solution. The post array has enough space for the droplet to diffuse and form a polymer–solvent interface.
The starting point of the derivation of the DDFT including hydrodynamic interactions is the n-component functional Langevin equation, which is given by40
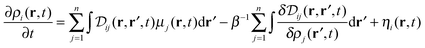 | (1) |
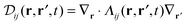 . Here ρi(r,t) represents the concentration field of each bead in polymer chains ρi(r,t) (i = 1,…,m), Λij is the Onsager kinetic coefficient, μi is the intrinsic chemical potential with μi(r,t) = δF[ρi(r,t)]/δρi(r,t), and ηi(r,t) is the noise field, which is dictated by the fluctuation–dissipation theorem as shown in ref. 41. F[ρ(r,t)] is the Helmholtz free-energy functional, and can be generalized as
. Here ρi(r,t) represents the concentration field of each bead in polymer chains ρi(r,t) (i = 1,…,m), Λij is the Onsager kinetic coefficient, μi is the intrinsic chemical potential with μi(r,t) = δF[ρi(r,t)]/δρi(r,t), and ηi(r,t) is the noise field, which is dictated by the fluctuation–dissipation theorem as shown in ref. 41. F[ρ(r,t)] is the Helmholtz free-energy functional, and can be generalized as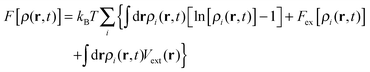 | (2) |
In order to simplify the calculation process, we correlate the diffusion of adjacent beads via the free-energy functional. As such, we introduce the local coupling approximation to the equation44
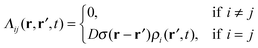 | (3) |
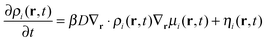 | (4) |
By constituting the fundamental, nonlinear, deterministic equation for the time-evolution of density ρ(r,t), the DDFT equation can be generalized in the following simplified form:
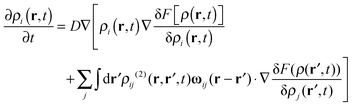 | (5) |
ρij(2)(r,r′,t) = ρi(r,t)ρj(r′,t)gij(|r − r′|, ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ) ) | (6) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ) is the pair correlation function at an appropriately averaged density
) is the pair correlation function at an appropriately averaged density ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) with gij(r) = ρi,j(r)/
with gij(r) = ρi,j(r)/![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , where ρi,j(r) is the density profile of bead i on the free molecules around the fixed bead j. ρi,j(r) can be obtained through the multi-point-density-based DFT. The distinct hydrodynamic tensor ωij(r) is approximated by the Rotne–Prager expression47
, where ρi,j(r) is the density profile of bead i on the free molecules around the fixed bead j. ρi,j(r) can be obtained through the multi-point-density-based DFT. The distinct hydrodynamic tensor ωij(r) is approximated by the Rotne–Prager expression47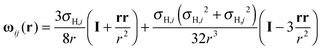 | (7) |
Structural function is used to measure nanofluid flows under constant or shear flow conditions, which can be written as49
| D(q,Δt) = 〈|ΔÎ(q,Δt)|2〉 | (8) |
D(q,Δt) = 〈|![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (q,Δt) − (q,Δt) − ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (q,0)|2〉 (q,0)|2〉 | (9) |
In order to make a quantitative assessment of the diffusion behaviors of polymer chains, the mean square displacement 〈ΔR2〉 is additionally calculated, which can be extracted from a simple statistical formula 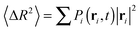 . Here P(r,t) is the probability of finding the diffusing polymer at a number of lattice space displacements r,50 and can be reasonably approximated by a line function of ρ(r,t), P(r,t) ∼ ρ(r,t). Therefore, the average mean square displacement is indicated as
. Here P(r,t) is the probability of finding the diffusing polymer at a number of lattice space displacements r,50 and can be reasonably approximated by a line function of ρ(r,t), P(r,t) ∼ ρ(r,t). Therefore, the average mean square displacement is indicated as
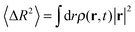 | (10) |
In three-dimensional calculations, the interactions of particle–particle and bead–bead of polymers are the sum of pair potential functions, which are simply expressed as the Lennard-Jones (LJ) form. For all calculations, we nondimensionalize the length by σbead and time by τB = σbead2/D0. The partial integro-differential equation governing the time evolution of density profile, eqn (5), is solved numerically by employing a finite-difference approximation with a fixed time step of 10−5τB.
Results and discussion
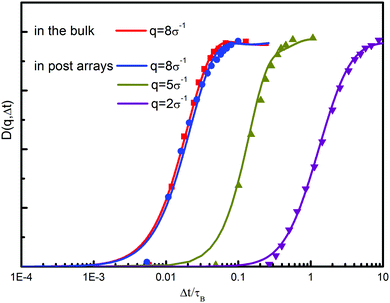
DFT allows for a reasonable description of the microscopic properties of polymers in terms of density distribution, which has been well addressed in our previous investigations.43 However, its extensive form, the DDFT model, should be tested to find the range of its applicability. Here we test the dynamic equation through the diffusion of nanoparticles in the bulk and in a similar nanopost array.51 The direct comparison of theoretical predictions and experimental values allows us to quantitatively evaluate the reliability of the current theoretical model. Fig. 2 shows the structural function D(q,Δt) as a function of delay time Δt. For each wavevector q, the magnitude of D(q,Δt) increases with time delay, indicating that the positions of particles became increasingly uncorrelated from their original positions. By comparing the structural functions in the bulk and in the nanopost array, it is apparent that the particles in the post array diffuse more slowly. On the other hand, the values of D(q,Δt) display a relatively large difference in the relaxation time between different values of q. In the considered four systems, a striking agreement has been achieved between the theoretical calculations and experimental measurements.51 The results imply that the theory is able to describe the dynamics of nanoparticles in a good solvent.We then calculate the structure of chain conformation as the prerequisite for chain diffusion. As shown in Fig. 3, the discrepancies of different segments have been considered to derive out the corresponding intermolecular correlation functions. In the theoretical calculations, a polymer chain is equivalent to a mixture of five polymeric components, as depicted in Fig. 1b. Of particular interest is the “correlation hole” structure of intermolecular correlation function, g(r), reflecting the partial expulsion of beads on different chains from inside a tagged polymer coil due to the intermolecular excluded volume interactions and intramolecular constraints. It can be observed that the correlation hole between middle segments is more pronounced than that between head segments or between a head segment and a middle segment. This could be induced by the close connection with the neighboring segments and the motion abilities of the segments. Such a phenomenon also reveals that the head segments tend to distribute on the surface of the polymer coil, and the middle segments are enveloped in the polymer coil.
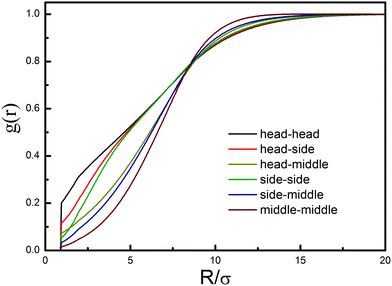 | ||
| Fig. 3 Intermolecular segment–segment distribution functions at the overall packing fractions of 0.05. | ||
To study chain dynamics, the effects of chain length and stiffness on chain diffusion should be clarified in advance. We analyse the chain flux through the mean square displacement of each segment in a nondimensionalized time scale to remove the influence of chain length on the diffusion coefficient. In Fig. 4, the values of 〈ΔR2〉 for head segments show trivial discrepancies among various chain lengths. It seems that the head segments are independent of the chain conformation, because they are lightly constrained by the steric hindrance and the connectivity effect of beads, thereby having the ability to cause the extra free volume in polymer melts. For other segments in short chains, however, the discrepancies have been enlarged, since their diffusion behaviors are susceptible to the end effect. As the chain length increases to N = 100, the effect is sufficiently diluted so that the average mobility becomes independent of the chain length. Accordingly, the chain length is set to N = 100 in the investigations thereafter.
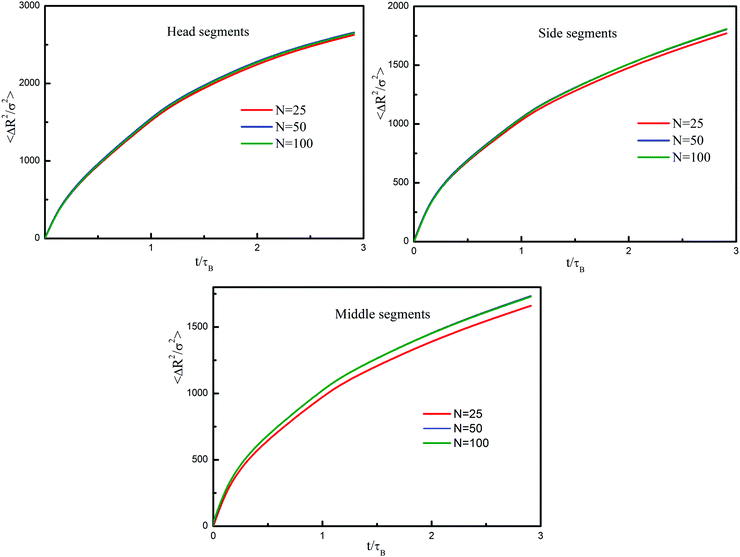 | ||
| Fig. 4 Time-evoluted mean square displacements of different segments in polymer chains with N = 25, 50, and 100. | ||
The influence of chain stiffness on the mean square displacements is shown in Fig. 5. As the time continues, the semiflexible chain shows a more pronounced swelling effect than the flexible one, which switches the larger mean end-to-end distances of the semiflexible chain. The result also suggests that there are more intermolecular contacts between semiflexible chains, which in turn may seem to suggest that the semiflexible chain system always exhibits larger pressure than the flexible chain system. By comparing the slopes of these two systems, one sees that they share the same scaling law, which means that chain stiffness influences the diffusion coefficient but not necessarily the translational behavior.
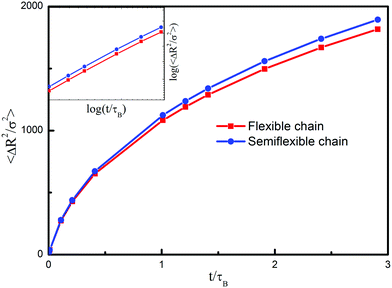 | ||
| Fig. 5 Mean square displacement of the single bead with different polymer chains as a function of time t. Insets: a log–log plot of the mean square displacement. | ||
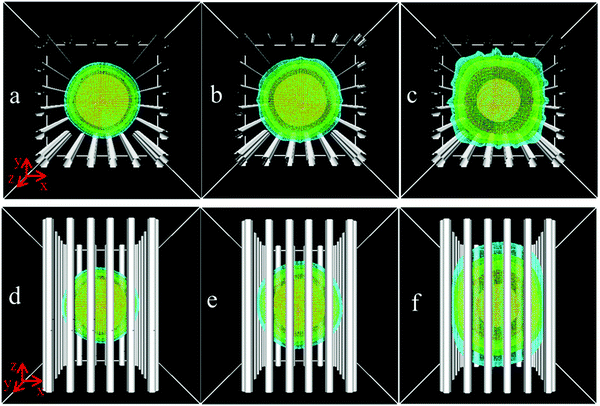
According to above analyses, we consider the diffusion of flexible chains with the length N = 100. Fig. 6 presents the spatial density distributions of polymer chains confined in the post array with S = 2.0σbead. The different diffusion behaviors in the xy-plane and along the z-axis direction are ascribed exclusively to evaluate the confinement effect. We suppose that the diffusion can be in one of two states, state 1, in which the polymer chains diffuse freely, and state 2, in which the chains are trapped and cannot move freely. At the initial stage (Fig. 6a and d), polymer chains are far from the posts, they diffuse in state 1 in different directions. When the outside segments of the polymer coil are in contact with the posts (Fig. 6b and e), all segments diffusing along the z-axis direction are in state 1, whereas the outer-layer segments diffusing perpendicular to the z-axis transform from state 1 into 2. As the time delays (Fig. 6c and f), the diffusion along the z-axis direction remains in state 1, but more and more segments diffusing perpendicular to the z-axis transfer to state 2. From the top-view, the segments around the posts are hard to escape from the confined nanoposts due to the chain connectivity, even though the space between two posts is big enough to let them pass through. From the side-view, one sees the polymer coil elongated parallel to the posts and compressed perpendicular to the posts with time evolution. Due to the confinement effect in the xy-plane, its preferential motion along the z-axis direction resembles the slithering of a snake.
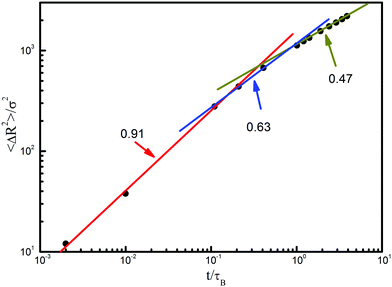
Fig. 7 shows the overall translational behavior of flexible chains. Over a short time scale, the displacement grows as 〈ΔR2〉 ∝ t0.91, where the chain motion during the relaxing process of the polymer coil displays a random walk. As the time goes on, one sees a crossover to subdiffusive behavior, which is induced by the connectivity of the chains and hydrodynamic interactions (Zimm mode dominated regime). The exponent of this regime is 0.63, quite similar to the Zimm prediction of 2/3. The slight deviation could mostly be attributed to the neglect of the kinetic coupling in the same chain. According to Fig. 6, the polymer coil has been in contact with the posts after t = 1.0τB, from which the exponent declines from 0.63 to 0.47. It is obviously induced by the confinement effect offered by the post array. Therefore, the confinement effect plays an important role in this region. The slope of 0.47 means that the Zimm mode and the reputation mode are combined in this region.
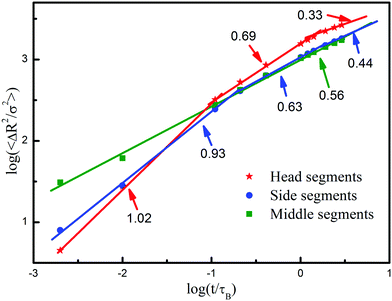
Fig. 8 illustrates the time-dependent mean square displacements of the head, side and middle segments for the flexible chains, from which we can analyze the individual translational behavior. The values of 〈ΔR2〉 for the three segments display different scaling indices. In the observation time window, three slopes have been clearly shown in the translational behaviors of the head and side segments, in contrast to only one slope for the middle segments. The exponent of the displacement of middle segments is approximately 0.56, which obeys the scaling law predicted by the Rouse model of 1/2. This phenomenon reveals the fact that the middle segments are restricted by the surrounding segments and are relatively difficult to be interfered by the effect of hydrodynamic interactions, which determine the difference between the Rouse model and the Zimm model. Using the fact that the scaling form 〈ΔR2〉 ∝ t (Fickian mode dominated regime), it is easy to see that, in the initial stage, the head and side segments display the random walk, and the side segments dragged by the middle segments move slower than the head ones. In this region, the polymer coil has not completely relaxed and the connectivity has trivial influence on the head segments. As the time continues, one sees a crossover from random walk to subdiffusive behavior, which is induced by the connectivity effect and hydrodynamic interactions included in both head and side segments. When the polymer coil expands and has been in contact with the posts, the free movement of head segments has to be fully restricted and the exponent decreases from 0.69 to 0.33, such that a reputation-like motion can be clearly observed. After the head segments have been confined, the side segments then show a similar phenomenon, and the exponent declines from 0.63 to 0.44, which is slightly higher than the value of head segments. It seems that some side segments are not in contact with the posts. In contrast, the diffusion of head segments is more sensitive to the environment. The results are consistent with those shown in Fig. 3. More importantly, they offer the reasonable evidence of how the different motions are combined.
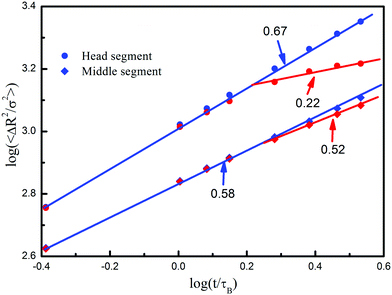
Fig. 9 presents the mean square displacements of the head and middle segments along different directions to further analyze the diffusion details of chains. Four straight lines are plotted, and the fitting exponents are 0.67 and 0.22 for the head segments and 0.58 and 0.52 for the middle segments, respectively. Before the polymer coil touches the posts, there is little difference between the power-laws along the two directions, which means that polymer chains diffuse homogeneously. As time passes (t > 1.0τB), the scaling exponents for the head segments along the two directions show an obvious difference, because the motion perpendicular to the posts has been extremely suppressed, and the diffusion of head segments transforms from homogeneity to inhomogeneity. For the middle segments, however, the exponents in the two directions show a slight difference, because the diffusion behavior is mostly interfered by other segments through the chain connectivity. These results offer additional evidence of the combining motion of polymer chains, in which the head segments move as the reputation type but the middle segments diffuse as the Zimm type.
Finally, we investigate the influence of the spacing crack on diffusion behavior. Fig. 10 compares the results in two different confinements. In the system with large space (S = 2.0σbead), the posts hinder the translational behavior in the direction perpendicular to the post but not affect it in the parallel direction. As the space decreases from 2.0σbead to 1.5σbead, the situation is different. One sees that the flux of polymer chains further slows down in the perpendicular direction but slightly accelerates in the parallel direction. The increase of the post number inevitably enhances the flux resistance of polymer chains, such that the packing density around the posts increases gradually with the time evolution. Due to the polymer depletion effect, some solvent molecules are pushed to move along the z-axis, which in turn hold polymer chains climbing along the z-axis. Such a climbing effect is an important result of non-Newtonian motion of polymer chains in high confinement.
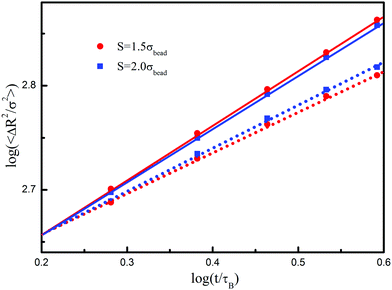 | ||
| Fig. 10 Time-evoluted mean square displacements of polymer chains. The fitted solid and dash lines correspond to the diffusion in parallel and perpendicular to the post direction, respectively. | ||
Conclusion
We have formulated a DDFT model to study the diffusive behaviors of polymer chains in a good solvent confined in different post arrays. Before its application, the dynamic equation has been fully tested with the experimental data for nanoparticles diffusing in a similar post array. Thereafter, the spatial diffusions of head, side, and middle segments in polymer chains before and after contact with the posts have been systematically analyzed to clarify the effect of array on the flux of different segments. We have demonstrated that chain diffusion displays a variety of dynamic characteristics. In particular, the motion of head segments crossovers from Zimm to reputation type in the direction perpendicular to the posts, whereas the middle segments almost retain the Zimm motion in all directions. As a result, the dynamics of the whole chains are a complex combination of Zimm and reputation models. In addition, an enhancement of the confinement effect could lead to polymer chains climbing along posts.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21476007 and 51525301) and Chemcloudcomputing of Beijing University of Chemical Technology.References
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- T. C. B. McLeish, Adv. Phys., 2002, 51, 1379–1527 CrossRef CAS.
- C.-F. Chou, O. Bakajin, S. W. Turner, T. A. Duke, S. S. Chan, E. C. Cox, H. G. Craighead and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13762–13765 CrossRef CAS.
- D. K. Schwartz, Annu. Rev. Phys. Chem., 2001, 52, 107–137 CrossRef CAS PubMed.
- V. Winstel, C. Liang, P. Sanchez-Carballo, M. Steglich, M. Munar, B. M. Bröker, J. R. Penadés, U. Nübel, O. Holst, T. Dandekar, A. Peschel and G. Xia, Nat. Commun., 2013, 4 Search PubMed.
- A. Muralidhar, D. R. Tree and K. D. Dorfman, Macromolecules, 2014, 47, 8446–8458 CrossRef CAS.
- M. Doi and S. F. Edwards, Theory of Polymer Dynamics, Clarendon, Oxford, 1986 Search PubMed.
- V. A. Harmandaris, V. G. Mavrantzas, D. N. Theodorou, M. Kröger, J. Ramírez, H. C. Öttinger and D. Vlassopoulos, Macromolecules, 2003, 36, 1376–1387 CrossRef CAS.
- P. Burgos, Z. Zhang, R. Golestanian, G. J. Leggett and M. Geoghegan, ACS Nano, 2009, 3, 3235–3243 CrossRef CAS PubMed.
- D. Mukherji, G. Bartels and M. Müser, Phys. Rev. Lett., 2008, 100, 068301 CrossRef PubMed.
- M. Kastantin, B. B. Langdon, E. L. Chang and D. K. Schwartz, J. Am. Chem. Soc., 2011, 133, 4975–4983 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- J.-L. Barrat and J.-P. Hansen, Basic Concepts for Simple and Complex Liquids, Cambridge University Press, New York, 2003 Search PubMed.
- J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 3rd edn, 1982 Search PubMed.
- S. Granick and S. C. Bae, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3434–3435 CrossRef CAS.
- M. Kröger and S. Hess, Phys. Rev. Lett., 2000, 85, 1128 CrossRef PubMed.
- K. D. Dorfman, S. B. King, D. W. Olson, J. D. P. Thomas and D. R. Tree, Chem. Rev., 2013, 113, 2584–2667 CrossRef CAS PubMed.
- W. Reisner, J. N. Pedersen and R. H. Austin, Rep. Prog. Phys., 2012, 75, 106601 CrossRef PubMed.
- A. Muralidhar and K. D. Dorfman, Macromolecules, 2015, 48, 2829–2839 CrossRef CAS PubMed.
- J. T. Del Bonis-O'Donnell, W. Reisner and D. Stein, New J. Phys., 2009, 11, 075032 CrossRef.
- Y. Zhang, J. J. de Pablo and M. D. Graham, Soft Matter, 2009, 5, 3694–3700 RSC.
- R. G. Larson, J. Rheol., 2005, 49, 1–70 CrossRef CAS.
- D. Wang, C. He, M. P. Stoykovich and D. K. Schwartz, ACS Nano, 2015, 9, 1656–1664 CrossRef CAS PubMed.
- M. J. Skaug, J. N. Mabry and D. K. Schwartz, J. Am. Chem. Soc., 2013, 136, 1327–1332 CrossRef PubMed.
- P. O. Brunn, J. Chem. Phys., 1984, 80, 5821–5826 CrossRef CAS.
- J. L. Harden and M. Doi, J. Phys. Chem., 1992, 96, 4046–4052 CrossRef CAS.
- R. Dessí, M. Pinna and A. V. Zvelindovsky, Macromolecules, 2013, 46, 1923–1931 CrossRef.
- B. H. Zimm, J. Chem. Phys., 1956, 24, 269–278 CrossRef CAS.
- S. Tripathi and W. G. Chapman, J. Chem. Phys., 2005, 122, 094506 CrossRef PubMed.
- E. S. Kikkinides and P. A. Monson, J. Chem. Phys., 2015, 142, 094706 CrossRef CAS PubMed.
- M. Rex and H. Löwen, Phys. Rev. Lett., 2008, 101, 148302 CrossRef CAS PubMed.
- B. D. Goddard, A. Nold, N. Savva, G. A. Pavliotis and S. Kalliadasis, Phys. Rev. Lett., 2012, 109, 120603 CrossRef PubMed.
- A. Donev and E. Vanden-Eijnden, J. Chem. Phys., 2014, 140, 234115 CrossRef PubMed.
- P. E. Rouse Jr, J. Chem. Phys., 1953, 21, 1272–1280 CrossRef.
- K. Binder, J. Chem. Phys., 1983, 79, 6387–6409 CrossRef CAS.
- K. Kawasaki and K. Sekimoto, Macromolecules, 1989, 22, 3063–3075 CrossRef CAS.
- N. M. Maurits and J. Fraaije, J. Chem. Phys., 1997, 107, 5879–5889 CrossRef CAS.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032–8044 CrossRef CAS.
- A. J. Archer and R. Evans, J. Chem. Phys., 2004, 121, 4246–4254 CrossRef CAS PubMed.
- B. A. C. van Vlimmere and J. G. E. M. Fraaije, Comput. Phys. Commun., 1996, 99, 21–28 CrossRef.
- C. W. Gardiner, Stochastic Methods for Physics, Chemistry and the Natural Sciences, Springer, Berlin, 1985 Search PubMed.
- Q. Zhao, X. Wang, C. Zhang, Z. Du, M. Tian and J. Mi, J. Phys. Chem. C, 2014, 118, 26808–26815 CrossRef CAS.
- Z. Wei, N. Ning, L. Zhang, M. Tian and J. Mi, Polymers, 2016, 8, 121 CrossRef.
- J. G. E. M. Fraaije, J. Chem. Phys., 1993, 99, 9202–9212 CrossRef CAS.
- S. Dietrich and A. Haase, Phys. Rep., 1995, 260, 1–138 CrossRef CAS.
- B. Götzelmann, A. Haase and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3456 CrossRef.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- M. Rex and H. Löwen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 139–146 CrossRef CAS PubMed.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef PubMed.
- Z. Zhang, Q. Ge, S. Li, B. D. Kay, J. M. White and Z. Dohnálek, Phys. Rev. Lett., 2007, 99, 126105 CrossRef PubMed.
- K. He, K. F. Babaye, S. T. Retterer, D. K. Thomas, J. C. Conrad and R. Krishnamoorti, ACS Nano, 2013, 7, 5122–5130 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2017 |