Conformational equilibrium and internal dynamics in the iso-propanol–water dimer

Abstract

The molecular complex between iso-propanol and water has been investigated by Fourier transform microwave spectroscopy. Two distinct rotational spectra have been assigned, corresponding to two different isomers of the adduct. In both cases the water molecule acts as a proton donor to the alcoholic oxygen atom of iso-propanol in its gauche arrangement. The isomer in which the water molecule is oriented along the symmetry plane of the iso-propanol molecule (inner) is more stable than the second isomer, where the water is positioned outside the iso-propanol symmetry plane (outer). The rotational transitions of the inner isomer display a doubling, due to the two equivalent minima related to the internal rotation of the hydroxyl group (concerted with a rearrangement of the water unit). The tunneling splitting has been determined to be 25.16(8) GHz, corresponding to a B₂ barrier of ∼440 cm⁻¹.

---

1. Introduction

The small size of the water monomer and its double-donor/double-acceptor capacities give it great flexibility in forming a variety of hydrogen bonds. A recent paper presents a cataloguing of the interactions of water with organic molecules, as obtained by the rotational spectra of their molecular complexes isolated in supersonic expansions.¹ In such complexes, water can undergo internal motions, where the dynamics depend on water's proton donor or proton acceptor role. These dynamics are generally enhanced, generating features such as the doubling of rotational transitions,^2,3 when water acts as a proton acceptor.

Adducts of water with alcohols are characterized by a relatively strong O–H⋯O hydrogen bond linking the two subunits. These alcohol–water structures may be further stabilized with weaker complementary hydrogen bonds between alkyl protons and the water oxygen.⁴ Internal dynamics often complicate the rotational spectra, but allow a determination of the intermolecular potential energy surfaces along the motions of interest. Due to the amphoteric nature of the water and alcohol hydroxyl groups, each can act either as the proton donor or the proton acceptor. In the pioneering rotational study of methanol–water it was shown that the observed species consisted of a water–donor, methanol–acceptor complex.⁵ The spectrum was complicated by the internal rotation of the methyl group, such that the spectroscopic parameters were reported only for the internal rotation A-state.

Similarly, water acts as proton donor in the adduct tert-butanol–water.¹ The tert-butanol hydroxyl group tunnels between two equivalent minima – involving also a considerable rearrangement of water – that generates splittings of the rotational transitions. From these splittings, the corresponding potential energy function has been estimated. The same hydrogen bonding motif (where water serves as the proton donor) has been recently found in the adduct of water with ethanol,⁶ and in glycidol–water, the water moiety acts both as a proton donor and a proton acceptor forming two strong O–H⋯O hydrogen bonds within a cyclic structure.⁷

A different behavior has been encountered in phenol–water,² where water has the role of proton acceptor. Here, water undergoes a two dimensional (2D) motion (a combination of internal rotation and inversion) between four (2 × 2 equivalent) minima on the 2D intermolecular potential energy surface.

Additional studies of the rotational spectra of adducts of water with larger aliphatic alcohols, such as water–propanol, would help to understand the interplay between the hydrophobic and -philic interactions in such clusters. Here we are interested in the adduct of water with iso-propanol (IP–W), a dimer with a conformational equilibrium taking place between the gauche and trans forms of the iso-propanol.⁸ In a related complex, hexafluoroisopropanol–water,⁹ only one conformer was observed, wherein trans-hexafluoroisopropanol acts as a proton donor to the water, a motif similar to phenol–water. Most likely, it is the high degree of fluorination that inverts the usual conformational behavior observed for the aliphatic alcohol–water complexes.

2. Experimental section

The rotational spectra of IP–W isotopologues have been measured in two different laboratories:

(a) UNIBO. Measurements were performed between 6–18.5 GHz using a pulsed jet Fourier Transform MicroWave (PJFTMW) spectrometer described elsewhere,¹⁰ based on the pioneering designs of Flygare¹¹ and Grabow.¹² Adducts were formed by flowing helium through a stainless steel reservoir containing a 50% by mole mixture of iso-propanol and water, and running the resulting gaseous mixture through a pulsed supersonic expansion. Rotational frequencies were determined after the Fourier transform of 8k-data point time domain free induction decays, recorded with 40 ns sampling intervals. The pulsed molecular beam was introduced parallel to the axis of the Fabry–Pérot resonator. Consequently, each observed transition appeared as a Doppler doublet, and the line frequency was determined as the arithmetic mean of the frequencies of the two Doppler components. The accuracy of frequency measurements is estimated to be better than 3 kHz.

(b) Caltech. Data were collected from 6–18 GHz using a previously described Chirped Pulse-Fourier Transform MicroWave (CP-FTMW) spectrometer.⁶ A reservoir nozzle was filled with a 1 : 1 molar mixture of iso-propanol and water, and heated to ∼40 Celsius. Argon at 46 psi pressurized the nozzle. The nozzle was pulsed at 10 Hz, creating a supersonic expansion perpendicular to two waveguide horns. Forty 1 microsecond duration chirps were broadcast with each gas pulse. Data were collected for 300 seconds at each local oscillator setting. Line centers were measured to an accuracy of 20 kHz.

3. Preliminary calculations of the conformational energies

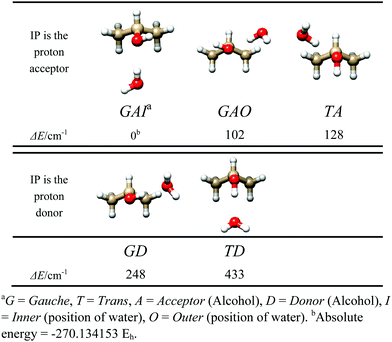
Before searching for the rotational spectrum, we ran several theoretical calculations, in order to constrain reliable starting conformations for spectral assignment. The MP2/6-311++G(d,p) level of theory was used, in Gaussian09.¹³

Five energy minima were found, shown in Fig. 1, corresponding to the trans or gauche conformation of iso-propanol, to the proton donor or proton acceptor role of water, and to the orientation of water with respect to the symmetry plane of gauche iso-propanol (inner indicates water is oriented along the IP symmetry plane; outer indicates water is oriented perpendicular to the IP symmetry plane). The corresponding spectroscopic parameters are listed in Table 1.

Fig. 1 Shapes and relative energies of the 5 most stable forms of IP–W.

Table 1 MP2/6-311++G(d,p) calculated spectroscopic parameters of the five most stable IP–W dimers

	GAI	GAO	TA	GD	TD
A/MHz	5121.4	8058.8	7528.5	8039.6	5188.1
B/MHz	2527.4	2073.1	2155.3	1996.1	2364.8
C/MHz	2388.2	1758.2	1837.5	1701.5	2225.1
μ a/D	1.95	−2.62	2.42	3.07	−2.69
μ b/D	0.20	−1.17	0.87	−0.83	0.00
μ c/D	1.51	−0.64	0.37	−0.48	1.62

---

As has been seen for the simpler aliphatic alcohol adducts, the complexes where the water acts as a proton donor are more stable, and, as for ethanol–water dimer, the gauche conformation of the alcohol is preferred. Cooperative water donor/iso-propanol acceptor structures (GAI, GAO, and TA) comprise the three lowest energy dimers, while anti-cooperative hydrogen bonding increases the GD and TD dimer energies by over 100 cm⁻¹. The relative energy difference between GAI, GAO, and TA indicates the trans/gauche position of the alcohol hydroxyl may account for ∼20 cm⁻¹ in energy. However, a significant stabilization of 100 cm⁻¹ occurs when the water is oriented symmetrically between the alcohol's two methyl groups, as in GAI. This stabilization is likely attributable to increased opportunities and/or improved alignment for secondary stabilizing C–H⋯OH₂ bonding interactions.

4. GAI (inner) isomer

Rotational spectrum

The rotational spectrum of this isomer was assigned at Caltech, using the SPFIT/SPCAT suite of programs¹⁴ and a graphical Python fitting program. Double resonance of assigned transitions was performed to validate the fit. Later on, complementary measurements were performed at UNIBO. Rotational transitions are split into two component lines, with an intensity ratio of about 5 : 1, corresponding to a vibrational splitting of about 1 cm⁻¹. The doublet of the 2_1,1 ← 1₁₀ transition is shown in Fig. 2.

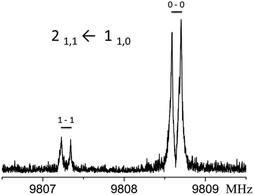Fig. 2 Tunneling components of the 2₁₁ ← 1₁₀ transition. Each of the peaks are further doubled by the Doppler effect.

Isotopologues were not assigned for the GAI isomer due to their complex spectra. Instead, the justification for our structural assignment comes from the good agreement between predicted and experimental rotational constants. The intensities of the GAI and GAO transitions also agree with relative populations consistent with the ab initio energies. Finally, the flexible model analysis based upon the GAI structure (mentioned next) faithfully reproduces splitting of transitions ascribed to that isomer.

The fitting of the transition frequencies was complicated by the Coriolis' interactions between the v = 0 and v = 1 vibrational levels. The following coupled Hamiltonian was therefore used:

H = H^R₀ + H^R₁ + H^CD + H^int (1)

where H^R₀ and H^R₁ account for the rotational energies for the 0 and 1 substates, respectively, H^CD represents the centrifugal distortion corrections (forced to the same value for v = 0 and v = 1), and H^int the interaction between the v = 0 and v = 1 states, expressed as:

H^int = ΔE₀₁ + F_bc × (P_bP_c + P_cP_b) + F_ab × (P_aP_b + P_bP_a) (2)

ΔE₀₁ is the energy difference between the 0 and 1 substates, while F_bc and F_ab are Coriolis' coupling parameters. The (P_cP_a + P_aP_c) Coriolis term was not used in the fit, consistent with an inversion motion through the b-axis. This inversion motion is further verified in the ab initio structure, which confirms that the proton movements occur along the b-axis.

Measured transition frequencies have been fitted using Pickett's SPFIT program.¹⁴ Since the GAI isomer is a near symmetric top, the S-reduction and I^r representation have been chosen.¹⁵ The fitted spectroscopic parameters are reported in Table 2. The measured transition frequencies are given in the ESI.†

Table 2 Experimental spectroscopic constants of IP–W–GAI (S-reduction, I^r representation)

v	0	1
a Errors in parenthesis are expressed in units of the last digit. b Standard deviation of the fit. c Number of fitted transitions.
A/MHz	5098.624(3)^a	5099.953(3)
B/MHz	2485.250(1)	2484.560(1)
C/MHz	2353.853(1)	2352.743(1)
D J/kHz	7.98(4)
D JK/kHz	21.6(2)
D K/kHz	−17.3(6)
d 1/kHz	0.27(2)
ΔE01/GHz	25.16(8)
F ab/MHz	47.87(2)
F bc/MHz	4.2(1)
σ /kHz	3.7
N	33

---

Flexible model analysis of the tunneling motion

The determined ΔE₀₁ splitting is related to the barrier connecting the two equivalent minima depicted in Fig. 3 as a function of the dihedral angle (τ) describing the internal rotation of the OH group, to the amplitude of the motion (in our case a ca. 120° rotation of the OH group), and to the reduced mass of the motion, which is a function of τ and also of the structural relaxation which takes place in the complex.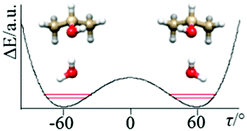

Fig. 3 The tunneling motion in of IP–W–GAI is predominantly due to the internal rotation of the hydroxyl group, accompanied by a structural relaxation of the “free” water hydrogen.

Meyer's flexible model¹⁶ is especially suitable to determining the basic properties of potential energy surfaces from rotational and vibrational experimental data. In our case we consider τ as the key parameter to describe the motion, with any structural relaxations of the dimer taken into account as a function of τ. In principle, the OH internal rotation should be described by a periodic function, but, considering the shape of the potential energy function (that is, when OH is in the trans position, the potential energy is very high), we can reasonably assume that the tunneling effects are produced ‘locally’ in the range of the HO–CH dihedral angle (τ) between ca. −120 and +120°. In this case, the potential can be described by the two parameters required in the following double minimum potential

V(τ) = B₂[1 − (τ/τ₀)²]², (3)

where B₂ is the barrier at τ = 0° and τ₀ is the equilibrium value of the inversion angle (see Fig. 3). Since we have only one data point, we fixed τ₀ at its ab initio value (62.7°). Guided by the ab initio structural differences between the energy minimum (τ = τ₀) and the transition state (τ = 0°), we took into account the structural relaxations of four structural parameters as a function of the leading parameter τ, according to the following expressions (see Fig. 4 for labelling):

H2O2–O1C1/° = 180 − 30.7·(τ/τ₀) (4)

HfO2–H2O1/° = 180 − 10.3·(τ/τ₀) (5)

H2O2O1/° = 15.3 − 3·(1 − cos 3τ). (6)

R(O2−O1)/Å = 2.843 + 0.006·(1 − cos 3τ). (7)

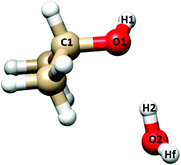Fig. 4 Labeling of the atoms involved in the flexible model analysis of IP–W–GAI. Hf indicates the “free” (not involved in the hydrogen bond) water hydrogen.

Applying Meyer's one-dimensional flexible model, a barrier of B₂ ∼ 440 cm⁻¹ best reproduced the experimental value of ΔE₀₁. In the flexible model calculations the τ coordinate has been considered in the ±120° range and solved into 81 mesh points.¹⁶

5. GAO (outer) isomer

Rotational spectra

The spectrum of this species was observed only at UNIBO, using He as carrier gas. It is possible that a supersonic expansion with Ar encourages GAO to conformationally relax into GAI.¹⁷ Here, the μ_a-dipole moment component has the highest value; for this reason we first scanned the frequency region expected to include the J = 2 ← 1 μ_a-bands of all species. We could identify only one triplet composed of the 2₁₂ ← 1₁₁, 2₀₂ ← 1₀₁, 2_1,1 ← 1₁₀ individual transitions. We could easily extend the assignment up to the J 4 ← 3 μ_a-band and to 4 additional μ_b- and μ_c-transitions, for a total of 16 rotational lines. The measured transition frequencies have been fitted with a semi-rigid Hamiltonian,¹⁵ obtaining the spectroscopic parameters (rotational constants and 4 quartic centrifugal distortion constants) reported in the first column of Table 3.

Table 3 Experimental spectroscopic parameters of the isotopologues of the GAO (outer) isomer of IP–W

	IP–H2O	IP–H2^18O	IP–DOH	IP–HOD	IP–D2O
a Error in parentheses in units of the last digit. b Values in brackets were fixed at the corresponding value of the parent species. c Number of lines in the fit. d Root-mean-square deviation of the fit.
A/MHz	7918.293(1)^a	7909.561(1)	7902.499(2)	7855.730(2)	7845.8(1)
B/MHz	2049.4385(7)	1928.2259(3)	2021.8056(3)	1960.3019(3)	1934.9157(3)
C/MHz	1745.1053(7)	1656.8025(3)	1724.2112(4)	1682.2996(4)	1662.5451(4)
D J/kHz	7.15(1)	6.878(5)	6.642(7)	7.485(7)	6.374(9)
D JK/kHz	−36.43(6)	−39.2(2)	−34.5(2)	−50.7(2)	[36.43]
d 1/kHz	−0.29(2)	[−0.29]^b	[−0.29]	[−0.29]	[−0.29]
d 2/Hz	−0.043(5)	[−0.043]	[−0.043]	[−0.043]	[−0.043]
N	16	15	12	12	9
σ /kHz	2.3	2.7	3.2	4.2	4.0

---

The experimental values of the rotational constants match best with those calculated for the GAO species, that is iso-propanol in the gauche isomer acting as a proton acceptor, and with H₂O in the outer position. This interpretation was confirmed by the assignment of the rotational spectra of four additional isotopologues, obtained by deuteration of the water hydrogens, or by replacing H₂O with H₂¹⁸O in the pre-expansion mixture. The rotational frequencies (generally a smaller number with respect to the parent species) of the isotopologues were fitted with the same procedure used for the parent species. Occasionally, some centrifugal distortion constants are not determinable and therefore have been fixed to the values of the parent species. All the obtained spectroscopic parameters are listed in Table 3, while the measured transition frequencies are given in the ESI.†

Structural information

Some structural information has been obtained from the six available rotational constants. First the Kraitchman coordinates¹⁸ of the water oxygen and of the water hydroxyl hydrogen atoms were calculated in the principal axis system of the parent species.

The obtained values are reported in Table 4 (see Fig. 5 for atom numbering), where the ab initio and the partial r₀ (see below) values are also given for comparison.

Table 4 Experimental (r_s and r₀), and ab initio (r_e, MP2/6-311++G(d,p)) coordinates of the substituted atoms of the GAO (outer) isomer of IP–W

		O5	H14	H15
a Error in parenthesis are in units of the last digits. b Calculated from the partial r0 structure of Table 5, combined with the ab initio structure given in the ESI.
|a|/Å	r s	2.8098(5)^a	1.8454(8)	3.2916(5)
	r 0	2.8240	1.9512	3.3367
	r e	2.8021	1.9283	3.3072
|b|/Å	r s	0.03(3)	0.370(4)	0.237(6)
	r 0	0.0189	0.3411	0.0355
	r e	0.0073	0.3550	0.1835
|c|/Å	r s	0.193(7)	0.07i	0.693(2)
	r 0	0.1983	0.0703	0.6119
	r e	0.1642	0.0667	0.6162

---

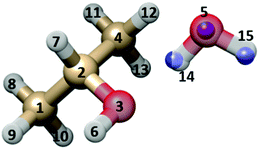Fig. 5 Sketch of the GAO (outer) isomer of IP–W, with atom numbering. The r_s substitution positions of the three water atoms are shown as blue spheres, superimposed to the MP2/6-311++G(d,p) geometry.

The ab initio values correspond to the bottom of the vibrational potential energy surface and are indicated by the notation r_e (or equilibrium structure).

A partial r₀ structure, suitable to reproduce the rotational constants in the vibrational ground state, has been determined by adjusting, with respect to the ab initio geometry (given in the ESI†), the O5–O3 distance and the ∠O5O3–C2C1 and ∠H15O5–O3C2 dihedral angles (see Table 5). The discrepancies between the experimental and calculated values of the rotational constants with such an effective structure have been reduced by 90% with respect to the pure ab initio geometry. The r₀ value of the O5–O3 distance is about 0.01 Å larger than the ab initio datum, according to the ground state vibrational effects for the stretching motion leading to dissociation.

Table 5 Partial r₀ and r_e geometry, and derived hydrogen bond length of the GAO (outer) isomer of IP–W

	r e	r 0
a MP2/6-311++G(d,p) values. b Error in parentheses in units of the last digit.
Fitted parameters
r O5O3/Å	2.8602	2.869(3)^b
∠O5O3–C2C1/°	178.3	184.0(2)
∠H15O5–O3C2/°	−144.6	−138(8)
Derived H-bond distance
r OH–O/Å	1.898	1.908

---

6. Conformational equilibrium

Relative intensity measurements of nearby a-type transitions of GAI v = 0 and GAO (in He) showed that the normalized intensities of the inner species were about 3 times higher than those of the outer adduct. Taking into account the values of the μ_a dipole moment component, one can extrapolate a population ratio ∼4/1 in favor of the inner isomer, in the v = 0 state. About 80% of the ground state population of the inner species is in the v = 0 state, while outer is doubly degenerate. Thus, we should increase this ratio by a factor 8/5, that is, a population ratio of ∼6/1.

Assuming that no conformational relaxation takes place during the supersonic expansion, a relative energy difference of 370 cm⁻¹ would be estimated (from ΔE_0,0 = kT ln(ratio)), where T is 297 Kelvin. This value is much larger than the ab initio value, but the formation and dissociation of the adduct is likely to take place many times during the supersonic expansion, significantly favoring the population of the most stable species.

It is somewhat surprising that the TA conformer was not observed as the energy difference is only 26 cm⁻¹ with respect to GAO. However, the absence of trans species seems to be a general feature of this kind of complex. For example: (i) in the dimer of iso-propanol we measured the rotational spectra of 5 conformers, but in only one of them the trans form was present. In addition, some conformers containing trans monomers, which have been calculated to be more stable than some of the observed species, have not been detected;¹⁹ (ii) in ethanol–water only the gauche form has been observed.⁶

Strong conformational relaxation of iso-propanol monomer from trans to gauche has been previously reported and may also help explain the lack of observed TA.¹⁷ Assuming the calculated energy difference between GAI and GAO (102 cm⁻¹) is roughly correct, the observed GAI/GAO population ratio suggests an effective temperature of ∼82 Kelvin. At 82 Kelvin we expect a TA/GAI population ratio of ∼1/10. Therefore, if present, TA transitions should be detectable given the experimental noise floor. However, no other observable transitions could be fit and attributed to the TA conformer. Given the strong relaxation of the iso-propanol monomer to the gauche conformation, there may be so little TA present in the expansion that the conformer is rendered undetectable. To fully analyze this question will involve detailed modeling of the interconversion barriers in the iso-propanol monomer and the iso-propanol–water dimer, which are outside the scope of this paper.

7. Conclusions

The present study confirms the inclination of aliphatic alcohols to play a proton acceptor role in their complexes with water, as observed in the previous investigations of this kind.^1,5–7 Such a trend appears to be inverted upon fluorination of the aliphatic chain, as shown by Shahi and Arunan in the case of hexafluoroisopropanol–water.⁹ In addition, aromatic alcohols (phenols) adopt a proton donor role upon complexation with one water molecule.²

Secondary weak hydrogen bonding interactions between alkyl protons also appear to play a stabilizing role. Orientation of the water to maximize the number of secondary CH–O interactions may stabilize the GAI isomer by a significant amount (prediction ∼100 cm⁻¹, experiment ∼370 cm⁻¹) compared to GAO. This is despite the known energetic cost of water accepting more than one hydrogen bond.⁴ The acceptance of more than one weak CH–O interaction by the water oxygen may be achieved by changes to hydrogen bond lengths in GAI cf. GAO. Ab initio structures indicate weak hydrogen bond lengths of 2.83 Å and 2.94 Å for GAI, and 2.79 Å for GAO. Therefore, we may conclude that multiple, comparatively weaker hydrogen bonding interactions may be favoured over a single stronger hydrogen bond in certain alcohol–water complexes. That ab initio calculations successfully predict the structures of iso-propanol–water dimers indicates appropriate consideration of weaker hydrogen bonds into structural calculations.

Acknowledgements

We thank Italian MIUR (PRIN project 2010ERFKXL_001) and the University of Bologna (RFO) for financial support. L. E. was supported by Marie Curie fellowship PIOF-GA-2012-328405. G. F. and Q. G. thank the China Scholarships Council (CSC) for a scholarship. We also thank the National Science Foundation Graduate Research Fellowship and CSDM (CHE-1214123) Programs.

Notes and references

1. L. Evangelisti and W. Caminati, Phys. Chem. Chem. Phys., 2010, 12, 14433–14441.
2. See, for example, S. Melandri, A. Maris, P. G. Favero and W. Caminati, Chem. Phys., 2002, 283, 185–192.
3. See, for example, S. Blanco, J. C. Lopez, J. L. Alonso, P. Ottaviani and W. Caminati, J. Chem. Phys., 2003, 119, 880–886.
4. G. R. Desiraju, and T. Steiner, The Weak Hydrogen Bond. Structural Chemistry, Oxford Science Publications, 1999, vol. 9.
5. P. A. Stockman, G. A. Blake, F. J. Lovas and R. D. Suenram, J. Chem. Phys., 1997, 107, 3782–3790.
6. I. A. Finneran, P. B. Carroll, M. A. Allodi and G. A. Blake, Phys. Chem. Chem. Phys., 2015, 17, 24210–24214.
7. A. R. Conrad, N. H. Teumelsan, P. E. Wang and M. J. Tubergen, J. Phys. Chem. A, 2010, 114, 336–342.
8. See, for example, E. Hirota and Y. Kawashima, J. Mol. Spectrosc., 2001, 207, 243–253 , and refs therein.
9. A. Shahi and E. Arunan, Phys. Chem. Chem. Phys., 2015, 17, 24774–24782.
10. W. Caminati, A. Millemaggi, J. L. Alonso, A. Lesarri, J. C. López and S. Mata, Chem. Phys. Lett., 2004, 392, 1–6.
11. T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45.
12. J.-U. Grabow, W. Stahl and H. Dreizler, Rev. Sci. Instrum., 1996, 67, 4072–4084.
13. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
14. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 . Current versions are described and available from: http://spec.jpl.nasa.gov.
15. J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier, New York/Amsterdam, 1977, vol. 6, pp. 1–89.
16. R. Meyer, J. Mol. Spectrosc., 1979, 76, 266; R. Meyer and W. Caminati, J. Mol. Spectrosc., 1991, 150, 229.
17. See for example: R. S. Ruoff, T. D. Klots, T. Emilson and H. S. Gutowski, J. Chem. Phys., 1990, 93, 3142.
18. J. Kraitchman, Am. J. Phys., 1953, 21, 17–24.
19. M. S. Snow, B. J. Howard, L. Evangelisti and W. Caminati, J. Phys. Chem. A, 2011, 115, 47–51.

---

Footnote

† Electronic supplementary information (ESI) available: Tables of experimental transition frequencies of all measured isotopomers of IP-W and table of MP2/6-311++G(d,p) principal axes coordinates (Å) of the observed isomers, and related sketches. See DOI: 10.1039/c6cp06315b

---