Analysis of contact area between water and irregular fibrous surface for prediction of wettability

Abstract

A characterization method, which allows visual observation of the surface area that is wet by a liquid on a roughened surface, called the solid fraction (f_s) in the Cassie–Baxter model was developed. To this end, superhydrophobic polystyrene (PS) webs (contact angles ∼170°, sliding angles ∼3°) were fabricated via electrospinning and subsequent coating with perfluorodecyltrichlorosilane (PFDTS). The theoretical solid fraction of the Cassie–Baxter model, f_s, was calculated from the equation. Microscopic images of the PS webs were converted into black and white binary images after adjusting the gray-scale of the images to match the bright area fraction with the theoretical f_s. For visual observation of the actual solid fraction, a drop of an aqueous solution with a hydrophobic fluorescent dye was rolled on the surface. Traces of the dye on the PS surface were analyzed by fluorescence microscopy to measure the actual solid fraction (f^dye_s) that was wet by the aqueous solution. The f^dye_s value corresponded well with the theoretical f_s for the webs with superhydrophobic characteristics.

---

1. Introduction

Superhydrophobic surfaces have gained significant scientific and industrial interest due to their potential applications in anti-fouling,¹ anti-fogging,² self-cleaning,³ and protective surfaces.^4,5 A common design strategy for a superhydrophobic surface is to implement micro- or nano-sized roughness onto a surface with low surface energy.^6–12 With an increased emphasis on forming the surface roughness to achieve a superhydrophobic surface, various fabrication methods have been employed to create surface roughness, including electrospinning,^13,14 lithography,¹⁵ particle-deposition,¹⁶ plasma etching,^11,12,17,18 and chemical etching.¹⁹ Among those methods, electrospinning is a convenient way to generate nano to micro-sized fibers with tunable morphology, such as beads, pores and wrinkles.^14,20

Surface wettability or anti-wettability is generally represented by a static contact angle (CA) and/or contact angle hysteresis. A surface with a high water contact angle (typically >150°) and low contact angle hysteresis (typically <5°) is regarded as being superhydrophobic.^6,21 For a flat surface, the contact angle is solely dependent on the surface energies of solid and liquid phases, as defined in Young's equation.²² For a roughened surface, the presence of surface roughness can either increase or decrease the wettability, depending on the surface energy of the solid, as explained by the Wenzel²³ and the Cassie–Baxter²⁴ models.

Particularly, the Cassie–Baxter equation²⁴ explains that the contact angle is increased as the fraction of the contact area between liquid and solid (solid fraction, f_s) is reduced. Knowing that the solid fraction, f_s, is a factor that explains the surface wettability in the Cassie–Baxter model,²⁴ efforts have been made to estimate the solid fraction, mostly by measuring the geometric dimensions of rough structures;^6,16,25,26 however, direct observation of the true solid fraction that a liquid is actually in contact with has not been made.

Kwon et al.¹¹ observed water droplets on a superhydrophobic fabric surface using an environmental scanning microscope (ESEM); however, the resolution of the ESEM was not high enough to observe the interface between water and the fabric surface. Also, the water droplets on the surface were not stably positioned, and they rolled off the surface during the ESEM observation. In the study by Park et al.,¹⁶ the upper surface area of nano-pillars formed on a superhydrophobic substrate was estimated, and the area fraction of the upper surface was used as an estimate of the solid fraction, f_s. However, this is not a true representation of the surface that is in contact with liquid, and little evidence was provided whether this geometric estimate of roughness truly represented f_s. Often low roll-off (or sliding) angle is suggested as an indirect evidence of the Cassie–Baxter wetting state,²⁴ where a liquid is held by the entrapped air, thereby allowing easy roll-off.²⁷ In this wetting state, the uppermost area of a roughened substrate would be a close estimate of the contact area between the liquid and solid, which is f_s.

In our study, it was attempted to visually observe the solid area fraction that the liquid is actually in contact with, by employing fluorescence microscopy with a hydrophobic fluorescent dye, coumarin. The solid fraction observed with the fluorescence microscope was compared with the theoretical solid fraction calculated by the Cassie–Baxter equation, in order to examine the validity of the developed characterization method. To this end, superhydrophobic rough surfaces were fabricated via electrospinning and vapor coating processes. The wettability of the fabricated surfaces was analyzed by contact angle and sliding angle measurements. The theoretical solid fraction, f_s, was calculated by the Cassie–Baxter equation²⁴ using the contact angles measured from both flat and rough surfaces. To visualize the predicted f_s on the surface, gray-scale SEM images were converted into black and white binary images using a certain threshold of gray-scale, such that the bright area fraction corresponded to the calculated f_s. To measure the actual solid fraction that is wet by water (f^dye_s), a drop of coumarin/water solution was rolled on the web surface; the coumarin-adhered surface area was then observed with a fluorescence microscope. The ultimate goal of this study is to develop a characterization method that allows direct observation of the solid fraction of the Cassie–Baxter model.²⁴ A schematic of the image analysis and estimation of the solid fraction is shown in Fig. 1.

Fig. 1 Process of image analysis, characterization of the solid fraction, and prediction of apparent contact angle.

2. Materials and method

2.1. Materials

Polystyrene (PS) pellets (M_w 192 000, >99%) and ACS grade solvents including N,N-dimethylformamide (DMF), tetrahydrofuran (THF), methylene iodide (MI), isopropanol, acetone, and toluene were purchased from Sigma-Aldrich (USA). Coumarin 314 (99%, laser grade, ACROS OrganicsTM) and n-hexane were purchased from Fisher Scientific (USA), and 1H,1H,2H,2H-perfluorodecyltrichlorosilane (PFDTS) (96%) was purchased from Alfa Aesar (USA).

2.2. Fabrication of flat film and electrospun web

A PS film with a smooth and flat surface was prepared using a spin coater (VTC-100, MTI Corporation, USA) on a 2 cm × 4 cm glass slide. A 12% (w/w) PS solution in toluene was prepared, and an aliquot of this solution was spin-coated on a glass slide at 2000 rpm for 60 s.

PS solutions of different concentrations (10 and 30% w/w) were prepared in a mixture of THF (vapor pressure, 19 065 Pa) and DMF (vapor pressure, 516 Pa) with different volume ratios. The volume ratios of THF : DMF used were 0 : 4, 1 : 3, 2 : 2, and 3 : 1. The electrospinning setup (Spraybase®, USA) consisted of a high voltage supply, a grounded aluminum drum-type collector, a syringe pump, and a 22 gauge needle. The collector was placed in front of the needle at a distance of 10 cm, and fibers were spun horizontally toward the collector, rotating at 100 rpm. The feeding rate of the PS solution was kept constant at 2.0 mL h⁻¹ throughout this study. The applied voltage was adjusted from 7 kV to 14 kV. The electrospinning process was conducted at room temperature at 45 ± 5% relative humidity.

2.3. Surface modification

To modify the surface energy, PS substrates underwent air plasma treatment and/or vapor coating. The substrates were exposed to air plasma (PDC-32G, Harrick Plasma, USA), at approximately 100 mTorr, 18 W for 3 min. Through this treatment, –OH functional groups are formed on the surface, increasing the surface energy of the PS substrates. Also, this process facilitates the later process of PFDTS chemical attachment.

To decrease the surface energy of PS substrates, PFDTS (surface energy, 17.2 mN m⁻¹) was deposited by a vapor coating process on the plasma-treated PS substrates. PFDTS was diluted to 5% (v/v) in hexane, and 5 mL of the diluted solution was placed into a vacuum desiccator, where the PS film or electrospun webs were placed. The pressure inside the desiccator was lowered to approximately 100 Torr, and the desiccator was placed in an oven at 70 °C for 1 h.²⁸ The chemical compositions of the PS substrates after air plasma treatment and PFDTS vapor coating were analyzed with a Cary 630 FTIR-ATR spectrometer (Agilent Technologies, USA). Specimen codes for different substrates and processes are shown in Table 1.

Table 1 Specimen codes

Code	Description
F	Untreated spin-coated film
Fpl	Film treated by air plasma
Fvc	Film treated by air plasma followed by PFDTS vapor coating
E	Untreated electrospun web
Epl	Electrospun web treated by air plasma
Evc	Electrospun web treated by air plasma followed by PFDTS vapor coating

---

2.4. Contact angle measurement

Static contact angles (CA) and sliding angles (SA) were measured at room temperature by an optical tensiometer (Attension Theta, Biolin Scientific, USA). For CA measurement, 4 μL of distilled water (WA) was dropped vertically from 1 cm above the specimen surface, and the contact angle was measured after 1 s. For sliding angle (SA) measurement, a specimen was fixed onto a stage, and a 10 μL water drop was placed on the specimen surface. The stage was tilted by 0.5° at a time, and the minimum tilting angle at which a water drop starts to roll away at least 1 cm was recorded as the SA. For CA and SA measurement, at least ten measurements were made from different locations of a specimen, and the mean value with standard deviation (SD) is presented. The theoretical solid fraction, f_s, of the Cassie–Baxter model²⁴ was calculated using the contact angles measured from a rough surface (electrospun web) and a flat surface (spin-coated film).

2.5. Surface energy estimation

Surface energies of untreated PS, PS treated by air plasma, and PS treated by PFDTS were estimated by Wu's method,²⁹ from the CAs measured for water and methylene iodide (MI) on flat film surfaces. The polar (γ^p_L) and dispersive (γ^d_L) components, and the total surface tension (γ_L) for water and MI are as follows: for water, γ^p_L 51.0 mN m⁻¹, γ^d_L 21.8 mN m⁻¹, and γ_L 72.8 mN m⁻¹; for MI, γ^p_L 0 mN m⁻¹, γ^d_L 50.8 mN m⁻¹, and γ_L 50.8 mN m⁻¹.³⁰

2.6. Microscopic analysis

The morphology and surface roughness of the PS films and the electrospun webs were observed with a field-emission scanning electron microscope (FE-SEM) (Versa 3D Dual Beam, FEI, USA). Prior to SEM analysis, specimens were coated with Au/Pd at 20 nm thickness using a sputter coater (150TS, Quorum, UK).

Based on the solid fraction, f_s, that was calculated from the contact angle measurement, a black and white binary image was generated from the SEM image by adjusting the threshold of gray-scale. For this image processing, ImageJ software (version 1.46r, NIH, USA) was used.

The actual contact area between water and the PS electrospun web was observed with a laser scanning confocal microscope (LSM 5 Pascal, Zeiss), using a hydrophobic fluorescent dye, coumarin 314. Although coumarin is a hydrophobic dye, a small amount is soluble in water (up to ∼1.7 g L⁻¹). An aqueous solution with coumarin dye was prepared with a concentration of 5 mM. A drop of the dye solution was rolled on an electrospun web and then removed from the surface. Due to the hydrophobic nature of coumarin, PS surface was stained by coumarin when it was in contact with the aqueous coumarin solution. The surface area that the coumarin adhered to was observed with a fluorescence microscope, and the area fraction of the fluoresced area (f^dye_s) was measured using ImageJ. For this analysis, at least four measurements of the fluorescence images per sample were used. This f^dye_s was regarded as the solid fraction that the water was actually in contact with. The f^dye_s was used to predict the apparent contact angle of the PS web, and the predicted CA was compared with the measured CA.

3. Results and discussion

3.1. Influence of surface morphology on wettability

To investigate the influence of surface roughness on wettability, electrospun webs with different morphologies were produced by varying the concentration of PS solution and solvent mixing ratio (Fig. 2). Beads were dominant at a lower polymer concentration (10%) and fibrous forms were dominant at a higher polymer concentration (30%). This morphological variation is attributed to the solution viscosity. When the viscosity of a solution is low (at low concentration), a jet collapses into droplets before the solvent evaporates, leading to bead formation.³¹ When the viscosity or polymer concentration reaches the critical point where chain entanglement occurs, jet break-up is prevented and uniform fibers can be produced.³²

Fig. 2 Morphology of the PS electrospun webs produced under different conditions: the water contact angle (CA) is presented as the mean value and standard deviation (SD). *All inserted yellow bars represent a length of 20 μm.

Solvent volatility also affects the surface morphology. A highly evaporative solvent reduces the time taken to solidify polymers, generally giving a coarse surface.³³ Also, a mixture of solvents with different volatilities is reported to form pores or corrugations by phase separation.^33,34 In this study, DMF and THF were chosen as less and more volatile solvents, respectively. With a higher ratio of DMF (THF : DMF, 0 : 4 and 1 : 3), fine pores or smooth surfaces were formed on beads and fibers. As the ratio of THF increased (3 : 1 THF : DMF), the surface of the beads or fibers became more corrugated or wrinkled. This phenomenon seemed to occur when THF evaporated more quickly, forming a solid skin, while the core of the polymer solution was not solidified as quickly. With further solvent evaporation, the core would lose the capability to support the skin, finally collapsing and forming a wrinkled structure.³⁵ The results in Fig. 2 demonstrate that the morphology and roughness structure of the electrospun web can be controlled by polymer concentration and solvent mixing ratio.

The wettability of the produced webs was measured using water contact angles (CA) (Fig. 2). Compared to the CA of the flat film (95°), the CAs of the electrospun webs were considerably increased (139–161°) due to the increased surface roughness resulting from fine fibers and beads on the web. In general, beaded webs produced higher CAs than the uniform fiber webs.

3.2. Modification of surface energy

PS film (F) and electrospun webs (E) were subjected to chemical modifications to modify the surface energy. To increase the surface energy by oxidation, substrates were treated with air plasma. To decrease the surface energy, plasma-treated PS substrates were subjected to chemical vapor deposition with PFDTS. The chemical compositions of the untreated PS and the modified PS surfaces were analyzed by FTIR (Fig. 3). Bands of the FTIR spectrum for PS correspond to aliphatic and aromatic C–H stretching at 2850–3100 cm⁻¹. After plasma treatment, bands at 1100–1300 cm⁻¹ appear, which correspond to the C–O functional group. With subsequent PFDTS vapor coating, bands at 1000–1300 cm⁻¹ appear, resulting from C–F stretching (PFDTS itself) and the chemical bonding between PS and PFDTS (Si–O–C stretching and Si–CH₃ bending). The peaks in the spectra corroborate the presence of functional groups that were introduced by the surface oxidation (by air plasma) and the hydrophobization (by PFDTS vapor coating).

Fig. 3 FTIR spectra of PS substrates: (bottom) untreated PS electrospun web, E; (middle) PS web treated by air plasma, E_pl; (top) PS web treated by air plasma followed by PFDTS vapor coating, E_vc.

The surface energy (SE) of a material was estimated using Wu's method.²⁹ The estimated surface energy components of the film samples, F, F_pl, and F_vc, are presented in Table 2 along with the CAs of water (WA) and methylene iodide (MI). Compared to the untreated PS substrate (SE 43.2 mN m⁻¹), the surface energy of the plasma-treated substrate was considerably increased to 81.7 mN m⁻¹, while that of the PFDTS-coated substrate was significantly reduced to 15.8 mN m⁻¹.

Table 2 Contact angle of water and methylene iodide, and the estimated surface energy^a

Specimen	Contact angle (°)		Surface energy (mN m^−1)
	WA	MI	γ S	γ ^dS	γ ^pS
a γ S, surface energy of PS; γ^dS, dispersive component of surface energy of PS; γ^pS, polar component of surface energy; γL, surface tension of liquid; γ^dL, dispersive component of surface tension of liquid; γ^pS, polar component of surface tension of liquid. For water, γL 72.8 mN m^−1; γ^dL 21.8 mN m^−1; γ^pS 51.0 mN m^−1.^30 For MI, γL 50.8 mN m^−1; γ^dL 50.8 mN m^−1; γ^pS 0 mN m^−1.^30
F	95°	39°	43.2	40.6	2.6
Fpl	21°	18°	81.7	48.4	33.3
Fvc	115°	99°	15.8	13.6	2.2

---

3.3. Combined effects of surface energy and morphology on wettability

Among the webs presented in Fig. 2, two webs with a high CA range (10% – 3 : 1, 30% – 3 : 1), one web with the lowest CA (30% – 0 : 4), and one web in between (10% – 1 : 3) were selected to further analyze the effect of surface modification on the wettability (Table 3). When the surface was treated with air plasma, all electrospun webs (ES) were completely wet. With PFDTS coating, E_vc exhibited superhydrophobic properties (water CA > 150°), while F_vc did not reach that level of hydrophobicity (CA ∼ 115°). From this result, it appears that there are limitations in achieving a superhydrophobic surface solely by lowering the surface energy, and the morphological parameters can have a substantial impact on anti-wettability.

Table 3 Water contact angles (CA) and sliding angles (SA) of PS substrates with different surface modifications

	Film (F)	Electrospun webs (ES)
PS conc.% (w/w)	12%	10%		30%
THF : DMF	Toluene	1 : 3	3 : 1	0 : 4	3 : 1
SEM image
CA untreated	95° (±1.1)	151° (±2.3)	161° (±2.6)	139° (±2.7)	155° (±2.1)
CA plasma-treated	21° (±1.4)	0° (all specimens were completely wet)
CA vapor coated	115° (±1.6)	171° (±2.5)	172° (±2.0)	163° (±1.5)	169° (±3.5)
SA vapor coated	N/A	3.5° (±0.5)	3° (±0.3)	9° (±1.8)	3° (±0.5)

---

When surface roughness is introduced to a low-surface-energy material, liquid is in contact with both the solid surface and the air pockets present between rough bumps, exhibiting the Cassie–Baxter state.²⁴ In this wetting state, the contact area between the liquid drop and solid surface is reduced, allowing easy roll-off of droplets. The roll-off ability is commonly evaluated using sliding angle (SA) measurement; a lower sliding angle represents easier roll-off and higher anti-wettability. On F_vc surface a water drop did not roll-off easily, and the SA was not measurable. However, E_vc surfaces with beads and corrugated fibers exhibited low SAs (3–3.5°). E_vc surfaces with smooth fibers gave relatively higher SAs (9°) (Table 3). From the SA measurements, it is speculated that surface patterns, such as beads and corrugations on the web, are beneficial with respect to reducing the contact area between water and the solid surface, leading to the Cassie–Baxter²⁴ wetting state.

3.4. Analysis of solid fraction and prediction of wettability

For the analysis of the solid fraction, f_s, in the Cassie–Baxter model,²⁴ the three most anti-wetting surfaces from Table 3 were chosen. With the presumption that the solid fraction, f_s, has a significant influence on the wettability, the Cassie–Baxter equation²⁴ explains the relationship between f_s, θ_e (Young's CA at a flat surface), and θ_CB (the apparent CA in Cassie–Baxter's wetting state) as follows:

cos θ_CB = f_s(cos θ_e + 1) − 1

The calculation of the solid fraction, f_s, is based on the assumption that a water drop is in contact only with the upper area of the roughened surface, leaving the air pockets unwet. This assumption would be valid when a liquid with high surface tension is placed on a superhydrophobic surface without penetrating into the pores and roughening bumps.

Based on the theoretical assumption, we attempted to visualize the solid fraction, f_s, or wet surface area, on SEM images (×500 magnification). Since the protruded regions in the sample have a higher chance of making contact with a water droplet and are brighter in SEM images, the protruded regions in the SEM images were segmented from the original SEM images by converting the gray-scale images into black and white binary images, using a threshold level so that the bright area fraction corresponds to the calculated f_s. In this procedure, the theoretical solid fraction, f_s, was calculated from the measured (apparent) contact angle and the Young's contact angle, assuming the Cassie–Baxter state. The calculated f_s was then used as a reference value to set the threshold level to convert SEM images into binary images. The image processing was performed with ImageJ. The calculated f_s and the converted binary images are shown in Fig. 4. Although this procedure does not provide an actual measurement of the solid fraction, it suggests a way of visualizing or estimating the location of liquid–solid interfaces on the surface.

Fig. 4 SEM binary images and f_s calculated from contact angles.

Of particular interest in this analysis is the solid area fraction of the beaded web. From the original gray-scale SEM image of the beaded web, this consists of both beads and fibers, where beads were more protruded than fine fibers. From the visualized solid fraction that appears white in the binary image, it was predicted that only the beads were in contact with water when the theoretical solid fractions were 6% and 1.7%.

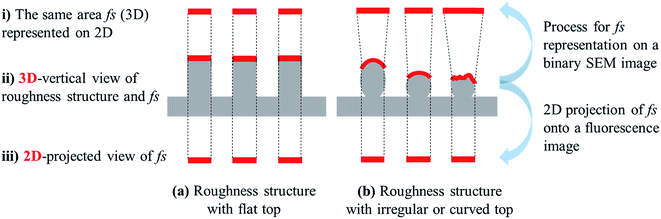
The visualized wetted surface area would correspond well to the actual f_s if the wetted surface is flat and exhibits the Cassie–Baxter state (Fig. 5a). In most cases, however, there would be discrepancies between the visualized and the actual wetted surface area, since this visualization process involves transformation of the area from three-dimensional (3D) shapes into two-dimensional (2D) space. In the process of generating the binary images in Fig. 4, the predicted surface area from the 3D shape (Fig. 5b-ii) was represented on 2D space, while keeping the same solid fractions (Fig. 5b-i). Thus, the wetted surface area appearing as white in the binary image (Fig. 4) should be “stretched,” to accurately reflect the predicted solid fraction onto 2D space. Thereby, the visualized wetted surface area would be distorted and enlarged. The degree of discrepancy depends on the surface shape of the 3D structure, and errors or distortions that could occur during 3D to 2D transformation are illustrated in Fig. 5b.

Fig. 5 3D and 2D representations of roughness and solid fraction f_s.

On the other hand, in the case of observing the surface area by fluorescence microscopy, which will be demonstrated in the following section, the wetted surface area is the 2D projection of 3D topography. Therefore, the f_s shown in the fluorescent image would be smaller than the actual f_s if the wetted surface is not flat (Fig. 5b, process from ii to iii).

In order to investigate the actual solid fraction that the liquid is in contact with, a novel yet simple characterization method was developed. In this method, an aqueous solution with a hydrophobic fluorescent dye, coumarin, was prepared, and a drop of coumarin/water solution was rolled on the PS web surface. When a drop of the dye solution rolled on the PS web, the coumarin molecules adhered to the hydrophobic PS surface, and this allowed the contact area between the liquid and the PS surface to be traced. The fluoresced area was observed by fluorescence microscopy. As the dye solution rolled on certain locations of the surface, the regions of microscopic images (mostly taken in ×500 magnifications) were cropped to ensure that the whole area of the selection was rolled over by the dye solution. The fraction of the fluoresced area from the image, f^dye_s, was measured using ImageJ and was regarded as the actual solid fraction in contact with water. In Fig. 6, the solid fraction, f^dye_s, was observed by fluorescence microscopy, with the predicted contact angle (CA) being obtained from this f^dye_s value.

Fig. 6 Fluorescent images for PS surfaces that coumarin dye is adhered to: the area fraction of the bright area was measured as f^dye_s from the image (f^dye_s, solid fraction analyzed by the fluorescence images; θ^dye, apparent contact angle predicted from f^dye_s).

For the beaded webs, only a portion of the beads were stained by coumarin, indicating that the majority of the protruded structures in the web were beads. This fluorescent image is similar to the binary images in Fig. 4, demonstrating the feasibility of this staining technique for measuring the actual wetted surface. For E_vc surfaces that showed superhydrophobic characteristics, f^dye_s and the predicted CAs corresponded fairly well with the theoretical f_s and the measured CAs, respectively. The prediction of the CA was more accurate for superhydrophobic E_vc samples than less hydrophobic E samples. As E_vc samples (CA ≥ 169°, SA ≤ 3.5°) are more anti-wetting than E samples, the surfaces of E_vc would fit more closely with the Cassie–Baxter wetting state,²⁴ resulting in more accurate predictions. The CAs of the untreated electrospun webs were not as high as those of the vapor coated webs, and their wetting state may have been in transition between the Wenzel and the Cassie–Baxter states, in which the liquid is partially penetrated through the rough structures. It is also possible that the dye has not fully adhered to its contacted surface, resulting in the solid fraction being underestimated, especially for the highly repellent surfaces. Thus, appropriate selection of a dye will be necessary for an accurate measurement of the solid fraction.

As shown in Fig. 5b (process ii to iii), when the coumarin-stained area from an irregular or curved surface is projected onto a 2D microscopic image, the surface area could be underestimated compared to the actual surface area that was in contact with liquid. As the topmost surface becomes flatter, the discrepancy between the actual f_s and the 2D-projected f_s becomes smaller. However, this tendency to underestimate the solid fraction on a 2D microscopic image is not clearly shown from the results in Fig. 6.

As the solid fraction measured by the staining method (Fig. 6) roughly matches up with the theoretical value, we further examined whether the stained area corresponded well with the estimated solid area fraction from the binary image. For this comparison, the same area from a gray-scale bright field image and a fluorescent image was selected. Then, the selected area of the gray-scale image was converted into a binary image, using the theoretical f_s. An example of this comparison is shown for a beaded web, E_vc in Fig. 7.

Fig. 7 Comparison of fluorescence image (wet solid fraction is stained in blue) and binary image (predicted solid fraction is presented in white area).

The stained area from the fluorescent image (f^dye_s) corresponded fairly well with the white area on the binary image, which is the f_s predicted by the Cassie–Baxter model. In the fluorescent image (Fig. 7, left), the solid fraction at the 3D surface was projected to the 2D microscopic image, and this projected area might be an underestimation of the actual f_s (illustrated in Fig. 5b, process ii to iii). In the binary image (Fig. 7, right), the theoretical f_s was directly represented on a 2D image, and this area may appear larger (or “stretched”) than the ones projected from 3D. This tendency is well presented in Fig. 7. From the traced regions (numbered 1–8) of the matching images, the binary image consistently shows larger areas of spots (corresponding to Fig. 5bi) than the fluorescence microscopy image (corresponding to Fig. 5biii).

The result from Fig. 7 demonstrates that the staining characterization method is feasible for tracing the actual solid fraction from a rough surface, and the binary image processing is a useful way of estimating the location of liquid–solid interfaces on a rough surface. Although this method was validated for the beaded surface, it was challenging to perform the same analysis for fibrous surfaces; the bright field images for fibers had the light transmitted through the fibers, thereby hindering the accurate depiction of fiber morphology in the desired gray-scale image, which is necessary to generate clear binary images.

The proposed characterization method will be useful to estimate the solid fraction and the apparent contact angle for a surface that follows the Cassie–Baxter state. However, further study is recommended to verify this method, by testing different surface structures with controlled and known geometric roughness. As illustrated in Fig. 5, this characterization method will provide more accurate estimation of the wetting state for roughness with a flat top (such as cylindrical pillars). To understand the possible distortion and errors of this characterization method, it is suggested that this method is tested on a standard roughness structure that exhibits the perfect Cassie–Baxter state. Also, this method gives only two-dimensional measurements. A method that allows the measurement of a three-dimensional interface will be beneficial for predicting wettability that may not follow the Cassie–Baxter wetting state.

4. Conclusions

Superhydrophobic PS webs with different surface morphologies were produced via electrospinning and vapor coating processes. At a low concentration of the polymer solution (∼10%), beads were dominant, while fibrous forms were dominant at a high polymer concentration (∼30%). In a mixed solvent system with THF and DMF, rougher surfaces were formed due to phase separation. Compared to a flat film (CA 95°), electrospun webs (CA > 139°) showed higher anti-wettability due to the surface roughness created by fibers and beads. The surface energy was modified by air-plasma and PFDTS coating. With PFDTS coating, the electrospun webs (E_vc) exhibited superhydrophobicity with CA ≥ 169°, while the PFDTS coated film (F_vc) exhibited CA of 115°. E_vc also exhibited low SAs (≤3.5°), implying that the introduced roughness reduced the contact area between water and the solid surface, leading to the Cassie–Baxter²⁴ wetting state.

The theoretical solid fraction of the Cassie–Baxter model, f_s, was calculated from the measured CAs from the rough and flat surfaces. The gray-scale SEM images were converted into black and white binary images so that the bright area fraction matched up with the theoretically calculated f_s. This theoretical f_s was compared with the solid fraction that was visually observed (f^dye_s) by staining the hydrophobic surface with the hydrophobic fluorescence dye. The measured f^dye_s and the CA predicted by this f^dye_s value corresponded fairly well with the actual measurement of the CA, especially for E_vc, for which the surface appears to follow the Cassie–Baxter wetting state. However, when the actual solid fraction from the 3D surface is projected onto the 2D surface, the projected area may underestimate the solid fraction, f_s, for an irregular or curved roughness structure. Future study is recommended to validate the characterization method for various roughness structures and to develop a characterization method that visualizes the wet surfaces in three dimensions for more accurate prediction of wettability.

Acknowledgements

This work is supported by the 3M Non-Tenured Faculty Grant; the Johnson Cancer Research Center Innovation Research Award; the University Small Research Grant (USRG) from the Kansas State University; and College of Human Ecology Sponsored Research Overhead Awards (CHE-SRO) from Kansas State University. The authors appreciate Dr Daniel L. Boyle at the Microscopy Facility of Kansas State University for the help with fluorescence microscopy.

References

1. J. Genzer and K. Efimenko, Recent Developments in Superhydrophobic Surfaces and Their Relevance to Marine Fouling: A Review, Biofouling, 2006, 22, 339–360.
2. Y. Lai, Y. Tang, J. Gong, D. Gong, L. Chi, C. Lin and Z. Chen, Transparent Superhydrophobic/Superhydrophilic TiO₂-based Coatings for Self-Cleaning and Anti-Fogging, J. Mater. Chem., 2012, 22, 7420–7426.
3. Y. Lu, S. Sathasivam, J. Song, C. R. Crick, C. J. Carmalt and I. P. Parkin, Robust Self-Cleaning Surfaces that Function When Exposed to Either Air or Oil, Science, 2015, 347, 1132–1135.
4. B. Leng, Z. Shao, G. de With and W. Ming, Superoleophobic Cotton Textiles, Langmuir, 2009, 25, 2456–2460.
5. S. Pan, A. K. Kota, J. M. Mabry and A. Tuteja, Superomniphobic Surfaces for Effective Chemical Shielding, J. Am. Chem. Soc., 2013, 135, 578–581.
6. A. K. Kota, W. Choi and A. Tuteja, Superhydrophobic Surfaces: Design and Durability, MRS Bull., 2013, 38, 383–390.
7. T.-S. Wong, T. Sun, L. Feng and J. Aizenberg, Interfacial Materials with Special Wettability, MRS Bull., 2013, 38, 366–371.
8. S. Nishimoto and B. Bhushan, Bioinspired Self-Cleaning Surfaces with Superhydrophobicity, Superoleophobicity, and Superhydrophilicity, RSC Adv., 2013, 3, 671–690.
9. A. Kota, J. M. Mabry and A. Tuteja, Superoleophobic Surfaces: Design Criteria and Recent Studies, Surf. Innovations, 2013, 1, 71–83.
10. T. Liu and C.-J. Kim, Turning a Surface Superrepellent Even to Completely Wetting Liquids, Science, 2014, 346, 1096–1100.
11. S.-O. Kwon, T.-J. Ko, E. Yu, J. Kim, M.-W. Moon and C. H. Park, Nanostructured Self-Cleaning Lyocell Fabrics with Asymmetric Wettability and Moisture Absorbency (Part I), RSC Adv., 2014, 4, 45442–45448.
12. J. Kim, H. S. Kim and C. H. Park, Contribution of Surface Energy and Roughness to the wettability of Polyamide 6 and Polypropylene Film in the Plasma-Induced Process, Text. Res. J., 2016, 86, 461–471.
13. M. Kang, R. Jung, H.-S. Kim and H.-J. Jin, Preparation of Superhydrophobic Polystyrene Membranes by Electrospinning, Colloids Surf., A, 2008, 313–314, 411–414.
14. I. Sas, R. E. Gorga, J. A. Joines and K. A. Thoney, Literature Review on Superhydrophobic Self-Cleaning Surfaces Produced by Electrospinning, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 824–845.
15. H.-J. Choi, S. Choo, J.-H. Shin, K.-I. Kim and H. Lee, Fabrication of Superhydrophobic and Oleophobic Surfaces with Overhang Structure by Reverse Nanoimprint Lithography, J. Phys. Chem., 2013, 117, 24354–24359.
16. Y. Park, C. H. Park and J. A. Kim, Quantitative Analysis on the Surface Roughness and the Level of Hydrophobicity for Superhydrophobic ZnO Nanorods Grown Textiles, Text. Res. J., 2014, 84, 1776–1788.
17. B. Shin, K.-R. Lee and M.-W. Moon, Extreme Water Repellency of Nanostructured Low-Surface-Energy Nonwoven Fabrics, Soft Matter, 2012, 8, 1817–1823.
18. T.-J. Ko, E. K. Her, B. Shin, H.-Y. Kim, K.-R. Lee and B. K. Hong, Water Condensation Behavior on the Surface of a Network of Superhydrophobic Carbon Fibers with High-Aspect-Ratio Nanostructures, Carbon, 2012, 50, 5085–5092.
19. C.-H. Xue, Y.-R. Li, P. Zhang, J.-Z. Ma and S.-T. Jia, Washable and Water-Resistant Superhydrophobic Surfaces with Self-Cleaning Property by Chemical Etching of Fibers and Hydrophobization, ACS Appl. Mater. Interfaces, 2014, 6, 10153–10161.
20. J. Lin, B. Ding, J. Yu and Y. Hsieh, Direct Fabrication of Highly Nanoporous Polystyrene Fibers via Electrospinning, ACS Appl. Mater. Interfaces, 2010, 2, 521–528.
21. M. Nosonovsky and B. Bhushan, Superhydrophobic Surfaces and Emerging Applications: Non-Adhesion, Energy, green Engineering, Curr. Opin. Colloid Interface Sci., 2009, 14, 270–280.
22. T. Young, An Essay on the Cohesion of Fluids, Philos. Trans. R. Soc. London, 1805, 95, 65–87.
23. R. N. Wenzel, Resistance of Solid Surfaces to Wetting by Water, Ind. Eng. Chem., 1936, 28, 988–994.
24. A. Cassie and S. Baxter, Wettability of Porous Surfaces, Trans. Faraday Soc., 1944, 40, 546–551.
25. Y. Rahmawan, M. W. Moon, K. S. Kim, K. R. Lee and K. Y. Suh, Wrinkled, Dual-Scale Structure of Diamond-Like Carbon (DLC) for Superhydrophobicity, Langmuir, 2010, 26, 484–491.
26. T. G. Cha, J. W. Yi, M.-W. Moon, K.-R. Lee and H.-Y. Kim, Nanoscale Patterning of Microtextured Surfaces to Control Superhydrophobic Robustness, Langmuir, 2010, 26, 8319–8326.
27. S. Park, J. Kim and C. H. Park, Analysis of wetting state for super-repellent fabrics to liquids in varied surface tensions, RSC Adv., 2016, 6, 45884–45893.
28. Z. Pan, H. Shahsavan, W. Zhang, F.-K. Yang and B. Zhao, Superhydro-oleophobic bio-inspired polydimethylsiloxane micropillared surface via FDTS coating/blending approaches, Appl. Surf. Sci., 2014, 324, 612–620.
29. S. Wu, Calculation of interfacial tension in polymer system, J. Polym. Sci., Polym. Symp., 1971, 34, 19–30.
30. M. Żenkiewicz, Methods for the Calculation of Surface Free Energy of Solids, Journal of Achievements in Materials and Manufacturing Engineering, 2007, 24, 137–145.
31. A. Frenot and I. S. Chronakis, Polymer Nanofibers Assembled by Electrospinning, Curr. Opin. Colloid Interface Sci., 2003, 8, 64–75.
32. P. Gupta, C. Elkins, E. L. Timothy and G. L. Wilkes, Electrospinning of Linear homopolymers of Poly(methylmethacrylate): Exploring Relationships between Fiber Formation, Viscosity, Molecular Weight and Concentration in a Good Solvent, Polymer, 2005, 46, 4799–4810.
33. T. Subbiah, G. S. Bhat, R. W. Tock, S. Parameswaran and S. S. Ramkumar, Electrospinning of Nanofibers, J. Appl. Polym. Sci., 2005, 96, 557–569.
34. Z. Qi, H. Yu, Y. Chen and M. Zhu, Highly Porous Fibers Prepared by Electrospinning a Ternary System of Nonsolvent/Solvent/Poly(L-lactic acid), Mater. Lett., 2009, 63, 415–418.
35. K. A. G. Katsogiannis, G. T. Vladisavljevic and S. Georgiadou, Porous Electrospun Polycaprolactone (PCL) Fibres by Phase Separation, Eur. Polym. J., 2015, 69, 284–295.

---