Polypharmacology modelling using proteochemometrics (PCM): recent methodological developments, applications to target families, and future prospects

Abstract

Proteochemometric (PCM) modelling is a computational method to model the bioactivity of multiple ligands against multiple related protein targets simultaneously. Hence it has been found to be particularly useful when exploring the selectivity and promiscuity of ligands on different proteins. In this review, we will firstly provide a brief introduction to the main concepts of PCM for readers new to the field. The next part focuses on recent technical advances, including the application of support vector machines (SVMs) using different kernel functions, random forests, Gaussian processes and collaborative filtering. The subsequent section will then describe some novel practical applications of PCM in the medicinal chemistry field, including studies on GPCRs, kinases, viral proteins (e.g. from HIV) and epigenetic targets such as histone deacetylases. Finally, we will conclude by summarizing novel developments in PCM, which we expect to gain further importance in the future. These developments include adding three-dimensional protein target information, application of PCM to the prediction of binding energies, and application of the concept in the fields of pharmacogenomics and toxicogenomics. This review is an update to a related publication in 2011 and it mainly focuses on developments in the field since then.

---

Isidro Cortés-Ciriano received a MSc in Biology and a MSc in Biochemistry from the University of Navarra (Spain) in 2011. Since 2012, he is a fellow of the Pasteur-Paris International PhD Programme in the Structural Bioinformatics Unit at the Institute Pasteur, where he works on the development and application of machine learning methods for predictive bioactivity modelling in the context of multi-target systems.

Qurrat Ul Ain is an IDB-CCT (Islamic Development Bank-Cambridge Commonwealth Trust) scholar for PhD in University of Cambridge since 2012. Her research focuses on bioactivity modelling approaches. She received her BS (HONS) in Bioinformatics from International Islamic University Islamabad and M.Phil in Bioinformatics from Quaid-i-Azam University Islamabad Pakistan.

Vigneshwari Subramanian studied Bioinformatics at the University of Helsinki, Finland and is currently doing her PhD in Computational Drug Discovery in the same university. Her research focuses on proteochemometric modelling involving 3D protein field-based descriptors.

Eelke B. Lenselink is currently pursuing his PhD at the LACDR in Leiden were he focuses on ligand and structure based design for GPCRs.

Oscar Méndez-Lucio received a BSc in pharmaceutical and biological chemistry and a MSc in chemistry from the National Autonomous University of Mexico (UNAM). Since 2012 he is a PhD student in the University of Cambridge working on the bioactivity and selectivity of kinase inhibitors.

Ad IJzerman is a full professor of medicinal chemistry at the Leiden Academic Centre for Drug Research of Leiden University, The Netherlands. He has a keen interest in using computer science methods for medicinal chemistry needs.

Gerd Wohlfahrt earned the PhD degree in chemistry, University of Braunschweig, Germany. Currently, he serves as a Principal Research Scientist, Computer-Aided Drug Design, Orion Pharma, Espoo, Finland. His areas of expertise include bioinformatics, chemoinformatics, drug discovery, and structural biology. His research interests comprise comparison of protein families, integration of protein- and ligand-based data for drug discovery, oncology target, and drug discovery.

Peteris Prusis defended his PhD thesis at Uppsala University, Sweden, which included discovery of proteochemometrics modeling approach. After many years of academic career at Uppsala University he shifted his focus to industry, starting as post-doc at AstraZeneca, Sweden and now as Senior Research Scientist at Orion, Finland.

Therese Malliavin defended her PhD at the Universite Paris-Sud and is a CNRS research fellow, working at the Institut Pasteur in Paris. Her main scientific interest concerns the relationship between biomolecules internal mobility and structure, and their interactions with other biomolecules and ligands.

Gerard JP van Westen finished a PhD in proteochemometrics at Leiden University (Netherlands) after an internship at Johnson and Johnson (Belgium). Subsequently he spent three years at the European Bioinformatics Institute in the ChEMBL Group (UK), and is returning to Leiden University.

Andreas Bender is a Lecturer for Molecular Informatics at the Centre for Molecular Informatics of the University of Cambridge, where he leads a research group comprising about ca. 20 members performing research on various aspects of chemical and biological data integration and analysis. He received his PhD from the University of Cambridge in 2005, and returned after a Presidential Postdoctoral Fellowship with Novartis in Cambridge/MA and an Assistant Professorship at the University of Leiden in The Netherlands to Cambridge.

---

1 Introduction

1.1 Available bioactivity data is growing: but can we make sense of it?

The cost of developing new drugs has been continuously increasing in recent years and it is now estimated to be in the order of $1.8 billion per drug. In addition, price pressure from health care providers has been increasing and there is a growing relevance of more targeted medicine. Hence, the ‘blockbuster model’ of the pharmaceutical industry is being challenged.^1,2 However, at the same time the amount of bioactivity data available both inside companies as well as in the public domain has significantly increased, for example with introduction of ChEMBL and PubChem Bioassay.^3,4 This trend can be expected to only pick up further speed in the future.³ The question now arises how this growing amount of bioactivity data can be used in real-world drug discovery and chemical biology projects, both to make drug discovery in commercial settings more efficient, but also to understand on a more fundamental level how we can use data in order to design a ligand with desired properties in a biological system.

Predictive bioactivity methods, such as Quantitative Structure–Activity Relationship (QSAR) models, are based upon the compound similarity principle.^5,6 However, it has been shown that the activity of a compound against a single target is not sufficient to understand its actions in a biological system. In fact promiscuity is intrinsic to chemical compounds,^7,8 bioactivity against related targets frequently needs to be considered for efficacy of e.g. CNS-active drugs and anti-cancer drugs,^9,10 and promiscuity has been used to anticipate side-effects.¹¹ Hence, only the simultaneous modelling of both the chemical and the target domain, across a series of protein targets, permits the meaningful mining of the compound–target interaction space.¹²

The term chemogenomics comprises techniques capable to capitalize on this huge amount of bioactivity data by considering compound and target information, in order to find unknown interactions between (new) compounds and their (new) targets.^13,14 Proteochemometrics (PCM) modelling describes methods where a computational description from the ligand side of the system is combined with a description of the biological side being studied and both are related to a particular readout of interest.^15,16

In this context, ligands are typically small molecules although biologics also have been explored. Conversely, the biological parameters in the model can comprise protein binding sites, but also e.g. gene expression levels of particular cell lines. The readout describes the biological effect of a particular ligand on the protein or cell line of interest (such as an IC₅₀ value of this particular combination of compound and biological system). Additionally, PCM relates to personalized medicine as it can predict the effect of a ligand on a complex biological system, e.g. cell line, from genotypic information.¹⁷

1.2 Synergy between ligand and target space

An analysis of the drug–target interaction network demonstrated that a given ligand interacts with six protein targets on average at therapeutic concentrations.⁷ Targets with correlated bioactivity profiles might be related or distant from a sequence similarity standpoint. It has been recently shown that for class A GPCRs protein classification based on ligand activity differs considerably from the classic description of proteins based upon sequence alignments.^18,19 Hence, full sequence similarity from multiple sequence alignments would not generally correlate with similar ligand affinity. Conversely, kinases exhibiting a sequence identity higher than 60% tend to have similar ATP-binding sites and hence they tend to be inhibited by similar compounds.²⁰ Similarly, compound binding is more conserved between human and rat orthologous proteins with respect to paralogues.^21,22 Thus, to better understand intra-family and inter-species selectivity both the target and the compound space need to be considered simultaneously.

In ligand space, chemogenomic approaches relying only on ligand data have shown that there is an unequal distribution of ligand data. This is due to the fact that some target classes (e.g. GPCRs or kinases) have been traditionally regarded as more interesting from a medicinal chemistry standpoint, and are thus overrepresented in bioactivity databases.²³ Moreover, while some chemogenomic methods implicitly consider target information using bioactivity profiles of groups of similar ligands, i.e. the interaction between these compounds and a panel of targets, they are outperformed by techniques that explicitly consider target information.^24,25 In addition, bioactivity profiles for related compounds are not always available.

In target space, techniques were employed which benefit from the structural or sequence information available and rely on groups of related targets with the aim to identify possible off-target effects and drug specificity for a particular target of interest.²⁵ Based on the inverse similarity principle, related proteins are likely to interact with similar compounds. As in the previous case, the unavailability of data also constitutes a limitation for target-based chemogenomics.

The combination of ligand and target data allows the creation of predictive models that can rationalize e.g. viral or cancer cell line selectivity, whereas models exclusively based on ligands cannot explain the role of the target in selectivity.²⁶ Merging data from ligand and target sources into the frame of a single machine learning model allows the prediction of the most suitable pharmacological treatment for a given genotype (personalized medicine), which ligand-only and protein-only approaches are not able to perform. This is precisely the underlying principle in proteochemometrics (PCM), which employs both ligand and target features simultaneously, and which therefore enables the deconvolution of both the target and the chemical spaces in parallel.^15,16

2 Proteochemometric modelling

2.1 PCM as a practical approach to use chemogenomics data

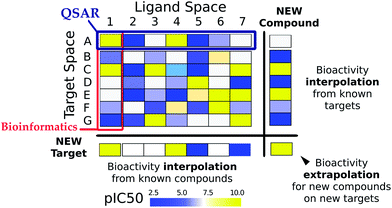
PCM modelling, is a computational technique which combines both ligand and target information within a single predictive model in order to predict an output variable of interest (usually the activity of a molecule in a particular biological assay).^15,16 It is this combination of orthogonous information that sets PCM apart from both QSAR and chemogenomics.^25,27 Generally, the term ‘target’ refers to proteins since the majority of PCM models in the literature have been devoted to the study of the activity of compounds on protein targets. Yet, target can also refer to a certain protein binding pocket (to allow distinction between binding modes, protein conformations, or allosteric/orthosteric binding), to a protein complex, or even to a cell line.^28,29 Each binding site and each binding mode can be regarded (computationally) as a ‘different target’.

A PCM model is trained on a dataset composed of a series of targets and compounds, where ideally compounds have been measured on as many targets as possible (illustrated in Fig. 1). The simultaneous modelling of the target and the ligand space permits to better understand complex drug–target interactions (e.g. selectivity)^30–33 than would be possible with chemogenomics as the effect of target and chemical variability can be evaluated (e.g. protein mutations or the effect of chemical substructures on bioactivity). Thus, the aim of PCM is the complete modelling of the compound–target interaction space (Fig. 1), including also the prediction of the bioactivity of novel compounds on yet untested targets.

Fig. 1 Ligand–target interaction space. The interaction between ligands (chemical compounds) and targets (biological macromolecules) can be envisioned as a matrix, where rows are indexed by target ids and columns by compound ids. Each matrix cell contains the binding affinity of a given compound on a given target, indicated by the following colors: blue means low affinity and yellow means high affinity. Traditional bioinformatics techniques have dealt with the similarity between targets, normally based upon sequence similarity. On the other hand, ligand based (QSAR) models have studied series of compounds acting on a given target. By contrast to both of them, PCM relates the chemical–target interaction space by describing targets and compounds with numerical descriptors permitting to predict activities of a given compound on a given target.

Initial attempts to incorporate description of several proteins and their ligands in a single QSAR model involved modelling of the interaction between mutated glucocorticoid receptors and DNA.^34,35 The first full scale PCM study involving different proteins was devoted to the interaction of chimeric melanocortin receptors with chimeric peptides at Uppsala University.³⁶ The name “proteochemometrics” was coined later by the same research group.¹⁵ Since then PCM has been applied on various diverse datasets (Table 1).^37,38 While the current review will focus on recent developments in the field, a comprehensive discussion of PCM-related work has been presented in a previous review by van Westen et al. from 2011 to which we would like to refer the reader.¹⁶

Table 1 An overview of recent PCM applications applied to a variety of datasets and the inferences made^a

Dataset (datapoints)	Receptor	Ligand descriptors	Target descriptors	Bioactivity type	Machine learning technique	In silico model validation	Prospective validation?	Remarks, inferences	References
a The wide applicability of PCM is evidenced by the increased coverage of drug targets in the studies of the last three years. Although traditional drug targets, such as GPCRs or kinases, are still widely represented, new applications (e.g. the modelling of viral genotypes or pharmacogenomics) are gaining ground steadily. BPN – Back Propagation Networks, BS – Bootstrapping Validation, CTD – composition and transition of amino acid properties, CV – Cross-Validation, DCNB – Dual Component Naive Bayes, DCSVM – Dual Component Support Vector Machines, DT – Decision Trees, DTV – Decoy Test Validation, ENR – Elastic Net Regression, EV – External Validation, GP – Gaussian Processes, KNN – K-Nearest Neighbors, LCO – Leave-Cluster-Out Validation, LOTO – Leave-One-Target-Out Validation, NB – Naïve-Bayes, NN – Neural Network, MLR – Multiple Linear Regression, OOB – Out-Of-Bag Validation, PCA – Principal Component Analysis, PLS – Partial Least Squares, Random Forest – RF, RS – Random Splitting, SVM – Support Vector Machines, SVR – Support Vector Regression, Y-Sc – Y-Scrambling.
PDBbind^170 (1300)	1300 protein–ligand complexes	Atom-type based	Atom-type based	K d, Ki	RF	Y-Sc, OoBV, EV	No	Increasing the training set size improves the model's predictability	Ballester et al., 2010 (ref. 208)
ProLINT database^209 (3595)	62 kinases	Structural fragments and 2D autocorrelation vectors	Sequence-based structural fragments and amino acid sequence autocorrelation	IC50	SVM	3-fold CV, EV	No	SVM based on autocorrelation descriptors perform better than fragment-based approaches	Fernandez et al., 2010 (ref. 210)
PDBbind^170 (1255)	Diverse proteins	Property-encoded shape distributions	Property-encoded shape distributions	K d, Ki	SVM	5-fold CV, EV	No	Training set enrichment and expansion enhances prediction accuracy	Das et al., 2010 (ref. 175)
Stanford HIV drug resistance database^211 (4495)	728 reverse transcriptases	Dragon descriptors^71	Z-scales^48	IC50	PLS	7-fold CV, EV	No	Receptor–ligand and receptor–receptor cross-terms improved model performance	Junaid et al., 2010 (ref. 149)
Immune epitope database^212 (31 992)	12 HLA-DRB1 proteins	Z-scales^48	Z-scales^48	IC50	PLS	7-fold CV, EV	No	Identified protein residues and peptide positions for binding predictions	Dimitrov et al., 2010 (ref. 213)
Karaman et al. dataset^214 (12 046)	317 human kinases	Dragon descriptors^71	Z-scales,^48 amino-acid composition, sequence order and CTD	K d	PLS, SVM, KNN, DT	Double CV	No	SVM outperforms all machine learning approaches	Lapins, et al., 2010 (ref. 215)
CSAR-NRC HiQ^176	346 protein–ligand complexes	Atom counts	Atom counts	K d	MLR	RS	No	Distance dependent atom descriptors make the regression models more robust	Kramer et al., 2011 (ref. 176)
Gold standard set (1933)	313 diseases (OMIM)^216	Diverse drug–drug similarity measures	Disease–disease similarity measure	Classifier score	Logistic regression classifier	10-fold CV, EV	No	Possibilities to include patient specific gene expression profiles make the models suitable for pharmacogenomics studies	Gottlieb et al., 2011 (ref. 217)
Sc-PDB^218 (2882)	581 targets	Hashed fingerprints	Protein sequence and 3-D structure based	Actives/inactives	SVM	5-fold CV, EV	No	Structure-based approaches perform better than sequence-based approaches	Meslamani et al., 2011 (ref. 60)
GLIDA database^119 (5207) and GVK kinase database (15 616)	317 GPCRs and 143 kinases	Dragon descriptors^71	Protein sequence and feature-based	K i, IC50, EC50	SVM	5-fold	9 compounds for ADRB2	Highly active compounds predicted by SVM not identified by ligand-based/structure-based approaches	Yabuuchi et al., 2011 (ref. 62)
							5 inhibitors for EGFR
Tibotec BVBA (4024)	14 HIV RT	Circular fingerprints	Hashed fingerprints	EC50	SVM	Y-Sc, E CV, LosoV	317 novel predictions were experimentally verified	Viral mutants PCM models can assist the development drugs for HIV infection	van Westen et al., 2011 (ref. 26)
Bioinfo-DB^61 (3 36 678)	Oxytocin receptor	MACCS structural keys	Fingerprints based on the properties of amino acids in active site	Actives/inactives	RF	10-fold CV, EV	Biological evaluation of 37 compounds (2 hits)	PCM models yield better hits than the conventional virtual screening procedures	Weill, et al., 2011 (ref. 61)
PDBbind refined set (1387)	23 protein families (1387 proteins)	Atom-type based	Atom-type based, distance-dependent protein ligand atom type pairs	K d	MLR, PLS	5-fold CV, LCO	No	Inclusion of descriptors from PCM models predict free energies more accurately than docking programs	Kramer et al., 2011 (ref. 169)
Stanford HIV drug resistance database (4794 protease and 4495 RT sequence-inhibitor combinations)	828 HIV-1 protease variants	GRIND alignment independent descriptors^219	Z-scales^48	Inhibitor concentration	PLS	Double loop CV, Y-Sc and EV	No	Intra-protease cross-terms improve model performance	Spjuth et al., 2011 (ref. 150)
Kinase SARfari^3 (85 908)	342 human kinase domains	Extended connectivity fingerprints (ECFP-6)^70	Fingerprints based on amino acid residues and physiochemical properties	IC50, Kd, Ki	DCSVM and DCNB	RS, EV	No	DCSVMs provide better activity prediction	Niijima et al., 2012 (ref. 94)
BindingDB^220 (1275)	5 HDAC isoforms	Physical properties and topological indices of compounds	Sequence similarity, structure similarity, geometry descriptors	IC50	SVR	10-fold CV, EV	No	SVR models with PUK kernels have stronger mapping capabilities	Wu et al., 2012 (ref. 92)
Docked complexes (2335 PDB structures & 3671 FDA drugs)	2335 human targets	Ligand shape descriptors	Binding site shape descriptors	Ligand contact point score	PCA	DTV, EV	VEGFR2 inhibition by Mebendazole and Cadherin 11 inhibition by Celecoxib were verified	TFMS PCM approach can assist in drug repositioning studies	Dakshanamurthy et al., 2012 (ref. 221)
Literature (160 protein–ligand complexes)	47 HIV-1 proteases	Physical properties, topological indices of compounds	Z-scales^48	K i	SVR	10-fold CV, EV	No	Protein–ligand interaction fingerprints improved models over cross-terms	Huang et al., 2012 (ref. 41)
CHEMBL 2^3 (10 999)	8 human and rat adenosine receptors	Circular fingerprints	Hashed fingerprints	K i	SVM	Y-Sc, EV, DTV	6 novel compounds were experimentally identified	Addition of orthologue information increased model quality	van Westen et al., 2012 (ref. 22)
CHEMBL 8^3 (81 689; 43 965)	136 GPCRs and 176 kinases	MACCS keys	Sequence descriptors	K i, IC50	SVM	5-fold CV, EV	No	Feature selection improved the predictive accuracy of the models	Cheng et al., 2012 (ref. 222)
GVK biosciences database^223 (628 120)	238 class A GPCRs	Chemical kernels based on ECFP-6 fingerprints and dragon descriptors	Protein kernels based on full length, TM and loop sequences	Agonists/antagonists	SVM	RS, DT, EV	No	Protein kernels based on TM sequences showed higher prediction accuracy	Shiraishi et al., 2013 (ref. 158)
GDSC dataset^224 (38 930)	639 cancer cell lines	PaDEL descriptors^72	CNV, sequence variation and microsatellite instability status	IC50	RF and NNs	8-fold CV, EV	No	PCM based on existing drugs allows drug repositioning and pharmacogenomics studies	Menden et al., 2013 (ref. 29)
Peptide library (180)	4 proteases	Binary and physiochemical descriptors	Binary descriptors	K i	PLS	5-fold CV	No	Inclusion of intra-peptide cross-terms improved model performance	Prusis et al., 2013 (ref. 151)
Kinase SARfari (54 012)	372 kinases	Topological fingerprints	Amino-acid composition and CTD	IC50, Kd, Ki	RF and NB	OOB, 5-fold CV, EV	No	Random forests outperform Näive Bayes	Cao, et al., 2013 (ref. 126)
Virco (300 000)	HIV mutants (10 700 NNRTI, 10 500 NRTI, 27 000 PI)	Circular fingerprints	Z-scales^48	IC50	SVM	Y-Sc, 5-fold CV, EV	No	Phenotypic resistance for novel mutants can be predicted via PCM	van Westen et al., 2013 (ref. 145)
GPCRDB^225 (310)	9 human amine GPCRs	Physical properties and topological indices of compounds	Z-scales^48 and TM identity descriptors	K i	SVR and GP	10-fold CV, EV	No	SVR is superior to GP	Gao et al., 2013 (ref. 112)
								TM identity descriptors perform better than Z-scales descriptors
PubChem BioAssay dataset^4 (63 391)	5 CYP 450 isoforms	Molecular signatures	CTD	AC50	KNN, SVM and RF	CV, EV	No	Non-linear methods (SVM and RF) perform better	Lapins et al., 2013 (ref. 88)
Binding and PDSP KI database^220 (13 079)	514 human targets	Topological fingerprints	Amino-acid composition and CTD	K i	RF and NB	OOB, 5-fold CV, EV	No	Random forests outperform KNN, SVM, NB and BPN	Cao et al., 2013 (ref. 226)
In vitro OATP modulation data (2000)	OATP1B1 and OATP1B3	Circular fingerprints	Z-scales^48 and feature-based ProtFP	K i	RF	OOB, EV	Agreement between experiment and prediction	4 class models are superior to 2-class models and provide information about selectivity	Bruyn et al., 2013 (ref. 54)
Karaman et al.,^214 Davis et al.^227 and Metz et al.^228 datasets	50 kinases	Mold 2,^229 open babel^230 and volsurf^231 descriptors	Knowledge-based fields 123 and watermap 124 derived fields	K d/Ki	PLS	7-fold CV, EV, LOTO, Y-Sc	No	Field-based models are superior to sequence-based models	Subramanian et al., 2013 (ref. 66)

---

2.2 Practical relevance of PCM

The novel way that PCM considers the unity of chemical and target space permits to better understand and predict the influence of target variability on compound activity. For instance, predicting compound activity on a cancer cell line panel can identify selective compounds towards a particular cell line.¹⁷ Similarly, the influence of viral proteins mutations in compound activity can be quantified.³⁹ Therefore, PCM opens new avenues: (i) to mine drug affinity databases with the goal to create multi-target and multispecies models, (ii) to integrate toxicogenomics and phenotypic data in predictive models, (iii) to identify designed or natural ligands for orphan receptors (receptor deorphanization), (iv) and to design personalized medicine for viral infections or a defined cancer type based on genotypic information. The ability of PCM to model these data depends on the structure of the input matrix, as we will elaborate on below, and concrete examples referring to the above fields will be presented in the subsequent sections.

2.3 Input data for PCM

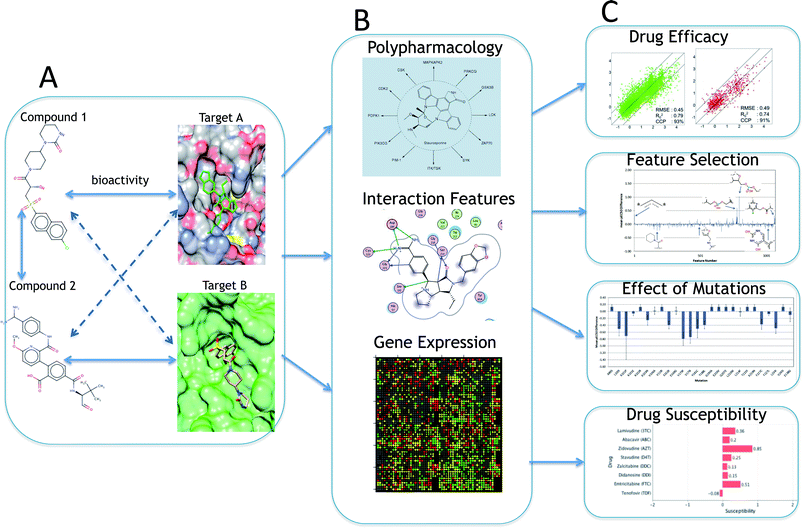
The ligand–target interaction space can be visualized as a matrix containing the activities of all possible ligand–target combinations (Fig. 1).⁴⁰ PCM attempts to predict the activity of a ligand on any target and vice versa, the activity of any ligand on a given target. The integration of these independent compound–target interactions is however possible in PCM due to the combination of chemical and target information in a single machine learning model. Fig. 2 gives an overview of how different sources of data can be integrated for modelling a particular aspect of bioactivity of a given ligand in different biological settings. Fig. 2A displays how compound and target information relate and are combined in a predictive model which permits the extrapolation in either (or both) the chemical or target space (to the extent the training data allows). These two input spaces are numerically described (Fig. 2B) by: compound bioactivity profiles or physicochemical descriptors (top panel, ligand space), cross-term descriptors, such as interaction fingerprints (middle panel, descriptors dependent on both spaces),^41,42 (lower panel, target space) binding pocket residues or gene expression profiles. Fig. 2C depicts some examples of practical applications of unifying chemical and biological sources of information. The top panel represents the observed against the predicted bioactivities calculated with a PCM model, illustrating how PCM can be used to predict compound potency. The second panel displays deconvolution of the chemical space by interpreting the influence of each compound descriptor. This approach can determine which chemical moieties are important for either potency or selectivity. The third panel displays interpretation of the target space, which can identify residues that are implicated in e.g. drug resistance of a viral protein. Thus, compounds can be developed by considering potency and selectivity towards a given target or target family. The final panel shows how PCM models can help to determine the best drug regime given a patients genotype (personalized medicine). Here, the activity of all drugs would be predicted on that genotype and the drug predicted to exhibit the highest activity would be preferentially selected.

Fig. 2 A systematic overview of proteochemometric modelling. (A) shows the similarity between ligands and drug targets and the utilization of both types of information in PCM. (B) is the representation of different types of input features of ligand and target space (shared bioactivity profiles of ligands, binding pocket residues, gene expression in cell lines, mutational stability, etc.) which could be employed in a PCM model depending on the type of output variable. The third block (C) shows the various possible applications of PCM models including measurement of drug efficacy and susceptibility, effect of mutations on activity and compound–target feature selection.

2.4 Target descriptors

As was touched upon above, PCM is rather flexible and can deal with a multitude of different target descriptors. Here, we will summarize some of the more common descriptors and later on in the review focus on novel descriptor types, for a full overview of established descriptors please see van Westen et al. 2011.¹⁶ By far the most common descriptors are alignment dependent sequence descriptors.⁴³ The authors refer the reader to a pair of benchmark studies recently published for more information on this type of descriptor.^44,45 This type of protein descriptor is usually obtained from a concatenation of individual amino acid descriptors and requires the individual sequences to be aligned. This can be done using full sequence alignment by established tools such as ClustalW and subsequently these alignments are converted to position-dependent numerical descriptors, e.g. the Z-scales by Sandberg.^46–48

When no reliable alignment is possible, target descriptors can be calculated using the whole protein sequence without aligning them.⁴⁹ The usage of only primary sequence descriptors to predict protein–protein interactions was shown efficient by Shen et al.⁵⁰ who were able to train a SVM model based on more than 16 000 protein–protein pairs described with conjoint triad feature amino acid descriptors. Similarly, analyses of sequence variability among targets exhibiting divergent bioactivity profiles, enabled the characterization of binding pocket residues energetically important for ligand binding and selectivity for GPCRs and kinases.^51–53

If present, structural information from crystallographic structures can be used by selecting residues near the ligand binding site (e.g. 5 or 10 Å sphere around the co-crystallized ligand).^21,43,44,47 Subsequently, the corresponding residues for other targets can be obtained from sequence alignment. This semi-structural method is less reliable than a full structural superposition and alignment gaps might appear. However, in practice, the former appears to have better resolution, which might be due to the fact that domains not involved in ligand binding are not considered.^22,54,55 To date, binding sites in PCM models have been derived from single crystallographic structures,^22,42,55,56 thus ignoring the intrinsically dynamic nature of proteins. However, databases such as Pocketome⁵⁷ might facilitate the introduction of dynamic properties of protein binding sites in PCM models as they contain ensembles of conformations for druggable binding sites extracted from co-crystal structures in the Protein Data Bank. To the knowledge of the authors, descriptors accounting for the dynamic properties of binding site amino acids have not been reported in the literature. Including this dynamic information might lead to a better description of protein targets in cases where small molecule binding is dependent on the binding site conformation, e.g. kinases.

Beyond sequence similarity, targets have also been described in different ways to model compound bioactivities on multiple targets.^58–62 Among others, targets have been characterized by: (i) the incorporation of biological tests and inverse virtual screening data; (ii) structural pocket similarity analyses; (iii) topology analyses of both compound–target and protein–protein interaction networks; (iv) the combination of pharmacophoric and interaction fingerprints; and (v) 3-dimensional alignment-free methods of binding sequences.^7,63–66 The availability of a plethora of target descriptors enables the application of PCM to target families where, for instance, little structural information is available. The advantages brought to the PCM field by each of these descriptor types will be reviewed in Sections 4 and 5. In cases where targets are not proteins, but more complex biological systems, such as cell lines, the target space can be described with ‘omics’ data, namely: copy-number variation (CNV) data, gene expression levels, exome sequencing data, cell line fingerprints, protein abundance, and miRNA expression levels.^17,29

2.5 Ligand descriptors

Similarly, from the ligand side a large number of descriptors have been employed in PCM in the last decade.^67,68 Circular fingerprints are the most commonly applied due to both their consistent good performance and interpretability when using the unhashed (keyed) version.^69,70 Keyed circular fingerprints, in both binary and counts format, where each bit in the descriptor accounts for the number of occurrences of a substructure in a given molecule, enable the interpretation of models and the identification of chemical substructures implicated in compound potency and selectivity. The performance of models trained on hashed and unhashed circular Morgan fingerprints do not vary significantly.⁵⁵ Therefore, we advocate for the customary usage of unhashed fingerprints in order to enhance the interpretability of PCM models.

Next to the circular fingerprint, physicochemical descriptors, such as DRAGON or PaDEL,^71,72 have been widely used in recent years (Table 1). Other ligand descriptors, such as atom types, topological indices, MACCs keys or ligand shape descriptors, have been also applied in the context of PCM.

In the experience of the authors, the description of compounds with circular Morgan fingerprints permits the generation of statistically validated PCM models but on several occasions the addition of physicochemical properties to fingerprints has been demonstrated to improve performance.⁵⁴ This was especially true on data sets with a large chemical diversity, e.g. resulting from screening a diverse set or resulting from covering a group of targets with diverse ligands.

2.6 Cross-term descriptors

Thirdly, some PCM studies have defined an additional class of descriptors, called cross-terms, by multiplying ligand and target descriptors. These descriptors serve as descriptors for the non-linear components in the interaction between ligand and target (e.g. a hydrogen bond that can be formed in one target but not in another).^43,73 Therefore, its application is advisable when using linear modelling techniques (such as Partial Least Squares (PLS)). In the case of non-linear techniques, cross-terms are not essential as the models should be able to capture this information.^22,74 Nonetheless, the experience of the authors indicates that they might be nevertheless useful to improve model performance when using SVM or GP even though their interpretability might not be straightforward. For further reading on different types of descriptors applied in PCM we refer the reader to van Westen et al.¹⁶

2.7 Validation of PCM models

Due to the previously mentioned bias in bioactivity data (both from a chemical point of view and target point of view) the ligand–target interaction matrix is virtually never complete.^23–25 The authors have trained PCM models on sparse datasets with a degree of matrix completeness in the 2–3% range that demonstrated good performance on the test set.⁷⁵ The statistical metrics proposed by Golbraikh and Tropsha⁷⁶ can be used (similar to QSAR) to validate models using observed and predicted values on the test set. Recent studies recommend the usage of nested cross-validation (NCV) to report model performance.^77–80 In NCV, two validation loops are nested: the inner one serves to optimize the values of the hyperparameters through traditional k-fold cross-validation, whereas the outer loop serves to assess the predictive ability of the model trained on the whole training set. This procedure is repeated k′ times, each time changing the composition of the training and the test sets. Thus, NCV does not provide the best parameter combination, as in each k′ round the best values of the hyperparameters might change due to the variance of the different training sets. Still, it provides the best estimate of the CV error as it provides an error interval, which can be wide depending on the dataset modeled.⁸⁰

However, the degree of completeness of the ligand–target interaction matrix is only one parameter influencing the predictive ability of a model. The variability on the chemical and the target side are the other two factors that need to be considered both in model validation and to assess its applicability domain.⁷⁵ Hence, the authors strongly suggest validating PCM models following a number of basic guidelines, which are in line with the recommendations from Park and Marcotte.⁷⁷ Firstly, external validation (e.g. 70–30 validation), a model is trained on 70% percent of the data (training set) and the bioactivity for the remaining 30% (test set) is predicted. In this case, all targets and compounds are present in both the training and the test set. This method corresponds to a Park and Marcotte C1 validation and serves to determine if a reliable model can be fit on the data set.

Secondly, Leave-One-Target-Out (LOTO) validation: all the bioactivity data annotated on a target is excluded from the training set. A model is subsequently trained on the training set, which is used to predict the bioactivities for the compounds annotated on the hold-out target. This process is repeated for each target. This validation scheme corresponds to a Park and Marcotte C2 validation and reflects the common situation in prospective validation where there is no information for a given target for which we intend to find hits.

Thirdly, Leave-One-Compound-Out (LOCO) validation: the bioactivity data for a compound on all targets is excluded from the training. Similarly to the LOTO validation, the PCM model trained on the remaining data is used to predict the bioactivity for the hold-out compound on each target. This data availability scenario corresponds to a Park and Marcotte C2 validation and resembles the situation where a PCM model is applied to novel chemistry in a e.g. prospective validation screening campaign. If the number of compounds in the training dataset is large, compound clusters can be used instead of single compounds, thus leading to the Leave-Once-Compound-Cluster-Out validation scenario (LOCCO).¹⁷

In addition to these scenarios, the authors suggest to compare the performance of the PCM model trained on all data to single-target QSAR models. The goal of this validation is twofold. Firstly a direct comparison to QSAR can determine whether it is wise to apply PCM to a data set. Secondly, as was touched upon above, bias in the data can be the cause of some targets being reliably modeled and some targets being poorly modeled (see Section 6).^23–25 When calculating validation parameters (such as the correlation coefficient) on the full test set, poorly modeled targets can be masked. In order to notice discontinuities, the authors recommend to not only calculate the validation parameters on the full test set. In addition, also calculate validation parameters on test set data points that are grouped per target and points that are grouped per ligand.⁴⁵ The values of the statistical metrics calculated per target can be directly compared with those obtained with single QSAR models (comparing values calculated on the full test set would not be an accurate comparison).

Ideally, the final validation is one where a target and all compounds that have been tested on this (and other targets) are iteratively excluded from the training set. This approach corresponds with a Park and Marcotte C3 validation. C3 validation is considered extrapolation rather than interpolation, as both parts of the pair (the ligand and the target) have not been seen in the training set by the model.

Taken together, these validation scenarios enable a thorough and earnest validation of PCM models and a comparison to the state of the art. Finally, the authors also suggest to calculate the statistical metrics on, at least, the predictions calculated with three models trained on different subsets of the complete dataset, and to accompany them with the standard deviation observed over the repetitions.⁷⁵ Similarly, it is advisable to carefully estimate the maximum achievable performance given the uncertainty of the data.^17,75

2.8 Review outline

Table 1 summarizes the main features of the PCM studies published between 2010 and 2013. In addition to traditional therapeutic targets (e.g. kinases or GPCRs), which continue to be well represented in recent PCM studies, other applications and techniques are gaining ground steadily, namely: (i) the modelling of the selectivity of viral protein mutants, mainly HIV; (ii) the inclusion of bioactivity information from mammal orthologues; (iii) the usage of 3-dimensional target information; and (iv) toxicogenomics and pharmacogenomics. In this review, we will focus on: (Section 3): (novel) machine learning techniques successfully applied in recent PCM studies (Table 2) and other predictive modelling contexts such as chemoinformatics; (Section 4): recent applications of PCM on established protein target classes; (Section 5): novel applications; (Section 6) pitfalls of PCM; (Section 7) future perspectives and concluding remarks close the review.

Table 2 Selection of machine learning prediction methods used for PCM^a

Machine learning method	Short description	Advantages	Disadvantages	References
a New algorithms have been introduced in PCM focusing on: (i) increasing interpretability; (ii) reducing training times; (iii) providing individual intervals of confidence for the predictions; and (iv) considering the experimental uncertainty in the modelling.
Support Vector Machine (SVM)	Maps the input space into a higher dimensional space where a hyper-plane is defined by ‘support vectors’, lying at the interface between classes	– Medium training time	– Optimize bandwidth hyper-parameter	Gao et al., 2013 (ref. 112)
		– PUK kernel uses an approximation of linear, polynomial and RBF kernels	– No consideration of experimental error	Hur et al., 2008 (ref. 87)
			– No Error bars for the predictions	Genton et al., 2001 (ref. 90)
				van Westen et al., 2012 (ref. 22)
Dual-component SVM (DC-SVM)	Amino acid residues and compound fragments are treated as two components	– Accurate prediction of active versus inactive	– Huge kernel matrix	Niijima et al., 2012 (ref. 94)
			– Reduced efficiency due to size
Transductive SVM (TSVM)	Semi-supervised text mining technique	– Effective with unbalanced datasets	– Difficult to implement without proper tuning	Kondratovich et al., 2013 (ref. 96)
		– Smoothen the decision boundaries		Wang et al., 2005 (ref. 97)
				Collobert et al., 2006 (ref. 98)
Relevant Vector Machine (RVM)	Probabilistic counterpart of SVM	– Contains sparse descriptors	– Non informative predicted variance	Tipping, 2001 (ref. 99)
		– Fast prediction		Lowe et al., 2011 (ref. 100)
		– Easy retrieval of important descriptors
Random Forest (RF)	– Constructs multiple decision trees with random selection of variables	– Computationally less expensive than SVM	– Requires relatively large amounts of memory	De Bruyn et al., 2013 (ref. 54)
		– Short training time
		– High interpretability
Gaussian Processes (GP)	– Non-parametric Bayesian technique	– Measureable interval of confidence (IC)	– Long training time	Schwaighofer et al., 2007 (ref. 113)
	– Gives each prediction as Gaussian distribution	– Consideration of experimental uncertainty		Cortes-Ciriano et al.^75
Matrix factorization (CF)	– Calculates activities as dot product of compound and target features	– Missing values are predicted efficiently	– Performance on sparse data	Gao et al.^115
		– Interpretability
	– Multi-task learning	– Inferred features could be used as descriptors in the activity model		Erhan et al.^117
		– Estimates relatedness between targets

---

3 Machine learning in PCM

Most of the currently used machine learning (PLS, rough set modelling, neural net modelling, Naïve Bayesian classifiers, and decision tree algorithms) as well as data preprocessing techniques in PCM have been described in recent reviews by Andersson et al.⁸¹ and van Westen et al.¹⁶ Moreover, feature selection methods and common algorithms have been recently benchmarked, with the overall conclusion that kernel and tree methods, such as SVM or RF, do not benefit from feature selection, and that no particular algorithm-feature selection pair appears to be preferable.^82–84 Therefore, only recent applications of novel techniques applied to PCM or chemoinformatic modelling will be discussed here, namely: Support Vector Machines (SVM), Random Forest (RF), Gaussian Processes (GP) and Collective Filtering (CF). A detailed description of the machine learning algorithms described in the following subsections is given in Table 2.

3.1 Support Vector Machines (SVM)

Support Vector Machines (SVMs) are a group of non-linear machine learning techniques commonly used in computational biology, and in PCM in particular.^16,22 SVMs became popular in the last decade due to their performance and efficient capacity to deal with large datasets also in high-dimensional variable spaces, even though interpretability can be challenging.^85–87 Furthermore SVMs require proper tuning of the so-called hyper parameters, usually determined by an exponential grid search.

In a recent study from Lapins et al.⁸⁸ Random Forest (RF), K-Nearest Neighbors (KNN), and SVMs were applied to construct a PCM model of Cytochrome P450 (CYP) inhibition. The models were trained on 5 CYPs and 17 143 compounds. CYPs were described with transition and composition description of amino acids, while compounds were described with structural signature descriptors. These PCM models were shown to outperform single target models in terms of Area Under the Curve (AUC: PCM: >0.90, QSAR: 0.79–0.89) that were constructed in parallel by Cheng et al.⁸⁹ Of the methods used, RF and SVM were shown to be comparable in terms of accuracy and AUC. The high performance of the SVM model in the external validation (AUC: 0.940) evidences the suitability of this approach to correctly extrapolate in both the target and compound space.

SVMs can use different internal methods (kernels) to derive bioactivity predictions, the most dominant being the Radial Basis Function (RBF) kernel.⁹⁰ Radial basis function kernels have been shown to perform well on PCM data.^16,22 Recently the VII Pearson function-based Universal Kernel (PUK)⁹¹ was also applied to PCM. Wu et al.⁹² showed that they were able to improve the mapping power of their PCM models for 11 histone deacetylases (HDAC's) by using a PUK kernel. Nonetheless, the radial kernel still constitutes a common option when inducting bioactivity models given the necessity to tune only one kernel parameter, i.e. σ, which in practice means shorter training times. Based on those results, the experienced user should keep in mind that although the radial kernel is a robust option with reliable results (in the experience of the authors), a proper kernel choice should be made on the basis of the data at hand.⁹³

Dual Component SVMs (DC-SVM) are an extension of the classical SVM and have been applied by Niijima et al.⁹⁴ to a kinase dataset spanning the whole kinome. They proposed a dual component naïve Bayesian model in which kinase–inhibitor pairs are represented by protein residues and ligand fragments that form dual components. Hence the probability of being active is simply estimated as the ratio of bioactivity values between active and inactive pairs. This method was further extended to SVMs by modifying a Tanimoto kernel to include compound fragments. PCM DC-SVMs outperformed ligand based SVMs (QSAR) in internal validation, as accuracies of 90.9% and 86.2% were respectively obtained. However the same level of accuracy was not achieved when using external datasets, which produced accuracies of 73.9% and 81.3% for DC-SVM and ligand based SVM. Therefore, these results do not permit to conclude that DC-SVM outperform SVM although this might happen with other datasets.

A second type of SVMs, Transductive SVMs (TSVMs), have been applied to model 10 small (between ∼1000 and ∼3000 datapoints) and unbalanced QSAR datasets from the Directory of Useful Decoys (DUD)⁹⁵ repository displaying a balanced accuracy higher than 30% on some datasets with respect to SVM.⁹⁶ The concept relies on transduction, allowing the modelling of partially labeled data which cannot be included using regular SVM. TSVMs could be potentially extended to PCM and have been shown to outperform SVMs in some cases.^97,98

A third flavor of SVMs are Relevance Vector Machines (RVMs).⁹⁹ The added value of RVM is the interpretability of the models, which is a consequence of their Bayesian nature. Each descriptor is associated to a coefficient, which determines its relevance for the model. Coefficients associated to low relevance descriptors are close to zero, hence the model becomes sparse and therefore permits shorter prediction times. Although the predicted variance is not informative in regression studies, class probabilities can be efficiently determined in classification.¹⁰⁰ RVMs have been demonstrated by binary classifiers trained on a subset of the MDDR database.¹⁰⁰ Therein, it was demonstrated that RVMs performed on par with ‘classic’ SVM, encouraging the authors to conclude that RVM should be added to the current chemoinformatic tools and as such potentially applied to future PCM studies.

On the basis of the above, SVM constitutes a useful algorithm in which initial drawbacks such as interpretability (e.g. the determination of which chemical substructures most contribute to compound bioactivity) can be overcome with new developments (e.g. RVM).

3.2 Random Forests (RF)

Random Forest (RF) models are often comparable in performance to SVMs,¹⁶ and are also non-linear. However, contrary to SVMs RFs tend to have relatively short training times and do not require extensive parameter tuning.¹⁰¹ Furthermore, in addition to their comparable performance, RFs permit an evaluation of both feature contribution and feature importance in PCM models, as shown by de Bruyn et al.⁵⁴ An example of such evaluation is given in the identification of organic anion-transporting polypeptide (OATP) inhibitors, where continuous descriptors, both Z-scales (proteins) and physiochemical features (compounds), were binned into discrete classes. For each feature (protein and ligand) the correlation to activity and importance was calculated for each target class. In that way, compound inactivity was correlated with the presence of chemical substructures positively charged at pH 7.4, number of atoms <20, and molecular weight <300. Conversely, chemical substructures with a number of ring bonds between 18 and 32, without atoms with positive charge, and with a log D value between 3.4 and 7.5 were found to favour OATP inhibition.

Although RFs have a high interpretability it should be noted that they do not output error estimates (as is also the case with SVM), although recent papers suggest the usefulness of the variance along the trees of a random forest model to determine its applicability domain.^102,103 Error estimates are of tremendous importance given the high levels of noise and error annotations in public bioactivity databases. Thus, fully informative predictions should be accompanied by individual uncertainties. This issue can be remediated by applying Quantile Regression Forests (QRF) which infer quantiles from the conditional distribution of the response variable.¹⁰⁴ To our knowledge QRFs have not been applied to QSAR or PCM yet. A machine learning technique that has been used in PCM with inherent error estimation capabilities are Gaussian processes, as described below.

3.3 Gaussian Processes (GP)

The determination of the applicability domain (AD) of a model (when are model predictions reliable or when can a model extrapolate) is one of the major concerns in bioactivity modelling (see previous studies^105–107 for comprehensive reviews). Major obstacles to the AD determination are the errors and uncertainties contained in bioactivity databases,^108–111 which are mainly due to data curation and experimental errors,¹¹⁰ as well as the accurate quantification of distances in the descriptor and the biological space, which would enable to anticipate prediction errors. Gaussian processes (GP) aim to address these concerns by permitting to handle data uncertainty as input into a probabilistic model.

Fig. 3 illustrates the basic idea underlying GP modelling. The prior probability distribution (Fig. 3A) covers all possible functions candidate to model the data, each of which has a different weight determined by the kernel (covariance) parameters. Subsequently, only those functions from the prior distribution in agreement with the experimental data are kept (Fig. 3B). The mean of this function is considered as the best fit to the data. Given that each prediction is a Gaussian distribution, different confidence intervals can be defined from its variance (Fig. 3B).

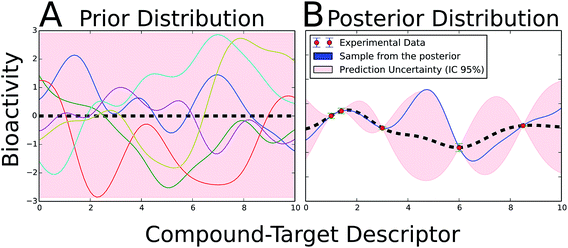Fig. 3 Illustrative example of GP theory in a two-dimensional problem. (A) The prior probability distribution embraces all possible functions which can potentially model the dataset. A subset of six prototypical functions is depicted. Normally, the mean of the distribution is set to zero (black dashed line). (B) The inclusion of bioactivity information (red dots) accompanied by its experimental uncertainty (blue error bars) updates the prior distribution into the posterior probability distribution. In the posterior probability distribution, only those functions in agreement with the experimental data are kept. The uncertainty (pink area) notably increases in those areas with little experimental information available. The mean of the posterior distribution (black dashed line) is considered the best fit to the data. A prototypical function from the posterior is shown in blue. For a new compound–target combination, the bioactivity is predicted as a Gaussian distribution, in which the mean is the best prediction and its variance the uncertainty. A radial-kernelled GP with σ = 1 was employed to generate the figure. The python infpy package helped to produce the plots.²⁰⁷

Gao et al.¹¹² showed that SVMs performed, in general, slightly better than GPs when modelling a dataset composed of 128 ligand and 9 human amine GPCRs, although the models trained on the best combination of descriptors exhibited Q² values of 0.744 and 0.742 for GP and SVM respectively. Worth of mention, the difference in performance between GP and SVM was not assessed neither statistically nor by comparing the results of a series models trained on different resamples of the whole dataset. Moreover, the predicted error bars by the GP PCM models were not considered. More recently, Cortes-Ciriano et al.⁷⁵ showed the actual potential of GPs by applying both SVMs and GPs implemented with a panel of diverse kernels to multispecies PCM datasets, namely: human and rat adenosine receptors, mammal GPCRs and Dengue virus proteases. GP and SVM performed comparably as absolute differences were statistically insignificant. However, GP provided notable added values via: (i) the determination of the model AD, (ii) the probabilistic nature of the predictions, and (iii) the inclusion of the experimental uncertainty in the model.

In the experience of the authors regarding the application of GP in PCM,⁷⁵ and in agreement with Schwaighofer et al.,¹¹³ the intervals of confidence (IC) calculated by GP are in accordance with the cumulative Gaussian distribution. Therefore, these intervals of confidence provide valuable information about individual prediction errors. In practice, knowing the error for each prediction can certainly guide decision-making about which compounds should be tested in prospective experimental validation of in silico PCM models. Overall, GP appear as an appealing approach for PCM in spite of the longer CPU time required for the training, as GP is an algorithm of O(N³) time complexity (i.e., it scales with the third power of the size of the dataset).¹¹⁴

3.4 Collaborative Filtering (CF)

One of the requirements for PCM is that target (protein) features need to be defined explicitly (usually by physicochemical characterization of amino acids). While this approach is effective, it nevertheless requires a certain level of information about target sequences and structures. An alternative approach would be to infer target features from an unsupervised approach and not use them as model input a priori. This was done quite recently in multi-target QSAR study of multiple cell lines for the hedgehog signalling pathway.¹¹⁵

Gao et al.¹¹⁵ incorporated a CF approach between 93 cyclopamine derivatives and four cell lines (BxPC-3, NCI-H446, SW1990 and NCI-H157), and showed that collaborative filtering multi-target QSAR outperforms normal QSAR for their dataset. The mean Root-Mean Squared Error (RMSE) for four cell lines was 0.65 log units for CF while it increased to 0.85 log units for (single target) SVR. The collaborative QSAR framework, combined with a feature selection methodology based on collaborative filtering and the content-based recommender systems (a system used by electronic retailers and content providers such as Amazon.com),¹¹⁶ enabled the definition of weights for the compound descriptors (drug-like index). When interpreting their models the authors could determine that molecular volume, polarity, and the cyclic degree are the most influent compound features for multi-cell line inhibitors for this particular pathway (which, from the chemical standpoint, would however be sometimes difficult to interpret structurally). Erhan et al.¹¹⁷ also used CF with a large library of compounds against a family of 12 related targets screened in AstraZeneca's HTS campaigns. The authors elegantly demonstrated how the principles of CF filtering can be used to derive a predictive model with the capability to extrapolate on the target side. However, better results were obtained when using target descriptors (binding pocket fingerprints of 14 bins in this case, where each bin accounts for a type of interaction – ionic, polar, or hydrophobic – in the binding site). Another novelty of this work was the introduction of the kernel-based method Jrank (a kernel perceptron algorithm), which was able to outperform the multi-task neural network in most cases and it never produced significantly worse models. Indeed, in 6 out of 7 cases, this kernel outperformed the random retrieval of compounds. Moreover, the authors also noted that improvements are still possible since Jrank not always outperformed the single-target models.

The overview presented above shows that PCM heavily draws on recent developments in the machine-learning field. However, given that the methods used are only the means to an end, we will in the following also summarize PCM applications in the medicinal chemistry and chemical biology fields, to different target classes as well as different types of biological readout.

4 PCM applied to protein target families

As was touched upon above, PCM has been applied to a very diverse selection of protein targets. Here we will focus on a small selection of targets relevant for drug discovery, namely G Protein-Coupled Receptors (GPCRs), kinases, epigenetic markers, viral enzymes, and human cancer cell lines.

4.1 G protein-coupled receptors

Early PCM virtual screening studies by Bock and Gough to identify ligands of orphan GPCRs (oGPCRs) used physiochemical properties of the amino acids of the entire primary sequence of GPCRs, such as accessible surface area or surface tension, rather than binding site residues. The authors screened 1.9 million ligand-oGPCRs combinations and were able to identify 4357 highly active ligands of oGPCRs. The method, based on SVM, outputs a ranked list of putative oGPCRs ligands. In practice, the most relevant feature of their predictive pipeline is the description of GPCRs with only physicochemical descriptors, thus avoiding the usage of exact 3-dimensional information of the receptors.³⁸ Subsequently, Jacob et al.¹¹⁸ demonstrated that the usage of bioactivity data from 4051 GPCR-ligand combinations (80 human GPCRs from classes A, B and C, and 2446 ligands) extracted from the GLIDA GPCR ligand database¹¹⁹ in PCM models improves the performance over single receptor models, leading to more reliable predictions. The authors used Tanimoto 2D and pharmacophore 3D kernels to describe the ligands, and 5 kernels to describe the GPCRs, namely: Dirac, multitask, hierarchy, binding pocket and poly binding pocket. The best combination thereof was shown to be 2D Tanimoto on the compound side and the binding pocket kernel for the GPCRs, as they reported an accuracy of 78.1% when predicting ligands for orphan receptors. These findings were further capitalized upon in the papers of Frimurer et al.,¹²⁰ and Weill and Rognan.¹²¹ Both papers devised features for the 7TM core ligand-binding site and cavity fingerprints to improve the structure guided drug discovery approaches and provide a general class A GPCR similarity metric.^120,121 The former approach introduced an in silico pipeline to relate 7TM GPCRs based upon the physicochemical properties of the ligand binding site, taken from the crystal structure of the bovine rhodopsin. The pipeline is composed of five steps, which are: (i) sequence alignment of the TM domain of the GPCRs of interest, (ii) selection of the residues in the core binding site important for ligand binding, (iii) definition of binding site signatures and generation of physicochemical descriptors for them, and (iv) use these descriptors to rank, cluster or compare 7TM GPCRs. The authors applied this pipeline to identify ligands for the rhodopsin-like receptor, CRTH2, which by that time only had one annotated ligand besides prostaglandin D2, namely indomethacin. The screening of a library of 1.2 million compounds yielded 600 candidate hit compounds. 10% thereof were confirmed as ligands in a CRTH2 receptor-binding assay, with a IC₅₀ cut-off value to consider a compound as active of 10 μM. On the other hand, Weill and Rognan¹²¹ introduced a new type of protein–ligand fingerprint (PLFP), which encodes pharmacophoric properties of ligands and their binding cavities. These fingerprints were applied to two GPCRs datasets, namely: (i) 168 536 GPCR-ligand combinations (160 286 inactive and 8250 active combinations), and (ii) 234 137 GPCR-ligand combinations (202 019 inactive and 32 118 active combinations). The total number of GPCRs considered was 160. The authors reported a cross-validated classification accuracy higher than 0.9 when using SVM, though the most predictive models on external datasets were not those presenting the highest accuracy values in cross-validation.¹²²

Overall, PCM models trained on GPCRs binding site amino acid descriptors have proven to be a powerful approach to identify the GPCRs targets for a given compound, and to predict ligands for orphan GPCRs. The increasing availability of bioactivity data on GPCRs of interest and orthologous sequences,⁷⁵ as well as the development of novel methodologies to assess GPCRs similarity, is likely to increase the application of PCM on this target family in drug discovery campaigns.

4.2 Kinases

Another important protein family in drug discovery subjected to PCM studies is the kinase superfamily which comprises more than 500 different human proteins.¹²³ The role of kinases in cell signalling and their involvement in more than 400 human diseases have rendered this protein family an attractive target.^124,125 Kinases generally contain a conserved kinase domain that binds ATP in their active site, though some contain more than one kinase domain. Inhibitors targeting this conserved binding site are known as Type I inhibitors. The activation loop of kinases, necessary for the transfer of a phosphate group, exhibits two different conformations, namely DFG-in and DFG-out (where DFG stands for the catalytic triad, Asp-Phe-Gly). Type II inhibitors bind to both the conserved ATP-binding site and to an adjacent pocket present in the DFG-out conformation. These compounds are more selective and thus attractive as drug candidates. Given the ability of PCM to model bioactivities against related targets, it is very well suited to model the affinity of small molecule inhibitors to the kinase family.¹⁶ Different PCM models have been reported to analyze drug selectivity and predict bioactivity profiles against kinases.^66,126

In a recent study by Cao et al.,¹²⁶ the full kinase sequence space was described by alignment-independent ‘Composition, Transition and Distribution’ (CTD) features,¹²⁷ along with topological features of compounds. The dataset comprised a total number of kinase–compound interactions of 54 012, with data from 22 229 compounds and 372 kinases. The best RF model exhibited a classification accuracy in five-fold cross-validation of 93.7%, and a sensitivity of 92.26%. Moreover, this high predictive power was maintained in the four validation levels suggested by Park and Marcotte,⁷⁷ as the following accuracies and sensitivities (respectively and in percentage units) were obtained: (i) L1: 93.15 and 91.23; (ii) L2: 89.53 and 88.24; (iii) L3: 90.71 and 89.48; and (iv) 87.30 and 85.82. Hence the statistically soundness of this PCM model enabled the classification of compound–kinase pairs as interacting, using a 100 nM concentration as cut-off, or non-interacting. The high predictive ability of the models should be considered nevertheless with caution as the degree of completeness of the bioactivity matrix used in the training was only 0.65%. Therefore, these PCM models should be iteratively updated as more bioactivity values become available. Interestingly, kinases similar in the sequence space exhibited high dissimilarity when assessing their similarity with the inhibitors bioactivities. This was assessed using 120 kinases with more than 15 bioactivity annotations, 14 400 datapoints in total. Thus, these data highlights the adequacy of considering chemical and target space to optimize kinase inhibitors.

While high affinity is generally desired for drugs (except possibly in case of multicomponent therapeutics),¹²⁸ selectivity is equally important when targeting a protein family with highly similar binding sites, such as in this case kinases. Subramanian et al.⁶⁶ applied PCM models to a kinase dataset comprising 50 different proteins in the DFG-in conformation to better understand both the residue and compound features which determined whether the ATP-binding site of kinases are involved in compound binding. The resulting PLS models, which included cross-terms (see Section 2.3), demonstrated the added value of PCM over ligand based approaches, as statistically satisfactory QSAR models were reported for only 44% of the targets. More importantly, the models could be visually interpreted, thus enhancing the practical usefulness of PCM for the optimization of compound selectivity. (Further details on the study are given in Section 4.4, as models targets were encoded with 3-dimensional information.)

The distinction between Type I and Type II inhibitors has been proved to be amenable to PCM by Mendez-Lucio et al.¹²⁹ In order to distinguish between Type I and Type II inhibitors, the authors trained a PCM model on a dataset consisting of 463 data points from the interaction matrix defined by 50 known kinase Type I (ATP-competitive) inhibitors against 12 different sequences of ABL1 (five of them) in both the phosphorylated and non-phosphorylated state.¹³⁰ The model exhibited sound predictive ability, assessed by cross-validation, with RMSE and Q² values of 0.420 and 0.887 respectively. In addition, the model allowed the full interpretation of both compound (inhibitor) and protein (kinase) features. Hence, along with the prediction of pK_d, a PCM model can provide information about the effect of both compound structural features and protein amino acid residues.^131–133 The importance of a given compound substructure, or a given amino acid residue, can be evaluated by the calculation of the difference in bioactivity between the predicted value for a compound with and without that substructure.⁷⁵Fig. 4 displays how this information can be presented in practice and shows the average (over the whole data set) effect of presence of a number of features on the pK_d of inhibitor – kinase pairs.

Fig. 4 The effect of presence of compound and amino acid features on bioactivity. (A) Bar plot showing the features of kinase Type I inhibitors and amino acids that affect the pK_d value. For this model, the electronic properties related to amino acid 315 and 317 have large impact on pK_d (shown as green bars), because of their relevance to enzyme–ligand interactions. (B) Kinase inhibitors containing the highlighted compound features responsible for change in pK_d value. The presence of ECFP4_7, ECFP4_34, ECFP4_57 and ECFP4_124 increase the activity, whereas ECFP4_24, ECFP4_41 and ECFP4_120 decrease it.¹³⁰

As shown by these recent PCM studies on the kinase superfamily, PCM can support new concepts for kinase inhibition implicating the simultaneous interaction of kinase inhibitors with several targets leading to multi-target kinase chemotherapy.^129,134 Therefore, PCM constitutes a suitable technique to help in the design of kinase inhibitors with respect to their potency and selectivity (Fig. 4).¹²⁹

4.3 Histone modification and DNA methylation

Epigenetic markers have been identified as emerging therapeutic targets in various malignancies and diseases by correlating phenotypes and differential expression patterns.¹³⁵ Key protein families involved in these processes are readers (bromodomains), writers (DNA modifying enzymes, histone acetylases, methyltransferases) and erasers (histone deacetylases).¹³⁶ Most of the bromodomain epigenetic targets have the ability to selectively modulate the gene expression pattern and contribute to post-translational modifications, chromatin binding, inflammation, oncogenesis.¹³⁷ Moreover there is a clear linkage to some diseases, e.g. multiple myeloma.^138–140 Vidler et al.¹⁴¹ studied the druggability of the different members of the bromodomain family focusing on amino acid signatures in the bromodomain acetyl-lysine binding site, which resulted in a bromodomain family classification more correlated with the binding of small molecules in comparison with a whole-sequence similarity classification. Numerous successful chemical probes like JQ1 have also been identified as bromodomain inhibitors by the Structural Genomics Consortium (SGC).¹⁴² However, the bromodomain family still has unexplored therapeutic potential. To date there are no PCM studies performed on this family.

Recently, Wu and co-workers utilized structural similarity between three classes of HDACs and generated a predictive model for a novel candidate anti-tumour drug.⁹² They implemented various descriptors (physicochemical properties) and similarity descriptors (sequence and structure) of compounds and targets in the PCM model and successfully identified the class-selective inhibitors for class-I and class-II HDACs. The best model exhibited high predictive ability, as the authors reported a Q² value on the external set of 0.754. Overall, the increasing importance of epigenetic targets in drug discovery as well as the availability of large-scale resources of epigenetic targets and its modulators,^143,144 will facilitate the application of PCM to this target family.

4.4 Viral mutants

Previous sections highlighted the ability of PCM to model bioactivities of several human protein superfamilies, yet PCM based approaches are not bound to human protein targets. PCM has also been applied in a number of studies to predict activity profiles of ligands against different viral protein variants.²⁶ In the field of HIV, van Westen et al.²⁶ used 451 compounds tested against 14 HIV reverse transcriptase sequences to train a model that was able to predict the bioactivity of 317 new compound–mutant pairs. Interestingly, when the prediction was validated prospectively with ‘wet lab’ experiments it was found that the prediction error (RMSE of 0.62 log units) was comparable to experimental uncertainty of the assay (0.50 log units). In a similar setting, Huang et al.⁴¹ showed that the inclusion of Protein–Ligand Interaction Fingerprints (PLIFs) of viral residues and ligand structures as cross-terms improved model predictive power over models lacking them. PCM models were trained on 92 compounds and 47 HIV-1 protease variants with about 160 K_i values. The best PCM model exhibited a Q² value of 0.827 on the external set.

Next to these applications, PCM has been used to model the sensitivity of viral mutants to antiretroviral drugs, which could potentially guide HIV treatment.¹⁴⁵ Resistance testing and prediction using these models is achieved by incorporating genotypic (protein) and drug (chemical) data and subsequently linking them to phenotypic data (resistance). PCM then allows the prediction of optimal treatment regimens. The advantage of PCM over established sequence-based approaches is that interpretation of a single model allows the combined elucidation of residues responsible for the change in efficacy and the complementary chemical features affected.^146–149 For instance, van Westen et al.¹⁴⁵ trained PCM models based on a large clinical dataset composed of circa 300 000 datapoints combining both phenotypic and genotypic data. The application of PCM enabled the integration of the similarity of marketed drugs together with protein sequence similarity. The best model exhibited a fold change error of 0.76 log units, which constitutes an improvement of 0.15 log units with respect to previously reported models trained on only protein sequence similarity (0.91 log fold change error). In addition, the authors identified novel mutations of both HIV reverse transcriptase and HIV protease conferring drug resistance, underlining the ability of PCM models not only to model bioactivity information, but to also learn about features relevant for activity from both the ligand and the protein target side.

Similarly, drug susceptibility profiles were predicted based on PCM. In that way, two models have been reported for the prediction of: (i) the susceptibility (bioactivity profile) of a given HIV protease genotype to seven commonly used protease inhibitors;¹⁴⁶ and (ii) the susceptibility of HIV reverse transcriptase to eight nucleoside/nucleotide reverse transcriptase inhibitors.¹⁴⁹ PCM models were trained on 4792 HIV protease–inhibitor combinations, being the Q² value on the external set for the best model 0.87. These models have been made publically available via web-services available at http://www.hivdrc.org/services, allowing free use of these algorithms.¹⁵⁰

While the ligands of most PCM studies discussed here were small molecules, protease peptide substrates are also amenable to PCM. This has been demonstrated recently by Prusis et al.^151,152 to study the enzyme kinetics parameters for designed small peptide substrates on four dengue virus NS3 proteases using PCM modelling. It was found that the PCM models for K_m and K_cat were significantly different. Therefore, by optimizing peptide amino acid properties important for K_m activity it was possible to improve peptide affinity to protease, while losing their catalytic activity, hence obtain peptides, which were dengue protease inhibitors.

These studies by Prusis et al. and van Westen et al. are some of the few reports in which predictions have been validated prospectively, demonstrating the predictive power of PCM in different scenarios.

5 Novel techniques and applications in PCM

5.1 Novel target similarity measure

In the context of GPCRs studies, developing better similarity metrics have helped to determine key binding residues within the GPCR trans-membrane (TM) helical bundle,^51,63,120 aided intra family similarity determination using cavity fingerprints,¹⁵³ and boosted high-throughput homology models that supported cavity detection programs.^65,153–155 PCM approaches including these features have also helped in off-target predictions, retrieval of new lead compounds, and target prediction for GPCR-focused combinatorial chemolibraries.^156,157

The binding site focused techniques used in above described studies allowed for the identification of orthosteric and allosteric sites on the same target for different ligand families. In this line, Gao et al.⁹³ showed the higher predictive ability of models trained on trans-membrane identity descriptors (Q² = 0.74) over Z-scales (Q² = 0.72) when modelling the inhibition constant of 9 human aminergic GPCRs and 128 ligands, (310 ligand–target combinations). Similarly, Shiraishi et al.¹⁵⁸ revealed specific chemical substructures binding to relevant TM pocket residues, which is not only relevant to mutational analysis but also serves as a complementary approach to Structure-Based Drug Discovery (SBDD).^62,158 TM identity descriptors and TM kernels behave more discriminatingly than Z-scales for GPCRs and allow identification and interpretation of GPCR residues associated with binding of ligands (of a particular chemotype). Therefore, the identification of chemical moieties and residues involved in ligand binding enables the development and optimization of GPCRs inhibitors with respect to both potency and selectivity.

5.2 Including 3D information of protein targets in PCM

The binding of a ligand to a protein is a complex process, governed on the structural level by the 3-dimensional (3-D) composition of the protein binding site, the 3-D conformation of the ligands approaching, and the complementarity of their pharmacophoric features. Hence it is expected that inclusion of spatial information from the protein binding sites would improve the predictive power of PCM. Unfortunately, this approach is frequently limited by the lack of high quality 3-D structures, poor understanding of ligand-induced conformational changes, and inaccurate superimposition of protein structures The latter can be (partly) overcome by the use of alignment-free protein descriptors,^65,81 but usually at the cost of lower resolution, loss of target-related information and poor interpretability.

Jacob et al.¹¹⁸ found no improvement through the use of 3-D information. In this study an analysis of 2446 ligands interacting with 80 human GPCRs was performed using a linear vector representing conserved amino acids in the binding pockets. While the binding pocket kernel implicitly encodes 3-D information, the spatial arrangements were derived from the comparison to only two template proteins. Overall, the 3-D kernels (∼77% prediction accuracy) did not show improvements compared to lower dimensional protein descriptions (∼77% prediction accuracy with a protein similarity kernel). Likewise Wassermann et al.¹⁵⁹ found little improvement using 3-D information in their analysis of interactions of 12 proteases with 1359 ligands using the TopMatch similarity score,¹⁶⁰ which used all amino acids within 8 Å around the catalytic residues to describe the target proteins. This 3-D description did not perform better (∼61% recovery rate) than the sequence (∼57%) and protein class-based (∼62%) kernels used in this publication.

Conversely, early work by Strömbergsson et al.¹⁶¹ used local protein substructures, encoded as motifs of 5 amino acid stretches, which are closer than 6.5 Å to each other. This local substructure method showed for a set of 104 enzymes an improvement over the use of global SCOP (Structural Classification of Proteins) folds and the RMSE values on the external validation set decreased from 2.06 to 1.44 pK_i units. Additionally, it was found that local substructures close to the ligand binding sites were assigned more importance in the models than more distant ones, which is intuitively understandable. Similarly, Meslamani and Rognan did find an improvement by using 3-D information.⁶⁰ 581 diverse proteins were described by the 3-D cavity descriptor FuzCav,⁶⁵ which is a vector of 4834 integers reporting counts of pharmacophoric feature triplets mapped to Cα-atoms of binding site-lining residues. The use of cavity 3-D kernels showed a clear advantage (F-measure 0.66) over sequence-based descriptions (F-measure 0.54) in predicting target-ligand pairings for a large external test set (>14 000 ligands, 531 targets), especially in local models. This difference seems to be even more pronounced for datasets with limited ligand data (<50 ligands). Likewise, a recent study by Subramanian et al.⁶⁶ described the superimposed binding sites of 50 (unique) kinases by molecular interaction fields derived from knowledge-based potentials and Schrödinger's WaterMaps.^162,163 Also in this example a significant improvement for 3-D methods (r² = 0.66, q² = 0.44) compared to sequence-based methods (r² = 0.50, q² = 0.34) was reported. Additionally, this combination of methods allows interpretation and easy visualization of PCM results within the context of ligands and binding pockets.

Earlier studies have not clearly shown the advantages of 3D PCM over solely sequence-based approaches, whereas more recent studies show that including 3D information appears to improve performance. The particular data set used (e.g. number of ligands), and the quality of the data provided, likely determines if there is a possible gain in this type of description. However, the constantly increasing number of protein structures, more robust alignment-free methods (e.g. Nisius and Gohlke¹⁶⁴ or Andersson et al.⁸¹), and introduction of protein descriptors with easier interpretability (e.g. Desaphy et al.¹⁶⁵), might help the interpretation and the visualization of PCM models in the future.

5.3 PCM in predicting ligand binding free energy

The application of PCM to docking might not be directly obvious. Yet, the concepts used in PCM, quantitatively relating ligand- and protein-side descriptors to affinity/activity, very much resemble empirical scoring functions. Molecular docking has led to the discovery of active compounds,¹⁶⁶ yet it suffers from several well described limitations, among which is the relatively low performance in prediction of interaction energies.^167,168 In contrast, PCM models can predict the difference in Gibbs free energy (ΔG = −RT ln K_d) between the initial state, where the protein and the compound do not interact, and the final ligand–target complex. Therefore, the principles of PCM can be applied to develop PCM-based scoring functions.

Kramer et al.¹⁶⁹ demonstrate this concept by building a structure-based PCM scoring function. Their method inducts a bagged stepwise multiple linear regression model with a subset of 1387 protein–ligand complexes extracted from the PDBbind09-CN database.¹⁷⁰ Subsequently a new compound–target interaction descriptor based upon distance-binned Crippen-like atom type pairs was introduced. The best model outperformed commercially available scoring functions assessed on the PDBbind09 database and was able to explain 48% of the variance of the external set, providing a RMSE equal to 1.44. Although similar methods had been previously proposed,^171–175 this was the first study where a sufficiently large validation was accomplished to ascertain model's predictive power. Additionally, the implementation of bagged stepwise multiple linear regression (MLR) and PLS enabled the evaluation of the importance of ligand and target descriptors for the PCM model.

Similarly, a subsequent study reported the development of a scoring function based upon the CSAR-NRC HiQ benchmark dataset (http://csardock.org).¹⁷⁶ The best model exhibited acceptable statistics with a cross-validated R² = 0.55 and RMSE = 1.49.¹⁷⁶ Finally, Koppisetty et al.¹⁷⁷ were able to predict for the first time ligand binding free energies where the enthalpic and entropic contributions for a given binding event were deconvoluted. Therein, the authors demonstrated the importance of including ligand descriptors (QIKPROP and LIGPARSE calculated in Schrödinger suite)¹⁷⁸ to the models in addition to 3-dimensional ligand–protein interaction descriptors.

As demonstrated above, PCM overlaps with methods that are originally coming from the structure-based field due to PCM describing in principle any method to relate ligand features and protein/target features on a large scale to an output variable of interest. Another source of complementary information is the information from divergent and convergent homologous sequences. This allows PCM models to extrapolate the bioactivity of ligands to the same protein target in different species as shown below.

5.4 PCM as an approach to extrapolate bioactivity data between species

Given that PCM considers bioactivity data from related targets, these related targets can also include similar targets from different species. Given a group of related targets, a distinction can be made from an evolutionary standpoint between gene pairs originated from intra-species gene duplication events (paralogy, within species) or from speciation events (orthology, across species).¹⁷⁹ Since orthologous genes will tend to maintain the original function, binding modes will also tend to be more conserved than in paralogues, where the original protein function is less conserved.

This has also been shown to be true for affinities of ligands binding to these orthologues by analyzing bioactivity data, such as in a recent study by Kruger et al.²¹ the authors demonstrate that the same small molecule exhibits similar binding affinities when acting on orthologues (though some exceptions were found, e.g. Histamine H₃ receptor). Moreover, the authors verified that larger differences in binding affinity are observed for paralogues with respect to orthologues by analyzing the differences in binding for a total number of 20 309 compounds on 516 human targets, with 651 being the final number of orthologous pairs. These observations aid in optimizing ligands for their interaction with conserved residues across a given protein family, thus making them more desirable lead compounds (thus avoiding their interaction with unrelated targets).¹⁸⁰

In the field of PCM, Lapinsh et al.³⁷ demonstrated for the first time the capability of PCM to successfully combine the pK_i values of 23 organic compounds on 17 human (paralogues) and 4 rat (orthologues) amine GPCRs. The authors were able to deconvolute the binding site interactions into two types, namely: those involved in specificity and those involved in affinity. Therefore, compound design can be envisioned from the viewpoint of affinity or specificity. Similarly, the contribution of TM regions involved in the interactions of amine GPCRs and compounds to compound affinity was also quantified. For example, TM regions 2, 3, 4, 6 and 7 are responsible for low overall affinity in β₂ receptors; however, the same regions are positive contributors to overall high affinity in α_1a receptors. van Westen et al.²² built on this by including in a PCM model bioactivity data from four human and rat adenosine receptors (A₁, A_2A, A_2B and A₃). The authors screened a commercial chemolibrary composed of 791 162 compounds with the most predictive PCM model obtained, which exhibited Q² and RMSE values of 0.73 and 0.61 pK_i units, respectively. Prospective experimental validation led to the discovery of new high-affinity inhibitors, among which a compound with a pK_i value of 8.1 on the A₁ receptor. Finally, the authors have applied PCM to model the pIC₅₀ value of 3228 distinct compounds on 11 mammalian cyclooxygenases (COX) using ensemble PCM.⁵⁵ The final ensemble PCM model, trained on the cross-validation predictions of a panel of 282 RF, SVM and Gradient Boosting Machine (GBM) models, each trained with different values of the hyperparameters, led to predictions on the test set with RMSE and R02 values of 0.71 and 0.65, respectively. Additionally, the description of compounds with unhashed Morgan fingerprints permitted a chemically meaningful model interpretation, which highlighted chemical moieties responsible for selectivity towards COX-2 in agreement with the literature.⁵⁵

The ability of PCM to embrace multispecies information using sequence descriptors allows the creation of models capable to predict compound activity on targets with little available data points on the human orthologue. The existing large body of bioactivity data collected on organisms other than human (e.g. rat and mouse) provides a good resource. This data was derived from the traditional usage of rodent tissues as a source of proteins for biochemical and pharmacological assays. Moreover, the difference in bioactivity between a compound acting on its human target with respect to its orthologue in another species (e.g. the CCR1 antagonist BX471) hampers the utilization of animal models to study human diseases at a molecular level.¹⁸¹ Thus, PCM can help not only to reduce the number of experiments required to complete the compound–target interaction matrix,²⁹ but also appears as a practical tool to understand complex diseases in scenarios where current experimental settings are insufficient (e.g. undeveloped enzymatic assays for a given protein). Similarly, PCM might be applied as a supporting tool in allometric scaling to predict the behavior of clinical candidate drugs in humans.^182,183 Nonetheless, the extrapolation capabilities of PCM models are subjected to the completeness of the bioactivity matrix (Fig. 1). In practice, even though high performance can be attained with a matrix completeness level below 3%, the variability of the chemical space plays a key role in determining the extrapolation capability of a PCM model on the chemical side.⁷⁵ Therefore, a balance has to be found between the coverage of chemical and target space, and the degree of completeness of the bioactivity matrix.

5.5 PCM applied to pharmacogenomics and toxicogenomics data

The biological space in a PCM model can be further extended from single proteins to whole cell lines. A step forward in this regard is the inclusion of cell line descriptors in a PCM model in order to model cell line sensitivity to cancer drugs or toxic compounds. Given that individual cell lines have been shown to demonstrate diverse profiles with respect to drug sensitivity, the variability on the cell line side, which constitutes now the target side of PCM, can be exploited to concomitantly predict both drug potency and cell line selectivity.¹⁷ Additionally, PCM can also facilitate the interpretation of differential gene expression or mechanism of toxicity of compounds,⁸⁸ as will be shown below.

The availability of pharmacogenomics and toxicogenomics data has enabled predictive modelling of cancer cell line sensitivity. These models consider as the dependent variable the response of a whole cell to a given drug, such as in the form of EC₅₀ values, which determines the concentration at which a chemical exerts half of its maximal effect. Therefore, the ‘target’ component in the PCM model is no longer a single protein, described in terms of binding site properties, but by more complex (usually genomic) features such as oncogene mutations, cell karyotypes or gene expression levels.

In the context of human cell lines, the work on the NCI-60 cell line panel, which covers cells from 9 different cancer types, has helped to find novel molecular determinants of drugs sensitivity, as well as to develop drugs targeting concrete tumor types (disease-oriented); e.g. 9-Cl-2-methylellipticinium acetate for central nervous system tumours.¹⁸⁴ However, the number of cancer cell lines with drug sensitivity data has vastly increased with the release in 2012 of two major cancer cell line panels, namely: the Cancer Cell Line Encyclopedia (CCLE) consisting of 947 cancer cell lines¹⁸⁵ and the Genomics of Drug Sensitivity in Cancer (GDSC) consisting of 727 cancer cell lines.¹⁸⁶ The setup of both cell line collections, sharing a total number of 471 cell lines, enabled large scale pharmacological profiling thereof. In that way, Barretina et al.¹⁸⁵ measured the chemotherapeutic effect of 24 drugs on the CCLE panel, while Garnett et al.,¹⁸⁶ tested 130 chemical compounds on the GDSC cell line collection. In both cases, the cell lines were further characterized genomically, by measuring gene expression data, chromosomal copy numbers, oncogene mutations, and microsatellite instability. Recently, Basu et al.¹⁸⁷ measured the sensitivity of 242 cell lines form the CCLE panel to an Informer Set composed of 354 diverse molecules, including 54 clinical candidates and 35 FDA-approved drugs. The sensitivity data is publicly available at the Cancer Therapeutics Response Portal (CTRP).¹⁸⁸

The availability of public bioactivity profiles for compounds in combination with detailed genetic information of the cell lines constitutes a scenario where ML can be applied for predictive cell line sensitivity modelling. In this area, Menden et al.²⁹ exploited cell line drug sensitivity information from the GDSC and incorporated genomic features in combination with chemical descriptors in non parametric models, i.e. neural networks and random forests. These models allowed the authors to determine the missing drug response (IC₅₀) values in the original cell-line compound matrix. The best model predicted the sensitivity on the external (blind) test with a correlation between observed and predicted of 0.64, while a value of 0.61 was obtained when predicting the response on a tissue unseen by the model in the training phase. Recently, the authors have integrated PCM random forest models with conformal prediction for the large-scale prediction of cancer cell line sensitivity with error bars.^17,189 Compounds were described with Morgan fingerprints, whereas a total of 16 cell line profiling datasets were benchmarked for their predictive signal. Gene expression data constantly led to the highest predictive power. Interestingly, the authors found statistically significant differences in predictive power between PCM models trained on cell line identity fingerprints (inductive transfer knowledge between cell lines)¹⁹⁰ and cell line profiling data, suggesting that the explicit inclusion of cell line information improves the prediction of cell line sensitivity. Of practical relevance, the predicted bioactivities enabled the prediction of growth inhibition patterns on the NCI60 panel and the identification of genomic markers of drug sensitivity.

The cancer cell line collections described above still remain to be fully exploited. While they constitute a great opportunity for PCM to integrate both drug sensitivity and genomics data in single models, this data integration still remains challenging due to the disagreement of drug sensitivity measurements between the CCLE and the GDSC.^191,192 Overall, the principles of PCM, namely the combination of chemical and cell line (target) information in single machine learning models, are suited to integrate and exploit the increasing availability of drug sensitivity measurements on cancer cell line panels. The application of PCM in pharmacogenomics is a recent sub-field of which the authors are certain it will grow in the near future. Moreover, in silico drug sensitivity prediction is a cost-efficient method capable to relate large-scale pharmacogenomics data, which is likely to foster the identification of chemotherapeutic lead compounds in both the academic and pharmaceutical cancer drug discovery pipeline.

5.6 Other potential PCM applications

As reviewed above PCM has been applied in a wide range of drug discovery settings, yet more applications remain unexplored. The prediction of compound toxicity on cell lines (toxicogenomics),^193–196 beyond the aforesaid cancer cell line collections, is also amenable to PCM. Recently, Kaggle,¹⁹⁷ a crowd-sourcing platform, hosted two competitions in the field of chemoinformatic modelling. Two pharmaceutical companies, Boehringer Ingelheim and Merck, provided structure–activity relationship datasets to the community in order to find the most predictive machine learning algorithms. The Merck challenge consisted of 15 datasets, each of which containing the bioactivities of a series of molecules on a different target. The winners of the competition applied restricted Boltzmann machines (deep learning).¹⁹⁸ Interestingly, the winning team noted that the similarity between the datasets (targets) could be exploited by inducting a single neural network with all datasets, which output a layer with fifteen different units (neurons). On the other hand, Boehringer Ingelheim provided a dataset with 1776 compound descriptors. The response variable was binary, 0 corresponded to a compound not eliciting the expected activity whereas 1 corresponded to a compound showing activity. In this case, the highest predictive ability was obtained with model ensembles (random forests, gradient boosting machines, and K-nearest neighbors). In a similar vein, the modelling challenge DREAM8 was proposed to the scientific community to model the toxicity of 106 compounds on 884 lymphoblastoid cell lines, which were characterized by SNP genotypes and gene transcript levels quantified by RNA sequencing.^199–201

As described in this review, a large variety of protein targets have been modelled using PCM. Beyond the modelling of the activity of compounds on targets of diverse nature, the interaction between nucleic acids and proteins is also amenable to PCM modelling. In this context, Bellucci et al. predicted protein–RNA interaction based upon the physicochemical properties of both the polypeptide and the nucleotide chains.²⁰² However, to date few studies have been published in this area.^50,202

6 PCM limitations

The usefulness of PCM in computational drug design has been extensively proven in silico (see Section 2.7) and in prospective experimental validation. Nevertheless, there are a number of limitations that should not be overlooked. Publicly available bioactivity databases contain a non-negligible degree of experimental uncertainty,^108–111 which should be certainly included in the modelling phase, as recently proposed by Cortes-Ciriano et al.⁷⁵ Similarly, intervals of confidence for individual predictions should be reported, which can be calculated with algorithm-dependent approaches, e.g. Gaussian processes,⁷⁵ or with algorithm-independent techniques, such as conformal prediction.^17,189

In addition to being informative for biologists, these confidence intervals constitute a valuable source of information about the applicability domain (AD) of a given model.⁷⁵ The AD is defined as the amount of ligand and target space to which a given model can be reliably applied. Thus, in addition to the model validation schemes presented above, an estimation of model AD should accompany any reported model in order to be of practical usefulness.

Another limitation which is often inherently related to bioactivity data is that of data skewness. Some datasets mostly report active²⁰³ or inactive molecules,²⁰⁴ and thus compound–target combinations untested experimentally are normally considered as inactive or active interactions, respectively. Moreover, public data in general tend to favor a relatively small number of proteins classes that have been extensively explored (e.g. GPCRs and kinases).^23–25,205 As such, for some targets the available data might not be sufficient for PCM projects given that imbalanced datasets can lead to models with high negative or false positive rates. Nevertheless, the modelling of cell line sensitivity has shown that PCM displays high interpolation power, as the accuracy of prediction reached a plateau when 20% of the whole compound-cell line matrix was included in the training set.²⁹

Beyond the quality of the data, the descriptor choice still constitutes a field of active research, specially with respect to protein descriptors, which development will deeply influence the success of PCM in the coming years.⁴⁵ A recent paper by Brown et al.¹⁹⁰ suggested that PCM mostly relies on inductive transfer knowledge and that protein descriptors mostly act as labels and do not account for structural differences among them. However, we have recently shown that both amino acid descriptors and cell line profiling datasets account for structural information of eukaryotic, mammal and bacterial DHFR, and cancer cell lines, where the difference in performance on the test set between inductive transfer and PCM models was statistically significant.^17,56

PCM requires the concatenation of ligand and target descriptors, and sometimes also cross-terms, which substantially increases the dimensionality of the input space with respect to QSAR. Although this higher dimensionality might lead to overfitting in PCM,²⁰⁶ in practice, PCM has been shown to exhibit higher predictive power on the test set than QSAR.^22,26,75

7 Conclusions

PCM is becoming a mature technique that allows the simultaneous use of both the chemical and the biological spaces in predictive bioactivity modelling. Both retrospective validation and prospective validation have underscored the advantages of PCM over ligand-based methods. However, it is the extensive expertise developed in the fields of QSAR and chemoinformatics on which PCM can build. Nowadays, a wide choice of properly benchmarked ligand and protein descriptors is available as well as different linear and nonlinear modelling algorithms. Nonetheless, conceptually diverse machine learning algorithms (e.g. GP), the inclusion of three-dimensional information of both ligands and targets, and the use of pharmacogenomics data are still under exploration.

Overall, the ability of PCM to become a customary technique in both the public and the private domain in the following years will certainly rest on its capability to capitalize on biological data of diverse nature, including personalized ‘omics’ data (personalized medicine), in combination with structural data of ligands, be those small molecules, antibodies or peptides.

Author Contributions

Primary attributions for the sections of this review are as follows: 1. I. Cortés-Ciriano, Q. U. Ain, T. Malliavin, G. J. P. Van Westen, and A. Bender; 2. I. Cortés-Ciriano, Q. U. Ain, T. Malliavin, J. P van Westen, and A. Bender; 3.1 E. B. Lenselink, and A. P. IJzerman; 3.2 E. B. Lenselink, and A. P. IJzerman; 3.3 I. Cortés-Ciriano; 3.4 E. B. Lenselink, and A. P. IJzerman; 4.1 I. Cortés-Ciriano, Q. U. Ain, and G. J. P. Van Westen; 4.2 I. Cortés-Ciriano, Q. U. Ain, and O. Méndez-Lucio; 4.3 I. Cortés-Ciriano and Q. U. Ain; 4.4 I. Cortés-Ciriano, Q. U. Ain, G. J. P. Van Westen, and P. Prusis; 5.1 G. Wohlfahrt, V. Subramanian, P. Prusis, and G. J. P. Van Westen; 5.2 G. Wohlfahrt, V. Subramanian, P. Prusis, and G. J. P. Van Westen; 5.3 I. Cortés-Ciriano; 5.4 I. Cortés-Ciriano; 5.5 I. Cortés-Ciriano, and Q. U. Ain; 5.6 I. Cortés-Ciriano, Q. U. Ain, E. B. Lenselink, T. Malliavin, G. J. P. Van Westen, and A. Bender; 6. I. Cortés-Ciriano; 7. I. Cortés-Ciriano, Q. U. Ain, T. Malliavin, G. J. P. Van Westen, and A. Bender. Figures 1 and 3 were done by I. Cortés-Ciriano. Figure 2 was done by Q. U. Ain. Figure 4 was done by Q. U. Ain, and O. Méndez-Lucio. Table 1 was compiled by V. Subramanian, I. Cortés-Ciriano, and Q. U. Ain. Table 2 was compiled by E. B. Lenselink, A. P. Ijzerman, I. Cortés-Ciriano, Q. U. Ain, and G. J. P. Van Westen. Final editing was accomplished by I. Cortés-Ciriano, Q. U. Ain, T. Malliavin, G. J. P. Van Westen, and A. Bender. All authors read and approved the final manuscript.

Abbreviations

3D	3-Dimensional
CF	Collaborative Filtering
GP	Gaussian Process
GPCR	G Protein-Coupled Receptor
IC50	Half Maximal Inhibitory Concentration
K d	Dissociation constant
K i	Inhibition constant
PCM	Proteochemometric(s)
PLS	Partial Least Squares
QSAR	Quantitative Structure–Activity Relationship
R&D	Research and Development
RF	Random Forests
SVM	Support Vector Machines
TM	Trans Membrane

Acknowledgements

ICC thanks the Pasteur-Paris International PhD Program and Institut Pasteur Paris for funding. QUA thanks the Islamic Development Bank and Cambridge Commonwealth Trust for funding. VS thanks the Finnish National Doctoral Program in Informational and Structural Biology for organizing graduate studies and Helsinki University Research Foundation for funding. API and EBL thank the Dutch Research Council (NWO) for financial support (NWO-TOP #714.011.001). OML is grateful to CONACyT (no. 217442/312933) and Cambridge Overseas Trust for funding. TM thanks the Institut Pasteur Paris and CNRS for funding. GJPvW thanks EMBL (EIPOD) and Marie Curie (COFUND) for funding. AB thanks Unilever and the European Research Commission (Starting Grant ERC-2013-StG 336159 MIXTURE) for funding.

References

1. L. B. Akella and D. DeCaprio, Curr. Opin. Chem. Biol., 2010, 14, 325–330.
2. S. M. Paul, D. S. Mytelka, C. T. Dunwiddie, C. C. Persinger, B. H. Munos, S. R. Lindborg and A. L. Schacht, Nat. Rev. Drug Discovery, 2010, 9, 203–214.
3. A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107.
4. Y. Wang, J. Xiao, T. O. Suzek, J. Zhang, J. Wang, Z. Zhou, L. Han, K. Karapetyan, S. Dracheva, B. A. Shoemaker, E. Bolton, A. Gindulyte and S. H. Bryant, Nucleic Acids Res., 2012, 40, 400–412.
5. A. Bender and R. C. Glen, Org. Biomol. Chem., 2004, 2, 3204–3218.
6. P. Willett, Annu. Rev. Inf. Sci. Technol., 2009, 43, 3–71.
7. J. Mestres, E. Gregori-Puigjané, S. Valverde and R. V. Solé, Mol. BioSyst., 2009, 5, 1051–1057.
8. J. Mestres, E. Gregori-Puigjané, S. Valverde and R. V. Solé, Nat. Biotechnol., 2008, 26, 983–984.
9. M. T. Bianchi and E. J. Botzolakis, BMC Pharmacol., 2010, 10, 3.
10. M. C. Shoshan and S. Linder, Cancer Ther., 2004, 2, 297–304.
11. A. Bender, J. Scheiber, M. Glick, J. W. Davies, K. Azzaoui, J. Hamon, L. Urban, S. Whitebread and J. L. Jenkins, ChemMedChem, 2007, 2, 861–873.
12. M. Bieler and H. Koeppen, Drug Dev. Res., 2012, 73, 357–364.
13. M. Bredel and E. Jacoby, Nat. Rev. Genet., 2004, 5, 262–275.
14. Computational Chemogenomics, ed. E. Jacoby, Pan Stanford Publishing, 2013.
15. M. Lapinsh, P. Prusis and A. Gutcaits, Biochim. Biophys. Acta, 2001, 1525, 180–190.
16. G. J. P. van Westen, J. K. J. K. J. K. Wegner, A. P. IJzerman, H. W. T. van Vlijmen and A. Bender, Med. Chem. Commun., 2011, 2, 16–30.
17. I. Cortes-Ciriano, G. J. P. van Westen, G. Bouvier, M. Nilges, J. P. Overington, A. Bender and T. E. Malliavin, in revision.
18. G. J. P. van Westen and J. P. Overington, Nat. Methods, 2013, 10, 116–117.
19. H. Lin, M. F. Sassano, B. L. Roth and B. K. Shoichet, Nat. Methods, 2013, 10, 140–146.
20. M. Vieth, J. J. Sutherland, D. H. Robertson and R. M. Campbell, Drug Discovery Today, 2005, 10, 839–846.
21. F. A. Kruger and J. P. Overington, PLoS Comput. Biol., 2012, 8, e1002333.
22. G. J. P. van Westen, O. O. Van Den Hoven, R. Van Der Pijl, T. Mulder-Krieger and A. Bender, J. Med. Chem., 2012, 55, 7010–7020.
23. E. Gregori-Puigjané and J. Mestres, Curr. Opin. Chem. Biol., 2008, 12, 359–365.
24. E. Gregori-Puigjané and J. Mestres, Comb. Chem. High Throughput Screening, 2008, 11, 669–676.
25. D. Rognan, Br. J. Pharmacol., 2007, 152, 38–52.
26. G. J. P. van Westen, J. K. Wegner, P. Geluykens, L. Kwanten, I. Vereycken, A. Peeters, A. P. IJzerman, H. W. T. van Vlijmen and A. Bender, PLoS One, 2011, 6, e27518.
27. E. van der Horst, J. E. Peironcely, G. J. P. van Westen, O. O. van den Hoven, W. R. J. D. Galloway, D. R. Spring, J. K. Wegner, H. W. T. van Vlijmen, A. P. IJzerman, J. P. Overington and A. Bender, Curr. Top. Med. Chem., 2011, 11, 1964–1977.
28. I. Bahar, C. Chennubhotla and D. Tobi, Curr. Opin. Struct. Biol., 2007, 17, 633–640.
29. M. P. Menden, F. Iorio, M. Garnett, U. McDermott, C. H. Benes, P. J. Ballester and J. Saez-Rodriguez, PLoS One, 2013, 8, e61318.
30. M. J. Keiser, B. L. Roth, B. N. Armbruster, P. Ernsberger, J. J. Irwin and B. K. Shoichet, Nat. Biotechnol., 2007, 25, 197–206.
31. G. V. Paolini, R. H. B. Shapland, W. P. van Hoorn, J. S. Mason and A. L. Hopkins, Nat. Biotechnol., 2006, 24, 805–815.
32. H. Geppert, J. Humrich, D. Stumpfe, T. Gärtner and J. Bajorath, J. Chem. Inf. Model., 2009, 49, 767–779.
33. X. Ning, H. Rangwala and G. Karypis, J. Chem. Inf. Model., 2009, 49, 2444–2456.
34. J. Zilliacus, A. P. Wright, U. Norinder, J. A. Gustafsson and J. Carlstedt-Duke, J. Biol. Chem., 1992, 267, 24941–24947.
35. S. Tomic, L. Nilsson and R. C. Wade, J. Med. Chem., 2000, 43, 1780–1792.
36. P. Prusis, R. Muceniece, P. Andersson, C. Post, T. Lundstedt and J. E. Wikberg, Biochim. Biophys. Acta, 2001, 1544, 350–357.
37. M. Lapinsh, P. Prusis, T. Lundstedt and J. E. S. Wikberg, Mol. Pharmacol., 2002, 61, 1465–1475.
38. J. R. Bock and D. A. Gough, J. Chem. Inf. Model., 2005, 45, 1114–1402.
39. G. J. van Westen, J. K. Wegner, P. Geluykens, L. Kwanten, I. Vereycken, A. Peeters, A. P. Ijzerman, H. W. van Vlijmen and A. Bender, PLoS One, 2011, 6, e27518.
40. M. L. Jarl and E. S. Wikberg, Chemogenomics in Drug Discovery, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, FRG, 2004.
41. Q. Huang, H. Jin, Q. Liu, Q. Wu, H. Kang, Z. Cao and R. Zhu, PLoS One, 2012, 7, e41698.
42. Q. U. Ain, O. Méndez-Lucio, I. Cortés Ciriano, T. E. Malliavin, G. J. P. van Westen and A. Bender, Integr. Biol., 2014 10.1039/C4IB00175C.
43. M. Lapinsh, S. Veiksina, S. Uhlén, R. Petrovska, I. Mutule, F. Mutulis, S. Yahorava, P. Prusis and J. E. S. Wikberg, Mol. Pharmacol., 2005, 67, 50–59.
44. G. van Westen, R. Swier, J. K. Wegner, A. P. IJzerman, H. W. van Vlijmen and A. Bender, J. Cheminf., 2013, 5, 41.
45. G. J. van Westen, R. F. Swier, I. Cortes-Ciriano, J. K. Wegner, J. P. Overington, A. P. IJzerman, H. W. van Vlijmen and A. Bender, J. Cheminf., 2013, 5, 42.
46. F. Sievers, A. Wilm, D. Dineen, T. J. Gibson, K. Karplus, W. Li, R. Lopez, H. McWilliam, M. Remmert, J. Söding, J. D. Thompson and D. G. Higgins, Mol. Syst. Biol., 2011, 7, 539.
47. D. S. Murrell, I. Cortes-Ciriano, G. J. P. van Westen, I. P. Stott, T. Malliavin, A. Bender and R. C. Glen, 2014, https://github.com/cambDI/camb.
48. M. Sandberg, L. Eriksson, J. Jonsson, M. Sjöström and S. Wold, J. Med. Chem., 1998, 41, 2481–2491.
49. H. B. Rao, F. Zhu, G. B. Yang, Z. R. Li and Y. Z. Chen, Nucleic Acids Res., 2011, 39, W385–W390.
50. J. Shen, J. Zhang, X. Luo, W. Zhu, K. Yu, K. Chen, Y. Li and H. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4337–4341.
51. J.-S. Surgand, J. Rodrigo, E. Kellenberger and D. Rognan, Proteins, 2006, 62, 509–538.
52. F. B. Sheinerman, E. Giraud and A. Laoui, J. Mol. Biol., 2005, 352, 1134–1156.
53. D. Kuhn, N. Weskamp, E. Hüllermeier and G. Klebe, ChemMedChem, 2007, 2, 1432–1447.
54. T. De Bruyn, G. J. P. van Westen, A. P. IJzerman, B. Stieger, P. de Witte, P. F. Augustijns and P. P. Annaert, Mol. Pharmacol., 2013, 83, 1257–1267.
55. I. Cortes-Ciriano, D. S. Murrell, G. J. P. van Westen, A. Bender and T. Malliavin, in revision, 2014.
56. S. Paricharak, I. Cortes-Ciriano, A. P. IJzerman, T. E. Malliavin and A. Bender, in revision.
57. I. Kufareva, A. V. Ilatovskiy and R. Abagyan, Nucleic Acids Res., 2012, 40, D535–D540.
58. O. Kalinina and O. Wichmann, PLoS Comput. Biol., 2011, 7, e1002043.
59. E. L. Willighagen, J. Alvarsson, A. Andersson, M. Eklund, S. Lampa, M. Lapins, O. Spjuth and J. E. Wikberg, J. Biomed. Semant., 2011, 2(suppl. 1), 1–24.
60. J. Meslamani and D. Rognan, J. Chem. Inf. Model., 2011, 51, 1593–1603.
61. N. Weill, C. Valencia, S. Gioria, P. Villa, M. Hibert and D. Rognan, Mol. Inf., 2011, 30, 521–526.
62. H. Yabuuchi, S. Niijima, H. Takematsu, T. Ida, T. Hirokawa, T. Hara, T. Ogawa, Y. Minowa, G. Tsujimoto and Y. Okuno, Mol. Syst. Biol., 2011, 7, 472–484.
63. D. E. Gloriam, S. M. Foord, F. E. Blaney and S. L. Garland, J. Med. Chem., 2009, 52, 4429–4442.
64. S. L. Kinnings and R. M. Jackson, J. Chem. Inf. Model., 2009, 49, 318–329.
65. N. Weill and D. Rognan, J. Chem. Inf. Model., 2010, 50, 123–135.
66. V. Subramanian, P. Prusis, L.-O. Pietilä, H. Xhaard and G. Wohlfahrt, J. Chem. Inf. Model., 2013, 53, 3021–3030.
67. R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, 2008.
68. M. Karelson, Molecular descriptors in QSAR/QSPR, vol. 1, 2000.
69. R. C. Glenn, A. Bender, C. H. Arnby, L. Carlsson, S. Boyer and J. Smith, I. Drugs, 2006, 9, 199–204.
70. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
71. V. C. Andrea Mauri, MATCH, 2006, 56, 237–248.
72. C. W. Yap, J. Comput. Chem., 2011, 32, 1466–1474.
73. P. Prusis, S. Uhlén, R. Petrovska, M. Lapinsh and J. E. S. Wikberg, BMC Bioinf., 2006, 7, 167.
74. M. R. Doddareddy, G. J. P. van Westen, E. van der Horst, J. E. Peironcely, F. Corthals, A. P. IJzerman, M. Emmerich, J. L. Jenkins and A. Bender, Stat. Anal. Data Min., 2009, 2, 149–160.
75. I. Cortes-Ciriano, G. J. van Westen, E. B. Lenselink, D. S. Murrell, A. Bender and T. Malliavin, J. Cheminf., 2014, 6, 35.
76. A. Golbraikh and A. Tropsha, J. Mol. Graphics Modell., 2002, 20, 269–276.
77. Y. Park and E. M. Marcotte, Nat. Methods, 2012, 9, 1134–1136.
78. T. Pahikkala, A. Airola, S. Pietilä, S. Shakyawar, A. Szwajda, J. Tang and T. Aittokallio, Briefings Bioinf., 2014 DOI:10.1093/bib/bbu010.
79. S. Varma and R. Simon, BMC Bioinf., 2006, 7, 91.
80. D. Krstajic, L. J. Buturovic, D. E. Leahy and S. Thomas, J. Cheminf., 2014, 6, 10.
81. C. R. Andersson, M. G. Gustafsson and H. Strömbergsson, Curr. Top. Med. Chem., 2011, 11, 1978–1993.
82. C. L. Bruce, J. L. Melville, S. D. Pickett and J. D. Hirst, J. Chem. Inf. Model., 2007, 47, 219–227.
83. M. Eklund, U. Norinder, S. Boyer and L. Carlsson, Mol. Inf., 2012, 31, 173–179.
84. M. Eklund, U. Norinder, S. Boyer and L. Carlsson, J. Chem. Inf. Model., 2014, 54, 837–843.
85. B. Schlkopf and A. J. Smola, Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond (Adaptive Computation and Machine Learning), The MIT Press, 2001.
86. B. Schölkopf, T. Koji and J.-P. Vert, Kernel Methods in Computational Biology, The MIT Press, 2004.
87. A. Ben-Hur and C. Ong, PLoS Comput. Biol., 2008, 4, e1000173.
88. M. Lapins, A. Worachartcheewan, O. Spjuth, V. Georgiev, V. Prachayasittikul, C. Nantasenamat and J. E. S. Wikberg, PLoS One, 2013, 8, e66566.
89. F. Cheng, Y. Yu, J. Shen, L. Yang, W. Li, G. Liu, P. W. Lee and Y. Tang, J. Chem. Inf. Model., 2011, 51, 996–1011.
90. R. W. Marc, G. Genton, N. Cristianini and J. Shawe-taylor, J. Mach. Learn. Res., 2001, 299–312.
91. B. Üstün, W. J. Melssen and L. M. C. Buydens, Chemom. Intell. Lab. Syst., 2006, 81, 29–40.
92. D. Wu, Q. Huang, Y. Zhang, Q. Zhang, Q. Liu, J. Gao, Z. Cao and R. Zhu, BMC Bioinf., 2012, 13, 212.
93. J. Gao, Q. Huang, D. Wu, Q. Zhang, Y. Zhang, T. Chen, Q. Liu, R. Zhu, Z. Cao and Y. He, Gene, 2013, 518, 124–131.
94. S. Niijima, A. Shiraishi and Y. Okuno, J. Chem. Inf. Model., 2012, 52, 901–912.
95. M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594.
96. E. Kondratovich, I. I. Baskin and A. Varnek, Mol. Inf., 2013, 32, 261–266.
97. J. Wang, X. Shen and W. Pan, J. Contemp. Mat., 2007.
98. R. Collobert, F. Sinz, J. Weston and L. Bottou, J. Mach. Learn. Res., 2006, 7, 1687–1712.
99. M. E. Tipping, J. Mach. Learn. Res., 2001, 1, 211–245.
100. R. Lowe, H. Y. Mussa, J. B. O. Mitchell and R. C. Glen, J. Chem. Inf. Model., 2011, 51, 1539–1544.
101. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan and B. P. Feuston, J. Chem. Inf. Comput. Sci., 2003, 43, 1947–1958.
102. R. P. Sheridan, J. Chem. Inf. Model., 2013, 53, 2837–2850.
103. R. P. Sheridan, J. Chem. Inf. Model., 2012, 52, 814–823.
104. N. Meinshausen, J. Mach. Learn. Res., 2006, 7, 983–999.
105. Z. Bosnić and I. Kononenko, Intell. Data Anal., 2009, 13, 385–401.
106. I. V. Tetko, P. Bruneau, H.-W. Mewes, D. C. Rohrer and G. I. Poda, Drug Discovery Today, 2006, 11, 700–707.
107. T. I. Netzeva, A. Worth, T. Aldenberg, R. Benigni, M. T. D. Cronin, P. Gramatica, J. S. Jaworska, S. Kahn, G. Klopman, C. A. Marchant, G. Myatt, N. Nikolova-Jeliazkova, G. Y. Patlewicz, R. Perkins, D. Roberts, T. Schultz, D. W. Stanton, J. J. M. van de Sandt, W. Tong, G. Veith and C. Yang, Altern. Lab. Anim., 2005, 33, 155–173.
108. C. Kramer and R. Lewis, Curr. Top. Med. Chem., 2012, 12, 1896–1902.
109. P. Tiikkainen, L. Bellis, Y. Light and L. Franke, J. Chem. Inf. Model., 2013, 53, 2499–2505.
110. C. Kramer, T. Kalliokoski, P. Gedeck and A. Vulpetti, J. Med. Chem., 2012, 55, 5165–5173.
111. T. Kalliokoski, C. Kramer, A. Vulpetti and P. Gedeck, PLoS One, 2013, 8, e61007.
112. J. Gao, Q. Huang, D. Wu, Q. Zhang, Y. Zhang, T. Chen, Q. Liu, R. Zhu, Z. Cao and Y. He, Gene, 2013, 518, 124–131.
113. A. Schwaighofer, T. Schroeter, S. Mika, J. Laub, A. ter Laak, D. Sülzle, U. Ganzer, N. Heinrich and K.-R. Müller, J. Chem. Inf. Model., 2007, 47, 407–424.
114. C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, Mit Press, 2006.
115. J. Gao, D. Che, V. W. Zheng, R. Zhu and Q. Liu, BMC Bioinf., 2012, 13, 186.
116. J. S. Breese, D. Heckerman and C. Kadie, Empirical analysis of predictive algorithms for collaborative filtering, 1998, pp. 43–52.
117. D. Erhan, P.-J. L'heureux, S. Y. Yue and Y. Bengio, J. Chem. Inf. Model., 2006, 46, 626–635.
118. L. Jacob, B. Hoffmann, V. Stoven and J.-P. Vert, BMC Bioinf., 2008, 9, 363.
119. Y. Okuno, J. Yang, K. Taneishi, H. Yabuuchi and G. Tsujimoto, Nucleic Acids Res., 2006, 34, D673–D677.
120. T. M. Frimurer, T. Ulven, C. E. Elling, L.-O. Gerlach, E. Kostenis and T. Högberg, Bioorg. Med. Chem. Lett., 2005, 15, 3707–3712.
121. N. Weill and D. Rognan, J. Chem. Inf. Model., 2009, 49, 1049–1062.
122. H. Kubinyi, F. A. Hamprecht and T. Mietzner, J. Med. Chem., 1998, 41, 2553–2564.
123. G. Manning, D. B. Whyte, R. Martinez, T. Hunter and S. Sudarsanam, Science, 2002, 298, 1912–1934.
124. I. Melnikova and J. Golden, Nat. Rev. Drug Discovery, 2004, 3, 993–994.
125. P. Cohen, Nat. Rev. Drug Discovery, 2002, 1, 309–315.
126. D.-S. Cao, G.-H. Zhou, S. Liu, L.-X. Zhang, Q.-S. Xu, M. He and Y.-Z. Liang, Anal. Chim. Acta, 2013, 792, 10–18.
127. D.-S. Cao, Q.-S. Xu and Y.-Z. Liang, Bioinformatics, 2013, 29, 960–962.
128. A. A. Borisy, P. J. Elliott, N. W. Hurst, M. S. Lee, J. Lehar, E. R. Price, G. Serbedzija, G. R. Zimmermann, M. A. Foley, B. R. Stockwell and C. T. Keith, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7977–7982.
129. O. Mendez-Lucio, M. A. Afzal, A. Q. Ul, I. Cortes Ciriano and Bender, unpublished work.
130. O. Méndez-Lucio, A. M. Avid, Q. U. Ain and A. Bender, unpublished work, 2013.
131. D. L. Gibbons, S. Pricl, H. Kantarjian, J. Cortes and A. Quintás-Cardama, Cancer, 2012, 118, 293–299.
132. C.-H. Yun, T. J. Boggon, Y. Li, M. S. Woo, H. Greulich, M. Meyerson and M. J. Eck, Cancer Cell, 2007, 11, 217–227.
133. S. W. Cowan-Jacob, G. Fendrich, A. Floersheimer, P. Furet, J. Liebetanz, G. Rummel, P. Rheinberger, M. Centeleghe, D. Fabbro and P. W. Manley, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2007, 63, 80–93.
134. T. S. Gujral, L. Peshkin and M. W. Kirschner, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5048–5053.
135. C.-W. Chung and J. Witherington, J. Biomol. Screening, 2011, 16, 1170–1185.
136. S. Knapp and H. Weinmann, ChemMedChem, 2013, 1885–1891.
137. R. K. Prinjha, J. Witherington and K. Lee, Trends Pharmacol. Sci., 2012, 33, 146–153.
138. S. R. Floyd, M. E. Pacold, Q. Huang, S. M. Clarke, F. C. Lam, I. G. Cannell, B. D. Bryson, J. Rameseder, M. J. Lee, E. J. Blake, A. Fydrych, R. Ho, B. a. Greenberger, G. C. Chen, A. Maffa, A. M. Del Rosario, D. E. Root, A. E. Carpenter, W. C. Hahn, D. M. Sabatini, C. C. Chen, F. M. White, J. E. Bradner and M. B. Yaffe, Nature, 2013, 498, 246–250.
139. J. E. Delmore, G. C. Issa, M. E. Lemieux, P. B. Rahl, J. Shi, H. M. Jacobs, E. Kastritis, T. Gilpatrick, R. M. Paranal, J. Qi, M. Chesi, A. C. Schinzel, M. R. McKeown, T. P. Heffernan, C. R. Vakoc, P. L. Bergsagel, I. M. Ghobrial, P. G. Richardson, R. A. Young, W. C. Hahn, K. C. Anderson, A. L. Kung, J. E. Bradner and C. S. Mitsiades, Cell, 2011, 146, 904–917.
140. G. Zhang and A. Plotnikov, J. Med. Chem., 2013, 56, 9251–9264.
141. L. R. Vidler, N. Brown, S. Knapp and S. Hoelder, J. Med. Chem., 2012, 55, 7346–7359.
142. M. Gruetter, Nature, 2012, 491, 40.
143. C. H. Arrowsmith, C. Bountra, P. V. Fish, K. Lee and M. Schapira, Nat. Rev. Drug Discovery, 2012, 11, 384–400.
144. Z. Huang, H. Jiang, X. Liu, Y. Chen, J. Wong, Q. Wang, W. Huang, T. Shi and J. Zhang, PLoS One, 2012, 7, e39917.
145. G. J. P. van Westen, A. Hendriks, J. K. Wegner, A. P. IJzerman, H. W. T. van Vlijmen and A. Bender, PLoS Comput. Biol., 2013, 9, e1002899.
146. M. Lapins, M. Eklund, O. Spjuth, P. Prusis and J. E. S. Wikberg, BMC Bioinf., 2008, 9, 181.
147. A. Kontijevskis, R. Petrovska, S. Yahorava, J. Komorowski and J. E. S. Wikberg, Bioorg. Med. Chem., 2009, 17, 5229–5237.
148. K. M. Doherty, P. Nakka, B. M. King, S.-Y. Rhee, S. P. Holmes, R. W. Shafer and M. L. Radhakrishnan, BMC Bioinf., 2011, 12, 477–496.
149. M. Junaid, M. Lapins, M. Eklund, O. Spjuth and J. Wikberg, PLoS One, 2010, 5, e14353.
150. O. Spjuth, M. Eklund, M. Lapins, M. Junaid and J. E. S. Wikberg, Bioinformatics, 2011, 27, 1719–1720.
151. P. Prusis, M. Junaid, R. Petrovska, S. Yahorava, A. Yahorau, G. Katzenmeier, M. Lapins and J. E. S. Wikberg, Biochem. Biophys. Res. Commun., 2013, 434, 767–772.
152. P. Prusis, M. Lapins, S. Yahorava, R. Petrovska, P. Niyomrattanakit, G. Katzenmeier and J. E. S. Wikberg, Bioorg. Med. Chem., 2008, 16, 9369–9377.
153. C. D. Andersson, B. Y. Chen and A. Linusson, Proteins, 2010, 78, 1408–1422.
154. S. Glinca and G. Klebe, J. Chem. Inf. Model., 2013, 53, 2082–2092.
155. Z. Liu, L. Wu, Y. Wang and X. Zhang, Int. J. Bioinf. Res. Appl., 2008, 4, 445–460.
156. N. Weill, Curr. Top. Med. Chem., 2011, 11, 1944–1955.
157. M. Reutlinger, T. Rodrigues, P. Schneider and G. Schneider, Angew. Chem., Int. Ed., 2014, 53, 582–585.
158. A. Shiraishi, S. Niijima, J. B. Brown, M. Nakatsui and Y. Okuno, J. Chem. Inf. Model., 2013, 53, 1253–1262.
159. A. M. Wassermann, H. Geppert and J. Bajorath, J. Chem. Inf. Model., 2009, 49, 2155–2167.
160. M. J. Sippl and M. Wiederstein, Bioinformatics, 2008, 24, 426–427.
161. H. Strömbergsson, A. Kryshtafovych, P. Prusis, K. Fidelis, J. E. S. Wikberg, J. Komorowski and T. R. Hvidsten, Proteins, 2006, 65, 568–579.
162. C. Hoppe, C. Steinbeck and G. Wohlfahrt, J. Chem. Inf. Model., 2006, 24, 328–340.
163. D. D. Robinson, W. Sherman and R. Farid, ChemMedChem, 2010, 5, 618–627.
164. B. Nisius and H. Gohlke, J. Chem. Inf. Model., 2012, 52, 2339–2347.
165. J. Desaphy, K. Azdimousa, E. Kellenberger and D. Rognan, J. Chem. Inf. Model., 2012, 52, 2287–2299.
166. E. Laine, C. Goncalves, J. C. Karst, A. Lesnard, S. Rault, W.-J. Tang, T. E. Malliavin, D. Ladant and A. Blondel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11277–11282.
167. E. Yuriev and P. A. Ramsland, J. Mol. Recognit., 2013, 26, 215–239.
168. E. Yuriev, M. Agostino and P. A. Ramsland, J. Mol. Recognit., 2011, 24, 149–164.
169. C. Kramer and P. Gedeck, J. Chem. Inf. Model., 2011, 51, 707–720.
170. R. Wang, X. Fang, Y. Lu and S. Wang, J. Med. Chem., 2004, 47, 2977–2980.
171. C. Sotriffer, P. Sanschagrin, H. Matter and G. Klebe, Proteins, 2008, 73, 395–419.
172. W. Deng, C. Brenema and M. Embrechts, J. Chem. Inf. Comput. Sci., 2004, 44, 699–703.
173. S. Zhang, A. Golbraikh and A. Tropsha, J. Med. Chem., 2006, 49, 2713–2724.
174. N. Artemenko, J. Chem. Inf. Model., 2008, 48, 569–574.
175. S. Das, M. M. P. Krein and C. M. C. Breneman, J. Chem. Inf. Model., 2010, 50, 298–308.
176. C. Kramer and P. Gedeck, J. Chem. Inf. Model., 2011, 51, 2139–2145.
177. C. A. K. Koppisetty, M. Frank, G. J. L. Kemp and P.-G. Nyholm, J. Chem. Inf. Model., 2013, 53, 2559–2570.
178. Small-Molecule Drug Discovery Suite 2013-3, QikProp, version 3.8, Schrödinger, LLC, New York, NY, 2013.
179. E. V. Koonin, Annu. Rev. Genet., 2005, 39, 309–338.
180. E. Lounkine, M. J. Keiser, S. Whitebread, D. Mikhailov, J. Hamon, J. L. Jenkins, P. Lavan, E. Weber, A. K. Doak, S. Côté, B. K. Shoichet and L. Urban, Nature, 2012, 486, 361–367.
181. R. Horuk, Nat. Rev. Drug Discovery, 2009, 8, 23–33.
182. L. Kagan, A. K. Abraham, D. E. Mager and J. M. Harrold, Pharm. Res., 2010, 27, 920–932.
183. D. Zhang, S. Surapaneni and L. Guan, in ADME-Enabling Technologies in Drug Design and Development, ed. D. Zhang and S. Surapaneni, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2012.
184. R. H. Shoemaker, Nat. Rev. Cancer, 2006, 6, 813–823.
185. J. Barretina, G. Caponigro, N. Stransky, K. Venkatesan, A. A. Margolin, S. Kim, C. J. Wilson, J. Lehár, G. V. Kryukov, D. Sonkin, A. Reddy, M. Liu, L. Murray, M. F. Berger, J. E. Monahan, P. Morais, J. Meltzer, A. Korejwa, J. Jané-Valbuena, F. A. Mapa, J. Thibault, E. Bric-Furlong, P. Raman, A. Shipway, I. H. Engels, J. Cheng, G. K. Yu, J. Yu, P. Aspesi, M. de Silva, K. Jagtap, M. D. Jones, L. Wang, C. Hatton, E. Palescandolo, S. Gupta, S. Mahan, C. Sougnez, R. C. Onofrio, T. Liefeld, L. MacConaill, W. Winckler, M. Reich, N. Li, J. P. Mesirov, S. B. Gabriel, G. Getz, K. Ardlie, V. Chan, V. E. Myer, B. L. Weber, J. Porter, M. Warmuth, P. Finan, J. L. Harris, M. Meyerson, T. R. Golub, M. P. Morrissey, W. R. Sellers, R. Schlegel and L. A. Garraway, Nature, 2012, 483, 603–607.
186. M. M. J. Garnett, E. E. J. Edelman, S. J. S. Heidorn, C. D. Greenman, A. Dastur, K. W. Lau, P. Greninger, I. R. Thompson, X. Luo, J. Soares, Q. Liu, F. Iorio, D. Surdez, L. Chen, R. J. Milano, G. R. Bignell, A. T. Tam, H. Davies, J. a. Stevenson, S. Barthorpe, S. R. Lutz, F. Kogera, K. Lawrence, A. McLaren-Douglas, X. Mitropoulos, T. Mironenko, H. Thi, L. Richardson, W. Zhou, F. Jewitt, T. Zhang, P. O'Brien, J. L. Boisvert, S. Price, W. Hur, W. Yang, X. Deng, A. Butler, H. G. Choi, J. W. Chang, J. Baselga, I. Stamenkovic, J. a. Engelman, S. V. Sharma, O. Delattre, J. Saez-Rodriguez, N. S. Gray, J. Settleman, P. A. Futreal, D. a. Haber, M. R. Stratton, S. Ramaswamy, U. McDermott and C. H. Benes, Nature, 2012, 483, 570–575.
187. A. Basu, N. E. Bodycombe, J. H. Cheah, E. V. Price, K. Liu, G. I. Schaefer, R. Y. Ebright, M. L. Stewart, D. Ito, S. Wang, A. L. Bracha, T. Liefeld, M. Wawer, J. C. Gilbert, A. J. Wilson, N. Stransky, G. V. Kryukov, V. Dancik, J. Barretina, L. A. Garraway, C. S.-Y. Hon, B. Munoz, J. A. Bittker, B. R. Stockwell, D. Khabele, A. M. Stern, P. A. Clemons, A. F. Shamji and S. L. Schreiber, Cell, 2013, 154, 1151–1161.
188. http://www.broadinstitute.org/ctrp, http://www.broadinstitute.org/ctrp.
189. U. Norinder, L. Carlsson, S. Boyer and M. Eklund, J. Chem. Inf. Model., 2014, 54, 1596–1603.
190. J. B. Brown, Y. Okuno, G. Marcou, A. Varnek and D. Horvath, J. Comput.-Aided Mol. Des., 2014, 1–22.
191. J. N. Weinstein and P. L. Lorenzi, Nature, 2013, 504, 381–383.
192. B. Haibe-Kains, N. El-Hachem, N. J. Birkbak, A. C. Jin, A. H. Beck, H. J. W. L. Aerts and J. Quackenbush, Nature, 2013, 504, 389–393.
193. W. H. M. Heijne, A. S. Kienhuis, B. van Ommen, R. H. Stierum and J. P. Groten, Expert Rev. Proteomics, 2005, 2, 767–780.
194. C. M. McHale, L. Zhang, A. E. Hubbard and M. T. Smith, Mutat. Res., 2010, 705, 172–183.
195. L. Suter, L. E. Babiss and E. B. Wheeldon, Chem. Biol., 2004, 11, 161–171.
196. S. R. Khan, A. Baghdasarian, R. P. Fahlman, K. Michail and A. G. Siraki, Drug Discov. Today, 2013, 19, 562–578.
197. https://www.kaggle.com/competitions .
198. G. E. G. E. Hinton, S. Osindero and Y.-W. Teh, Neural Comput., 2006, 18, 1527–1554.
199. T. C. Norman, C. Bountra, A. M. Edwards, K. R. Yamamoto and S. H. Friend, Sci. Transl. Med., 2011, 3, 88mr1.
200. G. Stolovitzky, D. Monroe and A. Califano, Ann. N. Y. Acad. Sci., 2007, 1115, 1–22.
201. DREAM8: Dialogue on Reverse Engineering Assessment and Methods project, http://www.the-dream-project.org/.
202. M. Bellucci, F. Agostini, M. Masin and G. G. Tartaglia, Nat. Methods, 2011, 8, 444–445.
203. J. Tang, A. Szwajda, S. Shakyawar, T. Xu, P. Hintsanen, K. Wennerberg and T. Aittokallio, J. Chem. Inf. Model., 2014, 54, 735–743.
204. Q. Li, Y. Wang and S. H. Bryant, Bioinformatics, 2009, 25, 3310–3316.
205. J. P. Overington, B. Al-Lazikani and A. L. Hopkins, Nat. Rev. Drug Discovery, 2006, 5, 993–996.
206. D. M. Hawkins, J. Chem. Inf. Model., 2004, 44, 1–12.
207. J. Reid, https://pypi.python.org/pypi/infpy/0.4.9.
208. P. J. Ballester and J. B. O. Mitchell, Bioinformatics, 2010, 26, 1169–1175.
209. A. S. Shandar Ahmad, K. Kitajima, S. Selvaraj, H. Kubodera, S. Sunada and J. An, Genome Inform., 2003, 14, 537–538.
210. M. Fernandez, S. Ahmad and A. Sarai, J. Chem. Inf. Model., 2010, 50, 1179–1188.
211. S.-Y. Rhee, M. J. Gonzales, R. Kantor, B. J. Betts, J. Ravela and R. W. Shafer, Nucleic Acids Res., 2003, 31, 298–303.
212. R. Vita, L. Zarebski, J. A. Greenbaum, H. Emami, I. Hoof, N. Salimi, R. Damle, A. Sette and B. Peters, Nucleic Acids Res., 2010, 38, D854–D862.
213. I. Dimitrov and P. Garnev, Eur. J. Med. Chem., 2010, 45, 236–243.
214. M. W. Karaman, S. Herrgard, D. K. Treiber, P. Gallant, C. E. Atteridge, B. T. Campbell, K. W. Chan, P. Ciceri, M. I. Davis, P. T. Edeen, R. Faraoni, M. Floyd, J. P. Hunt, D. J. Lockhart, Z. V. Milanov, M. J. Morrison, G. Pallares, H. K. Patel, S. Pritchard, L. M. Wodicka and P. Zarrinkar, Nat. Biotechnol., 2008, 26, 127–132.
215. M. Lapins and J. E. S. Wikberg, BMC Bioinf., 2010, 11, 339.
216. A. Hamosh, A. F. Scott, J. Amberger, C. Bocchini, D. Valle and V. A. McKusick, Nucleic Acids Res., 2002, 30, 52–55.
217. A. Gottlieb, G. Y. Stein, E. Ruppin and R. Sharan, Mol. Syst. Biol., 2011, 7, 496.
218. E. Kellenberger, P. Muller, C. Schalon, G. Bret, N. Foata and D. Rognan, J. Chem. Inf. Model., 2006, 46, 717–727.
219. M. Pastor, G. Cruciani, I. McLay, S. Pickett and S. Clementi, J. Med. Chem., 2000, 43, 3233–3243.
220. T. Liu, Y. Lin, X. Wen, R. N. Jorissen, M. K. Gilson and R. N. Jorrisen, Nucleic Acids Res., 2007, 35, D198–D201.
221. S. Dakshanamurthy, N. T. Issa, S. Assefnia, A. Seshasayee, O. J. Peters, S. Madhavan, A. Uren, M. L. Brown and S. W. Byers, J. Med. Chem., 2012, 55, 6832–6848.
222. T. Cheng, Q. Li, Z. Zhou, Y. Wang and S. H. Bryant, AAPS J., 2012, 14, 133–141.
223. GVK Biosciences Private Limited, Hyderabad, India, 2007.
224. W. Yang, J. Soares, P. Greninger, E. J. Edelman, H. Lightfoot, S. Forbes, N. Bindal, D. Beare, J. A. Smith, I. R. Thompson, S. Ramaswamy, P. A. Futreal, D. A. Haber, M. R. Stratton, C. Benes, U. McDermott and M. J. Garnett, Nucleic Acids Res., 2013, 41, D955–D961.
225. B. Vroling, M. Sanders, C. Baakman, A. Borrmann, S. Verhoeven, J. Klomp, L. Oliveira, J. de Vlieg and G. Vriend, Nucleic Acids Res., 2011, 39, D309–D319.
226. D.-S. Cao, Y.-Z. Liang, Z. Deng, Q.-N. Hu, M. He, Q.-S. Xu, G.-H. Zhou, L.-X. Zhang, Z.-X. Deng and S. Liu, PLoS One, 2013, 8, e57680.
227. M. I. Davis, J. P. Hunt, S. Herrgard, P. Ciceri, L. M. Wodicka, G. Pallares, M. Hocker, D. K. Treiber and P. P. Zarrinkar, Nat. Biotechnol., 2011, 29, 1046–1051.
228. J. T. Metz, E. F. Johnson, N. B. Soni, P. J. Merta, L. Kifle and P. J. Hajduk, Nat. Chem. Biol., 2011, 7, 200–202.
229. H. Hong, Q. Xie, W. Ge, F. Qian, H. Fang, L. Shi, Z. Su, R. Perkins and W. Tong, J. Chem. Inf. Model., 2008, 48, 1337–1344.
230. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
231. G. Cruciani, P. Crivori, P.-A. Carrupt and B. Testa, J. Mol. Struct., 2000, 503, 17–30.

---

Footnote

† Authors contributed equally to this work.

---