Effects of some salts on H₂O as probed by a thermodynamic signature of glycerol: towards understanding the Hofmeister effects (VII)

Abstract

The generality of the Hofmeister effects has been questioned of late, and doubts have been cast over their importance in understanding the specific ion effects on the chemistry and physics of biopolymers in aqueous solutions. Recent experimental evidence from modern non-linear spectroscopies points mostly to the direct interaction between the ion and the biopolymer in question that is more important for understanding the Hofmeister effects. On the other hand, our own contribution by higher order thermodynamical studies indicated that the effects of ions on H₂O itself may not be denied all together. Namely, we devised a methodology whereby the effect of an ion on H₂O is characterized by two orthogonal indices, hydrophobicity and hydrophilicity, by using a third order thermodynamic signature of hydrophobic 1-propanol (1P) as a probe, the 1P-probing methodology. The results indicated that the common anion ranking could be understood in terms of two indices, hydrophobicity and hydrophilicity of an individual ion. In the present work, we make an attempt at probing the effects of the same ions on H₂O by a typical hydrophile, glycerol (abbreviated as Gly in this article). Compared with the results of the 1P-probing methodology, we seek to determine how hydrophiles would react to the subtle modification of H₂O caused by the presence of an ion, since biopolymers are large amphiphiles with hydrophobic and hydrophilic surfaces. The results indicate that the Gly-probe is much less sensitive than the 1P-probe. We suggest therefore that it is the hydrophobic moieties of biopolymers that mainly give more conspicuous response to the modified H₂O by the presence of an ion.

---

Introduction

Ions and non-electrolyte solutes modify the molecular organization of H₂O in a specific manner. As one of their manifestations, they show marked differences in their solvent properties when used as mixed solvents. This was recognized back in 1887 by F. Hofmeister.^1–3 He ranked the effects of ions in the order from what reduces the solubility of lysozyme in aqueous solutions to what promotes it. Since then, almost the same ranking seems to apply to a large number of physical/chemical processes in aqueous solutions of biopolymers or colloids, particularly for anions. The left side of the ranking was named “kosmotropes” and the right “chaotropes” with Cl⁻ at about the null position.⁴ Thus, at the zero-th approximation, it was generally regarded to be the effect of each ion on H₂O that dictates the overall properties of the ternary systems. More recent investigations, however, tend to point to direct ion–biopolymer interactions that are more important for the ion-specific effects. Indeed, modern non-linear higher order spectroscopic studies suggested that the bulk H₂O away from hydration shells of common ions was left unperturbed.^5–11 Hence, the Hofmeister effects must be due to direct interactions between the specific ion and the biopolymer in question. Furthermore, the reversals of the Hofmeister ranking have been observed by modifying the end groups of the biopolymer,¹² or by changing the solution compositions.^13–15 With these the Hofmeister effects may become non-existent. The close relation between the Hofmeister series of biopolymers and the lyotropic series of colloids has been long noted. Lyklema pointed out in analogy with colloid science that the Hofmeister series ought to be re-examined by taking into account the surface conditions, hydrophobicity or hydrophilicity, of biopolymers in question.⁴¹ Meanwhile, Levin et al. claimed to have developed a theory of the surface density profile that could explain a variety of experimental results with a single adjustable parameter, and that could finally shed light on a century old enigma, the Hofmeister series.⁴²

Nonetheless, the effects of ions and non-electrolyte solutes on H₂O are interesting in their own right and important for fundamental investigations of the multicomponent aqueous solutions. We have recently devised what we call the 1-propanol (1P) probing methodology that was detailed elsewhere.^16,17 By applying it to aqueous solutions, we were able to characterize the effects of solutes, non-electrolytes and individual ions on H₂O using a pair of coordinates, hydrophobicity, a, and hydrophilicity, b, and thus to characterize the effect of a solute on a two-dimensional map with H₂O at the origin. For an individual species the former relates to its hydration number, n_H, and the latter to its effect on the degree of S–V cross fluctuation density (proportional to thermal expansivity) of the entire bulk of the solution.^18–21 Using this methodology, we found that there are five distinct classes of the effects of a solute on H₂O. In particular, the results of a series of studies on general ions by this methodology indicated that kosmotropes all belong either to “hydration centers” or “hydrophobes”, both being interpreted as forming hydration shells around them, while chaotropes were found to be all “hydrophiles” (see below). Furthermore, the anion Hofmeister ranking matched the decreasing order of the distance from the origin for “hydration centers” and “hydrophobes” and then the increasing order of the distance for “hydrophiles” with the null point being H₂O itself. Cl⁻, which is normally regarded as the null point, was found to belong to the “hydration center” and to be very close to the origin. According to our studies,^16,17 “hydration centers” were understood to form hydration shells but the bulk H₂O away from hydration shells is left unperturbed, while “hydrophobes” also form hydration shells with somewhat enhanced hydrogen bonding within them with concomitant reduction of the hydrogen bond probability of bulk H₂O.^20,21 “Hydrophiles”, on the other hand, form hydrogen bonds directly with the hydrogen bond network of H₂O and retard the degree of fluctuation inherent in pure H₂O.^18,22,23 Thus, we suggested that the effects of ions on H₂O must remain important in understanding the Hofmeister effects. Of course, the individuality of chemical and physical properties of biopolymers is not unimportant. After all, they are large amphiphiles with hydrophobic and hydrophilic moieties. It would therefore be interesting to investigate how a hydrophobe and a hydrophile react to the modification of H₂O caused by the presence of an individual ion. The probe 1-propanol (1P) we have used so far is a typical “hydrophobe” in our classification.^16,17 The present work shows how a hydrophile, glycerol (abbreviated as Gly in this paper), would react to the modification of bulk H₂O caused by the presence of a specific ion following the earlier preliminary study.²⁴

In dealing with aqueous solutions, particular consideration must be given to the composition. We earlier realized^20–22 that the solution properties are crucially dependent on the composition in general for aqueous solutions. We found that the aqueous solution generally consists of three distinctive regions, in each of which the mixing scheme (MS), the molecular level scenario of mixing, is qualitatively different from those of other regions. In the H₂O-rich region, H₂O is modified somewhat depending on the nature of the solute (the details of which were instrumental in classifying the solute into the five classes mentioned above)^16,17 but the basic integrity of liquid H₂O is retained inasmuch as the hydrogen bond network is connected fleetingly and yet permanently throughout the bulk. H₂O is here understood as a highly fluctuating hydrogen bonded assembly and yet hydrogen bonds are bond-percolated.^20,21,25,26 In the solute-rich region, the solute molecules tend to cluster together as in the pure state and H₂O interacts with such clusters as a single gas-like molecule. In the intermediate region, two kinds of clusters, one rich in H₂O and the other in solute, physically mix together. We name these three distinct mixing schemes Mixing Schemes I, II and III from the H₂O-rich end. The boundaries between the adjacent MSs are apparent from the anomalous behaviour of the third derivative thermodynamic quantity.^20–22 In special cases, the boundary could appear as liquid–liquid phase separation between MS I and MS II or precipitation of a solute at the MS II and MS III boundary.

In the original experiment conducted by Hofmeister,^1,3 the first cloud points with 2 wt% lysozyme were determined in terms of the salt composition. They occurred at the mole fraction of 0.056, 0.03, 0.061 and 0.09, respectively, for the Na-salts of SO₄²⁻, OAc⁻, Cl⁻, and ClO₃⁻. From the description in this paper, it is not clear whether the first cloud point is phase separation or precipitation. We interpret his first cloud point as corresponding to the MS I and II boundary for safety, and we limit our attention to MS I of the multi-component aqueous solutions.

As detailed earlier,^16,17 the methodology we use is applicable only to the limited H₂O-rich region, MS I. This is based on our earlier findings that within this limited H₂O-rich region, MS I, the effects of ions are additive and that the effects of hydrophobic and hydrophilic moieties of amphiphiles are also additive. Similarly, for a multi-component system the effects of each solute are additive as long as the total mole fraction is small enough so that a body of liquid H₂O maintains its integrity.^16,17

Here, following the previous Gly-probing study for Na-salts of some anions,²⁴ we apply it to Cl-salts of NH₄⁺, (CH₃)₄N⁺ (TMA⁺) and in addition NaCH₃COO (Na⁺OAc⁻). The latter was included, since we investigated recently how OAc⁻ works as a hydrophobe.^16,27

The details of the probing methodology were described elsewhere.^16,17 Very briefly, one of the thermodynamic signatures, H^E_BB (defined below), for the probing component B in the ternary aqueous solution of B and the test sample S is determined as a function of the mole fraction of B, x_B, at a fixed initial mole fraction of S, x⁰_S. H^E_BB shows the x_B-dependence pattern unique to the nature of B. For hydrophobic B, it displays a peak type and for a hydrophilic B a bend type anomaly reflecting a qualitative change in the molecular organization of H₂O. (See Fig. 5 in the Appendix.) The peak top or the bend point that we name point X is where the integrity of liquid H₂O is lost due to the presence of B at the value of x_B. We then observe how the H^E_BB pattern changes as S is added while the characteristic pattern of H^E_BB is retained. The induced changes, particularly those of the anomalous point, X, are indexed in two orthogonal directions in the graph of H^E_BBvs. x_B. Thus, the B-probing methodology is applicable only up to this mole fraction. The rate of westward shift (to the negative direction of the x_B-axis) of point X per unit increase in x⁰_S is defined as hydrophobicity, a. That of the southward shift (to the negative direction of H^E_BB-axis) is defined as hydrophilicity, b. The shifts in both directions are found generally to be linear to x⁰_S. By trying out a number of typical hydrophobes and hydrophiles for S, we catalogued the induced changes. Thus, we have a way to characterize the effect of an unknown solute S on H₂O using a pair of indices, a and b, and to display it in a two-dimensional map with H₂O defining its origin.

From the 1P-probing methodology, we drew the following conclusions for each ion studied here: Na⁺, NH₄⁺, and Cl⁻ are the “hydration centers” with the hydration number n_H, 5.2, 1 ± 1, and 2.3 ± 0.6, respectively, leaving the bulk H₂O away from hydration shells unperturbed.^16,17 The CH₃⁻ side of OAc– is a hydrophobe with the total hydration number 3.7 ± 0.7 and reducing progressively the hydrogen bond probability of bulk H₂O away from hydration shells. One out of 3.7 H₂O molecules hydrates the COO⁻ side of the ion as a hydration center without affecting the bulk H₂O.^16,27 TMA⁺ was found to act as a hydrophile which forms hydrogen bonds directly with the hydrogen bond network of H₂O and to pin down the fluctuation inherent in liquid H₂O.^16,28

As discussed in the Appendix, the Gly-probe has an intrinsic disadvantage in comparison with the 1P-probe. Namely, H^E_1P1P is directly proportional to the partial molar S–V cross fluctuation density of 1P, ^SVδ_1P, defined by eqn (2) and (3) in the Appendix. This signifies the effect of a solute on the mean square amplitude of the S–V cross fluctuation of bulk H₂O.^18,19 In other words, the mean square amplitude of the S–V cross fluctuation is monitored by perturbing the system by the infinitesimal increase of 1P. Thus, the behavior of H^E_1P1P, its increase/decrease, is directly proportional to that of ^SVδ_1P. H^E_GlyGly, on the other hand, is only partially proportional to the equivalent ^SVδ_Gly with an extra constant term.²³ Unless the behavior of the latter constant term is known, that of H^E_GlyGly cannot be directly connected to ^SVδ_Gly. Another practical disadvantage of the Gly-probe is that its point X is not as conspicuous as that of the 1P-probe, since the latter displays a peak top, while the former a bend point. (See Fig. 5 and 6 in the Appendix.) With these disadvantages we attempt to investigate how a hydrophile reacts to the subtle modification of H₂O caused by the presence of ions within MS I, in comparison with a hydrophobe. Most of the solutes of biological significance are amphiphilic, and it would be important to investigate how hydrophobic and hydrophilic moieties respond to subtle modification caused by an ion while the basic integrity of liquid H₂O is retained. As mentioned above, we have found that within the limited H₂O-rich region the hydrophobic and hydrophilic moieties respond additively to H₂O modification.^16–23

Experimental

Glycerol (abbreviated as Gly in this paper) (Sigma, >99%) was degassed in vacuo at 80 °C for about 30 min and then charged into a 1000 μL syringe in a dry N₂ atmosphere for the titration calorimetry described below. NH₄Cl (Merck, >99.8%), N(CH₃)₄Cl (TMACl) (Merck, >98%) and Na(CH₃COO) (NaOAc) (Sigma-Aldrich, >99.8%) were used to prepare stock solutions using Milli-Q water. The respective solutions were diluted to the desired initial mole fraction, x⁰_S, immediately before use.

The excess partial molar enthalpy of Gly, H^E_Gly, is determined by using a TAM III isothermal titration calorimeter (TA Instruments, New Castle, DE, USA) at 25.000 ± 0.005 °C. The titration procedure was modified to enable facile delivery of highly viscous Gly as described in the previous work.²⁴ Furthermore, a 30 min interval was given between successive titrations, in order to reduce a possible rheological effect of highly viscous Gly. The uncertainty in H^E_Gly was estimated to be ±0.03 kJ mol⁻¹.

Results and discussion

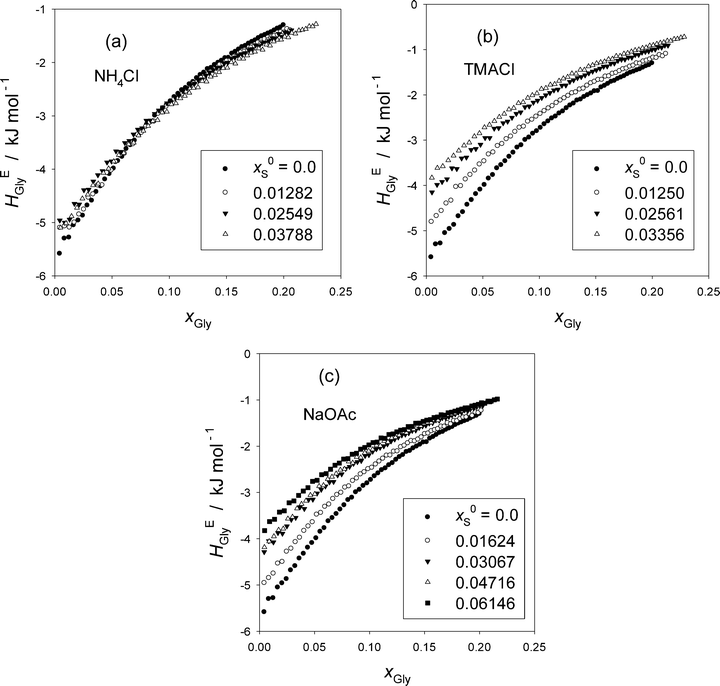
Fig. 1 shows the excess partial molar enthalpy of Gly, H^E_Gly, in the ternary Gly–S–H₂O at a given initial mole fraction of S in the mixed solvent, x⁰_S. The raw data are given in Table S1 in the ESI.† While H^E_Gly becomes more endothermic as x⁰_S increases for TMACl, Fig. 1(b), and NaOAc, Fig. 1(c), that for NH₄Cl shows a similar behavior at the low x_Gly range but becomes more exothermic at high x_Gly within the x_Gly range studied. But for all cases, the slopes of H^E_Gly against x_Gly seem to become less as x⁰_S increases. To see these trends more clearly, we evaluate H^E_GlyGly defined as,^{16,17,20–22}

H^E_GlyGly ≡ N(∂H^E_Gly/∂n_Gly) = (1 − x_Gly)(∂H^E_Gly/∂x_Gly), (1)

at given x⁰_S = n_S/(n_S + n_W). In the ternary system Gly–S–H₂O, n_S is the molar amount of S, n_Gly that of Gly which alone increases little by little through titration, n_W that of H₂O, N = n_Gly + n_S + n_W, and x_Gly = n_Gly/N. Of course for the 1P-probe, the equivalent definition is given by replacing subscripts Gly by 1P. For evaluating H^E_GlyGly, we perform graphical differentiation as for H^E_1P1P without resorting to curve-fitting an analytical function to the H^E_Gly data. By this treatment the random error in H^E_GlyGly inevitably increases to ±1 kJ mol⁻¹, but there is no danger of introducing a systematic error by a wrong choice of the analytical function. It is practically impossible to find a correct function.

Fig. 1 (a) Excess partial molar enthalpy of Gly, H^E_Gly, in Gly–S–H₂O (S = NH₄Cl) at 25 °C. (b) Excess partial molar enthalpy of Gly, H^E_Gly, in Gly–S–H₂O (S = TMACl) at 25 °C. (c) Excess partial molar enthalpy of Gly, H^E_Gly, in Gly–S–H₂O (S = NaOAc) at 25 °C.

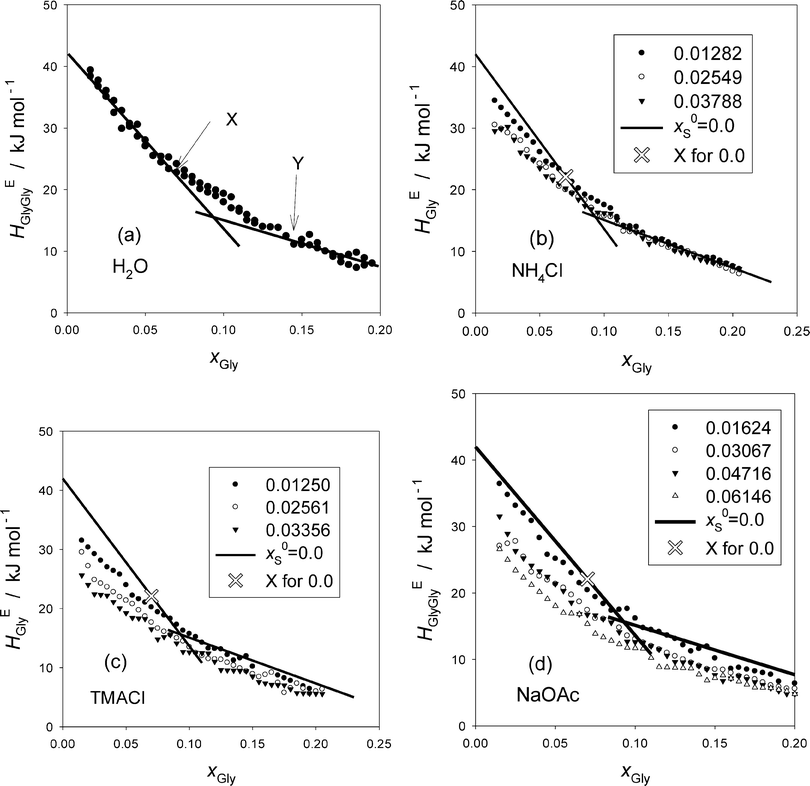
The resulting H^E_GlyGly data are plotted in Fig. 2. Fig. 2(a) shows H^E_GlyGly for the binary Gly–H₂O. It is apparent beyond the estimated uncertainty that the x_Gly-dependence pattern of H^E_GlyGly shows breaks in the slope at points X and Y at x_Gly = 0.073 and 0.14, respectively, indicated in the figure. The same behavior was observed in the previous Gly-probing study, though the x_Gly loci were at 0.08 and 0.015.²⁴ The existence of the breaks at points X and Y was confirmed recently²⁹ when we directly measured another third derivative quantity, the partial molar S–V cross fluctuation density of Gly in Gly–H₂O, ^SVδ_Gly, by differential pressure perturbation calorimetry.³⁰ Since this third derivative quantity is determined directly, we could take one more derivative graphically. The resulting fourth derivative quantity showed the onset of a step anomaly correctly at x_Gly = 0.076 and its end at 0.14 at 25 °C.²⁹ These should correspond to points X and Y in the third derivative quantity. As temperature increases, however, the step becomes progressively smaller and more obscure. The same observation was made in the previous Gly-probing study²⁴ in that as S is added and x⁰_S increases the break point X becomes more obscure to note in the H^E_GlyGly patterns.

Fig. 2 (a) Gly–Gly enthalpic interaction, H^E_GlyGly, in binary Gly–H₂O at 25 °C. The value of point X for the binary Gly–H₂O, x⁰_Gly, was found to be 0.073 and that of Y 0.14. (b) Gly–Gly enthalpic interaction, H^E_GlyGly, in Gly–S–H₂O at 25 °C for S = NH₄Cl. (c) Gly–Gly enthalpic interaction, H^E_GlyGly, in Gly–S–H₂O at 25 °C for S = TMACl. (d) Gly–Gly enthalpic interaction, H^E_GlyGly, in Gly–S–H₂O at 25 °C for S = NaOAc.

Fig. 2(b)–(d) show the results for the ternary Gly–S–H₂O systems. The binary Gly–H₂O system data are represented by two straight lines and its point X is indicated by a hollow X on the line. Point X is an important point that indicates the end of the dilute solution regime where the integrity of liquid H₂O is lost. We found from our earlier studies^20,23,31 that up to point X the integrity of liquid H₂O is retained such that the hydrogen bond network is still connected throughout the bulk H₂O. It is this dilute concentration range where the probing methodology by 1P or Gly is applicable.^16,17 Thus, it is unfortunate that with the present data at hand the loci of point X are not located with confidence.

We thus approach differently. From the previous 1P-probing methodology, we found how each solute, a non-electrolyte or an individual ion, modifies H₂O within the respective MS I. As mentioned above, Na⁺, NH₄⁺ and Cl⁻ belong to the class of “hydration centers” that are hydrated by 5.2, 1 and 2.3 molecules of H₂O, respectively, but leave the bulk H₂O away from hydration shells unperturbed. At least the same ions were shown not to alter the bulk H₂O away from hydration shells by femto-second pump probe spectroscopic studies.⁵ OAc⁻ is a “hydrophobe” that is hydrated by a total of 3.7 molecules of H₂O. The hydrogen bond probability within the hydration shells is enhanced somewhat, but that of the bulk H₂O away from the hydration shells is reduced progressively. The bulk H₂O has not yet lost the hydrogen bond percolation until the system reaches point X.^16,17,21

The distinction between hydration centers and hydrophobes was apparent in that the behavior of H^E_1P1P at x_1P = 0 was different in the 1P-probing studies.^16,17 Namely, for the hydration centers, the values of H^E_1P1P remain constant and independent of x⁰_S, while they increased as x⁰_S increased for the hydrophobes. Hence for salts consisting of counter ions in the “hydration center” such as, NaCl, and NH₄Cl, they remained constant. For the present Gly-probing study, on the other hand, NH₄Cl does not seem to stay constant as is evident in Fig. 2(b). The previous Gly-probing study²⁴ indicates the same observation for NaCl also. This discrepancy between the 1P- and Gly-probing methodologies could be related to our findings that H^E_1P1P is directly proportional to the solute's effect on the S–V cross fluctuation density,^16,17 while H^E_GlyGly is partially proportional with an extra constant term as discussed above and in the Appendix. The latter constant term, the origin of which is yet to be elucidated, may be responsible for the observed downward shift of H^E_GlyGly at x_Gly = 0 as x⁰_S increases.

TMA⁺ was found to act as a hydrophile^16,17,28 that forms hydrogen bonds directly with the existing (momentarily but perpetually) hydrogen bond network keeping the hydrogen bond connectivity intact. But it reduces the degree of fluctuation inherent in pure H₂O progressively by breaking the proton donor–acceptor symmetry of liquid H₂O. Probably reflecting this, Fig. 2(c) shows a little sharper decrease in the H^E_GlyGly value at x_Gly = 0, H^E_GlyGly (0), than the other two salts. NaOAc, on the other hand, with a hydrophobic OAc⁻ ion shows a decrease in H^E_GlyGly (0), the value of H^E_GlyGly at x_Gly = 0. This contrasts with the behavior of H^E_1P1P observed in the 1P-probing study, where the equivalent H^E_1P1P (0) increased.^16,17

To see these trends at x_Gly = 0 more clearly, the H^E_GlyGly data are extrapolated linearly to x_Gly = 0 and evaluated H^E_GlyGly (0) values. The results are plotted in Fig. 3(a). Also shown in the figure are the equivalent plots with hollow symbols taken from the previous Gly-probing study.²⁴ For S = Na₂SO₄, the raw data were not used for the analysis in ref. 24. We reproduce the data here with the permission of the original authors as Table S2 in the ESI.† Both graphs of H^E_Gly and H^E_GlyGly for S = Na₂SO₄ are also given as Fig. S3(a) and (b) (ESI†). Since the data points for H^E_GlyGly at x_Gly < 0.015 are not available for all cases, the uncertainty in the extrapolated results could amount to ±2 kJ mol⁻¹. Fig. 3(b) shows the same plots for non-electrolyte samples. In the latter figure, two typical cases for hydrophobes, TBA and 1P, are shown. H^E_GlyGly (0) decreases as x⁰_S increases, in contrast to the increase in H^E_1P1P (0), the value of H^E_1P1P at x_1P = 0.^16,17 This is only natural due to a geometrical reason. H^E_1P1P increases from x_1P = 0 to point X, while H^E_GlyGly decreases down to its point X. A hydrophobic sample S will shift the H^E_BB pattern including point X towards west, a smaller value of x_B (for B = 1P or Gly). Since a number, n_H, of H₂O molecules are used up for hydration, and they are not available for the probe B to interact, point X will be reached at a lesser value of x_B. Indeed, the dynamics of the hydrating H₂O was found to be several times slower than that of bulk H₂O.⁵ This westward shift will inevitably result in an increase in the value of H^E_BB for a line with a positive slope (for B = 1P) and a decrease for that with a negative slope (for B = Gly), unless there is a mechanism to pin down H^E_BB (0) at a constant value. This is what happens for the 1P-probing, B = 1P, for “hydration centers”. Going back to Fig. 3(b), it is surprising that the decreases in H^E_GlyGly (0) for both TBA and 1P show no difference, although TBA is a stronger hydrophobe than 1P.^16,17,20,21 This could indicate whether the Gly-probing is not as sensitive as 1P-probing or the effect of stronger TBA might be compensated for by its effect on the extra constant term discussed in the Appendix. Urea, a “hydrophile”, shows a marginal decrease in H^E_GlyGly (0) upon increasing its initial mole fraction, x⁰_S. This could be understood by the fact that the hydrophilicity indices determined by the 1P-probing are similar for urea and the probe Gly; the values of b being −1210 and −1180 respectively.¹⁶

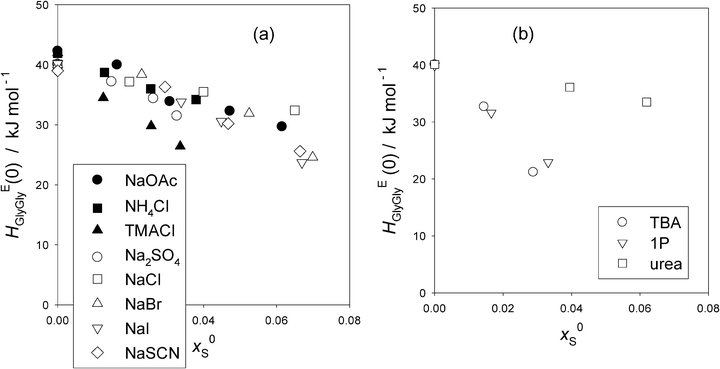Fig. 3 (a) The values of H^E_GlyGly at the infinite dilution, x_Gly = 0.0, H^E_GlyGly (0) against x⁰_S for various salts (S). The uncertainty is estimated to be ±2 kJ mol⁻¹. Filled symbols; this work, and hollow symbols; ref. 24. (b) The values of H^E_GlyGly at the infinite dilution, x_Gly = 0.0, H^E_GlyGly (0) against x⁰_S for non-electrolytes. The data are taken from the previous Gly-probing study.²⁴ The uncertainty is estimated to be ±2 kJ mol⁻¹.

Fig. 3(a) shows that for the hydration center salts, NH₄Cl and NaCl, H^E_GlyGly (0) decreases slightly, by just above the uncertainty upon increasing x⁰_S. They showed no change in H^E_1P1P (0) in the 1P-probing results.^16,17 This decrease could also be due to an unknown effect on the extra constant term discussed above. Furthermore, there seems to be no difference among all these two hydration center salts in their x⁰_S-dependence of H^E_GlyGly (0) in spite of the fact that the total hydration numbers are different; n_H = 7.5 for NaCl and 3.3 for NH₄Cl. This could also hint that the Gly-probe is not as sensitive as the 1P-probe towards subtle modification of H₂O caused by the presence of S. NaOAc, containing a hydrophobic anion, shows no difference in the decrease of H^E_GlyGly (0) with those of hydration centers. Na₂SO₄, SO₄²⁻ being a hydration center at x_1P = 0 found by the 1P-probing,^16,17 also shows the same trend. NaBr, NaI and NaSCN, consisting of Na⁺ and a hydrophilic anion with its hydrophilicity increasing in the order of Br⁻ < I⁻ < SCN⁻, do not show any difference among themselves nor from the hydration center group. TMACl is the only salt that stands out in terms of its decrease in H^E_GlyGly (0), as hydrophiles are expected to do. The hydrophilicity index of TMA⁺ is b = –1180, while those of other hydrophilic anions are −920, –2050, and –2800 respectively.¹⁶ Thus, TMA⁺ is only modestly hydrophilic, and yet the decrease of H^E_GlyGly (0) stands out. This must be due to the weaker effect of the counter ion Cl⁻ than Na⁺. The hydration number, n_H, for Cl⁻ is 2.3, while that for Na⁺ is 5.2. But it is more likely that all these observations among salts could be due to the effect of each S on the extra constant term in the proportionality between H^E_GlyGly and the ^SVδ_Gly.

Now that point X for the present H^E_GlyGly is hard to identify, we proceed our analysis by calculating the point X in the H^E_GlyGly pattern assuming that the shifts of x_Gly (X) and H^E_GlyGly (X) are both linear to x⁰_S as was the case for the 1P-probing methodology.^16,17 (X) indicates the respective coordinates at point X. Noting that the extrapolated value of x⁰_S to x_Gly (X) = 0, x⁰_S (0) is equal to 1/(n_H + 1), and using the x_Gly locus of point X for the binary Gly–H₂O determined in Fig. 2(a), we calculated the x_Gly-loci of point X at given x⁰_S, which are listed in Table 1 for the present data. The same data treatment is applied to the previous Gly-probing study,²⁴ and listed in Table S4 in the ESI.† We then read off the value of H^E_GlyGly in Fig. 2(b)–(d) for the present data and equivalent graphs of H^E_GlyGly against x_Gly for the previous work²⁴ at the calculated point X, x_Gly (X). The H^E_GlyGly (X) values are also listed in Table 1 and Table S4 (ESI†), and plotted in Fig. 4(a) for salts, and in Fig. 4(b) for non-electrolytes. The uncertainty of the resulting H^E_GlyGly (X) is estimated to be ±2 kJ mol⁻¹.

Table 1 The values of x_Gly at the presumed point X calculated using the total hydration number, n_H(tot), obtained by the 1P-probing methodology, and the value of x_Gly at the observed point X for the binary Gly–H₂O by the present Gly-probing. H^E_GlyGly at the presumed point X was read off the graph of H^E_GlyGly, Fig. 2(b)–(d). An assumption was made that the x_Gly-locus of point X is also linear to x⁰_S as the case of the 1P-probing

Salt	n H		x ^0S	x Gly (X)	H ^EGlyGly (X)
NH4Cl	+	1	0	0.073	21.1
	−	2.3	0.01282	0.06898	21
	(tot)	3.3	0.02549	0.06500	21
			0.03788	0.06111	21
TMACl	+	0	0	0.073	21.1
	−	2.3	0.01250	0.06999	20
	(tot)	2.3	0.02561	0.06683	18
			0.03356	0.06492	17
NaOAc	+	5.2	0	0.073	21.1
	−	3.7	0.01624	0.06126	23
	(tot)	8.9	0.03067	0.05084	22
			0.04716	0.03892	23
			0.06146	0.02852	23

---

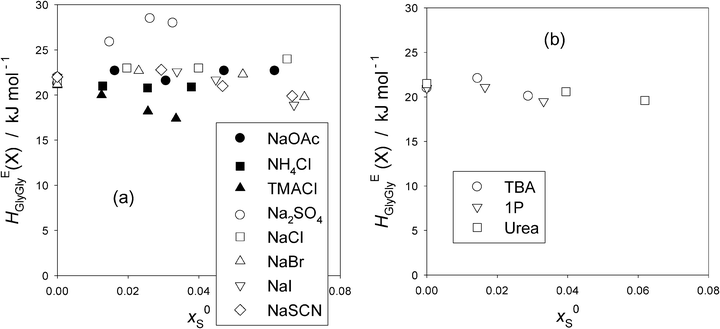Fig. 4 (a) The values of H^E_GlyGly at presumed point “X”, H^E_GlyGly (X) against x⁰_Sfor various salts (S). Filled symbols; present work and hollow symbols; ref. 24. The uncertainty is estimated to be ±2 kJ mol⁻¹. (b) The values of H^E_GlyGly at presumed point “X”, H^E_GlyGly (X), against x⁰_S for non-electrolytes. Evaluated using the data in the previous Gly-probing study.²⁴ The uncertainty is estimated to be ±2 kJ mol⁻¹.

For all other salts in Fig. 4(a) except for Na₂SO₄ and TMACl, H^E_GlyGly (X) may be regarded as remaining constant and independent of x⁰_S, taking into account the estimated uncertainty, ±2 kJ mol⁻¹. For Na₂SO₄, H^E_GlyGly (X) clearly increases as x⁰_S increases. This is an interesting and important finding. From the 1P-probing, SO₄²⁻ was found to belong to a special case of the “hydration center”.^16,32 As the mole fraction of the probe 1P, x_1P, increases, both S and 1P together were found to reduce the hydrogen bond probability of bulk H₂O just as a hydrophobe stronger than the probe 1P does, while in the absence of 1P (i.e. at x_1P = 0), SO₄²⁻ alone acts as purely a hydration center. Thus the present finding suggests that the increase in H^E_BB at point X is independent of the identity of the probe B. Namely, as x_B increases and hence the available bulk H₂O decreases, there must be some inherent mechanisms due only to SO₄²⁻ to reduce the hydrogen bond probability of bulk H₂O. Self-aggregation of SO₄²⁻ could be a reason, as observed for urea above x⁰_S > 0.08 (S = urea),³³ for the 1-butyl-2,3-dimethylimidazolium cation at x⁰_S > 0.006³⁴ and for the 1-butyl-3-methylimidazolium cation at x⁰_S > 0.014.³⁵ However, they all show a sudden decrease in the slope of H^E_BB (X) vs. x⁰_S in the respective 1P-probing studies. For Na₂SO₄ aqueous solutions, a dielectric relaxation study suggests the formation of H₂O separated cation–anion pairing as its concentration increases,³⁶ but this would also reduce H^E_BB (X) rather than increase as observed here. We rather speculate that as the availability of un-hydrated bulk H₂O decreases, SO₄²⁻ ions may start to interact more strongly with the existing hydrogen bond network of bulk H₂O rather than just forming hydration shells. This may be due to the fact that SO₄²⁻ ions presumably spread O atoms out in four tetragonal directions. As a result, the average hydrogen bond probability of bulk H₂O is reduced progressively. Recent studies using modern non-linear spectroscopic techniques aided by MD simulations^37,38 revealed how the ClO₄⁻ ion exchanges hydrogen bonds from a H₂O molecule with another in concentrated aqueous solutions of about 0.1 mole fraction. At this concentration, there are therefore hardly any H₂O molecules left to study the state of bulk H₂O away from hydration shells. Similar studies on SO₄²⁻ in H₂O could provide an important clue with more dilute aqueous solutions so that the state of bulk H₂O away from hydration shells could be studied.

In the case of TMACl, TMA⁺ being hydrophilic, slightly more so than Gly^16,28 and Cl⁻ being a weak hydration center,^16,17 the decrease in H^E_GlyGly (X) reflects the effect of TMA⁺ and indicates the reduction in the effect of the solute on the degree of fluctuation in the bulk H₂O.

For NH₄Cl and NaCl, the constituent ions are all hydration centers. Hence, these salts do not alter the bulk H₂O away from hydration shells, and hence the effect of the solute on the degree of the S–V cross fluctuation should remain constant independent of x⁰_S. This is exactly what we observe in Fig. 4(a). For the 1P-probe, however, not only at point X but also at x_B = 0 the values of H^E_BB were found to remain constant. For the present Gly-probe, the values of H^E_GlyGly (0) at x_Gly = 0 do not remain constant, as shown in Fig. 3(a). OAc⁻, on the other hand, was found to act as a hydrophobe with the total n_H = 3.7 and to reduce the hydrogen bond probability of bulk H₂O to the same degree as the probe 1P.^16,17,27Fig. 4(b) indicates the behavior of typical hydrophobes, TBA and 1P. They are hydrated by 20 and 29 H₂O molecules, respectively,¹⁶ and reduce the hydrogen bond probability of bulk H₂O away from hydration shells, more so for TBA than 1P. As a consequence, the effect of the solute on the degree of S–V cross fluctuation density increases due to a decrease in the negative contribution. Namely, as the hydrogen bond probability of liquid H₂O decreases, the chances for local and instantaneous formation of highly hydrogen bonded patches which contributes negatively to the S–V cross fluctuation decrease. Thus the net fluctuation increases, which should manifest in an increase in H^E_BB. It was indeed the case for the 1P-probing, B = 1P, and the value of H^E_BB (X) is larger for TBA at point X than for 1P.¹⁶Fig. 4(b) shows, on the other hand, that for the Gly-probing, the values of H^E_GlyGly (X) remain constant, independent of x⁰_S for both hydrophobes. Similarly, the values of H^E_GlyGly (X) for NaOAc remain constant as observed in Fig. 4(a).

The remaining three Na-salts are made of hydrophilic anions as found by the 1P-probing.^16,17 The hydrophilicity is stronger in the order of SCN⁻ > I⁻ > Br⁻, the values of hydrophilicity being b = −2800, −2050, and −920 respectively.¹⁶ In spite of the almost three-fold difference, the distinction in the x⁰_S-dependence of H^E_GlyGly (X) among them is not apparent. Thus, the Gly-probe appears to be insensitive to the difference in the modified H₂O by hydrophiles as well as by hydrophobes. Or it could be due to the constant additive term in the partial proportionality of the partial molar S–V cross fluctuation and H^E_GlyGly that makes the H^E_GlyGly (X) appear insensitive.

Thus, while the extra constant term in the partial proportionality between H^E_GlyGly and ^SVδ_Gly must be measured and its nature ought to be elucidated, we suggest that the behavior of H^E_GlyGly is not entirely inconsistent with the effects of S on H₂O deduced by the 1P-probing methodology.^16,17 It is clear, however, that the Gly-probe is not so sensitive as the 1P-counterpart. This would have an important implication for understanding the Hofmeister rankings, in that it is the hydrophobic part of a biological polymer that will respond more strongly to the slight modification of liquid H₂O caused by the presence of an ion.

Appendix

Fig. 5 shows the plots of H^E_1P1P and ^SVδ_1P for the binary 1P–H₂O system. The ordinate for ^SVδ_1P is scaled by a single factor ξ. The definition of H^E_1P1P is given in eqn (1) in the main text except for swapping subscripts Gly with 1P. H^E_1P1P signifies the 1P–1P interaction in terms of enthalpy in the solution. The S–V cross fluctuation density, ^SVδ, is defined as,^18,19,23

^SVδ ≡ 〈(ΔS)(ΔV)〉/k〈V〉 = Tα_p. (2)

ΔS and ΔV are the variation of the instantaneous value of S and V in a coarse grain containing a fixed number of molecules from their ensemble average 〈S〉 and 〈V〉 respectively. k is the Boltzmann constant, α_p the thermal expansivity and V_m the molar volume of the solution. This quantity is important for studying H₂O and aqueous solutions in that it contains a negative contribution due to putative formation of ice-like patches in H₂O, which contributes negatively to the S–V cross fluctuation density, ^SVδ. Its partial molar derivative is defined taking into account the fact that ^SVδ is an intensive quantity as,³⁹

^SVδ_1P ≡ N(∂^SVδ/∂n_1P) = (1 − x_1P)(∂^SVδ/∂x_1P). (3)

^SVδ_1P so defined is regarded as the effect of solute 1P on the S–V cross fluctuation density of the entire system. Of course, ^SVδ_Gly is also defined by swapping the subscript 1P with Gly.

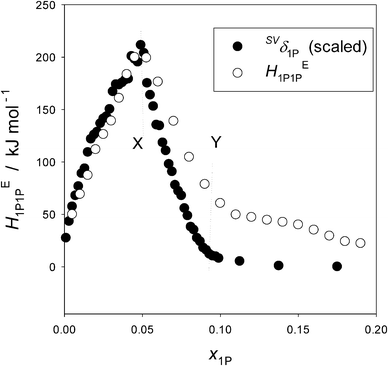Fig. 5 The partial molar S–V cross fluctuation density of 1P, ^SVδ_1P, and the enthalpic 1P–1P interaction, H^E_1P1P, in 1P–H₂O at 25 °C. The ordinate for ^SVδ_1P is scaled by a single factor. Reproduced with permission from ref. 18. Copyright (1999), NRC Research Press, National Research Council of Canada, Ottawa.

What Fig. 5 indicates then is that H^E_1P1P and ^SVδ_1P are directly proportional with a single factor ξ within the dilute region up to point X; namely,

H^E_1P1P = ξ^SVδ_1P. (4)

As discussed at some length elsewhere,^18,19 the 1P–1P enthalpic interaction and the effect of 1P on the S–V cross fluctuation density of the entire solution share the same fundamental cause and thus the enthalpic interaction is operative via bulk H₂O.^18,19 This finding was instrumental in devising the 1P-probing methodology.^16,17 The initial increase in H^E_1P1P up to point X is related to a net increase in ^SVδ_1P due to the decrease in the negative contribution in ^SVδ because the hydrogen bond probability of bulk H₂O is reduced progressively by the presence of a hydrophobic solute 1P.^20,21,31

The equivalent quantities of binary Gly–H₂O, H^E_GlyGly and ^SVδ_Gly are plotted in Fig. 6. The raw data of α_p determined by dilatometry⁴⁰ are used to calculate ^SVδ. A clear distinction is evident between Fig. 5 and 6 in their x_B-dependence patterns. The former pattern is unique to a hydrophobic solute, 1P, and the latter to a hydrophilic solute, Gly. Or rather, we used this qualitative difference in the x_B-dependence pattern of H^E_BB to distinguish “hydrophobes” and “hydrophiles”. Furthermore, H^E_GlyGly is only partially proportional to ^SVδ_Gly up to point X. Namely,

H^E_GlyGly = η^SVδ_Gly + ζ, (5)

with appropriate constants, η and ζ. Thus the Gly–Gly interaction is only partially proportional with an extra constant term, ζ, the nature and property of which are not yet elucidated. Further investigations on its T- or p-dependencies or the effect of the third component on these constants are required. For this purpose, systematic determination of H^E_GlyGly and ^SVδ_Gly is necessary.

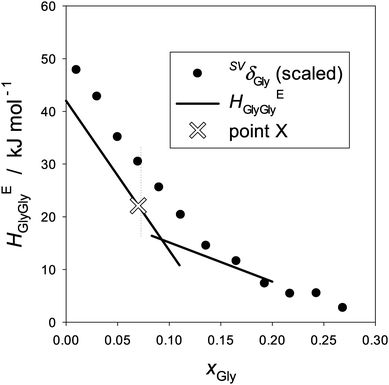Fig. 6 The partial molar S–V cross fluctuation density of Gly, ^SVδ_Gly, and the Gly–Gly enthalpic interaction, H^E_GlyGly, in binary Gly–H₂O at 25 °C. The ordinate for ^SVδ_Gly is scaled by a single factor. The data of α_p were taken from ref. 41. H^E_GlyGly data are represented by two straight lines as shown in Fig. 2(b)etc.

Acknowledgements

This work was supported by the Carlsberg Foundation.

References

1. F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1887, XXIV, 247–260.
2. F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, XXV, 1–30.
3. W. Kunz, J. Henle and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37.
4. K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323–422.
5. H. L. Bakker, Chem. Rev., 2008, 108, 1456–1473.
6. I. A. Heisler, K. Mazur and S. R. Meech, J. Phys. Chem. B, 2011, 115, 1863–1973.
7. I. A. Heisler and S. R. Meech, Science, 2010, 327, 857–860.
8. I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. M. Petersson and A. Nilsson, J. Chem. Soc., 2010, 134, 064513.
9. C. D. Cappa, J. D. Smith, K. R. Wilson, B. M. Messer, M. K. Gilles, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2005, 109, 7046–7052.
10. Y. S. Lin, B. M. Auer and J. L. Skinner, J. Chem. Phys., 2009, 131, 144511.
11. J. D. Smith and R. L. Saykally, J. Am. Chem. Soc., 2007, 129, 13847–13856.
12. J. Paterová, K. B. Rembert, J. Heyda, Y. Kurra, H. I. Okur, W. R. Liu, C. Hilty, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2013, 117, 8150–8158.
13. A. Salis, F. Cugia, D. F. Parsons, B. W. Ninham and M. Monduzzi, Phys. Chem. Chem. Phys., 2012, 14, 4343–4346.
14. Y. Zhamg and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249–15253.
15. P. Lo Nostro and B. W. Ninham, Chem. Rev., 2012, 112, 2286–2322.
16. Y. Koga, Phys. Chem. Chem. Phys., 2013, 15, 14548–14565.
17. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier B.V., Amsterdam, 2007, ch. VII and VIII, pp. 175–239.
18. Y. Koga, Can. J. Chem., 1999, 77, 2039–2045.
19. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier B.V., Amsterdam, 2007, Section V-3, pp. 117–130.
20. Y. Koga, J. Phys. Chem., 1996, 100, 5172–5181.
21. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, 2007, ch. V, pp. 89–150.
22. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier B.V., Amsterdam, 2007, ch. VI, pp. 151–173.
23. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier B.V., Amsterdam, 2007, Section VI-3, pp. 160–166.
24. P. Westh, E. L. Rasmussen and Y. Koga, J. Solution Chem., 2011, 40, 93–105.
25. Y. Koga, K. Nishikawa and P. Westh, J. Phys. Chem. A, 2004, 108, 3873–3877.
26. Y. Koga, Solution Thermodynamics and Its Application to Aqueous Solutions: A Differential Approach, Elsevier B.V., Amsterdam, 2007, Section IV-4, pp. 78–84.
27. T. Kondo, Y. Miyazaki, A. Inaba and Y. Koga, J. Phys. Chem. B, 2012, 116, 3571–3577.
28. Y. Koga, F. Sebe and K. Nishikawa, J. Phys. Chem. B, 2013, 117, 877–883.
29. K. Yoshida, A. Inaba and Y. Koga, J. Solution Chem. , accepted.
30. K. Yoshida, S. Baluja, A. Inaba, K. Tozaki and Y. Koga, J. Solution Chem., 2011, 40, 1271–1278.
31. Y. Koga, Netsu Sokutei, 2003, 30, 54–65 . Available in a pdf file on request to the author: E-mail: koga@chem.ubc.ca.
32. Y. Koga, T. Kondo, Y. Miyazaki and A. Inaba, J. Solution Chem., 2012, 41, 1388–1400.
33. Y. Koga, Y. Miyazaki, Y. Nagano and A. Inaba, J. Phys. Chem. B, 2008, 112, 11341–11346.
34. H. Kato, K. Miki, T. Mukai and K. Nishikawa, J. Phys. Chem. B, 2009, 113, 14754–14760.
35. K. Miki, P. Westh, K. Nishikawa and Y. Koga, J. Phys. Chem. B, 2005, 109, 9014–9019.
36. R. Buchner, S. G. Capewell, G. Hefter and P. M. May, J. Phys. Chem. B, 1999, 103, 1185–1192.
37. M. Ji, M. Odelius and K. J. Gaffney, Science, 2010, 328, 1003–1005.
38. S. Park, M. Odelius and K. J. Gaffney, J. Phys. Chem. B, 2009, 113, 7825–7835.
39. Y. Koga, J. Chem. Phys., 2012, 137, 124503.
40. E. C. H. To, J. V Davies, M. Tucker, P. Westh, C. Trandum, K. S. H. Suh and Y. Koga, J. Solution Chem., 1999, 28, 1137–1157.
41. J. Lyklema, Chem. Phys. Lett., 2009, 467, 217–222.
42. Y. Levin, A. P. dos Santos and A. Diehl, Phys. Rev. Lett., 2009, 103, 257802.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp53474j

---