First-principles study of the lattice dynamics of Sb2S3†
Yun
Liu
a,
Kun Ting
Eddie Chua
b,
Tze Chien
Sum
cde and
Chee Kwan
Gan
*a
aInstitute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632. E-mail: ganck@ihpc.a-star.edu.sg
bHarvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
cDivision of Physics and Applied Physics, School of Physical & Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, Singapore 637371
dEnergy Research Institute at NTU (ERI@N), 1 CleanTech Loop, #06-04, CleanTech One, Singapore 637141
eSingapore-Berkeley Research Initiative for Sustainable Energy (SinBeRISE), 1 Create Way, Singapore 138602
First published on 20th November 2013
Abstract
We present a lattice dynamics study of orthorhombic antimony sulphide (Sb2S3) obtained using density-functional calculations in conjunction with the supercell force-constant method. The effect of Born effective charges is taken into account using a mixed-space approach, resulting in the splitting of longitudinal and transverse optical (LO-TO) phonon branches near the zone center. Zone-center frequencies agree well with Raman scattering experiments. Due to the slow decay of the interatomic force constants (IFC), a minimal 2 × 4 × 2 supercell (Pnma setting) with 320 atoms is crucial for an accurate determination of the dispersion relations. Smaller supercells result in artificial acoustic phonon softening and unphysical lifting of degeneracies along high symmetry directions. We propose a scheme to investigate the convergence of the IFC with respect to the supercell sizes. The phonon softening can be attributed to the periodic images that affect the accuracy of the force constants, and the truncation of long-ranged forces. The commensuration of the q-vectors with the supercell size is crucial to preserve degeneracies in Sb2S3 crystals.
1 Introduction
Sb2S3 belongs to the group of metal chalcogenides (A2B3, A = As, Sb, Bi and B = S, Se, Te) that form an important class of semiconductors with extensive applications in photovoltaics1,2 and optoelectronics.3 They hold great promise as photovoltaic converters and thermoelectric cooling devices4,5 due to their small direct bandgaps, high thermoelectric power, and high absorption coefficient in the visible region.6,7 There is also a surge of interest in using Sb2S3 as a solid-state semiconductor-sensitized solar cell to replace the inorganic dye in dye-sensitized solar cells.7,8 Sb2S3 has been synthesized in various nanostructured forms, such as nanowires and nanotubes,9–11 which exhibit enhanced ferroelectric, piezoelectric, and conductive properties.So far, much focus has been placed on the synthesis and electronic properties12–15 of Sb2S3. To complement these known aspects, we present here a study of the lattice vibrational properties of Sb2S3 using density-functional theory (DFT). Phonon dispersion is one of the fundamental properties of crystals. The behavior of the branches reflects specific features of the crystal structure and the interactions between the constituent atoms. These lattice dynamical properties are indispensable in order to understand the properties of interest for device engineering and design, such as electronic transport and lattice specific heat.
We obtain phonon dispersions of Sb2S3 using the supercell force-constant method,16–20 fully taking into account the effect of Born effective charges. We note that a similar approach has been employed to study Bi2S3 in an earlier work.21 Due to the slow decay of IFC, we also investigate the effects of supercell sizes on the accuracy of dispersion relations, and propose a scheme to investigate the convergence of the IFC with respect to supercell sizes.
2 Methods
The orthorhombic phase of Sb2S3 belongs to the space group Pnma (#62) containing 20 atoms per primitive cell, five of which are inequivalent (Fig. 1). DFT calculations are carried out using the Quantum ESPRESSO22 suite within the local density approximation (LDA). We use pseudopotentials S.pz-bhs.UPF and Sb.pz-bhs.UPF from http://www.quantum-espresso.org. The electronic wavefunctions are expanded in a plane-wave basis set with a kinetic energy cutoff of 75 Ry. The Monkhorst–Pack23k-point sampling scheme used for Brillouin zone (BZ) integration has divisions of less than 0.03 Å−1. The total energies are tested to converge within 1 meV per atom.We relax the atomic coordinates and cell dimensions using a Broyden–Fletcher–Goldfarb–Shanno quasi-Newton algorithm to obtain optimized structures with residual forces of less than 10−3 eV Å−1 and stresses of less than 10−4 eV Å−3. The obtained equilibrium lattice parameters and atomic coordinates of inequivalent atoms are reported in Table 1 which show good agreement with experimental values. Note that the theoretical lattice constants a, b and c tend to be smaller than the experimental values, which is expected from a LDA calculation.13,14
| Lattice constants (Å) | Atomic positions | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| This work | Expt. | This work | Expt. | ||||||
| x/a | y/b | z/c | x/a | y/b | z/c | ||||
| a | 11.081 | 11.299 | Sb1 (4c) | 0.0200 | 0.25 | 0.6741 | 0.0290 | 0.25 | 0.6738 |
| b | 3.831 | 3.831 | Sb2 (4c) | 0.3437 | 0.25 | 0.4677 | 0.3503 | 0.25 | 0.4641 |
| c | 10.805 | 11.227 | S1 (4c) | 0.0508 | 0.25 | 0.1282 | 0.0493 | 0.25 | 0.1226 |
| b/a | 0.346 | 0.339 | S2 (4c) | 0.3738 | 0.25 | 0.0567 | 0.3745 | 0.25 | 0.0612 |
| c/a | 0.975 | 0.994 | S3 (4c) | 0.2133 | 0.25 | 0.8068 | 0.2077 | 0.25 | 0.8071 |
To obtain the full phonon dispersion within the BZ, we adopt a direct, supercell force-constant approach.17–20,25 We note that density-functional perturbation theory (DFPT)26,27 may also be employed to obtain the phonon dispersions. The relative merits of these two methods have been discussed in ref. 26. In the supercell force-constant approach, the sth atom in the primitive cell is displaced from its equilibrium position in the α direction by ±δαs = ±0.015 Å. The forces acting on the uth atom in the supercell, Fβu(±δαs) are calculated using the Hellmann–Feynman theorem. α and β denote the three spatial directions. We then use a finite central-difference scheme to evaluate the matrix elements of the IFC ϕ as
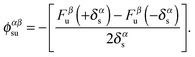 | (1) |
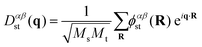 | (2) |
2.1 Symmetry reduction
In order to reduce the number of static DFT calculations, we use the symmetry properties of the crystals to transform the forces.17 Only the inequivalent atoms within the primitive cell are displaced to find the forces Fsu between the sth atom in the primitive cell and uth atom in the supercell, which can be represented by a 3 × 3 matrix. To obtain the forces between an equivalent atom and all other atoms in the supercell, we use the space group operation S that maps the sth inequivalent atom to the psth equivalent atom in the primitive cell. The forces between psth and puth atoms can be simply calculated as| Fpspu = G(S)FsuG(S−1) | (3) |
2.2 Non-analytical correction for q → 0
Due to the polar character of Sb2S3, the long-range dipole–dipole interaction gives rise to a macroscopic electric field that affects longitudinal optical (LO) phonon modes and not the transverse optical (TO) modes.28 The LO-TO splitting depends on the direction from which one approaches the Γ point in the BZ. This effect is reflected in the non-vanishing Born effective charge tensor Z*, taking the form of a non-analytical contribution![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) αβst to the dynamical matrix26,27,29,30 in the limit q → 0:
αβst to the dynamical matrix26,27,29,30 in the limit q → 0: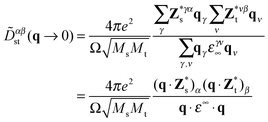 | (4) |
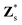 is the Born effective charge tensor for the sth atom. Z* and ε∞ may be calculated using density-functional perturbation theory (DFPT).26,27
is the Born effective charge tensor for the sth atom. Z* and ε∞ may be calculated using density-functional perturbation theory (DFPT).26,27
In order to include the non-analytical correction in the phonon dispersion, we add31 a correction factor ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) to the real space force-constant ϕ:
to the real space force-constant ϕ:
Φαβst(R) = ϕαβst(R) + ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) αβst αβst | (5) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) αβst by imposing the condition that
αβst by imposing the condition that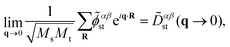 | (6) |
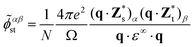 | (7) |
3 Results and discussion
3.1 Born effective charges
The Born effective charge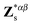 is the first derivative of the macroscopic polarization along the α direction with respect to the displacement of the sth atom along the β direction. This quantity is calculated using linear response theory at the zone center (Γ), and the non-zero values are shown in Table 2. The diagonal elements are different for each Sb and S atom, and off-diagonal elements are present, showing considerable anisotropy in the system.
is the first derivative of the macroscopic polarization along the α direction with respect to the displacement of the sth atom along the β direction. This quantity is calculated using linear response theory at the zone center (Γ), and the non-zero values are shown in Table 2. The diagonal elements are different for each Sb and S atom, and off-diagonal elements are present, showing considerable anisotropy in the system.
| xx | yy | zz | xz | zx | |
|---|---|---|---|---|---|
| ε ∞ | 9.33 | 18.7 | 13.0 | 0 | 0 |
| Z*(Sb1) | 2.89 | 5.62 | 7.36 | 0.07 | 1.53 |
| Z*(Sb2) | 3.33 | 7.25 | 4.50 | 0.28 | 0.09 |
| Z*(S1) | −2.35 | −4.18 | −4.07 | 1.07 | 0.83 |
| Z*(S2) | −1.83 | −4.80 | −4.44 | −0.45 | −0.33 |
| Z*(S3) | −2.03 | −3.90 | −3.36 | −0.20 | −1.34 |
The formal valence charges for Sb and S are + 3 and −2. Our calculation shows maximum effective charges of +7.36 and −4.80 for Sb and S respectively. From the study of ferroelectric compounds, it has been suggested that ions with effective charges close to the formal valence charge behave as closed-shell ions. Conversely, the presence of covalent character in the bonds causes a large amount of delocalized charge to flow through the structure during lattice displacements.28,32,33 In Sb2S3, the significantly larger effective charges suggest that there is substantial covalent character in the bonds. Sb atoms are able to donate electrons to S atoms during lattice displacements, and hence increase the magnitude of their respective Born effective charges. These results agree with X-ray photoelectron spectroscopy studies that describe the bonding in Sb2S3 as tight covalent.34
We also obtain the high-frequency dielectric tensor ε∞ which is diagonal as shown in Table 2. The anisotropy of ε∞ is an indication of the anisotropy of Sb2S3 structure.
3.2 Zone-center phonons
Since Pnma is a centrosymmetric space group, the Raman and infra-red (IR) modes of Sb2S3 are mutually exclusive, i.e., a mode cannot be simultaneously Raman and IR active. There are 60 phonon modes at Γ that respect the D2h point group symmetry:| Γ = 3Γacoustic + 30ΓRaman + 22ΓIR + 5Γsilent |
Currently there is no systematic study to assign the experimentally observed Raman modes in Sb2S3. Sereni et al.35 recently performed a polarization-dependent Raman scattering study on single crystal samples of Sb2S3 in the 90° and 180° geometries. Contributions from B1g spectrum were found in the experimental data for the Ag measurements. They also reported first-principles calculations of the zone-center phonons, but theoretical Raman scattering intensities were lacking. This makes the distinction between Ag and B2g modes, and that between B1g and B3g modes very challenging, as the effect of microtwinning makes the a and c directions indistinguishable.36 We present here the non-resonant Raman scattering coefficients which are computed from the second order derivative of the electronic density matrix with respect to a uniform electric field as implemented in Quantum ESPRESSO.37 To assign the modes, the phonon frequencies, scattering coefficients and the space group symmetries are taken into consideration. We find that 13 phonon modes are in good agreement with the experimental values, as shown in Table 3. However, experimental studies on additional scattering geometries are needed to provide a comprehensive assignment.
| Raman mode | Intensity (Å4 u−1) | DFPT (cm−1) | Supercell (cm−1) | Expt.21 (cm−1) |
|---|---|---|---|---|
| B1g | 267 | 47.7 | 47.7 | 43 |
| B3g | 1320 | 50.8 | 50.8 | 52 |
| Ag | 475 | 54.3 | 54.2 | 51 |
| B3g | 1140 | 69.1 | 69.0 | 60 |
| Ag | 1160 | 74.5 | 74.2 | 72 |
| B2g | 573 | 99.1 | 99.1 | 91 |
| Ag | 187 | 100.0 | 100.0 | 101 |
| B2g | 9.3 | 124.1 | 125.0 | 128 |
| Ag | 9970 | 196.7 | 197.4 | 192 |
| B1g | 1590 | 208.2 | 208.2 | 207 |
| B3g | 1390 | 231.4 | 231.4 | 239 |
| Ag | 4500 | 251.0 | 251.0 | 256 |
| Ag | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
277.9 | 278.0 | 283 |
3.3 Phonon dispersions
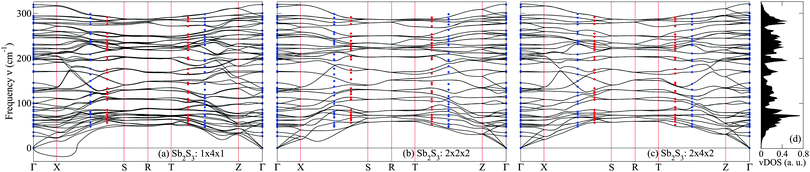
Periodic images of displaced atoms can exert sizable effects during the calculation of forces, hence decreasing the accuracy of the IFC. This is not an issue for q-vectors that are commensurate with the supercell, since the phonon frequencies calculated at these points are exact using the supercell method. In order to reduce the effects of periodic images on non-commensurate q-points, a huge supercell has to be used. However, large primitive cells such as that of Sb2S3 place a computational constraint on the largest supercells that can be used in DFT calculations. As a result, we investigate the effect of supercell sizes on the phonon dispersions by using sizes of 1 × 4 × 1 containing 80 atoms, 2 × 2 × 2 containing 160 atoms and 2 × 4 × 2 containing 320 atoms. We plot the dispersion relations along the high symmetry directions Γ→ X → S → R → T → Z → Γ as shown in Fig. 2, where we have used the q-vector convention in ref. 38 and 39. Fig. 2(c) shows our most accurate results from the 2 × 4 × 2 supercell calculation.There are in general 60 phonon modes present in the dispersions, as evident in the X → Γ and Z → Γ directions. Double degeneracy occurs along the high symmetry lines X → S and R → T → Z, resulting in only 30 distinct phonon frequencies. Along S → R, the phonon frequencies are quadruply degenerate and only 15 frequencies are present. These degeneracies are preserved in the 2 × 2 × 2 and 2 × 4 × 2 results whereby the zone boundary points (X, S, R, T and Z) are commensurate with the supercell sizes, i.e.,
| q·Li = 2πni | (8) |
As shown in Fig. 2, the zone-center phonon frequencies of Sb2S3 differ in the X → Γ and Z → Γ directions due to macroscopic electric fields in the polar crystals (the so-called LO-TO splitting). D =(½,¼,0) and B = (0,¼,½) are only commensurate with 2 × 4 × 2 supercell, and therefore the agreement between DFPT and supercell results are excellent. There are, however, huge discrepancies in the smaller supercells, showing that the dispersions are not accurate. (½,⅜,0) and (0,⅜,½) are not commensurate with any of the supercell sizes, but the results from the supercell force-constant method and DFPT show a good agreement in Fig. 2(c).
Apart from affecting the degeneracies, small supercell sizes also result in the artificial softening of phonon branches, as can be seen in Fig. 2(a) and (b). The softening becomes so severe in the 1 × 4 × 1 supercell that imaginary frequencies are introduced in the acoustic phonon modes. Soft modes are also displayed in the dispersions of 1 × 1 × 1 and 1 × 2 × 1 supercells (see the ESI†).
One of the biggest challenges in phonon calculations is to determine whether the soft modes are artificial (an artefact of the numerical methods, etc.) or genuine that are associated with unstable lattice structures and phase transitions.40,41 The occurrence of artificial phonon soft modes found in this work should serve as a caution that convergence with respect to supercell size must be checked carefully when using the supercell force-constant method. We conclude that softening is totally absent in the dispersions obtained with a 2 × 4 × 2 supercell for Sb2S3.
The vibrational density of states (vDOS) using the 2 × 4 × 2 supercell result is shown in Fig. 2(d). A dense 10 × 30 × 10 k-point mesh is used to sample the BZ and the effect of LO-TO splitting is included.
3.4 IFC analysis
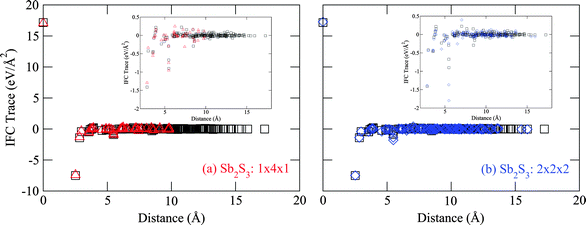
We now propose a scheme to analyze the IFC in order to understand the origin of the phonon softening. For each pair of atoms, a 3 × 3 force constant matrix is obtained, with elements corresponding to movements of the each atom along the Cartesian directions. As a measure of the strength of this interaction, we use the trace of the IFC tensor, Tr(Φsu) which has the advantage of being independent of the coordinate system used. The decrease of Tr(Φsu) with increasing interatomic distance rsu suggests a suitable range for the interatomic forces.42Fig. 3 shows the decay in Tr(Φsu) as a function of distances for different supercell sizes. The sth atom is the inequivalent S1 sulphur atom (Table 1), and u runs through all atoms within the supercell. Although not shown here, similar features are observed when the sth atom is replaced by other inequivalent atoms. Although the interactions are dominated by the on-site and the nearest neighbor terms, there are significant non-zero contributions at large distances which show the long ranged interactions in the crystals. The lattice dynamics of Sb2S3 thus cannot be approximated by a simple linear chain model considering only a few nearest neighbor interactions. To correctly describe the dispersions, a large supercell is needed to reduce the effect of periodic images and to capture the interactions at large distances.
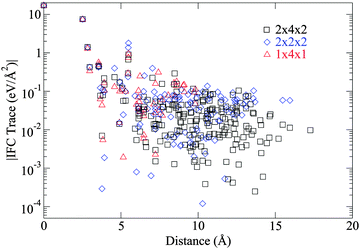
Due to the small sizes of 1 × 4 × 1 and 2 × 2 × 2 supercells, many values of IFC differ from those of 2 × 4 × 2 by a few orders of magnitude, as can be seen in Fig. 4. In addition, many interactions beyond ∼6 Å are not captured in the smaller supercells. We believe that these effects destabilize the crystal structure and result in the softening of the acoustic phonons. The softening is more pronounced in 1 × 4 × 1 supercells and less so in 2 × 2 × 2, due to the larger size of the supercell that reduces the effect of the periodic images and captures more long ranged interactions.
4 Conclusion
To the best of our knowledge, the phonon dispersion of Sb2S3 is obtained for the first time through a systematic lattice dynamics study using the supercell force-constant method. The Born effective charges give rise to LO-TO splitting at the zone center and elucidate the covalent character of the bonds. Both the high frequency dielectric tensor and Born effective charges show considerable anisotropy of the crystals. The use of small supercell sizes results in the softening of the phonon modes that is inconsistent with experiments. We attribute this to the effect of the periodic images on the force constants, as well as the truncation of long ranged interactions. We found that a minimal 2 × 4 × 2 supercell (Pnma setting) is required for an accurate determination of the dispersion relations of Sb2S3. Our results suggest that when using the supercell force-constant method, the supercell size has to be tested with other parameters such as the kinetic energy cut-off, the Brillouin-zone sampling or the self-consistent convergence criteria especially when dealing with low symmetry systems such as Sb2S3.Acknowledgements
The authors thank Peter Haynes of Imperial College London for useful discussions and pointing out ref. 13. Y.L and K.T.E.C acknowledge the financial support from the NSS programme, Singapore. T.C.S acknowledges the support by the following research grants: NTU start-up grant (M4080514); SPMS collaborative Research Award (M4080536); and the Singapore-Berkeley Research Initiative for Sustainable Energy (SinBeRISE) CREATE Programme. The authors gratefully acknowledge the use of resources at the A*STAR Computational Resource Centre, Singapore.References
- D. Aldakov, A. Lefrancois and P. Reiss, J. Mater. Chem. C, 2013, 1, 3756–3776 RSC.
- J. C. Cardoso, C. A. Grimes, X. Feng, X. Zhang, S. Komarneni, M. V. B. Zanoni and N. Bao, Chem. Commun., 2012, 48, 2818–2820 RSC.
- M. Schubert and W. Dollase, Opt. Lett., 2002, 27, 2073–2075 CrossRef CAS.
- E. Mãrquez, A. M. Bernal-Oliva, J. M. Gonzãlez-Leal, R. Prieto-Alcón and T. Wagner, J. Phys. D: Appl. Phys., 2006, 39, 1793 CrossRef.
- Z. Mandouh and S. Salama, J. Mater. Sci., 1990, 25, 1715–1718 CrossRef.
- Y. Itzhaik, O. Niitsoo, M. Page and G. Hodes, J. Phys. Chem. C, 2009, 113, 4254–4256 CAS.
- S.-J. Moon, Y. Itzhaik, J.-H. Yum, S. M. Zakeeruddin, G. Hodes and M. Grätzel, J. Phys. Chem. Lett., 2010, 1, 1524–1527 CrossRef CAS.
- J. A. Chang, J. H. Rhee, S. H. Im, Y. H. Lee, H.-j. Kim, S. I. Seok, M. K. Nazeeruddin and M. Gratzel, Nano Lett., 2010, 10, 2609–2612 CrossRef CAS PubMed.
- J. Varghese, S. Barth, L. Keeney, R. W. Whatmore and J. D. Holmes, Nano Lett., 2012, 12, 868–872 CrossRef CAS PubMed.
- Z. Deng, M. Mansuripur and A. J. Muscat, Nano Lett., 2009, 9, 2015–2020 CrossRef CAS PubMed.
- U. Jeong, P. H. C. Camargo, Y. H. Lee and Y. Xia, J. Mater. Chem., 2006, 16, 3893–3897 RSC.
- T. B. Nasr, H. Maghraoui-Meherzi, H. B. Abdallah and R. Bennaceur, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 406, 287–292 CrossRef PubMed.
- R. Caracas and X. Gonze, Phys. Chem. Miner., 2005, 32, 295–300 CrossRef CAS.
- M. R. Filip, C. E. Patrick and F. Giustino, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205125 CrossRef.
- C. E. Patrick and F. Giustino, Adv. Funct. Mater., 2011, 21, 4663–4667 CrossRef CAS.
- G. J. Ackland, M. C. Warren and S. J. Clark, J. Phys.: Condens. Matter, 1997, 9, 7861 CrossRef CAS.
- G. Kresse, J. Furthmüller and J. Hafner, Europhys. Lett., 1995, 32, 729 CrossRef CAS.
- W. Frank, C. Elsasser and M. Fahnle, Phys. Rev. Lett., 1995, 74, 1791–1794 CrossRef CAS.
- C. K. Gan, Y. P. Feng and D. J. Srolovitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235214 CrossRef.
- C. K. Gan, X. F. Fan and J.-L. Kuo, Comput. Mater. Sci., 2010, 49, S29 CrossRef CAS PubMed.
- Y. Zhao, K. T. E. Chua, C. K. Gan, J. Zhang, B. Peng, Z. Peng and Q. Xiong, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205330 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L. F. Lundegaard, R. Miletich, T. Balic-Zunic and E. Makovicky, Phys. Chem. Miner., 2003, 30, 463–468 CrossRef CAS PubMed.
- A. van de Walle and G. Ceder, Rev. Mod. Phys., 2002, 74, 11–45 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. D. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10337 CrossRef CAS.
- W. Zhong, R. D. King-Smith and D. Vanderbilt, Phys. Rev. Lett., 1994, 72, 3618–3621 CrossRef CAS.
- W. Cochran and R. Cowley, J. Phys. Chem. Solids, 1962, 23, 447–450 CrossRef CAS.
- P. Giannozzi, S. de Gironcoli, P. Pavone and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7231–7242 CrossRef CAS.
- Y. Wang, J. J. Wang, W. Y. Wang, Z. G. Mei, S. L. Shang, L. Q. Chen and Z. K. Liu, J. Phys.: Condens. Matter, 2010, 22, 202201 CrossRef CAS PubMed.
- M. Posternak, R. Resta and A. Baldereschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 8911–8914 CrossRef CAS.
- A. Roy, R. Prasad, S. Auluck and A. Garg, J. Phys.: Condens. Matter, 2010, 22, 165902 CrossRef PubMed.
- J. Grigas, E. Talik and V. Lazauskas, Phase Transitions, 2002, 75, 323–337 CrossRef CAS.
- P. Sereni, M. Musso, P. Knoll, P. Blaha, K. Schwarz and G. Schmidt, AIP Conf. Proc., 2010, 1267, 1131–1132 CrossRef.
- M. N. Iliev, M. V. Abrashev, H.-G. Lee, V. N. Popov, Y. Y. Sun, C. Thomsen, R. L. Meng and C. W. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2872–2877 CrossRef CAS.
- M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2003, 90, 036401 CrossRef.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef PubMed.
- K. Rao, S. Chaplot, V. Padmanabhan and P. Vijayaraghavan, Pramana, 1982, 19, 593–632 CrossRef CAS.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- Y. Duan and K. Parlinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104113 CrossRef.
- A. J. E. Foreman and W. M. Lomer, Proc. Phys. Soc., London, Sect. B, 1957, 70, 1143 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp53879f |
| This journal is © the Owner Societies 2014 |