Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The reactivity of CO2 on the MgO(100) surface
C. A.
Downing
*,
A. A.
Sokol
and
C. R. A.
Catlow
Department of Chemistry, University College London, Gower Street, London WC1E 6BT, UK. E-mail: christopher.downing.10@ucl.ac.uk
First published on 12th November 2013
Abstract
We investigate the adsorption of CO2 over an MgO(001) terrace, as calculated using an embedded cluster method. We find adsorbed geometries for CO2 on the perfect surface with energies which differ appreciably from previous studies, and observe that it is polarization of the surface rather than the inclusion of electron correlation which leads to this discrepancy. Our results suggest that both monodentate and tridentate carbonate formation on the MgO(001) surface are favourable processes, with the monodentate structure being of lower energy. Adsorption of CO2 is found to be favourable at both F0 and F+ terrace sites, but not at F2+. We also find that chemisorption at oxygen vacancy sites with a single localized electron (F+) could provide a route for the conversion of CO2 to other products, and that this system may be a useful model for other, more effective catalysts.
Introduction
Many investigations are currently focused on the reactivity of carbon dioxide with the hope of finding both an economical catalyst for CO2 conversion into industrially relevant products such as methanol, and also as a means to sequester CO2, e.g. by conversion to carbonate or storage within geological sinks as a supercritical fluid. Rocksalt alkali-earth oxides such as CaO and MgO are amongst the most important sorbent materials currently under investigation for this purpose.1,2The bulk and surface structures of magnesium oxide have been extensively studied, owing both to the simplicity of its rocksalt geometry and also the high degree of ionicity, which gives rise to a simple electronic structure. Additionally, basic oxides such as MgO are popular catalyst support materials which have been shown to display interesting reactivity when dopants or defects are included, opening up the possibility for their use as catalysts in their own right.
Previous computational studies of the interaction between CO2 and MgO have generally found the 5-coordinated oxygen on the [001] terrace to be an unfavourable adsorption site, with the 4 and 3-coordinated oxygens located at corners and edges being the preferred positions for chemical interactions to take place.3–5 The commonly stated reason for this difference between surface and defect sites is identical to the proposed cause of differing reactivities between MgO and CaO – the strength of the Madelung potential at the 5-coordinate oxygen atoms in the surface layer (O5c) of MgO is predicted to be so large that electron transfer onto the CO2 is unfavourable. Although this general conclusion has been reached by a number of authors, more recent work includes notable exceptions, which find CO2 adsorption at these sites to be weakly favourable.6,7
Experimental work on this topic is even less clear. Using measurements of oxygen exchange and infra-red spectra8–10 authors of ref. 8–11 tend to support the current theoretical models, which propose that carbonate formation only occurs at defect sites, i.e. kinks, corners, steps and vacancies, although no clear concensus exists as to what form the carbonate takes (monodentate, bidentate etc.)11 or which sites play a role in the interaction.
Other experimental work using temperature programmed desorption measurements suggests that the CO2 interaction with MgO is reasonably strong at 9.4 kcal mol−1 (0.41 eV, 39.33 kJ mol−1) although the authors interpret this result as a purely physical interaction.12 A combined experimental and theoretical investigation by Yanagisawa et al. found two distinct carbonate species on the MgO surface after room temperature adsorption of CO2, and identified one as monodentate while the other was suspected to include bidentate or tridentate character.13
In this study, we examine the mode of CO2 adsorption on O5c sites of the MgO[001] terrace using a hybrid quantum mechanical–molecular mechanical (QM/MM) embedding procedure. This method accurately models the long range electrostatic interactions and, crucially, the surface polarization, with the aim of providing an improved insight into possible adsorption mechanisms and energetics.
We also consider terrace (i.e. 5-coordinated) oxygen vacancies, i.e. F-centres,14 as adsorption sites, which may exhibit different charge states due to the localization of two (F0), one (F+) or no electrons (F2+) within the empty oxygen site. Oxygen vacancies containing trapped electrons have been identified as possible active sites for the conversion of CO to methanol using a Cu/ZnO/Al2O3 catalyst, with CO2 acting as a reactive intermediate species.15–20 Within the reaction process, CO2 is bound to the oxygen vacancy and undergoes a number of hydrogen addition steps, leading to the formation of methanol and the defect-free ZnO surface. The role of CO within the proposed mechanism is simply to regenerate the defect sites via its transformation to CO2, completing the catalytic cycle. The applicability of this mechanism to other oxides besides ZnO is of interest, as it is easy to imagine that the performance of such a reaction process would be highly tunable via modification of the surface with dopants or adatoms, stabilizing the oxygen vacancy and encouraging electron localization. MgO is a useful test case as its high Madelung potential causes electrons to be highly localized at its oxygen vacancies, with the trade-off that formation of such vacancies has a very high energetic cost.
Computational details
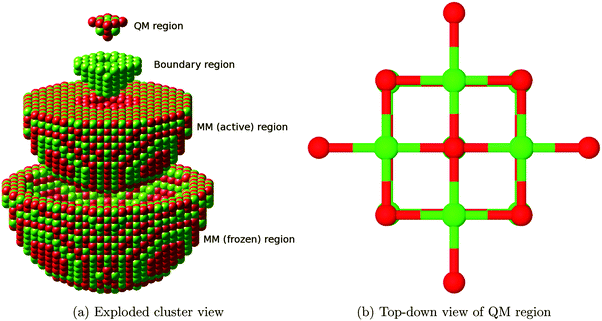
We use an embedded cluster approach, modelling atoms outside the QM region with a Born shell model potential using the QM/MM methodology17 as implemented in ChemShell,16,21 which also allows the embedding matrix to relax. Within this framework, an ab initio setup is coupled to an interatomic potentials based calculation, with energies and forces communicated between the two via the ChemShell module and structural optimization driven by the DL-FIND22 module. In the present work, GAMESS-UK23 and GULP24–26 were used as the QM and MM drivers, respectively.The full QM/MM cluster measured 60 Å in diameter, and was centred on an oxygen atom which was to be used as the site for adsorption or defect formation. In total, around 3700 atoms were free to undergo ionic relaxation in each calculation. Fig. 1a shows the full cluster broken down by region.
The outermost 5 Å of the cluster had all atoms frozen in their bulk positions (as determined by prior relaxation using GULP), whilst all other atoms within a radius of 25 Å of the cluster origin were allowed to relax. The accuracy of the treatment of the outermost 7 Å of relaxing MM atoms is reduced due to their interatomic potential cutoff values lying outside the range of frozen atoms present. However, the remaining 18 Å thick region surrounding the defect site remains, giving an accurate reproduction of the effect of long range polarization. The interatomic potential, reported in Table 1, consisted of Lennard-Jones and Buckingham terms, with rigid ion Mg atoms and polarizable shells on O atoms, optimised for embedded cluster calculations. The interatomic potential correctly reproduces the relaxation and rumpling of the MgO surface. No additional potential terms are included to account for the interactions of the adsorbate with the surface, as the CO2 molecule is always located directly above the QM part of the surface, with the closest MM atoms at least 5 Å away.
| Coulomb & harmonic | Core charge (e) | Shell charge (e) | k 2 | k 4 |
|---|---|---|---|---|
| Mg | +2.000 | n/a | n/a | n/a |
| O | +0.793 | −2.793 | 46.097 | 3589.7 |
| Buckingham | A | ρ | C | Cutoff (Å) |
|---|---|---|---|---|
| Mg–O shell | 798.394 | 0.324 | 0.000 | 12.000 |
| O shell–O shell | 22764.3 | 0.149 | 27.879 | 12.000 |
| Lennard-Jones | A | B | Cutoff (Å) |
|---|---|---|---|
| Mg–O shell | 182.25 | 0.000 | 12.000 |
The innermost QM region comprised those atoms described by the all-electron density functional theory calculation and ranged in size from 22 to 26 atoms depending on the presence of vacancies or adsorbate molecules. This QM region size was chosen to minimise computational cost while providing a calculation comparable with work already available in the literature. Tests were performed to determine how the F2+ defect formation energy varied with QM region size from one to six nearest neighbour shells surrounding the central oxygen atom, with no significant improvement found for cases larger than four nearest neighbour shells, leading to this value being chosen. The B3LYP27–29 exchange–correlation functional was used throughout this study due to its good representation of both molecular species and oxides in previous work.30 As a basis set we employed a modified version of the Def231 triple-zeta valence plus polarization (TZVP) for C and O atoms, and a similarly modified quadruple-zeta valence plus polarization (QZVP) basis set for Mg. The modification consisted of removing the most diffuse functions, specifically those uncontracted gaussians extending beyond 5 Å, to prevent the artificial spreading of charge density outside the QM region. Effective core potentials were placed on cations at the border of the QM region for the same purpose.
The QM/MM setup procedure begins by cutting an approximately hemispherical cluster of atoms from an MgO slab. The interior portion of the cluster is sampled in order to determine the necessary values for the point charges in the outermost layer to maintain the electrostatic field which would be expected at the surface of an infinite solid. Additionally, the group of atoms on the outermost edge of the cluster (excluding the terrace) have their charges modified to reflect their lower coordination numbers. The electrostatic fit and positioning of the point charges ensures charge neutrality for the surface cluster and minimises the dipoles in each of the cartesian directions. The cluster used in this study displays behaviour which is fully symmetric around the z-axis, with equivalent positions displaying a variance in their total charge of less than 0.001e. Bond distances between surface layer Mg and O atoms vary by less than 0.02 Å between the QM and MM regions after relaxation, suggesting that the interatomic potential provides a good match for the relaxation characteristics of the B3LYP functional.
When a charged defect was being modelled (i.e. F+ and F2+ centres), an additional correction term16,17 was included a posteriori to account for the polarization of atoms outside the sphere of relaxing MM atoms, given by eqn (1)
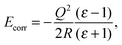 | (1) |
Reaction profiles for adsorption or configurational change were obtained using the nudged elastic band (NEB) method implemented within DL-FIND.22 A NEB spring constant of 0.05 eV Å−2 between the images was used throughout, with the end-points free to relax. Finite difference frequency calculations were performed for all minimum-energy geometries with the QM atoms as the active region. These calculations allowed us to confirm that each structure was a true minimum (indicated by the lack of imaginary frequencies). Task-farming parallelism was utilised when performing both NEB and frequency calculations.32
These calculations, like any other employing a localised basis set, suffer from the effects of basis set superposition error (BSSE), a phenomenon which arises where the electron density of a species benefits from the additional degrees of freedom provided by the basis functions of a second nearby species, leading to an artificial reduction of the energy of the interacting system relative to its isolated components. We have made use of the functional counterpoise correction procedure33,34 to estimate the effect of BSSE. An upper bound for the BSSE energy was obtained by making the approximations that the magnitude of BSSE is proportional to the distance between the two components in the cluster–adsorbate complex, and that the error is maximised in cases where the orientations of the involved species cause the overlap of diffuse functions to be maximised. Single point calculations for a range of distances were performed, each with orientations such that maximum overlap was achieved. The upper estimate for the BSSE as a function of distance was then used to determine the maximum necessary value of the counterpoise correction term. Fig. 2 shows how the calculated BSSE varied with distance, and the linear fit used throughout the study to determine counterpoise correction values. For calculations involving the interaction of CO2 with the MgO surface, the approximate counterpoise correction value was determined from the linear fitted function shown in Fig. 2, based on the surface-adsorbate separation distance after relaxation. These corrections generally fell within the range 0.15–0.18 eV. Final adsorption energies are corrected for BSSE, while NEB profiles are instead scaled relative to the energy of the non-adsorbed geometry with no correction. It is likely therefore that barrier heights shown are underestimated by approximately 0.10–0.15 eV (9.65–14.47 kJ mol−1) depending on the orientation and elevation of the transition state structure.
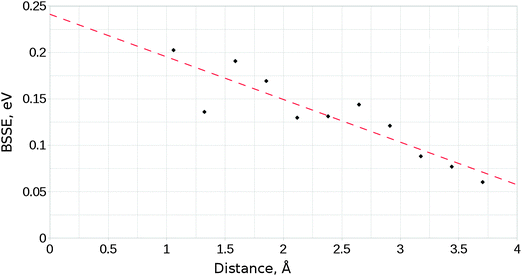 | ||
| Fig. 2 Variation of the basis-set superposition error with the distance between surface and adsorbate components for the unmodified MgO surface and a parallel orientated CO2 molecule. | ||
Results
We first report results for formation of surface F-centres in various charge states, where our calculations are in line with previous studies. We then consider CO2 adsorption on terrace and vacancy sites.Defect formation
The neutral F0 surface defect site, which corresponds to the removal of a neutral oxygen atom from the lattice to leave two electrons localized at the vacancy, was created by removing the central oxygen atom and maintaining the formal charge of the cluster. For the F+ and F2+ cases, the total charge of the cluster was increased by 1 and 2e respectively, equivalent to the removal of O− and O2−. As the O2− ion only exists within the solid phase and the conduction band for bulk MgO is above the vacuum level,38 the most common means of determining defect formation energies is to relate the energies of the defective clusters to pure MgO, a neutral oxygen atom, and isolated electrons, as in:| Ef = E(defect)n+ + E(Oat) + nE(e−) − E(MgOs) |
Defect formation energies for each of the charge states are given in Table 2 with results from previous work for comparison.39–41 The similarity between our results and those already published strongly suggests that our cluster model provides a suitable representation of the system. Results in ref. 40 were obtained using an embedded cluster method similar to ours, with special attention paid to the optimization of an added set of basis functions sited on the vacancy, which allow for better representation of electrons localized at the defect site. Ref. 41 also used an embedded cluster, but neither set of previous results included the full effects of long range relaxation, both having considerably fewer point charges outside the QM region than our cluster has MM atoms, with no shell model to account for the electronic polarization of these distant ions. Ref. 39 has results most readily comparable with ours, being based on a very similar embedded cluster technique with polarizable shells outside the QM region. The most significant differences in this case are in the number of point charges outside the relaxing region and the overall shape of the cluster.
| Defect | Uncorrected | Corrected | Ref. 39 | Ref. 40 | Ref. 41 |
|---|---|---|---|---|---|
| *Not given directly in reference as the authors used a different formalism for calculating defect formation energies. Value calculated from data given in Table 2 of ref. 41.a DFT (B3LYP) embedded cluster calculations with polarizable shells and a posteriori correction.b “Perturbed cluster embedding” Hartree–Fock calculations with no long-range polarization.c Hartree–Fock calculations with no long-range relaxation effects included. | |||||
| F0 | 9.23 | 9.23 | 9.07 | 9.35 | 7.67 |
| F+ | 11.14 | 10.90 | 11.57 | 10.78 | 12.38* |
| F2+ | 14.44 | 13.51 | 16.07 | 14.07 | 22.08* |
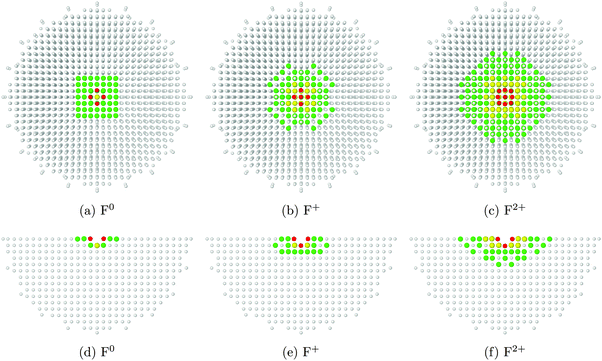
In Fig. 3, we see how the charge of the oxygen vacancy affects the relaxation of atoms in the surrounding area. Comparing images 3a–3c with their counterparts 3d–3f, we observe that the extent of relaxation is somewhat greater along the surface plane than down into the bulk. For comparison, a periodic supercell calculation would need dimensions of at least 4 × 4 × 2 unit cells (for F0) or 8 × 8 × 3 unit cells (for F2+) in order to capture the same information.
Physisorption of CO2
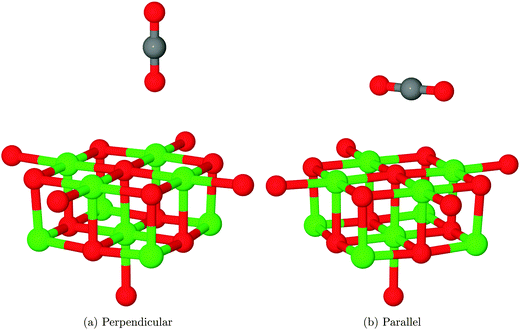
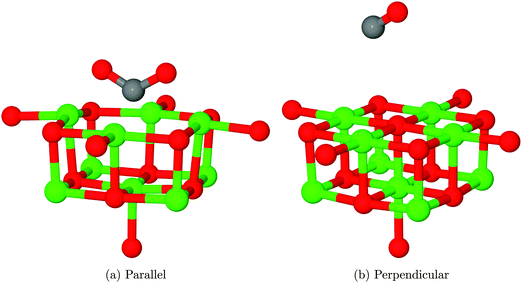
Two physisorption geometries, shown in Fig. 5, were identified for CO2 over the MgO(100) surface: one with an orientation perpendicular to the surface plane located over a 5-coordinate surface magnesium site (Mg5c), the other parallel to the surface but rotated 45° to the lattice axes and bridging two nearest-neighbour Mg5c sites. The interaction energies for the two structures after counterpoise correction were 0.075 eV (7.24 kJ mol−1), corresponding to a repulsive interaction and −0.046 eV (−4.44 kJ mol−1), corresponding to an attractive interaction, respectively. As no van der Waals correction term is included in the density functional theory part of this QM/MM calculation, it is likely that both structures are in reality more strongly adsorbed than this result would suggest. An estimate of 0.2–0.3 eV (19.30–28.5 kJ mol−1) for the van der Waals correction based on calculations of small molecules,42 for example, would completely outweigh the effects seen in the present calculations. Also, the magnitude of BSSE for the perpendicular orientation is likely to be significantly overestimated compared to the parallel geometry due to a different degree of overlap between basis functions. Assuming a stronger van der Waals correction for the parallel orientation but also a greater BSSE, we suggest that this interaction will be the more favourable of the two.Experimental work by Meixner et al. suggests that CO2 adsorbs on MgO with an energy of 29.7–39.3 kJ mol−1.12 The energies measured experimentally may be modified by lateral interactions between adsorbate molecules, but these effects are likely to be smaller than the discrepancy between calculations and experiment, and we suggest that the experimental result is more closely aligned with our proposed chemisorption model discussed in the next section than the physisorption values calculated here, even after the inclusion of a van der Waals correction and vibrational effects. We note, however, that the above conclusions are based on the expectation that experimental adsorption results were dominated by the effects of the defect-free surface, with lower coordinated sites such as edges and corners playing only a minor role in the measured adsorption behaviour.
Chemisorption of CO2
We have located stable chemisorbed geometries for the interaction of CO2 with the MgO(100) terrace O5c site, as well as F-centres in a number of charge states. In each case, the starting configurations corresponded to a CO2 molecule aligned perpendicular or parallel to the surface plane, with the latter aligned along the axes of the lattice.The adsorbate undergoes at least one favourable interaction with each of the O5c, F0 and F+ sites, with the identified structures in general agreement with previous work.4,43 In the case of the doubly positive charged oxygen vacancy F2+ however, neither parallel nor perpendicular alignments of CO2 resulted in any significant interaction with the defect. In both cases we observed a repulsive interaction between the adsorbate and the surface as the separation was decreased, with no local minima or barriers. Given the lack of reactivity and significantly higher defect formation energy, we can safely assume that the F2+ site plays no significant role in the adsorption of CO2 on MgO. Results for all sites considered are summarised in Table 3, with previous results also included for reference. Negative adsorption energies correspond to a favourable interaction relative to the isolated cluster and adsorbate.
| Defect | Orientation | This work | Previous work |
|---|---|---|---|
| None | Parallel | −0.68 (−65.61) | 0.77 (74.29),5 0.62 (59.82),4 0.135 (13),3 −0.09 (−8.68),44 −0.38 (−36.69)7 |
| Perpendicular | 0.12 (11.58) | n/a | |
| F0 | Parallel | −2.36 (−227.71) | −1.85 (−178.50)43 |
| Perpendicular | −3.52 (−339.63) | −3.23 (−311.65)43 | |
| F+ | Parallel | −0.71 (−68.50) | −0.23 (−22.19)43 |
| Perpendicular | −1.11 (−107.10) | −1.04 (−100.35)43 | |
| F2+ | Parallel | 0.11 (10.61) | n/a |
| Perpendicular | 0.04 (3.86) | n/a | |
O5c site
The interaction of a CO2 with the terrace O5c site is the most commonly studied of the reactions described in our work. Previous studies find the same carbonate-like adsorption geometry shown in Fig. 6a. Until recently the structure has generally been disregarded however, as it was found to be unstable with respect to dissociation. By contrast we find that the monodentate geometry is thermodynamically stable (by around 0.68 eV, 65.61 kJ mol−1). A NEB calculation to determine the reaction profile for adsorption, shown in Fig. 7, reveals a small barrier of around 0.1 eV (9.65 kJ mol−1), which increases to around 0.2 eV (19.30 kJ mol−1) if the effects of BSSE are included.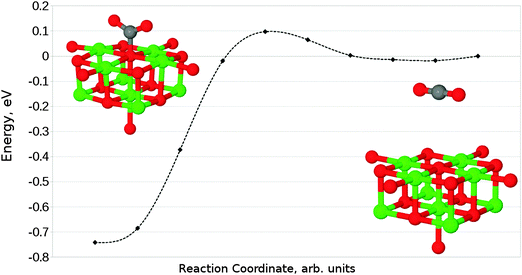 | ||
| Fig. 7 Reaction profile for the adsorption of CO2 at an O5c site obtained using the NEB method with 10 images. Counterpoise corrections not included. | ||
The difference in energy between our results and those of earlier investigators is particularly striking given the similarity of the adsorbed structures. A significant number of early studies (e.g. those by Pacchioni et al.) were carried out using the Hartree–Fock (HF) methodology, as opposed to the hybrid Density Functional Theory (DFT) approach used in our work. HF calculations do not include electron correlation effects, leading to the suspicion that this discrepancy could account for the difference in total energy observed. However, by repeating our calculations for CO2 adsorption at an O5c site using the same QM–MM system but with the DFT-based QM stage replaced by a HF calculation, we have been able to confirm that this is not the case. Eads for a HF QM/MM calculation was found to be around −1.43 eV (−137.97 kJ mol−1), suggesting that the inclusion of correlation actually destabilises the surface–adsorbate complex rather than stabilising it. Other effects must therefore be responsible for the difference in energy between our results and those published previously.
We are not aware of any previous study in which such a large volume was allowed to relax around the active site, leading to the possibility that long-range polarization is responsible for the observed differences. Given that early work which found the interaction to be most unfavourable included small clusters of QM atoms embedded in a static point charge array,5 and that the most recent comparable study which found the surface–adsorbate complex to be somewhat favourable used a larger 90-atom supercell,7 this appears at first glance to be a reasonable proposal.
We have performed additional test calculations in an attempt to verify this conjecture, involving the use of clusters with reduced relaxing MM regions. For a relaxation radius of 18 Å, we find an Eads of −0.68 eV (−65.61 kJ mol−1), identical to the original cluster. Given that approximately the same energy is found when the relaxation radius is further reduced to 15 Å, we can conclude that the polarization within the smallest relaxing region considered is accurately calculated. Indeed, we would expect the polarization of the cluster during CO2 adsorption to be comparable to that seen for the F0 defect formation in Fig. 3, although with lower symmetry due to the orientation of the molecule. We would therefore expect a relaxed region with a radius of at least 10–12 Å to be necessary, and the inclusion of any extra atoms within the MM part of the cluster would have had a negligible effect – hence the lack of distinction between results for the 15, 18 and 25 Å MM region radii that were tested. The use of the shell model potential gives our cluster calculations a significant advantage in this regard, as it allows us to include both ionic and electronic polarization effects for a large number of atoms with minimal additional cost.
The extent to which the polarization of the surface influences the final energy can be estimated using the Born–Onsager model for solvation of a dipole, given by eqn (2).
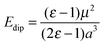 | (2) |
Modification of the Born–Onsager model is necessary in this case, as the “solvent” environment surrounding our cavity is hemispherical rather than spherical. Given that this term is analogous to the Jost correction described earlier (which accounts for polarization due to the presence of a charged species), and that the Jost term for a surface lies between 50 and 100% of the bulk value depending on the dielectric medium,17 we can be confident that the component of our total energy due to relaxation around the dipole is no less than half the calculated value of Edip.
Taking this approximation into account, we obtain a conservative value for the component of the adsorption energy due to relaxation around the dipole of 0.29 eV (28.37 kJ mol−1). This accounts for over 40% of the adsorption energy of CO2 at an O5c site.
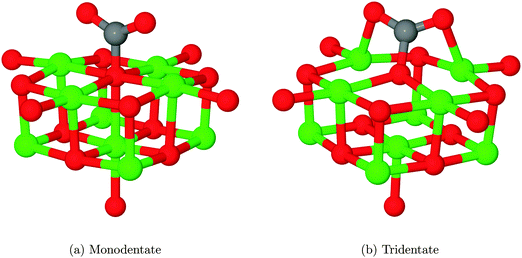
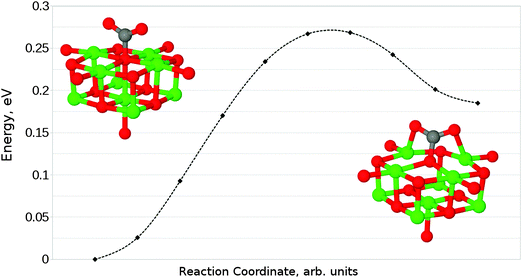
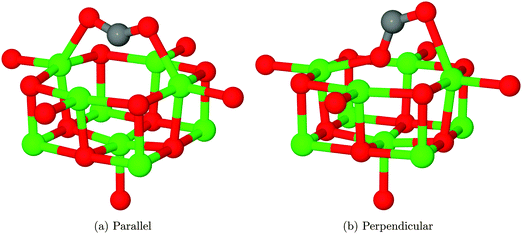
We have also identified a second adsorption geometry, which we define as tridentate, shown in Fig. 6b. The structure is a local minimum, around 0.18 eV (17.37 kJ mol−1) less stable in our calculations than the aforementioned monodentate configuration, with a barrier of 0.09 eV (8.68 kJ mol−1) for the tridentate–monodentate conversion (0.27 eV (26.05 kJ mol−1) for the reverse conversion) as shown in Fig. 8. The consideration of BSSE is not necessary in the case of monodentate–tridentate conversion shown in Fig. 8 as both structures would receive an approximately equal counterpoise correction. We are aware of only one case45 where a structure similar to the tridentate geometry of Fig. 6b has been identified previously, and the small cluster size used makes the results of the earlier study more easily comparable to those for low-coordinated edge and corner sites. Our vibrational frequency calculations identify modes at 922, 1291, 1669 cm−1 for the monodentate structure and 907, 1295, 1666 cm−1 for the tridentate structure, suggesting that distinguishing between the two would be very difficult using vibrational spectroscopy.
Despite speculation in previous experimental reports,9 no bidentate adsorbed structures have been observed in computational investigation of CO2 on the MgO(100) terrace, although recent work44 has shown that a pre-formed carbonate could adopt a bridging structure. We have attempted to find a structure similar to that postulated and shown in Scheme 1 of ref. 9 and Fig. 6 of ref. 11 where the carbon atom and one oxygen of CO2 are coordinated to adjacent O and Mg atoms, but in each case the structure relaxed to the monodentate structure, shown in Fig. 6a. Likewise, attempts to find a bridging bidentate structure between two adjacent Mg atoms resulted in the formation of either the tridentate chemisorbed configuration 6b or weakly physisorbed CO2 as in Fig. 5b.
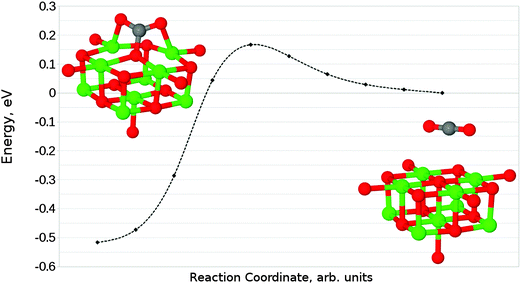
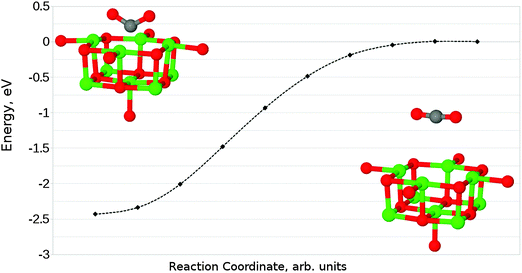
Given that the physisorbed and tridentate configurations have reasonably similar adsorbate oxygen atom positions, it is reasonable to postulate that the tridentate structure (Fig. 6b) could behave as an intermediate state between the physisorbed structure shown in Fig. 5b and the chemisorbed monodentate structure shown in Fig. 6a. A NEB adsorption pathway for this physisorbed–tridentate conversion is shown in Fig. 9, and a complete pathway from the physisorbed structure to the monodentate chemisorbed structure is given in Fig. 10. The multi-step adsorption route has an activation barrier which is slightly higher than that of direct adsorption to the monodentate structure from the gas phase, and so its relevance will depend heavily on the nature of the physisorption precursor when van der Waals forces are included, as they would be likely to shift both the physisorbed local minimum and the barrier to a lower energy.
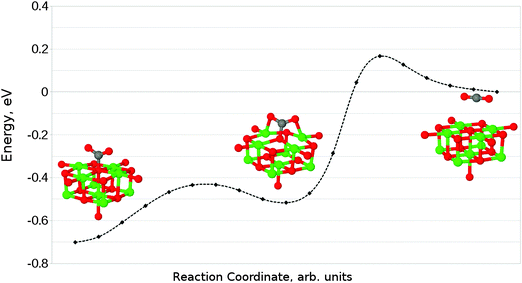 | ||
| Fig. 10 Reaction profile for an alternative adsorption process, from physisorbed CO2 to the monodentate chemisorbed species via a tridentate intermediate. | ||
F0-centre
In the case of the neutral F0 defect with two electrons localised within the vacancy, only one structure (shown in Fig. 11a) corresponding to CO2 adsorption in a parallel orientation was identified, with an adsorption energy of −2.36 eV (−227.71 kJ mol−1) – a considerably more favourable interaction than seen by Florez et al.,43 but as the minimum energy structures found in the two studies are essentially identical, we can conclude that the energy difference has a similar origin to that seen for the O5c site. The exothermic adsorption process seen here has no activation barrier in nudged elastic band calculations (Fig. 12). Mulliken analysis suggests that there is charge transfer onto the adsorbate, with approximately an additional 1.2 electrons being located on CO2 in the adsorbed geometry when compared to the molecule at a large degree of elevation above the surface.The relaxation of perpendicularly oriented CO2 (shown in Fig. 11b) in close proximity to the defect leads to the dissociation of CO2 to CO and Oat, with the oxygen atom filling the vacancy and reconstructing an unmodified MgO surface, in agreement with recent theoretical work.43
Based on the results described, the usefulness of F0 centres for CO2 conversion catalysis is expected to be limited: although the parallel adsorbed structure could feasibly behave as a reactive intermediate if another small molecule such as H2 were introduced, the reaction of the perpendicularly orientated adsorbate to form CO and a defect-free surface would poison the catalyst. The reverse reaction to generate an F0-centre by introducing CO is highly endothermic, and is therefore unlikely to make catalysis viable even if there were a highly efficient route from the parallel adsorbed CO2 complex to a useful product such as methanol.
F+-centre
Finally, we have considered the case of an oxygen vacancy with a single localised electron, designated as an F+ defect. The parallel adsorption of CO2 leads to a similar structure to that observed for an F0 site (Fig. 13a), with a reduction of charge transfer onto the adsorbate from 1.2 to 0.6 electrons. Mulliken analysis reveals that the majority of this electron localization occurs at the carbon atom. The adsorption energy for this interaction was found to be −0.71 eV (−68.50 kJ mol−1), with a barrier of around 0.05 eV (4.82 kJ mol−1).In the case of perpendicular adsorption (Fig. 13b), the observed structure is somewhat reminiscent of the CO2 bound to a surface oxygen vacancy in ZnO.15 An adsorption energy of −1.11 eV (−107.10 kJ mol−1) shows us that this is the preferred interaction orientation for CO2 over an F+ centre, being favoured over the parallel geometry by 0.4 eV (38.59 kJ mol−1) (Fig. 14). However, the barrier for perpendicular adsorption of around 0.16 eV (15.44 kJ mol−1) is approximately 0.1 eV (9.65 kJ mol−1) higher than that for parallel adsorption (Fig. 15). A greater degree of spin localization on the adsorbate is observed in the perpendicular case, with 0.72e located on the carbon atom and a further 0.15e on the upper oxygen atom.
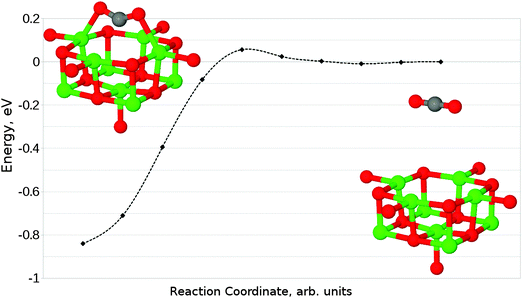 | ||
| Fig. 14 Reaction profile for the parallel adsorption of CO2 at an F+ centre on the MgO(100) terrace, obtained using the NEB method with 10 images. Counterpoise corrections not included. | ||
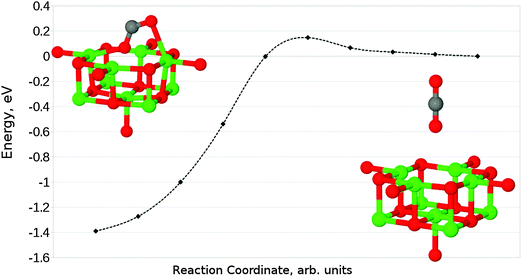 | ||
| Fig. 15 Reaction profile for the perpendicular adsorption of CO2 at an F+ centre on the MgO(100) terrace, obtained using the NEB method with 10 images. Counterpoise corrections not included. | ||
Given that neither interaction of CO2 with the F+ site leads directly to the regeneration of the defect-free surface, it is possible that subsequent reaction with a small molecule such as H2 could form part of a catalytic cycle for the transformation of CO2. Such a mechanism will require preserving or regenerating the single-electron F+ centre during later reaction steps, although the high defect formation energy (10.90 eV, 1051.70 kJ mol−1) could lead to preferential regeneration of the defect-free MgO(100) surface and the production of a cationic molecule. Giordano et al. have shown that in ultrathin MgO/Ag(100) films, F+ sites can be made to be more stable than F0 due to the occurrence of significant lattice distortion and polarization of the metal.46 Future work will investigate whether reactions at F+ centres can lead to a closed catalytic cycle.
Summary & conclusions
We have obtained a series of adsorption profiles and geometries for the interaction of CO2 with the MgO terrace. We find that adsorption of the molecule at surface oxygen atoms is favourable, and propose an adsorption process in which physisorbed CO2 may be converted to the monodentate chemisorbed species via a tridentate intermediate.Our results show that binding of CO2 with both F0 and F+ oxygen vacancy sites is exothermic. Perpendicular alignment of the CO2 molecule over the two-electron vacancy (F0) leads to electron transfer onto one of the oxygen atoms of the adsorbate, giving CO and the perfect MgO(100) surface. For the parallel orientation of the molecule over F0 and both orientations over F+, the binding of the adsorbate is accompanied by significant geometric distortion and electron transfer.
We have compared the results of earlier calculations,3–5 which suggested that there is no significant CO2–MgO interaction, with this work where we see two appreciably bound structures, as well as other recent investigations in the literature.7 The differences in the conclusions leads us to propose that the inclusion of long range polarization effects via the large relaxing volume of a QM/MM cluster play an important role in models of ionic oxide surfaces. However, we have also concluded that this does not fully account for the differences in energies observed, and that other effects such as a more comprehensive treatment of the electrostatics must also play a part.
We suggest that at least one structure (the perpendicular CO2 interaction with an F+ site) warrants further investigation with regard to its potential onward reactivity, for example with H2 or Hads similar to the catalytic formation of methanol at oxygen vacancy sites on ZnO.15,18 While the F+ centres of MgO are unlikely to form part of a directly useful catalytic process, a better understanding of the interaction between adsorbates and single electrons trapped at surface sites is likely to be crucial to finding a reaction process which can contribute to the conversion of CO2 into useful products.
Acknowledgements
CD would like to thank the Molecular Modelling and Materials Science Industrial Doctorate Centre (M3S IDC) and the Science and Technology Facilities Council (STFC) for funding. Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/F067496), this work made use of the facilities of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme.References
- S. Wang, S. Yan, X. Ma and J. Gong, Energy Environ. Sci., 2011, 4, 3805–3819 CAS.
- S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796–854 CrossRef CAS PubMed.
- M. Jensen, L. Pettersson, O. Swang and U. Olsbye, J. Phys. Chem. B, 2005, 109, 16774–16781 CrossRef CAS PubMed.
- G. Pacchioni, Surf. Sci., 1993, 281, 207–219 CrossRef CAS.
- G. Pacchioni, J. Ricart and F. Illas, J. Am. Chem. Soc., 1994, 116, 10152–10158 CrossRef CAS.
- W. Schneider, J. Phys. Chem. B, 2004, 108, 273–282 CrossRef CAS.
- J. Baltrusaitis, C. Hatch and R. Orlando, J. Phys. Chem. A, 2012, 116, 7950–7958 CrossRef CAS PubMed.
- D. Ochs, M. Brause, B. Braun, W. Maus-Friedrichs and V. Kempter, Surf. Sci., 1998, 397, 101–107 CrossRef CAS.
- H. Tsuji, A. Okamura-Yoshida, T. Shishido and H. Hattori, Langmuir, 2003, 19, 8793–8800 CrossRef CAS.
- H. Tsuji and H. Hattori, ChemPhysChem, 2004, 5, 733–736 CrossRef CAS PubMed.
- H. Tsuji, T. Shishido, A. Okamura, Y. Gao, H. Hattori and H. Kita, J. Chem. Soc., Faraday Trans., 1994, 90, 803–807 RSC.
- D. Meixner, D. Arthur and S. George, Surf. Sci., 1992, 261, 141–154 CrossRef CAS.
- Y. Yanagisawa, K. Takaoka and S. Yamabe, J. Chem. Soc., Faraday Trans., 1994, 90, 2561–2566 RSC.
- G. Pacchioni, ChemPhysChem, 2003, 4, 1041–1047 CrossRef CAS PubMed.
- S. French, A. Sokol, S. Bromley, C. Catlow, S. Rogers, F. King and P. Sherwood, Angew. Chem., Int. Ed., 2001, 40, 4437–4440 CrossRef CAS.
- P. Sherwood, A. de Vries, M. Guest, G. Schreckenbach, C. Catlow, S. French, A. Sokol, S. Bromley, W. Thiel, A. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjovoll, A. Fahmi, A. Schafer and C. Lennartz, THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- A. Sokol, S. Bromley, S. French, C. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712 CrossRef CAS.
- S. French, A. Sokol, S. Bromley, C. Catlow and P. Sherwood, Top. Catal., 2003, 24, 161–172 CrossRef CAS.
- S. Bromley, S. French, A. Sokol, C. Catlow and P. Sherwood, J. Phys. Chem. B, 2003, 107, 7045–7057 CrossRef CAS.
- C. Catlow, S. French, A. Sokol and J. Thomas, Philos. Trans. R. Soc., A, 2005, 363, 913–936 CrossRef CAS PubMed.
- ChemShell, a Computational Chemistry Shell, see www.chemshell.org.
- J. Kaestner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- M. Guest, I. Bush, H. Van Dam, P. Sherwood, J. Thomas, J. Van Lenthe, R. Havenith and J. Kendrick, Mol. Phys., 2005, 103, 719–747 CrossRef CAS.
- J. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- J. Gale and A. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- J. Gale, Z. Kristallogr., 2005, 220, 552–554 CrossRef CAS.
- A. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chablowski and M. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. W. Keal, P. Sherwood, G. Dutta, A. A. Sokol and C. R. A. Catlow, Proc. R. Soc. A, 2011, 467, 1900–1924 CrossRef CAS.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. Grimes, C. Catlow and A. Stoneham, J. Phys.: Condens. Matter, 1989, 1, 7367–7384 CrossRef CAS.
- C. Catlow, R. Bell, F. Cora, S. French, B. Slater and A. Sokol, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2005, 101, 513–547 Search PubMed.
- C. Catlow, Trans. Faraday Soc., 1978, 74, 1901–1908 RSC.
- G. Lewis and C. Catlow, J. Phys. C: Solid State Phys., 1985, 18, 1149–1161 CrossRef CAS.
- P. Cox and A. Williams, Surf. Sci., 1986, 175, L782–L786 CrossRef CAS.
- P. Sushko, A. Shluger and C. Catlow, Surf. Sci., 2000, 450, 153–170 CrossRef CAS.
- E. Scorza, U. Birkenheuer and C. Pisani, J. Chem. Phys., 1997, 107, 9645–9658 CrossRef CAS.
- A. Ferrari and G. Pacchioni, J. Phys. Chem., 1995, 99, 17010–17018 CrossRef CAS.
- R. W. Williams and D. Malhotra, Chem. Phys., 2006, 327, 54–62 CrossRef CAS PubMed.
- E. Florez, P. Fuentealba and F. Mondragon, Catal. Today, 2008, 133, 216–222 CrossRef PubMed.
- D. Cornu, H. Guesmi, J.-M. Krafft and H. Lauron-Pernot, J. Phys. Chem. C, 2012, 116, 6645–6654 CAS.
- Y. Yanagisawa, K. Takaoka, S. Yamabe and T. Ito, J. Phys. Chem., 1995, 99, 3704–3710 CrossRef CAS.
- L. Giordano, U. Martinez, G. Pacchioni, M. Watkins and A. L. Shluger, J. Phys. Chem. C, 2008, 112, 3857–3865 CAS.
| This journal is © the Owner Societies 2014 |