Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Site and bond-specific dynamics of reactions at the gas–liquid interface†
Maria A.
Tesa-Serrate
,
Kerry L.
King
,
Grant
Paterson
,
Matthew L.
Costen
and
Kenneth G.
McKendrick
*
Institute of Chemical Sciences, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, UK. E-mail: K.G.McKendrick@hw.ac.uk
First published on 7th November 2013
Abstract
The dynamics of the interfacial reactions of O(3P) with the hydrocarbon liquids squalane (C30H62, 2,6,10,15,19,23-hexamethyltetracosane) and squalene (C30H50, trans-2,6,10,15,19,23-hexamethyltetracosa-2,6,10,14,18,22-hexaene) have been studied experimentally. Laser-induced fluorescence (LIF) was used to detect the nascent gas-phase OH products. The O(3P) atoms are acutely sensitive to the chemical differences of the squalane and squalene surfaces. The larger exothermicity of abstraction from allylic C–H sites in squalene is reflected in markedly hotter OH rotational and vibrational distributions. There is a more modest increase in translational energy release. A larger fraction of the available energy is deposited in the liquid for squalene than for squalane, consistent with a more extensive geometry change on formation of the allylic radical co-product. Although the dominant reaction mechanism is direct, impulsive scattering, there is some evidence for OH being accommodated at both liquid surfaces, resulting in thermalised translation and rotational distributions. Despite the H-abstraction reaction being strongly favoured energetically for squalene, the yield of OH is substantially lower than for squalane. This is very likely due to competitive addition of O(3P) to the unsaturated sites in squalene, implying that double bonds are extensively exposed at the liquid surface.
Introduction
Chemical processes at gas–liquid interfaces have received increasing attention in recent years. The first dynamical studies on collisions of gas-phase species with liquid surfaces were conducted by Nathanson and co-workers in the early 1990s.1–4 The products of molecular-beam scattering were detected mass spectrometrically. Two separate distributions with different translational energies were commonly observed. It was consequently proposed that the scattering mechanism could be divided into two limiting processes. In an impulsive scattering (IS) mechanism, the incoming projectile undergoes one, or at most a few, collisions and returns directly into the gas phase with relatively high translational energy. In a thermal desorption (TD) event, the projectile interacts with the surface in multiple encounters and becomes thermalised, resulting in slower-moving products following a Maxwell–Boltzmann distribution of speeds. Experimental studies with spectroscopic detection5–8 have shown that scattered TD products also accommodate their rotational, but not vibrational, energy with the surface. The validity of this empirical binary division between IS and TD has later been questioned in theoretical studies, which have found intermediate types of trajectories with partial accommodation of the scattered products.9–12 Despite this, the “IS vs. TD” model has generally been found to effectively characterise many gas–liquid scattering processes.A considerable amount of experimental work has now been directed at interfacial scattering dynamics on surfaces such as polymers, liquid hydrocarbons and self-assembled monolayers.13 However, the majority of these studies have focused on scattering of nonreactive gas-phase species. Reactive scattering processes have been less extensively investigated. Aside from work on H–D exchange in the DCl–salty glycerol14,15 and HCl(Br)–D2SO4 systems,16 most of the existing studies have been on reactions with the partially branched hydrocarbon squalane (C30H62, 2,6,10,15,19,23-hexamethyltetracosane). Examples include the reactions with F,17,18 Cl,19 O(1D),20 and O(3P).21–29 Of these, the O(3P) + squalane reaction is the most thoroughly characterised. The reaction produces OH radicals by abstraction of a hydrogen atom. Experimental studies by Minton and co-workers21–23 employed mass-spectrometric detection to obtain the speed and angular distributions of the OH products. Their method also allowed detection of the inelastically scattered reactant O(3P) atoms, and of the secondary product H2O. All of these species exhibited two translational-energy distributions, in different proportions, that could be identified with IS and TD channels. We and earlier co-workers24–29 have adopted a complementary approach, detecting the internal-state distributions of the OH products by laser-induced fluorescence (LIF), with partial translational-energy resolution. A positive correlation between OH translational and rotational energy was found. Only the slower OH had a rotational temperature that was affected by the bulk temperature of the liquid. These observations indicate that there was some combined rotational and translational accommodation of OH products with the surface.
The well-characterised nature of the interfacial reaction of O(3P) with squalane allows it to be used as a benchmark against which to compare other hydrocarbon liquids. This has been exploited in subsequent work by our group on O(3P) reactions with other branched and linear liquid hydrocarbons,30 self-assembled monolayers31,32 and ionic liquids.33–35 In the present paper we pursue the same approach but increase the complexity of the system by introducing functional groups that will give rise to intrinsically different reaction dynamics. Specifically, we investigate here the reaction of O(3P) with squalane's unsaturated counterpart, squalene (C30H50, trans-2,6,10,15,19,23-hexamethyltetracosa-2,6,10,14,18,22-hexaene). The molecular structures of both liquids are shown in Fig. 1.
Squalene has the same basic structure as squalane, but six unsaturated sites are present along the backbone. The C(sp3)–H bonds are of two types, primary and secondary, but they are all allylic in character and in consequence have significantly lower bond energies than their equivalents in squalane. The H-abstraction reaction at these bonds is more exothermic and has a lower activation energy: the enthalpies of abstraction from allylic sites are typically between −56 and −86 kJ mol−1, while abstraction reactions from saturated hydrocarbons have values of ΔrH between −7 and −43 kJ mol−1, depending on the type of H abstracted.36 Abstraction of C(sp2)–H from squalene is energetically disfavoured. The contrasting energetics of the abstraction reactions from C(sp3)–H sites in squalane and squalene are illustrated schematically in Fig. 2. We shall discount below the primary C–H bonds in squalane as a source of a significant yield of OH. As illustrated in Fig. 2, their much higher measured activation energies suggest that they will be proportionately much less reactive than the weaker secondary or tertiary bonds with O(3P) atoms produced by 355 nm photolysis of NO2.37 This is confirmed by direct experimental observations on smaller alkanes in the gas phase37 and on isotopically labelled alkylthiolate self-assembled monolayers.31
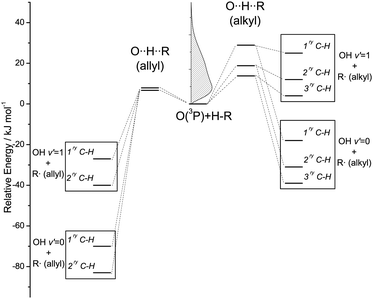 | ||
| Fig. 2 Energetics of H-abstraction from alkyl and allyl C–H bonds. The relative energies of the products have been estimated from bond dissociation energies for representative hydrocarbons tabulated in ref. 36. The barriers of abstraction for alkyl and allyl C(sp3)–H have been taken from ref. 46 and 66, respectively. The kinetic energy distribution of O(3P) produced by 355 nm photolysis of NO2 is presented in the inset graph. | ||
As well as the difference in energetics of the abstraction reaction, the double bonds provide an extra loss channel for O(3P) atoms. Addition to unsaturated alkene sites does not lead to significant OH production.38 The mechanism and product branching of the addition reaction has been extensively investigated in the gas phase for small alkenes.39–45 In substituted alkenes, both the H-abstraction and addition channels contribute. Previous studies have characterised the dynamics of H-abstraction,46,47 as well as the addition to the unsaturated site40,48–53 and the branching between mechanisms.54,55 The abstraction channel is thought to become important at high temperatures56 and will therefore be relevant in combustion environments.
Here we focus exclusively on the H-abstraction channel. There are no previous dynamical studies of the interfacial H-abstraction reaction by O(3P) at the surface of an unsaturated liquid hydrocarbon. Perhaps the closest relevant example is a study by Sibener and co-workers57 who examined the reaction of O(3P) with small alkenes adsorbed on metal and ice surfaces. However, they did not detect any OH products and focused instead on the addition reaction.
The present study aims to explore how the interfacial dynamics of H abstraction are affected when unsaturated sites are present in the liquid hydrocarbon. Previous inelastic scattering experiments using photolytically generated OH have shown that its survival probability is reduced by the presence of unsaturation at the surface.58,59 Reactive scattering of O(3P) might be expected to show more marked differences between saturated and unsaturated surfaces, in directions which are not easy to predict. The OH yield should be reduced in squalene by the presence of double bonds, but increased by the lower barrier associated with the allylic character of the C–H sites. The competition between these effects will be characterised by the relative OH yield with respect to squalane. In addition, the nascent products from squalene may possess more energy due to the larger exothermicity of the abstraction reaction, but there may also be competing changes in the deposition of energy into the liquid surface. We provide clear answers here to these previously unresolved questions.
Experimental
A similar experimental approach has been used in our previous work on reaction dynamics of O(3P) with liquid surfaces.24–26,28,30,35 Since a detailed description of the experimental setup has already been provided, only a brief account will be given here. The liquid of interest is contained in a copper bath at room temperature, located inside a vacuum chamber. A 5 cm diameter stainless steel wheel is partially submerged in the liquid. The wheel rotates at 0.5 Hz generating a continuously renewed liquid surface. Squalane and squalene were supplied by Aldrich. In addition, the perfluoropolyether Krytox 1506 (F-[CF(CF3)CF2O]14ave-CF2CF3, DuPont) was used as an inert blank liquid to confirm that all detected products originated exclusively from reaction at the liquid surface. All reactants were used as received without any further purification steps.O(3P) atoms were generated by photolysis of NO2 (BOC, 98.3%) at a carefully controlled pressure of nominally 1 mTorr. The 355 nm photolysis beam was generated by the third harmonic of a Nd:YAG laser (Continuum Surelite SLII-10), which produced pulses at 10 Hz with an approximate length of 5 ns. The photolysis energy was kept constant at approximately 90 mJ pulse−1 at the entrance to the chamber. The beam propagated through the centre of the chamber at a fixed distance of 6 mm from the wheel with an approximate diameter of 5 mm. The O(3P) atoms were produced with a known velocity distribution.60 The collision energy of the resulting O(3P) has an average value of 16 kJ mol−1 and FWHM of 26 kJ mol−1. The photolysis light was horizontally polarised in the lab frame so as to optimise the fraction of O(3P) directed towards the surface.
OH radicals escaping from the surface were detected by laser-induced fluorescence on the A2Σ+–X2Π (1,0) and (1,1) vibronic bands, probing OH ν′ = 0 and 1, respectively. This was achieved with a Nd:YAG-pumped dye laser (Sirah Pulsed Dye Laser, CSTR-LG-24, pumped by a Continuum Surelite II-10 laser) counter-propagating along the same axis as the photolysis laser with a beam diameter of either 3 mm (for the (1,0) band) or 4 mm ((1,1) band). Pulse energies were kept low to minimise saturation effects (125 μJ pulse−1 on the (1,0) band and 20 μJ pulse−1 for (1,1)). Fluorescence was collected by a liquid light guide situated 2 cm above the laser axis and detected by a photomultiplier tube (PMT). Dichroic filters were inserted in front of the PMT to isolate emission on the (1,1) band (when probing on (1,0)) or the (1,0) band (when probing on (1,1)).
For calibration purposes, as explained below, thermalised OH spectra were recorded by admitting 0.25 Torr N2 to the chamber and detecting OH at a photolysis-probe delay of 30 μs. This corresponds to an average of ∼75 collisions at a typical gas-kinetic collision frequency, easily sufficient to ensure rotational thermalisation.
Results
Appearance profiles
Fixing the probe wavelength on a particular transition and varying the delay between photolysis and probe pulses results in OH appearance profiles. These provide information on the translational energy distribution of the OH products in the selected rotational level. For the profiles presented here, lines in the main Q1 branch were used. These lines probe population in one lambda doublet of the lower (F1) spin–orbit manifold, but as we show below the rotational distributions are generally well-described by a temperature, or combination of temperatures. There is therefore no special significance to the branch chosen and we simply label the results by the corresponding value of N′. Each of the profiles presented here is an average of 22 measurements taken over at least 3 different days to ensure reproducibility. Caution should be exercised when interpreting the shapes of the appearance profiles at photolysis-probe delays longer than ∼30 μs, as the effects of secondary gas-phase collisions begin to become apparent beyond this delay.35Two types of background signals were present in all raw measurements. The first was scattered probe light, present at all delays. The second was a short-lived signal excited by the photolysis pulse (possibly originating from electronically excited NO2), in addition to the prompt scattered photolysis-laser light. These background signals were removed by recording separate profiles in turn with only one of the lasers firing. These “photolysis-only” and “probe-only” profiles were taken immediately after every set of measurements to minimise drifts in the experimental conditions. They were subtracted from the raw data to leave only the desired OH LIF signals. In addition, when detecting on the (1,0) band, an OH LIF signal was present at early delays, starting promptly at zero photolysis-probe delay and disappearing completely after approximately 4 μs. The intensity of this signal varied between sets of measurements. We infer this OH to be the product of photolysis of an impurity in the NO2 gas. A likely candidate is HONO, which is known to be formed in presence of H2O in the gas-lines or the reaction chamber.61 LIF excitation spectra recorded at early delays (3 μs) were indeed found to be consistent with the known results for OH ν′ = 0 produced by 355 nm photolysis of HONO.62 This early signal does not obscure the OH produced by reaction at the surface, as it is only present at delays shorter than the ∼5 μs onset of the first surface-scattered signals. Nevertheless, it was necessary to exclude the possibility that sufficient of this “pre-collision” OH would undergo inelastic scattering at the liquid surface to contribute appreciably to the appearance profiles. To investigate this, profiles were recorded with the unreactive liquid PFPE. The contribution of inelastically scattered OH to the appearance profiles here can be inferred from our own previous measurements of the ratio of inelastically scattered OH signal to the zero-delay signal from HONO photolysis.58 In those experiments the returning OH signal was naturally substantially smaller than the very large signal at early delays. Furthermore, the yield of inelastically scattered OH was lower for squalane and squalene in comparison with PFPE. In the present study, appearance profiles recorded with PFPE showed only a negligible scattered OH signal. We are therefore confident that all OH detected in our appearance profiles for squalane and squalene results from reaction of O(3P) at the surface of the liquid.
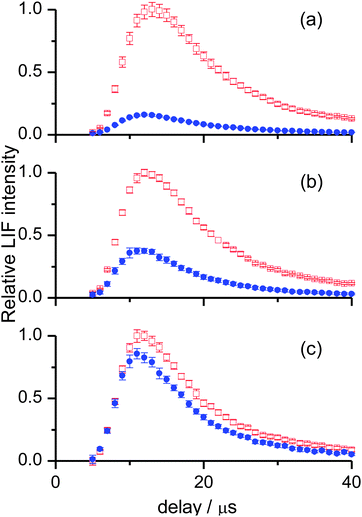
For OH ν′ = 0, appearance profiles were recorded on the Q1(1), Q1(5) and Q1(7) lines of the (1,0) band, probing the respective levels N′ = 1, 5 and 7, as shown in Fig. 3. (It should be noted for completeness that in the case of Q1(1) there is a small contribution from the overlapping R2(3) transition, but to avoid over-complication of the notation we simply label this as N′ = 1). There is a striking difference in the overall yields for the two liquids, with squalane producing much more OH ν′ = 0. However, this difference becomes smaller as the rotational level is increased. This indicates that the OH ν′ = 0 from squalene is considerably rotationally hotter than that from squalane. In addition, squalene also produces profiles which peak at slightly earlier times. This can be appreciated by carefully comparing the shapes of the two appearance profiles in any single panel of Fig. 3. It can also be seen in Fig. 3 that appearance profiles peak earlier for higher rotational levels, indicating a positive correlation between the translational and rotational energy of the products.
The corresponding measurements for OH ν′ = 1 are shown in Fig. 4. The slightly negative intensities of some of the profiles at 5 and 6 μs are an artefact resulting from imperfect photolysis background subtraction. The later peak arrival times for the profiles compared to those in Fig. 3 show that OH ν′ = 1 possesses on average less translational energy than OH ν′ = 0. The un-normalised intensities (not indicated in Fig. 3 or 4) were found to decline more rapidly with increasing N′ than for ν′ = 0. This will be confirmed in more detail by the excitation spectra below. It indicates that for both liquids OH ν′ = 1 is less rotationally excited.
These trends had been observed previously for squalane,26 but are reported here for the first time for squalene. Consequently, appearance profiles for ν′ = 1 were recorded only for rotational levels up to N′ = 5. For this vibrational level the OH yields from both liquids are comparable. From comparison with Fig. 3 it follows that squalene yields a higher proportion of vibrationally excited OH than squalane. Despite being rotationally colder than ν′ = 0, the OH ν′ = 1 from squalene is still substantially hotter than that from squalane, as revealed by the relative gain in yield from squalene with increasing N′. Lastly, the differences in translational energy between squalane and squalene are more evident for OH ν′ = 1, with larger shifts between the peak arrival times for the two liquids for a given N′. In contrast to ν′ = 0, there are no clear trends with rotational level in the translational energy of OH ν′ = 1.
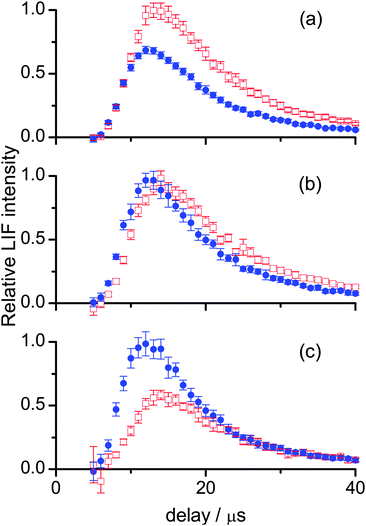
Fig. 5 presents a re-normalized comparison between appearance profiles for different vibrational and rotational levels for each liquid. The differences in translational energy can be more easily appreciated in this form. Also plotted is a Monte Carlo simulation of a thermal desorption (TD) OH distribution, constructed as described in previous work by our group.25,26,28,29,32,35 It is immediately clear from this comparison that all of the profiles correspond to translational energy distributions that are much hotter than a room temperature Maxwell–Boltzmann distribution. In Fig. 5(a) the OH ν′ = 1 profiles for squalane peak substantially later than for ν′ = 0, and for ν′ = 0 higher rotational levels have successively earlier appearance profiles. There is therefore a positive correlation between increasing translational and rotational energy in ν′ = 0, and a substantial decrease in translational energy in ν′ = 1. In contrast, in Fig. 5(b), the rising edges and peaks of the appearance profiles from squalene in ν′ = 0 and in ν′ = 1 are much more similar, representing smaller differences in the translational energy distributions for the two vibrational levels. Differences with rotational level are more subtle than for squalane, with a weaker tendency to increasing translation in the higher rotational levels for ν′ = 0 and no clear trend for ν′ = 1. Comparison of Fig. 5(a) and (b) at longer delays shows that the profiles decrease faster and with much less variation for squalene than for squalane. There appears to be less slow moving OH recoiling from the squalene surface than from squalane, and the relative fraction of slow OH produced is less sensitive to product quantum state for squalene.
Excitation spectra
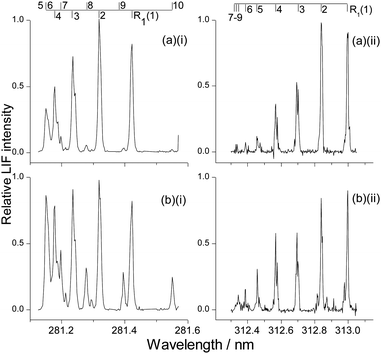
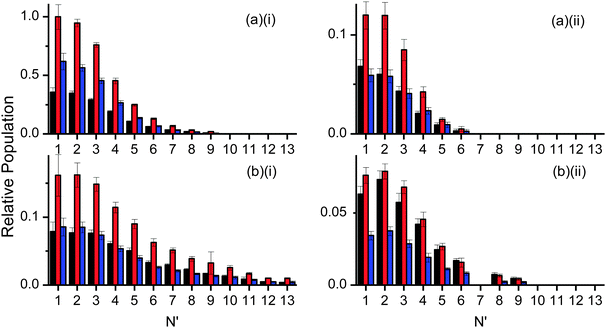
LIF excitation spectra were recorded on the A–X (1,0) and (1,1) bands at photolysis-probe delays corresponding to the rising edge, peak, and tail of the appearance profiles, respectively. These delays were 8, 12 and 20 μs for OH ν′ = 0; and 10, 14 and 22 μs for OH ν′ = 1. As for the appearance profiles, tests were carried out for OH ν′ = 0 to confirm that there was no significant contribution to these spectra from inelastic scattering of background OH produced by photolysis of the contaminant in the precursor. Example spectra (of the R1 branch) recorded at the peak of the appearance profile are shown in Fig. 6 for both squalane and squalene in ν′ = 0 and ν′ = 1 respectively. Comparison of the ν′ = 0 spectra (Fig. 6(a)(i) squalane vs.Fig. 6(b)(i) squalene) immediately shows that there is significantly higher rotational excitation in ν′ = 0 for squalene, consistent with the rotational level dependence of the appearance profiles already discussed. Comparison of ν′ = 0 spectra to ν′ = 1 (Fig. 6(a)(i) or (b)(i)vs.Fig. 6(a)(ii) or (b)(ii)) shows that the ν′ = 1 rotation is considerably colder than that in ν′ = 0. Closer comparison of Fig. 6(a)(ii) and (b)(ii) suggests that the rotational distribution from squalene in ν′ = 1 is also hotter than that from squalane.The population of each rotational level was extracted by fitting the experimental spectrum to a simulation using the program LIFBASE.63 Each of the rotational distributions shown here is an average from at least 6 spectra, recorded on different days. Only the main Q1 and R1 rotational branches were analysed as they had fewer blended lines for both vibrational bands. The populations within each rotational branch were obtained individually and averaged, resulting in separate distributions for Q1 and R1. Both branches were employed separately in the Boltzmann temperature analysis that follows, but they were averaged together to construct the rotational distributions plotted in Fig. 7 and 8.
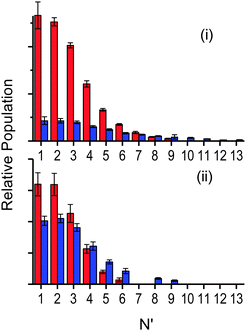 | ||
| Fig. 8 Relative OH rotational distributions at the peak of the appearance profile, from squalane (red bars) and squalene (blue bars). (i) OH ν′ = 0 at 12 μs, (ii) OH ν′ = 1 at 14 μs. | ||
The partially saturating probe fluences used in these experiments could in principle have an effect on the rotational distributions obtained by this analysis. The extent of any saturation effect was tested by recording spectra of OH that had been rotationally thermalised as described in the Experimental section, which were then analysed using LIFBASE, consistent with our previous work.24 Reassuringly, the population distribution of the thermalised OH within either the R1 or Q1 branch was found to be a good fit to a Boltzmann temperature of 303 ± 6 K, indicating that saturation does not substantially alter the result of our population analysis. It was found, however, that the relative intensities between rotational branches did not match those of the simulations. In consequence no attempt has been made to extract fine-structure or Λ-doublet populations from comparisons between branches.
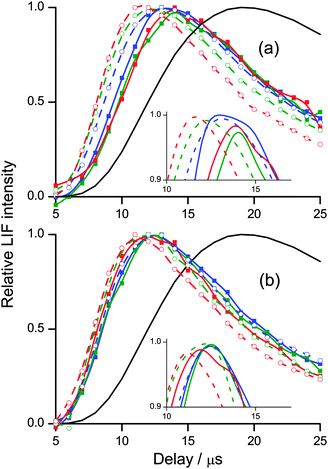
Fig. 7 shows the resulting rotational distributions for the OH reaction product at different times in the appearance profile. The populations have been scaled to match the relative signal intensities of the appearance profiles at each particular delay. These unnormalised data allow direct comparison between squalane and squalene within each vibrational level. However the yields for ν′ = 0 and ν′ = 1 cannot be compared directly, as the detection sensitivities on the (1,0) and (1,1) bands were different. Substantial differences between squalane and squalene are immediately apparent. Most notably, higher rotational levels are relatively more populated for squalene for both OH ν′ = 0 and ν′ = 1. Rotational distributions at early times also tend to be hotter than those at later delays.
Fig. 8 is allows a clearer comparison of the OH yields from squalane and squalene, measured at the peaks of their appearance profiles (12 and 14 μs, respectively). The relative squalene:squalane yield, summed over all contributing levels with smooth interpolation of any that are missing due to spectroscopic overlap, is 0.25 ± 0.01 for OH ν′ = 0 and 0.87 ± 0.13 for OH ν′ = 1. The OH ν′ = 1/ν′ = 0 vibrational branching ratio for squalane has previously been measured to be 0.07 ± 0.02 at the peak of the profile.25 Adopting this value for squalane and using the newly obtained relative OH yields gives a vibrational branching ratio of 0.24 ± 0.08 for squalene at the peak of the appearance profile. This is equivalent to a “two-point” vibrational temperature of 3600 ± 800 K, much hotter than the 1900 ± 200 K obtained for squalane. The overall squalene:squalane OH-yield ratio, summed over both OH vibrational levels, is 0.29 ± 0.03.
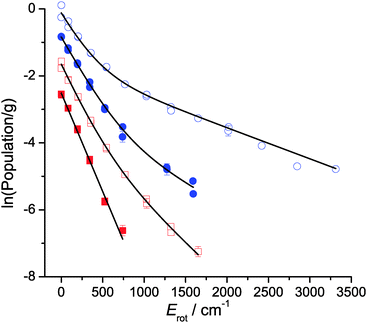
Rotational distributions can often be conveniently characterised by rotational temperatures, obtained by fitting the rotational populations to a Boltzmann distribution. However, many of the rotational distributions presented here do not correspond to a single rotational temperature. OH produced from squalene in particular presents a clearly bimodal rotational distribution. Consequently, the distributions were fitted to a 2-temperature Boltzmann model, as previously applied in other liquid surface scattering experiments.6,20,64 The model assumes contributions from high- and low-temperature components to the population, P(N):
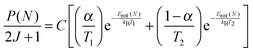 | (1) |
The rotational populations of OH produced from squalene are well described by the 2-temperature model with widely-separated values of T1 and T2. In contrast, this model was over-determined for OH ν′ = 1 from squalane, which as can be seen in Fig. 9 is well-described by a single temperature. In this case α was fixed to 1 to fit the distribution to a single temperature. Good fits to the data were found for all delays for both squalane and squalene. The resulting temperatures, T1 and T2, and branching fraction α are presented in Table 1. When comparing delays for the same liquid it should be noted that there are cross-correlations between the parameters, particularly T2 and α, and therefore the trends are not always well represented by any single parameter. However, it is clear that for both vibrational levels squalene has a substantially lower value of α, i.e. a phenomenologically larger fraction of the rotationally hot component is produced. The combined values of α, T1 and T2 also reflect the reduced rotational excitation at later delays for OH ν′ = 0 for both liquids.
| Delay (μs) | Squalane ν′ = 0 | Delay (μs) | Squalane ν′ = 1 | ||||
|---|---|---|---|---|---|---|---|
| α | T 1 (K) | T 2 (K) | α | T 1 (K) | T 2 (K) | ||
| 8 | 0.73 ± 0.12 | 290 ± 28 | 818 ± 239 | 10 | 1.00 | 243 ± 6 | — |
| 12 | 0.70 ± 0.13 | 256 ± 26 | 625 ± 124 | 14 | 1.00 | 245 ± 5 | — |
| 20 | 0.70 ± 0.20 | 249 ± 34 | 559 ± 143 | 22 | 1.00 | 267 ± 5 | — |
| Delay (μs) | Squalene ν′ = 0 | Delay (μs) | Squalene ν′ = 1 | ||||
|---|---|---|---|---|---|---|---|
| α | T 1 (K) | T 2 (K) | α | T 1 (K) | T 2 (K) | ||
| 8 | 0.35 ± 0.06 | 268 ± 38 | 1106 ± 275 | 10 | 0.63 ± 0.10 | 296 ± 28 | 1003 ± 251 |
| 12 | 0.43 ± 0.05 | 301 ± 34 | 1588 ± 128 | 14 | 0.74 ± 0.12 | 310 ± 33 | 1058 ± 405 |
| 20 | 0.53 ± 0.03 | 290 ± 19 | 1606 ± 216 | 22 | 0.67 ± 0.09 | 270 ± 30 | 1135 ± 318 |
The average rotational energy in either ν′ = 0 or 1 separately, and a weighted average over both, was obtained for each liquid. Populations of rotational levels that had not been determined experimentally were estimated by interpolation of the relevant one or two-temperature Boltzmann fit. The average vibrational energy of the products was obtained from the vibrational branching ratios presented above. The results are summarised in Table 2.
| 〈Erot〉 (ν′ = 0) | 〈Erot〉 (ν′ = 1) | 〈Erot〉 | 〈Evib〉 | |
|---|---|---|---|---|
| Squalane | 2.62 | 1.67 | 2.56 | 2.80 |
| Squalene | 6.42 | 3.58 | 5.89 | 8.29 |
Discussion
At a qualitative level, the answers to the questions we sought to address are now clear. Significant dynamical differences are observed in the interfacial reactions of O(3P) with fully and partially saturated liquid hydrocarbons. The unsaturated hydrocarbon produces a lower yield of OH, but one with higher translational, and especially internal, energies.We now consider each of these observations in more detail, beginning with the relative yields of OH. Squalene produces only ∼1/3 as much OH as squalane. This might naively be interpreted to result from the loss of potentially reactive H atoms on the introduction of six double bonds into the hydrocarbon chain, eliminating all six tertiary sites and replacing six methylenes with unreactive vinyl units. However the ratio of C(sp3)–H atoms available for abstraction (44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62) in squalene and squalane is still much higher than 1/3. In addition, the reaction is strongly energetically favoured for the C–H sites in squalene due to their allylic character, as noted in the introduction. We have previously shown in the reaction of O(3P) with labelled sites in alkylthiol SAMs that the much more modest difference in bond energies between primary and secondary sites has a large effect on their relative reactivities.31
62) in squalene and squalane is still much higher than 1/3. In addition, the reaction is strongly energetically favoured for the C–H sites in squalene due to their allylic character, as noted in the introduction. We have previously shown in the reaction of O(3P) with labelled sites in alkylthiol SAMs that the much more modest difference in bond energies between primary and secondary sites has a large effect on their relative reactivities.31
From this it follows that there must be some other explanation for the reduced OH production in squalene. The most likely candidate is a competitive loss channel for O(3P), namely the addition reaction at the unsaturated sites. A necessary condition would be that the double bonds are significantly exposed at the squalene surface. This has indeed been confirmed in our own recent MD simulations, which support the interpretation of experiments on inelastic scattering of OH from squalene.58,59 The equivalent loss of the products may also contribute to the reduced yield of OH from the O(3P) reaction with squalene, but we do not believe it is the major factor. Admittedly, there are differences in the falling edges of the profiles from squalane and squalene in Fig. 5, as noted above, consistent with preferential loss of slow-moving OH at the squalene surface. However, the differences in reactive uptake of OH on squalane and squalene are known to be quite modest from our inelastic scattering experiments,58,59 and considerably smaller than the observed reduction in OH yield in the O(3P) reaction here. Furthermore, there is overwhelming evidence, as noted in the Introduction, that O(3P) addition is a major channel in the gas-phase reaction with alkenes.40,49,50,54–56,65
It might be interesting to try to draw a comparison with these related gas-phase reactions to characterise how the competition between reaction channels might change at the liquid interface. However, the branching between OH formation and addition in the gas phase depends sensitively on the nature of the alkene molecule and the experimental conditions. Furthermore, all of the gas-phase studies have naturally involved much smaller alkenes than squalene. The most directly comparable study is by Bersohn and co-workers,55 who reported relative OH LIF intensities obtained for a range of gas-phase hydrocarbons under similar collision-energies to our experiments. For substituted alkenes capable of reacting via both channels, the addition reaction is always the dominant pathway. However, the faster overall rate constants for reaction with alkenes means that the OH yields from alkenes are still a substantial fraction of those observed from the equivalent alkanes. These ratios are interestingly of the same order as our value of ∼1/3 from squalene and squalane. This could imply that a substantial fraction of the OH detected from squalene is produced in single-collision events, similar to the gas-phase. We return to this aspect below in the context of dynamical attributes of the products that are more directly diagnostic of the reaction mechanism.
The average energies appearing in the internal modes of the OH at the peaks of the appearance profiles have been reported in Table 2. To appreciate the significance of the differences between squalane and squalene, it is necessary to estimate the respective energies available to the products. This is complicated by the fact that abstraction from different C–H sites will have different thresholds and excitation functions, which in principle would have to be convoluted with the broad distribution of O(3P) kinetic energies from the photolysis of NO2.60 Nevertheless, in practice the differences in total energy available are dominated by the large (50–60 kJ mol−1) differences in bond energy between the allylic sites in squalene and any of the sites in squalane (see Table 3 and Fig. 2). The difference in bond energies between primary and secondary allylic sites in squalene is, in comparison, only 13 kJ mol−1, and between secondary and tertiary sites in squalane is 7 kJ mol−1. (As above, we discount any significant contribution from the much less reactive primary sites in squalane). Therefore, for the purposes of this comparison it is sufficient to treat the average kinetic energy of the O(3P) atoms that react as being the same in all cases. We set this to 21 kJ mol−1, which corresponds to the kinetically determined activation energy for reaction at a secondary or tertiary site in squalane.37 The total energy available, Eav, is then simply equal to −ΔrH + 21 kJ mol−1.
| ΔrHa | E 0 | E av | 〈Et〉 | 〈Erot〉 | 〈Esur〉 | f t | f rot | f sur | |
|---|---|---|---|---|---|---|---|---|---|
| a Estimated from thermodynamic data in ref. 36. b Dynamic thresholds from ref. 45 and 66. | |||||||||
| Squalane | |||||||||
| OH ν′ = 0 | |||||||||
| 2y C–H | −19 | 19 | 40 | 12 | 3 | 25 | 0.31 | 0.07 | 0.62 |
| 3y C–H | −26 | 14 | 47 | 12 | 3 | 32 | 0.27 | 0.06 | 0.68 |
| Squalene | |||||||||
| OH ν′ = 0 | |||||||||
| 1y allylic C–H | −72 | 7 | 93 | 16 | 6 | 70 | 0.17 | 0.07 | 0.76 |
| 2y allylic C–H | −85 | 8 | 106 | 16 | 6 | 83 | 0.15 | 0.06 | 0.79 |
| OH ν′ = 1 | |||||||||
| 1y allylic C–H | −72 | 7 | 50 | 15 | 4 | 32 | 0.30 | 0.07 | 0.63 |
| 2y allylic C–H | −85 | 8 | 63 | 15 | 4 | 45 | 0.24 | 0.06 | 0.71 |
The corresponding fractions of the available energy appearing in rotation for each of the observed vibrational levels for squalane and squalene are listed in Table 3. This shows that for the OH at the peak of the appearance profile, the average energy that appears in rotation is a constant fraction, 6–7%, of the total energy available. This reinforces the conclusion that mechanistically the H-abstraction reactions with squalane and squalene are very similar. The significant differences in rotational energy release (see Fig. 7–9 and Tables 1 and 2) between liquids across both vibrational levels simply reflect the variations in the total energy available. Results from both liquids are consistent with a collinear O–H–C minimum-energy path that does not efficiently promote rotational excitation, as has been extensively inferred in previous studies on the gas-phase H-abstraction reaction.37,66,67
As noted above, there is a considerable difference in the vibrational branching ratio for the two liquids. It is not meaningful, though, to extend this to a calculation of the quantitative changes in the fraction of energy released to vibration on the basis of the simple assumption of a fixed contribution from O(3P) translation. The production of OH ν′ = 1 from squalane is energetically closed at an O(3P) energy of 21 kJ mol−1, and must result from the high-energy tail of the O(3P) distribution, and we have therefore omitted it from Table 3. Nevertheless, the increase in vibrational excitation from the more exothermic reaction with squalene is qualitatively entirely as expected in a direct process according to elementary Polanyi rules.
As is obvious from the comparison with the simulated profiles for thermal desorption at 300 K in Fig. 5, much of the OH is translationally hot. There is of course, as in the case of rotation, no a priori reason why the products of a direct process should conform to a Maxwell–Boltzmann distribution at a single temperature. However, as we show in the ESI,† it turns out that our appearance profiles are quite well described in this way. The best-fit single translational temperatures are around 1000 K and 900 K for OH ν′ = 0 and 1, respectively from squalane, and correspondingly 1300 K and 1200 K for squalene.
Interestingly, these temperatures vary proportionately less between liquids, and between vibrational levels, than the average rotational energies (see Table 2). They can be converted trivially to average energies in translation (through 〈E〉 = 3/2 kT), and are included in Table 3. The fraction of energy appearing in translation of OH ν′ = 0 for squalene is only around half that of squalane. A significant fraction of the additional energy available in the more exothermic reaction with squalene is therefore inferred to be deposited in the liquid surface. This could in principle reflect different physical properties, with the additional energy taken up in cooperative motion of the squalene surface. However, a more likely explanation is differences in the internal excitation of the radical co-product. This has been proposed in previous related gas-phase studies,46,47 and is consistent with the “vertical” abstraction mechanism proposed by Liu et al.68 The allylic radical fragment is resonance stabilised and undergoes a considerable geometry change on its formation from an unsaturated hydrocarbon such as squalene. In a sudden picture, this will result in vibrational excitation. In saturated hydrocarbons such as squalane the geometry of the radical fragment is more similar to that of the parent alkane, and is therefore expected to be produced with lower internal energy,46,47 consistent with our observations here.
It is clear from much of the discussion so far that the majority of our observations are consistent with a direct ‘IS’ reaction mechanism. What evidence is there of any TD-like collisional accommodation of OH at the liquid surface? The measured appearance profiles in Fig. 5 obviously extend to delays that overlap the simulated 300 K profile, so it would be possible in principle to fit the observed profile to a sum of the 300 K TD simulation and an IS component. However, in the absence of any independent measurement of the translational energy distribution of the IS component there is no clear justification for such a division into two discrete mechanisms.
However, the observed features of the profiles for different rotational levels do contain important mechanistic clues. For OH ν′ = 0 from squalane, there is a clear systematic progression towards an earlier peak for the higher rotational levels. This positive correlation between OH rotation and translation is also observed for squalene. It is consistent with at least partial collisional accommodation of some fraction of initially hotter-than-thermal nascent products, resulting in slower, rotationally relaxed molecules. It is the opposite effect to that of a total energy constraint, which is clearly present in the overall less rotationally excited and somewhat slower OH ν′ = 1 produced from both liquids, again more noticeably from squalane. We note also (see below) that the nascent OH ν′ = 1 from squalane is rotationally colder than thermal, consistent with observations in the gas phase.66 A combination of rotational warming and translational cooling in secondary collisions would also be consistent with the observations. Such subtle distinctions are interesting but clearly beyond what could be distinguished on the basis of the current limited translational energy resolution. For squalene, the ν′ = 1 profiles are also too similar to attempt to infer any significant trends.
The complementary LIF excitation measurements of rotational distributions at different points in the profiles in Fig. 7 confirm these correlations between OH rotation and translation. Moreover, there is bimodality in the distributions, as shown in Fig. 9. This is most pronounced in the more extended distribution in ν′ = 0 from squalene, but is also present for ν′ = 1 from squalene and ν′ = 0 from squalane. As noted above, the ν′ = 1 distribution from squalane fits to a single rotational temperature that is slightly sub-thermal, but gets slightly warmer at later points in the appearance profile. Otherwise, the lower of the temperatures, T1, in unconstrained two-temperature fits is quite close to thermal (see Table 1).
Such clear bimodality has not been identified in the rotational distributions in the corresponding gas-phase O(3P) reactions.37 We reiterate that we don't think it is the result of the relatively modest differences between the two types of reactive site that contribute significantly for each liquid (differences of 7 and 13 kJ mol−1 out of total energies of order 45 and 100 kJ mol−1, respectively, for squalane and squalene – see Table 3). However, it is a feature of the related, more strongly exothermic gas–liquid interfacial reactions of F and O(1D) with squalane.17,20 It has naturally been suggested that the rotationally colder components be associated with a TD mechanism. We agree that TD-like secondary accommodation is the most likely explanation. However, we caution against a literal interpretation of the weighting parameter, α, as a quantitative measure of the branching fraction between binary IS and TD mechanisms, at least in our experiments. The expected qualitative trend towards larger values of α at longer delays is indeed observed, but as we have noted above, the parameters are quite strongly correlated, particularly α and T2. The coupling is worse when the values of T1 and T2 are more similar, which is the case for the less exothermic reaction with squalane. Furthermore, inspection of Fig. 5 suggests that a limiting 300 K TD component should contribute little to rotational distributions measured at earlier delays, yet the fits yield significant values of α even at the rising edges of the profiles. This may again be related to the limited translational-energy resolution in our experiments, but more fundamentally may reflect a spectrum of collision types between the limiting IS and TD pictures, as has been suggested in some theoretical studies.9–12
Conclusions
We have shown that the presence of unsaturation in a liquid hydrocarbon has an important impact on the dynamics of the interfacial H-abstraction reaction with O(3P). The competition between the enhancement of H abstraction (due to the allylic character of the bonds) and the loss of O(3P) (due to addition at unsaturated sites) with squalene is reflected in the relative OH yield with respect to squalane. The measured ratio, 0.29 ± 0.03, shows that the additional loss channel dominates this balance. It also confirms that a significant fraction of the squalene surface must consist of exposed double bonds. Reaction at the allylic sites in squalene produces OH that is both rotationally and vibrationally hotter than from squalane. However, less of the extra energy available is partitioned to OH translation, with the balance taken up in the surface. This is consistent with the larger geometric rearrangement on formation of the allylic radical co-product, compared to that on formation of the alkyl radical. Most of the evidence points to a predominantly direct, impulsive scattering mechanism of OH formation. However, bimodal rotational distributions and positively correlated translational and rotational energies are consistent with some secondary accommodation of OH at the liquid surface.Acknowledgements
This work was supported by a research grant from the EPSRC, and MT-S thanks Heriot-Watt University for the award of a James-Watt PhD Scholarship.Notes and references
- M. E. Saecker, S. T. Govoni, D. V. Kowalski, M. E. King and G. M. Nathanson, Science, 1991, 252, 1421–1424 CAS
.
- M. E. Saecker and G. M. Nathanson, J. Chem. Phys., 1993, 99, 7056–7075 CrossRef CAS
.
- M. E. King, G. M. Nathanson, M. A. Hanninglee and T. K. Minton, Phys. Rev. Lett., 1993, 70, 1026–1029 CrossRef CAS
.
- M. E. Saecker and G. M. Nathanson, J. Chem. Phys., 1994, 100, 3999–4005 CrossRef CAS
.
- B. G. Perkins, T. Haber and D. J. Nesbitt, J. Phys. Chem. B, 2005, 109, 16396–16405 CrossRef CAS PubMed
.
- B. G. Perkins, Jr. and D. J. Nesbitt, J. Phys. Chem. B, 2006, 110, 17126–17137 CrossRef PubMed
.
- B. G. Perkins, Jr. and D. J. Nesbitt, J. Phys. Chem. A, 2007, 111, 7420–7430 CrossRef PubMed
.
- B. G. Perkins, Jr. and D. J. Nesbitt, J. Phys. Chem. B, 2008, 112, 507–519 CrossRef PubMed
.
- U. S. Tasić, T. Yan and W. L. Hase, J. Phys. Chem. B, 2006, 110, 11863–11877 CrossRef PubMed
.
- E. Martinez-Nunez, A. Rahaman and W. L. Hase, J. Phys. Chem. C, 2007, 111, 354–364 CAS
.
- D. Troya and G. C. Schatz, J. Chem. Phys., 2004, 120, 7696–7707 CrossRef CAS PubMed
.
- D. Kim and G. C. Schatz, J. Phys. Chem. A, 2007, 111, 5019–5031 CrossRef CAS PubMed
.
- J. W. Lu, B. S. Day, L. R. Fiegland, E. D. Davis, W. A. Alexander, D. Troya and J. R. Morris, Prog. Surf. Sci., 2012, 87, 221–252 CrossRef CAS PubMed
.
- A. H. Muenter, J. L. DeZwaan and G. M. Nathanson, J. Phys. Chem. B, 2006, 110, 4881–4891 CrossRef CAS PubMed
.
- A. H. Muenter, J. L. DeZwaan and G. M. Nathanson, J. Phys. Chem. C, 2007, 111, 15043–15052 CAS
.
- P. Behr, J. R. Morris, M. D. Antman, B. R. Ringeisen, J. R. Splan and G. M. Nathanson, Geophys. Res. Lett., 2001, 28, 1961–1964 CrossRef CAS
.
- A. M. Zolot, W. W. Harper, B. G. Perkins, P. J. Dagdigian and D. J. Nesbitt, J. Chem. Phys., 2006, 125, 021101 CrossRef PubMed
.
- A. M. Zolot, P. J. Dagdigian and D. J. Nesbitt, J. Chem. Phys., 2008, 129, 194705 CrossRef PubMed
.
- D. J. Garton, T. K. Minton, M. Alagia, N. Balucani, P. Casavecchia and G. G. Volpi, J. Chem. Phys., 2000, 112, 5975–5984 CrossRef CAS
.
- C. Waring, K. L. King, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2011, 115, 7210–7219 CrossRef CAS PubMed
.
- D. J. Garton, T. K. Minton, M. Alagia, N. Balucani, P. Casavecchia and G. G. Volpi, Faraday Discuss., 1997, 108, 387–399 RSC
.
- J. M. Zhang, D. J. Garton and T. K. Minton, J. Chem. Phys., 2002, 117, 6239–6251 CrossRef CAS
.
- J. M. Zhang, H. P. Upadhyaya, A. L. Brunsvold and T. K. Minton, J. Phys. Chem. B, 2006, 110, 12500–12511 CrossRef CAS PubMed
.
- H. Kelso, S. P. K. Köhler, D. A. Henderson and K. G. McKendrick, J. Chem. Phys., 2003, 119, 9985–9988 CrossRef CAS
.
- S. P. K. Köhler, M. Allan, H. Kelso, D. A. Henderson and K. G. McKendrick, J. Chem. Phys., 2005, 122, 024712 CrossRef PubMed
.
- S. P. K. Köhler, M. Allan, M. L. Costen and K. G. McKendrick, J. Phys. Chem. B, 2006, 110, 2771–2776 CrossRef PubMed
.
- S. P. K. Köhler, S. K. Reed, R. E. Westacott and K. G. McKendrick, J. Phys. Chem. B, 2006, 110, 11717–11724 CrossRef PubMed
.
- M. Allan, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, J. Phys. Chem. C, 2007, 111, 14833–14842 CAS
.
- M. Allan, P. A. J. Bagot, S. P. K. Köhler, S. K. Reed, R. E. Westacott, M. L. Costen and K. G. McKendrick, Phys. Scr., 2007, 76, C42–C47 CrossRef CAS
.
- M. Allan, P. A. J. Bagot, R. E. Westacott, M. L. Costen and K. G. McKendrick, J. Phys. Chem. C, 2008, 112, 1524–1532 CAS
.
- C. Waring, P. A. J. Bagot, M. W. P. Bebbington, M. T. Räisänen, M. Buck, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2010, 1, 1917–1921 CrossRef CAS
.
- C. Waring, P. A. J. Bagot, M. T. Räisänen, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2009, 113, 4320–4329 CrossRef CAS PubMed
.
- C. Waring, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2011, 2, 12–18 CrossRef CAS
.
- C. Waring, P. A. J. Bagot, J. M. Slattery, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2010, 1, 429–433 CrossRef CAS
.
- C. Waring, P. A. J. Bagot, J. M. Slattery, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2010, 114, 4896–4904 CrossRef CAS PubMed
.
-
D. R. Lide, CRC Handbook of Chemistry and Physics 2004–2005: A Ready-Reference Book of Chemical and Physical Data, CRC PressI LLC, 2004 Search PubMed
.
- F. Ausfelder and K. G. McKendrick, Prog. React. Kinet. Mech., 2000, 25, 299–370 CrossRef CAS
.
-
R. J. Cvetanović, Advances in Photochemistry, John Wiley & Sons, Inc., 1963, pp. 115–182 Search PubMed
.
- R. Atkinson and R. J. Cvetanovic, J. Chem. Phys., 1972, 56, 432–437 CrossRef CAS
.
- J. R. Kanofsky and D. Gutman, Chem. Phys. Lett., 1972, 15, 236–239 CrossRef CAS
.
- J. L. Gardner and S. M. Miller, J. Chem. Phys., 2004, 121, 5920–5928 CrossRef CAS PubMed
.
- A. M. Schmoltner, P. M. Chu, R. J. Brudzynski and Y. T. Lee, J. Chem. Phys., 1989, 91, 6926–6936 CrossRef CAS
.
- P. Casavecchia, G. Capozza, E. Segoloni, F. Leonori, N. Balucani and G. G. Volpi, J. Phys. Chem. A, 2005, 109, 3527–3530 CrossRef CAS PubMed
.
- B. Fu, Y.-C. Han, J. M. Bowman, F. Leonori, N. Balucani, L. Angelucci, A. Occhiogrosso, R. Petrucci and P. Casavecchia, J. Chem. Phys., 2012, 137, 22A532 CrossRef PubMed
.
- S.-H. Lee, W.-K. Chen and W.-J. Huang, J. Chem. Phys., 2009, 130, 054301 CrossRef PubMed
.
- K. Kleinermanns and A. C. Luntz, J. Chem. Phys., 1982, 77, 3533–3536 CrossRef CAS
.
- N. J. Dutton, I. W. Fletcher and J. C. Whitehead, Mol. Phys., 1984, 52, 475–483 CrossRef CAS
.
- R. J. Cvetanovic, D. F. Ring and L. C. Doyle, J. Phys. Chem., 1971, 75, 3056–3061 CrossRef CAS
.
- J. R. Kanofsky, D. Lucas and D. Gutman, Symp. (Int.) Combust., [Proc.], 1973, 14, 285–294 CrossRef
.
- B. Blumenberg, K. Hoyermann and R. Sievert, Symp. (Int.) Combust., [Proc.], 1977, 16, 841–852 CrossRef
.
- K. Kleinermanns and A. C. Luntz, J. Phys. Chem., 1981, 85, 1966–1968 CrossRef CAS
.
- S. Koda, Y. Endo, S. Tsuchiya and E. Hirota, J. Phys. Chem., 1991, 95, 1241–1244 CrossRef CAS
.
- J. D. Savee, O. Welz, C. A. Taatjes and D. L. Osborn, Phys. Chem. Chem. Phys., 2012, 14, 10410–10423 RSC
.
- R. Quandt, Z. Min, X. Wang and R. Bersohn, J. Phys. Chem. A, 1998, 102, 60–64 CrossRef CAS
.
- Z. Y. Min, T. H. Wong, H. M. Su and R. Bersohn, J. Phys. Chem. A, 2000, 104, 9941–9943 CrossRef CAS
.
- G. Y. Adusei and A. Fontijn, J. Phys. Chem., 1994, 98, 3732–3739 CrossRef CAS
.
- K. D. Gibson and S. J. Sibener, Surf. Sci., 2006, 600, L76–L79 CrossRef CAS PubMed
.
- C. Waring, K. L. King, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, Phys. Chem. Chem. Phys., 2011, 13, 8457–8469 RSC
.
- K. L. King, G. Paterson, G. E. Rossi, M. Iljina, R. E. Westacott, M. L. Costen and K. G. McKendrick, Phys. Chem. Chem. Phys., 2013, 15, 12852–12863 RSC
.
- R. P. Baker, M. L. Costen, G. Hancock, G. A. D. Ritchie and D. Summerfield, Phys. Chem. Chem. Phys., 2000, 2, 661–664 RSC
.
- K. A. Ramazan, D. Syomin and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2004, 6, 3836–3843 RSC
.
- R. Vasudev, R. N. Zare and R. N. Dixon, J. Chem. Phys., 1984, 80, 4863–4878 CrossRef CAS
.
- J. Luque and D. R. Crosley, SRI International, version 1.5 edn, 1999, pp. Report MP 99-009.
- C. C. Miller, R. D. van Zee and J. C. Stephenson, J. Chem. Phys., 2001, 114, 1214–1232 CrossRef CAS
.
- R. E. Huie, J. T. Herron and D. D. Davis, J. Phys. Chem., 1972, 76, 3311–3313 CrossRef CAS
.
- P. Andresen and A. C. Luntz, J. Chem. Phys., 1980, 72, 5842–5850 CrossRef CAS
.
- A. C. Luntz and P. Andresen, J. Chem. Phys., 1980, 72, 5851–5856 CrossRef CAS
.
- X. H. Liu, R. L. Gross, G. E. Hall, J. T. Muckerman and A. G. Suits, J. Chem. Phys., 2002, 117, 7947–7959 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp54107j |
| This journal is © the Owner Societies 2014 |