Predicted organic compounds derived from rare gas atoms and formic acid

Abstract

Organic insertion compounds of rare gas atoms into formic acid were investigated at the MP2(full)/aug-cc-pVTZ level. There are two configuration isomers for each molecule based on the location of H atoms: trans- and cis-HCOORgH (Rg = Ar, Kr, Xe). Their structures, harmonic frequencies, and decomposition energies have been calculated using the above ab initio method. Using trans-HCOOXeH as an example, natural bond orbital (NBO) and atom-in-molecules (AIM) analyses were also carried out to explore the binding nature of the rare gas atoms. The formation mechanism of molecular orbitals is also presented in this paper. The presented results indicate that HCOOXeH and HCOOKrH are potential candidates for experimental observation.

---

1. Introduction

Since the discovery of rare gas (Rg) atoms in the late 19th century, the Group VIII elements have attracted much attention because of their high chemical inertness. As a result, one major challenge in rare gas chemistry is whether these atoms can be activated to form a compound. In 1962, Barlett discovered the first rare gas compound xenon hexafluoroplatinate.¹ The further study pointed out that this compound is quite complex,² with a formula of Xe(PtF₆)_n (1 ≤ n ≤ 2). To date, hundreds of compounds containing Rg atoms have been reported both experimentally and theoretically.^3–8 Rare gas chemistry is currently ascendant, stimulated by the recent discovery of unprecedented compounds and bonding motifs.^9–18

One major advancement in this area is the recent fascinating finding of rare gas hydrides, pioneered by Räsänen's group.¹⁹ These compounds, namely, HRgY, where Y refers to an electronegative atom or group, are generally prepared at very low temperatures by the UV photolysis of suitable HY precursors in an Rg matrix. Although ab initio studies have shown that rare gas hydrides are metastable compared with the global minimum of HY + Rg,^20,21 an increasing number of HRgY molecules have been observed in matrix isolation experiments,²² with the recent additions of HXeOXeH,²³ HRgCCF (Rg = Kr, Xe),²⁴ HXeOBr²⁵ and HRgC₅N (Rg = Kr, Xe).²⁶ Quantum chemistry plays an important role in predicting new rare gas hydrides and their properties. In particular, the first chemically bonded argon compound, HArF²⁷ synthesized in 2000, was identified by comparing its vibrational spectrum with those obtained from quantum chemical calculations. At present, a number of theoretical studies have been devoted to understanding the properties of HRgY molecules, including their electronic structures, nature of bonding, spectroscopic properties, and reaction mechanisms.^28–38 Theoretical analysis has shown that the HRgY stabilization may be derived from the strong coulomb attraction between the (HRg)⁺ and Y⁻ fragments, where H–Rg and Rg–Y bonds are dominated by covalent and electrostatic interactions, respectively.^21,22,25

As an extension of the organic rare-gas hydrides family, several insertion compounds of Xe into alkynes, such as HXeCCH and HXeCCXeH, were firstly predicted by ab initio calculations³⁹ and successfully synthesized soon afterwards.^40,41 Slightly later, HKrCCH,⁴² HXeC₄H, and HKrC₄H⁴³ were also prepared in succession. The existence of organic Rg compounds has strongly stimulated theoretical studies predicting that a series of related molecules and their derivatives, including HRnCCH,^44,45 HCCXeCCH and HCCKrCCH,⁴⁶ HArC₄H,⁴⁷ HArC₆N,⁴⁸ FRgCCH,^49,50 HRgCCCN (Rg = Kr, Xe),⁵¹ HRgYRgH⁺ (Y = H, F; Rg = Ar, Kr, Xe)^52,53 and HRgC₅N (Rg = Kr, Xe)²⁶ should be stable based on DFT or ab initio calculations. Among them, FRgCCH, HRgCCCN (Ng = Kr, Xe) and HRgC₅N (Rg = Kr, Xe) have been observed in low-temperature Rg matrices.^24,26,51 This development introduces a very interesting class of organic rare gas compounds with considerable promise for future extensions. Formic acid is a valuable molecule from a physical, chemical, and biological aspect. Due to the fact that it is the simplest of the carboxylic acids, there are many fundamental studies in both theory and experiment.^54,55 The trans and cis configurations of formic acid have been studied and the trans-HCOOH is more stable. In this paper, we present an ab initio study of organic Rg-insertion compounds, i.e., HCOORgH (Rg = Ar, Kr, Xe).

2. Computational method

The equilibrium structures of HCOORgH (Rg = Ar, Kr, Xe) and their harmonic vibrational frequencies were calculated at the MP2(full) level. The standard Dunning's correlation consistent all-electron basis set aug-cc-pVTZ was used for H, C, O, Ar, and Kr atoms. The combination of the relativistic effective core pseudopotentials aug-cc-pVTZ-PP together with the corresponding triple zeta valence basis set was employed to describe the xenon atom. For simplicity, the basis set used in this paper is denoted as AVTZ. The transition states (TS) for two- and three-body decomposition reactions were also located at the MP2(full)/AVTZ level. Intrinsic reaction coordinate (IRC) calculations were therefore carried out to ensure that the TS connect the appropriate local minima. The relative energies were corrected by the CCSD(T)/AVTZ method. The vibrational zero-point energy (ZPE) was also considered in the energetics calculations. The Gaussian 03⁵⁶ electronic structure package was used for all ab initio calculations. Natural bond orbital (NBO) analysis was performed using the NBO 5.9 program.⁵⁷ The topological properties of the predicted molecules have also been investigated using the atoms-in-molecules (AIM)⁵⁸ approach.

3. Results and discussion

3.1. Structures and frequencies

Fig. 1 shows the MP2(full)/AVTZ optimized structures of HCOORgH (Rg = Ar, Kr, Xe), which feature two geometrical isomers, i.e., trans- and cis-forms, according to the location of the H atoms. The trans-HCOORgH is more stable than cis-HCOORgH; the stability energies are 9.05, 8.31, and 8.13 kcal mol⁻¹ for Rg = Ar, Kr, and Xe, respectively, as presented in Table 1. This result is consistent with the finding that the trans-formic acid is more stable than cis-form by approximately 4.02 kcal mol⁻¹ at the same MP2(full)/AVTZ level. Our study mainly focuses on the trans-HCOORgH molecules (Rg = Ar, Kr, Xe). The bond lengths of H–Xe and Xe–O in trans-HCOOXeH are 1.651 and 2.307 Å, respectively, which are similar to the corresponding values (1.666 and 2.322 Å) given by MP2 calculations.⁵⁹ In 2005, G. M. Chaban investigated the similar insertion compounds of Rg atoms (Rg = Ar, Kr, Xe) into the O–H bond of glycine using ab initio methods,⁶⁰i.e. NH₂CH₂COORgH (Rg = Ar, Kr, Xe), where the H–Rg lengths are 1.334, 1.489 and 1.669 Å, and the O–Rg lengths are 2.195, 2.224 and 2.310 Å for Ar, Kr, and Xe, respectively. Compared to (Rg = Ar, Kr, Xe), the Rg compounds derived from formic acid have shorter H–Rg and O–Rg distances. Generally, in trans-HCOORgH (Rg = Ar, Kr, Xe), the H–Rg bond lengths were predicted to be sensitive to the Rg atom size; the bond lengths are 1.315, 1.464, and 1.651 Å for Rg = Ar, Kr, and Xe, respectively, exhibiting an obvious increasing trend. However, the O–Rg bond lengths are less sensitive to the Rg atom size, increasing only approximately 0.1 Å from Rg = Ar to Xe. The slight difference between the O–Ar and O–Xe distances implies that the bonding between O and Ar is weak because the Ar atom has a shorter atomic radius than the Xe atom.

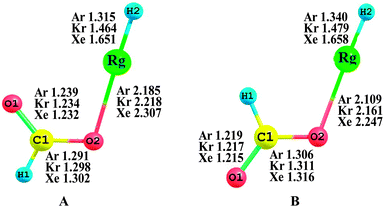Fig. 1 Equilibrium geometries of trans-HCOORgH (A) and cis-HCOORgH (B) (Rg = Ar, Kr, Xe) at the MP2(full)/AVTZ level. The bond lengths and angles are in angstroms and degrees, respectively.

Table 1 Primary frequencies (cm⁻¹) and intensities (km mol⁻¹) of the H–Rg and Rg–O bonds for HCOORgH (Rg = Ar, Kr, Xe) and relative energies (E_RE = E_cis-HCOORgH − E_{trans-HCOORgH}, in kcal mol⁻¹) at the MP2(full)/AVTZ level

Compound	Stretching mode		Intensity		E RE
	Rg–H	Rg–O	Rg–H	Rg–O
trans-HCOOArH	2307.96	333.88	1073.72	201.01	—
cis-HCOOArH	2062.90	349.09	1696.96	232.65	9.05
trans-HCOOKrH	2158.30	334.09	868.15	152.20	—
cis-HCOOKrH	2055.89	327.20	968.32	147.13	8.31
trans-HCOOXeH	2049.48	327.35	567.04	124.79	—
cis-HCOOXeH	2015.53	312.38	512.03	123.77	8.13

---

The MP2(full)/AVTZ calculated frequencies for the six HCOORgH (Rg = Ar, Kr, Xe) molecules, including the trans- and cis-structures, are all positive, confirming that these structures correspond to the local minima of their corresponding potential energy surfaces. Table 1 shows the primary frequencies and their intensities, i.e., the H–Rg and Rg–O stretching modes. In trans-HCOOXeH, the frequencies of H–Xe and Xe–O bonds are 2049.48 and 327.35 cm⁻¹, respectively, and the intensities are 567.04 and 124.79 km mol⁻¹, respectively. Similarly, the stretching modes of H–Kr (H–Ar) and O–Kr (O–Ar) were calculated as 2158.30 (2307.96) and 334.09 (333.88) cm⁻¹, respectively, with intensities of 868.15 (1073.72) and 152.20 (201.01) km mol⁻¹, respectively. These values represent fairly stiff frequencies, corresponding to chemically bound molecules rather than weakly interacting van der Waals complexes. Due to its strong infrared intensity, the H–Rg stretching mode may serve as an experimental fingerprint for identifying these compounds. Interestingly, Olbert-Majkut et al.⁶¹ and Lundell et al.⁶² have systematically studied the photochemistry of formic acid and observed the quite complicated spectra upon photolysis of HCOOH in Ar, Kr, and Xe matrices, respectively. Several distinct bands measured around 2100 cm⁻¹ are assigned to the stretching modes of complexes of H₂O and CO. The photolysis of deuterated HCOOH in rare gas matrices was also observed in the previous experiments.⁶² However, identifying the predicted rare gas compounds in this paper is still challenging and further observations would be helpful. In addition, we also calculated the frequencies of deuterated rare gas compounds of trans-HCOORgD (Rg = Kr and Xe). The detailed information is in the ESI.† In particular, the stretching modes of Kr–D and Xe–D are 1500.7 and 1445.0 cm⁻¹, respectively.

3.2. Decomposition reaction barriers

The barriers against different decomposition channels, e.g., “two-body” and “three-body” decompositions, are very important for the stability of the rare gas hydrides. Consequently, the two decomposition pathways for the predicted species are calculated at the MP2(full)/AVTZ level. Fig. 2 presents the geometric structures of the transition states in the dissociation reactions. All transition states (TS) were confirmed by only one imaginary frequency and intrinsic reaction coordinate (IRC) calculations. The MP2-calculated frequencies of the HCOORgH (Rg = Ar, Kr, Xe) and TS are provided in detail as ESI.†⁶³Fig. 3 presents the potential energy profiles for the two decomposition reaction pathways for trans-HCOORgH (Fig. 3a) and cis-HCOORgH (Fig. 3b). As shown in Fig. 3a, trans-HCOORgH are higher in energy than the global minimum of trans-HCOOH and Rg atom by approximately 126.08, 106.60, and 84.35 kcal mol⁻¹ for Rg = Ar, Kr, and Xe, respectively. However, these molecules are protected from “two-body” decay by a high barrier, reaching 21.69 kcal mol⁻¹ for xenon species and 13.59 and 5.96 kcal mol⁻¹ for the Kr and Ar compounds, respectively. Like other experimentally observed rare gas hydrides, the currently predicted molecules are also metastable species. With respect to the “three-body” dissociation channels (A → C), the energy barriers are even higher than those of “two-body” decomposition, with values of 44.16, 23.79, and 10.42 kcal mol⁻¹ for Rg = Xe, Kr, and Ar, respectively. However, our MP2(full)/AVTZ calculations show that trans-HCOOArH lies well above the HCOO + Ar + H “three-body” products by approximately 8.97 kcal mol⁻¹, which is corrected as 6.77 kcal mol⁻¹ at the CCSD(T)/AVTZ level (using the MP2 optimized geometries). The experimental and theoretical studies show that when the “three-body” pathway is highly exothermic, the HNgY molecule does not seem to exist,²² possibly because its formation from the three fragments by annealing is unfavorable under these conditions. Compared to their “three-body” products, i.e., HCOO + Rg+ H, the trans-HCOOXeH and trans-HCOOKrH molecules are energetically stable by approximately 32.76 and 10.51 kcal mol⁻¹, respectively, which become 34.89 and 12.52 kcal mol⁻¹ at the CCSD(T)/AVTZ level (using the MP2 optimized geometries). Thus, the generation of trans-HCOORgH (Rg = Xe, Kr) from the three fragments is thermodynamically preferred. There are also two decomposition pathways for each cis-HCOORgH (Rg = Ar, Kr, Xe) molecule, and similar results are obtained from Fig. 3b. However, the HCOO radical is a highly reactive species, the three fragments undergo further reactions to yield the Rg, H₂, and CO₂ final products. At the MP2(full)/AVTZ level, the decomposition barriers are 6.55, 7.27, and 7.96 kcal mol⁻¹ for Rg = Xe, Kr, and Ar, respectively. The final products (H₂, and CO₂) of HCOORgH (Rg = Xe, Kr) decomposition are in agreement with the observation results of J. Lundell and M. Räsänen. In their experiments,⁶² the H₂ and CO₂ products were detected upon the photolysis of HCOOH in Xe, Kr, and Ar. In particular, the H₂ and CO₂ were the dominant products in a xenon matrix. There are also two decomposition pathways for each cis-HCOORgH (Rg = Ar, Kr, Xe) molecule, and similar results are obtained from Fig. 3b. The cis-HCOOH first are activated by a rare atom, via TS3, to form the cis-HCOORgH. Through TS4, the cis-HCOORgH decomposed to the three fragments (HCOO + Rg + H).

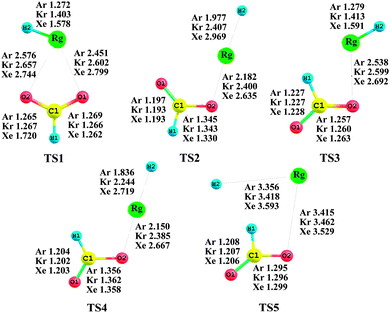Fig. 2 Equilibrium geometries of transition states for the dissociation reaction pathways at the MP2(full)/AVTZ level. The bond lengths and angles are in angstroms and degrees, respectively.

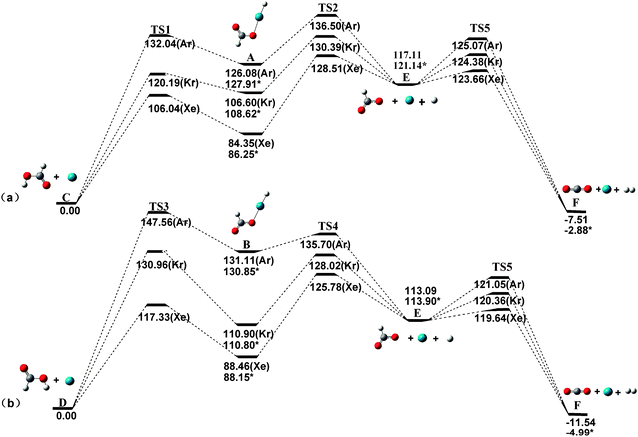Fig. 3 Dissociation reaction pathways of trans-HCOORgH (a) and cis-HCOORgH (b) (Rg = Ar, Kr, Xe) at the MP2(full)/AVTZ level (kcal mol⁻¹). The CCSD(T)/AVTZ energy corrections are marked by asterisks.

It is well known that the stability of the HCOORgH compounds with respect to the three-body dissociation channel (HCOO + Rg + H) is very important, such study poses particular challenges to theoretical study because it requires more reliable multi-configurational techniques. At present, the ab initio calculations like CASPT2 and MRCI are definitely beyond our computing power capabilities. As mentioned in a previous study,⁶⁴ however, the DFT method often gives better estimates for the HY bond energy than MP2. As is widely used to predict rare gas compounds,^23,26,30,53 the B3LYP method^65,66 was used to calculate the relative energies of three-body decomposition. These B3LYP results showed similar trends to the MP2 results, as listed in Table 2.

Table 2 The relative energies (in kcal mol⁻¹) of HCOORgH → HCOO + Rg + H

Compound	MP2/AVTZ	CCSD(T)^a/AVTZ	B3LYP/AVTZ
a Using the MP2 optimized geometries.
trans-HCOOArH	8.97	6.77	6.98
cis-HCOOArH	18.02	16.95	15.18
trans-HCOOKrH	−10.51	−12.52	−8.77
cis-HCOOKrH	−2.19	−3.10	−0.89
trans-HCOOXeH	−32.76	−34.89	−27.38
cis-HCOOXeH	−24.63	−25.75	−19.71

---

3.3. NBO analysis

Our NBO analysis was performed at the HF/AVTZ level for trans-HCOORgH (Rg = Ar, Kr, Xe). The NBO partial atomic charges are summarized in Table 3. In trans-HCOORgH, each rare gas atom has a positive charge (Q_Rg), which is 0.57, 0.70, and 0.86 for Rg = Ar, Kr, and Xe, respectively. The oxygen atom adjacent to the Rg atoms becomes more negative than that of formic acid, and the Q_O values are −0.93, −0.93, and −0.95 in the trans-HCOORgH species for Rg = Ar, Kr, and Xe, respectively. Correspondingly, the H–Rg groups of trans-HCOORgH have positive partial charges of 0.90, 0.87, and 0.87 for Rg = Ar, Kr, and Xe, respectively. Generally, the charge distribution in cis-HCOORgH is almost same as that in trans-HCOORgH. The NBO charge distribution suggests that these species may be described as (HCOO)⁻(RgH)⁺, which is also consistent with the general characteristics of the previously prepared HNgY compounds. In particular, the first rare gas compound, Xe(PtF₆)_n (1 ≤ n ≤ 2), was also suggested as a XeF⁺ salt of polymeric (PtF₅⁻)_n.

Table 3 NBO charge (Q) of HCOORgH (Rg = Ar, Kr, Xe) at the HF/AVTZ level

Compound	Q (Rg)	Q (O2)	Q (H2)
trans-HCOOArH	0.57	−0.93	0.33
cis-HCOOArH	0.56	−0.93	0.30
trans-HCOOKrH	0.70	−0.93	0.17
cis-HCOOKrH	0.70	−0.94	0.15
trans-HCOOXeH	0.86	−0.95	0.01
cis-HCOOXeH	0.86	−0.97	0.01

---

The NBO analysis confirmed that in HCOORgH molecules, H–Rg and Rg–O bonds are dominated by covalent and electrostatic interactions, respectively. Table 4 lists the orbital occupancy and hybrid composition of the H–Rg bond for trans-HCOORgH (Rg = Ar, Kr, Xe). The H–Rg bond orbital occupancy is 1.99, which is almost full, suggesting that the H–Rg interaction is a typical covalent bond. The NBO bond orbital (H_H–Rg) can be written in terms of two directed valence hybrids, h_H and h_Rg, on the bond centers H and Rg, respectively. That is, H_H–Rg = c_Hh_H + c_Rgh_Rg. The coefficients c_H and c_Rg vary from the covalent (c_H = c_Rg) to ionic limit (c_H ≫ c_Rg or c_Rg ≫ c_H). Using trans-HCOOXeH as an example, the bonding (BD) orbital can be expressed as H_H–Xe = 0.6805h_H + 0.7327h_Xe. The coefficients c_H (0.6805) and c_Xe (0.7327) of the H–Xe bond for trans-HCOOXeH are clearly close to the covalent criteria (c_H = c_Rg), which implies that the H–Xe bond is the covalent interaction. The NBO analysis further suggests that the H–Rg bond results from the overlap of the p orbital on Rg and the s orbital on the H atom.

Table 4 Occupancy and composition of the H–Rg bond orbital for trans-HCOORgH (Rg = Ar, Kr, Xe) at the HF/AVTZ level

Compound	Orbital occupancy	Composition
trans-HCOOArH	1.99	0.5483sH + 0.8363pAr
trans-HCOOKrH	1.99	0.6124sH + 0.7906pKr
trans-HCOOXeH	1.99	0.6805sH + 0.7327pXe

---

To understand the bonding nature of H–Rg and Rg–O more clearly, we used natural resonance theory (NRT)⁶⁷ to analyze the total bond order and the covalent and electrovalent (i.e., ionic) contributions, as listed in Table 5. The results show that in trans-HCOOXeH, the total NRT bond order of H–Rg is 0.9319 (H–Xe), 0.9379 (H–Kr), and 0.9524 (H–Ar), which correspond to a formal chemical bond. Its covalent character is approximately 92.63% based on the covalent (0.8632) and ionic (0.0687) components. Similarly, the covalent character of H–Kr and H–Ar bonds are 75.00% and 60.13% in trans-HCOOKrH and trans-HCOOArH, respectively. Their covalent character is obviously less than that of the H–Xe bond, but they are certainly covalent in nature.

Table 5 Total NRT bond order and covalent and electrovalent (i.e., ionic) contributions for trans-HCOORgH (Rg = Ar, Kr, Xe) at the HF/AVTZ level

Compound	H–Rg			Rg–O
	Total	Covalent	Ionic	Total	Covalent	Ionic
trans-HCOOArH	0.9524	0.5727	0.3797	0.0381	0.0008	0.0373
trans-HCOOKrH	0.9379	0.7034	0.2344	0.0530	0.0018	0.0512
trans-HCOOXeH	0.9319	0.8632	0.0687	0.0390	0.0018	0.0372

---

The NBO-calculated extra stabilization energies, i.e., the second-order perturbation energies (E₂), are presented in Table 6, where LP and σ* denote the lone pair and antibonding sigma, respectively. As observed, the E₂ value of LP(O2) → σ*(H–Xe) reaches 48.13 kcal mol⁻¹ (4.65 + 43.48 kcal mol⁻¹), which strongly enhances the stability of trans-HCOOXeH. The corresponding values are 42.17 and 27.43 kcal mol⁻¹ for trans-HCOOKrH and trans-HCOOArH, respectively. In a recent study of RgAuF (Rg = He, Ar, Kr, and Xe),⁶⁸ the authors suggested a new type of weak interaction, i.e., the lone pair (LP) of Rg interacting with the unoccupied valence Au–F antibond (LP(Rg) → σ*(Au–F)). As their E₂ values increased, the stability of RgAuF increases strongly in the order of He, Ar, Kr, Xe. In our studied HCOORgH system, the LP donor becomes the oxygen atom next to the Rg atom, and the acceptor is the unoccupied valence H–Rg antibond, i.e., LP(O2) → σ*(H–Rg), which play an important role in the existence of HCOORgH molecules.

Table 6 NBO-calculated stabilization energy (E₂, kcal mol⁻¹) of trans-HCOORgH (Rg = Ar, Kr, Xe) at the HF/AVTZ level

Compound	Donor	Acceptor	E 2
trans-HCOOArH	LP1(O2)	σ*(H–Ar)	2.32
	LP2(O2)	σ*(H–Ar)	25.11
trans-HCOOKrH	LP1(O2)	σ*(H–Kr)	3.52
	LP2(O2)	σ*(H–Kr)	38.65
trans-HCOOXeH	LP1(O2)	σ*(H–Xe)	4.65
	LP2(O2)	σ*(H–Xe)	43.48

---

3.4. Molecular orbital (MO) formation

There are two formation schemes for HRgY molecular orbitals. One is based the classical Pimentel–Rundle three-center model; Last and George⁶⁹ suggested that one electron transfers from the Rg atom to the Y group and forms the neutral Rg⁺Y⁻ subunit and that the unpaired electron in a p-type orbital of Rg⁺Y⁻ interacts with the s electron of the H atom. The other scheme is given by Merino et al.,^38,45 who suggested that the HRgY bonding results from Rg⁺ interacting with [H⋯Y]⁻, i.e., one p-electron transferred from Rg to HY before the bonding. Considering that HCOORgH (Rg = Ar, Kr, Xe) is a derivative of formic acid with high ionic character, we believe that their bonding orbital formation begins with the interaction between H⁺ and Xe. Using trans-HCOOXeH as an example, its MO formation is shown in Fig. 4. We can see that the hybridization between the empty 1s orbital of H⁺ and a filled 5p orbital of Xe (e.g., 5p_z) generated a sigma bonding and antibonding orbitals of the [HXe]⁺ group while the other two 5p orbitals of Xe (e.g., 5p_x and 5p_y) formed the two non-bonding orbitals of the [HXe]⁺ group. In the next step, the frontier orbitals of [HCOO]⁻ correspondingly interacted with the orbitals of [HXe]⁺ to form the MO of HCOOXeH. In particular, a lone pair of electrons in the p-orbital of the oxygen atom in HCOO⁻ back-donate into the σ*(H–Xe) orbital, which strongly increases the stability of the HCOOXeH molecule. A similar MO formation mechanism has also been found in the argon and krypton derivatives.

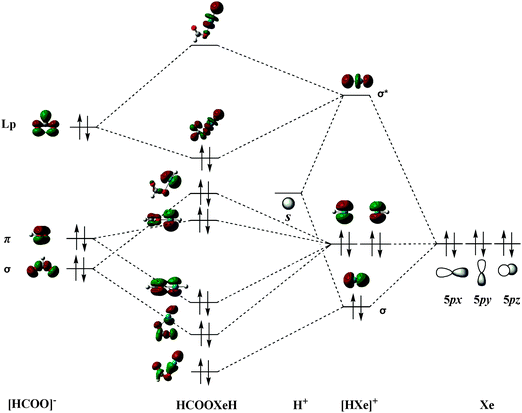Fig. 4 Formation of molecular orbitals for trans-HCOOXeH.

3.5. AIM analysis

The AIM approach given by Bader and co-workers⁵⁸ was also used to calculate the topological parameters and analyze the bonding nature of the constituent atoms in HCOORgH molecules. The AIM analysis and the wave functions for the calculations were extracted from the Gaussian calculations at MP2/AVTZ level. Table 7 lists the calculated values of the electron density (ρ), the Laplacian of the electron density (∇²ρ), and the total electronic energy density Ed(r) at the bond critical points (BCPs). Fig. 5 shows the contour line diagrams of the Laplacian distribution ∇²ρ of trans-HCOORgH (Rg = Ar, Kr, Xe). The shape of ∇²ρ indicates the nature of the bonding interaction: ∇²ρ < 0 corresponds to shared-type interactions, i.e., a covalent bond, whereas ∇²ρ > 0 corresponds to ionic, hydrogen bond, or van der Waals interactions. For the H–Rg bonds of the HCOORgH system, all the calculated ∇²ρ values are negative at different BCPs, suggesting that they are covalent interactions. This conclusion is consistent with NBO analysis, which showed a full occupancy and high covalent contribution of the H–Rg bond orbital. However, in the case of Rg–O bonding, the completely positive ∇²ρ values indicate that they are electrostatic interactions, which also coincides with the high NBO charge of the oxygen atom and [HRg] group and low electron occupancy of the Rg–O bond orbital. Another important AIM parameter is the total electronic energy density, defined as Ed(r) = G(r) + V(r), where G(r) and V(r) correspond to the gradient kinetic energy density and the potential energy density, respectively. The sign of Ed(r) determines whether accumulated charge at a given point (r) is stabilizing (Ed(r) < 0) or destabilizing (Ed(r) > 0). The Ed values at the BCPs are −0.021, −0.017, and −0.012 Ha/a₀³ for Xe–O, Kr–O, and Ar–O bonds, respectively, which, combined with the ∇²ρ values (0.149, 0.181, and 0.207 ea₀⁻⁶), indicate a slight partial covalent interaction, which may be attributed to the interaction LP(O2) → σ*(H–Xe), as shown in Fig. 4. As a result, the stability of the Rg–O bond is mostly due to the electrostatic interaction.

Table 7 Topological properties at bond critical points for HCOORgH (Rg = Ar, Kr, Xe) at the MP2(full)/AVTZ level

Bond	trans-HCOOArH			trans-HCOOKrH			trans-HCOOXeH
	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)
H–Rg	0.227	−0.716	−0.238	0.194	−0.453	−0.169	0.154	−0.216	−0.117
Rg–O2	0.070	0.207	−0.012	0.076	0.181	−0.017	0.075	0.149	−0.021

---

Bond	cis-HCOOArH			cis-HCOOKrH			cis-HCOOXeH
	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)	ρ (ea0^−3)	∇^2ρ (ea0^−6)	E d (a.u.)
H–Rg	0.216	−0.601	−0.210	0.188	−0.422	−0.160	0.152	−0.210	−0.114
Rg–O2	0.084	0.225	−0.019	0.086	0.189	−0.024	0.084	0.157	−0.028

---

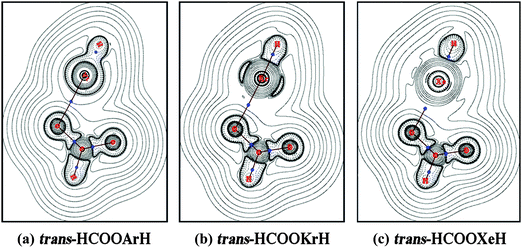Fig. 5 Contour line diagrams of ∇²ρ(r) for trans-HCOORgH. Dashed lines indicate areas of charge concentration (∇²ρ(r) < 0), while solid lines indicate areas of charge depletion (∇²ρ(r) > 0). The blue dots are BCPs.

4. Conclusion

In this paper, we have investigated the equilibrium structures, harmonic frequencies, and stabilities of HCOORgH (Rg = Ar, Kr, Xe) using the MP2(full)/aug-cc-pVTZ (aug-cc-pVTZ-PP) method. There are two structural isomers for each HCOORgH molecule, i.e., trans- and cis-configurations, based the position of the hydrogen atom. The ab initio calculations suggested that the compounds containing Kr and Xe are metastable and could be observed in matrix isolation experiments using the fingerprint of the H–Rg stretching mode. In contrast, the argon derivatives are rarely observed in experiments due to their thermodynamic instability relative to the three-body decomposition products. NBO and AIM analyses further confirmed that H–Rg bonds are definitively covalent interactions, and Rg–O bonding is mostly attributed to the electrostatic force as well as the electron delocalization of LP(O2) → σ*(H–Rg), which plays an important role in the Rg–O bonding and may be considered a new type of atomic interaction.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC, Grant No. 20903029), the Natural Scientific Research Innovation Foundation of the Harbin Institute of Technology (HIT.NSRIF 2011024), and the Scientific Research Foundation for the Returned Overseas Chinese Scholars (SRF for ROCS), State Education Ministry, China.

References

1. N. Bartlett, Proc. Chem. Soc., 1962, 218.
2. L. Graham, O. Graudejus, N. K. Jha and N. Bartlett, Coord. Chem. Rev., 2000, 197, 321.
3. J. H. Holloway and E. G. Hope, Adv. Inorg. Chem., 1998, 46, 51.
4. J. F. Lehmann, H. P. A. Mercier and G. J. Schrobilgen, Coord. Chem. Rev., 2002, 1, 233.
5. B. E. Pointner, R. J. Suontamo and G. J. Schrobilgen, Inorg. Chem., 2006, 45, 1517.
6. K. O. Christe, Angew. Chem., Int. Ed., 2001, 40, 1419.
7. W. Grochala, Chem. Soc. Rev., 2007, 36, 1632 , and references therein.
8. W. Grochala, L. Khriachtchev and M. Räsänen, Physics and Chemistry at Low Temperatures, Pan Stanford Publishing, 2011, ch. 13, pp. 419–446.
9. S. Seidel and K. Seppelt, Science, 2000, 290, 117.
10. P. Pyykkö, Science, 2000, 290, 64.
11. (a) G. Frenking, Nature, 2000, 406, 836; (b) C. Ó. C. Jiménez-Halla, I. Fernández and G. Frenking, Angew. Chem., Int. Ed., 2009, 48, 366; (c) L. A. Muck, A. Y. Timoshkin, M. v. Hopffgarten and G. Frenking, J. Am. Chem. Soc., 2009, 131, 3942; (d) R. Tonner, G. Frenking, M. Lein and P. Schwerdtfeger, ChemPhysChem, 2011, 12, 2081; (e) I. Fernández and G. Frenking, Phys. Chem. Chem. Phys., 2012, 14, 14869.
12. (a) J. Li, B. E. Bursten, B. Liang and L. Andrews, Science, 2002, 295, 2242; (b) L. Andrews, B. Liang, J. Li and B. E. Bursten, J. Am. Chem. Soc., 2003, 125, 3126; (c) B. Liang, L. Andrews, J. Li and B. E. Bursten, Inorg. Chem., 2004, 43, 882.
13. (a) C. J. Evans, D. J. Rubinoff and M. C. L. Gerry, Phys. Chem. Chem. Phys., 2000, 2, 3943; (b) S. A. Cooke and M. C. L. Gerry, Phys. Chem. Chem. Phys., 2004, 6, 3248; (c) J. M. Thomas, N. R. Walker, S. A. Cooke and M. C. L. Gerry, J. Am. Chem. Soc., 2004, 126, 1235; (d) J. M. Michaud and M. C. L. Gerry, J. Am. Chem. Soc., 2006, 128, 7613.
14. (a) J. Roithová and D. Schröder, Angew. Chem., Int. Ed., 2009, 48, 8788; (b) J. F. Lockyear, K. Douglas, S. D. Price, M. Karkowska, K. J. Fijalkowski, W. Grochala, M. Remeš, J. Roithová and D. Schröder, J. Phys. Chem. Lett., 2010, 1, 358.
15. (a) M. D. Moran, D. S. Brock, H. P. A. Mercier and G. J. Schrobilgen, J. Am. Chem. Soc., 2010, 132, 13823; (b) D. S. Brock and G. J. Schrobilgen, J. Am. Chem. Soc., 2011, 133, 6265.
16. (a) I. H. Krouse and P. G. Wenthold, Inorg. Chem., 2003, 42, 4293; (b) I. H. Krouse, C. Hao, C. E. Check, K. C. Lobring, L. S. Sunderlin and P. G. Wenthold, J. Am. Chem. Soc., 2007, 129, 846.
17. (a) M. W. Justik, Annu. Rep. Prog. Chem., Sect. A: Inorg. Chem., 2009, 105, 165; (b) H. Li, D. Xie and H. Guo, J. Chem. Phys., 2004, 120, 4273; (c) T. Arppe, L. Khriachtchev, A. Lignell, A. V. Domanskaya and M. Räsänen, Inorg. Chem., 2012, 51, 4398.
18. (a) A. Nakayama, K. Niimi, Y. Ono and T. Taketsugu, J. Chem. Phys., 2012, 136, 054506; (b) T. Takayanagi, H. Motegi, Y. Taketsugu and T. Taketsugu, Chem. Phys. Lett., 2008, 454, 1; (c) Y. Taketsugu, T. Taketsugu and T. Noro, J. Chem. Phys., 2006, 125, 154308; (d) Y. Ono and T. Taketsugu, Chem. Phys. Lett., 2004, 385, 85; (e) T. Takayanagi, T. Asakura, K. Takahashi, Y. Taketsugu, T. Taketsugu and T. Noro, Chem. Phys. Lett., 2007, 446, 14; (f) T. Tanaka, T. Takayanagi, T. Taketsugu and Y. Ono, Chem. Phys. Lett., 2012, 539–540, 15.
19. (a) M. Pettersson, J. Lundell and M. Räsänen, J. Chem. Phys., 1995, 102, 6423; (b) M. Pettersson, J. Lundell and M. Räsänen, J. Chem. Phys., 1995, 103, 205.
20. R. B. Gerber, Annu. Rev. Phys. Chem., 2004, 55, 55 , and references therein.
21. R. B. Gerber, E. Tsivion, L. Khriachtchev and M. Räsänen, Chem. Phys. Lett., 2012, 545, 1.
22. L. Khriachtchev, M. Räsänen and R. B. Gerber, Acc. Chem. Res., 2009, 42, 183 , and references therein.
23. L. Khriachtchev, K. Isokoski, A. Cohen, M. Räsänen and R. B. Gerber, J. Am. Chem. Soc., 2008, 130, 6114.
24. L. Khriachtchev, A. Domanskaya, J. Lundell, A. Akimov, M. Räsänen and E. Misochko, J. Phys. Chem. A, 2010, 114, 4181.
25. L. Khriachtchev, S. Tapio, A. V. Domanskaya, M. Räsänen, K. Isokoski and J. Lundell, J. Chem. Phys., 2011, 134, 124307.
26. M. Turowski, M. Gronowski, J. C. Guillemin and R. Kołos, J. Mol. Struct., 2012, 1025, 140.
27. L. Khriachtchev, M. Pettersson, N. Runeberg, J. Lundell and M. Räsänen, Nature, 2000, 406, 874.
28. H. Q. Wu, R. L. Zhong, Y. H. Kan, S. L. Sun, M. Zhang, H. L. Xu and Z. M. Su, J. Comput. Chem., 2013, 34, 952.
29. Q. Z. Li, J. L. Zhao, B. Jing, R. Li, W. Z. Li and J. B. Chen, J. Comput. Chem., 2011, 32, 2432.
30. V. Poterya, O. Votava, M. Farnik, M. Ončak, P. Slaviček, U. Buck and B. Friedrich, J. Chem. Phys., 2008, 128, 104313.
31. H. Schneider, K. Takahashi, T. R. Skodje and J. M. Weber, J. Chem. Phys., 2009, 130, 174302.
32. G. Q. Liu, Y. L. Zhang, Z. X. Wang, Y. Z. Wang, X. X. Zhang and W. X. Zhang, Comput. Theor. Chem., 2012, 993, 118.
33. T. Y. Lai, C. Y. Yang, H. J. Lin, C. Y. Yang and W. P. Hu, J. Chem. Phys., 2011, 134, 244110.
34. A. Avramopoulos, H. Reis, J. M. Luis and M. G. Papadopoulos, J. Comput. Chem., 2013, 34, 1446.
35. P. Antoniotti, E. Bottizzo, L. Operti, R. Rabezzana, S. Borocci and F. Grandinetti, J. Phys. Chem. Lett., 2010, 1, 2006.
36. L. Bučinský, S. Biskupič, M. Ilčin, V. Lukeš and V. Laurinic, J. Comput. Chem., 2011, 32, 356.
37. E. Tsivion and R. B. Gerber, Phys. Chem. Chem. Phys., 2011, 13, 19601.
38. N. Pérez-Peralta, R. Juárez, E. Cerpa, F. M. Bickelhaupt and G. Merino, J. Phys. Chem. A, 2009, 113, 9700.
39. J. Lundell, A. Cohen and R. B. Gerber, J. Phys. Chem. A, 2002, 106, 11950.
40. L. Khriachtchev, H. Tanskanen, J. Lundell, M. Pettersson, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 4696.
41. V. I. Feldman, F. F. Sukhov, A. Y. Orlov and I. V. Tyulpina, J. Am. Chem. Soc., 2003, 125, 4698.
42. L. Khriachtchev, H. Tanskanen, A. Cohen, R. B. Gerber, J. Lundell, M. Pettersson, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 6876.
43. H. Tanskanen, L. Khriachtchev, J. Lundell, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 16361.
44. E. Tsivion and R. B. Gerber, Phys. Chem. Chem. Phys., 2010, 12, 11791.
45. R. Juarez, C. Zavala-Oseguera, J. O. C. Jimenez-Halla, F. M. Bickelhaupt and G. Merino, Phys. Chem. Chem. Phys., 2011, 13, 2222.
46. T. Ansbacher and R. B. Gerber, Phys. Chem. Chem. Phys., 2006, 8, 4175.
47. L. Sheng, A. Cohen and R. B. Gerber, J. Am. Chem. Soc., 2006, 128, 7156.
48. C. Cheng, L. Sheng and Z. S. Li, Mol. Phys., 2012, 110, 293.
49. A. Cohen, J. Lundell and R. B. Gerber, J. Chem. Phys., 2003, 119, 6415.
50. T. H. Li, Y. L. Liu, R. J. Lin, T. Y. Yeh and W. P. Hu, Chem. Phys. Lett., 2007, 434, 38.
51. L. Khriachtchev, A. Lignell, H. Tanskanen, J. Lundell, H. Kiljunen and M. Räsänen, J. Phys. Chem. A, 2006, 110, 11876.
52. S. Borocci, N. Bronzolino, M. Giordani and F. Grandinetti, J. Phys. Chem. A, 2010, 114, 7382.
53. S. Borocci, M. Giordani and F. Grandinetti, Comput. Theor. Chem., 2011, 964, 318.
54. L. Khriachtchev, J. Mol. Struct., 2008, 880, 14.
55. Z. Y. Zhou, Y. Shi and X. M. Zhou, J. Phys. Chem. A, 2004, 108, 813.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Bur-ant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Strat mann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Lia-shenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E. 01, Gaussian, Inc., Wallingford, CT, 2004.
57. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2012.
58. (a) R. F. W. Bader, Atoms in Molecules-A. Quantum Theory, Oxford University Press, Oxford, 1990; (b) F. W. Klieger-Konig, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317.
59. J. Lundell, M. Pettersson and M. Räsänen, Comput. Chem., 2000, 24, 325.
60. G. M. Chaban, Chem. Phys. Lett., 2005, 401, 318.
61. A. Olbert-Majkut, J. Ahokas, J. Lundell and M. Pettersson, Phys. Chem. Chem. Phys., 2010, 12, 7138.
62. (a) J. Lundell and M. Räsänen, J. Mol. Struct., 1997, 436–437, 349; (b) J. Lundell and M. Räsänen, J. Phys. Chem., 1995, 99, 14301.
63. See ESI† for the MP2-calculated frequencies of HCOORgH (Rg = Ar, Kr, Xe) and the transition states.
64. A. Lignell, L. Khriachtchev, J. Lundell, H. Tanskanen and M. Räsänen, J. Chem. Phys., 2006, 125, 184514.
65. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
66. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
67. (a) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593; (b) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 610; (c) E. D. Glendening, J. K. Badenhoop and F. Weinhold, J. Comput. Chem., 1998, 19, 628.
68. W. L. Zou, D. N. Shargh and J. E. Boggs, J. Phys. Chem. A, 2013, 117, 207.
69. I. Last and T. F. George, J. Chem. Phys., 1988, 89, 3071.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp52175c

---