Experimental and computational insights into the conformations of tunicyclin E, a new cycloheptapeptide from Psammosilene tunicoides

Abstract

Tunicyclin E (1), a new cyclic heptapeptide, cyclo(Pro¹–Ser²–Trp³–Leu⁴–Val⁵–Gly⁶–Ser⁷), was isolated from the root of Psammosilene tunicoides. The presence of two sets of resonance signals in its NMR spectra (1a:1b, ∼3 : 1 abundance) indicated that it has two conformations in solution, while only one conformation was found in its crystal state by X-ray diffraction. To explore the molecular basis of the two conformations of 1 in solution and their interconversion mechanism, X-ray diffraction, NMR experiments, and theoretical calculations were performed. The results disclosed that two conformers of 1 in solution were derived from the cis/trans isomers of the Ser⁷–Pro¹peptide bond (1a, trans; 1b, cis). The fast interconversion of the two conformations in solution is explained by an intramolecular catalysis mechanism and solvent effects. Furthermore, the existence of several unusual pseudo turns characterized for the first time plays a key role for dominant trans conformation in solution.

---

Introduction

Owing to their bioactivities and a continuous number of transitions over the NMR timescale, intense efforts have focused on the exploration of bioactive conformations of macrocyclic compounds and the mechanisms involved in their conformational changes by a combined NMR/MD/QM approach.¹ This is especially important as many cyclic peptides containing the proline residue exist as cis/trans isomers in solution because of small energy differences between the isomers and high barriers for rotation about peptidyl–prolyl bonds.² As a result, cyclic peptides serve as useful models in studies of cis/transisomerization of peptidyl–prolyl bonds, which play a unique role in peptide and protein folding and signal transduction.³ However, until now few investigations of this process in macrocyclic cyclopeptides, especially plant cyclic peptides, have been undertaken. Also, no study has been involved in the role of the hydroxyl of the amino acid side chain to form pseudo turns and stabilize the conformations of the cyclic peptides and intrinsically unstructured proteins (IUPs).

As part of the effort aimed at seeking structurally and pharmacologically interesting secondary metabolites from Chinese medicinal plants, a new cyclic heptapeptide, tunicyclin E (1) (Fig. 1), was isolated as a crystalline substance from the root of Psammosilene tunicoides (Caryophyllaceace).⁴ The presence of two sets of resonances in its NMR spectra indicate that 1 exists in two conformations 1a : 1b (ca. 3 : 1) (Fig. 2) in the solution state while only one conformation with a transSer⁷–Pro¹peptide bond in the crystalline state. By using NMR (in C₅D₅N) and chemical methods, the structure of 1 was shown to be cyclo(L–Pro¹–L–Ser²–L–Trp³–L–Leu⁴–L–Val⁵–Gly⁶–L–Ser⁷). Based on the NOE correlations and the chemical shifts of the β and γ carbons of Pro¹, the two conformations 1a and 1b, derived from trans and cisSer⁷–Pro¹peptide bond, respectively in solution were elucidated. In order to explore the molecular basis of the two conformations of 1 in solution and their interconversion mechanism, X-ray diffraction, NMR experiments, theoretical calculations, and kinetic and thermodynamic experiments were performed. Below, we describe the results of this investigation, in which the conformations of tunicyclin E in crystalline and solution states have been elucidated, and the mechanism of fast interconversion of two solution conformations has been explained.

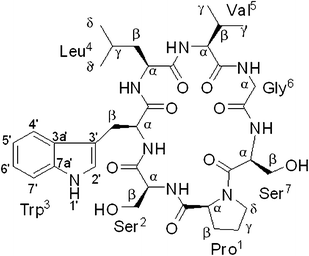Fig. 1 Chemical structure of tunicyclin E (1).

Fig. 2 ¹H–MMR spectrum of tunicyclin E (1) at 300 K (C₅D₅N, 600 Hz).

Results

Assignment of NMR Resonances

Compound 1 was isolated as colorless crystal ([α]²⁰_D −2, c 0.13, MeOH) with the molecular formula C₃₅H₅₀N₈O₉ as established by negative HR-ESI-MS (m/z [M − H]⁻ 725.3625, calcd 725.3623). Two sets of proton resonances with a ratio of 3 : 1 in ¹H NMR spectrum implicated the presence of two conformations in solution (1a and 1b). By 1D and 2D NMR experiments, two sets of NMR data (1a and 1b) were unambiguously assigned. In 1a, the appearance of six main-chain amide protons (δ_H 10.03, 9.36, 8.81, 8.63, 8.41, and 8.15) in ¹H NMR spectrum and seven carbonyls (δ_C 174.49, 172.74, 172.60, 171.98, 171.31, 170.38, and 169.36) and seven α-carbon atom resonances (δ_C 61.25, 61.18, 56.77, 56.41, 53.49, 53.40 and 43.80) in the ¹³C NMR spectrum indicated that 1a is a cyclic heptapeptide (Table 1). In addition, the 1D NMR spectra established the presence of four methyl groups (two isopropyl groups), four methylene groups, two methine groups, one CH₂N group, two CH₂OH groups, and a 3-substituted indolyl group. From ¹H–¹H COSY and TOCSY experiments, six amino acid spin systems of Pro, Ser, Leu, Val, Gly, and Ser were determined (Fig. 3). The HMBC correlations of proton resonance at δ_H 3.87 (2H, d, J = 7.14 Hz, H–β of Trp) with carbon resonances at δ_C 111.23, 124.50 and 128.02 identified the Trp residue. Furthermore, the carbonyl carbons of Pro¹, Ser², Trp³, Leu⁴, Val⁵, Gly⁶, and Ser⁷ were undoubtedly assigned to δ_C 171.98, 171.31, 172.60, 174.49, 172.74, 169.36, and 170.38 based on HMBC correlations between carbonyl carbons and the α or βprotons of the same amino acid residues, respectively. The amino acid sequence of 1a was established by the following the HMBC crosspeaks: Ser²–NH/CO–Pro¹, Trp³–NH/CO–Ser², Leu⁴–NH/CO–Trp³, Val⁵–NH/CO–Leu⁴, Gly⁶–NH/CO–Val⁵ and Ser⁷–NH/CO–Gly⁶ (Fig. 3). The gross structure obtained was also supported by ROESY data, as indicated in Fig. 4. The presence of strong NOE correlations between the αproton of Ser⁷ and both of the δ, δ′ protons of Pro¹ suggested that the amide bond of Ser⁷–Pro¹ was trans. The β and γcarbon chemical shifts of Pro¹ at 28.39 and 24.92 ppm further supported the presence of a transpeptidyl–prolyl bond.⁵

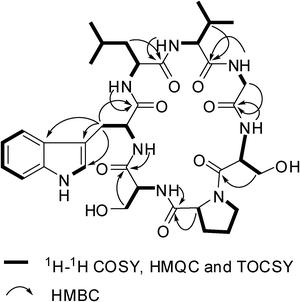Fig. 3 Selected 2D NMR correlations for 1.

Fig. 4 Key ROESY correlations for 1a and 1b respectively.

Table 1 ¹H (600 MHz) and ¹³C NMR (150 MHz) spectroscopic data of 1a (in C₅D₅N, J in Hz, δ in ppm)^a

	δ H	δ C		δ H	δ C
Pro^1			Leu^4
a All proton signals integrate to 1 H, unless otherwise indicated
CO		171.98	CO		174.49
α	4.75 (dd, 8.10, 5.70)	61.25	NH	8.15 (d, 7.80)
β	2.07 (m)	28.39	α	4.90 (ddd, 10.40, 7.80, 4.69)	53.40
β′	1.92 (m)		β	1.95 (ddd, 13.99, 10.40, 6.37)	40.64
γ	1.70 (m)	24.92	β′	1.87 (ddd, 13.99, 8.70, 4.69)
γ′	1.50 (m)		γ	1.78 (m, 8.70, 6.78, 6.54, 6.37)	24.79
δ	3.62 (dt, 9.36, 7.20)	47.31	δ	0.76 (3H, d, 6.54)	22.93
δ′	3.40 (dt, 9.36, 6.90)		δ′	0.73 (3H, d, 6.78)	21.52
Ser^2			Val^5
CO		171.31	CO		172.74
NH	8.41 (d, 7.44)		NH	9.36 (d, 4.80)
α	4.97 (dt, 7.44, 5.10)	56.41	α	4.31 (dd, 8.49, 4.80)	61.18
β	4.17 (2H, d, 5.10)	62.14	β	2.28 (m, 8.49, 6.72, 6.66)	30.05
Trp^3			γ	1.05 (3H, d, 6.72)	19.25
CO		172.60	γ′	1.02 (3H, d, 6.66)	19.44
NH	8.81 (d, 7.38)		Gly^6
α	5.10 (dt, 7.38, 7.14)	56.77	CO		169.36
β	3.87 (2H, d, 7.14)	27.90	NH	10.03 (dd, 7.71, 4.74)
1′ NH	11.77 (d, 3.91)		α	4.84 (dd, 16.45, 7.71)	43.80
2′ CH	7.70 (d, 3.91)	124.50	α′	3.88 (dd, 16.45, 4.74)
3′ C		111.23	Ser^7
3a′ C		128.02	CO		170.38
4′ CH	7.92 (d, 7.80)	118.93	NH	8.63 (d, 8.70)
5′ CH	7.07 (dd, 7.80, 7.14)	119.09	α	5.36 (ddd, 8.70, 4.92, 4.50)	53.49
6′ CH	7.16 (dd, 7.14, 7.98)	121.61	β	4.27 (dd, 11.28, 4.92)	63.80
7′ CH	7.49 (d, 7.98)	111.83	β′	4.08 (dd, 11.28, 4.50)
7a′ C		137.33

---

In 1b, the same amino acid residues of Pro, Ser, Trp, Leu, Val, Gly, and Ser as those in 1a were also deduced by 1D and 2D NMR experiments. The complete assignment for the ¹H and ¹³C NMR data of 1b (Table 2) was similar that of 1a. In addition, the amino acid sequence of 1b was established to be identical with that of 1a on the basis of HMBC and ROESY experiments. However, the β and γcarbon chemical shifts of Pro¹ in 1b at δ_C 31.59 and 22.50 ppm respectively suggested the presence of a cispeptidyl–prolyl bond in 1b.⁵ This was further confirmed by the strong NOE correlation between αproton of Pro¹ and αproton of Ser⁷ (Fig. 4). The result indicated that 1a and 1b were cis/transpeptidyl–prolyl bond isomers.

Table 2 ¹H (600 MHz) and ¹³C NMR (150 MHz) spectroscopic data of 1b (in C₅D₅N, J in Hz, δ in ppm)^a

	δ H	δ C		δ H	δ C
a All proton signals integrate to 1 H, unless otherwise indicated
Pro^1			Leu^4
CO		172.74	CO		173.67
α	5.31 (d, 9.06)	61.51	NH	8.45 (d, 7.74)
β	2.38 (dd, 15.31, 7.11)	31.59	α	4.87 (ddd, 10.10, 7.74, 4.25)	54.41
β′	2.02 (m)		β	1.75 (ddd, 13.19, 8.04, 4.25)	41.80
γ	1.63 (m)	22.50	β′	1.65 (ddd, 13.19, 10.10, 6.59)
γ′	1.58 (m)		γ	1.64 (m, 8.04, 6.96, 6.59, 6.18)	24.95
δ	3.66 (m)	47.15	δ	0.77 (3H, d, 6.18)	22.50
δ′	3.65 (m)		δ′	0.74 (3H, d, 6.96)	21.70
Ser^2			Val^5
CO		173.44	CO		171.60
NH	8.83 (d, 8.88)		NH	7.81 (d, 9.36)
α	5.33 (ddd, 8.88, 8.06, 4.55)	55.10	α	4.96 (dd, 9.36, 5.58)	58.45
β	4.45 (dd, 11.13, 8.06)	62.44	β	2.90 (m, 6.84, 6.72, 5.58)	29.95
β′	4.31 (dd, 11.13, 4.55)		γ	1.10 (3H, d, 6.72)	17.23
Trp^3			γ′	0.98 (3H, d, 6.84)	19.76
CO		172.60	Gly^6
NH	9.73 (d, 5.06)		CO		170.63
α	5.17 (ddd, 8.58, 5.06, 4.92)	56.59	NH	8.00 (dd, 8.37, 2.68)
β	3.68 (dd, 15.30, 4.92)	27.22	α	4.79 (dd, 14.91, 8.37)	43.35
β′	3.62 (dd, 15.30, 8.58)		α′	3.75 (dd, 14.91, 2.68)
1′ NH	11.80 (d, 3.97)		Ser^7
2′ CH	7.65 (d, 3.97)	124.43	CO		171.01
3′ C		110.24	NH	9.13 (d, 3.42)
3a′ C		128.21	α	4.94 (ddd, 8.11, 7.32, 3.42)	55.30
4′ CH	7.78 (d, 7.83)	118.78	β	4.21 (dd, 11.77, 8.11)	62.79
5′ CH	7.09 (dd, 7.83, 7.14)	119.17	β′	4.16 (dd, 11.77, 7.32)
6′ CH	7.16 (dd, 7.14, 7.90)	121.61
7′ CH	7.50 (d, 7.90)	111.83
7a′ C		137.17

---

The absolute configurations of Pro¹, Ser², Leu⁴, Val⁵ and Ser⁷ were identified as L (S) on the basis of HPLC-ESI-MS analysis of the retention times and m/z values of the chiral derivatives of amino acid residues in acid hydrolysate of 1 (detailed information is given in the ESI†).⁶ Taken together with the relative configuration, established by X-ray crystallography, all amino acid residues had the L (S) configuration. Thus, 1 was determines to be cyclo(L–Pro¹–L–Ser²–L–Trp³–L–Leu⁴–L–Val⁵–Gly⁶–L–Ser⁷).

Conformational analysis

Crystal structure investigation. The single crystal X-ray diffraction was performed to study the structure of 1, and only one conformation with the transSer⁷–Pro¹peptide bond was found in the crystal of 1. This conformation was studied in detail based on X-ray diffraction results (crystal data, structure refinement and the final atomic parameters of 1 are given in the ESI†) (Fig. 5). The conformations of the backbone and side chains for each residue were well described by conformational parameters given in Table 3. In the crystal, all peptide bonds are trans (t) conformation based on their ω angles. And the almost pairs of ϕ, ψ values fall within the allowed regions for Lamino acid residues in the Ramachandran plot except for Ser² with ϕ = −127.8, ψ = −97.4, appreciably higher in energy. However, the Ser² residue is able to form two additional hydrogen bonds (Trp³–NH…HO–Ser² and Ser²–NH…HO–Ser⁷) to stabilize the conformation. The side chain conformational parameters of other residues are very close to those usually found in peptides in crystal state.⁷

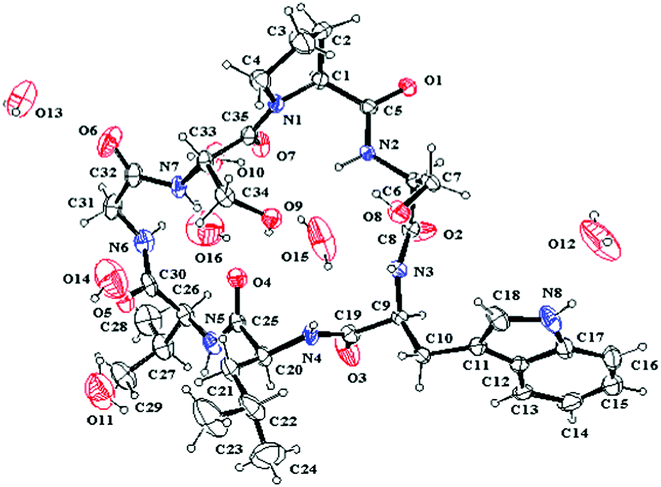Fig. 5 ORTEP structure of 1 with atom labels.

Table 3 Torsion angles (deg) for 1 in crystal

	Pro1	Ser2	Trp3	Leu4	Val5	Gly6	Ser7
ϕ i	−90.8	−127.8	−98.9	−77.8	−56.1	88.0	−112.2
ψ i	9.2	−97.4	−53.0	146.1	140.1	−6.6	173.1
ω i	−176.3	−172.2	−171.9	176.6	−177.7	−177.6	176.3
χ i ^11	32.3	70.1	−65.3	−61.2	−164.2		85.1
χ i ^12					70.3
χ i ^21	−36.6		89.9	−177.9
χ i ^22			−89.0	−56.0
χ i ^3	25.2
χ i ^4	−4.2
χ i ^5	−17.0

---

Details on the key intramolecular hydrogen bonds in crystal were reported in Table 4. One type II β-turn is observed in the crystal structure of 1 based on a trans-annular hydrogen bond (Leu⁴–C=O…NH–Ser⁷) and the observed backbone angles.⁸ In addition, the hydroxyl group of the Ser⁷ side chain is positioned at the center of the molecular plane as a hydrogen bond acceptor to form an unusual C9 (nine-membered) pseudo inverse γ-turn with Ser²–NH, and as a hydrogen bond donor to form an unusual C13pseudo β-turn with Leu⁴–C=O, respectively. The hydrogen bond of the C9 pseudo inverse γ-turn is of intermediate strength with d(N…O) = 3.15 Å, d(H…O) = 2.33 Å and the bond angle (N–H…O) = 160.6°. However, the hydrogen bond of C13 pseudo β-turn is of high strength with d(N…O) = 2.73 Å, d(H…O) = 1.98 Å and the bond angle (N–H…O) = 152.3°. The C13 pseudo β-turn and C9 pseudo inverse γ-turn were first characterized in the cyclic peptide. Although the pseudo turns are not found in classic secondary structures, they can stabilize the conformations of cyclic peptides or intrinsically unstructured proteins (IUPs) by forming hydrogen bonds between the hydroxyl of the amino acid side chain and the amide or carbonyl group of other amino acid residues. To form the pseudo inverse γ-turn, the dihedral angles of Pro¹ have to adopt the following dihedral angles: ϕ = −90.8° and ψ = 9.2°, resulting in the proton of NH–Ser² spatially proximate to the nitrogen of Pro¹ to form a hydrogen bond with d(N…N) = 2.77 Å, d(H…N) = 2.40 Å and bond angle (N–H…N) = 106.4°.

Table 4 Intramolecular hydrogen bonds for 1 in crystal

donor	acceptor	Distance, Å (D–H)	Distance, Å (H…A)	Distance, Å (D…A)	Angle, deg (D–H–A)
Ser^7–OH	Leu^4–CO	0.82	1.98	2.73	152.3
Ser^2–NH	Pro^1–N	0.86	2.40	2.77	106.4
Ser^2–NH	Ser^7–OH	0.86	2.33	3.15	160.6
Trp^3–NH	Ser^2–OH	0.82	2.13	2.76	133.8
Ser^7–NH	Leu^4–CO	0.84	2.26	3.02	149.8

---

Solution conformation investigation. The solution conformations (1a, trans; 1b, cis) were studied in detail based on the temperature dependence of NH chemical shifts (Table 5), coupling constants (Table 1 and 2), and NOE effects. The NH/αH coupling constants of Ser², Trp³, Leu⁴, and Ser⁷ of 1a were directly determined from the ¹H–NMR spectrum. While NH/αH coupling constants of Gly⁶ and Val⁵ residues and all αH/βH coupling constants of 1a were obtained from the MQF-COSY spectrum because NH–Val⁵ are being fast exchanged with trace water in solution or being heavily overlapped in the ¹H–NMR spectrum. The NH/αH and αH/βH coupling constants of 1b were also similarly obtained. The coupling constants can serve as dihedral angle constrains to determine the backbone or side chain conformations using the Karplus equation.⁹ To further determine interproton distances, an off-resonance ROESY experiment was performed by employing a ROESYPHPR.2 pulse sequence to suppress TOCSY type magnetization transfer.¹⁰ The interproton distances were calibrated by the distance from indole NH proton to the 7′CH proton (d = 2.82 Å) (see detailed information in ESI†).^8b,11 The unambiguous interproton distances of 1a and 1b were shown in Table 6.

Table 5 Temperature dependence of the NH chemical shifts (−Δδ/ΔT) in ppb K⁻¹

	Ser^2	Trp^3	Leu^4	Val^5	Gly^6	Ser^7
−Δδ/ΔT for 1a	5.49	13.11	10.58	15.87	12.60	8.17
−Δδ/ΔT for 1b	15.67	16.99	9.18	3.45	1.50	14.26

---

Table 6 The key interproton distances obtained from the ROESY spectrum and those from crystal structure

1a		1b		Crystal
Involved protons	Distance (Å)	Involved protons	Distance (Å)	Involved protons	Distance (Å)
Pro^1 Hα–Ser^2 NH	2.81	Pro^1 Hα–Ser^7 Hα	2.20	Pro^1 Hα–Ser^2 NH	3.10
Pro^1 Hδ–Ser^2 NH	3.05	Pro^1 Hδ–Ser^2 NH	3.03	Pro^1 Hδ–Ser^2 NH	3.29
Pro^1 Hδ–Ser^7 Hα	2.47	Ser^2 Hα–Trp^3 NH	2.27	Pro^1 Hδ–Ser^7 Hα	2.72
Pro^1 Hδ–Ser^7 Hβ	2.15	Ser^2 Hβ–Val^5 NH	3.12	Pro^1 Hδ–Ser^7 Hβ	2.10
Pro^1 Hδ′–Ser^7 Hα	2.08	Ser^2 Hβ–Gly^6 NH	3.14	Pro^1 Hδ′–Ser^7 Hα	2.40
Pro^1 Hδ′–Ser^7 Hβ	3.00	Trp^3 NH–Leu^4 NH	2.39	Pro^1 Hδ′–Ser^7 Hβ	3.09
Ser^2 NH–Trp^3 NH	2.99	Trp^3 Hα–Leu^4 NH	2.82	Ser^2 NH–Trp^3 NH	3.24
Ser^2 NH–Ser^7 Hβ	3.30	Trp^3 Hα–Gly^6 NH	3.47	Ser^2 NH–Ser^7 Hβ	3.39
Ser^2 Hα–Trp^3 NH	2.73	Trp^3 Hβ′–Leu^4 NH	3.07	Ser^2 Hα–Trp^3 NH	3.40
Trp^3 NH–Leu^4 NH	2.69	Leu^4 NH–Val^5 NH	2.32	Trp^3 NH–Leu^4 NH	2.56
Trp^3 Hα–Leu^4 NH	3.14	Leu^4 Hα–Val^5 NH	3.03	Trp^3 Hα–Leu^4 NH	3.49
Leu^4 Hα–Val^5 NH	2.56	Val^5 NH–Gly^6 NH	2.34	Leu^4 Hα–Val^5 NH	2.29
Val^5 Hα–Gly^6 NH	2.23	Val^5 Hα–Gly^6 NH	2.93	Val^5 Hα–Gly^6 NH	2.41
Val^5 Hα–Ser^7 NH	3.73	Gly^6 NH–Ser^7 NH	3.19	Val^5 Hα–Ser^7 NH	3.48
Gly^6 NH–Ser^7 NH	2.28			Gly^6 NH–Ser^7 NH	2.49
Ser^7 Hα–Ser^7 Hβ	2.28			Ser^7 Hα–Ser^7 Hβ	2.22

---

The temperature dependence of the NH chemical shifts of 1a indicated the NH protons of Trp³, Val⁵ and Gly⁶ to be oriented externally, because of a large −Δδ/ΔT coefficient.^8b Although the coefficients of the Ser²–NH and Ser⁷–NH protons of 1a lie in intermediate range because of the flexible backbone, it seemed that these protons were involved in two intramolecular hydrogen bonds. In 1a, the strong NOE correlations of Val⁵–αH/NH–Gly⁶ and Gly⁶–NH/NH–Ser⁷ (Fig. 4) indicated the presence of a type II β-turn due to the hydrogen bond Leu⁴–C=O…NH–Ser⁷. And the NOE correlations of Ser²–NH/δH–Pro¹, Ser²–NH/βH–Ser⁷ and Ser⁷–αH/δ,δ′H–Pro¹ could established the same pseudo C9 γ-turn due to the hydrogen bond Ser⁷–OH…NH–Ser² as that of the crystal structure of 1. Further evidence came from the observation that the side chain of the Ser⁷ residue has restricted rotation: the chemical shifts of two βprotons are very different (δ_H 4.27, Ser–βH; 4.08, Ser–β′H). Comparing the key interproton distances of 1a from the ROESY experiment with those from the crystal structure of 1 (Table 6), it indicated that the solution conformation 1a was quasi-identical with that of crystal structure of 1.

As to 1b, the temperature dependence of the NH chemical shifts of 1b exhibited that the NH protons of Ser², Trp³, Leu⁴ and Ser⁷ were oriented externally, while the NH protons of Val⁵ and Gly⁶ were involved in two intramolecular hydrogen bonds (Table 5). Based on the NOE correlations of Trp³–NH/NH–Leu⁴, Leu⁴–NH/NH–Val⁵ and Leu⁴–NH/βH–Leu⁴ (Fig. 4) and the small temperature dependence coefficient of Val–NH in 1b, an unambiguous type I β-turn due to a trans-annular hydrogen bond Ser²–C=O…NH–Val⁵ was deduced. The very low temperature dependence coefficient of Gly⁶ (1.50 ppb K⁻¹) indicated that NH–Gly⁶ was involved in a hydrogen bond with Ser²–C=O to form an α-turn, which was strongly supported by the NOE cross peak between βH–Ser² and NH–Gly⁶ (Fig. 4).

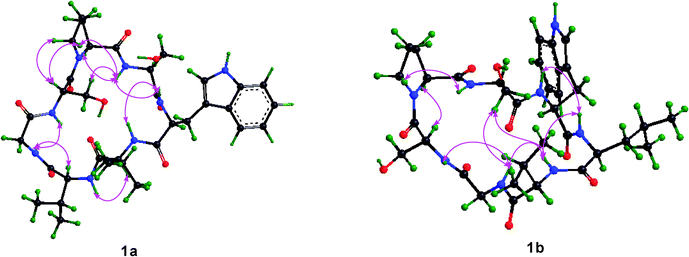
Although the solution conformations 1a and 1b have been interpreted by NOE effects, the precise solution conformation was still unclear because of the flexible backbone. Chemical calculations were then performed. The crystal structure of 1 provided the seed structure for molecular dynamics simulation of 1a. Since the crystal structure for 1b was unavailable, a random structure was generated and then optimized based on the constraints of the key interproton distances and the torsion angles. The structure obtained from this process was used as input file for the molecular dynamics simulation of 1b. Starting from the initial structures mentioned above, 10 ns restrained molecular dynamics simulation was performed for both 1a and 1b. The results were represented by two ensembles of the 20 lowest energy conformers within 5.21 kcal mol⁻¹ of the global minimum for 1a and 6.86 kcal mol⁻¹ for 1b (Fig. 6). The low-energy conformations of 1a and 1b without dramatic violations of experimentally validated restraints were relocated and confirmed at B3LYP approximation level employing the 6-31G basis set of Gaussian 03W (Fig. 7).¹²

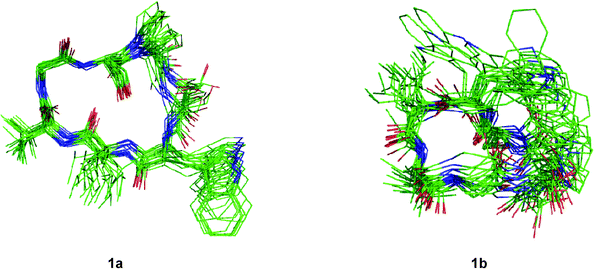Fig. 6 Overlays of the 20 lowest energy conformers for 1a and 1b respectively.

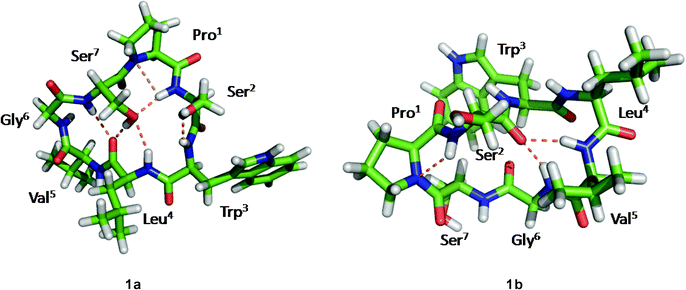Fig. 7 The B3LYP/6-31G–optimized solution structures of 1a and 1b, with the intramolecular hydrogen bonds.

The well-defined ensemble of the 20 lowest energy conformers of 1a indicated that it has a relatively rigid conformation in solution, with the root mean square deviation (RMSD) value of 0.87 ± 0.15 Å over all 52 heavy atoms of the residual violation statistics. In addition, the 20 lowest energy conformers of 1a, although not perfectly, nicely match the crystal structure with a RMSD value of 0.67 Å obtained upon superposition of the 21 backbone atoms. Inspection of the 3D structure of 1a, refined by density functional theory (DFT) with a 6-31G basis set, revealed that the type II β-turn, the pseudo C9 inverse γ-turn, the pseudoC13β-turn, and the side chains orientations of amino acid residues are quasi-identical with those in crystal structure. Furthermore, the refined 3D structure also reveals that six intramolecular hydrogen bonds exist. The hydrogen bond network significantly increases the stability of the trans conformation. The differences between the refined solution structure 1a and crystal structure of 1 (Table 7) are small except for the significantly different ψ angles of Trp³ (5.3° in solution and −53.0° in crystal) and ϕ angles of Leu⁴ (−135.3° in solution and −77.8° in crystal). The altered ψ value of Trp³ and ϕ value of Leu⁴ indicate that the Leu⁴–NH points toward the hydroxyl group of the Ser⁷ side chain to form an intramolecular hydrogen bond (d(N…O) = 3.22 Å and d(H…O) = 2.26 Å and the bond angle (N–H…O) = 157.5°), which is involved in the unusual pseudoC15α-turn, rather than forming an intermolecular hydrogen bond with Pro¹–C=O of another molecule in crystal. However, as a result of the small difference in the ψ value of Pro¹ in 1a (29.1°) and crystal structure of 1 (9.2°), the NH–Ser² proton remains spatially proximate to the nitrogen atom of Pro¹ and forms a hydrogen bond (d(N…N) = 2.85 Å, d(H…N) = 2.55 Å and the bond angle (N–H…N) = 96.2°) similar to that in crystal.

Table 7 The torsion angles (deg) in the solution and crystal conformation of 1

		Pro1	Ser2	Trp3	Leu4	Val5	Gly6	Ser7
1a	ϕ i	−93.9	−130.1	−116.1	−135.3	−55.5	100.7	−129.1
	ψ i	29.1	−96.4	5.3	150.5	130.8	−4.8	168.3
	ω i	177.6	−168.1	175.0	164.8	−174.0	177.8	163.0
1b	ϕ i	−65.1	−83.5	−57.8	−60.4	−117.1	170.2	−147.9
	ψ i	−21.6	97.9	−24.1	−33.9	−15.7	−117.0	151.1
	ω i	−175.9	−169.8	178.2	−179.6	−176.3	170.9	−5.4
crystal	ϕ i	−90.8	−127.8	−98.9	−77.8	−56.1	88.0	−112.2
	ψ i	9.2	−97.4	−53.0	146.1	140.1	−6.6	173.1
	ω i	−176.3	−172.2	−171.9	176.6	−177.7	−177.6	176.3

---

The significant fluctuation seen in the 20 lowest energy conformers (RMSD value of 2.19 ± 0.31 Å over all 52 heavy atoms of the residual violation statistics) indicates that its isomer 1b possesses a more flexible backbone in solution. Analysis of the structure of 1b, refined by using B3LYP/6-31G, reveals that the conformational change of Ser⁷–Pro¹peptide bond from trans (ω = 163.0°) to cis (ω = −5.4°) is accompanied by a complete change in the hydrogen bond network and orientations of the amino acid side chains. Especially, the orientations of the side chain of Ser⁷, Ser⁷–NH and Leu⁴–C=O change from inward in 1a to outward in 1b, while the orientations of Ser²–C=O and Val⁵–NH from outward in 1a to inward in 1b. In addition, only three intramolecular hydrogen bonds are present in the cis conformation. The hydrogen bonds of Ser²–C=O…NH–Val⁵ and Ser²–C=O…NH–Gly⁶ in 1b, which form the type I β-turn and the α-turn respectively, are stronger than any in 1a. This feature results in a sterically more crowded conformation and higher in energy. The conformational analysis of 1b indicate that nearly all pairs of ϕ, ψ values fall within typical regions in the Ramachandran plot. An exception is found for Gly⁶ which has ϕ = 170.2°, ψ = −117.0°, values within the forbidden region. However, this conformation favors formation of the Ser²–C=O…NH–Gly⁶hydrogen bond. Although the solution conformation of 1b is markedly different from that of 1a, the ψ value of Pro¹ in 1b (ψ = −21.6°) remains close to that in the crystal structure. The hydrogen bond Pro¹–N…NH–Ser² in 1b (d(N…N) = 2.83 Å, d(H…N) = 2.44 Å) and the N–H…N bond angle (102.3°) is highly similar to that in the crystal structure of 1.

Thermodynamics and kinetics study. The thermodynamics and kinetics parameters for cis/transisomerization of 1 in C₅D₅N solution were determined by using inversion-magnetization transfer experiments over a range of temperatures (300–320 K, 5 K intervals) (detailed information is given in the ESI†).¹³ The pair of cis/trans proton resonances of Ser⁷–NH were subjected for the thermodynamic and kinetic measurements. The equilibrium constants (Table 8) for trans/cisisomerization (K_e = k_ct/k_tc = [trans]/[cis]) were obtained from inversion-magnetization transfer experiment measured with a mix time t ≥ 5T₁. The thermodynamic parameters (ΔH° = 0.490 ± 0.066 kcal mol⁻¹, ΔS° = 3.972 ± 0.213 cal mol⁻¹ K⁻¹ and ΔG°= −0.702 ± 0.066 kcal mol⁻¹) for the isomerization of 1 were calculated using a van't Hoff plot. The positive ΔH° indicates that 1a is more stable than 1b. Moreover, the 1a becomes increasingly favored as the temperature increases. The rate constants for cis-to-transisomerization (k_ct) were determined by employing a nonlinear least squares fit of the inversion-magnetization transfer data to the equations, as described in ref. 5b (detailed information and figures are given in ESI†). The rate constants for trans-to-cisisomerization (k_tc) were then calculated based on k_ct and K_e (k_tc = k_ct/K_e) (Table 8). The results indicate that the rate constant of the cis/transpeptidyl–prolyl bond isomerization of 1 is considerably large in comparison with those of cyclic peptides containing a disulfide bond in aqueous solution.^13a The activation parameters (ΔH_ct^≠ = 13.853 ± 2.106 kcal mol⁻¹, ΔS_ct^≠ = −13.438 ± 6.800 cal mol⁻¹ K⁻¹, ΔG_ct^≠ = 17.884 ± 2.106 kcal mol⁻¹ at 300 K; and ΔH_tc^≠ = 13.365 ± 2.163 kcal mol⁻¹, ΔS_tc^≠ = −17.402 ± 6.982 cal mol⁻¹ K⁻¹, ΔG_ct^≠ = 18.586 ± 2.163 kcal mol⁻¹ at 300 K) derived from the Eyring plot are smaller than those of dipeptides and cyclotetrapeptides (about 20 kcal mol⁻¹ in aqueous solution).^13a,14. The large negative ΔS^≠ leads to the significant decrease in ΔH^≠ to offset the change of ΔS^≠.

Table 8 Equilibrium constants and rate constants for cis/transpeptidyl–prolyl bond isomerization of 1

T/K	K e	k ct	k tc
300	3.228 ± 0.012	0.697 ± 0.048	0.216 ± 0.015
305	3.300 ± 0.004	0.772 ± 0.052	0.234 ± 0.016
310	3.353 ± 0.022	1.085 ± 0.074	0.324 ± 0.022
315	3.365 ± 0.010	1.815 ± 0.083	0.539 ± 0.025
320	3.408 ± 0.014	3.056 ± 0.133	0.897 ± 0.039

---

Discussion

In the cyclopeptide conformations, the hydrogen bond is one of the key factors in stablizing the conformations and influencing the populations of both the cis and trans isomers. In the trans conformation (1a), there are six intramolecular hydrogen bonds in total. Among of them, three intramolecular hydrogen bonds are formed by the hydroxyl of the side chain of the Ser⁷ residue with Ser²–NH, Leu⁴–NH and Leu⁴–C=O, respectively. The three hydrogen bonds, together with the hydrogen bond Leu⁴–C=O…NH–Ser⁷, construct a trans-annular hydrogen bond network. The hydrogen bond network greatly enhances the rigidity of the cyclopeptide skeleton, and significantly increases the stability of the trans conformation (1a). In contrast, the conformational change of the Ser⁷–Pro¹peptide bond is accompanied by complete changes of the hydrogen bond network and the side chains orientations of amino acid residues. There are only three intramolecular hydrogen bonds to stabilize the cis conformation (1b). Although the hydrogen bonds of Ser²–C=O…NH-Val⁵ and Ser²–C=O…NH–Gly⁶ are more tight than any one of 1a, it is still not enough to support a relatively rigid cis conformation, but still results in a more crowded spatial conformation and higher energy. Moreover, on the basis of hydrogen bond network analysis of 1a and 1b, several unusual pseudo turns were characterised for the first time, which might bring us a better understanding about the role of the hydroxyl of the amino acid side chain stabilizing the secondary structure of peptides or proteins.

Because of the lone electron pair of the nitrogen atom and the electrophilic capability of the adjacent carbonyl, the peptide bond, including the peptidyl–prolyl bond, has partial double bond character. Essentially, the cis/transisomerization of peptidyl–prolyl bond is derived from the rotation of the C–N bond by forcing electrons to leave the C–N bond accompanying the change in the nitrogen of proline from a partial planed sp² hybrid state to a pyramidalized sp³ hybrid state.^2,13a Thus, the cis/transisomerization of the peptidyl–prolyl bond is a relatively slow process with a rotational enthalpy barrier of about 20 kcal mol⁻¹.¹⁴ However, the cis/transisomerization rate can be accelerated by chemical or enzymic catalysis. In vivo, peptidyl prolylcis/trans isomerases (PPIases) play key role for cis/transisomerization of proline-containing oligopeptides and proteins.¹⁵ By forming a pyramidalized proline imide of the transition state and distorting the imide bond to destabilize the ground state, the peptidyl–prolylcis/trans isomerases (PPIs) can lower the enthalpy barrier of the peptidyl–prolylcis/transisomerization to 5–6 kcal mol⁻¹.^15a However, in some special proteins or dipeptide models, the rates of cis/transisomerization of the peptidyl–prolyl bond can also be accelerated by an intramolecular catalysis mechanism.¹⁶ The process involves a shift of the lone electron pair of the prolyl imide from a p_z orbital to an sp³ orbital by forming a hydrogen bond between the prolyl imide and a pinpointed spatial proximate hydrogen of amide group or other groups of other residue in the molecule and then rotating around the C–N bond to give a twisted transition state with the proline ring arranged perpendicular to the carbonyl group (ω ≈ 90°) (Fig. 8).^13a The hydrogen bond can lower the enthalpy barrier of cis/transisomerization of the peptidyl–prolyl bond by 1.4 kcal mol⁻¹ by stabilizing the pyramidalized proline imide of the transition state according to the theoretical calculations.¹⁴

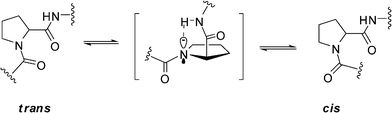Fig. 8 The intramolecular catalysis mechanism of cis/transisomerization of peptidyl–prolyl bond.

In our study, the proton of NH–Ser² is spatially proximate to the nitrogen of Pro¹ to form a hydrogen bond in the crystal of 1 based on the small ψ value of Pro¹. Similarly, the same hydrogen bonds of Pro¹–N…NH–Ser² were also observed in both refined conformations of 1a and 1b. Just the same as the similar studies about several dipeptides and cyclotetrapeptides previously reported,^13a,14 the weak Pro¹–N…NH–Ser² hydrogen bonds are associated with a shift of the lone pair electrons of the prolyl nitrogen from a p_z orbital to a pyramidalized sp³ orbital to decrease the partial C–N double bond character of the Ser⁷–Pro¹peptide bond. Furthermore, deuterated pyridine with less dielectric constant and less hydrogen-bond-donating ability relative to water also stabilizes the less polar, twisted Ser⁷–Pro¹peptide bond in its transition state, wherein amide resonance is disrupted and charge separation diminished.¹⁷ Therefore, the intramolecular catalysis mechanism and the solvent effects contribute the decrease in ΔG^≠. The significant negative ΔS^≠ of 1a and 1b likely arises from two factors. First, solvent molecules are bound to the NH and hydroxyl protons which participate in the intramolecular hydrogen bond in its ground state, and rupture in transition state.¹⁸ Second, some intramolecular hydrogen bonds including Pro¹–N…NH–Ser² are reorganized in transition state.

Conclusion

In summary, the conformations of tunicyclin E (1), including crystal conformation and two solution conformations (1a and 1b), were discussed in our study. Conformational analysis disclosed that two solution conformers of 1 are derived from the Ser⁷–Pro¹peptide bond cis/trans isomers (1a, trans; 1b, cis), while conformation of the trans isomer (1a) was quite similar to the crystal conformation of 1. In both the trans and cis solution conformations of 1, the protons of Ser²–NH are spatially proximate to the nitrogens of Pro¹ to form intramolecular hydrogen bonds, accelerating the cis/transisomerization of the Ser⁷–Pro¹peptide bond. This finding will light up the road to understand the mechanism of intramolecular catalysis of cis/transisomerization of the peptidyl–prolyl bond in peptide scaffolds. Moreover, new types of turns first characterized herein also increase some novel secondary structure elements of peptides or proteins.

Because of their molecular size and a number of possible conformations in solution, the conformations of macrocyclic cyclopeptides from the molecular dynamics (MD) simulations cannot be relied upon without experimental data, while the results from the ab initio method are more accurate but quite computationally-expensive. In addition, the conformations of macrocyclic cyclopeptide from solution NMR experiments are only the average values of a large number of transitions over the NMR timescale and cannot afford more detailed information of the conformations.¹⁹ Thus, the structural complexity of the macrocyclic cyclopeptide presents a great challenge to their conformational analysis. The approach used in the investigation described above, has led to more details of multiple conformation macrocyclic cyclopeptides and peptidyl bond cis/transisomerization.

Experimental Section

General experimental procedures

Optical rotation was measured on Perkin-Elmer 341 polarimeter. IR and UV spectra were taken on Bruker Vector 22 instrument and Varian Cary 300 Bio, respectively. ¹H and ¹³C NMR spectra were recorded on Bruker Avance 600 MHz NMR spectrometer in C₅D₅N, with chemical shifts (δ) reported in ppm. ESI-MS and HR-Q-TOF-MS were measured on LC/MSD Trap XCT (Agilent, USA) and Q-TOF micro mass spectrometer (Waters, USA), respectively.

Plant material

The roots of Psammosilene tunicoides (40 kg) were collected in Lijiang, Yunnan province, China, in 2006. The botanical identification was made by Prof. Li-Shan Xie, Kunming Institute of Botany, Chinese Academy of Sciences. A voucher specimen (herbarium No. 2006071015) is deposited in School of Pharmacy, Second Military Medical University, China.

Extraction and isolation

The air-dried powdered material was refluxed with 80% alcohol. The residue obtained by concentrating alcohol was partitioned between H₂O and CHCl₃. The CHCl₃ soluble extract (285 g) was chromatographed by a silica gel (100–200 mush) column, and eluted successively with gradient petroleum ether—EtOAc (1%, 5%, 10%, 20%, 30%, and 40%), then eluted with 10% CH₃OH–CHCl₃ to yield nine fractions (F1 to F9). The H₂O soluble extract was chromatographed by a macroporous resin (HP-20) column and eluted successively with H₂O, 70% alcohol and acetone to yield two fractions. The acetone fraction was combined with the F9 fraction to afford fraction M. The fraction M was chromatographed by a MCI gel column eluted successively with H₂O, 70% CH₃OH, and CH₃OH to yield two fractions (M-1 and M-2). The fraction M-1 was subjected to a chromatograph over a silica gel column eluting with CH₃OH–CHCl₃ (5%, 10%, 15%, 20%, and 30%) to give four subfractions (M-1-1 to M-1-4). The M-1-3 was further purified by repeated reverse-phase (ODS) columns and Sephedex (LH-20) columns, finally chromatographed over a reverse-phase (ODS) column eluting with H₂O–MeOH (1 : 1) to afford compound 1 (1357 mg).

Tunicyclin E (1). Colorless crystal; [α] −2 (c 0.13, MeOH); UV (MeOH): λ_max = 281, 290 nm; IR (KBr): ν = 3308, 3062, 2933, 2874, 1652, 1522, 1457, 1437, 1339, 1236, 1128, 1061, 878, 745, 667, 562, 425 cm⁻¹; ¹H and ¹³C NMR data (see Table 1 and 2 for 1a and 1b, respectively); ESI-MS: m/z: 727 [M + H]⁺, 749 [M + Na]⁺; HR-ESI-MS: m/z: calcd for C₃₅H₄₉N₈O₉ [M − H]⁻: 725.3623; found: 725.3625.

X-ray data for Tunicyclin E (1). C₃₅H₅₀N₈O₉·6H₂O, M_r = 834.93, orthorhombic, space groupP2₁2₁2₁, a = 10.798 (17), b = 15.09 (2), c = 27.46(4) Å, V = 4473(12) ų, Z = 4, ρ_c = 1.240 g cm⁻³, crystal dimensions 0.20 × 0.12 × 0.10 mm⁻³ was used for measurements on a CAD4 DIFFACTIS 586 diffractometer with graphite monochromator (ω-2θ scans, 2θ_max = 52.98°), Mo_Kα radiation. The total number of independent reflections measured was 17 448, of which 5080 were observed (|F|² ≥ 2σ|F|²). Final indices: R₁ = 0.0810, WR₂ = 0.1884. The crystal structure was refined by the full-matrix least-squares on F². CCDC-787350 contains the supplementary crystallographic data for this paper. This data can be obtained free of charge from the Cambridge Crystallographic Data Center via www.cam.ac.uk/data_request/cif.

Computational methods

The seed structure of 1a was extracted from the crystal structure of 1, while the initial structure of 1b was generated and then optimized by using SYBYL 6.8 software package (Tripos Inc., St. Louis, MO). For the minimization process, the following parameters were used: Tripos force field and Gasteiger–Hückel charge, distant-dependent dielectric constant of 4.0 R, 8 Å cutoff for non-bonded calculations, and conjugate gradient minimization until the RMS gradient in the energy was less than 0.05 kcal mol⁻¹. 10 ns restrained MD simulations were carried out on both 1a and 1b separately using the AMBER package (version 9.0) and the Parm99 force field.²⁰ Before simulations, the initial structure of both 1a and 1b was solvated using a box of TIP3P²¹water molecules extending at least 8 Å away from the boundary of any molecule atoms. The Particle Mesh Ewald (PME) method²² was employed to calculate the long-range electrostatics interactions. Both the MD runs were set up using the same protocol. First, each solvated conformation was subjected to steps of 1000 minimization using the steepest descent method followed by conjugate gradient to remove conflicts possibly existing between the solvent water and the molecules (1a and 1b). During this process, the molecules were fixed. Then, a second minimization of 1000 steps was performed on the entire molecule-water system.

The relaxed structures were then subjected to MD simulations. Each system was gradually heated from 0 K to 300 K in 20 ps, followed by a data collection run, giving a total simulation time of 10 020 ps. The non-bonded cutoff was set to 10.0 Å, and the non-bonded pairs were updated every 25 steps. The SHAKE²³ method was applied to constrain all covalent bonds involving hydrogen atoms. Each simulation was coupled to 300 K thermal bath at 1.0 atm pressure by applying the algorithm of Berendsen.²⁴ The temperature and pressure coupling parameters were set as 1 ps and 2 ps separately. An integration timestep of the MD simulations was 2 fs. In the energy minimizations and MD simulations, periodic boundary conditions were applied in all directions. In order to achieve an optimal low-energy conformer, ab initio quantum mechanics were applied in a second round of geometry optimization using Gaussian03 program.¹² The low-energy conformations of 1a and 1b without dramatic violations of experimentally validated restraints were relocated and confirmed by density functional theory (DFT) at B3LYP approximation level employing the 6-31G basis set.

Acknowledgements

We gratefully thank for the financial support from the program of NCET Foundation, the National Natural Science Foundation of China (30725045, 20972174 and 91029704), the Special Program for New Drug Innovation of the Ministry of Science and Technology, China (2009ZX09308-005, 2009ZX09311-001, 2008ZX09308-005), Shanghai Leading Academic Discipline Project(B906) and in part by the Scientific Foundation of Shanghai, China (09DZ1975700, 09DZ1971500), the State Key Program of Basic Research of China grant (2009CB918502).

References

1. (a) O. Atasoylu, G. Furst, C. Risatti and A. B. Smith III, Org. Lett., 2010, 12, 1788–1791; (b) A. Caporale, M. Sturlese, L. Gesiot, F. Zanta, A. Wittelsberger and C. Cabrele, J. Med. Chem., 2010, 28, 8072–8079; (c) H. Kessler, Angew. Chem., Int. Ed. Engl., 1982, 21, 512–523.
2. (a) G. Fischer, Chem. Soc. Rev., 2000, 29, 119–127; (b) C. Cox and T. Lectka, Acc. Chem. Res., 2000, 33, 849–858.
3. (a) E. K. Asciutto, J. D. Madura, S. S. Pochapsky, B. OuYang and T. C. Pochapsky, J. Mol. Biol., 2009, 388, 801–814; (b) A. H. Andreotti, Biochemistry, 2003, 42, 9515–9524; (c) W. J. Wedemeyer, E. Welker and H. A. Scheraga, Biochemistry, 2002, 41, 14637–14644; (d) P. Sarkar, C. Reichman, T. Saleh, R. B. Birge and C. G. Kalodimos, Mol. Cell, 2007, 25, 413–426.
4. (a) H. M. Zhong, W. Ni, Y. Hua and C. X. Chen, Acta Botanica Yunanica, 2002, 24, 781–786; (b) Z. T. Ding, Y. C. Wang, J. Zhou, N. H. Tan and H. M. Wu, Chin. Chem. Lett., 1999, 10, 1037–1040; (c) J. M. Tian, Y. H. Shen, X. W. Yang, S. Liang, J. Tang, L. Shan and W. D. Zhang, Org. Lett., 2009, 11, 1131–1133; (d) J. M. Tian, Y. H. Shen, X. W. Yang, S. Liang, L. Shan, H. L. Li, R. H. Liu and W. D. Zhang, J. Nat. Prod., 2010, 73, 1987–1992.
5. A. Wele, C. Mayer, Q. Dermigny, Y. Zhang, A. Blond and B. Bodo, Tetrahedron, 2008, 64, 154–162.
6. K. Fujii, Y. Ikai, H. Oka, M. Suzuki and K. I. Harada, Anal. Chem., 1997, 69, 5146–5151.
7. D. L. Herald, G. L. Cascarano, G. R. Pettit and J. K. Srirangam, J. Am. Chem. Soc., 1997, 119, 6962–6973.
8. (a) E. Vass, M. Hollosi, F. Besson and R. Buchet, Chem. Rev., 2003, 103, 1917–1954; (b) H. Kessler, J. W. Bats, C. Griesinger, S. Koll, M. Will and K. Wagner, J. Am. Chem. Soc., 1988, 110, 1033–1049.
9. (a) V. F. Bystrov, Prog. Nucl. Magn. Reson. Spectrosc., 1976, 10, 41–82; (b) H. Kessler, C. Griesinger and K. Wagner, J. Am. Chem. Soc., 1987, 109, 6927–6933.
10. T. Hwang and A. J. Shaka, J. Am. Chem. Soc., 1992, 114, 3157–3159.
11. E. Ammalahti, M. Bardet, D. Molko and J. Cadet, J. Magn. Reson., Ser. A, 1996, 122, 230–232.
12. M. J. Frisch, ( 2003)Gaussian 03, revision B.05 Gaussian, Inc, .
13. (a) T. S. Shi, S. M. Spain and D. L. Rabenstein, J. Am. Chem. Soc., 2004, 126, 790–796; (b) J. R. Alger and J. H. Prestegard, J. Magn. Reson., 1977, 27, 137–141.
14. S. Fischer, R. L. Dunbrack, Jr. and M. Karplus, J. Am. Chem. Soc., 1994, 116, 11931–11937.
15. (a) S. Fischer, S. Michnick and M. Karplus, Biochemistry, 1993, 32, 13830–13837; (b) J. Kallen and M. D. Walkinshaw, FEBS Lett., 1992, 300, 286–290.
16. (a) F. L. Texter, D. B. Spencer, R. Rosenstein and C. R. Matthews, Biochemistry, 1992, 31, 5687–5691; (b) U. Reimer, N. Mokdad, M. Schutkowski and G. Fischer, Biochemistry, 1997, 36, 13802–13808.
17. (a) C. K. Larive and D. L. Rabenstein, J. Am. Chem. Soc., 1993, 115, 2833–2836; (b) C. Cox and T. Lectka, J. Org. Chem., 1998, 63, 2426–2427.
18. E. Haslinger, H. Kalchhauser and P. Wolschann, Monatsh. Chem., 1984, 115, 779–783.
19. A. E. Aliev, D. Courtier-Murias, S. Bhandal and S. Zhou, Chem. Comm., 2010, 46, 695–697.
20. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
21. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
22. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
23. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
24. H. J. C. Berendsen, J. P. M. Postma, W. F. V. Gunsteren, A. DiNole and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.

---

Footnotes

† Electronic supplementary information (ESI) available: the detailed experimental and computational information and the NMR spectra of 1. CCDC reference number 787350. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1ra00593f

‡ These authors contributed equally to this work.

---