Towards a robust description of intrinsic protein disorder using nuclear magnetic resonance spectroscopy†
Robert
Schneider
,
Jie-rong
Huang
,
Mingxi
Yao
,
Guillaume
Communie
,
Valéry
Ozenne
,
Luca
Mollica
,
Loïc
Salmon
,
Malene
Ringkjøbing Jensen
and
Martin
Blackledge
*
Protein Dynamics and Flexibility, Institut de Biologie Structurale Jean-Pierre Ebel, CEA, CNRS, UJF UMR 5075, 41 Rue Jules Horowitz, Grenoble 38027, France. E-mail: martin.blackledge@ibs.fr; Tel: +33 4 38789554
First published on 26th August 2011
Abstract
In order to understand the conformational behaviour of Intrinsically Disordered Proteins (IDPs), it is essential to develop a molecular representation of the partially folded state. Due to the very large number of degrees of conformational freedom available to such a disordered system, this problem is highly underdetermined. Characterisation therefore requires extensive experimental data, and novel analytical tools are required to exploit the specific conformational sensitivity of different experimental parameters. In this review we concentrate on the use of nuclear magnetic resonance (NMR) spectroscopy for the study of conformational behaviour of IDPs at atomic resolution. Each experimental NMR parameter is sensitive to different aspects of the structural and dynamic behaviour of the disordered state and requires specific consideration of the relevant averaging properties of the physical interaction. In this review we present recent advances in the description of disordered proteins and the selection of representative ensembles on the basis of experimental data using statistical coil sampling from flexible-meccano and ensemble selection using ASTEROIDS. Using these tools we aim to develop a unified molecular representation of the disordered state, combining complementary data sets to extract a meaningful description of the conformational behaviour of the protein.
Introduction
One of the most remarkable discoveries of protein science over the last decade concerns the revelation that a large fraction of functional proteins encoded by the human genome is either fully disordered or contains long disordered regions.1–4 Intrinsically disordered proteins (IDPs) remained beyond the scope of classical structural biology, and therefore escaped the attention of the multiplication of structural genomics projects that have emerged in the hope of classifying all protein folds. IDPs are biologically functional despite a lack of stable, well-defined three-dimensional structural fold, and as such they impose a different perspective on the relationship between primary protein sequence and function. IDPs are also strongly involved in numerous human pathologies, and the development of pharmacological solutions to these problems awaits a molecular description of the role of flexibility in the development of disease.5–7Proteins present a vast spectrum of flexibility in their physiological states, from stable enzymes to highly flexible chains. In analogy to folded proteins, the primary sequence predetermines the functional behaviour of the protein, but in this case, rather than focussing on a unique fold that stabilizes the protein, and considering the role of local structure and dynamics relative to this scaffold, we are forced to consider the more central role that conformational flexibility plays in the function of the intrinsically disordered state. The determination of a single structure has no real physical relevance, at least in the free form of such proteins, and there is therefore a pressing need for the development of an entirely new set of experimental and descriptive approaches to describe the conformational behaviour of IDPs.8–11One obvious aim of a structural description of IDPs is to determine rules that define the behaviour of the flexible protein in terms of probability to populate a defined region of conformational space. This is often achieved by evoking an explicit ensemble description of interconverting structures, whose populations are interpreted in terms of a population-weighted distribution that represents the true conformational equilibrium. However the definition of this distribution is no easy task. IDPs populate a vast conformational space, and the mapping of this potential energy landscape represents a classical ill-posed problem, in which the number and complexity of the available degrees of conformational freedom far outweigh the accessible experimental data that can be measured for a particular system. Some caution therefore needs to be exercised when treating such under-determined systems, where the development of an ensemble description that is in agreement with the experimental data may not ensure that the associated conformational sampling is correct. The development of robust procedures that address this issue is of paramount importance.
NMR of intrinsically disordered proteins
Characterisation of the diverse conformational properties of the unfolded protein cannot be based solely on a single experimental technique, but necessarily relies on the exploitation of complementary approaches reporting on both short range and long-range structural parameters. It is also essential to consider the time scales that characterise local and global motions and the inter-conversion rates of different members of a conformational ensemble. Nuclear magnetic resonance (NMR) spectroscopy is particularly rich in both short range and long-range structural information that can be exploited to accurately define the behaviour of IDPs.12 Despite a comparatively restricted amide proton chemical shift dispersion, NMR signals retain the spectroscopic characteristics of small molecules, because of the flexibility of the chain, so that heteronuclear chemical shift assignment remains possible, even for very large intrinsically disordered proteins.13 Molecular weight restrictions that apply to folded proteins therefore do not extend in the same way to intrinsically disordered proteins of the same number of amino acids.Most importantly NMR provides access to ensemble and time averaged conformationally dependent parameters at atomic resolution. The measurement of structurally dependent parameters inherently provides a basic tool to study local conformational propensities that may be important for folding upon binding,14 and transient or persistent long-range contacts or tertiary structure that may also play a role in molecular interactions.14–16 In this article we describe advances of some NMR-based techniques that have taken place in recent years for the description of the conformational behaviour of IDPs.17–19
The chemical shift of a specific nucleus reports on the local physico-chemical environment of the nucleus, and in the presence of conformational flexibility, depends on a population-weighted average over local conformations sampled by all molecules in the ensemble that are exchanging on timescales faster than the millisecond. This timescale therefore dictates our interpretation of all NMR parameters that are measured from this chemical shift averaging process. The chemical shift can also provide information about the local structural propensity20 that can be detected in intrinsically disordered proteins by analyzing the deviation of measured parameters from the expected value that would be measured in the absence of any local structure (the so-called ‘random coil’ value).21,22 The absolute definition of a random coil remains open to argument, in most cases amino-acid specific values are measured experimentally from small peptides with no apparent local structure.23–25 The chemical shift provides a sensitive probe of local structural sampling, in particular 13C shifts, whose values depend, in order of importance, on the covalent structure (13Cα, 13Cβ or 13C′), the type of amino acid, and finally on the local structural propensity which is the parameter of interest. The difference between the measured shift and the amino-acid specific random coil shift, known as the ‘secondary’ chemical shift, is commonly used to identify the presence of transient structure in flexible chains.26–28 Scalar couplings between nuclei on the backbone of the protein also depend on backbone dihedral angles and average in a similar way to chemical shifts.29–31 Again random coil values have been measured in small peptides and these values can be compared to experimental values to determine the level of transient local structure.
Residual dipolar couplings (RDCs), measured between pairs of nuclei, are also extremely promising tools for studying the conformational behaviour of disordered proteins.32–36 RDCs become measurable when the protein of interest is dissolved in a dilute liquid crystalline medium, such that the average dipolar coupling, normally averaged to zero in free solution, has a residual, non-zero value.37–39 Under these conditions RDCs depend on the average over the ensemble of orientations of the vector connecting the two spins in the following way:
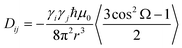 | (1) |
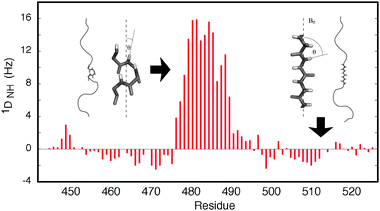 | ||
| Fig. 1 Illustration of the sensitivity of RDCs to the presence of local structure. The orientational dependence shown in eqn (1) results in positive 1DNH RDCs for the central helical element, where the NH bond vectors tend to be aligned with the field, while in the disordered regions the RDCs are negative, because the average orientation is perpendicular to the direction of the chain. | ||
Disordered proteins often exhibit evidence of fluctuating long-range tertiary structure, that may be important for physiological interactions, for example via so-called fly-casting interactions,16 in the control of early folding events, or to provide protection from aggregation or proteolysis. While it is difficult to detect such transient contacts via standard approaches to the measurement of internuclear distances, using 1H–1H cross relaxation, the detection of such long-range information is possible by exploiting the strength of the dipolar relaxation between the nuclear spin and an unpaired electron that can be introduced into the protein by attaching a nitroxide group to a cysteine mutant.48–50 Because the gyromagnetic ratio of the electron spin is over 600 times higher than the proton spin, the observed line broadening due to the paramagnetic relaxation enhancement provides long-range probes of intra- and intermolecular distances and distance distribution functions that can be detected even if only weakly populated.51–57
A number of additional NMR parameters can be used to characterize the unfolded state: the most common are pulse-field gradient spin echo experiments,58 that report on the population weighted average translational diffusion properties of the chain and heteronuclear spin relaxation, that report on local order on picosecond to nanosecond timescales.59–61 The complementary information available from small angle X-ray scattering that reports on the average mass distribution in three dimensional space, and therefore the dimensions of the ensemble of structures, is also often exploited in combination with NMR data to provide a more complete picture of the disordered state.62–68
Ensemble descriptions of IDPs from NMR data
Despite remarkable progress in recent years, the transformation of these highly diverse experimental parameters into a meaningful conformational description remains a key challenge for contemporary structural biologists. The most common approach that has been applied over recent years borrows tools developed for the determination of the structure of proteins in solution, where additional terms are incorporated into a physical potential energy function to bias the conformational sampling. A restrained molecular dynamics (MD) simulation, run in parallel over different members of the ensemble, is then used to drive the ensemble into a region of conformational space that is in agreement with experimental data.69–74 Despite the popularity of such techniques, a number of key questions remain open with respect to their generalisation. It is not clear how the introduction of non-physical parameters into the force field will affect the ability of the molecular dynamics engine to efficiently search conformational phase space, or its ability to sample a Boltzmann-weighted distribution of conformers. It is also unclear how to optimize the number of structures present in the ensemble average, a feature that will depend strongly on the density and information content of the experimental parameters. A more general problem, that is shared by all approaches to the interpretation of experimental data from disordered states, concerns the characteristic averaging timescales of each experimental parameter that must be properly accounted for within the conformational ensemble.An entirely different approach does not use the experimental data to drive the individual members of the ensemble into a conformation in agreement with the experimental data, but instead samples conformational space as broadly as possible, and then exploits the experimental data to define the region of conformational space that is appropriate for the system under investigation. Enhanced molecular dynamics approaches such as accelerated molecular dynamics have been used in this way to study intrinsic dynamics in folded proteins,44,75,76 although the potential extent of conformational space available to IDPs complicates the successful application of such approaches to these highly flexible systems. An alternative strategy is to attempt to flood conformational space by creating a statistical coil model of the protein based on the intrinsic conformational behaviour of each amino acid, derived for example from backbone dihedral angle distributions found in loop regions of protein structures.77–79
An explicit ensemble description of IDPs, called flexible-meccano, builds multiple copies of the protein that are ensemble designed to represent all possible states that are relevant for the NMR observable.35Flexible-meccano randomly samples amino-acid-specific backbone dihedral angle {ϕ/ψ} propensities derived from non-secondary structural elements of high-resolution X-ray crystallographic structures,80 and thereby assembles a conformational ensemble from which experimental values can be calculated. Amino-acid specific hard-sphere steric clashes are used to provide a physically reasonable model of repulsive interatomic forces, and no attractive forces are explicitly used. The simplicity of the model allows for highly efficient structure ensemble assembly (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures of a 100 amino acid protein can be created in 30 minutes on a single processor). The ensembles are randomly sampled from population-weighted distributions that are taken to represent the potential energy surface of each amino acid. Although this does not guarantee a Boltzmann distribution, the absence of additional constraints in this sampling phase avoids distortions due to additional potential energy terms such as those used in restrained MD calculations.
000 structures of a 100 amino acid protein can be created in 30 minutes on a single processor). The ensembles are randomly sampled from population-weighted distributions that are taken to represent the potential energy surface of each amino acid. Although this does not guarantee a Boltzmann distribution, the absence of additional constraints in this sampling phase avoids distortions due to additional potential energy terms such as those used in restrained MD calculations.
The presence of a single set of signals detected in NMR spectra of denatured and intrinsically disordered proteins imposes the implicit assumption that all conformers used to predict an experimental value are in rapid exchange on timescales faster than the millisecond. The ensemble of structures can then be used to predict experimental values that would be measured if the statistical coil model were relevant. For the prediction of chemical shifts and scalar couplings, local structural information is sufficient to predict the expected value, while for RDCs the calculation of the expected alignment of each conformer is necessary before averaging over the ensemble. In the most common case of steric alignment this calculation is performed on the basis of the three dimensional shape of the protein.81
RDCs simulated using this very simple approach predict values in reasonable agreement with experimental couplings measured in both intrinsically disordered and chemically denatured proteins. Initial studies already indicated that the orientational space sampled by inter-nuclear bond-vectors from RDCs is sensitive enough to pick up differences in amino-acid specific backbone dihedral angle distributions, even in the absence of secondary structural propensity.10,35Flexible-meccano has also been used in combination with molecular dynamics based simulations, to quantify the level of β-turn propensity in the K18 domain of the protein Tau82 and α-helical propensity in the transactivation domain of the protein p53.83
While N–HN RDCs alone have been shown to provide evidence for local structural propensity, the measurement of multiple RDCs from each peptide unit provides the necessary information to make quantitative estimates of the detail and population of the structural elements. Thus, the combination of RDCs from different bond-vectors (N–HN, Hα–Cα, C′–HN, Cα–C′) was also shown to be crucial to the description of the length and population of different helical structures that form the rapidly exchanging conformational equilibrium of the molecular recognition element of the disordered C-terminal domain of the nucleoproteins from Sendai and measles viruses.84,85 In this case entire ensembles of all possible helical elements were calculated, and the minimum combination that could reproduce the experimental data was determined, along with their associated populations. Remarkably, in both cases, the helical elements present in the molecular recognition elements that were significantly populated in solution were found to follow amino acids with known propensity to stabilize helices in free solution.85 An extensive set of RDCs, including a large number of long-range 1H–1H couplings, were measured in the protein Ubiquitin in its denatured state,87 and used in combination with flexible-meccano to identify modifications of the statistical coil model that are appropriate to account for conformational sampling of the unfolded chain in the presence of the denaturant.88,89
The statistical coil description of the disordered state thus provides a relatively straightforward approach for calculating RDC profiles that would be expected if the protein behaved as a random coil. The establishment of such approaches is essential in order to develop a clear understanding of the origin of experimentally observed fluctuations in the absence and in the presence of specific or persistent local or long-range structure. However the next step, requiring the quantitative interpretation of departures from expected random coil values in terms of specific local or long-range conformational behaviour, is of equal importance and fundamentally more challenging.10,90,91
Determination of meaningful ensembles in agreement with experimental data
A number of studies have applied a rational, hypothesis-based approach, calculating explicit ensembles containing tens of thousands of conformers from different conformational sampling regimes and comparing the ensemble-averaged couplings to experimental data. In some case this is achieved with the aid of molecular dynamics simulation to create alternative conformational sampling that provides agreement with experimental data.82,83 While these studies are informative and important to advance our understanding of the field, in order to generalize the methodology it is necessary to take the analysis one step further, and develop approaches that can accurately define the conformational sampling of the peptide chain directly from the experimental NMR data.In order to address this issue, the ensemble selection algorithm, ASTEROIDS (A Selection Tool for Ensemble Representation Of Intrinsically Disordered States) has been developed to determine appropriate regions of conformational space populated by the IDP by selection of conformers from the flexible-meccano ensemble using experimental NMR data.92–94 The ASTEROIDS algorithm is based on an efficient genetic algorithm that is used to propose conformational ensemble descriptions selected from a large pool of possible conformers that are in agreement with the experimental data. In order to identify conditions under which an approach that evokes a sub-ensemble of structures can be accurately applied to describe a pseudo-continuum of conformers, we systematically adopt the following simple procedure that clearly quantifies the conformational accuracy of such approaches: (1) Data are simulated under specific conditions of conformational sampling and appropriately averaged over an ensemble of a very large number of conformers (between 50 and 100 thousands). (2) Sub-ensembles of tractable size are generated using ASTEROIDS to be in agreement with these data, and the conformational sampling represented in these ensembles is compared to the target sampling used in step (1) to generate the data.
One of the most important problems encountered in the treatment of RDCs derives from the large number of structures required before a simple arithmetic average reaches convergence. The reason for this is that, in addition to the obvious dependence on local conformational sampling, the RDCs for each individual conformer depend on conformational degrees of freedom throughout the molecule, that each define the shape of the protein, and therefore the size and distribution of the RDCs. Indeed, convergence of RDCs from a 76 amino acid chain is not yet achieved in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures. More rapid convergence of RDCs can be achieved using a smaller number of conformers if the protein were divided into short, uncoupled segments (Local Alignment Windows—LAWs) and the RDCs are calculated using the alignment tensor of these segments.95 This is an important result: the ability to describe the conformational properties using fewer structures renders ensemble selection more tractable.
000 structures. More rapid convergence of RDCs can be achieved using a smaller number of conformers if the protein were divided into short, uncoupled segments (Local Alignment Windows—LAWs) and the RDCs are calculated using the alignment tensor of these segments.95 This is an important result: the ability to describe the conformational properties using fewer structures renders ensemble selection more tractable.
However there are important aspects that need to be addressed before such approaches can be used to explain experimental data. Adopting the procedures described above, RDCs were calculated using specific conformational sampling regimes averaged over a large ensemble.92 The average RDCs were then used, in combination with a 15 amino acid window, to select different sized ensembles of conformers from a large pool in agreement with the data. The results demonstrated that ensembles that evoked only 20 structures reproduced the experimental data, but critically did not reproduce the backbone dihedral angle distributions that were at the origin of the average. Only when at least 200 structures were used in the average was the conformational behaviour sufficiently well reproduced. The reason for this is the instability of adding additional RDCs to an ensemble where the average is not yet converged.
The revelation that experimental data can be reproduced by an ensemble of structures that does not represent the correct conformational sampling was initially surprising to us, although this appears to be a predictable manifestation of the potential pit-falls of deriving ensembles under such under-determined conditions. The result has particular importance, and highlights the risks of reducing the number of members of a conformational average until the data are reproduced. Such a procedure can clearly produce ensembles whose local conformational sampling is quantitatively incorrect, while reproducing experimental data.
Secondly, and possibly more critically, approaches that only use a LAW to analyze RDCs patently ignore the fact that RDCs are affected both by the local conformational sampling and long-range order. This is important even in the absence of specific long-range contacts, because the chain-like nature of the unfolded protein induces an effective baseline reflecting the increasing degrees of freedom available towards the ends of the chain (Fig. 2a and h). Long-range information is necessarily absent from an approach that only employs LAWs to predict the RDCs. If this approach is employed the simulated data need to be corrected for the effects of the unfolded chain. This can be achieved when LAW-predicted RDCs are multiplied by the expected baseline of an unfolded chain, whose bell-shaped dependence can be parameterised by fitting to numerical simulation.
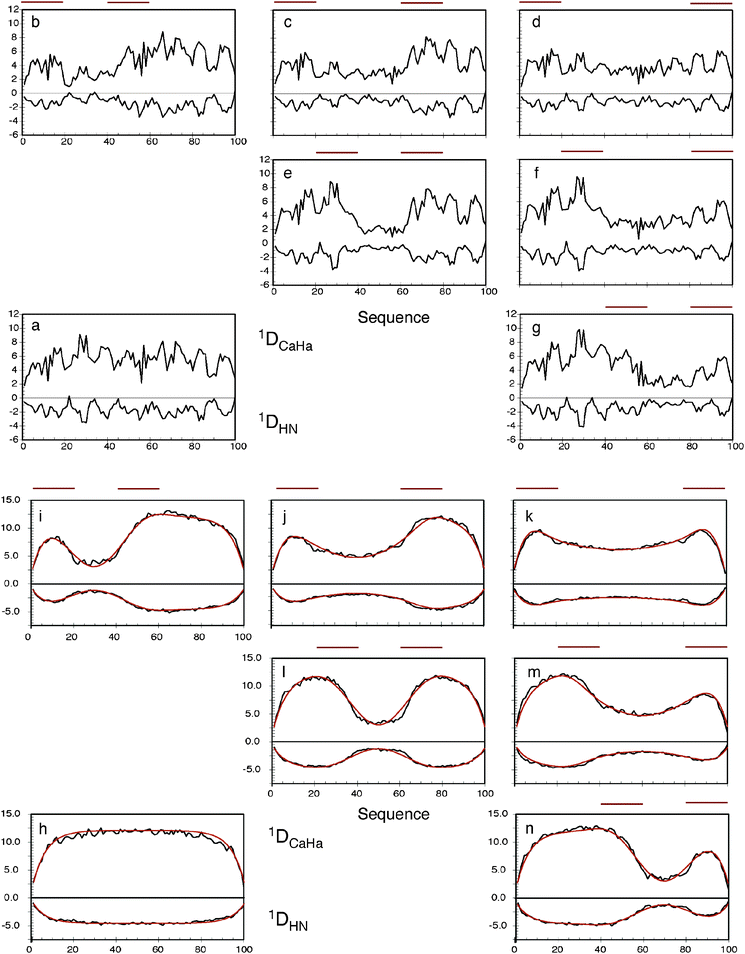 | ||
Fig. 2 The effects of long-range contacts on expected RDC profiles. Top: (a) 1DNH and 1DCaHa RDCs calculated for a 100 amino acid sequence in the absence of specific contacts. The program PALES was used to calculate RDCs from each conformer. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformers were used in this and each average shown in figures (b–n). (b–g) The same calculation is performed, but conformers are only retained in the ensemble if at least one inter-Cβ distance exists between the primary sequence ranges shown below the red lines: (b) i = 1–20, j = 41–60, (c) i = 1–20, j = 61–80, (d) i = 1–20, j = 81–100, (e) i = 21–40, j = 61–80, (f) i = 21–40, j = 81–100, (g) i = 41–60, j = 81–100. Bottom: (h) 1DNH and 1DCaHa RDCs calculated for a 100 amino acid poly-valine sequence in the absence of specific contacts. (i–n) The same calculation is performed, but conformers are only retained in the ensemble if at least one inter-Cβ distance exists between the primary sequence ranges shown below the red lines: (i) i = 1–20, j = 41–60, (j) i = 1–20, j = 61–80, (k) i = 1–20, j = 81–100, (l) i = 21–40, j = 61–80, (m) i = 21–40, j = 81–100, (n) i = 41–60, j = 81–100. The dark red curves show the analytical reproduction of the long-range effects on the RDCs with the contact positioned in the centre of each region. Reprinted with permission from the Journal of the American Chemical Society.93 000 conformers were used in this and each average shown in figures (b–n). (b–g) The same calculation is performed, but conformers are only retained in the ensemble if at least one inter-Cβ distance exists between the primary sequence ranges shown below the red lines: (b) i = 1–20, j = 41–60, (c) i = 1–20, j = 61–80, (d) i = 1–20, j = 81–100, (e) i = 21–40, j = 61–80, (f) i = 21–40, j = 81–100, (g) i = 41–60, j = 81–100. Bottom: (h) 1DNH and 1DCaHa RDCs calculated for a 100 amino acid poly-valine sequence in the absence of specific contacts. (i–n) The same calculation is performed, but conformers are only retained in the ensemble if at least one inter-Cβ distance exists between the primary sequence ranges shown below the red lines: (i) i = 1–20, j = 41–60, (j) i = 1–20, j = 61–80, (k) i = 1–20, j = 81–100, (l) i = 21–40, j = 61–80, (m) i = 21–40, j = 81–100, (n) i = 41–60, j = 81–100. The dark red curves show the analytical reproduction of the long-range effects on the RDCs with the contact positioned in the centre of each region. Reprinted with permission from the Journal of the American Chemical Society.93 | ||
The effects of ignoring long-range contacts when analyzing RDCs from disordered chains can however be much more severe when preferential long-range contacts exist in the protein, as demonstrated by the following simulations: RDCs were predicted from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 strong ensembles using the flexible-meccano simulations of a 100 amino acid model sequence in the presence of weakly defined long-range contacts, defined as a contact between any of two 20 amino acid strands (Fig. 2). In comparison to the expected values for a chain with no specific long-range contacts, the effect is significant, even for such diffuse long-range contacts. Simulation predicts significant quenching of RDC values in regions between the two contact regions. Importantly, although the local conformational sampling is not measurably affected by the contacts, the resulting RDCs are very different because of the transient long-range order that is also present. This again demonstrates that extreme caution needs to be exercised when interpreting RDCs uniquely in terms of the local structure. Comparison with identical simulations for a poly-valine indicates that the actual effect of diffuse long-range contacts is to convolute a more complex ‘baseline’ on the local structure of the expected RDCs. Fortunately a generic mathematical expression that accurately models the form of this baseline can be derived that reproduces the numerically predicted baselines shown in Fig. 2, which depends only on the position of the contacts and the length of the chain. The consequences of this are that long-range information, for example derived from paramagnetic relaxation enhancement (vide infra), can be combined with the efficient sliding window approach, to simultaneously account for both aspects within the same ensemble average (Fig. 3).93
000 strong ensembles using the flexible-meccano simulations of a 100 amino acid model sequence in the presence of weakly defined long-range contacts, defined as a contact between any of two 20 amino acid strands (Fig. 2). In comparison to the expected values for a chain with no specific long-range contacts, the effect is significant, even for such diffuse long-range contacts. Simulation predicts significant quenching of RDC values in regions between the two contact regions. Importantly, although the local conformational sampling is not measurably affected by the contacts, the resulting RDCs are very different because of the transient long-range order that is also present. This again demonstrates that extreme caution needs to be exercised when interpreting RDCs uniquely in terms of the local structure. Comparison with identical simulations for a poly-valine indicates that the actual effect of diffuse long-range contacts is to convolute a more complex ‘baseline’ on the local structure of the expected RDCs. Fortunately a generic mathematical expression that accurately models the form of this baseline can be derived that reproduces the numerically predicted baselines shown in Fig. 2, which depends only on the position of the contacts and the length of the chain. The consequences of this are that long-range information, for example derived from paramagnetic relaxation enhancement (vide infra), can be combined with the efficient sliding window approach, to simultaneously account for both aspects within the same ensemble average (Fig. 3).93
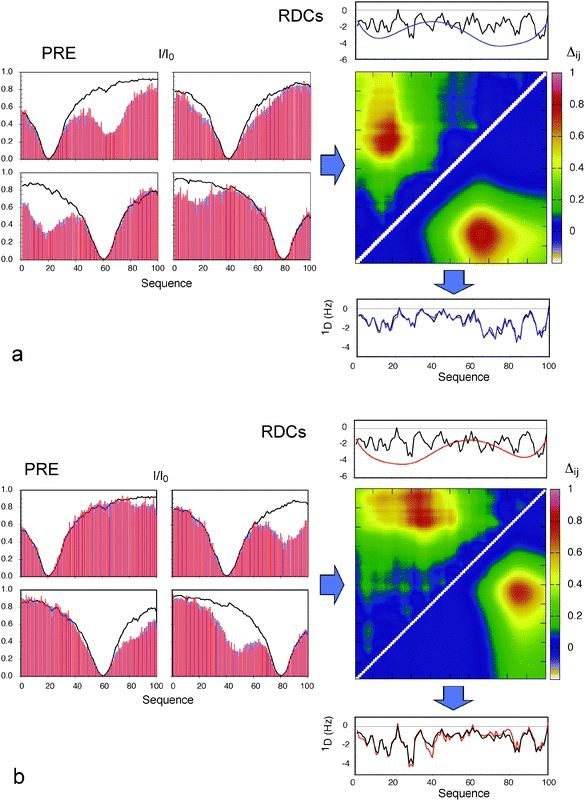 | ||
Fig. 3 Combination of effects of long-range order derived from PREs with local conformational sampling using local alignment windows for the interpretation of RDCs. (a) Blue: Data averaged over the target ensemble where each conformer has a contact between 11–20 and 61–70. Red: Average PREs over an ensemble of 80 structures selected using ASTEROIDS. The four boxes show the PRE data for simulated spin labels at residues 20 (top left), 40 (top right), 60 (bottom left) and 80 (bottom right). Lines show the PREs calculated from a control ensemble with no specific contacts. The distance matrix shows the chain proximity in the ensembles selected using ASTEROIDS (above the diagonal), compared to target ensembles (below the diagonal). Average distances between sites are shown in terms of: Δij = log(〈d0ij〉/〈dij〉) where dij is the distance in any given structure of the ASTEROIDS ensemble between sites i and j, and d0ij is the distance in any given structure of the reference ensemble between sites i and j. Values above the diagonal have been multiplied by 2 for ease of identification of the contact. Top: Black: RDCs calculated using the local alignment window (LAW). Blue: Predicted effect of the long-range contact detected using the ASTEROIDS interpretation of the PREs. Bottom: Combination (purple) of the two curves shown in the top panel and RDCs averaged over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 full length conformers where each structure has a contact between 41–50 and 81–90 (black). (b) Blue: Data averaged over the target ensemble where each conformer has a contact between 41–50 and 81–90. Red: Average PREs over an ensemble of 80 structures selected using ASTEROIDS. The four boxes show the PRE data for simulated spin labels at residues 20 (top left), 40 (top right), 60 (bottom left) and 80 (bottom right). Lines show the PREs calculated from a control ensemble with no specific contacts. The distance matrix shows the chain proximity in the ensembles selected using ASTEROIDS (above the diagonal), compared to target ensembles (below the diagonal). Values above the diagonal have been multiplied by 2 for ease of identification of the contact. Top: Black: RDCs calculated using the local alignment window (LAW). Blue: Predicted effect of the long-range contact detected using the ASTEROIDS interpretation of the PREs. Bottom: Combination (purple) of the two curves shown in the top panel and RDCs averaged over 100 000 full length conformers where each structure has a contact between 41–50 and 81–90 (black). (b) Blue: Data averaged over the target ensemble where each conformer has a contact between 41–50 and 81–90. Red: Average PREs over an ensemble of 80 structures selected using ASTEROIDS. The four boxes show the PRE data for simulated spin labels at residues 20 (top left), 40 (top right), 60 (bottom left) and 80 (bottom right). Lines show the PREs calculated from a control ensemble with no specific contacts. The distance matrix shows the chain proximity in the ensembles selected using ASTEROIDS (above the diagonal), compared to target ensembles (below the diagonal). Values above the diagonal have been multiplied by 2 for ease of identification of the contact. Top: Black: RDCs calculated using the local alignment window (LAW). Blue: Predicted effect of the long-range contact detected using the ASTEROIDS interpretation of the PREs. Bottom: Combination (purple) of the two curves shown in the top panel and RDCs averaged over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 full length conformers where each structure has a contact between 11–20 and 61–70 (black). Reprinted with permission from the Journal of the American Chemical Society.93 000 full length conformers where each structure has a contact between 11–20 and 61–70 (black). Reprinted with permission from the Journal of the American Chemical Society.93 | ||
Combining RDCs and PREs in a single conformational ensemble
Similar analyses were applied to the interpretation of paramagnetic relaxation enhancements in disordered systems. We again use flexible-meccano, in combination with ASTEROIDS, to model intermolecular contacts giving rise to experimental PRE in disordered proteins. One important result demonstrates that even in the presence of highly diffuse, ill-defined target interactions, explicit modelling of spin label mobility significantly improves reproduction of conformational sampling, both for experimental and simulated data. We find that intermolecular contacts can be identified using 4 strategically placed spin labels in a 100 amino acid protein (Fig. 3) (and that two contacts can be identified using 8 spin labels in a 200 amino acid protein). Of course the ability to detect the transient contacts, and more importantly to estimate their population, strongly depends on the number of cysteine mutants that are available for the study.71 Using cross validation of an entire data set that is not used in the analysis, we are also able to determine the appropriate number of structures necessary to define the system.The ability to combine long-range information from PREs and RDCs in this way represents a major step forward in our ability to describe highly disordered systems. As an example, we applied these methods to experimental PRE and RDC data from α-Synuclein.57,96 Experimentally measured RDCs agree significantly better when a long-range contact between the N and C terminal domains, derived from PREs, is included in the RDC analysis (rmsd of 0.51 compared to 0.75). This not only validates the predicted effects on RDC profiles due to long-range transient contacts in disordered systems, but also demonstrates that PREs and RDCs can be meaningfully combined to understand experimental data (Fig. 4).
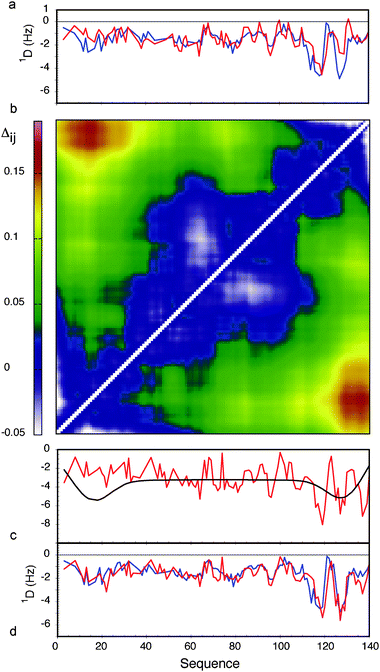 | ||
| Fig. 4 Combined analysis of PREs and RDCs in the context of experimental data from α-synuclein. (a) Comparison of experimental 1DNH RDCs with couplings calculated using a standard flexible-meccano prediction (red). The rmsd between the two distributions is 0.78 Hz. (b) Contact map showing the relative proximity of different parts of the chain in α-synuclein, derived from experimental PRE data. Average distances between sites are shown in terms of: Δij = log(〈dij〉〈d0ij〉) where dij is the distance in any given structure of the ASTEROIDS ensemble between sites i and j, and d0ij is the distance in any given structure of the reference ensemble between sites i and j. (c) LAW-predicted RDCs (red) and effective baseline derived from the distance matrix shown in (b). (d) Combination of the curves shown in (c) (red) in comparison to the experimental 1DNH RDCs (rmsd = 0.52 Hz). Reprinted with permission from the Journal of the American Chemical Society.93 | ||
Defining conformational ensembles of IDPs from chemical shifts
Finally we have applied the flexible-meccano/ASTEROIDS combination to explore the possibility of using chemical shifts alone to map local backbone conformational sampling of intrinsically disordered and partially folded proteins (Fig. 5).9713Cα, 13Cβ, 13C′ and 15N chemical shifts have different backbone ϕ/ψ dihedral angle dependences that are complementary in terms of the mapping of different regions of the Ramachandran space. 13Cα and 13Cβ secondary shifts report essentially on the Ramachandran space sampled by the observed amino acid, while both 13C′ and 15N are also sensitive to the sampling properties of the neighbouring amino acids. ASTEROIDS is used to select a 200-strong sub-ensemble out of a larger pool (typically 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures) constructed by flexible-meccano that is in agreement with the experimental 13Cα, 13Cβ, 13C′ and 15N chemical shifts (Fig. 6). The program SPARTA98 is used to calculate chemical shifts for each member of the ensemble. No assumptions are made about the secondary structural propensity, with the first ensemble containing only unfolded structures derived from the statistical coil database. The local conformational bias is identified automatically on the basis of chemical shifts, and the resulting propensities are then used to assemble the new database for the next iteration. The algorithm thus automatically resolves the backbone dihedral angle distributions for the construction of entire secondary structural elements, as well as identifying local conformational sampling in unfolded domains. The analysis was applied to the study of NTAIL, the C-terminal domain of the Sendai virus nucleoprotein, which contains a conformationally fluctuating helical element at its centre. Excellent agreement with experimental shifts is observed throughout the protein. Here again we are able to cross-validate the conformational description against independent data sets (1DNH dipolar couplings or 15N chemical shifts) to demonstrate both the accuracy of the description and the predictive power of the approach (Fig. 6). Although the conformational information is not as rich as that provided by RDCs, this approach raises the exciting prospect of probing the conformational behaviour of disordered proteins under more demanding conditions where additional parameters cannot be easily measured, for example when studying IDPs in situ.86
000 structures) constructed by flexible-meccano that is in agreement with the experimental 13Cα, 13Cβ, 13C′ and 15N chemical shifts (Fig. 6). The program SPARTA98 is used to calculate chemical shifts for each member of the ensemble. No assumptions are made about the secondary structural propensity, with the first ensemble containing only unfolded structures derived from the statistical coil database. The local conformational bias is identified automatically on the basis of chemical shifts, and the resulting propensities are then used to assemble the new database for the next iteration. The algorithm thus automatically resolves the backbone dihedral angle distributions for the construction of entire secondary structural elements, as well as identifying local conformational sampling in unfolded domains. The analysis was applied to the study of NTAIL, the C-terminal domain of the Sendai virus nucleoprotein, which contains a conformationally fluctuating helical element at its centre. Excellent agreement with experimental shifts is observed throughout the protein. Here again we are able to cross-validate the conformational description against independent data sets (1DNH dipolar couplings or 15N chemical shifts) to demonstrate both the accuracy of the description and the predictive power of the approach (Fig. 6). Although the conformational information is not as rich as that provided by RDCs, this approach raises the exciting prospect of probing the conformational behaviour of disordered proteins under more demanding conditions where additional parameters cannot be easily measured, for example when studying IDPs in situ.86
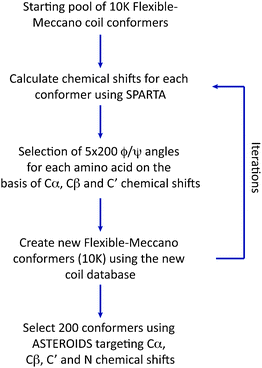 | ||
| Fig. 5 Flowchart showing the iterative construction of a conformational ensemble using ASTEROIDS on the basis of heteronuclear chemical shifts. | ||
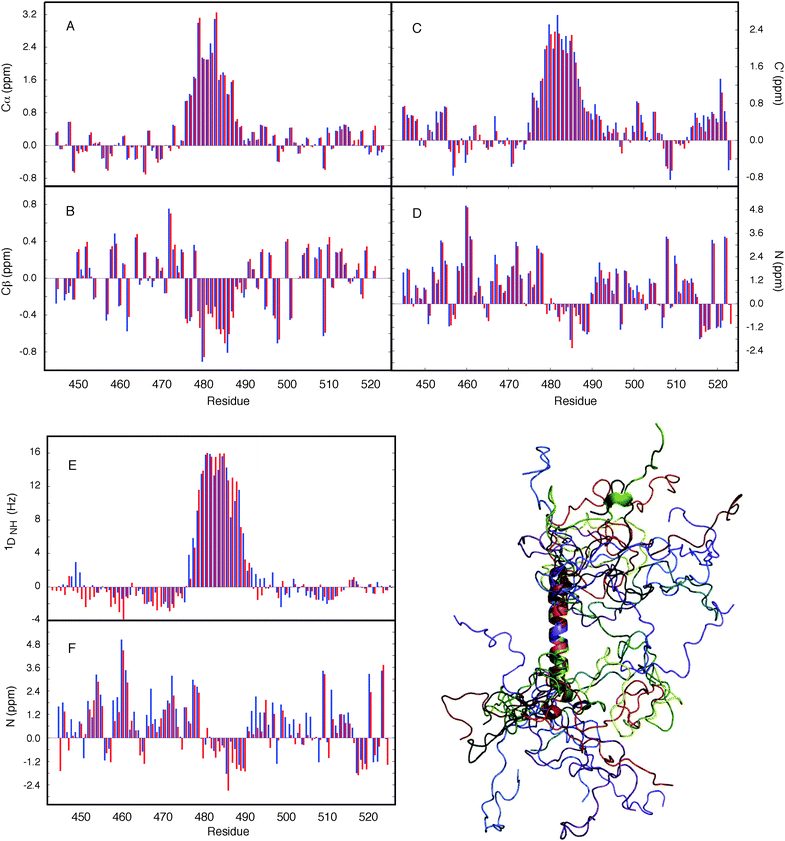 | ||
Fig. 6 Application of ASTEROIDS to ensemble representation on the basis of chemical shifts. Secondary chemical shifts from an ensemble of 200 structures determined using the ASTEROIDS algorithm compared to experimental secondary chemical shifts (blue). Red: secondary chemical shifts averaged over the final ensemble. (A) α carbon, (B) β carbon, (C) carbonyl, (D) amide nitrogen. (E, F) Reproduction of independent parameters by the ensemble based on chemical shift selection. (E) 15N–1H residual dipolar couplings (RDCs) measured in sterically aligned NTAIL compared to averages over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformers calculated using the amino acid specific description of NTAIL determined from the chemical shifts. Simulated data (red) were scaled uniformly to best match experiment (blue). (F) Reproduction of 15N secondary chemical shifts (blue: experiment, red: simulation), calculated using an ensemble determined from only 13C shifts. Reprinted with permission from the Journal of the American Chemical Society.97 000 conformers calculated using the amino acid specific description of NTAIL determined from the chemical shifts. Simulated data (red) were scaled uniformly to best match experiment (blue). (F) Reproduction of 15N secondary chemical shifts (blue: experiment, red: simulation), calculated using an ensemble determined from only 13C shifts. Reprinted with permission from the Journal of the American Chemical Society.97 | ||
Conclusions
In order to understand the conformational behaviour of IDPs, a molecular representation of the partially folded state is required. We have developed ensemble approaches that characterize the disordered state, initially comparing free statistical coil simulations with measured data in order to understand expected random coil values of the different experimental parameters. Deviations from expected values allowed us to identify the presence of secondary structural propensity in a number of IDPs. We have then developed an ensemble description approach, initially for the study of helical elements in viral proteins from Sendai and Measles, then applied more generally for any disordered system. This problem is highly underdetermined, and each experimental NMR parameter requires specific consideration of the relevant averaging properties of the physical interaction responsible for the experimental observable, before valid parameter ranges and procedures can be established. The resulting approach, ASTEROIDS, can now be used to combine different sources of experimental NMR data, for example RDCs, PREs and chemical shifts, to define the conformational behaviour of the protein, and hopefully to follow the changes in conformational equilibrium that accompany physiologically relevant interactions.References
- V. N. Uversky, Protein Sci., 2002, 11, 739–756 CrossRef CAS.
- A. K. Dunker, C. J. Brown, J. D. Lawson, L. M. Iakoucheva and Z. Obradović, Biochemistry, 2002, 41, 6573–6582 CrossRef CAS.
- P. Tompa, Trends Biochem. Sci., 2002, 27, 527–533 CrossRef CAS.
- H. J. Dyson and P. E. Wright, Curr. Opin. Struct. Biol., 2002, 12, 54–60 CrossRef CAS.
- A. K. Dunker and V. N. Uversky, Curr. Opin. Pharmacol., 2010, 10, 782–788 CrossRef CAS.
- M. M. Babu, R. van der Lee, N. S. de Groot and J. Gsponer, Curr. Opin. Struct. Biol., 2011, 21, 432–440 CrossRef CAS.
- M. Vendruscolo and C. M. Dobson, Nature, 2007, 449, 555 CrossRef CAS.
- T. Mittag and J. D. Forman-Kay, Curr. Opin. Struct. Biol., 2007, 17, 3–14 CrossRef CAS.
- D. Eliezer, Curr. Opin. Struct. Biol., 2009, 19, 23–30 CrossRef CAS.
- M. R. Jensen, P. R. L. Markwick, S. Meier, C. Griesinger, M. Zweckstetter, S. Grzesiek, P. Bernadó and M. Blackledge, Structure, 2009, 17, 1169–1185 CrossRef CAS.
- C. K. Fisher and C. M. Stultz, Curr. Opin. Struct. Biol, 2011, 21, 426–431 CrossRef CAS.
- H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208 CrossRef CAS.
- M. D. Mukrasch, S. Bibow, J. Korukottu, S. Jeganathan, J. Biernat, C. Griesinger, E. Mandelkow and M. Zweckstetter, PLoS Biol., 2009, 7, e34 Search PubMed.
- K. Sugase, H. J. Dyson and P. E. Wright, Nature, 2007, 447, 1021–1025 CrossRef CAS.
- V. N. Uversky, Chem. Soc. Rev., 2011, 40, 1623–1634 RSC.
- B. A. Shoemaker, J. J. Portman and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8868–8873 CrossRef CAS.
- S. Meier, M. Blackledge and S. Grzesiek, J. Chem. Phys., 2008, 128, 052204 CrossRef.
- P. E. Wright and H. J. Dyson, Curr. Opin. Struct. Biol., 2009, 19, 31–38 CrossRef CAS.
- P. Tompa, Curr. Opin. Struct. Biol., 2011, 21, 419–425 CrossRef CAS.
- D. S. Wishart and B. D. Sykes, J. Biomol. NMR, 1994, 4, 171–180 CrossRef CAS.
- H. Zhang, S. Neal and D. S. Wishart, J. Biomol. NMR, 2003, 25, 173–195 CrossRef CAS.
- J. A. Marsh, V. K. Singh, Z. Jia and J. D. Forman-Kay, Protein Sci., 2006, 15, 2795–2804 CrossRef CAS.
- S. Schwarzinger, G. J. Kroon, T. R. Foss, J. Chung, P. E. Wright and H. J. Dyson, J. Am. Chem. Soc., 2001, 123, 2970–2978 CrossRef CAS.
- Y. Wang and O. Jardetzky, J. Am. Chem. Soc., 2002, 124, 14075–14084 CrossRef CAS.
- W. Peti, L. J. Smith, C. Redfield and H. Schwalbe, J. Biomol. NMR, 2001, 19, 153–165 CrossRef CAS.
- J. Yao, J. Chung, D. Eliezer, P. E. Wright and H. J. Dyson, Biochemistry, 2001, 40, 3561–3571 CrossRef CAS.
- M. Kjaergaard, K. Teilum and F. M. Poulsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12535–12540 CrossRef CAS.
- K. Modig, V. W. Jürgensen, K. Lindorff-Larsen, W. Fieber, H. G. Bohr and F. M. Poulsen, FEBS Lett., 2007, 581, 4965–4971 CrossRef CAS.
- L. J. Smith, K. A. Bolin, H. Schwalbe, M. W. MacArthur, J. M. Thornton and C. M. Dobson, J. Mol. Biol., 1996, 255, 494–506 CrossRef CAS.
- H. Schwalbe, K. M. Fiebig, M. Buck, J. A. Jones, S. B. Grimshaw, A. Spencer, S. J. Glaser, L. J. Smith and C. M. Dobson, Biochemistry, 1997, 36, 8977–8991 CrossRef CAS.
- L. Serrano, J. Mol. Biol., 1995, 254, 322–333 CrossRef CAS.
- D. Shortle and M. S. Ackerman, Science, 2001, 293, 487–489 CrossRef CAS.
- R. Mohana-Borges, N. K. Goto, G. J. A. Kroon, H. J. Dyson and P. E. Wright, J. Mol. Biol., 2004, 340, 1131–1142 CrossRef CAS.
- W. Fieber, S. Kristjansdottir and F. M. Poulsen, J. Mol. Biol., 2004, 339, 1191–1199 CrossRef CAS.
- P. Bernadó, L. Blanchard, P. Timmins, D. Marion, R. W. H. Ruigrok and M. Blackledge, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17002–17007 CrossRef.
- A. K. Jha, A. Colubri, K. F. Freed and T. R. Sosnick, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13099–13104 CrossRef CAS.
- N. Tjandra and A. Bax, Science, 1997, 278, 1111–1114 CrossRef CAS.
- M. Blackledge, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 46, 23–61 CrossRef CAS.
- J. Tolman and K. Ruan, Chem. Rev., 2006, 106, 1720–1736 CrossRef CAS.
- J. Meiler, J. J. Prompers, W. Peti, C. Griesinger and R. Brüschweiler, J. Am. Chem. Soc., 2001, 123, 6098–6107 CrossRef CAS.
- S. A. Showalter and R. Brüschweiler, J. Am. Chem. Soc., 2007, 129, 4158–4159 CrossRef CAS.
- O. F. Lange, N.-A. Lakomek, C. Farès, G. F. Schröder, K. F. A. Walter, S. Becker, J. Meiler, H. Grubmüller, C. Griesinger and B. L. de Groot, Science, 2008, 320, 1471–1475 CrossRef CAS.
- L. Salmon, G. Bouvignies, P. Markwick, N. Lakomek, S. Showalter, D.-W. Li, K. Walter, C. Griesinger, R. Brüschweiler and M. Blackledge, Angew. Chem., Int. Ed., 2009, 48, 4154–4157 CrossRef CAS.
- P. R. L. Markwick, G. Bouvignies, L. Salmon, J. A. McCammon, M. Nilges and M. Blackledge, J. Am. Chem. Soc., 2009, 131, 16968–16975 CrossRef CAS.
- M. Louhivuori, K. Pääkkönen, K. Fredriksson, P. Permi, J. Lounila and A. Annila, J. Am. Chem. Soc., 2003, 125, 15647–15650 CrossRef CAS.
- K. Fredriksson, M. Louhivuori, P. Permi and A. Annila, J. Am. Chem. Soc., 2004, 126, 12646–12650 CrossRef CAS.
- O. I. Obolensky, K. Schlepckow, H. Schwalbe and A. V. Solov'yov, J. Biomol. NMR, 2007, 39, 1–16 CrossRef CAS.
- J. L. Battiste and G. Wagner, Biochemistry, 2000, 39, 5355–5365 CrossRef CAS.
- J. R. Gillespie and D. Shortle, J. Mol. Biol., 1997, 268, 170–184 CrossRef CAS.
- G. M. Clore, C. Tang and J. Iwahara, Curr. Opin. Struct. Biol., 2007, 17, 603–616 CrossRef CAS.
- A. N. Volkov, J. A. R. Worrall, E. Holtzmann and M. Ubbink, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18945–18950 CrossRef CAS.
- C. Tang, J. Iwahara and G. M. Clore, Nature, 2006, 444, 383–386 CrossRef CAS.
- G. M. Clore and J. Iwahara, Chem. Rev., 2009, 109, 4108–4139 CrossRef CAS.
- J. Iwahara and G. M. Clore, Nature, 2006, 440, 1227–1230 CrossRef CAS.
- S. Kristjansdottir, K. Lindorff-Larsen, W. Fieber, C. M. Dobson, M. Vendruscolo and F. M. Poulsen, J. Mol. Biol., 2005, 347, 1053–1062 CrossRef CAS.
- K. Lindorff-Larsen, S. Kristjansdottir, K. Teilum, W. Fieber, C. Dobson, F. Poulsen and M. Vendruscolo, J. Am. Chem. Soc., 2004, 126, 3291–3299 CrossRef CAS.
- C. W. Bertoncini, Y.-S. Jung, C. O. Fernandez, W. Hoyer, C. Griesinger, T. M. Jovin and M. Zweckstetter, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1430–1435 CrossRef CAS.
- D. K. Wilkins, S. B. Grimshaw, V. Receveur, C. M. Dobson, J. A. Jones and L. J. Smith, Biochemistry, 1999, 38, 16424–16431 CrossRef CAS.
- B. Brutscher, R. Brüschweiler and R. R. Ernst, Biochemistry, 1997, 36, 13043–13053 CrossRef CAS.
- J. Klein-Seetharaman, M. Oikawa, S. B. Grimshaw, J. Wirmer, E. Duchardt, T. Ueda, T. Imoto, L. J. Smith, C. M. Dobson and H. Schwalbe, Science, 2002, 295, 1719–1722 CrossRef CAS.
- S. Schwarzinger, P. E. Wright and H. J. Dyson, Biochemistry, 2002, 41, 12681–12686 CrossRef CAS.
- W.-Y. Choy, F. A. A. Mulder, K. A. Crowhurst, D. R. Muhandiram, I. S. Millett, S. Doniach, J. D. Forman-Kay and L. E. Kay, J. Mol. Biol., 2002, 316, 101–112 CrossRef CAS.
- J. E. Kohn, I. S. Millett, J. Jacob, B. Zagrovic, T. M. Dillon, N. Cingel, R. S. Dothager, S. Seifert, P. Thiyagarajan, T. R. Sosnick, M. Z. Hasan, V. S. Pande, I. Ruczinski, S. Doniach and K. W. Plaxco, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12491–12496 CrossRef CAS.
- I. S. Millett, S. Doniach and K. W. Plaxco, Adv. Protein Chem., 2002, 62, 241–262 CrossRef CAS.
- P. Bernadó and M. Blackledge, Biophys. J., 2009, 97, 2839–2845 CrossRef.
- J. Lipfert and S. Doniach, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 307–327 CrossRef CAS.
- E. Mylonas, A. Hascher, P. Bernado, M. Blackledge, E. Mandelkow and D. Svergun, Biochemistry, 2008, 47, 10345–10353 CrossRef CAS.
- P. Bernadó, E. Mylonas, M. V. Petoukhov, M. Blackledge and D. I. Svergun, J. Am. Chem. Soc., 2007, 129, 5656–5664 CrossRef.
- A. M. Bonvin, J. A. Rullmann, R. M. Lamerichs, R. Boelens and R. Kaptein, Proteins, 1993, 15, 385–400 CrossRef CAS.
- J. Gsponer, H. Hopearuoho, S. B.-M. Whittaker, G. R. Spence, G. R. Moore, E. Paci, S. E. Radford and M. Vendruscolo, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 99–104 CrossRef CAS.
- D. Ganguly and J. Chen, J. Mol. Biol., 2009, 390, 467–477 CrossRef CAS.
- J. R. Allison, P. Varnai, C. M. Dobson and M. Vendruscolo, J. Am. Chem. Soc., 2009, 131, 18314–18326 CrossRef CAS.
- K.-P. Wu, D. S. Weinstock, C. Narayanan, R. M. Levy and J. Baum, J. Mol. Biol., 2009, 391, 784–796 CrossRef CAS.
- S. Esteban-Martín, R. B. Fenwick and X. Salvatella, J. Am. Chem. Soc., 2010, 132, 4626–4632 CrossRef.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS.
- P. R. L. Markwick, G. Bouvignies and M. Blackledge, J. Am. Chem. Soc., 2007, 129, 4724–4730 CrossRef CAS.
- N. C. Fitzkee, P. J. Fleming and G. D. Rose, Proteins, 2005, 58, 852–854 CrossRef CAS.
- J. F. Leszczynski and G. D. Rose, Science, 1986, 234, 849–855 CAS.
- A. K. Jha, A. Colubri, M. H. Zaman, S. Koide, T. R. Sosnick and K. F. Freed, Biochemistry, 2005, 44, 9691–9702 CrossRef CAS.
- S. C. Lovell, I. W. Davis, W. B. Arendall 3rd, P. I. W. de Bakker, J. M. Word, M. G. Prisant, J. S. Richardson and D. C. Richardson, Proteins, 2003, 50, 437–450 CrossRef CAS.
- M. Zweckstetter and A. Bax, J. Am. Chem. Soc., 2000, 122, 3791–3792 CrossRef CAS.
- M. D. Mukrasch, P. Markwick, J. Biernat, M. von Bergen, P. Bernadó, C. Griesinger, E. Mandelkow, M. Zweckstetter and M. Blackledge, J. Am. Chem. Soc., 2007, 129, 5235–5243 CrossRef CAS.
- M. Wells, H. Tidow, T. Rutherford, P. Markwick, M. Jensen, E. Mylonas, D. Svergun, M. Blackledge and A. Fersht, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5762–5767 CrossRef CAS.
- M. R. Jensen and M. Blackledge, J. Am. Chem. Soc., 2008, 130, 11266–11267 CrossRef CAS.
- M. R. Jensen, K. Houben, E. Lescop, L. Blanchard, R. W. H. Ruigrok and M. Blackledge, J. Am. Chem. Soc., 2008, 130, 8055–8061 CrossRef CAS.
- M. R. Jensen, G. Communie, E. A. Ribeiro Jr, N. Martinez, A. Desfosses, L. Salmon, L. Mollica, F. Gabel, M. Jamin, S. Longhi, R. W. H. Ruigrok and M. Blackledge, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9839–9844 CrossRef CAS.
- S. Meier, M. Strohmeier, M. Blackledge and S. Grzesiek, J. Am. Chem. Soc., 2007, 129, 754–755 CrossRef CAS.
- S. Meier, S. Grzesiek and M. Blackledge, J. Am. Chem. Soc., 2007, 129, 9799–9807 CrossRef CAS.
- F. Gabel, M. R. Jensen, G. Zaccaï and M. Blackledge, J. Am. Chem. Soc., 2009, 131, 8769–8771 CrossRef CAS.
- J. A. Marsh and J. D. Forman-Kay, J. Mol. Biol., 2009, 391, 359–374 CrossRef CAS.
- C. K. Fisher, A. Huang and C. M. Stultz, J. Am. Chem. Soc., 2010, 132, 14919–14927 CrossRef CAS.
- G. Nodet, L. Salmon, V. Ozenne, S. Meier, M. R. Jensen and M. Blackledge, J. Am. Chem. Soc., 2009, 131, 17908–17918 CrossRef CAS.
- L. Salmon, G. Nodet, V. Ozenne, G. Yin, M. R. Jensen, M. Zweckstetter and M. Blackledge, J. Am. Chem. Soc., 2010, 132, 8407–8418 CrossRef CAS.
- M. R. Jensen, P. Bernadó, K. Houben, L. Blanchard, D. Marion, R. W. H. Ruigrok and M. Blackledge, Protein Pept. Lett., 2010, 17, 952–960 CrossRef CAS.
- J. A. Marsh, J. M. R. Baker, M. Tollinger and J. D. Forman-Kay, J. Am. Chem. Soc., 2008, 130, 7804–7805 CrossRef CAS.
- P. Bernadó, C. W. Bertoncini, C. Griesinger, M. Zweckstetter and M. Blackledge, J. Am. Chem. Soc., 2005, 127, 17968–17969 CrossRef.
- M. R. Jensen, L. Salmon, G. Nodet and M. Blackledge, J. Am. Chem. Soc., 2010, 132, 1270–1272 CrossRef CAS.
- Y. Shen and A. Bax, J. Biomol. NMR, 2007, 38, 289–302 CrossRef CAS.
Footnote |
| † Published as part of a Molecular BioSystems themed issue on Intrinsically Disordered Proteins: Guest Editor M. Madan Babu. |
| This journal is © The Royal Society of Chemistry 2012 |
