Network forming units in alkali borate and borophosphate glasses and the mixed glass former effect
Michael
Schuch
a,
Christian
Trott
b and
Philipp
Maass
*a
aFachbereich Physik, Universität Osnabrück, Barbarastraße 7, 49076, Osnabrück, Germany
bInstitut für Physik, Technische Universität Ilmenau, 98684, Ilmenau, Germany
First published on 4th October 2011
Abstract
A theoretical approach is presented for relating structural information to transport properties in ion conducting borophosphate glasses. It relies on the consideration of the different types of glass forming units and the charges associated with them. First it is shown how changes of the unit concentration with the overall glass composition can be understood. Then it is demonstrated how the changes in the unit concentrations upon borate–phosphate mixing lead to a re-distribution of Coulomb traps for the mobile ions and a subsequent change in long-range ionic mobilities. The theories are tested against experiments and yield good agreement with the measured data both for the unit concentrations and the variation of the activation energy.
1 Introduction
The chemical composition of ion conducting glasses can be varied to a large extent and this offers many possibilities to optimise these materials with respect to different demands, in particular to high ionic conductivities.1 One important method for enhancing ionic conductivities in glasses is by mixing different glass formers such as silicates, borates, phosphates, etc. The occurrence of a maximum in the ionic conductivity or minimum in the conductivity activation energy upon mixing is commonly referred to as the mixed glass former effect (MGFE). The MGFE has been found in a number of different systems as, for example, the alkali borosilicates,2 alkali borophosphates,3,4 as well as GeS2 + SiS2,5P2O5 + TeO2,6TeO2 + B2O3,7MoO3 + TeO2,8 and GeO2 + GeS29,10 mixed network former glasses with different types of mobile ions (Li, Na, Ag). It is, however, not always observed. For example, Maia and Rodrigues11 did not find a maximum in the conductivity in a lithium borosilicate system similar to the one investigated by Tatsumisago et al.2The origin of the MGFE is not well understood. For the glass system 0.3Li2S + 0.7[(1 − x)SiS2 + xGeS2], Pradel et al.5 showed that the MGFE in the composition range 0.5 ≲ x ≲ 0.65 is caused by a phase separation into an almost Li free GeS2 glass and a Li2S + SiS2 glass. The enhancement of Li mobility can thus be traced back to the enrichment of Li ions in the SiS2 component.12,13 When the MGFE is not induced by phase separation, we recently suggested to distinguish between two situations I and II,14 where in situation I the network forming units (NFUs) remain the same during glass former mixing (as, for example, when germanates are mixed with their thio-analogues), while in situation II different types of NFUs exist for each glass former, which change their concentrations upon mixing. For situation I, it was shown14 that the MGFE can be caused by reduced activation barriers for ionic jumps in heterogeneous environments containing both glass formers.
In this article we present a theoretical approach applicable to situation II, which relies on the NFUs building the host structure for the ionic motion. We argue that the charges associated with the NFUs and the way that they are localised are of crucial relevance for characterising the statistical properties of the energy landscape that govern the long-range ionic transport properties. This view is in line with earlier findings that changes of dc-conductivities correlate with the concentration of BO4 tetrahedra.3,15
To demonstrate the new approach we apply it to the mixed glass former effect in sodium borophosphate glasses, where detailed information on the NFU concentrations has been gained recently by magic angle spinning nuclear magnetic resonance (MAS-NMR).3,16 We first show how the observed changes of NFU concentrations with the borate-to-phosphate mixing ratio can be understood from a general modelling. Then we will use this structural information on the NFUs to calculate changes of the conductivity activation energy upon the mixing ratio.
2 NFU concentrations in alkali borate glasses
Before developing a model for the NFU concentrations in the more complex ternary alkali oxide-borate-phosphate glass compositions, we first revisit here the situation in the simpler binary alkali oxide-borate glasses. Since the pioneering work of Bray and coworkers17,18 and further subsequent experimental investigation and theoretical modelling (for a recent overview, see Wright19) the behaviour of the NFUs in the alkali borate glasses has been clarified to some extent. Overall, three types of NFUs can be distinguished,† see Fig. 1: the trigonal, neutral B(3) unit with three bridging oxygens (bOs), the tetrahedral, negatively charged B(4) unit with four bOs, and the trigonal, negatively charged B(2) unit with two bOs and one non-bridging oxygen (nbO). Since the bOs are shared by two boron atoms, the total number of oxygens attributed to these NFUs is 4 × (1/2) = 2 for the B(4) unit, 3 × (1/2) = 3/2 for the B(3) unit, and 2 × (1/2) + 1 = 2 for the B(2) unit. | ||
| Fig. 1 Sketch of the NFUs in alkali borate glasses: Below the chemical representations the charge numbers of the NFUs are given. The charge of the B(4) unit is delocalised over the four bOs, while the charge of the B(2) unit is more localised at the site of the nbO. | ||
For convenient notation let us denote by {B(n)}, n = 2,3,4, the fraction of units {B(n)}, i.e. {B(n)} = [B(n)]/[B], where [B(n)] is the concentration of NFUs of type B(n) and [B] = [B(2)] + [B(3)] + [B(4)] the total number concentration of NFUs. The NFU fractions {B(4)} as a function of the alkali ion fraction {M} = [M]/[B] = y/(1 − y) (M = Li, Na, K, Rb, or Cs) in glasses of composition yM2O-(1 − y)B2O3, as measured by MAS-NMR17,20–24 and neutron scattering25 are redrawn in Fig. 2. For small {M} ≲ 0.4, each alkali ion M (or, more precisely, each MO1/2) converts one B(3) to a B(4) unit, and accordingly {B(4)} = {M} in Fig. 2. This well-known behaviour leads to the so-called “borate anomaly”, which refers to the fact that a better connected glassy network (and a correspondingly higher glass transition temperature) is found for larger modifier contents, in contrast to what is commonly seen in other types of modified network glasses, where the cations of the modifier generate nbOs and hence a reduced connectivity.
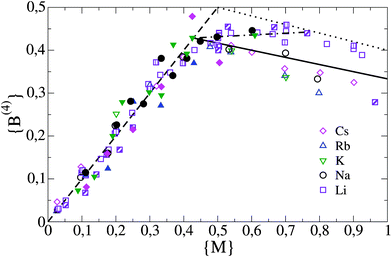 | ||
| Fig. 2 B(4) fraction as a function of alkali fraction {M} in alkali borate glasses. The symbols refer to results from MAS-NMR measurements17,20–24 and neutron scattering.25 Different fillings for the same symbols correspond to different studies. Results from the theoretical modelling are indicated by lines. The dashed line corresponds to the regime of low alkali content ({M} ≤ {M}*). The solid line marks the Beekenkamp result in the regime of high alkali content ({M} > {M}*) and the dashed line marks the modified Beekenkamp model with f = 1/4. The dashed-dotted line indicates the result from the refined modelling in section 2.3 for K = 1.3. | ||
For large {M} ≳ 0.4, the one-to-one replacement of B(3) by B(4) units with each addition of M ceases to be valid due to the emergence of B(2) units that compensate for the charges of the alkali ions. As a consequence, {B(4)} becomes smaller than {M} in Fig. 2. The number of charge compensating B(2) units (and the associated reduction of {B(4)} with respect to the line {B(4)} = {M}) depends on the type of alkali ion, with a trend of becoming larger with larger alkali ion size, although the {B(4)} data for Rb in Fig. 2 lie below those for Cs.
2.1 Beekenkamp model
A good theoretical description of the overall behaviour seen in Fig. 2 has been given by Beekenkamp26 already in 1965. He assumed that the B(4) units are preferentially compensating the charges of the alkali ions, but cannot be directly linked by a bO. This avoidance of B(4)–B(4) linkages likely has its origin in a high effective dipolar interaction between the O–B, B–O bonds forming the links. The NFU fractions then have to obey the following set of relations:| {B(2)} + {B(3)} + {B(4)} = 1 | (1a) |
 | (1b) |
| 4{B(4)} ≤ 3{B(3)} + 2{B(2)} | (1c) |
The first eqn (1a) follows from the given total boron content and the second eqn (1b) from the requirement of charge neutrality. The relation (1c) expresses that the number of bOs linked to B(4) units must be smaller than or equal to the number of bOs linked to B(3) and B(2) units, since a bO bonded to a B(4) has to be linked to either a B(3) or B(2) unit due to the B(4)–B(4) avoidance. Let us note that the two eqn (1a) and (1b) automatically imply that the fraction {O} of oxygens given by the stoichiometry ({O} = 3/2 + {M}/2) equals the one calculated from the units ({O} = 2{B(2)} + 3{B(3)}/2 + 2{B(4)}). This condition could thus by used as an equivalent alternative to the requirement of charge neutrality.
For small {M}, only the favoured B(4) units are needed for charge compensation ({B(2)} = 0) and eqn (1b) and (1a) yield {B(4)} = {M} and {B(3)} = 1 − {M}. This is valid as long as relation (1c) is satisfied, i.e. for 4{M} ≤ 3(1 − {M}) or {M} ≤ 3/7 ≅ 0.429. For {M} > 3/7, in addition B(2) units are needed for charge compensation. Since the B(4) are favoured over the B(2) units, the number of B(4) units has to be taken as large as possible under the constraint (1c), i.e. this relation becomes an equation. Inserting it into eqn (1a) yields {B(4)} = [3 − {B(2)}]/7, and inserting this into eqn (1b) gives {B(2)} = 7{M}/6 − 1/2 and {B(3)} = 1 − {M}. In summary, the Beekenkamp model predicts
 | (2a) |
| {B(3)} = 1 − {M} | (2b) |
 | (2c) |
The predicted behaviour for {B(4)} is indicated by the dashed and solid lines in Fig. 2. The terminal point (intersection of dashed with solid line) {M}* = 3/7 of {B(4)} = {M} is in good agreement with the measurements. Except for the lithium borates, the line {B(4)} = 1/2 − {M}/6 captures quite well the behaviour for {M} > {M}*, although there is a tendency of the measured {B(4)} to be smaller, in particular at larger {M} ≳ 0.7.
The measured {B(4)} data for Li are significantly higher than that predicted by the Beekenkamp model. This points to the fact that the constraint of forbidden B(4)–B(4) linkages is too strict in this case. It has been conjectured that the small Li ions can come closer to the bOs in these linkages and thereby are able to stabilise them.24 With respect to the two other unit types B(2) and B(3), let us note that the result {B(3)} = 1 − {M} follows already from eqn (1a), (1b) and simply expresses the fact that for each additional M, a neutral B(3) unit needs to be replaced by one of the two charged units. With {B(4)} and {B(3)} known, {B(2)} is fixed by the overall boron content.
2.2 Constant fraction of B(4)–B(4) linkages
In order to account for the discrepancies between the Beekenkamp model and the measurements, one may release the constraint of strict absence of linkages between B(4) units. In fact, it is known that in crystalline alkali borates such linkages exist19 and there is evidence that this is the case also in vitreous systems.27 Gupta28 proposed a model, where all B(4) are sharing a bO with exactly one other B(4), leading to a replacement of relation (1c) by 3{B(4)} ≤ 3{B(3)} + 2{B(2)}, since each of the remaining three bOs bonded to a B(4) unit has to be linked to either a B(3) or a B(2) unit.More generally, we can introduce the fraction f of B–O bonds belonging to B(4) units that are part of B(4)–B(4) linkages. We then have to replace relation (1c) by
| 4(1 − f){B(4)} ≤ 3{B(3)} + 2{B(2)} | (3) |
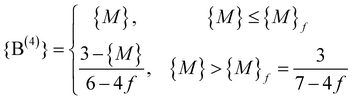 | (4) |
As before, {B(3)} = 1 − {M} and {B(2)} = 0 for {M} ≤ {M}f, while {B(2)} = 1 − {B(3)} − {B(4)} for {M} > {M}f.
According to eqn (4), when increasing f from f = 0, one obtains a shift of {M}* from 3/7 to a higher value {M}f = 3/(7 − 4f) and a steeper fall of {B(4)} for {M} > {M}f, corresponding to a change in slope from (−1/6) to [−1/(6 − 4f)]. As an example, we have indicated the result for f = 1/4 as a dotted line in Fig. 2. This line overestimates {B(4)} in the interval 0.43 < {M} < 0.7 but it appears as a limiting line of the B(4) fraction for {M} ≥ 0.7 in lithium borate glasses. This suggests that the Gupta model corresponds to a limiting case in the sense that a B(4) unit can have at most one linkage to another B(4) unit.
2.3 Balancing mutually linked B(4) with B(2) units
While the approach of fixing the fraction f is a straightforward extension of the Beekenkamp model, it is not clear why f should be independent of {M}. For a refinement of the theoretical treatment, we now assume that a B(4) unit can have at most one linkage to another B(4) unit and invoke the often applied concept that concentrations of different structural subgroups in a glass are balanced via chemical reactions.‡ Let us consider network configurations with mutually linked B(4) units in balance with network configurations without such linkages but with additional B(2) units according to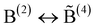 | (5) |
Here  denotes a B(4) unit that is linked to another B(4). The reaction (5) represents the most simple one by which a balancing of the respective units is described under conservation of both the charge and the number of oxygens (2 × (1/2) + 1 = 4 × (1/2)).
denotes a B(4) unit that is linked to another B(4). The reaction (5) represents the most simple one by which a balancing of the respective units is described under conservation of both the charge and the number of oxygens (2 × (1/2) + 1 = 4 × (1/2)).
Applying the law of mass action to the reaction (5) gives
 | (6) |
Since the  units are linked through one bO to another B(4) (
units are linked through one bO to another B(4) ( ) unit, the number of bOs to be connected to either B(2) or B(3) units is proportional to
) unit, the number of bOs to be connected to either B(2) or B(3) units is proportional to  . Relation (1c) then has to be replaced by
. Relation (1c) then has to be replaced by
 | (7) |
Eqn (1a), (1b), (6) together with relation (7) form a complete set to determine the NFU fractions under the principle of B(4) preference for charge compensation. It is clear that the reaction is only relevant when the  units form and accordingly the low alkali regime described in eqn (2) is not modified, including its end point {M}* = 3/7. For {M} > {M}* (and {M} ≤ {M}K, see eqn (9) below) we obtain
units form and accordingly the low alkali regime described in eqn (2) is not modified, including its end point {M}* = 3/7. For {M} > {M}* (and {M} ≤ {M}K, see eqn (9) below) we obtain
 | (8a) |
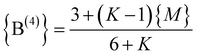 | (8b) |
 increases until
increases until 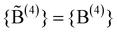 , where {M} equals§
, where {M} equals§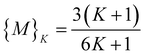 | (9) |
For {M} > {M}K,  , that means the limit described by the Gupta model is reached with {B(4)} = (3 − {M})/5.
, that means the limit described by the Gupta model is reached with {B(4)} = (3 − {M})/5.
A success of the refined model is that it can comfortably describe the measured {B(4)} in lithium borate glasses when taking K = 1.3, see Fig. 2. It is interesting to note that a fitting of the {B(4)} dependence on {M} in lithium borate glasses by three linear regimes was already shown to give a good description by Feller et al. in 1982.29 The refined model allows one to reason this finding. Moreover, the model still includes the results of the Beekenkamp model in the limit K → 0 (no linkages between B(4) units), which describes the behaviour fairly well for the other types of alkali ions (K could be also fitted for each type).
Finally, let us note that it is possible to obtain B(4) fractions below the line of the Beekenkamp model for {M} > 3/7 [eqn (2a)] and thus a possibly better agreement with the measured data. B(4) fractions below this line result, for example, when assuming that B(2)–B(4) linkages are less likely and B(2)–B(3) linkages are formed. A more detailed discussion of such further refinements and predictions for linkages will be presented elsewhere.
3 NFU concentrations in alkali borophosphate glasses
We now develop a model to describe the NFU concentrations in alkali borophosphate glasses with general composition yM2O–(1 − y)[xB2O3–(1 − x)P2O5]. Detailed comparisons with experiments are made for sodium borate glasses of composition 0.4Na2O–0.6[xB2O3–(1 − x)P2O5] as a function of the borate to phosphate mixing parameter x. In these glasses, NFU concentrations were determined recently by MAS-NMR3,16 and the results of these measurements has served as a reference in our modelling approach.Seven NFUs could be distinguished in the work by Zielniok et al.:3 in addition to the three borate units shown in Fig. 1, there are four tetrahedral phosphate units P(n), n = 0, … 3 with n bOs, (4 − n) nbOs, and charges (n − 3), see Fig. 3. The total number of oxygens attributed to the P(n) unit is (n/2) + (4 − n) = 4 − n/2. Extending the definition of the previous section, we denote by {X} (X = B(n) or P(n)) the fraction of network units with respect to the network forming cations, i.e. {X} = [X]/([B] + [P]).
 | ||
| Fig. 3 Sketch of the phosphate NFUs with their charge numbers. The charges are considered to be equally spread over the nbOs. | ||
The equations for fixing the total boron content, the total phosphorus content, and the charge neutrality are
| {B(4)} + {B(3)} + {B(2)} = x | (10a) |
| {P(3)} + {P(2)} + {P(1)} + {P(0)} = (1− x) | (10b) |
| {B(4)} + {B(2)} + {P(2)} + 2{P(1)} + 3{P(0)} = {M} | (10c) |
 . Accordingly, this condition could by used as an equivalent alternative to the requirement of charge neutrality. Eqn (10a)–(10c) are three determining equations for the seven unknown NFU fractions. To proceed, we thus need to include additional information in the theoretical modelling.
. Accordingly, this condition could by used as an equivalent alternative to the requirement of charge neutrality. Eqn (10a)–(10c) are three determining equations for the seven unknown NFU fractions. To proceed, we thus need to include additional information in the theoretical modelling.
Corresponding additional information can be included by considering the rank order by which the NFU types are favoured with respect to charge compensation of the alkali ions. We assume that the relevant parameter controlling this rank order is the charge delocalisation, where higher delocalisation makes an NFU type more favourable. As a measure of the delocalisation, we take |qα|/kα, where qα and kα denote the charge and the number of “charge carrying oxygens” of NFUα, respectively. For the NFUs B(2), P(2), P(1), and P(0), kα equals the number of nbOs. Note that this implies that the delocalisation of electrons belonging to the double bond in the charged P(n) units is taken into account. This means that the nbOs of the P(n) units are considered to be equivalent, which is in agreement with results from ab initio molecular orbital calculations30,31 and diffraction studies.32,33 For the B(4) unit, the charge (−1) is shared equally between all four bOs. Hence we find |qα|/kα = 1/4, 1/2, 2/3, 3/4, and 1 for the B(4), P(2), P(1), P(0), and B(2) unit, respectively, giving the corresponding rank order for charge compensation.
How far this rank order is pivotal for the preferred selection of the charged NFUs depends upon what extent the charge delocalisation is reflected in certain differences between formation energies of these NFUs (see the Appendix for a further discussion of this point). In the following we first assume that the relevant differences between the formation energies are large compared to the thermal energy (with exceptions to be discussed further below). This leads to the occurrence of different x-regimes, where one particular NFU is replaced by another one and only a limited number of the NFU types need to be considered. As long as this number is small, the three eqn (10a)–(10c) are sufficient to predict the NFU concentrations.
In the alkali phosphate glass (x = 0), P(2) units are the most favourable NFUs for charge compensation and the network is formed by these units with fraction {P(2)} = {M} and the neutral P(3) units with fraction {P(3)} = 1 − {M}. When some phosphate is partially substituted by borate, B(4) units become more favourable for the charge compensation. Accordingly, P(2) are replaced by B(4) units rather than P(3) by B(3) units (more precisely, the free energy change for P(3) by B(3) substitution has to be larger than the free energy change for P(2) by B(4) substitution, see the Appendix). For small x we thus need to consider only the NFUs P(2), P(3), and B(4). Eqn (10a)–(10c) then yield
| {B(4)} = x | (11a) |
| {P(2)} = {M} − x | (11b) |
| {P(3)} = 1 − {M} | (11c) |
The question is, at which x = x1 value does this simple behaviour terminate? Since {P(2)} must be positive, we find
| x1 = {M} | (12) |
 | (13) |
That the same critical value {M}* is obtained here as in the Beekenkamp model is due to the fact that the number of bOs in the P(2) and P(3) units equals those in the B(2) and B(3) units.
When {M} ≤ {M}* and phosphate is replaced by borate beyond x = x1, a second x-regime is entered. Since all alkali charges are now compensated by the most favourable B(4) units, {B(4)} stays constant at the value {B(4)}* = x1 = {M}, while the neutral B(3) replace the neutral P(3) units. According to eqn (10a)–(10b) we hence obtain for x ≥ x1
| {B(4)} = {B(4)}* = {M} | (14a) |
| {P(3)} = 1 − x | (14b) |
| {B(3)} = x − {B(4)}* = x − {M} | (14c) |
There is no further x-regime, since the replacement of P(3) by B(3) terminates at x = 1, when {P(3)} = 0.
Eqn (11), (12), and(14) describe the NFU concentrations for low alkali contents {M} ≤ {M}* with {M}* given in eqn (13). A plot of these NFU fractions as a function of x is shown in Fig. 4a. This predicted behaviour has to be considered with some care though, since in alkali borophosphate glasses with a small alkali content, it is also possible that a positively charged P(4) unit is built into the network structure.16 These units are known to occur in pure borophosphate crystals.34 In the presence of P(4) units the analysis needs to be modified, but we will not pursue this further here.
![Theoretical NFU fractions as a function of x in alkali borophosphate glasses yM2O–(1 − y)[xB2O3–(1 − x)P2O5] for (a) low alkali content {M} = 1/3 (y = 0.25) as predicted by eqn (11)–(14), and (b) large alkali content {M} = 2/3 (y = 0.4) as predicted by eqn (11), eqn (20)–(26). The open symbols in (b) refer to f = 0 and the full symbols to f = 1/4.](/image/article/2011/RA/c1ra00583a/c1ra00583a-f4.gif) | ||
| Fig. 4 Theoretical NFU fractions as a function of x in alkali borophosphate glasses yM2O–(1 − y)[xB2O3–(1 − x)P2O5] for (a) low alkali content {M} = 1/3 (y = 0.25) as predicted by eqn (11)–(14), and (b) large alkali content {M} = 2/3 (y = 0.4) as predicted by eqn (11), eqn (20)–(26). The open symbols in (b) refer to f = 0 and the full symbols to f = 1/4. | ||
When {M} exceeds {M}*, as in the sodium borophosphate glasses studied by Zielniok et al.,3 where {M} = 2/3, the theoretical treatment becomes more complicated, since we have to address the question how to deal with the B(4)–B(4) linkages. Similar to section 2, we start in section 3.1 by introducing a constant (x independent) fraction f of B–O bonds belonging to B(4) units that are part of B(4)–B(4) linkages. In addition we assume that the appearance of the charged NFUs units is solely controlled by the rank order. As shown below, this leads to different x-regimes, where one particular NFU is replaced by another one. When comparing to the experimental results reported by Zielniok et al.,3 there is already an overall agreement for f ≅ 1/10 (see Fig. 5), but finer details are not reproduced. In a next step of the modelling presented in section 3.2 we let the fractions of different phosphate units partially balance each other and this leads to a good agreement with the experimental data.
![NFU concentrations in the glass 0.4Na2O–0.6[xB2O3–(1 − x) P2O5]. The symbols mark MAS-NMR results from Zielniok et al.3 and the open symbols at x = 1 correspond to the MAS-NMR measurements by Michaelis et al.24 The lines mark the results from the modelling in section 3.1 with f = 1/10 [eqn (11), eqn (20)–(26)].](/image/article/2011/RA/c1ra00583a/c1ra00583a-f5.gif) | ||
| Fig. 5 NFU concentrations in the glass 0.4Na2O–0.6[xB2O3–(1 − x) P2O5]. The symbols mark MAS-NMR results from Zielniok et al.3 and the open symbols at x = 1 correspond to the MAS-NMR measurements by Michaelis et al.24 The lines mark the results from the modelling in section 3.1 with f = 1/10 [eqn (11), eqn (20)–(26)]. | ||
From a theoretical point of view, it is, however, not fully satisfactory to use a constant fraction f. It can be conjectured that f is in fact weakly dependent on x, since in the only known sodium borophosphate crystal with composition Na5B2P3O15, the structure exhibits B(4)–B(4) linkages.16,35 This suggests that local network configurations resembling this crystalline structure are more likely to occur in the glass at higher phosphate contents. In fact, guided by the crystalline structure one can refine the analysis further and constrain the B(4) fraction to the P(2) fraction. This refined modelling presented in section 3.3 provides a theory for the NFU concentrations, where there is no need to specify an f parameter, at least in those cases where the Beekenkamp model is considered to be a valid description of the pure borate system (forbidden B(4)–B(4) linkages at x = 1).
3.1 {M} ≥ {M}*: Constant fraction of B(4)–B(4) linkages
With the fraction f, the general relation constraining the B(4)–B(4) linkages is | (15) |
This implies that the analysis on the termination of regime 1 given by the set of eqn (11) has to be repeated with the result that {M}* from eqn (13) is modified to
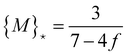 | (16) |
 | (17) |
The NFU fractions in regime 1 are given by eqn (11) and the P(2) fraction reached at x = x1 is {P(2)} = {M} − x1 = (7 − 4f)(6 − 4f)−1({M} − {M}*) > 0.
Since B(4) is the most favourable NFU for charge compensation, as much as possible B(4) should be kept upon further replacement of phosphate by borate. Relation (15) hence becomes an equation for x ≥ x1. When expressing the fractions {P(3)} and {B(3)} of the neutral NFUs by the fractions of the charged NFUs viaeqn (10a), (10b), and inserting these into eqn (15), the charged NFUs in the resulting equation appear only in a linear combination that is identical to the left hand side of eqn (10c). This means that with eqn (10a)–(10c), eqn (15) becomes a closed equation for {B(4)} with solution
 | (18) |
As a consequence, we can, in the following further discussion of the regimes for x ≥ x1, disregard relation (15) and set {B(4)} = {B(4)}* in eqn (10a)–(10c).
Moreover, when defining the subsequent second regime x1 ≤ x ≤ x2 as the one, where the least favourable B(2) unit is still not needed for charge compensation ({B(2)} = 0), we obtain from eqn (10a)
| {B(3)} = x − {B(4)}* | (19) |
 : Replacement of P(3) by B(3).
Since {B(4)} has saturated and B(2) is the least favourable NFU for charge compensation, B(3) are replacing P(3) units and the network is formed by the B(3), B(4), P(2), and P(3) units. Eqn (10b) and (10c) provide a closed pair for the left unknown {P(2)} and {P(3)} with solution
: Replacement of P(3) by B(3).
Since {B(4)} has saturated and B(2) is the least favourable NFU for charge compensation, B(3) are replacing P(3) units and the network is formed by the B(3), B(4), P(2), and P(3) units. Eqn (10b) and (10c) provide a closed pair for the left unknown {P(2)} and {P(3)} with solution| {P(2)} = {M} − {B(4)}* | (20a) |
| {P(3)} = (1 − {M} + {B(4)}*) − x | (20b) |
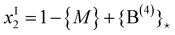 | (21) |
 Replacement of P(2) by P(1).
According to the rank order, P(2) are replaced by P(1) units with further increasing x and the network is formed by the B(3), B(4), P(1), and P(2) units. Eqn (10b) and (10c) yield
Replacement of P(2) by P(1).
According to the rank order, P(2) are replaced by P(1) units with further increasing x and the network is formed by the B(3), B(4), P(1), and P(2) units. Eqn (10b) and (10c) yield| {P(1)} = x − (1 − {M} + {B(4)}*) | (22a) |
| {P(2)} = (2 − {M} + {B(4)}*) − 2x | (22b) |
The replacement of P(2) by P(1) terminates when P(2) is no longer available, i.e. at
 | (23) |
 : Replacement of P(1) by P(0).
P(1) are replaced by P(0) units and the network is formed by the B(3) and B(4) units, and the P(0) and P(1) units with fractions
: Replacement of P(1) by P(0).
P(1) are replaced by P(0) units and the network is formed by the B(3) and B(4) units, and the P(0) and P(1) units with fractions| {P(0)} = 2x − (2 − {M} + {B(4)}*) | (24a) |
| {P(1)} = (3 − {M} + {B(4)}*) − 3x | (24b) |
The replacement terminates when {P(1)} = 0, i.e. at
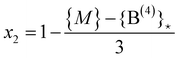 | (25) |
| {B(2)} = 3x − (3 − {M} + {B(4)}*) | (26a) |
| {B(3)} = (3 − {M}) − 2x | (26b) |
| {P(0)} = 1 − x | (26c) |
The NFU fractions as a function of x, as predicted by eqn (11), (17)–(26) for high alkali contents {M} > {M}* with {M}* given by eqn (16), are shown in Fig. 4b for two different fractions f = 0 and 1/4. By its definition f controls the saturation value {B(4)}* [eqn (18)], and with a change of f goes along a small shift of the regimes [cf.eqn (17), (21), (23), (25)]. The slopes of the one-to-one replacement lines in the various regimes are not affected by f [cf.eqn (11), (20), (22), (24), (26)], since these are fixed by the condition of charge neutrality (or, equivalently, by the oxygen content).
We thus have found that the behaviour of the NFU concentrations becomes quite simple also for large alkali contents, once f is fixed and the rank order of the charged NFUs for charge compensation is known. In principle there is no freedom to choose f, when fixing it by its value in the pure alkali borate glass (x = 1), see section 2. However, as discussed above, we should expect f to be only approximately constant in the borophosphate glass and for comparison with experiments it can be more practical to determine f from the (mean) value of {B(4)} measured on the boron rich side (e.g. for x > 0.5).
Fig. 5 shows such comparison with the MAS-NMR measurements3 on sodium borophosphate glasses with composition 0.4Na2O–0.6[xB2O3–(1 − x)P2O5], where we find f = 1/10, corresponding to {B(4)}* = 5/12 ≅ 0.417, to give a good account of the indeed almost constant B(4) fraction on the boron rich side for x in the range 0.5–0.9. For x = 1, the value for {B(4)} reported in Zielniok et al.3 is much smaller than {B(4)}* but in view of the analysis of the alkali borate glasses in section 2, we believe that this discrepancy is due to a measurement error or a consequence of some peculiarity in the glass preparation. In fact, MAS-NMR measurements for sodium borate glasses reported by Michaelis et al.24 give {B(4)} = 0.40 for {M} = 0.53 and {B(4)} = 0.39 for {M} = 0.7 (see Fig. 3), from which we can estimate {B(4)} = 0.39 for {M} = 2/3 = 0.66 in the system investigated by Zielniok et al.3 The corresponding NFU fractions are marked by the open symbols in Fig. 5, which are in agreement with the general behaviour discussed in section 2. For x = 1 we will use these data for further comparison in the following. Note that the unexpected low value of {B(4)} at x = 1 reported in Zielniok et al.,3 necessarily affects also the B(2) and B(3) fractions.
While the overall behaviour of the measured NFU fractions in Fig. 5 is captured by the modelling (with the values at x = 1 taken as those reported by Michaelis et al.24), the following deviations can be identified:
(i) In the experimental data, P(1) units start to emerge between x = 0.6 and 0.7, that means at a significantly lower value than 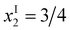 predicted by eqn (21) for {M} = 2/3 and f = 1/10 ({B(4)}* = 5/12 ≅ 0.417). Correlated with this behaviour is a corresponding decrease of {P(2)} when approaching the end of subregime I. This is in contrast to eqn (20a) that predicts {P(2)} = 1/4 to stay constant in this regime.
predicted by eqn (21) for {M} = 2/3 and f = 1/10 ({B(4)}* = 5/12 ≅ 0.417). Correlated with this behaviour is a corresponding decrease of {P(2)} when approaching the end of subregime I. This is in contrast to eqn (20a) that predicts {P(2)} = 1/4 to stay constant in this regime.
(ii) In the experimental data, P(2), P(1) and P(0) units occur simultaneously in subregimes II and III (no strict rank order of their appearance).
3.2 {M} ≥ {M}*: Mutual balancing of phosphate unit fractions
The simultaneous appearance of charged phosphate units suggests that the relevant differences in the formation energies of these units are not much larger than the thermal energy.¶ To account for this effect we can consider, as earlier suggested in polyphosphate glasses,36,37 the disproportionation reactions | (27a) |
 | (27b) |
 | (28a) |
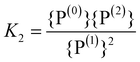 | (28b) |
Note that the charge and the oxygen number are conserved in the reactions (27a) and (27b). In general, both K1 and K2 will depend on the composition (x and {M}) but we may assume that this dependence is weak and can be neglected.
Reaction (27a) implies that, if P(2) and P(3) are present in the network, P(1) units are also present. For consistency we hence should include this reaction in regime 1 as well. However, if K1 is very small, {P(1)} = K1{P(2)}2/{P(3)} will become negligible as long as {P(3)} does not become small too. Hence, for K1 < 1, we can ignore the influence of (27a) in regime 1. In an approximation where K1 is set to zero, subregime I would be left unchanged and only subregimes II and III were modified according to reaction (27b), without change of the terminal points 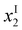 and x2 given in eqn (21), (25).
and x2 given in eqn (21), (25).
Eqn (28a) and (28b) together with eqn (10b) and (10c), form a complete set of determining equations for the fractions {P(0)}, {P(1)}, {P(2)}, and {P(3)} in regime 2. Due to the two coupled quadratic eqn (28a) and (28b), the analytical solution becomes unhelpful and it is more convenient to use a numerical root finding procedure. Fig. 6 shows results for K1 = 0.01 and K2 = 0.29 (dashed lines) in comparison with the experimental data for the sodium borophosphate glass. As can be seen from the figure, the measured fractions for the phosphate units in the regime 0.6 < x < 0.9 are now better accounted for than by the model with a strict rank order. It would be interesting to check if a temperature dependence of these fractions can be observed because of a temperature dependence of the reaction constants K1 and K2. Whether the reactions (27a) and (27b) are taking place in the glassy phase is, however, not clear. We note that the non-equilibrium glassy state does not preclude this, since local structural configurations may rearrange, while long-range structural disorder is frozen on all accessible time scales. It is on the other hand possible that the reactions (27a) and (27b) are only relevant during the glass formation. Then we except them to be reflected in a cooling rate dependence of the respective NFU fractions.
![NFU concentrations in the glass 0.4Na2O–0.6[xB2O3–(1 − x) P2O5]. The symbols mark MAS-NMR results3,24 and the lines indicate results from the theoretical modelling. The dashed lines refer to the first refinement in section 3.2 and the solid lines to the second refinement in section 3.3.](/image/article/2011/RA/c1ra00583a/c1ra00583a-f6.gif) | ||
| Fig. 6 NFU concentrations in the glass 0.4Na2O–0.6[xB2O3–(1 − x) P2O5]. The symbols mark MAS-NMR results3,24 and the lines indicate results from the theoretical modelling. The dashed lines refer to the first refinement in section 3.2 and the solid lines to the second refinement in section 3.3. | ||
3.3 {M} ≥ {M}*: B(4)–B(4) linkages constrained by P(2) units
So far f has to be taken as an a priori unknown parameter, although it can be estimated from its value in the pure borate glass (x = 1) or, for closer description of the experimental data, it can be determined from the mean B(4) fraction for x > 0.5. A further refinement of the modelling allows us to avoid the use of f. The idea is to assume that the B(4)–B(4) linkages are, as in the crystal with composition Na5B2P3O15, associated with the diborate configuration shown in Fig. 7.|| To include this rule in the modelling, we denote, as in section 2, by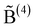 a B(4) unit that is linked to another B(4), i.e. in the present case one that is part of a diborate configuration. As discussed above in connection with eqn (11)–(13), B(4)–B(4) linkages can be avoided for all x, when {M} ≤ {M}* = 3/7. For {M} > {M}*, the formation of such linkages is now constrained to the condition
a B(4) unit that is linked to another B(4), i.e. in the present case one that is part of a diborate configuration. As discussed above in connection with eqn (11)–(13), B(4)–B(4) linkages can be avoided for all x, when {M} ≤ {M}* = 3/7. For {M} > {M}*, the formation of such linkages is now constrained to the condition | (29) |
 unit must be linked to P(2) units, cf.Fig. 7. B(4) units can replace P(2) units in regime 1 [eqn (11)] until all P(2) units are used for the formation of
unit must be linked to P(2) units, cf.Fig. 7. B(4) units can replace P(2) units in regime 1 [eqn (11)] until all P(2) units are used for the formation of  in diborate configurations and the maximal fraction
in diborate configurations and the maximal fraction  is reached. At this point x = x1, the other B(4) units are all linked to P(3) units, yielding
is reached. At this point x = x1, the other B(4) units are all linked to P(3) units, yielding  . With the NFU fractions from eqn (11), this gives
. With the NFU fractions from eqn (11), this gives | (30) |
 | ||
| Fig. 7 Schematic view of a diborate superstructural unit in Na5B2P3O13-crystals. | ||
For x > x1, relation (29) becomes an equation to generate the maximal B(4) fraction for charge compensation, and inserting this into 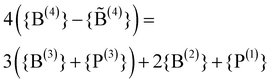 (condition for linkages of B(4) not connected to other B(4) if all P(2) are linked to
(condition for linkages of B(4) not connected to other B(4) if all P(2) are linked to  ), we obtain
), we obtain
 | (31) |
Note that this implies that the B(4) fraction for x → 1 is approaching the result of the Beekenkamp model discussed in section 2. If necessary, one can include in the modelling also the refinements discussed there with respect to the {B(2)}–{B(4)} balancing.
Eqn (31) replaces eqn (15) for x > x1 and one can proceed as in section 3.1 or section 3.2 to determine the NFU concentrations. We refrain from giving here the explicit formulas corresponding to eqn (20)–(26). For comparison with experiment, we have included in Fig. 6 the results (solid line), when using the approach in section 3.2 with the same reaction constants K1 and K2 used before to fit the experimental data. The measured B(4) fraction is well reproduced now without parameter adjustment. Otherwise, there are only small changes of the NFU fractions compared to the model considered before in section 3.2.
Conceptually the theoretical modelling presented in this section relies on a rank order of the NFUs for compensating the charges of the alkali ions and simple constraints given by the stoichiometry and with respect to B(4)–B(4) linkages. The simultaneous appearance of certain NFUs can be taken into account by a balancing of their concentrations via reactions. It would be interesting to clarify whether the assumed balancing can occur in the glassy phase or whether it is taking place in the melt during the cooling process.
The same underlying concepts can be introduced into a statistical mechanics approach, which we present in the Appendix. An advantage of this approach is that it starts out with the formation energies as parameters and that it allows one to include interactions in a systematic manner. Future experiments on the temperature dependence or cooling rate dependence of the NFU concentrations could give access to corresponding energy parameters. Particular values of the formation energies, however, become irrelevant if certain differences between them become much larger than the thermal energy.
4 Modelling of the effect of different NFU types on the activation energy
Next we show how one can, based on the information on the NFU concentrations, successfully model long-range ionic transport properties. To this end we developed a model, which we call the Network Unit Trapping (NUT) model. It relies on the following idea: the nbOs create localised Coulomb traps for the mobile ions, while delocalised charges, as those of the B(4) units, give a partial Coulomb contribution to several neighbouring ion sites. In this way the structural energy landscape for the ionic pathways is modified with the mixing concentration x and this effect can be conjectured to govern the change of the activation energy Ea(x) for the long-range ionic transport.To test this model we randomly distribute the NFUs with their concentrations from the model in section 3.3 on the sites of a simple cubic lattice, see Fig. 8. These sites are called NFU sites. The mobile ions are considered to perform a hopping motion between the centres of the lattice cells, which represent the ion sites.
 | ||
| Fig. 8 Two-dimensional sketch of the NUT model. The arrows indicate charge transfer to ion sites as described in the text. | ||
An NFUα with kα > 0 nbOs and charge qα adds a Coulomb contribution ∝ qα/kα to kα distinct and randomly selected neighbouring ion sites, as illustrated in Fig. 8. The delocalised charge of a B(4) unit is spread equally among the neighbouring ion sites, which implies k = 8 for this unit. The neutral B(3) and P(3) units give no Coulomb contribution. Finally, Gaussian fluctuations are added to the site energies in order to take into account the disorder in the glassy network.40 In summary we can write for the energy of ion site i
 | (32) |
 is equal to one, if an NFUα on site j contributes a Coulomb contribution ∝ qα/kα to ion site i; otherwise it is equal to zero. The ηi are independent Gaussian random numbers with zero mean and standard deviation Δ. The parameter E0 > 0 sets an energy scale and is irrelevant if we are interested in the relative change of the activation energy with the mixing, i.e. the normalised activation energy Ea(x)/Ea(0). The standard deviation Δ is then the only tunable parameter in the modelling.
is equal to one, if an NFUα on site j contributes a Coulomb contribution ∝ qα/kα to ion site i; otherwise it is equal to zero. The ηi are independent Gaussian random numbers with zero mean and standard deviation Δ. The parameter E0 > 0 sets an energy scale and is irrelevant if we are interested in the relative change of the activation energy with the mixing, i.e. the normalised activation energy Ea(x)/Ea(0). The standard deviation Δ is then the only tunable parameter in the modelling.
To determine Ea(x) we have chosen a lattice with 643 sites,41 occupied all NFU sites according to the occupation probabilities derived in section 3.3, and the ion sites randomly with concentration {M} = y/(1 − y). The mobile ions can jump to vacant nearest neighbour sites and the energetic barriers for these jumps are following from eqn (32) by calculating the total energy difference ΔE between the (attempted) target configuration after a jump and the initial configuration before this jump. To model the jump motion, kinetic Monte Carlo simulations with periodic boundary conditions and Metropolis transition rates are performed, as described, for example, in Porto et al.42 Since the ion concentration is high, it is, for the technical implementation, advantageous here to use a vacancy algorithm. In this algorithm, one of the vacancies is picked randomly in each elementary step and attempted to move to a randomly selected neighbouring ion site. If this site is empty, the attempt is rejected. If the site is occupied by an ion, the attempt is accepted with a probability min[1,exp(−ΔE/kBT)]. After each attempt, the time is incrementally increased by (νNV)−1, where v ≅ 1012s−1 is an attempt frequency and NV is the number of vacancies. After thermalisation the time-dependent mean-square displacement R2(t) of the mobile ions and the diffusion coefficient D = limt→∞R2(t)/6t are determined. Averages are performed over typically 10 realisations of the disorder.
The diffusion coefficient is shown for Δ = 0.25 and various x in an Arrhenius plot in Fig. 9a. From the slopes of the straight lines we calculated the activation energy Ea(x), and the behavior of the normalized activation energy Ea(x)/Ea(0) is compared with the experimental results from Zielniok et al.3 in Fig. 9b. The overall agreement between the theoretical (open squares, solid line) and the experimental data (full squares) is surprisingly good. Note that we needed to fit only the parameter Δ to achieve this agreement. A significant difference between the theoretical and experimental curve can be seen for x → 1: while the theoretical Ea(x) decreases, the experimental Ea(x) finally rises to a higher value in the sodium borate glass at x = 1. Interestingly, this rise is reproduced by the NUT model (dashed line), if instead of the NFU concentrations shown in Fig. 6, the NFU concentrations reported by Zielniok et al.3 are used. On the other hand, a much smaller experimental value Ea = 0.54 eV for the sodium borate glass has been reported by Doweidar et al.,43 corresponding to a ratio Ea(1)/Ea(0) = 0.6. The differing measured Ea values likely result from varying NFU concentrations as a consequence of different glass preparation processes.
![(a) Arrhenius plot of the simulated Na+ diffusion coefficients D in 0.4Na2O–0.6[xB2O3–(1 − x)P2O5] for various x and Δ = 0.25 in the case, where no ionic sites were blocked. D is given in units of νa2, where ν is the attempt frequency of the ion jumps and a is the lattice constant (mean jump distance). The slope of the regression lines yields the activation energies. (b) Comparison of simulated activation energies (open symbols) with the measured conductivity activation energy from Zielniok et al.3 (full squares). The open squares and open triangles refer to the results for the modelling without and with blocked sites, respectively, and the solid and dotted lines are least square fits of sixth order polynomials to these data. For the system without blocked sites Δ = 0.25, and for the system with blocked sites Δ = 0.3. The open circle at x = 1 (connected with the dashed line) corresponds to the simulated Ea without blocked sites, if the NFU concentrations from Zielniok et al.3 are taken.](/image/article/2011/RA/c1ra00583a/c1ra00583a-f9.gif) | ||
| Fig. 9 (a) Arrhenius plot of the simulated Na+ diffusion coefficients D in 0.4Na2O–0.6[xB2O3–(1 − x)P2O5] for various x and Δ = 0.25 in the case, where no ionic sites were blocked. D is given in units of νa2, where ν is the attempt frequency of the ion jumps and a is the lattice constant (mean jump distance). The slope of the regression lines yields the activation energies. (b) Comparison of simulated activation energies (open symbols) with the measured conductivity activation energy from Zielniok et al.3 (full squares). The open squares and open triangles refer to the results for the modelling without and with blocked sites, respectively, and the solid and dotted lines are least square fits of sixth order polynomials to these data. For the system without blocked sites Δ = 0.25, and for the system with blocked sites Δ = 0.3. The open circle at x = 1 (connected with the dashed line) corresponds to the simulated Ea without blocked sites, if the NFU concentrations from Zielniok et al.3 are taken. | ||
It is obvious that the model presented here does not take into account important aspects of ion motion in glasses. In this respect we should in particular address the following questions:
(i) Why should a hopping between regular sites of a simple cubic lattice be appropriate for a modelling of the ionic jump motion between irregularly distributed sites in a disordered glassy network?
(ii) How can one reason that the energy barriers, or “doorways”, between the ionic sites should not be considered in more detail?
(iii) Why should it be allowed to neglect the long-range Coulomb interaction between the mobile ions?
The answer to the question (i) is twofold. Firstly, we are interested in the long-range ionic motion, where the chosen regular lattice structure for ionic sites becomes of minor importance. Secondly, by the random distribution of the NFUs and the additional Gaussian energy fluctuations in eqn (32) the sites are in fact not equivalent so that, dependent on the realization of the disorder, favorable pathways without regular structure are formed.
Question (ii) is answered by noting that the Gaussian energy fluctuations are in effect generating disorder in the jump barriers. One could, in addition to the Gaussian fluctuations in eqn (32), also add a random barrier distribution for the jumps. As long as the width of these distributions is sufficiently small compared to the site energy fluctuations induced by the NFU charges, the behavior of Ea is dominated by the latter. We note that the assumption of a dominant role of the trapping effect by the NFU charges is the actual starting point of our approach as we discussed in the Introduction when considering the two different situations I and II as possible origins for the MGFE.
The answer to question (iii) is more subtle. One could argue that the Coulomb interaction can, due to its long range nature, be treated in a mean-field approximation as a weakly varying, almost constant contribution to the energy of the alkali ions.44 However, results from molecular dynamics (MD) simulations suggest that the Coulomb part has a decisive influence on the differences between the energies of the mobile ions on their sites. The interesting point on the other hand is, that in the same MD simulations it was also found that in a vacancy (hole) description the structural energy part (i.e., the part without Coulomb interactions between the mobile ions) is indeed largely determining the energy of the vacancies.45
The fraction of vacancies found in molecular dynamics simulations, with respect to all available ion sites, is smaller than 10%.45–47 This result is in line with the picture that a glass constitutes a dense system with a low free energy and hence should not exhibit too many empty sites.48–50 It is also supported by a theoretical explanation of the occurrence of surprisingly large internal friction peaks in some mixed alkali glasses upon small exchanges of one type of alkali ion by another.51 In our lattice modelling described above, we have occupied two-thirds of the ionic sites (cell centers between the NFUs) with the ions in order to ensure the overall charge neutrality for the stoichiometry of our experimental reference system. The other one-third of ionic sites, however, were left empty, implying that the vacancy concentration is indeed too large compared to the ones found in MD simulations.
In order to see how the results of our modelling change when decreasing the vacancy fraction to a typical value of 7% found in MD simulations, we have performed additional kinetic Monte Carlo simulations, in which 26% of the ionic sites are randomly blocked. This blocking of the cell centers is done before the NFUs are distributed among the lattice sites. Thereafter the NFUs are randomly placed on their sites as before, but their charges are distributed randomly among the neighboring non-blocked sites only. Hence, if an NFUα with kα nBOs on site i is surrounded by mi non-blocked ion sites, kα of these sites are now randomly selected and the Coulomb contribution ∝ qα/kα added to them.** The delocalized charge of a B(4) unit on site i is spread equally among the mi neighboring nonblocked ion sites, implying that a Coulomb contribution ∝ (−1/mi) is added to them. Finally, the Gaussian fluctuations from eqn (32) are added to the site energies resulting from this procedure.
In the same way as described above, the activation energy Ea for this refined model with 7% vacancy fraction was determined from the temperature dependence of the long-time diffusion coefficients of the mobile ions at different x. Interestingly, this activation energy shows almost the same behavior as the model with 33% vacancies, when the parameter Δ is increased from Δ = 0.25 to Δ = 0.3, see Fig. 10. This finding thus gives us some confidence in our modelling with neglect of the Coulomb interaction between the mobile ions. It also demonstrates, as discussed above, that with respect to long-range transport properties the parameter Δ effectively takes into account modifications of the randomness (more irregular topology of ionic sites here).
![NFU concentrations from the statistical mechanics approach with f = 1/10 (lines) for the glass 0.4Na2O–0.6[xB2O3–(1 − x)P2O5] in comparison with MAS-NMR results3,24 (symbols).](/image/article/2011/RA/c1ra00583a/c1ra00583a-f10.gif) | ||
| Fig. 10 NFU concentrations from the statistical mechanics approach with f = 1/10 (lines) for the glass 0.4Na2O–0.6[xB2O3–(1 − x)P2O5] in comparison with MAS-NMR results3,24 (symbols). | ||
5 Summary
In summary we have presented a theoretical approach for the mixed glass former effect in borophosphate glasses. This approach is based on a consideration of the properties of the different NFUs building the network structure with respect to total charge and charge delocalization. In addition we showed how NFU concentrations can be successfully modelled.We believe that our approach is applicable also to other mixed glass former systems, where concentrations of different types of NFUs associated with the glass formers vary with the mixing ratio. Due to its generality, the basic concept may have even wider applicability for describing other compositional effects, as, for example, changes of ionic mobilities with the content of the network modifier.
We would like to thank H. Eckert and S. W. Martin for very valuable discussions and gratefully acknowledge financial support of this work by the Deutsche Forschungsgemeinschaft in the Materials World Network (DFG Grant number MA 1636/3-1).
Appendix: Statistical mechanics approach to NFU concentrations
Without detailed consideration of the network topology, the NFUs can be considered to occupy N sites i in the glass, where N = NB + NP is the total number of boron and phosphorous atoms. To specify the distribution of the NFUs among the sites, we introduce the occupation numbers , where
, where  if an NFU of type α (α = B(2), B(3), etc.) is occupying site i and zero otherwise. Using a coarse-grained Landau-type description, we introduce a free energy
if an NFU of type α (α = B(2), B(3), etc.) is occupying site i and zero otherwise. Using a coarse-grained Landau-type description, we introduce a free energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (n) as a function of the set
(n) as a function of the set 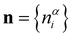 of occupation numbers,
of occupation numbers, | (33) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) '(n) accounts for interactions between the NFUs. For example, for sites i and j being neighbours one could include a term
'(n) accounts for interactions between the NFUs. For example, for sites i and j being neighbours one could include a term  to describe the unlikelihood of B(4)–B(4) linkages. The formation energies f(α) depend in general on the composition (x and {M}) and they are expected to depend also on the cooling rate. One can question whether an equilibrium type description underlying this coarse-grained approach can at all be appropriate for glasses whose structures are frozen into a non-equilibrium state. The hope is that on small length scales the glass structure has found sufficient time to equilibrate during the cooling process and that this equilibration can be accounted for by an effective temperature T′. The structural disorder on large length scales should have no significant influence on the NFU concentrations.
to describe the unlikelihood of B(4)–B(4) linkages. The formation energies f(α) depend in general on the composition (x and {M}) and they are expected to depend also on the cooling rate. One can question whether an equilibrium type description underlying this coarse-grained approach can at all be appropriate for glasses whose structures are frozen into a non-equilibrium state. The hope is that on small length scales the glass structure has found sufficient time to equilibrate during the cooling process and that this equilibration can be accounted for by an effective temperature T′. The structural disorder on large length scales should have no significant influence on the NFU concentrations.
If only the ideal part in eqn (33) is kept, the NFU fractions can be calculated under the constraints eqn (10a)–(10c). These constraints can be rewritten in the form
 | (34a) |
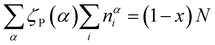 | (34b) |
 | (34c) |
 | (35) |
| u(α) = g(α) − ζB(α)μB − ζP(α)μP − ζM(α)μM | (36) |
 | (37) |
The generalised chemical potentials entering the u(α) [see eqn (36)] are to be determined from the constraints eqn (34a)–(34c).
With respect to the appearance of the NFUs at a given composition only certain differences between the formation energies are relevant. If these are much larger than kBT′, the change of the NFU concentrations with x can be inferred from a T′ → 0 limit.
To demonstrate the procedure, we consider a situation similar to the one addressed in section 3.2. The rank order of the NFUs with respect to charge compensation introduced in section 3 implies f(B(4)) < f(P(2)), 2f(P(2)) < f(P(1)), 3f(P(2)) < f(P(0)), 3f(P(1)) < 2f(P(0)), and f(P(0)) < 3f(B(2)). In order that the P(2) are replaced by the B(4) units rather than the P(3) by the B(3) units for small x, it should hold [f(B(4)) − f(P(2))] < [f(B(3)) − f(P(3))]. All these conditions can be fulfilled by introducing just one energy parameter δ and by setting
| f(B(3)) = f(P(3)) = f(B(4)) = 0 | (38a) |
| f(P(2)) = δ, f(B(2)) = 3δ | (38b) |
| f(P(1)) = 3δ, f(P(0)) = 5δ | (38c) |
The parameter δ is just a convenient tool to evaluate the low temperature limit T′ → 0 under the chosen conditions and does not have any physical meaning.
For determining the NFU fractions {α} we insert the f(α) from eqn (38a)–(38c) into eqn (37) and calculate the chemical potentials numerically from eqn (34a)–(34c). To extract the values in the limit (β′δ) → ∞, the calculations are performed for successively increasing (β′δ) until changes in the NFU fractions become negligible. In order to include the additional constraint (15) into the description, it is checked if the resulting B(4) fraction fulfils relation (15). If it does, the solution is taken. Otherwise, {B(4)} is set equal to [4(1 − f)]−1 times the right hand side of (15) [the calculations have to be done self-consistently by using the corresponding expressions for the determination of μB in eqn (34a)].
The NFU fractions calculated in this way for f = 1/10 are compared to the experimental data for the sodium borophosphate glass in Fig. 10. Note that, different from the situation shown in Fig. 5, the P(0) units occur before the P(2) units have disappeared. The simultaneous appearance of P(0), P(1), and P(2) units in an interval around x = 0.8 is caused by the fact that, for the parameters in eqn (38b), (38), the compensation of 4 charges by either two P(1) units or by one P(0) and one P(2) unit are energetically equivalent. Since the same basic ingredients have been included in the theoretical description as in section 3, the agreement between model and experiment is of comparable quality as in Fig. 6.
The formulation by the statistical mechanics approach is valuable to our view, since it gives additional insight into the underlying assumptions and indicates a way how to access energy parameters. Knowledge of these parameters would allow one to make contact to another theoretical modelling, which has been successfully applied to predict thermodynamic (and some other) properties of borate, silicate, and borosilicate glasses.52,53
References
- M. D. Ingram, Phys. Chem. Glasses, 1987, 28, 215–234 CAS.
- M. Tatsumisago, N. Machida and T. Minami, Yogyo Kyokaishi, 1987, 95, 197–201 CrossRef CAS.
- D. Zielniok, C. Cramer and H. Eckert, Chem. Mater., 2007, 19, 3162–3170 CrossRef CAS.
- P. S. Anantha and K. Hariharan, Mater. Chem. Phys., 2005, 89, 428–437 CrossRef CAS.
- A. Pradel, N. Kuwata and M. Ribes, J. Phys.: Condens. Matter, 2003, 15, S1561–S1571 CrossRef CAS.
- D. Coppo, M. J. Duclot and J. L. Souquet, Solid State Ionics, 1996, 90, 111–115 CrossRef CAS.
- B. V. R. Chowdari and P. P. Kumari, Solid State Ionics, 1996, 86–8, 521–526 CrossRef.
- B. V. R. Chowdari and P. P. Kumari, J. Phys. Chem. Solids, 1997, 58, 515 CrossRef CAS.
- Y. Kim, J. Saienga and S. W. Martin, J. Phys. Chem. B, 2006, 110, 16318–16325 CrossRef CAS.
- Y. Kim and S. W. Martin, Solid State Ionics, 2006, 177, 2881–2887 CrossRef CAS.
- L. F. Maia and A. C. M. Rodrigues, Solid State Ionics, 2004, 168, 87–92 CrossRef CAS.
- P. Maass, A. Bunde and M. D. Ingram, Phys. Rev. Lett., 1992, 68, 3064 CrossRef CAS.
- A. Bunde, M. D. Ingram and P. Maass, J. Non-Cryst. Solids, 1994, 172–174, 1222 CAS.
- M. Schuch, C. R. Müller, P. Maass and S. W. Martin, Phys. Rev. Lett., 2009, 102, 145902 CrossRef.
- R. D. Banhatti, C. Cramer, D. Zielniok, A. H. J. Robertson and M. D. Ingram, Z. Phys. Chem., 2009, 223, 1201–1215 CrossRef CAS.
- D. B. Raskar, M. T. Rinke and H. Eckert, J. Phys. Chem. C, 2008, 112, 12530 CrossRef CAS.
- P. J. Bray and J. G. O'Keefe, Phys. Chem. Glasses, 1963, 4, 37 Search PubMed.
- P. J. Bray and M. L. Liu, in Structure and Bonding in Noncrystalline Solids, ed. G. E. Walrafen and A. G. Revesz, Plenum Press, New York, 1986 Search PubMed.
- A. C. Wright, Phys. Chem. Glasses, 2010, 51, 1.
- E. Ratai, J. C. C. Chan and H. Eckert, Phys. Chem. Chem. Phys., 2002, 4, 3198 RSC.
- J. Epping, H. Eckert, A. W. Imre and H. Mehrer, J. Non-Cryst. Solids, 2005, 351, 3521 CrossRef CAS.
- S. Kroeker, P. M. Aguiar, A. Cerquiera, J. Okoro, W. Clarida, J. Doerr, M. Olesiuk, G. Ongie, M. Affatigato and S. A. Feller, Eur. J. Glass Sci. Technol. B: Phys. Chem. Glasses, 2006, 47, 393 Search PubMed.
- P. M. Aguiar, S. Kroeker and J. Non-Cryst, Solids, 2007, 353, 1837 Search PubMed.
- V. K. Michaelis, P. M. Aguiar, S. Kroecker, P. J. Bray, J. G. O'Keefe and J. Non-Cryst, Solids, 2007, 353, 2582 Search PubMed.
- L. Cormier, G. Calas, B. J. Beuneu and J. Non-Cryst, Solids, 2007, 353, 1779 Search PubMed.
- P. Beekenkamp, in Physics of Non-Crystalline Solids, ed. J. A. Prins, North-Holland, Amsterdam, 1965, p. 512 Search PubMed.
- E. I. Kamitsos, M. A. Karakassides and G. D. Chryssikos, J. Phys. Chem., 1987, 91, 1073 CrossRef CAS.
- P. K. Gupta, Collected Paper XIV Int.Congr. Glass, 19861.
- S. A. Feller, W. J. Dell and P. J. Bray, J. Non-Cryst. Solids, 1982, 51, 21 CrossRef CAS.
- T. Uchino and Y. Ogata, J. Non-Cryst. Solids, 1995, 181, 175 CrossRef CAS.
- A. F. Zatsepin, V. S. Kortov and Y. V. Shchapova, Phys. Solid State, 1997, 39, 1212 CrossRef.
- K. Suzuki and M. Ueno, J. Phys. Paris, 1985, 46, C8–261 Search PubMed.
- U. Hoppe, W. Walter, D. Stachel and A. C. Hannon, Z. Naturforsch., 1996, A51, 179 Search PubMed.
- J. Haines, O. Cambon, R. Astier, P. Fertey and C. Chateau, Z. Kristallogr., 2004, 219, 314 CrossRef CAS.
- B. Ewald, Y.-X. Huang, R. Kniep and Z. Anorg, Z. Anorg. Allg. Chem., 2007, 633, 1517–1740 CrossRef CAS.
- R. K. Brow, D. R. Talland, S. T. Meyers and C. C. Phifer, J. Non-Cryst. Solids, 1995, 191, 45 CrossRef CAS.
- R. K. Brow and J. Non-Cryst, Solids, 2000, 263, 1–28 Search PubMed.
- D.-B. Xiong, H.-H. Chen, X.-X. Yang and Y.-T. Zhao, J. Solid State Chem., 2007, 180, 233–239 CrossRef CAS.
- B. Ewald, Y. Prots, P. Menezes and A. C. Wright, Inorg. Chem., 2005, 44, 6431 CrossRef CAS.
- The Gaussian fluctuations are needed, since, by using a regular arrangements of sites, we disregard the complex network topology. For long-range ionic motion at large length scales, we do not expect our results to be strongly influenced by the lattice structure.
- By varying the box size it was confirmed that the results are not affected by finite size effects.
- M. Porto, P. Maass, M. Meyer, A. Bunde and W. Dieterich, Phys. Rev. B: Condens. Matter, 2000, 61, 6057 CrossRef CAS.
- H. Doweidar, Y. M. Moustafa, G. M. El-Damrawi and R. M. Ramadan, J. Phys.: Condens. Matter, 2008, 20, 035107 CrossRef.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- H. Lammert and A. Heuer, Phys. Rev. Lett., 2010, 104, 125901 CrossRef.
- J. Habasaki and Y. Hiwatari, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144207 CrossRef.
- C. Müller, E. Zienicke, S. Adams, J. Habaski and P. Maass, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 014203 CrossRef.
- A. Cormack, J. Du and T. R. Zeitler, Phys. Chem. Chem. Phys., 2002, 4, 3193 RSC.
- J. C. Dyre and J. Non-Cryst, Solids, 2003, 324, 192 Search PubMed.
- H. Lammert, M. Kunow and A. Heuer, Phys. Rev. Lett., 2003, 90, 215901 CrossRef.
- R. Peibst, C. Schott and P. Maass, Phys. Rev. Lett., 2005, 95, 115901 CrossRef.
- B. A. Shakhmatkin, N. M. Vedisheva, M. M. Schultz and A. C. Wright, J. Non-Cryst. Solids, 1994, 177, 249 CrossRef CAS.
- N. M. Vedisheva, B. A. Shakhmatkin and A. C. Wright, Adv. Mater. Res., 2008, 39, 103 CrossRef.
Footnotes |
| † In borate glasses with very high alkali content (larger than 50 mole percent), B(1) and B(0) units were also reported,19 but we will not consider such high alkali contents here, where the glassy matrix can be viewed to change from a network to a “salt glass” structure. |
| ‡ The balancing should occur before the glass structure becomes frozen into a non-equilibrium state, meaning that the corresponding reaction constant is expected to depend on an effective temperature that varies weakly with the cooling rate. |
| § Since we are not considering {B(0)} and {B(1)} units here, the validity of the treatment is restricted {M} ≤ 1, see the comment above. |
| ¶ Note that the charge delocalisations |qα|/kα discussed above differ by 1/6 = 0.167 between the P(1) and P(2) units and by 1/12 = 0.083 between the P(0) and P(1) units, while there is a larger difference 1/4 = 0.25 both between the P(2) and B(4) units and between the B(2) and P(0) units. Hence one could argue that the phosphate NFUs should more likely occur simultaneously in the network formation than the charged borate and phosphate NFUs in regimes 1 and 3. This view is supported by the behaviour observed in the sodium borophosphate glasses. However, whether the charge delocalisation discussed above can be really used also for a quantitative estimate of differences between relevant formation energies, see the Appendix, is not clear. It would be interesting to conduct electronic structure calculations for small clusters to get more insight into the correlation between charge delocalisation and formation energies. |
| || The Na5B2P3O13 system is the most prominent crystalline alkali ion borophosphate structure. Crystals with compositions Na3BP2O8 and Na3B6PO13 where one-dimensional borophosphate chains are hold together by sodium ions were reported more recently by Xiong et al.38 With respect to alkali types other than sodium, crystalline structures were obtained for a few borophosphate-hydroxide compounds,39 as, for example, Li[B3PO6(OH)2] or K[B6PO10(OH)4]. |
| ** In the rare case, where the number mi of surrounding non-blocked sites is smaller than kα, an attempt is made to exchange the NFUα on site i with another randomly selected NFUα′ on site i′. If, after the attempted exchange, the numbers kα and kα′ of nbOs should be still smaller than the number of surrounding non-blocked sites, another attempt is started until all partial charges carried by the nBOs can be assigned to neighboring non-blocked ion sites. |
| This journal is © The Royal Society of Chemistry 2011 |
