Local structure relaxation, quantum trap depression, and valence charge polarization induced by the shorter-and-stronger bonds between under-coordinated atoms in gold nanostructures
Xi
Zhang
a,
Jer-lai
Kuo
b,
Mingxia
Gu
c,
Xiaofeng
Fan
d,
Ping
Bai
c,
Qing-Gong
Song
e and
Chang Q.
Sun
*a
aSchool of Electrical and Electronic Engineering, Nanyang Technological University, Singapore 639798, Singapore. E-mail: ecqsun@ntu.edu.sg
bInstitute of Atomic and Molecular Sciences, Academia Sinica, Taipei 10617, Taiwan
cAdvanced Photonics and Plasmonics Division, A*STAR Institute of High Performance Computing 1 Fusionopolis Way, Singapore, 138632
dSchool of Physical and Mathematical Science, Nanyang Technological University, Singapore 639798, Singapore
eCollege of Science, Civil Aviation University of China, Tianjin 3000300, China
First published on 2nd December 2009
Abstract
Relativistic density functional theory calculations have been conducted to examine the effect of atomic under-coordination on the crystal structure, binding energy, and electron configuration of cuboctahedral and Marks decahedral gold clusters. Trend consistency between calculations and experimental observations confirmed the predictions made using BOLS correlation theory, suggesting that the shorter-and-stronger bonds between under-coordinated atoms induce local structure relaxation, potential well depression, and the associated local charge and energy densification, as well as the polarization of the otherwise conducting s-electrons (valence charge) by the densely- and tightly-trapped core electrons of which the binding energy shifts positively to deeper energies. Findings are in good agreement with scanning tunneling microscopy/spectroscopy results from monomers, dimers, chain ends, and nanostructures of gold and other metals.
1. Introduction
Metallic nanoparticles (NPs) have inspired increasing interest recently because of their intriguing properties that cannot be observed for their bulk counterparts. As the sizes of the NPs decrease, the volume ratio of surface layers to the entire body, called the surface-to-volume ratio, increases up to 90% for a gold NP with a diameter of 1 nm, for instance. The involvement of the interaction between under-coordinated atoms, which distinguishes the NPs from their bulk counterparts in performance, is indeed fascinating. For instance, Au NPs manifest magnetism1–3 while the bulk gold is diamagnetic; a phase transition from conductor to insulator occurs at the size of a few nanometres;4 nanoscale gold meets the demand of local surface plasmons;5,6 and the catalytic ability for CO oxidation of gold is greatly enhanced at small sizes.7–9 Other intriguing properties for applications include RNA-delivery, localized surface plasma resonance for Raman spectroscopy,10,11 laser applications in medicine,12 enhancement of photoluminescence,13etc. Accompanied by the structure evolution from the face-centered-cubic of bulk to strained structures such as icosahedral or decahedral,14,15 substantial bond contraction occurs to the outermost few atomic shells16 which can be described as an elastic cover sheet of “skin”.17Besides the bond length contraction, the potential trap depth, charge density, energy density, and electronic configurations of the NPs differ from their bulk counterpart as well. Transmission electron microscopy (TEM) measurements have revealed that the inner muffin-tin potential of gold NPs becomes deeper when the particle size is reduced.18 As a consequence of potential well depression, the Au 4f binding energy, for instance, also goes deeper when the solid dimensions are reduced.19 A single-electron tunneling spectroscopy experiment revealed the generation of an energy gap whose width is inversely proportional to the diameter of Au NPs and Pd NPs.4,20 Meanwhile, the peaks of the valence local density of states (LDOS) of Au monomers and dimers,21 Au–Au chains,21,22 Au nanowires,23 and Ag adatoms,24,25 organic nanowires on Ag substrates,26 Fe chains on InSe substrates,27 and Cu chains on Cu substrates28 all move to upper energies as revealed using scanning tunneling microscopy/spectroscopy (STM/S).
Although metal NPs or metal atoms at the edges or at the chain ends demonstrate so many fascinating properties, the mechanism behind them remains yet unclear despite the possible mechanisms such as Coulomb blockade,4 size-dependent dynamic effects,20 and standing wave effects.29 A consistent understanding of the fascinating effects of under-coordination and its electronic origin remains a great challenge.
In recent decades, ab initio density function theory (DFT) has become an elegant tool to investigate the properties of materials. With the simplification of inserting a vacuum slab into the periodical structure or by neglecting the edge potentials or edge states, DFT calculations can be applied to non-periodical systems. Here, we report the consistency in trend between DFT calculations and the experimental observations on the bond contraction, potential well depression, core level shift, and the valence charge polarization of gold nanostructures. Agreement in trends between calculations and experimental observations confirms the expectations of the bond-order-length-strength (BOLS) correlation theory30 regarding the performance of the localized edge states. It is stressed that the edge atomic under-coordination induces local strain, quantum trap depression, charge densification and valence charge polarization, which provide perturbation to the Hamiltonian and hence the related properties and observations.
2. Theory: BOLS expectations
Extended from the “atomic coordination-atomic radius” correlation premise of Goldschmidt31 and Pauling,32 the BOLS correlation30,33 deals with under-coordinated systems such as adatoms, defects, edges, grain boundaries, atomic chains, atomic ribbons, atomic tubes, surfaces and nanostructures as an additional inspection to the classical and the quantum approximations. According to the BOLS theory, within skin depth of the outermost atomic shells in the NPs, the curvature K−1 (with K being the number of atoms lined along the radius of a spherical dot) dependence of the effective coordination number (CN or zi), bond length (di), charge density (ni), and the potential trap depth (also bond energy, Ei), energy density (Ei/d3i) follow the relations:30,33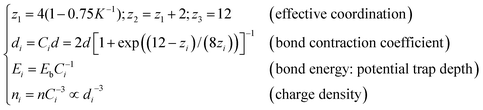 | (1) |
The subscript i denotes the ith atomic layer counted from the outermost to the center of the sphere and the subscript b represents the corresponding bulk values. Eqn (1) indicates that bonds between under-coordinated atoms at the ith shell of NPs will contract spontaneously by Ci associated simultaneously with a C−1i times bond energy gain. As the consequence of bond contraction and bond energy gain, the local charge density will rise by C−3i for a three-dimensional specimen and the local potential well will be deepened by C−1i.
By taking the average over the entire nanostructure with a core–shell configuration, the size dependence of the energy density (which is proportional to the elastic modulus34) and potential trap depth (corresponds to the core level shift19) of a specimen,
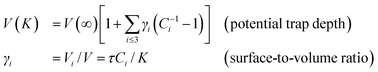 | (2) |
The parameter τ = 3, 2, and 1 represents the dimensionality of a spherical dot, a cylindrical rod and a thin slab, respectively. In eqn (2), the potential trap depth in the surface of up to three atomic layers in depth of a nanostructure is strongly correlated through the bond length and bond energy.35
Increasing experimental evidence17,19 favors the quantitative reliability of the BOLS expectation:
(a) Bonds between the under-coordinated atoms become shorter31,32 and stronger. The bond contraction has happened globally to adatoms,36 dimers,37,38 atomic chains,21 two-dimensional atomic sheets,39,40nanotubes,41nanoribbons,42 atomic vacancies,23 terrace edges,43 dislocations,44 grain boundaries,16,35 nanoislands,45 liquid skins,46 and nanostructures.30 Local strain and curvature-resolved charge and energy quantum trapping do occur near the under-coordinated atoms,39 which provides strong perturbation to the Hamiltonian, binding energy density, and atomic cohesive energy of the system.
(b) The densely- and tightly-trapped charges will polarize the otherwise conducting electrons such as those in the half-filled s-orbital of metals47 or the π-electrons of sp2 hybridized carbon.42 The localized polarization of the s-electrons makes Au(4f145d106s1), Ru(4d75s1), Rh(4d85s1), and Ag(4d10 5s1) nanocrystals nonconductive and magnetic2 because the otherwise-conducting electrons become the tightly-locked monopoles, which are expected to play an important role in quantum friction.48
3. DFT calculations
In order to verify the BOLS predictions of the broken-bond-induced quantum trapping and the associated charge polarization, we conducted DFT calculations of the bond length, Mulliken charge transfer in the skins and the valence charge distribution of Au clusters. As the size decreases, metallic NPs will evolve into some distorted structures such as icosahedra14,49 or decahedra.50,51Recently, a 49-atom core of a Marks decahedral (MD) structure in a thiol monolayer-protected gold nanoparticle was experimentally confirmed.15 However, some researchers claimed that fcc-like cuboctahedral (CO) structures are still stable at small sizes.14 Hence, we chose CO13, CO55, CO147 and the MD13, MD49, MD75, as shown in Fig. 1 for our calculations. Nevertheless, the selection of particular structures does not affect the conclusion as we examined the under-coordination effect only. The calculations focus mainly on the change of bond length between atoms of different effective CNs, the charge transfer using Mulliken population analysis, and the energetic distribution of the valence states.
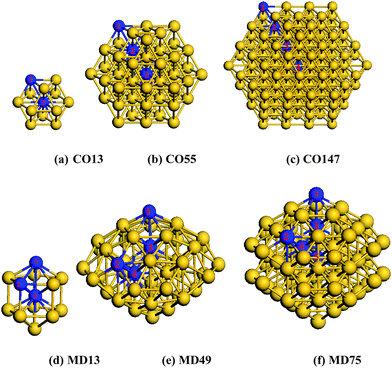 | ||
| Fig. 1 Gold nanoclusters of cuboctahedral (CO) and Marks decahedral (MD) structures. Indicated numbers are atomic positions in different atomic layers. | ||
The relativistic DFT calculations were conducted using the the DMol3 code with a double numeric plus polarization basis set.52 The DFT semi-core pseudopotential53 was chosen as approximations for gold, to deal with the core potentials including some degree of relativistic effects. Geometric and electronic structures were obtained on the basis of the localized density approximation in the PWC form of the functional.54 During calculations, the self-consistency threshold of the total energy was set at 10−6 au. The tolerance limit for the energy, forces and displacement in geometry optimizations were set, respectively, at 10−5 Hartree, 0.002 Hartree/Å and 0.005 Å, respectively.
4. Results and discussion
4.1 Coordination-resolved bond length contraction
As the BOLS theory expected, the spontaneous Au–Au bond contraction at the surface has been confirmed by the current DFT calculations, as listed in Table 1, in addition to the experimental measurements of Huang et al.35 Using electron cohesive diffraction, Huang and coworkers discovered that the Au–Au bond contraction happens only to the outermost three atomic layers of a gold nanosolid in a radial way, which is further supported by molecular dynamics simulations.16 The CN dependence of Au–Au bond contraction is insensitive to the type of substrate support.55 The spontaneous bond contraction depends uniquely on the coordination and has nothing to do with the structural phase or particular elements or the nature of the bond.17,30 It has been proven that the equilibrium Au–Au bond in the monatomic chain contracts by 30% from the bulk value of 0.29 nm to 0.20 nm.56| Structure | Position: atom 1 ∼ atom 2a | Effective zi | d i | d 0 | C −1 i (%) | Shell i | Charge Transfer (e) |
|---|---|---|---|---|---|---|---|
| a The atomic positions are indicated in Fig. 1. | |||||||
| CO13 | 1∼2 | 2.00 | 2.694 | 2.883 | −6.56 | 1 | −1.50 |
| CO55 | 1∼2 | 2.80 | 2.699 | 2.883 | −6.37 | 1 | −0.75 |
| 2∼3 | 4.80 | 2.783 | 2.883 | −3.47 | 2 | 0.653 | |
| CO147 | 1∼2 | 3.14 | 2.788 | 2.883 | −3.29 | 1 | −1.272 |
| 2∼3 | 5.14 | 2.812 | 2.883 | −2.46 | 2 | 1.236 | |
| 3∼4 | 12.00 | 2.829 | 2.883 | −1.86 | 3 | 0.035 | |
| MD13 | 2∼3 | — | 2.759 | 2.883 | −4.31 | — | — |
| 1∼3 | 2.43 | 2.784 | 4.077 | −31.71 | 1 | −0.127 | |
| MD49 | 2∼4 | — | 2.779 | 2.883 | −3.62 | — | — |
| 1∼3 | 2.86 | 2.893 | 4.077 | −29.06 | 1 | −0.613 | |
| MD75 | 2∼4 | — | 2.742 | 2.883 | −4.89 | — | — |
| 1∼3 | 3.10 | 2.910 | 4.077 | −28.62 | 1 | −1.005 | |
| 4∼5 | — | 2.838 | 2.883 | −1.57 | — | — | |
| 3∼5 | 5.10 | 3.354 | 4.077 | −17.74 | 2 | 0.912 | |
In the current DFT geometrical optimization, the bond length of surface Au atoms is shortened with respect to that of the bulk Au atoms (see Table 1). Moreover, Au–Au bonds of the outermost atomic layer, with smaller curvature-dependent CN, shrink more than those in the core interior. The Au–Au distance contracts up to 30%, being in line with experimental observations, as discussed in ref. 56 for Au monatomic chains. The DFT-optimized Au–Au bond lengths follow the trend of the BOLS prediction, but generally, the bond contraction does not reach the derived extent of the BOLS. This quantitative deviation arises from the artifact of the commercial DFT code that needs to include the edge boundary conditions where localized potential depression and charge and energy densification become dominant. Simply inserting a vacuum slab in the calculation may not represent the true situation of edge quantum trapping, which is why we stress the trend consistency between prediction, calculation and measurement throughout the context.
4.2 Potential trap depression and charge transfer from center to edge
According to the principle of least energy, any spontaneous process proceeds towards the direction of energy reduction. Therefore, the spontaneous process of bond contraction is associated simultaneously with the interatomic potential well depression, or the single bond energy gain. The depth of the potential well (Vi) at the surface or edge is proportional to the equilibrium bond energy (Ei), i.e., Vi/Vb ∝ Ei/Eb = C−1i, with subscript b representing the bulk case. Due to the potential well deepening at the surface, valence charges tend to ‘flow’ from the core interior to the surface. Energetically, the binding energy of core electrons will go deeper, also called the ‘positive core level shift’, that is determined uniquely by the overlap and exchange integrals, or the coupling of the interatomic potential and the specific Bloch wave functions.19 Excitingly, as shown in Fig. 2(a), TEM measurement has confirmed18 the size dependence of the muffin-tin inner potential quantum trapping of gold NPs. The mean depth of the inner potential (the volume-averaged electrostatic part of the crystal potential) is increasingly deepened as the diameter of the Au cluster decreases. The trend of inner-potential-well depression is in accordance with the size-induced core level shift. As a result of the surface-potential-well depression, the energy levels of the core electrons will go correspondingly deeper and hence the charge tends to be localized and pinned in the surface layer. The charge transfer of the six considered different nanoclusters is demonstrated (see Table 1) in the calculations using Mulliken charge population analysis.57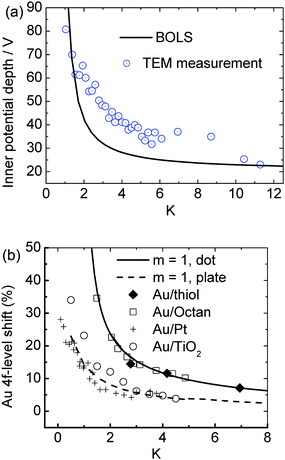 | ||
| Fig. 2 (a) Comparison of the BOLS-derived quantum trapping with the mean inner-potential-well depression as a function gold NP size detected by TEM.18 (b) BOLS reproduction of the size-induced Au 4f core level shift of gold nanostructures on different substrates, which leads to the energy level of an isolated Au atom as 81.505 eV and its bulk shift of 2.865 eV.19 | ||
The negative values in Table 1 represents charge gain, and the positive values charge loss. It can be seen that, for the considered structures, the electrons transfer from the inner to the outer shells of the clusters, consistent with the DFT results for Ag nanoclusters.58
4.3 Core level shift and valence charge polarization
As a consequence of BOLS, the core-level binding-energy shifts to deeper energies because of the Hamiltonian perturbation. Trapping of the 4f charge with a decrease in size, or thickness, of Au on octane and octanedithiol,59 Au on TiO260 and on Pt61 substrates has been observed using X-ray photoelectron emission spectroscopy.Fig. 2(b) shows the BOLS reproduction of the measured shape and size dependence of the Au 4f core level shift using a least-root-mean-square linearization method,19 which led to the quantitative information of the 4f energy level of an isolated Au atom as 81.505 eV and its shift of 2.865 eV upon bulk formation. Interested readers are referred to ref. 19 for more details about the calculations and discussion on the surface and size-induced core level shift of a number of samples.
Meanwhile, according to BOLS, the originally conductive s-electrons of Au are expected to be polarized and locally-pinned by the densely- and tightly-trapped core charges. The extent of polarization increases when one goes from the center to the edge with even lower atomic coordination numbers, which is exactly the case of graphenenanoribbons,42 Au and Ag monomers, dimers, and chain ends.21,22,24,25 Gold monatomic chains are an ideal prototype for one-dimensional structures and the graphenenanoribbon is an ideal a prototype for two-dimensional structures. They demonstrate the same feature of valence charge polarization at the chain end or at the ribbon edge even though they are different materials. Most strikingly, recent progress47 revealed that the under-coordinated Pt(5d106s0) and Rh(5s14d8) adatoms do induce trapped states as additional peaks in the XPS spectra of both the Pt 4f7/262 and the Rh 3d5/263 energies, but polarization only happens to the Rh adatoms because of the presence of the half-filled Rh 5s electrons. The trapped and polarized states due to adatoms are located, respectively, at energies below and above the bulk component of the XPS spectra.
Fig. 3 shows the typically shell-resolved LDOS for the MD75 and CO147 structures. It can be seen from Fig. 3 that the valence electrons in the outermost shells are centered at the upper edge of the valence band while electrons in the inner shells are trapped at the lower edge. The maximum LDOS of atoms at the outermost shell are polarized by the inner electrons. The resultant DOS in Fig. 4 demonstrates that the polarization is more significant in the smaller size. For example, the peak shifts from −2.8 eV to −1.7 eV if the CO147 evolves into CO13. Similarly, the peak of the MD47 shifts from −2.2 to −1.8 eV when MD13 is formed. The calculated results agree exceedingly well with the experimentally observed polarization trends of end and edge states.21,23,24 For an Ag monomer or a Ag dimer, the unoccupied DOS peaks are detected at 2.9 and 2.3 eV, respectively, while the quasi-dimer/monomer state is at 2.7 eV, demonstrating the CN effect on the charge polarization. The monomer and quasi dimer (which retains of the monomer nature) of Ag adatoms exhibit stronger polarization effects than the dimer,24 because the latter has one more coordinated atom.
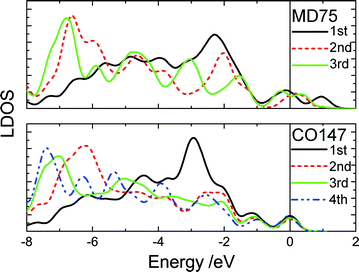 | ||
| Fig. 3 The shell-resolved LDOS for the CO147 and MD75 clusters. The electrons of the outermost shell transfer to the upper edge near the EF (positioned at 0) while the inner-shell electrons remain at lower energies. | ||
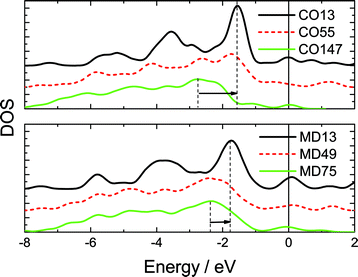 | ||
| Fig. 4 Comparison of the resultant valence DOS of all six calculated clusters. The valence charge polarization is more significant in the smaller size, which agrees with the STM/S observations of gold islands of different sizes23 and from the gold monatomic chain.21 The STS DOS moves up the most for the smallest island and the polarization is more apparent at the chain end. The convoluted LDOS moves to the upper edge near the EF (positioned at 0), and the smallest cluster moves most. | ||
STM/S investigation21 shows that the Au–Au chain end atoms exhibit significant polarization near the EF compared with atoms in the chain interior. Au nanowires of different widths demonstrate that the valence LDOS shifts up and that of the thinnest wire shifts most.23 The common feature of these experimental observations is that the extent of polarization (energy and density) is more pronounced at sites of even lower-coordinated atoms, which are in good accordance, in trend, with the BOLS expectations and the DFT calculations. The shorter-and-stronger bonds between under-coordinated atoms not only cause local strain, but also quantum trap depression, charge and energy densification, and polarization of the otherwise conducting electrons in the outermost, half-filled, s-orbital of gold.
5. Conclusion
Consistency between the current DFT calculations and the TEM, XPS, and STM/S observations of the size trends of the surface lattice strain, muffin-tin inner potential depression, core level shift, chain end and island charge polarization of gold nanostructures confirmed the predictions made using the BOLS approximation. An incorporation of the BOLS correlation with the DFT calculations and experimental observations has led to a consistent insight into the physical origin of the generation of the strongly localized edge states of gold nanoclusters. The consistency between BOLS expectations and the observed trends of charge localization and the LDOS polarization near the EF witnesses the significance of the under-coordination, or broken bond. It is particularly emphasized that the under-coordinated atoms are so important that they result in local strain, quantum trap depression, charge densification and valence charge polarization. The understanding herewith and the previously reported findings may extend to other situations with a large proportion of under-coordinated atoms, which should further shed light on other intrinsic properties such as catalytic enhancement, magnetism presence and surface plasmon response of gold NPs.Acknowledgements
Financial support from the Institute of High Performance Computing, A*Star, Singapore and NSF (No. 60979008), China, are gratefully acknowledged.References
- J. S. Garitaonandia, M. Insausti, E. Goikolea, M. Suzuki, J. D. Cashion, N. Kawamura, H. Ohsawa, I. Gil de Muro, K. Suzuki, F. Plazaola and T. Rojo, Nano Lett., 2008, 8, 661–667 CrossRef CAS.
- Y. Yamamoto, T. Miura, M. Suzuki, N. Kawamura, H. Miyagawa, T. Nakamura, K. Kobayashi, T. Teranishi and H. Hori, Phys. Rev. Lett., 2004, 93, 116801 CrossRef CAS.
- R. J. Magyar, V. Mujica, M. Marquez and C. Gonzalez, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144421–144427 CrossRef.
- B. Wang, X. D. Xiao, X. X. Huang, P. Sheng and J. G. Hou, Appl. Phys. Lett., 2000, 77, 1179–1181 CrossRef CAS.
- O. A. Yeshchenko, I. M. Dmitruk, A. A. Alexeenko, M. Y. Losytskyy, A. V. Kotko and A. O. Pinchuk, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235438–235438 CrossRef.
- J. Sancho-Parramon, Nanotechnology, 2009, 20, 235706 CrossRef CAS.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. I. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981–983 CrossRef CAS.
- M. Valden, M. X. Lai and D. W. Goodman, Science, 1998, 281, 1647 CrossRef CAS.
- A. Wittstock, B. Neumann, A. Schaefer, K. Dumbuya, C. Kübel, M. M. Biener, V. Zielasek, H.-P. Steinrück, J. M. Gottfried, J. Biener, A. Hamza and M. Bäumer, J. Phys. Chem. C, 2009, 113, 5593–5600 CrossRef CAS.
- Y. B. Zheng, L. L. Jensen, W. Yan, T. R. Walker, B. K. Juluri, L. Jensen and T. J. Huang, J. Phys. Chem. C, 2009, 113, 7019–7024 CrossRef CAS.
- A. Elbakry, A. Zaky, R. Liebl, R. Rachel, A. Goepferich and M. Breunig, Nano Lett., 2009, 9, 2059–2064 CrossRef CAS.
- V. A. B. V. K. Pustovalov, Laser Phys. Lett., 2004, 1, 516–520 Search PubMed.
- G. Sun, J. B. Khurgin and R. A. Soref, Appl. Phys. Lett., 2009, 94, 101103–101103 CrossRef.
- K. P. McKenna, Phys. Chem. Chem. Phys., 2009, 11, 4145 RSC.
- P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430–433 CrossRef CAS.
- W. H. Qi, B. Y. Huang and M. P. Wang, J. Comput. Theor. Nanosci., 2009, 6, 635–639 CrossRef CAS.
- C. Q. Sun, Prog. Mater. Sci., 2009, 54, 179–307 CrossRef CAS.
- P. Donnadieu, S. Lazar, G. A. Botton, I. Pignot-Paintrand, M. Reynolds and S. Perez, Appl. Phys. Lett., 2009, 94, 263116–263113 CrossRef.
- C. Q. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 045105 CrossRef.
- B. Wang, K. D. Wang, W. Lu, J. L. Yang and J. G. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205411 CrossRef.
- J. N. Crain and D. T. Pierce, Science, 2005, 307, 703–706 CrossRef CAS.
- N. Nilius, T. M. Wallis and W. Ho, Science, 2002, 297, 1853–1856 CrossRef CAS.
- K. Schouteden and et al, Nanotechnology, 2009, 20, 395401 CrossRef CAS.
- A. Sperl, J. Kröger, R. Berndt, A. Franke and E. Pehlke, New J. Phys., 2009, 11, 063020 CrossRef.
- A. Sperl, J. Kroger, N. Neel, H. Jensen, R. Berndt, A. Franke and E. Pehlke, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085422–085427 CrossRef.
- L. Chen, H. Li and A. T. S. Wee, Nano Lett., 2009 DOI:10.1021/nl902527d.
- T. Matsui, C. Meyer, L. Sacharow, J. Wiebe and R. Wiesendanger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165405–165405 CrossRef.
- S. Fölsch, P. Hyldgaard, R. Koch and K. H. Ploog, Phys. Rev. Lett., 2004, 92, 056803 CrossRef CAS.
- B. G. Briner, P. Hofmann, M. Doering, H. P. Rust, E. W. Plummer and A. M. Bradshaw, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 13931–13943 CrossRef CAS.
- C. Q. Sun, Prog. Solid State Chem., 2007, 35, 1–159 CrossRef CAS.
- W. T. Goldschmidt, Ber. Deut. Chem. Ges., 2007, 60, 1270 Search PubMed.
- L. J. Pauling, J. Am. Chem. Soc., 1947, 69, 542 CrossRef CAS.
- C. Q. Sun, Y. Sun, Y. G. Nie, Y. Wang, J. S. Pan, G. Ouyang, L. K. Pan and Z. Sun, J. Phys. Chem. C, 2009, 113, 16464–16467 CrossRef CAS.
- X. J. Liu, J. W. Li, Z. F. Zhou, L. W. Yang, Z. S. Ma, G. F. Xie, Y. Pan and C. Q. Sun, Appl. Phys. Lett., 2009, 94, 131902 CrossRef.
- W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Nat. Mater., 2008, 7, 308–313 CrossRef CAS.
- O. Mironets, H. L. Meyerheim, C. Tusche, V. S. Stepanyuk, E. Soyka, H. Hong, P. Zschack, N. Jeutter, R. Felici and J. Kirschner, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035406 CrossRef.
- Y.-C. Tsai, C.-W. Hsu, J.-S. K. Yu, G.-H. Lee, Y. Wang and T.-S. Kuo, Angew. Chem., Int. Ed., 2008, 47, 7250–7253 CrossRef CAS.
- C.-W. Hsu, J.-S. K. Yu, C.-H. Yen, G.-H. Lee, Y. Wang and Y.-C. Tsai, Angew. Chem., Int. Ed., 2008, 47, 9933–9936 CrossRef CAS.
- F. Matsui, T. Matsushita, Y. Kato, M. Hashimoto, K. Inaji, F. Z. Guo and H. Daimon, Phys. Rev. Lett., 2008, 100, 207201–207204 CrossRef.
- T. Kizuka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155401–155411 CrossRef.
- C. Q. Sun, H. L. Bai, B. K. Tay, S. Li and E. Y. Jiang, J. Phys. Chem. B, 2003, 107, 7544–7546 CrossRef CAS.
- C. Q. Sun, S.-Y. Fu and Y. G. Nie, J. Phys. Chem. C, 2008, 112, 18927–18934 CAS.
- M. V. Rastei, B. Heinrich, L. Limot, P. A. Ignatiev, V. S. Stepanyuk, P. Bruno and J. P. Bucher, Phys. Rev. Lett., 2007, 99, 246102 CrossRef CAS.
- C. Deng and F. Sansoz, Appl. Phys. Lett., 2009, 95, 091914–091913 CrossRef.
- O. Mironets, H. L. Meyerheim, C. Tusche, V. S. Stepanyuk, E. Soyka, P. Zschack, H. Hong, N. Jeutter, R. Felici and J. Kirschner, Phys. Rev. Lett., 2008, 100, 096103 CrossRef CAS.
- O. G. Shpyrko, A. Y. Grigoriev, C. Steimer, P. S. Pershan, B. H. Lin, M. Meron, T. Graber, J. Gerbhardt, B. Ocko and M. Deutsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 224206 CrossRef.
- C. Q. Sun, Adatom-induced local strain, quantum trap depression, and charge polarization at Pt and Rh surfaces, J. Phys. Chem. C, 2009 Search PubMed , in press.
- C. Q. Sun et al., J. Phys. Chem. C, 2009, 113, 20009 CrossRef.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856–3863 CrossRef CAS.
- C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Phys. Rev. Lett., 1997, 79, 1873 CrossRef CAS.
- L. D. Marks, J. Cryst. Growth, 1983, 61, 556–566 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS.
- B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244 CrossRef.
- J. T. Miller, A. J. Kropf, Y. Zha, J. R. Regalbuto, L. Delannoy, C. Louis, E. Bus and J. A. van Bokhoven, J. Catal., 2006, 240, 222 CrossRef CAS.
- C. Q. Sun, C. M. Li, S. Li and B. K. Tay, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 245402 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1846 CAS.
- D. Liu, J. S. Lian and Q. Jiang, J. Phys. Chem. C, 2009, 113, 1168–1170 CrossRef CAS.
- T. Ohgi and D. Fujita, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 115410 CrossRef.
- A. Howard, D. N. S. Clark, C. E. J. Mitchell, R. G. Egdell and V. R. Dhanak, Surf. Sci., 2002, 518, 210–224 CrossRef CAS.
- M. Salmerón, S. Ferrer, M. Jazzar and G. A. Somorjai, Phys. Rev. B: Condens. Matter, 1983, 28, 1158 CrossRef CAS.
- L. Bianchettin, A. Baraldi, S. de Gironcoli, E. Vesselli, S. Lizzit, L. Petaccia, G. Comelli and R. Rosei, J. Chem. Phys., 2008, 128, 114706 CrossRef.
- A. Baraldi, L. Bianchettin, E. Vesselli, S. de Gironcoli, S. Lizzit, L. Petaccia, G. Zampieri, G. Comelli and R. Rosei, New J. Phys., 2007, 9(5), 143 CrossRef.
| This journal is © The Royal Society of Chemistry 2010 |
