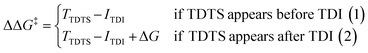Open Access Article
Open Access ArticleMachine learning-based screening of Mn-PNP catalysts for the CO2 reduction reaction using a region-wise ligand-encoded feature matrix†
Amitabha
Das‡
 a,
Diptendu
Roy‡
a,
Diptendu
Roy‡
 a,
Shyama Charan
Mandal§
a,
Shyama Charan
Mandal§
 ab and
Biswarup
Pathak
ab and
Biswarup
Pathak
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Indore, Indore 453552, India. E-mail: biswarup@iiti.ac.in
bSUNCAT Center for Interface Science and Catalysis, SLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
First published on 18th March 2024
Abstract
The CO2 reduction reaction is a promising way to reduce the CO2 level in the environment and most importantly to produce C1-based chemicals (HCOOH and CH3OH) that can be used as liquid fuels and industrial chemicals. In this regard, homogeneous Mn-PNP based catalysts are found to be suitable for the reaction and show promising potential for enhancing activity through ligand modification. Herein, a novel ligand encoded feature matrix enabled machine learning (ML) model has been developed to screen efficient catalysts from a large search space of earth-abundant aromatic Mn-PNP catalysts using the effects of different ligands present on the different ligand sphere of the catalysts. The ML models based on gradient boosting (GBR and XGBR) were found to be the best performing ML models with a density functional theory (DFT) level of accuracy. Potential catalysts for HCOOH and CH3OH formation are identified based on the overall reaction free energy barrier through ML + DFT. The importance of different regions (R1 and R2) and the effect of ligand substituents (+I/−I) in the catalyst are unleashed. Furthermore, a favorable mechanism to produce HCOOH has been ascertained.
Introduction
Homogeneous catalyst-driven reduction of CO2 into value-added C1 based chemicals and liquid fuels (CO, HCOOH, CH3OH, etc.) represents a sustainable route for the direct utilization of CO2.1–4 However, the hydrogenation of CO2 is challenging due to its high thermodynamic stability.5 In this regard, homogeneous catalysts based on noble metals such as Ru and Ir have been utilized to overcome thermodynamic stability and product selectivity.3,6–10 However, such noble metal-based catalysts are not sustainable for industrial scale usage due to the cost associated with them. In recent years, earth abundant Mn-based catalysts made of aromatic PNP catalyst have been studied and found to show promising activity for CO2 reduction reactions (CO2RR) to produce HCOOH and CH3OH and also for other hydrogenation reactions.11–14 Kirchner and co-workers have found the aromatic Mn-PNP catalyst to be active for aldehyde hydrogenation.11 Gonsalvi and co-workers have reported that, aromatic Mn-PNP catalysts with different ligand substituents can hydrogenate CO2 to HCOOH and CH3OH with good turnover number (TON).12,13 Similarly, Saouma et al. have also reported the good catalytic activity of the analogous catalyst for the conversion of CO2 to formate.14 Therefore, aromatic Mn-PNP catalysts are a suitable choice for HCOOH and CH3OH formation, but their activity is not up to the mark to be used as an industrial catalyst. Therefore, finding suitable earth abundant metal-based catalysts for the CO2RR is a need of the hour.It was reported that a subtle change in the ligand sphere can change the overall activity of the catalyst.12,15,16 Similarly, the electronic environment of the ligand has a huge influence on the catalyst activity. Thus, the activity of any catalyst can be significantly enhanced through ligand substitution. The various possibilities in the unknown ligand space are then confronted with the challenge of choice from the vast structural possibilities. As a result, there has been a long-standing interest in predicting a given ligand's likely impact on the structure and reactivity of organometallic complexes through parameterization. In the absence of insight into the correlation between ligand and catalyst, new catalysts are developed mostly through a series of tedious trial and error cycles guided by chemical intuition either using density functional theory (DFT) methods or experiments. It takes a lot of time, money, and effort to complete the process. The possibilities of catalyst combinations are vast considering the available ligand space. Therefore, the existing strategies clearly fail to address the full scope of the challenge. This raises the importance of developing faster, efficient, and more reliable data-driven catalyst design techniques to guide future experiments. In this regard, machine learning (ML)-based regression techniques have emerged as a promising tool.17–19 Through specific strategies, ML algorithms are able to learn underlying principles behind vast amounts of data through mathematical theory and rigorous data analysis. These laws are used to achieve the purpose of prediction. Thus, the active catalyst search for the reaction can be accelerated using ML models. Furthermore, the activity of the catalyst or any chemical transformations are evaluated through the activation barriers. For the ML prediction of the activation barriers, the mostly used features are the DFT calculated features, which are in a way time consuming and computationally expensive.20–22 Moreover, some features suffer due to the lack of interpretation. Thus, it is necessary to develop a feature that does not require DFT calculations and can alone predict the activation energy barrier.
Herein, under the assumption of the great influence of the ligand in the aromatic Mn-PNP catalysts for CO2 conversion to C1 products (HCOOH and CH3OH), we set out to identify the best set of ligands and overall catalysts for the reactions. To accomplish this, we used regression models using ligand encoded matrix-based features for all the considered ligands and further tested the reliability of the best fitted ML models through cross-validation (CV) analysis and DFT calculated results.
Methods
For the CO2 hydrogenation to HCOOH and CH3OH, an appropriate model was implemented using the Gaussian 09 D.01 package.23 Previous studies show the good accuracy of the Becke's three-parameter hybrid exchange Lee–Yang–Parr's (B3LYP) functional for the Mn based systems for the hydrogenation of CO2.4,24 Thus, all the density functional theory (DFT) based calculations were executed with the B3LYP correlation functional. The Pople diffused basis set 6-31++G(d,p) was considered for all the non-metals (P, F, O, N, C and H) beside the LANL2DZ effective core potential (ECP) for Mn metal.25–30 Grimme's DFT-D3 potential has been utilized in our study to include all the non-covalent interactions (NCI).31 The common solvent for these reactions is tetrahydrofuran (THF) and thus all the structures were optimized using the implicit conductor-like polarizable continuum model (CPCM) for the THF solvent (e = 7.58) in order to mimic the experimental conditions.32,33 To obtain the accurate reaction free energy, zero-point vibrational energy (ZPVE) and entropy correction (TΔS) have been included in the total calculated electronic energy at 298.15 K temperature and 1 atm pressure. All the intermediates were optimized and identified through the absence of imaginary frequency. The structure of all transition states (TSs) has been optimized and validated by frequency calculations with a single imaginary frequency. The overall reaction free energy change (ΔG) and the total reaction free energy barriers (ΔG‡) have been evaluated based on the Shaik–Kozuch energetic span model, where ΔΔG‡ of a catalytic cycle depends on the TOF-determining transition state (TDTS) and TOF-determining intermediate (TDI):34Natural bond orbital (NBO) analysis is done to understand the charge distribution of different atoms.35
Results and discussion
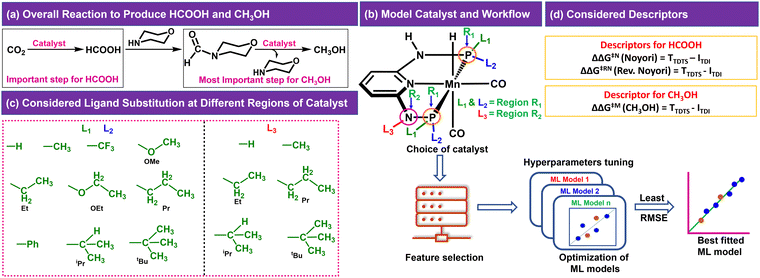
In the CO2RR, CO2 can be converted to HCOOH in the presence of a catalyst, which can be then converted to CH3OH through direct or indirect mechanisms.4,8,10 We have considered the indirect mechanistic approach employing morpholine as a co-catalyst in our study (Fig. 1a) to produce CH3OH.10 We first considered a Mn-PNP based aromatic catalyst (Fig. 1b) and identified two specific regions on the catalyst. We have divided the regions as R1 and R2 based on the distance from the metal centre as well as based on the ligands bonded to the P or N atoms (R1 → P and R2 → N), respectively, where the foreign ligand can be attached. For the R1 and R2 region, a set of 10 (R1: L1 and L2) and 6 (R2: L3) ligands (Fig. 1c) are considered, respectively based on the experimental reports of PNP and other catalysts.13,36–39 The P atom sites in the catalysts were found to be the most preferable sites for a variety of ligand substitutions and thus the number of considered ligands for the R2 region is less compared to the R1 region.36–41 The PNP catalysts typically exhibit either complete symmetry with four identical ligand substituents across two P (L1 = L2) sites or a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of two different ligands across both P sites (L1 ≠ L2) (Fig. 1b).13,36–39,42,43 The number of possible catalysts that came out from the considered ligands at the R1 region with respect to each ligand present on the R2 region is 330.
1 ratio of two different ligands across both P sites (L1 ≠ L2) (Fig. 1b).13,36–39,42,43 The number of possible catalysts that came out from the considered ligands at the R1 region with respect to each ligand present on the R2 region is 330.
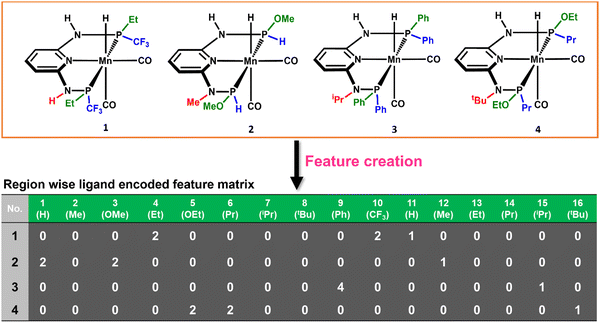
The consideration of the DFT calculated features would take a great deal of time and resources for such a large number of possible catalysts. Therefore, we introduced a ligand encoded matrix-based feature for simplicity and better adaptability of the model like the microstructural feature introduced in heterogeneous catalysis.44,45 The newly introduced matrix-based feature can speed up the process of training and prediction as the matrix contains only the information about variable parts i.e., ligand substituents. This feature is obtained for each catalyst through a ligand encoding technique considering the kind of ligand and the number of specific ligands present on different substitution sites R1 (L1 and L2) and R2 (L3) in the catalysts. These variants of substitution sites are decided according to the distance of the ligands from the metal centre. An illustration of the feature matrix with a few catalysts is shown in Fig. 2. Furthermore, each catalyst's individual matrices are combined into a large matrix capable of containing all the structural information. A total of 16 features (Fig. 2) have been considered and these features are the different ligands present in a specific region of the catalysts. In catalyst 1 (Fig. 2), two Et and two CF3 groups are present in the R1 region, and one H is present in the R2 region and therefore the feature values for these features are 2, 2 and 1, respectively and the rest of the feature values are 0 in the matrix for the catalyst. In this way, a feature matrix has been prepared for 330 catalysts for our machine learning study. The newly introduced feature matrix can reduce the time and cost of feature selection and feature engineering.
Two different reaction mechanisms such as Noyori and revised Noyori (RN) are reported for the conversion of CO2 to HCOOH (Scheme 1a).4,24 The subsequent step involves the reaction between the HCOOH and the co-catalyst (morpholine) to form N-formylmorpholine.10,24 There are two competing pathways for the hydrogenation of N-formylmorpholine and we have considered the most favorable mechanism for the formation of CH3OH (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond hydrogenation followed by C–N bond; Scheme 1b).24,46 There are three important transition states for the formation of HCOOH and CH3OH from CO2, namely hydride transfer to CO2 (TS1), heterolytic H2 cleavage to regenerate the active catalyst (TS2) and heterolytic H2 cleavage to transfer a proton (TS3) to HCOO− (Scheme 1a). In the RN mechanism, either TS1 or TS3 can contribute to the overall reaction free energy barrier (ΔΔG‡RN),8,24,47 whereas TS2 is the most important step that controls the overall reaction free energy barrier of the Noyori type mechanism (ΔΔG‡N).3,7 Similarly, CH3OH can be produced through the indirect mechanism (free energy barrier: ΔΔG‡M), where TS2 is the most important transition state.3,24 Therefore, in all the cases, the calculated ΔΔG‡ for (Fig. 1d) each individual mechanism using the transition state model is considered to be a suitable descriptor of the overall reactions (ΔΔG‡RN, ΔΔG‡N and ΔΔG‡M). Additionally, the activation barrier (ΔG‡) for each of these transition states (TS1: ΔG‡TS1; TS2: ΔG‡TS2; and TS3: ΔG‡TS3) can also be a suitable descriptor to identify the activity of the catalyst for a specific step of the reaction.
O bond hydrogenation followed by C–N bond; Scheme 1b).24,46 There are three important transition states for the formation of HCOOH and CH3OH from CO2, namely hydride transfer to CO2 (TS1), heterolytic H2 cleavage to regenerate the active catalyst (TS2) and heterolytic H2 cleavage to transfer a proton (TS3) to HCOO− (Scheme 1a). In the RN mechanism, either TS1 or TS3 can contribute to the overall reaction free energy barrier (ΔΔG‡RN),8,24,47 whereas TS2 is the most important step that controls the overall reaction free energy barrier of the Noyori type mechanism (ΔΔG‡N).3,7 Similarly, CH3OH can be produced through the indirect mechanism (free energy barrier: ΔΔG‡M), where TS2 is the most important transition state.3,24 Therefore, in all the cases, the calculated ΔΔG‡ for (Fig. 1d) each individual mechanism using the transition state model is considered to be a suitable descriptor of the overall reactions (ΔΔG‡RN, ΔΔG‡N and ΔΔG‡M). Additionally, the activation barrier (ΔG‡) for each of these transition states (TS1: ΔG‡TS1; TS2: ΔG‡TS2; and TS3: ΔG‡TS3) can also be a suitable descriptor to identify the activity of the catalyst for a specific step of the reaction.
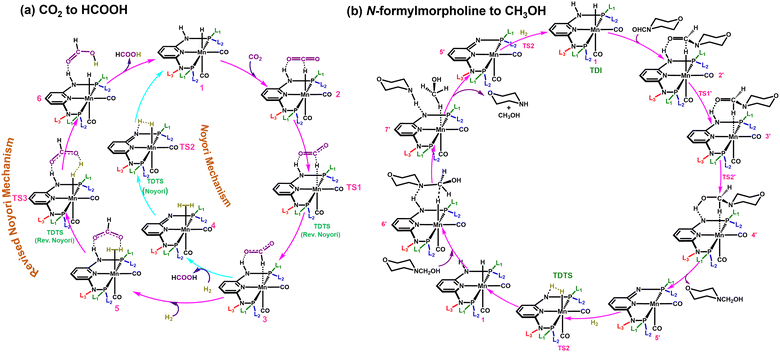 | ||
| Scheme 1 Possible CO2 hydrogenation mechanisms to (a) produce HCOOH and (b) the hydrogenation of N-formylmorpholine to CH3OH with an aromatic Mn-PNP based catalyst. | ||
Through DFT calculations, a training dataset (44 catalysts) was generated with proper sampling of the catalysts to make sure all the ligand substituents are present in both the regions of the catalysts (Table S1, ESI†). Herein, several regression models were used to achieve all the considered output descriptors. Initially considered ML models were trained and evaluated using an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-test split of the DFT calculated datasets.45,48 The workflow is summarized in Fig. 1b. The performance of each regression mode is estimated with train-test root-mean-square error (RMSE) to avoid the overfitting condition.
20 train-test split of the DFT calculated datasets.45,48 The workflow is summarized in Fig. 1b. The performance of each regression mode is estimated with train-test root-mean-square error (RMSE) to avoid the overfitting condition.
Five ML models were implemented, namely ordinary linear regressor, kernel ridge regressor (KRR: kernel-based algorithm), Random-forest regressor (RFR: tree-based algorithm made of bagging technique) implemented in the scikit-learn package49 and gradient boosting frameworks such as gradient boosting regressor (GBR) and eXtreme gradient boosting regressor (XGBR).50 The NumPy and Pandas libraries were used for the mathematical functions and data pre-processing, respectively, along with Matplotlib and Seaborn for the plotting of numerical data and visualization.51–53 Through the hyperparameter tuning of all the algorithms, we achieved the best possible values of the hyperparameters, resulting in optimized algorithms (Table S2, ESI†). The performance of all the considered models is given in Table S3 (ESI†). The best performing ML model for each descriptor was chosen based on the lowest train-test errors. We have found that the optimized XGBR has the lowest train-test RMSE for both ΔΔG‡RN and ΔΔG‡M and the GBR model for ΔΔG‡N (Table 1). The plots of DFT calculated versus predicted ΔΔG‡ are shown in Fig. 3. Similarly, for other descriptors (ΔG‡TS1, ΔG‡TS2 and ΔG‡TS3), either of the gradient boosting regressors (GBR or XGBR) performed well with the least test RMSE (Table 1 and Fig. S1, ESI†). All the train-test RMSEs for the best fitted models are reasonable enough to be considered for suitable predictions of unknown catalysts. In the case of ΔΔG‡RN, the calculated RMSE is slightly higher compared to the other cases, underlying the fact that either TS1 or TS3 can contribute in the ΔΔG‡RN and both of these transition states are chemically different from each other. In contrast, for the individual case of the ΔG‡TS1 and ΔG‡TS3 the test RMSE is significantly low (Table 1). Taking all these results into account, it appears that the learning complexity rises to the ML model for the training data of descriptor ΔΔG‡RN, resulting in a slightly higher RMSE.
| Name | ΔΔG‡N | ΔΔG‡RN | ΔΔG‡M | ΔG‡TS1 | ΔG‡TS2 | ΔG‡TS3 |
|---|---|---|---|---|---|---|
| Method | GBR | XGBR | XGBR | XGBR | GBR | GBR |
| Train (RMSE) | 0.01 | 0.08 | 0.03 | 0.04 | 0.01 | 0.01 |
| Test (RMSE) | 0.09 | 0.14 | 0.12 | 0.07 | 0.10 | 0.08 |
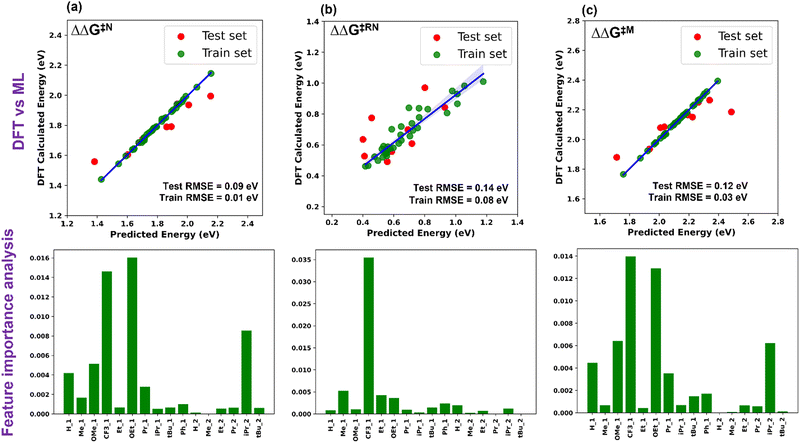 | ||
| Fig. 3 Plot of DFT calculated vs. ML predicted ΔΔG‡ and feature importance for (a) Noyori, (b) revised Noyori and (c) CH3OH formation mechanisms. | ||
To ensure the stability and generalizability of the best fitted ML models, we have performed 5-fold CV analysis (Fig. S2, ESI†). The average RMSE of CV in each case is close to the test RMSE (Fig. 4a and Table S4, ESI†). This reflects that all the best fitted ML models are suitable and generalizable even though the training dataset is small. The reliable performance of the ML models could be due to the proper sampling of all the data points to prepare the training dataset.54,55 Considering the best fitted ML models for individual descriptors with optimized hyperparameters, all the descriptors (overall reaction free energy barriers (ΔΔG‡) and activation barriers (ΔG‡) of individual transition states) were predicted for the rest of the 286 catalysts (Table S5, ESI†). Further validation of our predictions is also carried out with 5 arbitrary catalysts (Fig. S3, ESI†) from the predicted data points calculating all the considered output descriptors using the DFT method. Interestingly, it was observed that the predicted values closely matched with the DFT calculated values (Fig. 4b and Table S6, ESI†), which again suggests that all the best fitted models are stable and suitable for prediction.
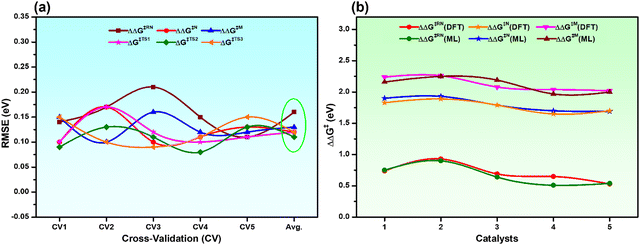 | ||
| Fig. 4 (a) 5-fold CV analysis with the best fitted ML models for all the descriptors and the Avg. is the mean RMSE of the CV, and (b) comparison of DFT calculated vs. ML predicted ΔΔG‡ of all the catalysts considered in Fig. S3 (ESI†). | ||
Based on DFT calculation and ML prediction, the RN type mechanism was found to be the favourable pathway over the Noyori type mechanism for aromatic Mn-PNP catalysts to produce HCOOH.3,24 The TS2 accounted for the overall high ΔΔG‡N for the Noyori-type mechanism, thus making the mechanism not suitable for HCOOH formation (Scheme 1a and Table S1, ESI†). In contrast, in the RN-type mechanism, the barriers for both TS1 and TS3 are low (Scheme 1a and Table S1, ESI†), thereby making the pathway more favourable for HCOOH formation.
The permutation feature importance analysis (Fig. 3) shows the contribution of different ligands present on different positions of the catalysts towards ΔΔG‡ for the considered reactions.54 The ligands present in the first region have higher contributions as compared to the second region, which shows that the former is the most important part to tune the activity of aromatic Mn-PNP for a specific reaction. Ligands having a stronger/moderate −I effect are found to adversely affect the activation barriers of the reactions (Table S1, ESI†). Conversely, groups with +I effects are observed to be beneficial for the reactions. Using DFT+ML, we have identified the top-performing catalysts for the formation of CH3OH and HCOOH from CO2 (Fig. 5 and Fig. S4, ESI†). For the HCOOH formation, along with the three top performing catalysts (1 to 3) (Fig. S4, ESI†), we have proposed two symmetric catalysts (4 and 5) from the ease of synthesis perspective, which are found to be comparable in terms of activity with top performing catalysts.
For the CH3OH formation, the suitable ligands (–iPr and –tBu) mostly have a strong/moderate +I affect, in agreement with the experimentally reported suitable catalysts for the reaction.10,12 The –iPr is the most suitable ligand substitution in both the regions though –tBu is the group having the strongest +I effect. The presence of a –tBu group in both the regions together creates steric hindrance, which reduces the available space for reactants to approach the active center. This, in turn, has an adverse effect on the overall ΔΔG‡ of the reactions. In the case of HCOOH formation, the two different transition states (TS1 and TS3) play an important role and both these steps are chemically different in nature. Thus, catalysts having moderate +I and weak −I effecting groups are found to be the most suitable.
The natural bond orbital (NBO) analysis of the two catalysts having strong +I/−I effecting (Fig. S5, ESI†) groups showed that the presence of such groups largely affects the overall charge distribution of the catalysts. In the case of TS2, the +I effecting groups shifted the electron density towards the aromatic ring, thus stabilizing the overall transition state. At the same time, the higher positive charges on the P-atoms helped the heterolytic hydrogen cleavage, whereas the −I effecting groups pull the electron density from the ring thereby destabilizing the overall transition states for CH3OH formation. On the other hand, good catalysts for HCOOH formation should have an overall balanced charge distribution, which can control both TS1 and TS3. Therefore, moderate +I and weak −I effecting groups are suitable for the HCOOH formation. This proof-of-concept model may be very helpful for experimentalists to design catalysts in no time for the conversion of CO2 to HCOOH and CH3OH.
Conclusions
In summary, we have developed an ML prediction model based on a DFT database. This scheme can significantly expedite the exploration of a vast catalyst search space, leading to the identification of promising homogeneous aromatic Mn-PNP catalysts for converting CO2 into HCOOH and CH3OH in solvent medium. The newly proposed feature matrix and the proper sampling of the dataset are the backbone of the remarkable predictive capability of the used ML model. The ML models based on gradient boosting (GBR and XGBR) were found to be the best performing and well-trained ML models with high accuracy. The utility and predictive capability of the best fitted model were tested through cross-validation and DFT calculations. Our model shows that the revised Noyori-type mechanism is favourable compared to the Noyori mechanism for HCOOH formation. The first region of the catalysts is found to be the most important position to tune their activity. The ligand substituents having a strong +I effect are found to be suitable for CH3OH formation. In contrast, the moderate +I and weak −I effecting groups are found to be suitable for HCOOH. We believe that our model and feature matrix-based approach may be able to speed up the catalyst search process.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB (Project Number CRG/2018/001131), CSIR (Project 01(3046)/21/EMR-II), and BRNS (Project Number 2023-BRNS/12356). A. D. thanks UGC, and D. R. thanks MoU for the research fellowship.References
- S. Zhang, Q. Fan, R. Xia and T. J. Meyer, Acc. Chem. Res., 2020, 53, 255 CrossRef CAS PubMed.
- E. E. Benson, C. P. Kubiak, A. J. Sathrum and J. M. Smieja, Chem. Soc. Rev., 2009, 38, 89–99 RSC.
- S.-T. Bai, G. De Smet, Y. Liao, R. Sun, C. Zhou, M. Beller, B. U. W. Maes and B. F. Sels, Chem. Soc. Rev., 2021, 50, 4259–4298 RSC.
- A. Das, S. C. Mandal and B. Pathak, Catal. Sci. Technol., 2021, 11, 1375–1385 RSC.
- I. Omae, Catal. Today, 2006, 115, 33 CrossRef CAS.
- Y.-N. Li, R. Ma, L.-N. He and Z.-F. Diao, Catal. Sci. Technol., 2014, 4, 1498–1512 RSC.
- W.-Y. Chu, Z. Culakova, B. T. Wang and K. I. Goldberg, ACS Catal., 2019, 9, 9317–9326 CrossRef CAS.
- S. Wesselbaum, V. Moha, M. Meuresch, S. Brosinski, K. M. Thenert, J. Kothe, T. Vom Stein, U. Englert, M. Hoelscher, J. Klankermayer and W. Leitner, Chem. Sci., 2015, 6, 693 RSC.
- S. Kar, A. Goeppert, J. Kothandaraman and G. K. S. Prakash, ACS Catal., 2017, 7, 6347–6351 CrossRef CAS.
- A. Weilhard, S. P. Argent and V. Sans, Nat. Commun., 2021, 12(1), 231 CrossRef CAS PubMed.
- Y.-Q. Zou, S. Chakraborty, A. Nerush, D. Oren, Y. Diskin-Posner, Y. Ben-David and D. Milstein, ACS Catal., 2018, 8, 8014–8019 CrossRef CAS PubMed.
- F. Bertini, M. Glatz, N. Gorgas, B. Stöger, M. Peruzzini, L. F. Veiros, K. Kirchner and L. Gonsalvi, Chem. Sci., 2017, 8, 5024–5029 RSC.
- F. Bertini, M. Glatz, B. Stöger, M. Peruzzini, L. F. Veiros, K. Kirchner and L. Gonsalvi, ACS Catal., 2019, 9, 632–639 CrossRef CAS.
- K. Schlenker, E. G. Christensen, A. A. Zhanserkeev, G. R. McDonald, E. L. Yang, K. T. Lutz, R. P. Steele, R. T. VanderLinden and C. T. Saouma, ACS Catal., 2021, 11, 8358–8369 CrossRef CAS.
- D. A. Kuß, M. Hölscher and W. Leitner, ACS Catal., 2022, 12(24), 15310–15322 CrossRef.
- L. Piccirilli, B. Rabell, R. Padilla, A. Riisager, S. Das and M. Nielsen, J. Am. Chem. Soc., 2023, 145, 5655–5663 CrossRef CAS PubMed.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K.-I. Shimizu, ACS Catal., 2020, 10, 2260–2297 CrossRef CAS.
- D. Roy, S. C. Mandal and B. Pathak, ACS Appl. Mater. Interfaces, 2021, 13(47), 56151–56163 CrossRef CAS PubMed.
- D. Roy, A. Das, S. Manna and P. Pathak, J. Phys. Chem. C, 2023, 127(2), 871–881 CrossRef CAS.
- S. Choi, Y. Kim, J. W. Kim, Z. Kim and W. Y. Kim, Chem. – Eur. J., 2018, 24, 12354–12358 CrossRef CAS PubMed.
- X. Li, S. Zhang, L. Xu and X. Hong, Angew. Chem., Int. Ed., 2020, 59(32), 13253–13259 CrossRef CAS PubMed.
- K. Jorner, T. Brinck, P. O. Norrby and D. Buttar, Chem. Sci., 2021, 12(3), 1163–1175 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Revision B.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- S. C. Mandal, K. S. Rawat, S. Nandi and B. Pathak, Catal. Sci. Technol., 2019, 9, 1867–1878 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- F. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO, Version 3.1 Search PubMed.
- M. Mastalir, M. Glatz, B. Stöger, M. Weil, E. Pittenauer, G. Allmaier and K. Kirchner, Inorg. Chim. Acta, 2017, 455, 707–714 CrossRef CAS.
- Z. Yang, X. Wei, D. Liu, Y. Liu, M. Sugiya, T. Imamoto and W. Zhang, J. Organomet. Chem., 2015, 791, 41–45 CrossRef CAS.
- T. Takao, H. Suzuki and R. Shimogawa, Organometallics, 2021, 40(9), 1303–1313 CrossRef CAS.
- B. C. Gruver, J. J. Adams, S. J. Warner, N. Arulsamy and D. M. Roddick, Organometallics, 2011, 30, 5133–5140 CrossRef CAS.
- M. Glatz, B. Stöger, D. Himmelbauer, L. F. Veiros and K. Kirchner, ACS Catal., 2018, 8, 4009–4016 CrossRef CAS PubMed.
- D. Himmelbauer, B. Stöger, L. F. Veiros and K. Kirchner, Organometallics, 2018, 37, 3475–3679 CrossRef CAS.
- R. Huber, A. Passera, E. Gubler and A. Mezzetti, Adv. Synth. Catal., 2018, 360, 2900–2913 CrossRef CAS.
- I. Arenas, O. Boutureira, M. I. Matheu, Y. Diaz and S. Castillón, Eur. J. Org. Chem., 2015, 3666–3669 CrossRef CAS.
- J. K. Pedersen, T. A. A. Batchelor, A. Bagger and J. Rossmeisl, ACS Catal., 2020, 10, 2169–2176 CrossRef CAS.
- D. Roy, S. C. Mandal and B. Pathak, J. Phys. Chem. Lett., 2022, 13(25), 5991–6002 CrossRef CAS PubMed.
- L. A. Suarez, Z. Culakova, D. Balcells, W. H. Bernskoetter, O. Eisenstein, K. I. Goldberg, N. Hazari, M. Tilset and A. Nova, ACS Catal., 2018, 8, 8751–8762 CrossRef.
- K. S. Rawat and B. Pathak, Catal. Sci. Technol., 2017, 7, 3234–3242 RSC.
- A. Nandy, C. Duan and H. J. Kulik, J. Am. Chem. Soc., 2021, 143(42), 17535–17547 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Chen and C. Guestrin, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, pp. 785–794.
- C. R. Harris, et al. , Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- J. D. Hunter, et al. , Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- M. Waskom, mwaskom/seaborn: v0.8.1, 2017 Search PubMed.
- C. J. Ren, S. H. Lu, Y. L. Wu, Y. X. Ouyang, Y. H. Zhang, Q. Li, C. Y. Ling and J. L. Wang, J. Am. Chem. Soc., 2022, 144, 12874–12883 CrossRef CAS PubMed.
- Y. Jiao, H. Li, Y. Jiao and S. Z. Qiao, J. Am. Chem. Soc., 2023, 145(28), 15572–15580 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00520h |
| ‡ A.D. and D.R. have contributed equally. |
| § Present address: SUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, 443 Via Ortega, Stanford, CA 94305, USA. |
| This journal is © The Royal Society of Chemistry 2024 |