Open Access Article
Open Access ArticleA multi-FLP approach for CO2 capture: investigating nitrogen, boron, phosphorus and aluminium doped nanographenes and the influence of a sodium cation†
Maxime
Ferrer
ab,
Ibon
Alkorta
 *a,
José
Elguero
a and
Josep M.
Oliva-Enrich
c
*a,
José
Elguero
a and
Josep M.
Oliva-Enrich
c
aInstituto de Química Médica (CSIC), Juan de la Cierva, 3, E-28006 Madrid, Spain. E-mail: ibon@iqm.csic.es
bPhD Program in Theoretical Chemistry and Computational Modeling, Doctoral School, Universidad Autónoma de Madrid, 28049 Madrid, Spain
cInstituto de Química-Física Blas Cabrera (CSIC), Serrano, 119, E-28006 Madrid, Spain
First published on 27th March 2024
Abstract
The reactivity of B3N3-doped hexa-cata-hexabenzocoronene (B3N3-NG), Al3N3-NG, B3P3-NG and Al3P3-NG, models of doped nanographenes (NGs), towards carbon dioxide was studied with density functional theory (DFT) calculations at the M06-2X/6-311++G(3df,3pd)//M06-2X/6-31+G* level of theory. The NG systems exhibit a poly-cyclic poly-frustrated Lewis pair (FLP) nature, featuring multiple Lewis acid/Lewis base pairs on their surface enabling the capture of several CO2 molecules. The capture of CO2 by these systems was investigated within two scenarios: (A) sequential capture of up to three CO2 molecules and (B) capture of CO2 molecules in the presence of a sodium cation. The resulting adducts were analyzed in terms of the activation barriers and relative stabilities. The presence of aluminium atoms changes the asynchrony of the reaction favoring the aluminium-oxygen bond and influences the regioselectivity of the multi-capture. A cooperative effect is predicted due to π-electron delocalization, with the sodium cation stabilizing the stationary points and favoring the addition of CO2 to the NGs.
Introduction
Carbon dioxide (CO2) is a highly stable molecule commonly produced from the oxidation of mineral carbon or organic carbon chains. It is also a major greenhouse effect gas released as a result of human activities.1–3 Various small molecules, including carbenes,4–9 guanidines,10,11 and phosphines,12–15 have been studied for their ability to form adducts with CO2. However, the surplus production of CO2 calls for more efforts to reduce its impact. For example, in 2022, the atmospheric CO2 concentration reached an alarming new record, with an average yearly concentration of 417 ppm.16,17The scientific community is heavily focused on searching for new techniques and methods to reduce the concentration of CO2 in the atmosphere, and the main technologies being developed for its trapping can be categorized into three groups: absorption, adsorption, and membrane technologies.16 Among the most widely used methods in industry is the absorption of CO2 using amine solutions, typically monoethanolamine (MEA).18,19 However, the energy-intensive process of regenerating the solvent after CO2 capture makes this method fall short of the ambitious goal of achieving a CO2 capture cost of $20 per ton, as proposed by various research programs in the USA and Europe.16,20 Reducing the costs of CO2 capture is crucial for widespread implementation and to make it economically viable on a large scale.
One promising alternative for CO2 capture and activation is the use of frustrated Lewis pairs (FLPs).21–23 FLP systems, characterized by their inability to form traditional Lewis acid–Lewis base adducts, have shown the notable capability to activate stable molecules like CO2, N2, or H2.24–26 Experimental and theoretical studies on the activation and sequestration of CO2 by FLPs have been reported.27–32
Recently, a derivative of hexabenzo[a,d,g,j,m,p]coronene, or hexa-cata-hexabenzocoronene, with N–B atoms in relative para positions has been synthesized33 (Refcode: FEWKIE in CSD34). Nanographenes (NGs) and doped nanographenes have also been studied for their interaction with CO2, forming non-covalent complexes where the CO2 molecule remains relatively unactivated.35–39 In a recent theoretical study, it was suggested that a B3P3-doped NG could capture up to three CO2 molecules, making it an attractive system for carbon dioxide capture32 in agreement with other P/B FLPs reported in the literature.40–42 However, the previous study only considered the influence of the Lewis base substitution. In this work, we focus on the effect of the Lewis acid substitution on the CO2 capture. The reaction of four doped NGs, namely B3N3-NG, Al3N3-NG, B3P3-NG and Al3P3-NG (Fig. 1), with up to three CO2 molecules was investigated. Additionally, considering the growing interest in using charged FLPs43–45 for CO2 reactions, the influence of a cation (Na+) interacting with the doped NG on the CO2 capture was also considered.
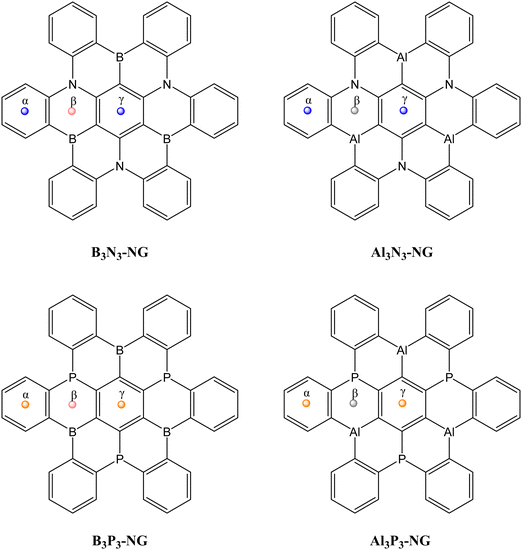 | ||
| Fig. 1 Structure of the multi-FLP B3N3-NG, Al3N3-NG, B3P3-NG and Al3P3-NG used in this study. The centroids of the 6-member rings are indicated as α, β, and γ. | ||
Computational details
The structures under study, depicted in Fig. 1, were optimized with the scientific software Gaussian1646 using the M06-2X DFT functional47 and the 6-31+G(d) basis set.48 The Berny optimization algorithm49 and the synchronous transit-guided quasi-Newton (STQN) method50 were used to locate the stationary points (energy minima and TSs, respectively). The optimized geometries were checked as energy minima (no imaginary frequency) or transition states (one imaginary frequency) by performing frequency calculations at the M06-2X/6-31+G(d) computational level. In order to obtain more accurate energies, single-point energy calculations were performed at the M06-2X/6-311++G(3df,3pd)51 level of theory using the M06-2X/6-31+G(d) optimized geometries. This computational procedure gives similar results to the ones provided by the DLPNO-CCSD(T) computational level in the reaction of other FLPs with CO2.52 The frequency calculations at the M06-2X/6-31+G(d) computational level were also used to obtain the enthalpy and entropy corrections.The molecular electrostatic potential (MEP) was calculated in order to identify regions of favorable interaction with a positive point charge (negative regions of the MEP) and those with a negative charge (positive regions of the MEP). The MEP was calculated on the 0.001 a.u. electron density isosurface using the M06-2X/6-311++G(3df,3pd)//M06-2X/6-31+G(d) wavefunction and the Multiwfn software.53
The topological properties of the electron density were analyzed using the quantum theory of atoms in molecules (QTAIM)54,55 as implemented in the AIMAll scientific software.56 Electron density critical points (CPs), where the density gradient vanishes with respect to electron coordinates, were identified. These CPs are classified based on the number of non-zero eigenvalues (rank, w) and the sum of the eigenvalue signs (signature, s) as CP(w,s). Points of interest include attractor (3,−3), bond (3,−1), ring (3,+1), and cage critical points (3,+3). The covalent character of the interactions associated with bond critical points can be determined by examining the values of the electron density, Laplacian of the electron density, potential energy density, and kinetic energy density.57,58 The molecular graphs were computed using the M06-2X/6-311++G(3df,3pd)//M06-2X/6-31+G(d) wavefunctions.
The natural bond orbital methodology,59 as implemented in the NBO program (version 7.0),60 was used to obtain a Lewis-like structure as regards to electron distribution of the systems and to compute the stabilization due to the charge transfer between occupied and empty orbitals.
The binding energy of the adducts (Eb) was calculated as the difference between the adduct energy and the sum of the isolated monomers in their energy minimum configuration (eqn (1)). In order to quantify the cooperative effect when multiple molecules of CO2 interact with an NG, the total binding energy of the adducts was decomposed (eqn (2)) into deformation energy of the monomers (Edef) (eqn (3)), two-body interaction energy [Δ2E(ij)] (eqn (4)), and a cooperative energy (C). Here, E(i) represents the energy of the isolated monomer in its minimum energy state, and E′(i) represents the energy in the geometry of the supermolecule. This method is similar to the many-body energy analysis,61,62 but it truncates the expansion in the two-body interaction term and includes the higher terms in the cooperativity component.
| Eb = E(adduct) − E(NG) − n × E(CO2) | (1) |
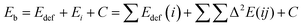 | (2) |
| Edef(i) = E(i) − E′(i) | (3) |
| Δ2E(ij) = E(ij) − E′(i) − E′(j) | (4) |
| [NG–H]+ → NG + H+; proton affinity (PA) = H(NG) + H(H+) − H([NG+H]+) | (5) |
| [NG–F]− → NG + F−; fluoride ion affinity (FIA) = H(NG) + H(F−) − H([NG+F]−) | (6) |
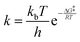 | (7) |
Results and discussion
We consider the sequential capture of up to three CO2 molecules on nanographene (NG) surfaces (Fig. 1). The capture of each CO2 molecule comprises the initial formation of a pre-reactive complex, which, after a transition state (TS), produces the adduct where the CO2 molecule forms covalent bonds between the oxygen atom and the Lewis acid atoms, as well as between the carbon atom in CO2 and the Lewis base atoms. The first step of these processes is shown in Fig. 2 with two examples.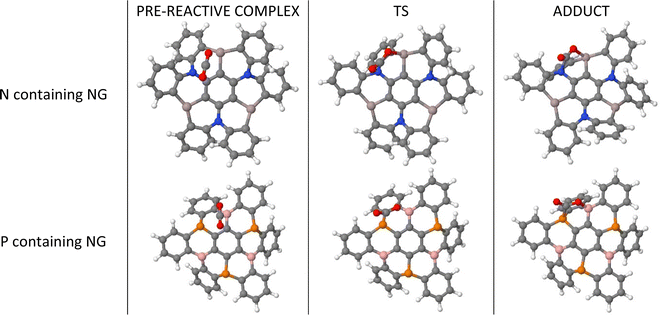 | ||
| Fig. 2 Geometries of the stationary points for the first capture of CO2 by Al3N3-NG and B3P3-NG systems. | ||
This section has been divided into four subsections. First, we present the general properties of the four NG systems. Second, one CO2 molecule approached the NG systems and formed an adduct. The candidates considered as reactive toward CO2 will be further studied for multi-CO2 capture. Finally, we analyze the effect of the presence of a Na+ cation, on both faces of the NG.
Properties of isolated NGs
The potential reactivity of FLPs can be predicted by examining the acidity and basicity values of their molecular electrostatic potential (MEP). The four systems have C3 symmetry, i.e., the LA/LB pairs are equivalent through a 120° rotation. Additionally, the nitrogen-containing NG species possess a planar environment around the nitrogen atoms, with both faces equivalent. Conversely, the NG species containing phosphorus do not have equivalent faces, but the most stable conformation has the lone pairs of the phosphorus atoms oriented in the same direction, making only one face reactive (see Fig. 3).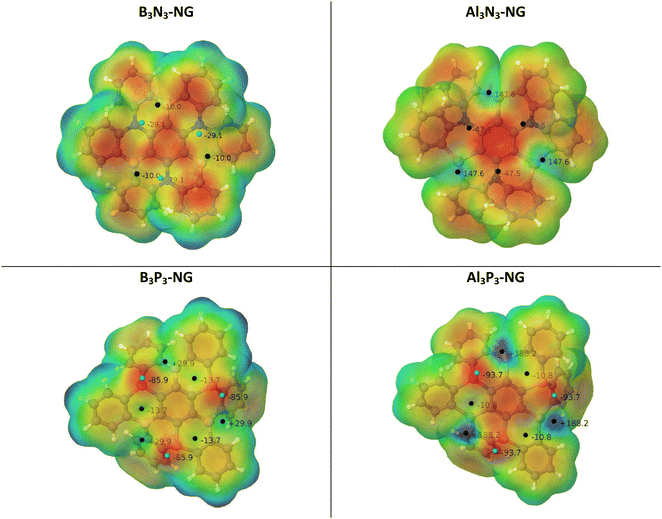 | ||
| Fig. 3 MEP of the four NG systems. The location of the MEP maxima and minima is identified by black and cyan spheres and their values are indicated in kJ mol−1. | ||
The geometry of B3N3-NG is available in the CSD database34 (Refcode FEWKIE33), and our optimized geometry is in agreement with the experimental X-ray structure within an RMDS of 0.02 Å (Fig. S1, ESI†).
The geometries of the B3N3-NG and Al3N3-NG species are similar, with the lateral phenyl rings displaying similar orientations. The nitrogen atoms exhibit sp2 hybridization due to the delocalization of the lone pairs into the aromatic rings. NBO calculations reveal that the nitrogen atoms in the C–N bonds have an average hybridization of sp2.03 for B3N3-NG and sp2.08 for Al3N3-NG. Furthermore, the interaction between the nitrogen lone pairs and the π antibonding orbitals stabilizes the system by approximately 523.0 kJ mol−1 and 397.0 kJ mol−1, for B3N3-NG and Al3N3-NG, respectively. Regarding the MEP minima and maxima, the two systems show different features. The B3N3-NG systems have MEP maxima on boron atoms with values of −10.0 kJ mol−1, while the nitrogen atoms have MEP minima of −29.1 kJ mol−1. In contrast, Al3N3-NG shows three MEP maxima (+147.6 kJ mol−1) on the aluminium atoms and three MEP minima on the nitrogen atom (−47.5 kJ mol−1). The larger values of the MEP on the nitrogen atoms are in agreement with the NBO results, indicating that the nitrogen lone pairs in B3N3-NG are more delocalized than those in Al3N3-NG. Additionally, the larger acidity of aluminium compared to boron shows up, with boron atoms with MEP maxima of −10 kJ mol−1, while aluminium atoms have an MEP maximum value of +147.6 kJ mol−1. Based on this analysis, we can confirm that Al3N3-NG should be a better candidate for CO2 capture, as compared to B3N3-NG.
The phosphorus-containing NG species (B3P3-NG and Al3P3-NG) exhibit a similar arrangement of MEP maxima and minima. The phosphorus atoms have an MEP negative minimum with values of −85.9 and −93.7 kJ mol−1 for the B3P3-NG and Al3P3-NG systems, respectively. The region close to boron atoms shows an MEP maximum of +29.9 kJ mol−1 in the B3P3-NG molecule, whereas near aluminium atoms there is an MEP maximum of +188.2 kJ mol−1 in the Al3P3-NG system. In the NG with phosphorus atoms, three FLP systems over six are deactivated by the presence of a negative MEP maximum, with −10.8 kJ mol−1 and −13.7 kJ mol−1 for B3P3-NG and Al3P3-NG, respectively. These MEP maxima are not found for the nitrogen-containing NGs (B3N3-NG and Al3N3-NG). As previously reported,32 this observation can be related to the angle between the α, β, and γ centroids of the 6-member rings (Fig. 1). In the case of B3N3-NG and Al3N3-NG, the α–β–γ angles have values of 162° and 155°, respectively. As for B3P3-NG, the angles alternate between 148° and 175°. The same is observed for Al3P3-NG, but with an alternation from 147° to 176°. The most deactivated FLPs are those with the most planar angles (175° and 176°). Based on this analysis alone, we can infer that the Al3P3-NG system should be more reactive towards CO2 than B3P3-NG.
In order to evaluate the acidity and basicity of the boron/aluminium and nitrogen/phosphorus atom pairs, respectively, we computed the fluoride ion affinity (FIA) and the proton affinity (PA) (Table 1). The NG systems with Al exhibit higher FIA values compared to those with boron, in agreement with the reported values of the phenyl derivatives: FIA[B(C6H5)3] = 320 kJ mol−1 and FIA[Al(C6H5)3] = 427 kJ mol−1.65 As regards to basicity, the systems with P display higher basicities than those with N, in good agreement with the experimental PA values69 of N(C6H5)3 (908.9 kJ mol−1) and P(C6H5)3 (972.8 kJ mol−1). The enhanced basicity of the P-NG systems as compared to N-NG can be attributed to the lower delocalization of the phosphorus lone pairs, leading to their higher availability as previously discussed. The trends in FIA and PA values are in agreement with the MEP values previously discussed (Fig. 3).
| System | B3N3-NG | Al3N3-NG | B3P3-NG | Al3P3-NG |
|---|---|---|---|---|
| FIA | 295.8 | 435.6 | 354.6 | 450.2 |
| PA | 859.8 | 933.8 | 967.8 | 995.2 |
First CO2 capture
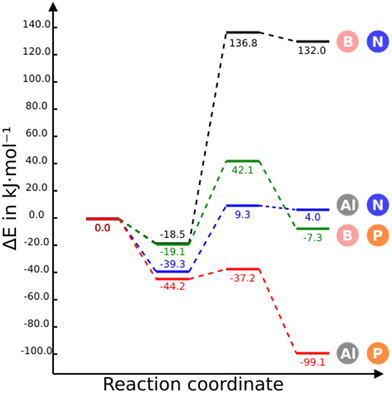
The stationary points of the first CO2 capture with two NGs are shown in Fig. 2. The energy and free energy profiles for the four NGs are displayed in Fig. 4 and Fig. S2 (ESI†), respectively. The CO2 adsorption on B3N3-NG is feasible and relatively stable, resulting in the formation of a complex with an energy of −18.5 kJ mol−1, as previously found.35,36 However, the formation of a covalent adduct is unfavorable, as indicated by the positive and large relative energy (+132.0 kJ mol−1). It can be anticipated that this adduct has a very low probability of existence, due to the small rate constant associated with the corresponding barrier (8.06 × 10−20 s−1).The substitution of nitrogen by phosphorus (B3P3-NG) does not significantly change the stability of the adsorption complex, −19.1 for B3P3-NG vs. −18.5 kJ mol−1 for B3N3-NG. However, the adduct is now slightly above the reactant energies (Erel = −7.3 kJ mol−1) and the TS is also stabilized (from 137 kJ mol−1 in B3N3-NG to 42 kJ mol−1 in B3P3-NG), reducing the activation barrier. Although the adduct (Erel = −7.3 kJ mol−1) is below the complex, a rate constant of 3.07 × 102 s−1 suggests that the reaction should take place.
The energetic profiles of Al3N3-NG and B3N3-NG share several similarities: a stable pre-reactive complex with stabilization energies of −19 and −39 kJ mol−1 respectively, TS and final product with positive relative energies and small energy difference between them (about 5 kJ mol−1). However, the replacement of B by Al decreases significantly the above energy values of the TS and final products.
The substitution of nitrogen with phosphorus to form Al3P3-NG results in a highly reactive system towards CO2. As shown in Fig. 4, all stationary points in this system are below the entrance channel. The reaction rate constant is considerably large (k = 1.01 × 1011 s−1), an indication that the CO2 capture by Al3P3-NG is both thermodynamically and kinetically favorable, making it the most promising candidate so far.
If the free energy at 298 K is considered (Fig. S2, ESI†) then only the Al3N3-NG and Al3P3-NG complexes are more stable than the entrance channel and the Al3P3-NG-CO2 is very stable (−52 kJ mol−1). These results clearly indicate that the reaction is enthalpy driven.
Regarding the geometry of the stationary points and their electron density (Table 2), the higher stability of the aluminium-containing complexes can be attributed to the closer contact between aluminium and oxygen atoms compared to the B–O contact (3.11, 2.36, 2.88, and 2.18 Å for B3N3-NG, Al3N3-NG, B3P3-NG and Al3P3-NG respectively). In fact, when passing from boron to aluminium, CO2 undergoes a more significant bending in the complex (179.0° to 177.9° in B3N3-NG and Al3N3-NG, respectively, and 178.9° to 174.8° in B3P3-NG and Al3P3-NG, respectively), and turns into a more activated molecule. Additionally, the AIM analysis reveals the presence of BCP between oxygen and aluminium in the complex of aluminium systems, whereas no BCP was found between boron and oxygen in the complexes with B3N3-NG and B3P3-NG. These results confirm Ashley et al.'s statement: “in Al-based FLP, CO2 activation proceeds by initial Al⋯O1/4C1/4O interaction in a van der Waals complex, which stands in contrast to other P/B examples where CO2 interacts with the Lewis base component first”.22
| Geometry | Complex | TS | Adduct | |
|---|---|---|---|---|
| B3N3-NG | B–O | 3.11 | 1.66 (0.0885) | 1.60 (0.1032) |
| C–N | 3.37 | 1.87 (0.1132) | 1.73 (0.1527) | |
| O–C–O | 179.2 | 141.2 | 135.7 | |
| α–β–γ | 163.0 | 140.7 | 138.1 | |
| Al3N3-NG | Al–O | 2.36 (0.0192) | 1.93 (0.0571) | 1.89 (0.0641) |
| C–N | 2.99 | 1.92 (0.1025) | 1.75 (0.1476) | |
| O–C–O | 177.9 | 143.1 | 136.6 | |
| α–β–γ | 150.3 | 135.9 | 134.1 | |
| B3P3-NG | B–O | 2.89 | 2.25 (0.0276) | 1.58 (0.1134) |
| C–P | 3.33 (0.0085) | 2.15 (0.0967) | 1.90 (0.1599) | |
| O–C–O | 178.9 | 144.4 | 129.8 | |
| α–β–γ | 148.4 | 145.6 | 137.0 | |
| Al3P3-NG | Al–O | 2.19 (0.0265) | 2.07 (0.0366) | 1.87 (0.0693) |
| C–P | 3.17 (0.0125) | 2.74 (0.0314) | 1.92 (0.1558) | |
| O–C–O | 174.8 | 161.2 | 30.0 | |
| α–β–γ | 143.9 | 142.3 | 141.6 |
The TSs and adduct geometries with the nitrogen-containing NG systems are very similar, with B/Al–O and N–C bonds formed by 96% and 92% in the TS of B3N3-NG and 97% and 91% in the case of the Al3N3-NG TS with respect to the bond length computed in the adducts. In contrast, the bond formations in the TSs for B3P3-NG are 70% and 88%, and 90% and 70% in Al3P3-NG. This indicates that in B3P3-NG FLPs, phosphorus attacks first, while in the case of Al3P3-NG FLPs, it is the aluminium atom that interacts first. This difference in bond formation is also reflected in the electron density at the BCPs, higher and closer to the final values in the nitrogen-containing systems compared to the phosphorus-containing NGs (Table 2). An excellent exponential correlation is found for the six BCPs obtained for the Al–O and C–P contacts vs. the interatomic distances (Fig. S3, ESI†), in agreement with previous reports.58,70,71
One possible reason for the difference in TS energies, aside from the differences in acidity and basicity, could be the deformation of the NG system and the bending of the lateral phenyl ring. The calculated deformation energy of the two monomers (NG plus CO2) in the TS accounts for 281, 194, 143 and 48 kJ mol−1 for B3N3-NG, Al3N3-NG, B3P3-NG and Al3P3-NG, respectively. These results are in agreement with the difference between this angle on the three centroids α, β, γ (Fig. 1) in the complex and this angle at the corresponding TS angle, with values of 22.3°, 14.4°, 2.8° and 1.6°, respectively.
Multi capture
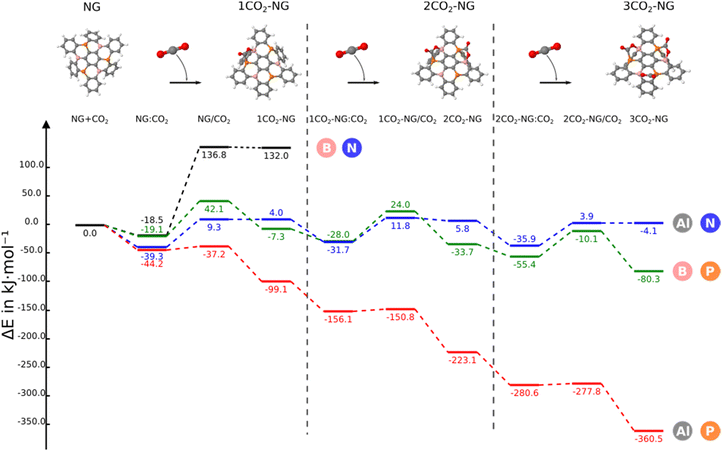
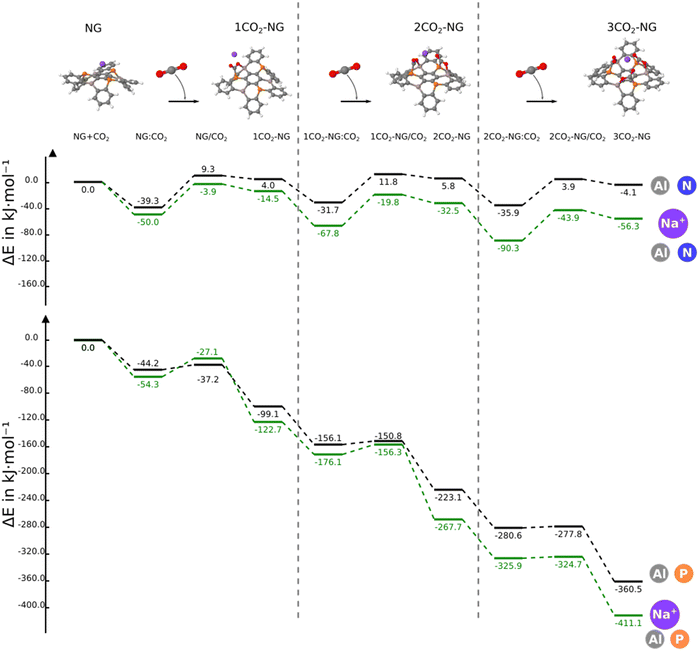
In this section, we consider the sequential reaction of the NG system with up to three CO2 molecules. The B3N3-NG system is excluded from further studies since it is not able to form a stable adduct with CO2. Thus, this section only considers the B3P3-NG, Al3N3-NG and Al3P3-NG systems.The reaction profiles are depicted in Fig. 5; as the number of interacting CO2 molecules with Al3P3-NG increases, the systems become more stabilized. The energies of the different minima become more negative leading to the formation of an adduct with three CO2 molecules and a relative energy of −360.5 kJ mol−1. A similar profile is observed for the reaction of B3P3-NG except for the first CO2 addition where the complex is more stable than the adduct (–19.1 vs. −7.3 kJ mol−1, respectively), with the relative energy of the adduct with three CO2 molecules being −80.3 kJ mol−1. Finally, in Al3N3-NG, all complexes are more stable than the corresponding adducts, with no significant stabilization gain after the addition of three CO2 molecules and a relative energy of the final product of −4.1 kJ mol−1.
When the second capture occurs, a regioselectivity question arises in the TS when choosing between the remaining FLP sites. However, the product of the second CO2 addition is the same, independently of the adduct formed in any of the two remaining FLP couples. The two TSs have been explored for the three NGs and only the most stable one (from 1 to 5 kJ mol−1) has been included in Fig. 5.
In the case of B3P3-NG, the fixation of the second CO2 molecule on the right (see Fig. 6) enables a stabilization of the TS by 5 kJ mol−1, while the complexes have the same energies. Considering the reaction of Al3N3-NG and Al3P3-NG, the most favorable TS is the one that yields the adduct on the left (see Fig. 6). The complexes are more stable by 2 and 5 kJ mol−1, and the TSs are more stable by 1 and 3 kJ mol−1 for Al3N3-NG and Al3P3-NG, respectively. The differences are not large, but they can still be at the origin of a certain kinetic regioselectivity. In order to gain insights into the regioselectivity of CO2 fixation, the FIA and PA of the isolated NG and adducts are calculated and summarized in Fig. 6. The difference in the TS regioselectivity can be attributed to the fact that in Al/P or Al/N FLP systems, CO2 initially forms a strong interaction with the aluminium atom. The FIA of these compounds determines which FLP is more likely to react. In the case of P/B NG, the interaction of the phosphorus with the carbon of CO2 is more dominant, and consequently, the phosphorous with the highest PA will have the smallest activation barrier.
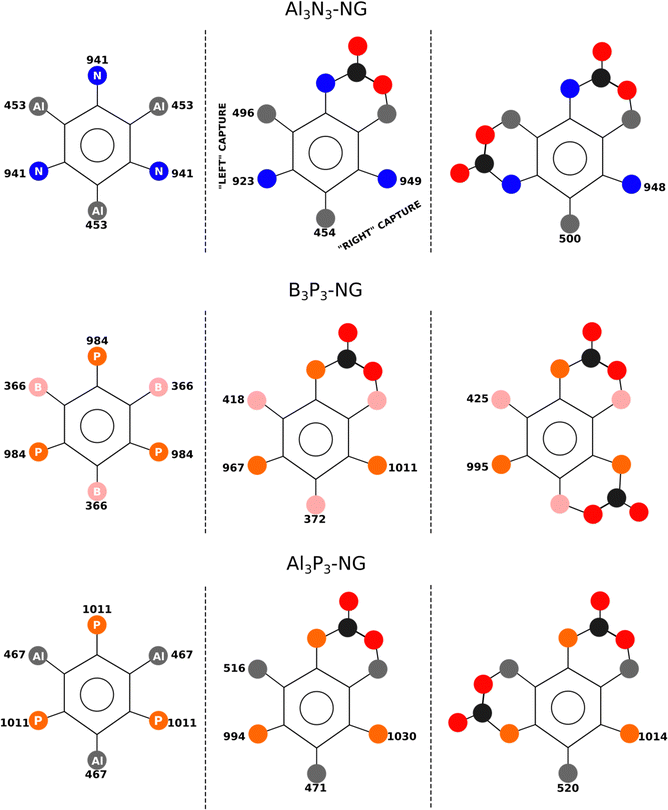 | ||
| Fig. 6 FIA and PA of the different stationary points in kJ mol−1. The 2CO2-NG adduct associated with the lowest TS barrier is shown in the third column. | ||
As regards the stability of the adduct and the TS, the relationship is not straightforward as their energies are correlated with both acidity and basicity. A linear correlation is obtained between the adduct energy and the FIA and the PA, with R2 = 0.83, and a correlation with R2 = 0.80 for the TS, in both cases with n = 9. As previously mentioned, both FIA and PA contribute to stabilizing these stationary points.
The energy terms obtained using the decomposition scheme from the methods section are gathered in Table S9 (ESI†). Depending on the NG systems studied, the relationship between the deformation energy and the absolute value of the two-body interaction energy is as follows: in the Al3N3-NG adducts, the deformation energy is larger than the two-body interaction energy; in the B3P3-NG systems, the deformation energy is slightly larger than the two-body interaction energy and, finally, in the Al3P3-NG adducts, the two-body interaction energy is clearly larger than those of the deformation energy. As regards to cooperativity effects, their values in the 2CO2-NG adducts are −5.8, −24.1 and −8.1 kJ mol−1 for Al3N3-NG, B3P3-NG and Al3P3-NG, respectively, and the corresponding ones in the 3CO2-NG adducts are −21.6, −80.4 and −26.9 kJ mol−1, respectively. An analysis of the geometries of the LA–O and LB–C bonds (Table 3) in the addition products as a function of the number of CO2 molecules shows that the LA–O distances decrease, an indication that these bonds become stronger with the number of CO2 molecules attached. Otherwise, the LB–C contact remains unaltered or slightly elongated. Thus, the LA–O bond evolves in line with the energetic results obtained for the cooperativity effect in the adducts with two and three CO2 molecules.
| NG-CO2 | NG-(CO2)2 | NG-(CO2)3 | |
|---|---|---|---|
| a Average values of the two CO2 molecules. | |||
| Al3N3-NG | d(C–N) = 1.750 | 1.744a | 1.750 |
| d(O–Al) = 1.891 | 1.879a | 1.849 | |
| k = 3.07 × 102 | 2.18 × 103 | 9.57 × 103 | |
| B3P3-NG | d(C–P) = 1.900 | 1.903a | 1.907 |
| d(O–B) = 1.581 | 1.570a | 1.560 | |
| k = 3.47 | 2.18 × 102 | 2.41 × 102 | |
| Al3P3-NG | d(C–P) = 1.920 | 1.928a | 1.927 |
| d(O–Al) = 1.868 | 1.858a | 1.847 | |
| k = 5.93 × 1010 | 2.51 × 10+11 | 3.79 × 1011 | |
A systematic reduction in the reaction energy barriers is also observed in the Al3P3-NG system with the number of CO2 molecules, which is also reflected in an increase in the reaction constant k (Table 3).
CO2 capture in the presence of Na+
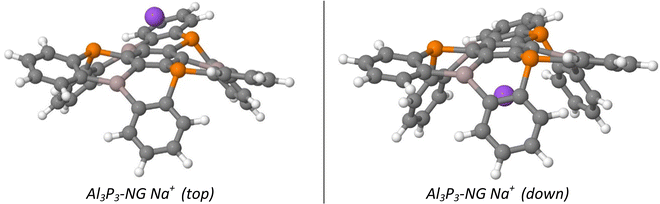
In this subsection, we discuss the influence of a cation (Na+) in the capture of CO2 molecules by NG systems. Two possible locations are considered for the cation (Fig. 7). In the first one (top), the cation interacts with the NG systems and the approaching CO2 molecules. In the second approach (bottom), the cation interacts with the NG system only, whereas the CO2 molecules interact with the NG on its opposite face.The interaction energy of the cation with the isolated NGs on the two sides is the same for the B3N3-NG (−167 kJ mol−1) and Al3N3-NG (−200 kJ mol−1), whereas in the B3P3-NG, the down complex is more stable (top, −175 and down, −183 kJ mol−1) and in Al3P3-NG is the opposite with the top complex being more stable (−194 and −185 kJ mol−1). The complex formation does not change the geometry of the NG in the nitrogen-containing NG (B3N3-NG and Al3N3-NG). In contrast, in the phosphorous NG, the deformation of the system is responsible for their stability (Fig. S4, ESI†).
The two possible adducts of three CO2 molecules approaching the NG in the presence of Na+ have been explored. Their stability is listed in Table 4. In the B3N3-NG, it is possible to locate the adducts in the presence of Na+ which are absent without the cation, but with very high relative energy as an indication of their instability. In the other three NG systems, the adducts with Na+ in down orientation give stabilization energies which are very similar to those without the cation. In contrast, a significant stabilization takes place if the Na+ cation is located in top orientation/location.
| Na+ disposition | B3N3-NG | Al3N3-NG | B3P3-NG | Al3P3-NG |
|---|---|---|---|---|
| Na+ (top) | +258.4 | −90.6 | −167.0 | −422.6 |
| Na+ (down) | +273.6 | −21.8 | −122.3 | −379.3 |
| — | Not found | −25.8 | −107.2 | −373.5 |
We now discuss the reaction to yield the adducts with the Na+ in the top arrangement, with those with the Na+ in the down orientation included in the ESI.†
The energy profile for the addition of three CO2 molecules in the presence of the Na+ cation shows three stationary points per added CO2 molecule: non-covalent complex, adduct and TS connecting them (Fig. 8). Only in the NG system with boron, additional stationary points are found due to the Na+–OCO interactions in analogy to those found for the pentacene/K+ system (Fig. S5, ESI†).32,52 The comparison of the energy profiles with and without Na+ in the same NG system shows that the presence of the cation reduces the relative energy of the stationary points with the exception of TS1 of Al3P3-NG, 10 kJ mol−1 less stable in the presence of the cation.
 | ||
| Fig. 8 Comparative energy profiles for the reaction of Al3N3-NG and Al3P3-NG in the absence/presence of Na+ with three CO2 molecules. | ||
An interesting effect due to the presence of the cation is the activation of the CO2 molecule even before the adduct. In addition, the TSs show that the LB–C bond is more advanced in all cases than the LA–O.
The adduct formation modifies the geometries and the electronic distribution of the NGs and CO2 molecules. Thus, a significant dipole moment enhancement is observed in the adducts up to 6.2 and 6.3 Debyes for the Al3P3-NG-(CO2)2 and Al3P3-NG-(CO2)3 adducts, respectively. This effect is mostly due to the distortion in the CO2 molecules that contribute around 1.3 Debye per molecule. This polarity increase should favor adducts vs. complex in polar environments.15,30,72
Conclusions
The electronic structure computations carried out in this work with doped nanographenes (NGs) with up to three CO2 molecules, with and without the presence of a sodium cation, can be summarised as follows:– In the case of NG systems containing aluminium as a LA, the CO2 molecule first interacts with the LA. In contrast, in NGs based on boron, the LB is the first to attack CO2.
– The LB species is directly involved in the general shape of the reaction profile. Due to π-electron delocalization, the NG systems containing nitrogen form non-stable adducts that evolve back to the complex.
– The nitrogen-containing NG systems tend to exhibit larger deformation energy and, consequently, larger activation energies due to the delocalization of the nitrogen lone pairs. These NGs also tend to have TSs close to the adducts. Conversely, the Al3P3-NG systems are highly reactive towards CO2 and exhibit the TS close to the pre-reactive complexes.
– The FIA and PA of atoms involved in the first reactions determine the kinetic regioselectivity of the studied multi-FLPs. In NG systems with aluminium, CO2 reacts with the more acidic free aluminium, while in the other NG cases, the CO2 molecule reacts with the more basic LB.
– There is a cooperative effect in Al3N3-NG and Al3P3-NG systems in the third CO2 capture, and in B3P3-NG in the second and third capture. The cooperativity can be attributed to shrinkage of the LA–O bonds.
– B3P3-NG and Al3P3-NG exhibit interesting properties for the capture of up to three CO2 molecules, indicating their potential as promising candidates for CO2 sequestration.
The presence of a cation on the same side where the adduct formation takes place stabilizes these adducts by activating the electrophilicity of the CO2 non-covalent complex and interacting with the highly polar CO2 molecule in the adducts.
These findings provide valuable insights into the reactivity and regioselectivity of doped nanographenes with CO2 fixation and highlight the impact of LAs and LBs in driving the reactions. Finally, we should emphasize that the combination of Al and P atoms seems to be the most suitable for the activation/sequestration of CO2 in doped nanographenes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades (Project PID2021-125207NB-C32). We are also grateful to the Centro de Supercomputación de Galicia (CESGA), CTI (CSIC) and the Irish Centre for High-End Computing (ICHEC, Dublin) for their continued computational support.References
- P. Nejat, F. Jomehzadeh, M. M. Taheri, M. Gohari and M. Z. Abd. Majid, Renew. Sust. Energ. Rev., 2015, 43, 843–862 CrossRef CAS.
- A. Kijewska and A. Bluszcz, J. Sustain. Min., 2016, 15, 133–142 CrossRef.
- J. Xu, M. Zhou and H. Li, Resour., Conserv. Recycl., 2018, 129, 326–332 CrossRef.
- N. Kuhn, M. Steimann and G. Weyers, Z. Naturforsch. B, 1999, 54, 427–433 CrossRef CAS.
- H. A. Duong, T. N. Tekavec, A. M. Arif and J. Louie, Chem. Commun., 2004, 112–113 RSC.
- Y. Kayaki, M. Yamamoto and T. Ikariya, Angew. Chem., Int. Ed., 2009, 48, 4194–4197 CrossRef CAS PubMed.
- S. Wang and X. Wang, Angew. Chem., Int. Ed., 2016, 55, 2308–2320 CrossRef CAS PubMed.
- I. Alkorta, M. M. Montero-Campillo and J. Elguero, Chem. – Eur. J., 2017, 23, 10604–10609 CrossRef CAS PubMed.
- M. M. Montero-Campillo, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2018, 20, 19552–19559 RSC.
- C. Villiers, J.-P. Dognon, R. Pollet, P. Thuéry and M. Ephritikhine, Angew. Chem., Int. Ed., 2010, 49, 3465–3468 CrossRef CAS PubMed.
- S. Anila and C. H. Suresh, Phys. Chem. Chem. Phys., 2021, 23, 13662–13671 RSC.
- F. Buß, P. Mehlmann, C. Mück-Lichtenfeld, K. Bergander and F. Dielmann, J. Am. Chem. Soc., 2016, 138, 1840–1843 CrossRef PubMed.
- P. Mehlmann, C. Mück-Lichtenfeld, T. T. Y. Tan and F. Dielmann, Chem. – Eur. J., 2017, 23, 5929–5933 CrossRef CAS PubMed.
- I. Alkorta, C. Trujillo, G. Sánchez-Sanz and J. Elguero, Inorganics, 2018, 6, 110 CrossRef.
- G. Sánchez-Sanz, I. Alkorta, J. Elguero and C. Trujillo, Chem. Phys. Chem., 2019, 20, 3195–3200 CrossRef PubMed.
- R. J. Krupadam and S. S. Rayalu, Emergent Mater., 2021, 4, 545–563 CrossRef CAS.
- J. A. Rudd, Nat. Chem., 2022, 14, 360 CrossRef CAS PubMed.
- S. Freguia and G. T. Rochelle, AlChE J., 2003, 49, 1676–1686 CrossRef CAS.
- P. Luis, Desalination, 2016, 380, 93–99 CrossRef CAS.
- F. d’Amore and F. Bezzo, Int. J. Greenhouse Gas Control, 2017, 65, 99–116 CrossRef.
- E. Gerhard and W. S. Douglas, Frustrated Lewis Pairs I, Springer, Berlin, Heidelberg, 2013 Search PubMed.
- E. Gerhard and W. S. Douglas, Frustrated Lewis Pairs II, Springer, Berlin, Heidelberg, 2013 Search PubMed.
- J. C. Slootweg and A. R. Jupp, Frustrated Lewis Pairs, Springer Chem, 2020 Search PubMed.
- A. L. Travis, S. C. Binding, H. Zaher, T. A. Q. Arnold, J.-C. Buffet and D. O'Hare, Dalton Trans., 2013, 42, 2431–2437 RSC.
- G. Kehr and G. Erker, Chem. Rec., 2017, 17, 803–815 CrossRef CAS PubMed.
- R. Pal, M. Ghara and P. K. Chattaraj, Catalysts, 2022, 12, 201 CrossRef CAS.
- N. Von Wolff, G. Lefèvre, J.-C. Berthet, P. Thuéry and T. Cantat, ACS Catal., 2016, 6, 4526–4535 CrossRef CAS.
- D. Zhuang, A. M. Rouf, Y. Li, C. Dai and J. Zhu, Chem. – Asian J., 2020, 15, 266–272 CrossRef CAS PubMed.
- G. Sharma, P. D. Newman and J. A. Platts, J. Mol. Graphics Modell., 2021, 105, 107846 CrossRef CAS PubMed.
- M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, J. Phys. Chem. A, 2021, 125, 6976–6984 CrossRef CAS PubMed.
- S. Soroudi and M. Z. Kassaee, J. Phys. Org. Chem., 2022, 35 Search PubMed.
- M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, Sci. Rep., 2023, 13, 2407 CrossRef CAS PubMed.
- K. Matsui, S. Oda, K. Yoshiura, K. Nakajima, N. Yasuda and T. Hatakeyama, J. Am. Chem. Soc., 2018, 140, 1195–1198 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B, 2016, 72, 171–179 CrossRef CAS PubMed.
- R. Balasubramanian and S. Chowdhury, J. Mater. Chem. A, 2015, 3, 21968–21989 RSC.
- D. Saha, K. Nelson, J. Chen, Y. Lu and S. Ozcan, J. Chem. Eng. Data, 2015, 60, 2636–2645 CrossRef CAS.
- A. A. Salari, C. R. Chim, 2017, 20, 758–764 CrossRef CAS.
- V. Babar, S. Sharma and U. Schwingenschlögl, J. Phys. Chem. C, 2020, 124, 5853–5860 CrossRef CAS.
- G. Wang, J. Yu, K. Zheng, Y. Huang, X. Li, X. Chen and L. Q. Tao, IEEE Electron Device Lett., 2020, 41, 1404–1407 CAS.
- C. Appelt, H. Westenberg, F. Bertini, A. W. Ehlers, J. C. Slootweg, K. Lammertsma and W. Uhl, Angew. Chem., Int. Ed., 2011, 50, 3925–3928 CrossRef CAS PubMed.
- G. Ménard and D. W. Stephan, Angew. Chem., Int. Ed., 2011, 50, 8396–8399 CrossRef PubMed.
- P. Federmann, R. Müller, F. Beckmann, C. Lau, B. Cula, M. Kaupp and C. Limberg, Chem. – Eur. J., 2022, 28, e2022004 CrossRef PubMed.
- E. Von Grotthuss, S. E. Prey, M. Bolte, H.-W. Lerner and M. Wagner, Angew. Chem., Int. Ed., 2018, 57, 16491–16495 CrossRef CAS PubMed.
- S. E. Prey and M. Wagner, Adv. Synth. Catal., 2021, 363, 2290–2309 CrossRef CAS.
- J. E. Barker, A. D. Obi, D. A. Dickie and R. J. Gilliard, Jr., J. Am. Chem. Soc., 2023, 145, 2028–2034 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16; Revision, A.03, Gaussian, Inc., Wallingford, CT, USA, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, Phys. Chem. Chem. Phys., 2023, 25, 22512–22522 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- P. L. A. Popelier, F. M. Aicken and S. E. O'Brien, in Chemical Modelling: Applications and Theory, ed. A. Hinchliffe, The Royal Society of Chemistry, 2000, vol. 1, pp. 143–198 Search PubMed.
- T. A. Keith, AIMAll, 19.10.12 Version (aim.tkgristmill.com), 2019 Search PubMed.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- S. S. Xantheas, J. Chem. Phys., 1994, 100, 7523–7534 CrossRef CAS.
- D. Hankins, J. W. Moskowitz and F. H. Stillinger, J. Chem. Phys., 2003, 53, 4544–4554 CrossRef.
- A. K. Chandra and A. Goursot, J. Phys. Chem., 1996, 100, 11596–11599 CrossRef CAS.
- I. B. Sivaev and V. I. Bregadze, Coord. Chem. Rev., 2014, 270–271, 75–88 CrossRef CAS.
- P. Erdmann, J. Leitner, J. Schwarz and L. Greb, Chem. Phys. Chem., 2020, 21, 987–994 CrossRef CAS PubMed.
- Z. Wang, F. Wang, X.-S. Xue and P. Ji, Org. Lett., 2018, 20, 6041–6045 CrossRef CAS PubMed.
- M. Ferrer, I. Alkorta, J. Elguero and J. M. Oliva-Enrich, ChemPhysChem, 2022, 23, e202200204 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- NIST Chemistrt WebBook, 2023.
- G. Sánchez-Sanz, I. Alkorta and J. Elguero, Mol. Phys., 2011, 109, 2543–2552 CrossRef.
- I. Alkorta, M. Solimannejad, P. Provasi and J. Elguero, J. Phys. Chem. A, 2007, 111, 7154–7161 CrossRef CAS PubMed.
- M. Ferrer, I. Alkorta and J. Elguero, Struct. Chem., 2024, 35, 393–405 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00496e |
| This journal is © the Owner Societies 2024 |