 Open Access Article
Open Access ArticleAn extended model for chirality selection in single-walled carbon nanotubes
Nigora
Turaeva
ab,
Yoosuk
Kim
a and
Irma
Kuljanishvili
 *a
*a
aSaint Louis University, Department of Physics, 3511 Laclede Avenue, St Louis, MO 63103, USA. E-mail: irma.kuljanishvili@slu.edu
bWebster University, Department of Biological Sciences, 470 East Lockwood Avenue, St. Louis, Missouri 63119, USA
First published on 23rd June 2023
Abstract
The chirality selective production of single-walled carbon nanotubes (SWCNTs) continues to represent one of the most important technological challenges. In this study, an extended model which considers all steps of the SWCNT growth process, including adsorption, decomposition, diffusion, and incorporation, is applied, for the first time, to obtain chirality selection in the SWCNT populations. We show that the dependence of the population distribution on chirality, defined as a product of the nucleation probability and the growth rate, has a volcano-shape. The model is in good agreement with the reported experimental studies and supports the results which show the surplus of near armchair or near zigzag SWCNTs. The present work emphasizes the role of the catalyst in chirality selection via optimization of chemisorption strength between the carbon species and the catalyst surface needed to achieve stable nucleation and fast growth rates. The obtained results can be used in catalyst designs to define the pathways towards the growth of SWCNTs with specific chiralities exhibiting distinguished electronic properties.
Introduction
Single-walled carbon nanotubes (SWCNTs) are fascinating one-dimensional (1D) carbon nanomaterials that possess remarkable mechanical characteristics along with high electrical and heat conductivities.1–4 These unique fundamental characteristics are due to the strong covalent bonds between the carbon atoms and because of the ways the carbon sheet is folded into a hollow cylindrical shape. The latter characteristic is called chirality specified by two chiral indices (n,m) or a specific chiral angle (χ) between the circumference and the zigzag axis in the graphene sheet. SWCNTs are classified as armchair (n,n), zigzag (n,0) or chiral (n,m) with n ≠ m based on how they are wrapped into the tubes.3 Chirality of a SWCNT governs its chemical, mechanical and electronic properties and thus defines its potential applications.3–8 They exhibit either metallic (n − m = 3i) or semiconducting (n − m = 3i ± 1) features. For example, semiconducting SWCNTs are highly regarded due to their structural integrity and sizable and controllable band gap, which allows for lower resistance and much less heat generation,6,7 while metallic SWCNTs are desirable substitutes for transparent conducting films and electrodes, 1D interconnects or other active elements of future devices.8 Hence, SWCNTs with specific chirality are highly desirable for a variety of applications.While in recent years, post growth processing techniques have demonstrated significant improvements in separating metallic and semiconducting SWCNTs according to their chiralities and geometric properties,9–14 it is more cost effective to directly synthesize SWCNTs of a certain chirality by using arc-discharge15 or laser ablation methods.16 At the same time, the chemical vapor deposition (CVD) method is a scalable and industrially relevant method that allows various SWCNTs to be grown via selection of catalysts and growth conditions.17–19 This route is uniquely relevant for site-specific synthesis of SWCNTs while also allowing for control over their chiral selectivity.18,19 So far, published reports have implied that high-quality SWCNTs with a single chirality abundance over 90% can be attained on well-designed catalysis.20–24 It is important to note that the published studies have assumed that the morphology and crystalline facets of the solid catalyst influence the nucleation and growth of SWNTs, accounting for their chirality distributions.24 However, the recent work by Zang et al.25 showed that three different catalysts with different symmetries generated similar near-(2n,n) chirality SWCNTs, which implies that other mechanisms beyond the symmetry-matching theory could be in play. The experiments showed that at low temperatures most major species synthesized on solid catalysts such as Fe, Co, Ni, FeRu, FeCo, CoPt, etc. are centered at (n,n − 1) SWCNTs.24 At high temperatures the catalyst is in the liquid state; due to its structural mobility, the nucleation of carbon nanotubes shows little dependence on the catalyst and occurs with low interfacial formation energy. The growth rate of the nanotubes is proportional to their chiral angle as the energy of kink generation is near zero on the armchair edge, and thus, the growth kinetics determines the chirality distributions.24,26–29
At a low reaction temperature the catalyst is in the solid state, and a SWCNT–catalyst structural match facilitates the nucleation of SWCNTs with low formation energy, but their tight contact has a very low growth rate, resulting in one-index off SWNTs that is a compromise between the rapid kinetics and stable nucleation.22–24 So, the selective growth of (n,n − 1) carbon nanotubes is possible because of the formation of a favorable armchair nanotube–catalyst interface. However, on the other hand, by using catalysts that favor the zigzag nanotube–catalyst interface, the (n,1) family of nanotubes can be selectively grown.22,30 Thus, we can note that chirality selectivity depends upon the synthesis parameters: carbon precursors, its pressure, the type of catalyst, its size and composition, and the type of support.24,31
Based on the combination of experimental results and computer simulations, several models have been constructed to interpret the effects of thermodynamical and kinetic factors on the chirality preference. For example, computer simulations performed over Ni catalysts19,20 showed the stability of lattice matched caps and catalyst surfaces. DFT simulations by Li's group revealed matching SWCNTs of different chiralities with the different planes of W6Co7.20,32,33 Ding et al.24,34 showed a symmetry match between the SWCNTs and catalyst surface in growth dynamics. In another study using ab initio density functional theory (DFT) calculations, Hofmann et al.35 studied the dissociation energy of precursor carbon gases on the catalyst surface. DFT calculations of carbon diffusion on different catalyst surfaces36–39 revealed the lower energy barrier for surface diffusion compared to bulk diffusion. Ding et al.28 proposed the application of the screw dislocation model, established widely for crystal growth, to the growth of the SWCNTs, considering the periodic crystal carbon structure of SWCNTs. It was shown that while on a liquid catalyst, the SWCNT growth rate is proportional to the chiral angle, favoring armchair SWCNTs, on the solid catalyst, the growth rate becomes bimodal with minima for achiral SWCNTs and a maximum for (2n,n) SWCNTs with a chiral angle of 19.1. Artyukhov et al.22 proposed a unifying model by combining the nanotube–catalyst interface thermodynamics with energetic preference towards achiral SWCNTs and the kinetic growth theory with the fastest growth kinetics of chiral nanotubes. For the growth rate, they augmented the screw dislocation model by including the thermal kinks for achiral nanotubes and accounting for the energy penalty ∼1/d2 from the wall curvature. The interplay between the thermodynamic and kinetic arguments leads to emerging near-armchair peaks. They received a simple function, X × e−X, for the narrow distribution of the SWCNT abundancy as a function of chirality, that exhibits the peaked behavior. This model, considering both kinetic and thermodynamic aspects of SWCNT growth, had explained the origins of chirality and diverse experimental results from the broader chiral distributions to the narrow ones. More general models, where the dislocation theory was a specific case, were proposed in other studies.34,40 These models describe the “etching-dependent” growth kinetics of SWCNTs on solid catalyst particles. According to the model,34 in the presence of a sufficient amount of ‘etchants’ (H2, O2, and H2O), most of the decomposed carbon atoms are removed by the etching molecules in competition with carbon participating in nanotube growth. Thus, it was shown that the concentration of carbon atoms on the catalyst surface is independent of the SWCNT chiral angle, the growth rate is proportional to the number of active sites, and SWCNT growth follows the screw dislocation model. If there is insufficient ‘etching agent’ during the SWCNT growth, most decomposed carbon atoms are incorporated into the growing SWCNTs, and the concentration of carbon atoms staying on the catalyst surface is the smallest when the number of active sites of the nanotube rim is approaching the maximum value, that is when the chirality is (2n,n). In the latter case, the growth rate is independent of the number of active sites and will be proportional to the ratio of the active catalyst surface to the tube diameter. Hence, the excessive carbon atoms on the catalyst surface would lead to the encapsulation of the catalyst particles by a carbon layer, and the termination of SWCNT growth. Thus, SWCNTs with the maximum active sites consume carbon atoms faster and are less likely to be deactivated.
It must be noted, however, that several key challenges have remained and should be considered in the theoretical model of chirality selective growth of SWCNTs. The key parameters such as the chemical nature of the catalysts, their size, the synthesis temperature, gas precursors and various support substrates,24,31,34 all have been shown to have profound impact on chirality of the resulting SWCNTs. We note here that while in several published theoretical studies close attention has been devoted to some critical parameters mentioned above, there is a lack of theoretical studies that consider all steps of the growth process in the growth kinetics.
In our work here, we present a model which considers all steps of the SWCNT growth kinetics, including adsorption and decomposition of carbon precursor gases and diffusion and incorporation of carbon atoms into the growing nanotube. This approach also considers the presence of weak and strong chemisorbed carbon species, the relative concentrations of which are defined by the Fermi level of the catalysts participating in adsorption, decomposition, diffusion, and incorporation processes. We show that the growth rate depends on the chirality of the nanotubes using the screw dislocation model. The probability of nanotube nucleation depends on the chirality via the relationship between the free energy of the nanotube–catalyst interaction and the chiral angle. As a result of the combination of the nucleation and the growth processes, the dependence of the nanotube population on the chirality will take a volcano-shape. In our work two special cases were considered corresponding to strong and weak adsorption and decomposition of the precursor gas molecules and slow and fast carbon atom diffusion and incorporation into the growing nanotube. In the first case, the growth rate does not depend on the chirality, while in the second case there is a linear dependence of the growth rate on the chirality. Thus, accounting for the catalyst–tube interfaces by introducing weak and strong chemisorption of intermediates during the nucleation and all steps of nanotube growth provides an analytical expression for the abundance of the nanotube of a certain chirality as a nonmonotonic function of chirality.
Results and discussion
In general, the growth of SWCNTs occurs in three steps: (1) adsorption of carbon gaseous species onto the surface of the catalyst; (2) dissociation of the adsorbents into carbon atoms; (3) surface diffusion of adsorbed carbon atoms and incorporation of carbon atoms from the catalyst surface into the root of the nanotube. In our previous work,41 the following mechanism, which accounted for weak and strong chemisorption of adsorbents, was considered for nanotube growth from the methane (CH4) precursor gas.It was assumed that the decomposition of reagent gas molecules occurs in strong chemisorbed states while desorption of adsorbents and diffusion of carbon adatoms take place in weak chemisorbed states. This mechanism includes two electronic steps (steps 1′ and 2′) corresponding to the electron exchange between weak and strong chemisorbed carbon species and the catalyst. The following expression for the carbon deposition rate R corresponding to the mechanism outlines in Table 1 was obtained
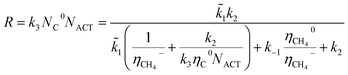 | (1) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) 1 = k1CCH4, CCH4 is the concentration of methane in the gas phase; η0 and η− are fractions of weak and strong chemisorbed carbon intermediates, accordingly; NACT is the number of active sites at the SWCNT–catalyst interface; k1, k2, and k3 are the kinetic constants of the corresponding forward reactions; k−1 is the kinetic constant of the desorption of methane.
1 = k1CCH4, CCH4 is the concentration of methane in the gas phase; η0 and η− are fractions of weak and strong chemisorbed carbon intermediates, accordingly; NACT is the number of active sites at the SWCNT–catalyst interface; k1, k2, and k3 are the kinetic constants of the corresponding forward reactions; k−1 is the kinetic constant of the desorption of methane.
| Step 1 | CH4 + Z ↔ ZCH40 | Forward reaction, k1 |
| Backward reaction, k−1 | ||
| Electronic step 1′ | ZCH40 ↔ ZCH4− | |
| Step 2 | ZCH4− → ZC− + 2H2 | Forward reaction, k2 |
| Electronic step 2′ | ZC− ↔ ZC0 | |
| Step 3 | ZC0 + ZCNT → ZCNT + Z | Forward reaction, k3 |
Next, we will discuss what parameters in eqn (1) for the growth rate will depend on the chiral angle. Here, the number of active sites at the SWCNT–catalyst interface depends upon the chiral angle. The dependence comes from the screw dislocation model of growth, according to which the kinks at the tube rim serve as the active sites for carbon incorporation, and the number of kinks is a basic characteristic of the chiral angle.22,28,34 Dumlich et al.42 theoretically revealed the growth rate dependence of SWCNT chirality by the combination of a geometric approach based on the dependence of the number of growth sites on chirality with calculated energy differences for carbon dangling bonds on metals. By coupling laser-induced CVD with Raman spectroscopy, Rao et al.26 experimentally showed a positive correlation between the linear growth rate and the SWCNT chiral angle. From the basic characteristics of the SWCNTs,22,28,34 in the case when a zigzag SWCNT is considered as structurally perfect, the chiral ones are regarded as a zigzag SWCNT with a screw dislocation, where the number of active sites NACT determined by the kink number m is expressed by the chiral angle X in the following way
| NACT ≈ m ∝ sin(X) ∼ X (0 ≤ X ≤ 30°) | (2) |
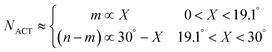 | (3) |
According to the unified model developed by Artyukhov et al.,22,43 the kinks created by thermal fluctuations on A and Z edges can be taken into account by including the additional term e−EAC,ZZ/kT, where EAC,ZZ is the activation energy for achiral (armchair and zigzag) nanotubes. As a result, the number of active sites is determined by using the following expression:
| NACT = (a × (Nmax − |X − 19.1°|) + e−EAC/kBT + e−EZZ/kBT) | (4) |
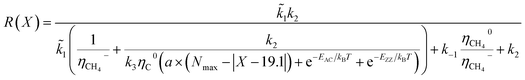 | (5) |
| N(x) ∝ e(−G*/kBT) = e−GZZ/kTe−bX/kT + e−GAC/kTec(X−19.1)/kT | (6) |
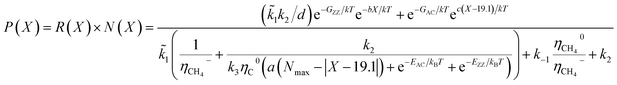 | (7) |
Let's consider two special cases: (1) k3 is very large and (2) k3 is very small. In the first case, when diffusion and incorporation of neutral carbon atoms into the nanotube active sites occur much faster than adsorption of precursor gas molecules and their decomposition, the growth rate does not depend upon X and is given by
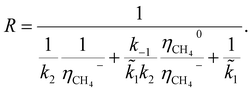 | (8) |
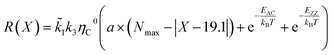 | (9) |
In general, it is seen from eqn (7), that the population of a specific type of SWCNT depends non-monotonically on the chiral angle and has a volcano-shape near (ZZ) and (AC) chiralities (Fig. 2).
The role of catalysts in chirality-selective growth of SWCNTs can be interpreted in two ways: stimulation of adsorption and decomposition of carbon precursors and nucleation of nanotubes with tight low energy contact from one side, and stimulation of diffusion and incorporation of carbon atoms into the growing nanotube from another side. For the former processes, the carbon atoms should form strong chemical bonds with the active sites of the catalyst, while for the latter processes weaker bonds are preferably stimulated. When the bond of carbon atoms with the catalyst is very strong, a lower amount of neutral carbon atoms is available for diffusion and incorporation into the growing nanotube, and the growth rate should be small, but nucleation of achiral nanotubes with a strong carbon–catalyst interface energy is highly probable. We assume that the low population of achiral nanotubes observed in experiments24,31,34 is not only because of the high energy barrier for carbon atom incorporation into the growing nanotube but also due to the low concentration of neutral carbon atoms available for incorporation. In the case of a high amount of neutral carbon atoms on the surface of the catalyst due to the weaker bonds with the catalysts, the growth rate should be high for chiral nanotubes with more kinks; however, the nucleation process in this case occurs with the lower probability. Thus, we assume that there should be an optimal strength of the chemical bond between the carbon atoms and the catalyst which allows the nucleation to take place at the optimal growth rate resulting in the abundance of the nanotubes of a certain chirality. It was shown that the dependence between the population of the SWCNTs and the chiral angle has a volcano-shape with the maximum value at the optimal chiral angle near the edges of the chiral angle range (0 < X < 30°), as depicted in Fig. 1. We note here that the size of catalyst particles can be chosen as a parameter which can control the adsorption strength of carbon-precursor gas molecules and, hence the fractions of carbon atoms with strong and weak adsorption. Since neutral carbon atoms are involved in diffusion and incorporation processes during growth, while the carbon atoms with larger binding energy mostly stay on the surface of the catalyst, we can assume that the size of catalyst particles will affect the population distributions of SWCNTs with a specific chirality. These results are in good agreement with the experimental studies which show the abundance of the near-armchair nanotubes, or the near-zigzag nanotubes,24,31,34 depending on the difference in nucleation energy of armchair nanotubes on certain catalyst surfaces in comparison with that of zigzag nanotubes, as shown in Fig. 2, where metallic and semiconducting species achieved so far by direct chirality selection synthesis are indicated by blue hexagons.
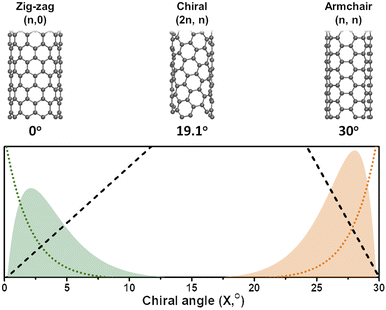 | ||
| Fig. 1 (Bottom panel) The SWCNT population distributions (y-axis) calculated as a product of nucleation probability (dotted) and the growth rate (dashed) shown for near ZZ (green) and near-AC (orange) chiralities (similar to ref. 22), and (top panel) the schematic of the SWCNTs corresponding to the chiral angles shown below. | ||
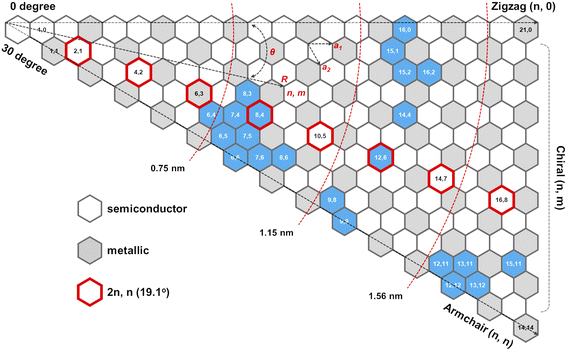 | ||
| Fig. 2 Semiconducting and metallic SWNT species: (n,m) SWCNTs (blue hexagon) achieved so far by direct chirality selection synthesis.24 | ||
Note here that single chirality nanotube synthesis can be achieved by moving the reaction zone and dissolution processes.44 According to the model, the feedstock gas propagation speed determines whether all the CNT ensembles can keep up or only the faster species survive and grow while the slower ones fall behind and terminate. So, by the choice of the zone speed, the separation of the CNTs by the rate constants as a function of chirality was obtained. It was also indicated in ref. 44 that in the reverse process (etching and gasification), the reaction zone will eliminate all types of chiralities, leaving only the selected chirality.
The presented approach is directly applicable to solid catalysts that are used in vapor–solid–solid (VSS) synthesis of SWCNTs.34 It must be noted here that at high temperatures, when the catalysts are in a liquid state in vapor–liquid–solid (VLS) synthesis, all types of SWCNTs nucleate with equal probability, and the kinetic route of the chirality selection becomes dominant.
Thus, the presented model considers all steps of nanotube growth on the catalyst surface, including adsorption of the carbon precursor gas and its decomposition into carbon atoms, which subsequently diffuse and incorporate into the growing nanotube. Catalysts play an important role in each step of the growth process, determining the fractions of weakly and strongly adsorbed carbon species. The growth rate increases at both ends of the chiral angle range (0 < X < 30°) due to the linear dependence of active sites along the nanotube rim on the chiral angle which comes from the screw dislocation theory. On the one hand, a strong adsorption of carbon precursor gas molecules onto the surface of catalysts is desirable for their decomposition into carbon atoms and the subsequent nucleation stage which we believe is critical in determining SWCNT chirality. On the other hand, weakly adsorbed carbon atoms participate in diffusion on the catalyst surface and incorporate into the active sites during SWCNT growth. As a result, at the optimal adsorption strength, stable/steady nucleation and fast growth of the SWCNTs with given chiralities could be achieved.
Conclusion
In this study, we present an extended model of chirality-selective growth of SWCNTs which comprehensively explains the abundance of nanotubes with certain chiralities depending upon different parameters, such as carbon gas precursors, the chemical nature of catalysts and their size, the growth temperature, etc. Our model considers all steps of growth, including adsorption, decomposition, diffusion, and incorporation. According to this model, the population distribution of nanotubes by chirality, determined by an interplay of the thermodynamic nucleation and the growth kinetics, has a volcano-shape at both ends of the chiral angle range. These theoretical results are in good agreement with the experiments, which demonstrate the dependence of the peak values of the SWCNT population on chirality of near armchair or near zigzag SWCNTs.24 It is important to note here that the probability of SWCNT nucleation with certain chirality and the yield in each step of the growth process depend on the strength of chemical bonds between the carbon atoms and the catalyst surface. For example, strong chemical bonds improve adsorption of precursor gas molecules and their decomposition into carbon atoms and promote stable nucleation. At weak chemisorption, nucleation of the CNTs is impaired, but the diffusion of neutral carbon atoms facilitates their growth. The stronger the chemical bond between the nanotube and the catalyst, the larger the probability of nucleation, which results in the reduction of the growth rate. Thus, for the growth of SWCNTs with certain chirality, it is important to consider an optimal strength of chemical bonds between the nanotube and catalysts to provide good adsorption and decomposition of precursor carbon gases on the catalyst surface, along with the facilitated diffusion and incorporation of neutral carbon atoms into the growing nanotube. We discussed two special cases: in the first case, when adsorption and decomposition of precursor gas molecules are hindered due to the strong bonds, while the neutral carbon atoms are easily incorporated into the nanotube active sites, the growth rate does not depend on X (the chirality), and therefore, the chirality dependence of SWCNT-abundance is defined by the chirality-dependent nucleation probability. In the second case, when the adsorption and decomposition occur effectively, but the carbon atom diffusion and incorporation are very slow, we have a linear dependence of the growth rate on X, and as a result, the chirality dependence of the SWCNT-abundance takes a volcano-shape.This study also showed that the size of the catalyst could be chosen to control the strength of adsorption of carbon precursors to optimize their decomposition into carbon atoms, and the subsequent facilitated diffusion and incorporation into the tube–catalyst interfaces. Our theoretical results will contribute to the better understanding of the nucleation and growth processes and help in controlling the abundance of chiral SWCNTs. Thus, the presented model can be used in the catalyst designs for the growth of SWCNTs with certain chiralities exhibiting specific electronic properties aimed at various applications.
Conflicts of interest
There are no conflicts to declare.References
- S. Iijima, Helical Microtubules of Graphitic Carbon, Nature, 1991, 354(6348), 56–58, DOI:10.1038/354056a0.
- A. D. Franklin, The Road to Carbon Nanotube Transistors, Nature, 2013, 498(7455), 443–444, DOI:10.1038/498443a.
- R. Saito and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, 1998, p. 272, DOI:10.1142/p080.
- C. T. White and J. W. Mintmire, Fundamental Properties of Single-Wall Carbon Nanotubes, J. Phys. Chem. B, 2005, 109(1), 52–65, DOI:10.1021/jp047416+.
- M. Ouyang, J.-L. Huang and C. M. Lieber, Fundamental Electronic Properties and Applications of Single-Walled Carbon Nanotubes, Acc. Chem. Res., 2002, 35(12), 1018–1025, DOI:10.1021/ar0101685.
- A. D. Franklin, M. Luisier, S.-J. Han, G. Tulevski, C. M. Breslin, L. Gignac, M. S. Lundstrom and W. Haensch, Sub-10 Nm Carbon Nanotube Transistor, Nano Lett., 2012, 12(2), 758–762, DOI:10.1021/nl203701g.
- M. F. L. D. Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Carbon Nanotubes: Present and Future Commercial Applications, Science, 2013, 339(6119), 535–539, DOI:10.1126/science.1222453.
- Z. Wu, Z. Chen, X. Du, J. M. Logan, J. Sippel, M. Nikolou, K. Kamaras, J. R. Reynolds, D. B. Tanner, A. F. Hebard and A. G. Rinzler, Transparent, Conductive Carbon Nanotube Films, Science, 2004, 305(5688), 1273–1276, DOI:10.1126/science.1101243.
- M. S. Arnold, A. A. Green, J. F. Hulvat, S. I. Stupp and M. C. Hersam, Sorting Carbon Nanotubes by Electronic Structure Using Density Differentiation, Nat. Nanotechnol., 2006, 1(1), 60–65, DOI:10.1038/nnano.2006.52.
- S. Ghosh, S. M. Bachilo and R. B. Weisman, Advanced Sorting of Single-Walled Carbon Nanotubes by Nonlinear Density-Gradient Ultracentrifugation, Nat. Nanotechnol., 2010, 5(6), 443–450, DOI:10.1038/nnano.2010.68.
- X. Tu, S. Manohar, A. Jagota and M. Zheng, DNA Sequence Motifs for Structure-Specific Recognition and Separation of Carbon Nanotubes, Nature, 2009, 460(7252), 250–253, DOI:10.1038/nature08116.
- H. Liu, D. Nishide, T. Tanaka and H. Kataura, Large-Scale Single-Chirality Separation of Single-Wall Carbon Nanotubes by Simple Gel Chromatography, Nat. Commun., 2011, 2(1), 309, DOI:10.1038/ncomms1313.
- T. Lei, I. Pochorovski and Z. Bao, Separation of Semiconducting Carbon Nanotubes for Flexible and Stretchable Electronics Using Polymer Removable Method, Acc. Chem. Res., 2017, 50(4), 1096–1104, DOI:10.1021/acs.accounts.7b00062.
- C. Luo, D. Wan, J. Jia, D. Li, C. Pan and L. Liao, A Rational Design for the Separation of Metallic and Semiconducting Single-Walled Carbon Nanotubes Using a Magnetic Field, Nanoscale, 2016, 8(26), 13017–13024, 10.1039/c6nr03928f.
- S. Iijima and T. Ichihashi, Single-Shell Carbon Nanotubes of 1-Nm Diameter, Nature, 1993, 363(6430), 603–605, DOI:10.1038/363603a0.
- T. Guo, P. Nikolaev, A. Thess, D. T. Colbert and R. E. Smalley, Catalytic Growth of Single-Walled Nanotubes by Laser Vaporization, Chem. Phys. Lett., 1995, 243(1–2), 49–54, DOI:10.1016/0009-2614(95)00825-o.
- M. José-Yacamán, M. Miki-Yoshida, L. Rendón and J. G. Santiesteban, Catalytic Growth of Carbon Microtubules with Fullerene Structure, Appl. Phys. Lett., 1993, 62(6), 657–659, DOI:10.1063/1.108857.
- Y. Li, W. Kim, Y. Zhang, M. Rolandi, D. Wang and H. Dai, Growth of Single-Walled Carbon Nanotubes from Discrete Catalytic Nanoparticles of Various Sizes, J. Phys. Chem. B, 2001, 105(46), 11424–11431, DOI:10.1021/jp012085b.
- S. Reich, L. Li and J. Robertson, Control the Chirality of Carbon Nanotubes by Epitaxial Growth, Chem. Phys. Lett., 2006, 421(4–6), 469–472, DOI:10.1016/j.cplett.2006.01.110.
- F. Yang, X. Wang, D. Zhang, J. Yang, D. Luo, Z. Xu, J. Wei, J.-Q. Wang, Z. Xu, F. Peng, X. Li, R. Li, Y. Li, M. Li, X. Bai, F. Ding and Y. Li, Chirality-Specific Growth of Single-Walled Carbon Nanotubes on Solid Alloy Catalysts, Nature, 2014, 510(7506), 522–524, DOI:10.1038/nature13434.
- J. R. Sanchez-Valencia, T. Dienel, O. Gröning, I. Shorubalko, A. Mueller, M. Jansen, K. Amsharov, P. Ruffieux and R. Fasel, Controlled Synthesis of Single-Chirality Carbon Nanotubes, Nature, 2014, 512(7512), 61–64, DOI:10.1038/nature13607.
- V. I. Artyukhov, E. S. Penev and B. I. Yakobson, Why Nanotubes Grow Chiral, Nat. Commun., 2014, 5(1), 4892, DOI:10.1038/ncomms5892.
- S. Zhang, L. Kang, X. Wang, L. Tong, L. Yang, Z. Wang, K. Qi, S. Deng, Q. Li, X. Bai, F. Ding and J. Zhang, Arrays of Horizontal Carbon Nanotubes of Controlled Chirality Grown Using Designed Catalysts, Nature, 2017, 543(7644), 234–238, DOI:10.1038/nature21051.
- M. He, S. Zhang, Q. Wu, H. Xue, B. Xin, D. Wang and J. Zhang, Designing Catalysts for Chirality-Selective Synthesis of Single-Walled Carbon Nanotubes: Past Success and Future Opportunity, Adv. Mater., 2019, 31(9), 1800805, DOI:10.1002/adma.201800805.
- X. Zang, B. Graves, M. De Volder, W. Yang, T. Johnson, B. Wen, W. Su, R. Nishida, S. Xie and A. Boies, High-precision solid catalysts for investigation of carbon nanotube synthesis and structure, Sci. Adv., 2020, 6(40), 1–8, DOI:10.1126/sciadv.abb6010.
- R. Rao, D. Liptak, T. Cherukuri, B. I. Yakobson and B. Maruyama, In Situ Evidence for Chirality-Dependent Growth Rates of Individual Carbon Nanotubes, Nat. Mater., 2012, 11(3), 213–216, DOI:10.1038/nmat3231.
- B. Liu, J. Liu, X. Tu, J. Zhang, M. Zheng and C. Zhou, Chirality-Dependent Vapor-Phase Epitaxial Growth and Termination of Single-Wall Carbon Nanotubes, Nano Lett., 2013, 13(9), 4416–4421, DOI:10.1021/nl402259k.
- F. Ding, A. R. Harutyunyan and B. I. Yakobson, Dislocation Theory of Chirality-Controlled Nanotube Growth, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(8), 2506–2509, DOI:10.1073/pnas.0811946106.
- E. S. Penev, K. V. Bets, N. Gupta and B. Yakobson, Transient Kinetic selectivity in nanotubes growth on solid Co-W catalyst, Nano Lett., 2018, 18(8), 5288–5293, DOI:10.1021/acs.nanolett.8b02283.
- S. Zhang, X. Wang, F. Yao, M. He, D. Lin, H. Ma, Y. Sun, Q. Zhao, K. Liu, F. Ding and J. Zhang, Controllable Growth of (n, n − 1) Family of Semiconducting Carbon Nanotubes, Chem, 2019, 5(5), 1182–1193, DOI:10.1016/j.chempr.2019.02.012.
- M. V. Kharlamova, Investigation of Growth Dynamics of Carbon Nanotubes, Beilstein J. Nanotechnol., 2017, 8(1), 826–856, DOI:10.3762/bjnano.8.85.
- F. Yang, X. Wang, D. Zhang, K. Qi, J. Yang, Z. Xu, M. Li, X. Zhao, X. Bai and Y. Li, Growing Zigzag (16,0) Carbon Nanotubes with Structure-Defined Catalysts, J. Am. Chem. Soc., 2015, 137(27), 8688–8691, DOI:10.1021/jacs.5b04403.
- F. Yang, X. Wang, J. Si, X. Zhao, K. Qi, C. Jin, Z. Zhang, M. Li, D. Zhang, J. Yang, Z. Zhang, Z. Xu, L.-M. Peng, X. Bai and Y. Li, Water-Assisted Preparation of High-Purity Semiconducting (14,4) Carbon Nanotubes, ACS Nano, 2017, 11(1), 186–193, DOI:10.1021/acsnano.6b06890.
- L. Qiu and F. Ding, Understanding Single-Walled Carbon Nanotube Growth for Chirality Controllable Synthesis, Acc. Mater. Res., 2021, 2(9), 828–841, DOI:10.1021/accountsmr.1c00111.
- S. Hofmann, G. Csányi, A. C. Ferrari, M. C. Payne and J. Robertson, Surface Diffusion: The Low Activation Energy Path for Nanotube Growth, Phys. Rev. Lett., 2005, 95(3), 036101, DOI:10.1103/physrevlett.95.036101.
- S. Helveg, C. López-Cartes, J. Sehested, P. L. Hansen, B. S. Clausen, J. R. Rostrup-Nielsen, F. Abild-Pedersen and J. K. Nørskov, Atomic-Scale Imaging of Carbon Nanofibre Growth, Nature, 2004, 427(6973), 426–429, DOI:10.1038/nature02278.
- S. Hofmann, R. Sharma, C. Ducati, G. Du, C. Mattevi, C. Cepek, M. Cantoro, S. Pisana, A. Parvez, F. Cervantes-Sodi, A. C. Ferrari, R. Dunin-Borkowski, S. Lizzit, L. Petaccia, A. Goldoni and J. Robertson, In Situ Observations of Catalyst Dynamics during Surface-Bound Carbon Nanotube Nucleation, Nano Lett., 2007, 7(3), 602–608, DOI:10.1021/nl0624824.
- R. T. K. Baker, M. A. Barber, P. S. Harris, F. S. Feates and R. J. Waite, Nucleation and Growth of Carbon Deposits from the Nickel Catalyzed Decomposition of Acetylene, J. Catal., 1972, 26(1), 51–62, DOI:10.1016/0021-9517(72)90032-2.
- O. V. Yazyev and A. Pasquarello, Effect of Metal Elements in Catalytic Growth of Carbon Nanotubes, Phys. Rev. Lett., 2008, 100(15), 156102, DOI:10.1103/physrevlett.100.156102.
- L. Qiu and F. Ding, Contact-Induced Phase Separation of Alloy Catalyst to Promote Carbon Nanotube Growth, Phys. Rev. Lett., 2019, 123(25), 256101, DOI:10.1103/physrevlett.123.256101.
- N. Turaeva and I. Kuljanishvili, Effects of Electronic Structure of Catalytic Nanoparticles on Carbon Nanotube Growth, Carbon Trends, 2021, 5, 100092, DOI:10.1016/j.cartre.2021.100092.
- H. Dumlich and S. Reich, Chirality-Dependent Growth Rate of Carbon Nanotubes: A Theoretical Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(8), 085421, DOI:10.1103/physrevb.82.085421.
- V. I. Artyukhov, Y. Liu and B. I. Yakobson, Equilibrium at the edge and atomistic mechanisms of graphene growth, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(38), 15136–15140, DOI:10.1073/pnas.1207519109.
- B. I. Yakobson and K. V. Bets, Single-chirality nanotube synthesis by guided evolutionary selection, Sci. Adv., 2022, 8, eadd4627 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |
