Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of capillary fluid flow on single cancer cell cycle dynamics, motility, volume and morphology†
Hubert M.
Taïeb
 *a,
Guillaume
Herment
a,
Tom
Robinson
*a,
Guillaume
Herment
a,
Tom
Robinson
 *b and
Amaia
Cipitria
*b and
Amaia
Cipitria
 *acd
*acd
aDepartment of Biomaterials, Max Planck Institute of Colloids and Interfaces, 14476 Potsdam, Germany. E-mail: hubert.taieb@mpikg.mpg.de; amaia.cipitria@mpikg.mpg.de
bDepartment of Theory and Bio-Systems, Max Planck Institute of Colloids and Interfaces, 14476 Potsdam, Germany. E-mail: tom.robinson@mpikg.mpg.de
cGroup of Bioengineering in Regeneration and Cancer, Biodonostia Health Research Institute, 20014 San Sebastian, Spain
dIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Spain
First published on 30th November 2022
Abstract
From primary tumours and disseminating to secondary organs, cancer cells experience a wide variety of fluid flow profiles when passing through blood vessels or the lymphatic system before extravasation. Sinusoidal capillaries are a common site for extravasation. Therefore, we aim to investigate how metastatic cancer cells react to a biophysical cue such as capillary fluid flow by quantifying its effect on metastatic cell cycle progression, motility, cell and nuclear volume, and morphology. We use MDA-MB-231 breast cancer cells genetically modified with fluorescent ubiquitination-based cell cycle indicator 2 (FUCCI2) as a model system. Single cells are trapped using a microfluidic device and exposed to different laminar flows. Quantitative time-lapse imaging in both 2D epifluorescence and 3D confocal microscopy is performed using in-house software FUCCItrack. In addition, 3D time-lapse with cell and nuclear segmentation is performed with a deep learning approach to streamline the image processing of big datasets. We show that at a single cell level, faster fluid flow leads to a shorter S/G2/M phase and an overall shorter cell cycle, as well as increase in cell motility irrespective of the flow direction. 3D time-lapse confocal imaging of MDA-FUCCI2 single cells reveals the evolution of cell and nuclear volume and morphology as a function of a specific cell cycle phase. Both cell and nuclear volume increase linearly over time. Cell morphology elongates more strongly during the S/G2/M phase, whereas the nuclear shape remains constant. Under the highest flow conditions, only during the S/G2/M phase can we observe a more elongated nucleus, while the cell sphericity remains similar to the control. Collectively, this data, together with the deep learning approach, provides new insights into the potential impact of fluid flow at a single cell level.
Introduction
Many molecular pathways drive metastasis,1 yet it is becoming increasingly acknowledged that mechanical forces also modulate tumour progression.2–4 Solid stress, fluid flow shear stress, fluid pressure, stiffness and microarchitecture are some physical factors known to affect biological cancer hallmarks.5 Prior to metastasis, tumour cells are exposed to three main body fluids: blood, lymph and interstitial fluid.6–8 The terms “hemodynamic” or “mechanical” theory describe the notion that fluid-based mechanics could shape metastasis.9 In the context of brain cancer, it was reported that fluid flow could stimulate invasion as well as proliferation.10,11 On the other hand, after extravasation it was demonstrated that specific cancer cells could remain dormant for years to decades in niches.12 Metastatic onset or dormancy requires physical intravascular arrest of disseminated tumour cells (DTCs) before they actively extravasate to the interstitial matrix,13 where they can stay dormant14 or generate life-threatening growing metastasis.15Given that the bone marrow (BM) is a preferential site for breast cancer metastasis and that stable microvasculature can provide a dormant niche,12 this region appears to be of great interest to study the impact of fluid flow on breast cancer cell dormancy. The BM microvasculature is composed of a fairly irregular network of microvessels.16,17 In long bones, these microvessels connect to a complex and irregular network of arterial vessels and sinusoidal capillaries.16,18 Recently, intravital two-photon imaging was used in vivo to quantify blood flow dynamics and velocities in these arterial vessels and sinusoidal capillaries,19 thus providing an accurate fluid flow profile in this region. Slower velocities in sinusoidal capillaries favoured hematopoietic stem and progenitor cells rolling, adhering, and transmigration into the bone marrow interstitial matrix.19
To the best of our knowledge, the effect of fluid flow on single cancer cell motility, volume and cell shape as a function of cell cycle phases has not been documented. It is therefore of great interest to have a model system to accurately investigate cancer cell response to flow in both 2D and 3D in real time. To mimic these condition, microfluidics is an essential tool that allows 1) isolation of single cells and 2) control over tuneable fluid flow velocity and shear stress, while allowing cell monitoring in vitro and in real time.20–23
Here, we aim to investigate the effect of capillary flow on metastatic breast cancer cell cycle progression, motility, cell and nuclear volume, as well as morphology, all correlated and time-resolved. To this end, we used a microfluidic device with integrated traps to capture and isolate single breast cancer cells for long term monitoring. We used a deep learning approach to streamline the image processing of big datasets containing 3D time-lapse multi-channel images.
Experimental
Cell lines
Human metastatic breast cancer cells MDA-MB-231 (ATCC, #HTB-26) with the FUCCI2 reporter24,25 (MDA-FUCCI2) were generated as reported previously.26 MDA-FUCCI2 cells were cultured in low glucose Dulbecco's modified Eagle's medium (DMEM) (Sigma, #D6046) supplemented with 1% penicillin/streptomycin (Gibco, #15140-122, 104 units per mL of penicillin and 10 mg mL−1 of streptomycin) and 10% foetal bovine serum superior (Sigma, #S0615). They were grown at 37 °C with 5% CO2 on Nunc™ 100 × 17 mm Petri dishes (Thermo Fisher, #150350) with regular passaging.Cell actin staining
The SiR-Actin Kit (Spirochrome, #SC-001) was used as a live F-actin cell staining. After passaging, a 1 mL cell suspension of 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per mL was incubated in a 1.5 mL Eppendorf for 6 hours with the cell culture media containing the SiR-Actin at a concentration of 100 nmol L−1. The cell suspension was then mixed every 1.5 hours. Cells were then seeded for experiments with the media containing the SiR-Actin to allow a consistent and stable F-actin staining over time and throughout the different cell generations.
000 cells per mL was incubated in a 1.5 mL Eppendorf for 6 hours with the cell culture media containing the SiR-Actin at a concentration of 100 nmol L−1. The cell suspension was then mixed every 1.5 hours. Cells were then seeded for experiments with the media containing the SiR-Actin to allow a consistent and stable F-actin staining over time and throughout the different cell generations.
Wafer master mold fabrication
Microfluidic devices were adapted and modified from previously reported designs.27,28 Silicon wafers (Siegert wafer, #BW14001) was used to create the master mold of 30 μm in height via soft photolithography (Fig. S1†). Briefly, the wafer was dehydrated at 200 °C for 30 minutes and then spin-coated with 4 mL SU-8 photoresist (Microchem, SU8-3025) at 500 RPM for 15 seconds followed by 2600 RPM for 30 seconds (Laurell, #WS-650-23). The wafer was then soft-baked at 95 °C and inserted into the mask aligner (KLOE, UV-KUB3) along with the film mask (Micro Lithography Services) containing our design for UV exposure at 35 mW cm−2 for 6 seconds. The wafer was then post-baked at 95 °C and developed (Micro resist technology, #mr-Dev 600) to remove the non-cured SU-8. A final hard bake was performed at 200 °C for 30 minutes and the wafer was silanised to avoid PDMS adhesion. This was done by having the wafer overnight inside a 150 mbar desiccator with 50 μL of 1H,1H,2H,2H-perfluorodecyltrichlorosilane (abcr, #AB111155). Every wafer contains 10 designs to create 10 individual chips.Microfluidic device fabrication
To produce the microfluidic chips, PDMS and curing agent (Dow Corning, Sylgard 184 Silicone Elastomer Kit) were mixed with a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (70 g PDMS monomer, 7 g curing agent). The mixture was degassed for 30 minutes in a 150 mbar desiccator and then poured over the wafer master. The mixture was degassed once more for 15 minutes in a 150 mbar desiccator and cured at 80 °C for 2 hours. The 10 designs were cut out from the cured PDMS and holes for the inlet and outlet were made with a 1.5 mm biopsy puncher (Kai Europe GmbH). A reservoir made from a cut 1000 μL pipette tip was placed above the inlet, sealed with liquid PDMS and cured at 80 °C for 30 minutes. The PDMS microfluidic devices and glass coverslips (24 × 40 mm, Thermo Fischer, #10180035) were then placed in a plasma oven (Plasma Cleaner PDC-002-CE, Harrick Plasma) at 0.6 mbar for 60 seconds. Following the plasma activation, the PDMS and the coverslip were attached manually and kept on a hot plate at 60 °C for 30 minutes to help the bonding. Before an experiment, the microfluidic device was sterilized under UV radiation for one hour.
1 ratio (70 g PDMS monomer, 7 g curing agent). The mixture was degassed for 30 minutes in a 150 mbar desiccator and then poured over the wafer master. The mixture was degassed once more for 15 minutes in a 150 mbar desiccator and cured at 80 °C for 2 hours. The 10 designs were cut out from the cured PDMS and holes for the inlet and outlet were made with a 1.5 mm biopsy puncher (Kai Europe GmbH). A reservoir made from a cut 1000 μL pipette tip was placed above the inlet, sealed with liquid PDMS and cured at 80 °C for 30 minutes. The PDMS microfluidic devices and glass coverslips (24 × 40 mm, Thermo Fischer, #10180035) were then placed in a plasma oven (Plasma Cleaner PDC-002-CE, Harrick Plasma) at 0.6 mbar for 60 seconds. Following the plasma activation, the PDMS and the coverslip were attached manually and kept on a hot plate at 60 °C for 30 minutes to help the bonding. Before an experiment, the microfluidic device was sterilized under UV radiation for one hour.
Complete microfluidic setup
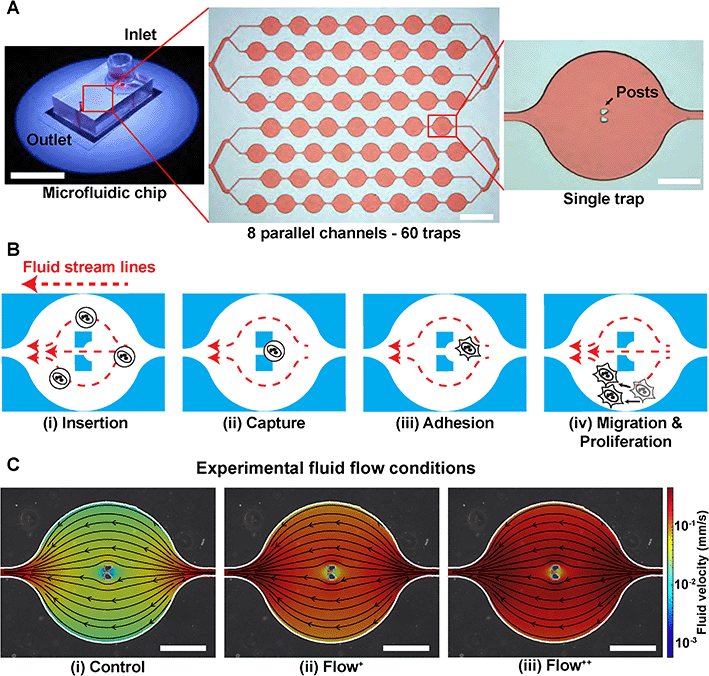
A microfluidic device can be seen in Fig. 1A. It consists of 8 parallel channels (coloured with red dye for visualisation) accounting for 60 traps in total. Each trap contains two posts to capture and immobilize single cells in the chip (Fig. 1B).Firstly, the microchannels were flushed with a cell culture media solution (200 μL) with centrifugation for 10 minutes at 900 RPM. The microfluidic device with its channels filled with cell culture media was then placed in a stage top incubator at 37 °C and 5% CO2 (Okolab, UNO-T-H-CO2). We used an aluminium custom-made sample holder to make sure no movement occurred during the time-lapse imaging. The outlet was then connected via a metal connector to a 1 mL (control and Flow+) or 2.5 mL (Flow++) syringe (Agilent, #5190-1530 and #5190-1534) mounted on a pump (Chemyx, Fusion 200) in withdraw mode (Fig. S2†). Once everything was connected, the device was kept for 30 minutes to reach the targeted temperature and concentration of CO2 inside the chamber and inside the microfluidic device. Two containers filled with Millipore water were inserted inside the top stage incubator to have a 100% humid environment, thus reflecting the conditions of the incubator used for regular cell culture and avoiding media evaporation.
Microfluidic device operation
The complete setup (Fig. S2†) was prepared and checked so that no apparent air bubbles were present in any of the channels. Then the process of trapping the cells inside the microfluidic device started as follows. From the master cell suspension at 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per mL that received the SiR-Actin, another cell suspension was created by dilution to reach 100
000 cells per mL that received the SiR-Actin, another cell suspension was created by dilution to reach 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per mL. The microfluidic device operation was divided in four steps (Fig. 1B):
000 cells per mL. The microfluidic device operation was divided in four steps (Fig. 1B):
(i) Insertion. From the cell suspension of MDA-FUCCI2 stained with SiR-Actin, 50 μL were taken (∼5000 cells) and inserted into the reservoir. The flow rate was set to 20 μL min−1 for 5 minutes for maximum trapping efficiency.
(ii) Capture. The streamlines in the microfluidic device went around and between the two posts until a suspension cell occupied the space between the posts. After this point, other cells only went around the posts and filled the next trap. Cells were then hydrodynamically trapped for the duration of the experiments.
(iii) Adhesion. A visual check with the microscope was done to ensure that at least 80% of the traps were occupied with a cell since this yielded enough single cells per experiments. The flow rate of the chosen experimental group was then applied. The remaining cells in suspension still in the reservoir were removed by 3 exchanges of media in the reservoir. Finally, the reservoir was filled with media containing SiR-Actin and parafilm was added to prevent evaporation. The trapped suspension cells (hydrodynamically trapped between the two posts) were then incubated overnight to allow adhesion.
(iv) Migration and proliferation. Once the cells adhered to the glass, they migrated within the trap and proliferated while being imaged during time-lapse experiments.
Fluid flow
The level of fluid flow was controlled by modifying the syringe pump. To investigate the effect of sinusoidal fluid flow on metastatic breast cancer cells, several experimental groups were defined as follows. The control group (flow rate: 0.02 μL min−1) was defined as the minimum value of flow inside the microfluidic device that would provide sufficient nutrients and permit cell proliferation comparable to conventional Petri dishes as previously reported.26,29 No significant differences in division time were found in cells upstream or downstream from the inlet (Fig. S3†). In addition, two experimental fluid flow conditions were chosen (Flow+: 0.1 μL min−1 and Flow++: 0.2 μL min−1) to create a region of fluid velocity that resembled sinusoidal capillaries in the bone marrow microvasculature19 (Fig. 1C). The values of velocities inside the microfluidic trap were computed with 3D computational fluid dynamic (CFD) simulations using the open-source software OpenFOAM (ESI†) and are on average between [0–0.01] mm s−1 for the control, [0–0.05] mm s−1 for the Flow+ and [0–0.10] mm s−1 for the Flow++.2D time-lapse image acquisition
The 2D time-lapse images were acquired using a Zeiss AxioObserver 7 epifluorescence and a 10x, 0.45 numerical aperture (NA) objective (Zeiss, #420641-9910-000). One field of view was taken for each trap containing a cell. Fluorescence channels mVenus, mCherry and SiR-Actin were recorded with 100% LED intensity at 511, 555 and 630 nm illumination wavelength, respectively. The following filter sets were used: (i) Zeiss #46 HE (500/25 nm excitation and 535/30 nm emission) for mVenus, (ii) Zeiss #45 (560/40 nm excitation and 630/75 nm emission) for mCherry and (iii) Zeiss #50 (640/30 nm excitation and 690/50 nm emission) for SiR-Actin. All fluorescence channels were recorded at 300 ms exposure time. The phase contrast channel was recorded with transmitted light at 20% light intensity and without any filter set. Time-lapse images were acquired with intervals of 30 minutes for 90 hours (corresponding to 3 times the normal cell division time26).Single cell tracking and cell cycle dynamics
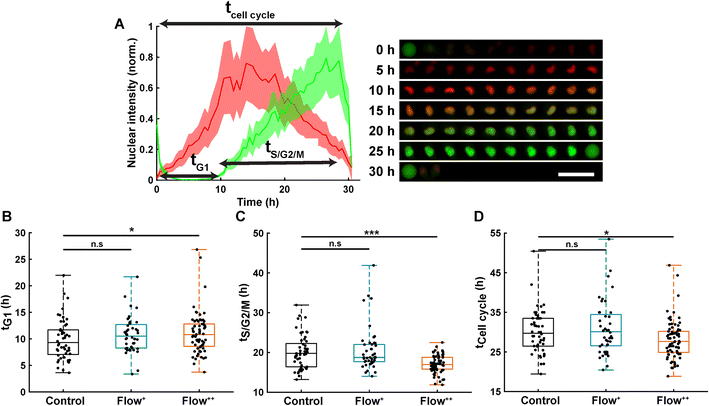
Automatic single cell tracking and cell cycle dynamics quantification was done using our custom-made FUCCItrack software.29 Mitosis events were tracked for 30 hours, and single cell cycle dynamics were then recorded for the first generation of daughter cells, where time 0 hour for each single cell was defined by the first frame after division of the parent cell. This way, the total duration of the cell cycle could be measured from mitosis to mitosis. This was necessary as the readout tG1 and tCell cycle are defined with respect to the beginning of the cell cycle.Briefly, the nuclei were automatically segmented, and the nuclear fluorescence intensity as well as nuclear area were recorded over time. To account for cell variability, the intensity for each channel was independently normalized with respect to its maximum value during the whole cell cycle, for each channel mCherry and mVenus separately (Fig. 2A). Using the normalized nuclear intensity as a function of time, the duration of cell cycle, G1 and S/G2/M phases were quantified. In accordance with our previous work,26,29 the beginning of the S/G2/M phase was then defined as the time when the intensity of mVenus exceeds 5% of the maximum intensity for each individual cell. The same method applies for the beginning of the G1 phase.
3D time-lapse image acquisition
The 3D time-lapse images were acquired using a Leica SP8 confocal microscope and a 63x, 1.2 NA water immersed objective (Leica, #11506356). An automatic water immersion micro dispenser (Leica, #15640019) was used along with the objective to prevent drying and allow for time-lapse imaging for 90 hours. For every trap, a 2 × 2 tile image was acquired (with 10% overlap) and then merged using the LASX (Leica) software. Fluorescence channels mVenus, mCherry and SiR-Actin were recorded with 1% laser intensity at 488, 552 and 638 nm laser excitations. Emission was recorded for the three channels as follows: (i) mVenus [493–547 nm], (ii) mCherry [588–633 nm] and (iii) SiR-Actin [651–707 nm]. Sequential acquisitions were performed to record all channels independently, and bright field transmission images were also obtained. Voxel size were 0.48 μm per pixel for X and Y direction whereas 1.0 μm per pixel resolution was achieved for the Z direction. 3D time-lapse images were acquired in intervals of 2 hours and for 90 hours. An illustrative example of a single cell during its cell cycle is showed in Fig. S4.†Deep learning for 3D multi-channel time-lapse segmentation
3D time-lapse multi-channel images were recorded as follows: mCherry (red), mVenus (green) and the SiR-Actin (magenta). Considering the large amount of data to be processed for every cell, time point and for every experimental group, a deep learning approach was chosen to automatically segment the respective channels. To perform this approach, both FUCCItrack29 (for the preparation of the data) and DragonFly (ORS, V2021.1.0.977) software (for segmentation) were used.The data preparation to reduce the size of the datasets was achieved as follows: using the single cell tracking data from FUCCItrack, each single cell was localized, and the field of view corresponding to each cell was cropped to produce 3D time-lapse stack images stored in one big .tif file per cell.
Then, a total of 7 different time-lapse cells were used to train the SiR-Actin U-net neural network30 (obtained by manual segmentation performed on 1710 2D slices). For the FUCCI2 U-net neural network, 4 different time-lapse cells were used for the training, accounting for 434 manually segmented 2D slices. All 2D slices were subsequently cropped down to the minimum region of interest containing the manual segmentation to reduce class imbalance. Data augmentation was performed by flipping, rotating and scaling the original dataset to increase the number of training images.
Statistical analysis
All data were analyzed using MATLAB R2019b, v9.7. The plots represent the median, 1st and 3rd quartiles and extrema. Statistical analysis was done with respect to the control using a non-parametric two-tailed Wilcoxon rank sum test except when stated otherwise, n.s: p > 0.05, *: p < 0.05, **: p < 0.01 and ***: p < 0.001.Results
Fluid flow accelerates cell cycle by decreasing S/G2/M duration
Thanks to the FUCCI2 technology,24,25 the cell cycle phase duration could be monitored in real time (Fig. 2B). While cells are in the G1 phase of the cell cycle, only mCherry fluorescence is expressed in the nucleus since it is linked to part of the Cdt1 protein. Then, when cells enter the S/G2/M phase, the mVenus fluorescence can be detected since it is linked to part of the Geminin protein. Hence, by measuring the fluorescence intensity inside the nucleus over time, the duration of the G1 phase (tG1, Fig. 2B), the S/G2/M phase (tS/G2/M, Fig. 2C) and the whole cell cycle (tCell cycle, Fig. 2D) were evaluated.Under control conditions, all MDA-FUCCI2 cells took a median value of 30 hours to run through a full cell cycle (Fig. 2A and D). Interestingly, under higher fluid flow (Flow+) cell cycle dynamics (tG1, tS/G2/M and tCell cycle) were not altered and no significant difference could be measured compared to the control group (Fig. 2B–D). However, the highest fluid flow (Flow++) triggered a response in cell cycle dynamics resulting in a slight significant increase of tG1 (+2 h, Fig. 2B) and a more pronounced decrease in tS/G2/M (−3 h, Fig. 2C) leading to a significantly shorter overall cell cycle (−2 h, Fig. 2D).
Fluid flow increases cell motility in a non-directional manner
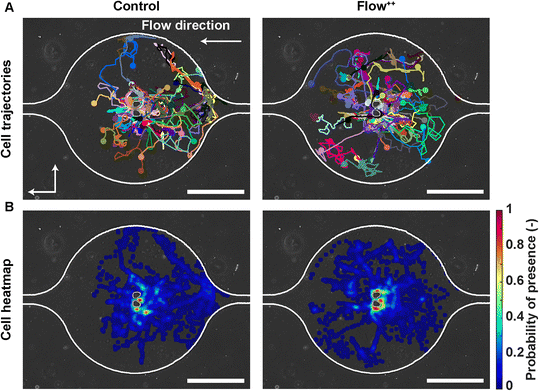
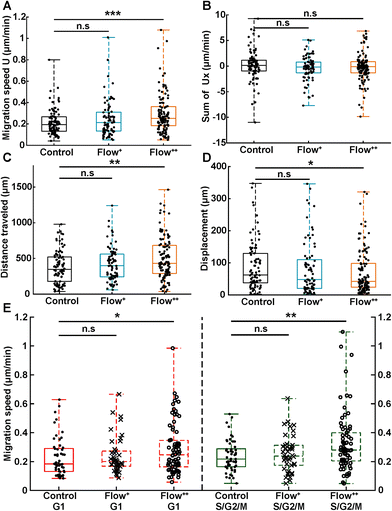
To investigate whether the shortened cell cycle for the highest flow condition correlated with an impact on cell motility, we examined single cell motility using the FUCCI2 marker. The centre of the nucleus of every cell was tracked with our custom-made software FUCCItrack and their trajectories were recorded over time (Movie S1†). Fig. 3A is a representation of an exemplary trap in phase contrast overlaid with cell trajectories coming from different traps and two biological repeats for the control and Flow++ groups. The cell dispersion within a trap was also represented with a heatmap of cell probability (Fig. 3B). Every time a cell went to a certain position within a trap, the probability of its presence increased so that the resulting heatmap displayed the most likely regions for cells. In both cases, the highest probability of presence was around the two posts. However, the highest flow condition (Flow++) displayed a slightly shifted heatmap in the x direction, following the flow direction.In addition, motility related parameters were measured and analyzed for the three experimental groups (Fig. 4). The migration speed U (μm min−1) was computed as the median of instantaneous speed of cells throughout their trajectory. The x component of the speed vector (Ux) was summed up throughout each cell trajectory to determine if the flow direction influenced the cell motility direction. Finally, the distance travelled was computed as the total distance a cell travelled over time, whereas the displacement was defined as the distance between the beginning and the end of the tracking.
Analogous to cycle dynamics, the slow Flow+ experimental group did not show any significant difference with respect to the control group for all motility related parameters (Fig. 4A–E). However, in the highest flow condition (Flow++), the median speed increased up to 30% with respect to control (Fig. 4A). This increase occurred in a non-directed fashion (Fig. 4B), since the sum of Ux did not show any significant difference with respect to the control group. More specifically, the increase in speed was different in the G1 and the S/G2/M phase, with the more significant increase recorded for the S/G2/M phase (Fig. 4E). Interestingly, within each experimental condition, cells moved at similar speeds in both G1 and S/G2/M phase with no significant difference between phases (Fig. 4E, red and green box).
In addition, the total distance travelled by the cells also increased by 23% (from 350 μm to 430 μm) between the control and the Flow++ group respectively (Fig. 4C). Inversely, the displacement slightly decreased for the highest flow condition with respect to the control (Fig. 4D). It is worth noting that the slower Flow+ group did not show any significant difference with respect to the motility or the cell cycle dynamics with respect to the control. To summarize thus far, the highest flow condition accelerated cell cycle dynamics and cell motility, with no influence on migration directionality.
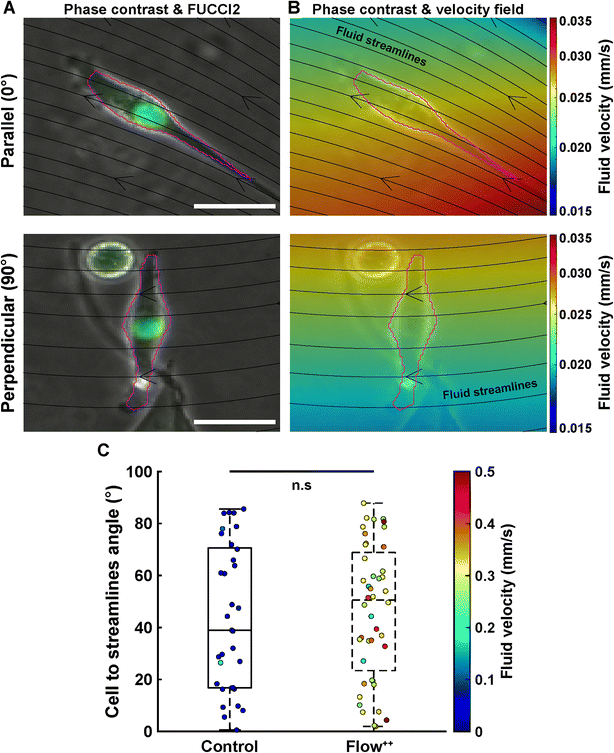
Cell main axis does not align with fluid streamlines before division
We then investigated whether there is a preferential cell alignment with respect to flow right before mitosis. For this purpose, we quantified the orientation of the cell main axis with respect to the fluid streamlines (obtained with the CFD simulation) right before division occurred (Fig. 5). An angle of 0° would represent the cell being parallel to the fluid streamlines, while 90° would indicate the cell being perpendicular to the fluid streamlines (Fig. 5A). There was no significant difference in the angle between the cell main axis and the fluid streamlines for the control vs. Flow++ group (Fig. 5C, boxplot) and for different velocities right before division in both groups (Fig. 5C, colormap). The dispersion of angle covered the smallest (0.1 mm s−1) to the highest (0.5 mm s−1) velocity without any distinctive pattern.Linear increase of cell and nuclear volume during the cell cycle is not affected by flow
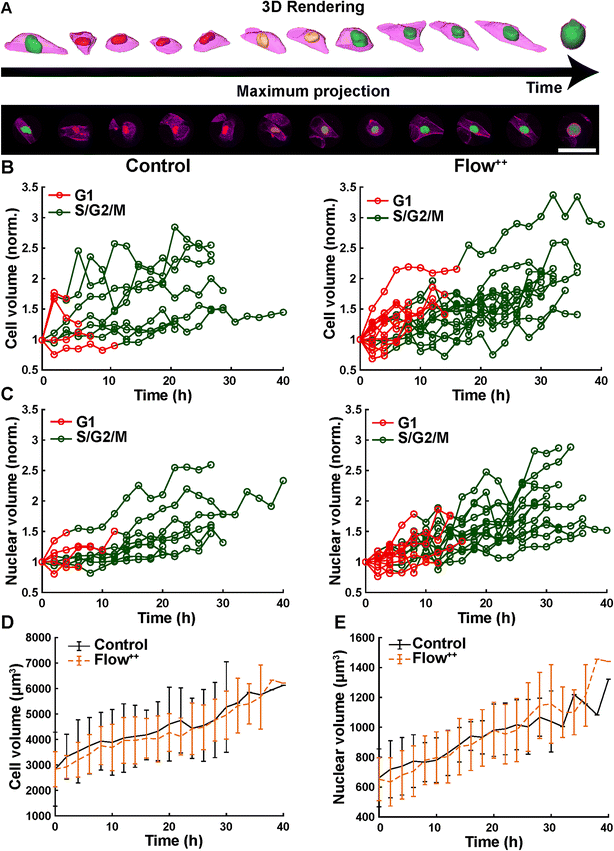
We further investigated cell and nuclear volume changes under flow (Flow++) compared to control with 3D confocal time-lapse imaging. After a mitosis event, daughter cells were tracked and segmented to obtain the cell and nuclear volume of every single cell throughout entire cell cycle (Fig. 6, Movie S2†). For every time point, the cells were segmented using deep learning in three channels: the SiR-Actin (magenta) was used to approximate the cell volume and mVenus/mCherry (green, red) were used to measure the nuclear volume as well as the cell cycle phases (Fig. 7). Because we could isolate single cells inside a confined field of view (i.e., the microfluidic trap) suitable for confocal imaging, tracking single cells over a long period of time with 3D confocal microscopy was successful.The cell volume roughly doubled linearly from first mitosis (t = 0 h) to the next cell division event, in both the control and Flow++ groups (Fig. 7B). In absolute values, the cell volume started at 3000 μm3 and ended at 6000 μm3 (Fig. 7D) with a similar growth rate in both experimental conditions. More specifically during G1, cell volume increased from 3000 μm3 to 4000 μm3, and during S/G2/M from 4000 μm3 to 6000 μm3.
Similarly, nuclear volume roughly doubled for every cell (Fig. 7C) starting at 650 μm3 and growing to 1200 μm3 (Fig. 7E), in both control and Flow++ groups. During G1, the volume increased from 650 μm3 to 800 μm3, and continued in S/G2/M reaching 1200 μm3 before division.
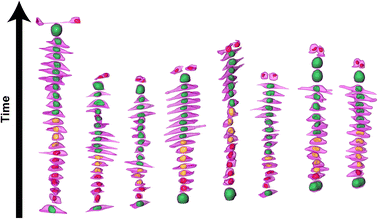
Time-resolved 3D shape analysis shows increasingly elongating cells not accompanied by nuclear shape changes
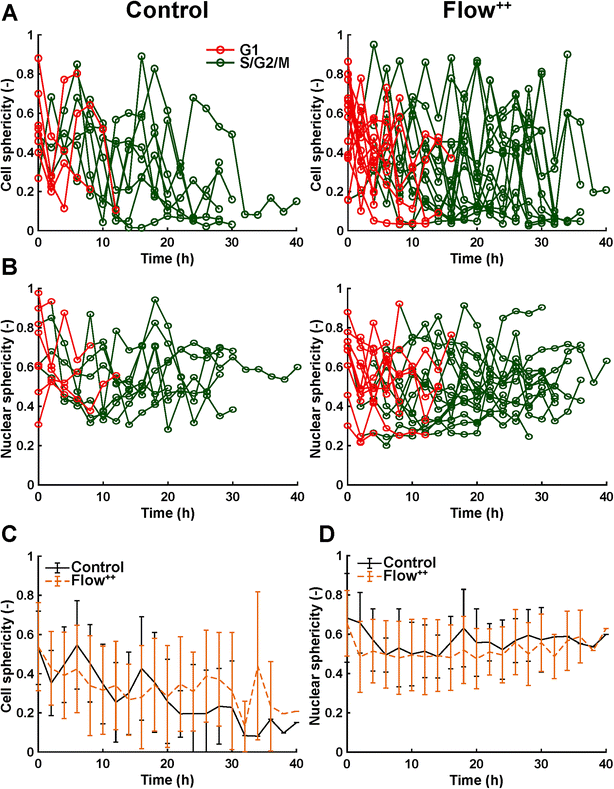
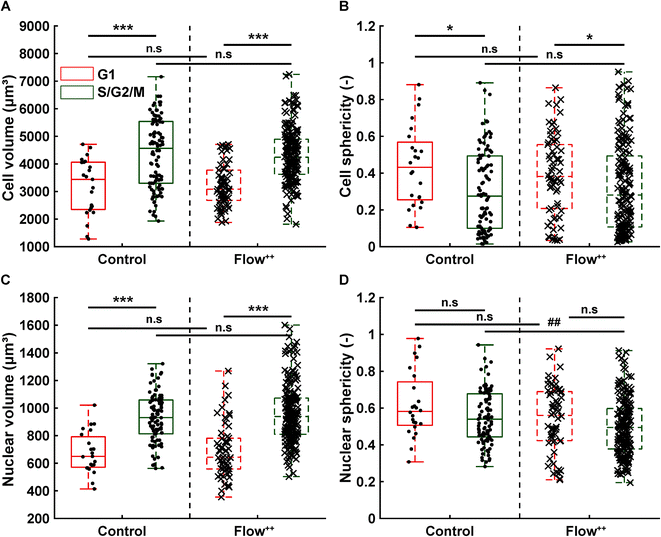
We then further investigated the cell and nuclear time-resolved morphology changes coming from the same 3D confocal time-lapse multi-channel images. Using MATLAB, we calculated the Eigenvalues of the voxels representing every segmented cell. We then defined the sphericity as the ratio of the second Eigenvalue with respect to the first Eigenvalue (Fig. 8), with 1 meaning a perfect spherical shape and 0 a really elongated cell (eqn (1)).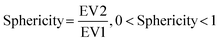 | (1) |
Moreover, thanks to the FUCCI2 signal, the nuclear sphericity could also be measured (Fig. 8B). For both experimental groups, nuclear sphericity over time displayed a smaller fluctuation compared to the cell sphericity. The extrema values ranged from 1 to 0.3 for the control to 0.9 to 0.2 for the Flow++ group (Fig. 8D). However, and in contrast to the cell sphericity, the average nuclear sphericity remained roughly constant with an average value reaching ∼0.5. Similar to cell shape analysis, the nuclear sphericity variance was broader in Flow++ than in the control group.
The FUCCI2 signal provided additional information since we could distinguish the cell and nuclear sphericity at every phase of the cell cycle (Fig. 9). For this, we pooled all data points as a function of the cell cycle phase. It means that every data point in the boxplot corresponds to one cell for one time point in its respective cell cycle phase (G1, S/G2/M). The cell (Fig. 9A) and nuclear (Fig. 9C) volume increased significantly between the G1 and the S/G2/M (red vs. green boxplots) phase but we could not observe any significant differences between the control and the Flow++ groups. In terms of cell shape, we found a similar trend, meaning that between the G1 and the S/G2/M phase, the cell sphericity significantly decreased for both the control (plain lines) and the Flow++ (dashed lines) groups (Fig. 9B). We could not see a significant difference in cell sphericity, neither in G1 nor S/G2/M phase. Additionally, the nuclear sphericity was similar between the control and the Flow++ in G1 and did not show significant differences (Fig. 9D, red boxplots). However, in S/G2/M the nuclear sphericity significantly decreased for the Flow++ group (Fig. 9D, green boxplots) with respect to the control.
Conclusions & discussion
Fluid flow and resulting shear stress is a physiologically important biophysical cue that is involved in several processes in cancer metastasis, such as dissemination of tumour cells to distant sites and their survival.31 Here we investigate the effect of fluid flow from sinusoidal capillaries on metastatic breast cancer cells, since this dynamic environment is characteristic of regions where cells can adhere, roll and extravasate into the bone marrow interstitial matrix.19 With the specific microfluidic design, we can isolate single cells and monitor several aspects of their cell cycle dynamics in correlation with migration and morphology in real time and in 3D for long periods of time, as a function of shear stress. This design has the best trapping efficiency, single cells are quasi-isolated and our CFD simulation inside the trap (Fig. 1C) shows that the velocities correspond to what was measured in vivo in the bone marrow sinusoidal capillaries.19Our findings on 2D single cell analysis identify sinusoidal fluid flow (Flow++) as a biophysical cue that can modulate cell cycle dynamics by reducing the S/G2/M phase duration, hence the overall division time and thus accelerating the proliferation of metastatic cancer cells (Fig. 2). This is accompanied by faster cell motility, which does not correlate with the direction of the flow (Fig. 4). During the experiments and irrespective of the flow conditions, a few cells were washed away during rounding up leading to mitosis. Since we could not capture the entire duration of their cell cycle, these were excluded from the analysis. A small number of cells show distinct behaviours in term of migration or cell cycle phase duration in all three experimental groups. Since we are working with a highly metastatic breast cancer cell line, it is possible that heterogeneity arises, and it could be of interest to test these experiments with another cell line in the future.
Furthermore, we investigated time-resolved volume and shape changes of single cells and their nuclei using 3D time-lapse single cell analysis (Fig. 6–9). Cell and nuclear volume linearly increased with time and no difference was found for cells under flow (Fig. 7). Previous studies have shown that cell cycle arrest induced by hyperosmotic pressure is accompanied by impaired nuclear growth.26 This is not the case under sinusoidal fluid flow, where cell and nuclear volume growth are analogous to the control group, which is consistent with similar cell cycle dynamics for the Flow+ group and slightly faster dynamics for the Flow++ group.
To understand what could cause faster cell division under Flow++, we investigated cell shape evolution with respect to the flow direction. In particular, we hypothesized that cells could elongate perpendicular to the flow direction and the resulting shear forces could support and promote cell division. We analyzed the angle between the cell main axis and flow direction right before division in 2D experiments (Fig. 5), as well as time-resolved cell and nuclear sphericity in 3D experiments (Fig. 8 and 9). However, we found no trend of high (90°) angle between the cell main axis and flow direction that could support this hypothesis. The 3D analysis revealed increasingly elongated cell shape with time, particularly in the S/G2/M phase. Yet, no significant difference was found between control and Flow++ groups. Nuclear sphericity was also monitored with progressing cell cycle, with no apparent difference between control and Flow++ groups (Fig. 8D). Only when pooling all data points according to cell cycle, significantly more elongated nuclei were found for the S/G2/M phase under Flow++. Cell motility is often associated with cell morphology,32 we thus investigated whether cell volume and/or sphericity would be correlated with cell migration speed at each time point (Fig. S5†). We could not observe any significant trend in both the control and the Flow++ groups.
Such detailed time-resolved single cell analysis in 2D and 3D was made possible thanks to artificial intelligence during image analysis of large datasets. Most methods for cell or nuclear segmentation involve a compromise between automation and flexibility. It can be done completely with manual labelling,33 with customized pipelines involving user-specific parameters34–36 or with fully automated methods based on deep learning networks containing parameters estimated on large training datasets.37,38 Here we propose an approach based on the deep learning network U-net for 3D time-lapse cell and nucleus segmentation with minimal training datasets. By doing so, we significantly decreased the processing time of our large datasets. Still, our method was trained on a specialized dataset, and it will be interesting to see how it can be generalized to other cell lines. A large international competition (Data Science Bowl) was held recently to gather datasets of varied images of nuclei from many different laboratories and a deep learning method outperformed other methods on segmentation tasks.39 Very recently, a similar approach was taken to gather images of cells from many laboratories and create a universal deep learning model to perform cell segmentation without requiring parameter adjustments, new training data or network retraining.40
Our findings are in agreement with previous work done with prostate cancer cells that demonstrated an acceleration of proliferation under similar range of wall shear stress.41 To evaluate the wall shear stress in our experiment, we used the real shape of the cell from the 3D time-lapse segmentation together with computational fluid dynamics (CFD) simulations (Fig. S6 and S7 in the ESI†). Lee et al.41 identified that under flow, the transcriptional coactivator with PDZ-binding motif (TAZ) positively influenced cancer cell proliferation, whereas silencing of TAZ under flow reduced proliferation with respect to control. Indeed, TAZ can act as a promotor and amplify genes that have roles in cell proliferation and other cellular functions42,43 and its activation under fluid flow could explain the observed acceleration in the cell cycle. While accelerated proliferation under sinusoidal flow was previously reported,41 to the best of our knowledge it is the first time that quantification of cell cycle phase duration in real time, in conjunction with cell motility, volume and morphology of the cell and nucleus, is being reported thanks to the FUCCI2 system.
In contrast, higher fluid flow and shear stress (∼12 dynes per cm2), which are values found in vivo in intermediate capillaries,19 could induce a cell cycle arrest via G2/M in DTCs. This occurs through an increase in the expression of cyclin B1 and p21, decreasing expressions of cyclin A, D1 and E, CDK-1, −2, −4 and −6, as well as p27, in three bone cancer cell lines and one tongue cancer cell line.44 This result can also be put in perspective with the emergence of quiescent hematopoietic stem cells preferentially found adjacent to small arterioles in the BM,18 regions where shear stress is higher than sinusoidal capillaries (>20 dyne per cm2).19 Unfortunately, our system in its current state does not allow to reach such high shear stresses and would require design modifications. The platform nevertheless allows us to investigate physiologically relevant shear stress values found in sinusoids capillaries.19
Acting not only as a cell cycle reporter, the FUCCI2 system can also be used to track single cell motility thanks to our FUCCItrack software.29 We show that irrespective of the flow condition, MDA-FUCCI2 generally had similar speed in G1 and in S/G2/M phase, matching previous work with HeLa FUCCI cells.45 Moreover, under Flow++ the speed and distance travelled increased significantly compared to control, despite not exhibiting any preferred direction with respect to the direction of the flow. A previous study with MDA-MB-231 cells in a microfluidic device also confirmed an increase in speed as well as a more mobile behaviour under flow.46 More specifically, they identified the transient receptor potential melastatin 7 (TRPM7) as being activated by fluid-shear through deformation of the plasma membrane. This promoted extracellular calcium influx, which in turn activated several pathways coordinating cell motility. Indeed, it has been shown that biophysical cues such as shear stress can activate mechanosensitive ion channels to enable uptake of extracellular Ca2+ into the cell.47 This could explain some of the results we are observing, although further experiments would be needed to confirm this.
In conclusion, taking advantage of FUCCI2, microfluidics and a deep learning approach altogether, we could perform quantitative 2D and 3D time-lapse multi-channel imaging. Here, our findings on 2D single cell analysis identify fluid flow mimicking sinusoidal capillaries as a biophysical cue that can slightly modulate single cell cycle dynamics by reducing the S/G2/M phase duration, hence the overall division time, as well as increasing cell motility irrespective of the flow direction. These two results could have important repercussions in the context of cancer progression. The increased motility of adherent cells could facilitate the crossing of the endothelial barrier48 by spanning more area of the sinusoids. Further, faster dividing cells could cause a physical occlusion of small capillaries facilitating cell extravasation.15 This way, more motile and faster dividing cells under capillary fluid flow could facilitate metastasis progression. It would be of great interest to visualize our FUCCI2 cancer cells in vivo inside an animal model such as zebrafish49,50 to help translate our findings to a more physiological setting. For instance, Goetz et al. recently uncovered the cellular and molecular mechanisms driving blood flow dependent arrest of circulating tumour cells, endothelial remodelling and extravasation thanks to this model.51,52 The evolution of cell and nuclear volume as well as morphology throughout the cell cycle was also revealed thanks to the impressive efficiency of deep learning-based approach for 3D time-lapse multi-channel segmentation.
Data availability
All raw and processed data, microfluidic design masks and custom-made code is available in a publicly accessible repository of the Max Planck Society (https://doi.org/10.17617/3.658NWI).Author contributions
H. M. T., T. R. and A. C. conceived the idea and designed the experiments. H. M. T. and G. H. performed the experiments. H. M. T. and G. H. designed the simulation workflow. H. M. T, T. R. and A. C. analyzed and discussed the data. H. M. T., T. R. and A. C. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. M. T. thanks the International Max Planck Research School (IMPRS) on Multiscale Bio-Systems for financial support. A. C. acknowledges the funding by the Deutsche Forschungsgemeinschaft (DFG) Emmy Noether Grant CI 203/2-1 and the IKERBASQUE Basque Foundation for Science. T. R. acknowledges funding from the MaxSynBio consortium, which is jointly funded by the Federal Ministry of Education and Research of Germany and the Max Planck Society. The authors would like to acknowledge the technical assistance of Christine Pilz with cell culture at the MPICI. We thank Sadra Bakhshandeh, Sarah Young, Luca Bertinetti, Emanuel Schneck, Peter Fratzl and Roland Lauster for scientific discussion. Open Access funding provided by the Max Planck Society.References
- S. Valastyan and R. A. Weinberg, Cell, 2011, 147, 275–292 CrossRef PubMed.
- J. D. Martin, G. Seano and R. K. Jain, Annu. Rev. Physiol., 2019, 81, 505–534 CrossRef.
- H. Mohammadi and E. Sahai, Nat. Cell Biol., 2018, 20, 766–774 CrossRef PubMed.
- J. J. Northey, L. Przybyla and V. M. Weaver, Cancer Discovery, 2017, 7, 1224–1237 CrossRef PubMed.
- H. T. Nia, L. L. Munn and R. K. Jain, Science, 2020, 370, eaaz0868 CrossRef PubMed.
- D. Wirtz, K. Konstantopoulos and P. C. Searson, Nat. Rev. Cancer, 2011, 11, 512–522 CrossRef PubMed.
- P. Koumoutsakos, I. Pivkin and F. Milde, Annu. Rev. Fluid Mech., 2013, 45, 325–355 CrossRef.
- M. A. Swartz and A. W. Lund, Nat. Rev. Cancer, 2012, 12, 210–219 CrossRef.
- L. Weiss, J. Bronk, J. W. Pickren and W. W. Lane, Invasion Metastasis, 1981, 1, 126–135 Search PubMed.
- J. M. Munson, R. V. Bellamkonda and M. A. Swartz, Cancer Res., 2013, 73, 1536–1546 CrossRef.
- R. C. Cornelison, C. E. Brennan, K. M. Kingsmore and J. M. Munson, Sci. Rep., 2018, 8, 17057 CrossRef PubMed.
- C. M. Ghajar, H. Peinado, H. Mori, I. R. Matei, K. J. Evason, H. Brazier, D. Almeida, A. Koller, K. A. Hajjar, D. Y. R. Stainier, E. I. Chen, D. Lyden and M. J. Bissell, Nat. Cell Biol., 2013, 15, 807–817 CrossRef CAS PubMed.
- A. B. Al-Mehdi, K. Tozawa, A. B. Fisher, L. Shientag, A. Lee and R. J. Muschel, Nat. Med., 2000, 6, 100–102 CrossRef CAS PubMed.
- M. S. Sosa, P. Bragado and J. A. Aguirre-Ghiso, Nat. Rev. Cancer, 2014, 14, 611–622 CrossRef CAS PubMed.
- Y. Kienast, L. von Baumgarten, M. Fuhrmann, W. E. F. Klinkert, R. Goldbrunner, J. Herms and F. Winkler, Nat. Med., 2010, 16, 116–122 CrossRef CAS.
- A. P. Kusumbe, S. K. Ramasamy and R. H. Adams, Nature, 2014, 507, 323–328 CrossRef CAS.
- F. Lassailly, K. Foster, L. Lopez-Onieva, E. Currie and D. Bonnet, Blood, 2013, 122, 1730–1740 CrossRef.
- Y. Kunisaki, I. Bruns, C. Scheiermann, J. Ahmed, S. Pinho, D. Zhang, T. Mizoguchi, Q. Wei, D. Lucas, K. Ito, J. C. Mar, A. Bergman and P. S. Frenette, Nature, 2013, 502, 637–643 CrossRef.
- M. G. Bixel, A. P. Kusumbe, S. K. Ramasamy, K. K. Sivaraj, S. Butz, D. Vestweber and R. H. Adams, Cell Rep., 2017, 18, 1804–1816 CrossRef PubMed.
- M. B. Chen, J. A. Whisler, J. S. Jeon and R. D. Kamm, Integr. Biol., 2013, 5, 1262 CrossRef.
- S. Regmi, A. Fu and K. Q. Luo, Sci. Rep., 2017, 7, 39975 CrossRef.
- C. Hajal, L. Ibrahim, J. C. Serrano, G. S. Offeddu and R. D. Kamm, Biomaterials, 2021, 265, 120470 CrossRef CAS PubMed.
- M. Urbanska, H. E. Muñoz, J. Shaw Bagnall, O. Otto, S. R. Manalis, D. Di Carlo and J. Guck, Nat. Methods, 2020, 17, 587–593 CrossRef CAS PubMed.
- A. Sakaue-Sawano, H. Kurokawa, T. Morimura, A. Hanyu, H. Hama, H. Osawa, S. Kashiwagi, K. Fukami, T. Miyata, H. Miyoshi, T. Imamura, M. Ogawa, H. Masai and A. Miyawaki, Cell, 2008, 132, 487–498 CrossRef CAS PubMed.
- A. Sakaue-Sawano, T. Kobayashi, K. Ohtawa and A. Miyawaki, BMC Cell Biol., 2011, 12, 2 CrossRef CAS PubMed.
- H. M. Taïeb, D. S. Garske, J. Contzen, M. Gossen, L. Bertinetti, T. Robinson and A. Cipitria, Sci. Rep., 2021, 11, 13455 CrossRef PubMed.
- K. Eyer, P. Kuhn, S. Stratz and P. S. Dittrich, J. Visualized Exp., 2013, 80, 50618 Search PubMed.
- T. Robinson, P. Kuhn, K. Eyer and P. S. Dittrich, Biomicrofluidics, 2013, 7, 044105 CrossRef.
- H. M. Taïeb, L. Bertinetti, T. Robinson and A. Cipitria, PLoS One, 2022, 17, e0268297 CrossRef PubMed.
- O. Ronneberger, P. Fischer and T. Brox, in Lecture Notes in Computer Science, Springer, Cham, 2015, vol. 9351, pp. 234–241 Search PubMed.
- G. Follain, D. Herrmann, S. Harlepp, V. Hyenne, N. Osmani, S. C. Warren, P. Timpson and J. G. Goetz, Nat. Rev. Cancer, 2020, 20, 107–124 CrossRef PubMed.
- D. Imoto, N. Saito, A. Nakajima, G. Honda, M. Ishida, T. Sugita, S. Ishihara, K. Katagiri, C. Okimura, Y. Iwadate and S. Sawai, PLoS Comput. Biol., 2021, 17, e1009237 CrossRef PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef PubMed.
- C. Sommer, C. Straehle, U. Kothe and F. A. Hamprecht, in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, IEEE, 2011, pp. 230–233 Search PubMed.
- S. Berg, D. Kutra, T. Kroeger, C. N. Straehle, B. X. Kausler, C. Haubold, M. Schiegg, J. Ales, T. Beier, M. Rudy, K. Eren, J. I. Cervantes, B. Xu, F. Beuttenmueller, A. Wolny, C. Zhang, U. Koethe, F. A. Hamprecht and A. Kreshuk, Nat. Methods, 2019, 16, 1226–1232 CrossRef PubMed.
- C. McQuin, A. Goodman, V. Chernyshev, L. Kamentsky, B. A. Cimini, K. W. Karhohs, M. Doan, L. Ding, S. M. Rafelski, D. Thirstrup, W. Wiegraebe, S. Singh, T. Becker, J. C. Caicedo and A. E. Carpenter, PLoS Biol., 2018, 16, e2005970 CrossRef PubMed.
- Y. Al-Kofahi, A. Zaltsman, R. Graves, W. Marshall and M. Rusu, BMC Bioinf., 2018, 19, 365 CrossRef PubMed.
- J. Funke, L. Mais, A. Champion, N. Dye and D. Kainmueller, in Lecture Notes in Computer Science, Springer, Cham, 2019, vol. 11134 LNCS, pp. 437–445 Search PubMed.
- J. C. Caicedo, A. Goodman, K. W. Karhohs, B. A. Cimini, J. Ackerman, M. Haghighi, C. Heng, T. Becker, M. Doan, C. McQuin, M. Rohban, S. Singh and A. E. Carpenter, Nat. Methods, 2019, 16, 1247–1253 CrossRef.
- C. Stringer, T. Wang, M. Michaelos and M. Pachitariu, Nat. Methods, 2021, 18, 100–106 CrossRef.
- H. J. Lee, A. Ewere, M. F. Diaz and P. L. Wenzel, Cell Cycle, 2018, 17, 147–153 CrossRef PubMed.
- F. Zanconato, M. Forcato, G. Battilana, L. Azzolin, E. Quaranta, B. Bodega, A. Rosato, S. Bicciato, M. Cordenonsi and S. Piccolo, Nat. Cell Biol., 2015, 17, 1218–1227 CrossRef.
- Q.-Y. Lei, H. Zhang, B. Zhao, Z.-Y. Zha, F. Bai, X.-H. Pei, S. Zhao, Y. Xiong and K.-L. Guan, Mol. Cell. Biol., 2008, 28, 2426–2436 CrossRef.
- S.-F. Chang, C. A. Chang, D.-Y. Lee, P.-L. Lee, Y.-M. Yeh, C.-R. Yeh, C.-K. Cheng, S. Chien and J.-J. Chiu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3927–3932 CrossRef.
- M. Panagiotakopoulou, M. Bergert, A. Taubenberger, J. Guck, D. Poulikakos and A. Ferrari, ACS Nano, 2016, 10, 6437–6448 CrossRef.
- C. L. Yankaskas, K. Bera, K. Stoletov, S. A. Serra, J. Carrillo-Garcia, S. Tuntithavornwat, P. Mistriotis, J. D. Lewis, M. A. Valverde and K. Konstantopoulos, Sci. Adv., 2021, 7, eabh3457 CrossRef PubMed.
- C. Wei, X. Wang, M. Chen, K. Ouyang, L.-S. Song and H. Cheng, Nature, 2009, 457, 901–905 CrossRef.
- N. Reymond, B. B. D'Água and A. J. Ridley, Nat. Rev. Cancer, 2013, 13, 858–870 CrossRef.
- M. Sugiyama, A. Sakaue-Sawano, T. Iimura, K. Fukami, T. Kitaguchi, K. Kawakami, H. Okamoto, S. Higashijima and A. Miyawaki, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20812–20817 CrossRef.
- C. Yan, D. C. Brunson, Q. Tang, D. Do, N. A. Iftimia, J. C. Moore, M. N. Hayes, A. M. Welker, E. G. Garcia, T. D. Dubash, X. Hong, B. J. Drapkin, D. T. Myers, S. Phat, A. Volorio, D. L. Marvin, M. Ligorio, L. Dershowitz, K. M. McCarthy, M. N. Karabacak, J. A. Fletcher, D. C. Sgroi, J. A. Iafrate, S. Maheswaran, N. J. Dyson, D. A. Haber, J. F. Rawls and D. M. Langenau, Cell, 2019, 177, 1903–1914 CrossRef , e14.
- G. Follain, N. Osmani, A. S. Azevedo, G. Allio, L. Mercier, M. A. Karreman, G. Solecki, M. J. Garcia Leòn, O. Lefebvre, N. Fekonja, C. Hille, V. Chabannes, G. Dollé, T. Metivet, F. Der Hovsepian, C. Prudhomme, A. Pichot, N. Paul, R. Carapito, S. Bahram, B. Ruthensteiner, A. Kemmling, S. Siemonsen, T. Schneider, J. Fiehler, M. Glatzel, F. Winkler, Y. Schwab, K. Pantel, S. Harlepp and J. G. Goetz, Dev. Cell, 2018, 45, 33–52 CrossRef PubMed , e12.
- G. Follain, N. Osmani, V. Gensbittel, N. Asokan, A. Larnicol, L. Mercier, M. J. Garcia-Leon, I. Busnelli, A. Pichot, N. Paul, R. Carapito, S. Bahram, O. Lefebvre and J. G. Goetz, Sci. Rep., 2021, 11, 13144 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00322h |
| This journal is © The Royal Society of Chemistry 2023 |