Mo₂B₂ MBene-supported single-atom catalysts as bifunctional HER/OER and OER/ORR electrocatalysts

Abstract

Searching for highly efficient and cost-effective bifunctional electrocatalysts for the oxygen evolution reaction (OER), oxygen reduction reaction (ORR) and hydrogen evolution reaction (HER), which can be applied to water splitting, fuel cells and metal–air batteries, is critical for developing clean and renewable energies. Yet it remains a great challenge. By means of first-principles calculations, we have studied the OER, ORR and HER catalytic activity of Mo₂B₂ MBene-supported single-atom catalysts (SACs) by embedding a series of transition metal atoms in the Mo vacancy (TM@Mo₂B₂, TM = Ti, V, Cr, Mn, Fe, Co, Ni and Cu) as electrocatalysts. All TM@Mo₂B₂ SACs show excellent metallic conductivity, which would be favorable for the charge transfer in electrocatalytic reactions. Importantly, Ni@Mo₂B₂ can be used as a HER/OER bifunctional electrocatalyst with a lower |ΔG_H| (−0.09 eV) for the HER under 1/4H coverage and a lower overpotential (η_OER = 0.52 V) than that of IrO₂ (η_OER = 0.56 V) for the OER, while Cu@Mo₂B₂ can be used as an OER/ORR bifunctional electrocatalyst with a lower overpotential (η_OER = 0.31 V) than that of IrO₂ (η_OER = 0.56 V) and RuO₂ (η_OER = 0.42 V) for the OER and a lower overpotential of 0.34 V than that of Pt (η_ORR = 0.45 V) for the ORR, for both of which the transition metal atoms serve as the active sites. This work could open up an avenue for the development of non-noble-metal-based bifunctional MBene electrocatalysts.

---

1. Introduction

Clean and renewable energy technologies, such as water splitting, fuel cells and metal–air batteries, are crucial to mitigate environmental pollution and the energy crisis.^1–10 The bases of these technologies are the oxygen evolution reaction (OER), oxygen reduction reaction (ORR) and hydrogen evolution reaction (HER), the efficiency of which mainly depends on the performance of the catalysts. Currently, the most effective catalysts are Pt (for the ORR and HER) and IrO₂/RuO₂ (for the OER).^11–14 However, the scarcity and high price prevent their large-scale usage. Although great effort has been made in the research on OER, ORR and HER catalysts, such as nanostructured metal carbides,^15–17 graphene doped with heteroatoms,^18,19 carbon-based hybrids,^20–22 and transition metal chalcogenides,^23,24 searching for non-noble metal catalysts with high catalytic performance comparable to that of the above-mentioned Pt and IrO₂/RuO₂ is still a great challenge. In addition, compared with two separate unifunctional catalysts, for which the optimal working conditions are not always the same, bifunctional catalysts operating under optimal and identical conditions have many obvious advantages,²⁵ such as reducing costs and simplifying the systems.⁵ According to previous work,^3,26,27 HER/OER bifunctional catalysts and OER/ORR bifunctional catalysts have attracted widespread attention because HER/OER bifunctional catalysts can be used for water splitting and OER/ORR bifunctional catalysts be used in fuel cells and metal–air batteries.

On account of the special physical and chemical properties and the large specific area, two-dimensional (2D) materials have been highly attractive in the past few years.^28,29 Recently, 2D transition metal borides, known as MBenes, have been extensively studied.^30–35 MBenes can be obtained by selectively removing the A atomic layer in MAB phases experimentally, where A represents aluminum in most cases, M represents a transition metal and B represents boron. So far, some MBenes including Mo₂B₂,³³ Cr₂B₂ (ref. ³¹) and Ti₂B₂ (ref. ³⁵) have been experimentally produced. Importantly, according to previous work,^30,32,35 all the reported MBenes show good metallic conductivity to ensure electron transfer efficiency as electrodes and electrocatalysts. In addition, with the exploration and development of materials synthesis methods, the rational design of catalysts with high efficiency has become more intriguing. Among various catalyst designs, single-atom catalysts (SACs) have attracted significant attention, due to the unique electronic structure originating from the strong interaction and large charge transfer between the single metal atoms and the coordination species of the supports.^36–38 Moreover, SACs have fully exposed and dispersed active sites.^39–42 The unique electronic-structural properties and the exposure of the active sites make SACs exhibit remarkable enhancements in the catalytic performance in a variety of reactions.³⁶ Inspired by the good metallic conductivity and the large specific area of MBenes and the advantages of SACs, it is of significance to investigate MBene-supported SACs.

In this work, we rationally embedded transition metal atoms in the Mo vacancies of Mo₂B₂ MBenes (TM@Mo₂B₂) to construct SACs to study their OER, ORR and HER performance at different surface active sites by first-principles calculations, where the transition metals refer to Ti, V, Cr, Mn, Fe, Co, Ni and Cu. With good structural stability and metallic conductivity, Ni@Mo₂B₂ and Cu@Mo₂B₂ can be used as bifunctional HER/OER and OER/ORR catalysts, respectively.

2. Computational methods

In this work, all the first-principles calculations were performed using spin-polarized density-functional theory (DFT) as implemented in the Vienna ab-initio simulation package (VASP) code.⁴³ The generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PBE) functional⁴⁴ was applied to describe the electron exchange–correlation interactions. To describe the long-range van der Waals interactions, the DFT+D2 method was used in this work.⁴⁵ The DFT+U correction was considered during the electronic structure calculations for the systems. The cut-off energy was set to 500 eV and 4 × 4 supercells were used. The structural optimizations and electronic properties were all studied with the energy converged to 1.0 × 10⁻⁴ eV per atom and the force converged to 0.01 eV Å⁻¹. In addition, the Brillouin zones were sampled with a 4 × 4 × 1 k-point grid for structural optimizations, a 7 × 7 × 1 k-point grid for static self-consistent calculations and a denser 11 × 11 × 1 k-point grid for the density of states (DOS) calculations. To evaluate the stability of the catalysts, ab initio molecular dynamics (AIMD) simulations were performed. The AIMD simulations lasted for 10 ps with a time step of 2.0 fs at 300 K. The climbing-image nudged elastic band (NEB) method was used to investigate the diffusion pathway and energy barrier of intermediates for the OER and ORR, respectively.

The formation energy of Mo vacancies in Mo₂B₂ is calculated using the following equation:

E_f(V_Mo) = E_Mo2B2–VMo − E_Mo2B2 + nμ_Mo (1)

where E_Mo2B2–VMoand E_Mo2B2 represent the total energy of the Mo₂B₂ monolayer with and without Mo vacancies, respectively, μ_Mo is the chemical potential of a Mo atom, and n stands for the number of Mo vacancies, which is 1 here to study the formation energy of a monovacancy.

The binding energy (E_b) of transition metal atoms (TM = Ti, V, Cr, Mn, Fe, Co, Ni and Cu) embedded in the Mo monovacancy of Mo₂B₂ was calculated according to the equation:

E_b = E_TM+S − E_S − E_TM (2)

where E_TM+S and E_S represent the total energy of the defective Mo₂B₂ with and without the embedded transition metal atoms, respectively, and E_TM represents the total energy of the transition metal atom from its most stable bulk phase.

The pathways of the OER, ORR and HER have been summarized in detail. In an acid electrolyte, the OER can be decomposed into the following elementary steps:

H₂O(l) + * → OH* + H⁺ + e⁻ (3)

OH* → O* + H⁺ + e⁻ (4)

O* + H₂O(l) → OOH* + H⁺ + e⁻ (5)

pOOH* → * + O₂(g) +H⁺ + e⁻ (6)

where * represents the active site on the surfaces of the catalysts and l and g represent the liquid phase and the gas phase, respectively.

The ORR process can be regarded as the inverse of the OER process, which proceeds via the four-electron-transfer pathway as shown below:

* + O₂(g) + H⁺ + e⁻ → OOH* (7)

OOH* + H⁺ + e⁻ → O* + H₂O(l) (8)

O* + H⁺ + e⁻ → OH* (9)

OH* + H⁺ + e⁻ → H₂O(l) + * (10)

For each elementary step of the OER and ORR, the free energies have been calculated according to the method proposed by Norskov et al.¹² The free energy change from the initial state to the final state of the reaction is defined as:

ΔG = ΔE + ΔE_ZPE − TΔS + ΔG_U + ΔG_pH (11)

where ΔE, ΔE_ZPE and ΔS are the differences in the total energy obtained from DFT calculations, zero-point energy and entropy between the reactants and the products, respectively. T represents temperature (298.15 K). ΔG_U = −neU, where U is the applied electrode potential, e is the charge transferred and n is the number of proton–electron transferred pairs. In addition, ΔG_pH = −k_BTln[H⁺] = pH × k_BTln 10, where k_B is the Boltzmann constant.

The free energy change for the four elementary OER steps can be obtained as: ΔG₁ = ΔG_OH*, ΔG₂ = ΔG_O* − ΔG_OH*, ΔG₃ = ΔG_OOH* − ΔG_O* and ΔG₄ = 4.92 − ΔG_OOH*. For the ORR steps: ΔG_a = −ΔG₄, ΔG_b = −ΔG₃, ΔG_c = −ΔG₂ and ΔG_d = −ΔG₁. Therefore, the overpotential that evaluates the performance of the OER and ORR is applied according to the following equations:

η_OER =max{ΔG₁, ΔG₂,ΔG₃, ΔG₄}/e − 1.23 (12)

η_ORR = max{ΔG_a, ΔG_b, ΔG_c, ΔG_d}/e + 1.23 (13)

where 1.23 represents the equilibrium potential.¹¹

Under acidic conditions, the overall reaction scheme of the HER can be written as:

H⁺ + e⁻ + * → H* (14)

H* →½H₂(g) + * (15)

The HER catalytic activity is described using the computed Gibbs free energy change of (14), which was obtained by using the equation:

ΔG_H = ΔE_H + ΔE_ZPE − TΔS (16)

where ΔE_H is the adsorption energy of hydrogen and ΔE_ZPE and ΔS are the differences in the zero-point energy and entropy between the adsorbed hydrogen and the gas phase hydrogen.

3. Results and discussion

3.1 Stability and active sites

First of all, the structural stability of TM@Mo₂B₂ was studied. The atomic structure of TM@Mo₂B₂ is shown in Fig. 1a. We calculated the vacancy formation energy of the Mo monovacancy of Mo₂B₂, E_f(V_Mo), which is 0.98 eV. Generally, the smaller the value of the vacancy formation energy, the more possible the formation of the vacancy. Comparing the vacancy formation energy of MoS₂ (5.85 eV for the S monovacancy)⁴⁶ and graphene (7.69 eV for the C monovacancy),⁴⁷ it is evident that Mo₂B₂ MBene shows greater possibility to form the Mo monovacancy with a relatively low vacancy formation energy. Besides, the vacancy formation energy of Mo₂B₂ MBene is comparable to that of M₂C-type MXenes ranging from 0.96 to 2.85 eV, which make it easy to form vacancies.⁴⁸ Then, the binding energy (E_b) of the transition metal atoms in TM@Mo₂B₂ was calculated, and the results are depicted in Fig. 1b and Table S1.† As is well-known, the negative E_b indicates the high stability of the recombinant systems. The binding energy of Ti@Mo₂B₂, V@Mo₂B₂, Cr@Mo₂B₂, Mn@Mo₂B₂, Fe@Mo₂B₂, Co@Mo₂B₂, Ni@Mo₂B₂ and Cu@Mo₂B₂ is −6.99, −5.97, −5.38, −4.55, −5.02, −4.74, −6.12 and −5.73 eV, respectively, implying that all the studied materials possess excellent structural stability. In addition, as shown in Fig. 1c, the charge accumulation between TM and B atoms indicates the formation of TM-B bonds, which is consistent with the above-mentioned negative binding energy. In addition, we performed AIMD simulations and the result is shown in Fig. S1,† indicating that Ni@Mo₂B₂ and Cu@Mo₂B₂ are both thermally stable.

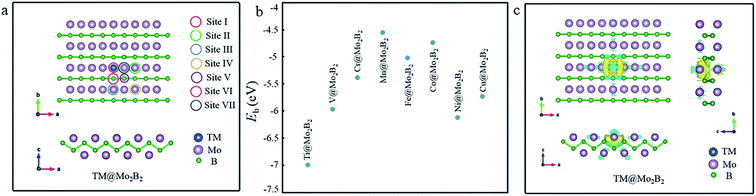Fig. 1 (a) The structure and seven possible active sites of TM@Mo₂B₂. (b) The binding energy diagram of different TM@Mo₂B₂ (TM = Ti, V, Cr, Mn, Fe, Co, Ni and Cu). (c) The charge density difference of TM@Mo₂B₂, where yellow and blue regions indicate the charge density accumulation and depletion, respectively.

Next, the active sites for the OER, ORR, and HER need to be studied. In Mo₂B₂ MBenes, embedding the transition metal atoms in the Mo vacancies causes changes in the chemical environment around the embedded transition metal atoms. As shown in Fig. 1a, seven possible active sites of TM@Mo₂B₂ are marked. According to previous work,^28,30 the HER always occurs on the metal atoms instead of boron atoms of MBenes. Hence, the Mo atoms (including the Mo atoms on the surface and Mo atom on the bridge sites) and TM atoms are selected to be the possible active sites for the HER, including sites I, II, III, IV and VII. For the OER and ORR, apart from the above active sites, the B atoms on the bridge sites are also included. Therefore, we studied the OER, ORR and HER catalytic activity of TM@Mo₂B₂ at the embedded transition metal site (site I), Mo atoms on the surface around the TM (site II, III and IV), B atoms on the bridge sites (site V and VI) and Mo atom on the bridge sites (site VII).

3.2 Electronic properties

Electrical conductivity is vital for electrocatalysts to guarantee electron transfer efficiency during the electrocatalytic reactions. On account of this, the electronic properties of the pristine Mo₂B₂, Mo₂B₂ with Mo monovacancies (Mo₂B₂–V_Mo) and TM@Mo₂B₂ were investigated. Fig. 2 shows the total density of states (TDOS) and projected density of states (PDOS), of Mo₂B₂, Mo₂B₂–V_Mo, Ni@Mo₂B₂ and Cu@Mo₂B₂ (the other TM@Mo₂B₂ are depicted in Fig. S2†). Obviously, the pristine Mo₂B₂ exhibits metallic conductivity with the Fermi energy falling into a continuum of energy states, which is consistent with previous work.³⁰ Meanwhile, Mo₂B₂–V_Mo, Ni@Mo₂B₂, Cu@Mo₂B₂ and all the TM@Mo₂B₂ are metallic. According to the projected density of states (PDOS), the metallic conductivity of the studied materials is mainly contributed by the Mo-4d orbitals near their Fermi levels.

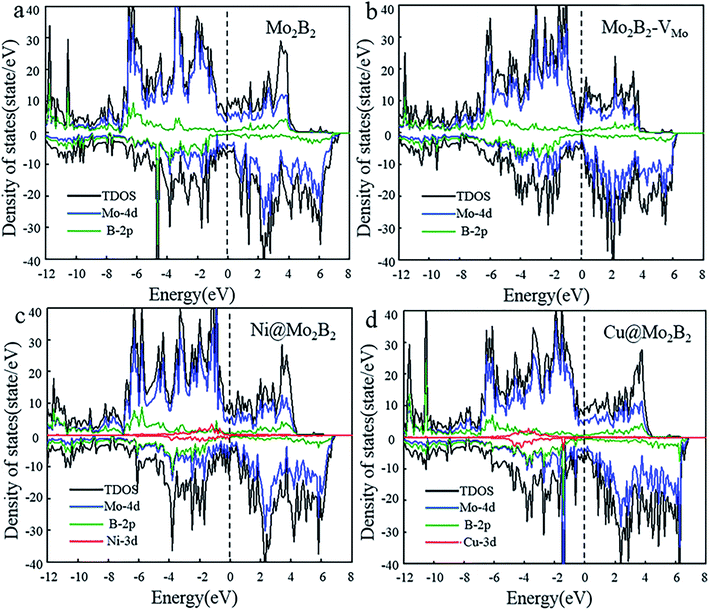Fig. 2 The total density of states (TDOS) and the projected density of states (PDOS) of (a) pristine Mo₂B₂, (b) Mo₂B₂–V_Mo, (c) Ni@Mo₂B₂ and (d) Cu@Mo₂B₂, where the Fermi level is set to 0 eV.

3.3 OER and ORR catalytic activity

After verifying the stability and electrical conductivity of TM@Mo₂B₂, we studied the catalytic activity of TM@Mo₂B₂ for the OER and ORR. As depicted in Fig. 3, there are four elementary steps of the OER, which is also the inverse process of the ORR. Firstly, we studied which of the four sites mentioned above is the active site for the OER and ORR. As listed in Tables S2–S15†, for Ti@Mo₂B₂, V@Mo₂B₂, Fe@Mo₂B₂, Co@Mo₂B₂, Ni@Mo₂B₂ and Cu@Mo₂B₂ in the OER, site I is the optimal active site with a lower overpotential than that of the other six sites, while for Cr@Mo₂B₂ and Mn@Mo₂B₂ in the OER, site III is the optimal active site with a lower overpotential than that of the other six sites. In addition, for Co@Mo₂B₂, Ni@Mo₂B₂ and Cu@Mo₂B₂ in the ORR, site I is the optimal active site with a lower overpotential than that of the other six sites, while for Ti@Mo₂B₂, V@Mo₂B₂ and Cr@Mo₂B₂ in the ORR, site IV is the optimal active site with a lower overpotential than that of the other six sites, and for Mn@Mo₂B₂ and Fe@Mo₂B₂ in the ORR, site VI is the optimal active site with a lower overpotential than that of the other six sites.

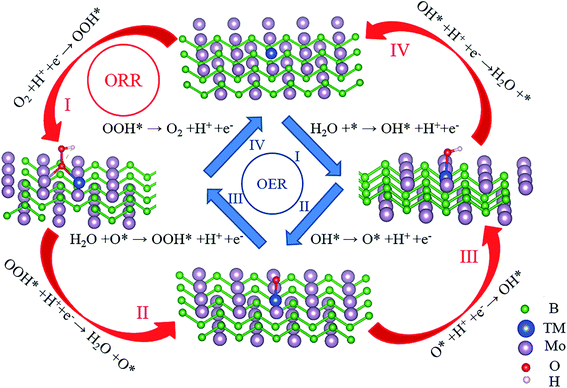Fig. 3 Elementary reaction steps of the OER and ORR process for TM@Mo₂B₂ at site I.

For the OER, we calculated the Gibbs free energy change for each elementary reaction to draft the Gibbs free energy diagrams, as shown in Fig. 4 and Fig. S3.† From the free energy diagrams, we can see that for Ti@Mo₂B₂, V@Mo₂B₂, Cr@Mo₂B₂, Mn@Mo₂B₂, Fe@Mo₂B₂, Co@Mo₂B₂ and Ni@Mo₂B₂, the third step of O* reacting with H₂O to form OOH* is the most energy-consuming step of the entire OER with ΔG₃ values of 3.86, 3.80, 3.32, 2.84, 2.26, 2.13 and 1.75 eV, respectively. In the OER process with Cu@Mo₂B₂ as the catalyst, the step of OH* dissociating to H⁺ and O* (the second step), is the most energy-consuming step and ΔG₂ is 1.54 eV. In addition, we calculated the overpotential for TM@Mo₂B₂ which is the most important indicator to determine the OER performance. Ni@Mo₂B₂ (η_OER = 0.52 V) has better catalytic performance for the OER with a lower overpotential than that of IrO₂ (η_OER = 0.56 V).⁴⁹ It is worth noting that the overpotential for Cu@Mo₂B₂ (η_OER = 0.31 V) is the lowest in this work, even lower than that of the state-of-the-art IrO₂ (η_OER = 0.56 V) and RuO₂ (η_OER = 0.42 V),⁴⁹ indicating that the OER catalytic activity of Cu@Mo₂B₂ is better than that of IrO₂ and RuO₂. Furthermore, it is notable that for the pristine Mo₂B₂, η_OER was calculated to be 2.67 V, as listed in Table S16.† Based on the above results, we can conclude that the OER catalytic activity of Mo₂B₂ MBene is significantly improved after embedding with the above transition metal atoms.

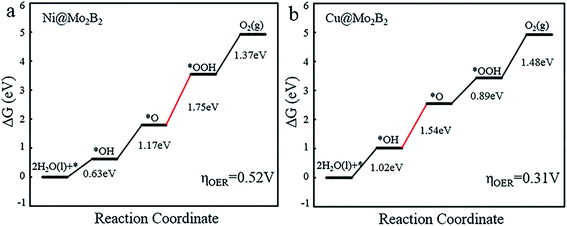Fig. 4 The Gibbs free energy diagrams for the OER pathway of (a) Ni@Mo₂B₂ and (b) Cu@Mo₂B₂ at site I, where the red lines represent the most energy-consuming step of the OER.

Next, we further evaluated the reaction mechanism for the ORR. Generally, there are two possible reaction mechanisms for the ORR in acidic media, i.e., the associative and dissociative mechanism, the difference of which depends on whether the adsorbed O₂ molecule on the catalytic site can be dissociated into two separate O atoms. If so, it is the dissociative pathway, otherwise it is the associative pathway. Before calculating the dissociation barrier, we studied the most stable O₂ adsorption configuration. It is found that the O₂ adsorption energy for the end-on configuration is 7.93 eV lower than that for the side-on configuration, indicating that O₂ prefers to adsorb on Cu@Mo₂B₂ with the end-on configuration. As shown in Fig. S7,† by calculating the dissociation barrier of the adsorbed O₂ molecule at site I of Cu@Mo₂B₂ to form two separate O*, we can find that the dissociation process for Cu@Mo₂B₂ would overcome a large energy barrier of 7.94 eV, which is higher than the associative barrier (0.07 eV, Fig. S6 (a)†). Therefore, in this work, we research the associative pathway for the ORR, rather than the dissociative pathway.

The Gibbs free energy diagrams of the ORR process are presented in Fig. 5 and Fig. S4.† It is obvious that for Ti@Mo₂B₂, V@Mo₂B₂, Cr@Mo₂B₂, Mn@Mo₂B₂, Fe@Mo₂B₂, Co@Mo₂B₂ and Ni@Mo₂B₂ at site I, the fourth step of OH* reacting with H⁺ to form H₂O is the most energy-consuming step of the entire ORR with ΔG_d values of 1.32, 0.98, 1.29, −0.44, 0.45, −0.16 and −0.63 eV, respectively, while for Cu@Mo₂B₂, the most energy-consuming step is the second step, that is, the step of OOH* reacting with H⁺ to form H₂O and O* (ΔG_b are −0.89 eV). Importantly, Cu@Mo₂B₂ has the lowest overpotential (η_ORR = 0.34 V) for the ORR among all the studied TM@Mo₂B₂, which is even lower than that of Pt (η_ORR = 0.45 V). Hence, Cu@Mo₂B₂ also exhibits good ORR catalytic activity apart from OER activity. Similarly, we computed the overpotential of pristine Mo₂B₂ for the ORR, as listed in Table S16,† and the result (η_ORR = 1.50 V) indicates that the ORR performance for pristine Mo₂B₂ is greatly improved by embedding Mn, Co, Ni and Cu. In terms of kinetics, for the four elementary steps of the ORR proceeding on Cu@Mo₂B₂, the whole process is kinetically favorable, as shown in Fig. S6.† The third electron transfer step (O* reacting with H⁺ to form OH*) is the rate-limiting step with a moderate activation energy barrier of 0.75 eV. For the reverse process of the ORR, i.e., the OER, the third electron transfer step (O* reacting with H₂O to form OOH* and H⁺) is the rate-limiting step with an activation energy barrier of 1.04 eV.

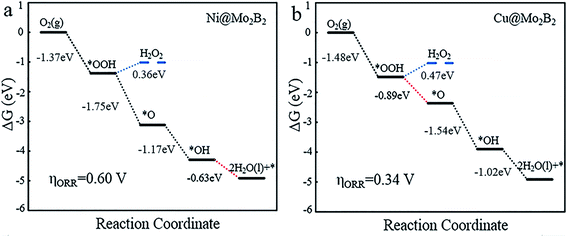Fig. 5 The Gibbs free energy diagrams for the 4e⁻ and 2e⁻ ORR processes of (a) Ni@Mo₂B₂ and (b) Cu@Mo₂B₂ at site I, where the blue lines represent the 2e⁻ ORR process, the black lines represent the 4e⁻ ORR process, and the red dashed lines represent the most energy-consuming step of the ORR.

The most energy-consuming steps of the OER and ORR are both the third steps (ΔG₃ = 3.9 eV, ΔG_c = 0.27 eV) for Mo₂B₂. However, ΔG₃ decreases to 1.75 and 0.89 eV while ΔG_c decreases to −1.17 and −1.54 eV for Ni@Mo₂B₂ and Cu@Mo₂B₂, respectively, indicating that the catalytic activity of Mo₂B₂ is enhanced after embedding Ni or Cu. It is found that the valence state of Mo atoms is +0.61 in bare Mo₂B₂, while the valence states of Ni and Cu are only +0.22 and +0.20 in Ni@Mo₂B₂ and Cu@Mo₂B₂, respectively. The large positive net charges (high valence states) of Mo atoms result in strong adsorption between *O and the adjacent Mo atom in bare Mo₂B₂, leading to large ΔG₃ and ΔG_c. However, the bonding strength between *O and Ni/Cu atoms is moderate due to the relatively small positive net charges (low valence states) of Ni/Cu, contributing to decreased ΔG₃ and ΔG_c in Ni@Mo₂B₂ and Cu@Mo₂B₂.

In addition, from *OOH, there are several pathways to proceed, such as to form *O, HOOH or *OH + *OH. Notably, in acidic media, the 2e⁻ reduction process forming HOOH is the competitive side reaction of the 4e⁻ reduction process, which consists of the following steps:

O₂ + H⁺ + e⁻ + * → OOH* (17)

OOH* + H⁺ + e⁻ → H₂O₂ (18)

To reveal the competitive relationship between the 4e⁻ and 2e⁻ processes, we plotted the Gibbs free energy diagrams of the two different processes for Ni@Mo₂B₂ and Cu@Mo₂B₂. As shown in Fig. 5, in the 2e⁻ process, ΔG of the second elementary reaction of the 2e⁻ reduction process (eqn (18)) is 0.36 and 0.47 eV for Ni@Mo₂B₂ and Cu@Mo₂B₂, respectively, which are both positive. However, in the 4e⁻ process, the ΔG_b values are −1.75 and −0.89 eV for Ni@Mo₂B₂ and Cu@Mo₂B₂, respectively, which are both negative. Therefore, Ni@Mo₂B₂ and Cu@Mo₂B₂ are highly selective for the 4e⁻ process forming H₂O rather than the 2e⁻ process forming H₂O₂. Furthermore, as displayed in Fig. S5,† for Ni@Mo₂B₂, ΔG values from *OOH to *OH + *OH (0.29 eV) or *OH + *O (0.17 eV) are all positive. However, ΔG_b is −1.75 eV for Ni@Mo₂B₂. Hence, Ni@Mo₂B₂ tends to the pathway from *OOH to *O rather than from *OOH to *OH + *OH or *OH + *O. For Cu@Mo₂B₂, ΔG from *OOH to *OH + *OH (−0.20 eV) is negative, but ΔG_b from *OOH to *O (−0.89 eV) is more negative. In addition, ΔG from *OOH to *OH + *O (7.19 eV) is positive. Based on this, Cu@Mo₂B₂ is highly selective for the pathway from *OOH to *O rather than that from *OOH to *OH + *OH. Thus, Ni@Mo₂B₂ and Cu@Mo₂B₂ also possess high selectivity for the process of forming *O from *OOH.

In previous work,^5,14,26 the Gibbs free energies (ΔG_OH*, ΔG_O* and ΔG_OOH*) of three intermediates have been considered as the possible descriptors for the binding strength between the active atoms of the catalyst and the intermediates. During the construction of free energy diagrams for TM@Mo₂B₂, a linear scaling relationship between ΔG_OH* and ΔG_O*, ΔG_OOH* was observed. As shown in Fig. 6a, ΔG_O* showed strong linear correlation with ΔG_OH*, which can be described by the following expressions: ΔG_O* = 1.69ΔG_OH* + 0.74 eV with a coefficient of determination (R²) of 0.972. However, the linear relationship between ΔG_OOH* and ΔG_OH* is not strong. Therefore, ΔG_OH* and ΔG_OH* can be adopted as the descriptor for the binding strength between the active atoms of the catalyst and the intermediates. Based on the above relationship, a dual volcano plot for the ORR and OER was constructed, as shown in Fig. 6b. The dual volcano plot has unique advantages in describing the bifunctional activity for reversible OER/ORR processes (the strategy of the dual volcano plot is shown in the ESI†). When the OER and ORR locate more to the right on the branch of the volcano plot, the OH* binding strength is weaker. Located near the top of the OER volcano plot, Ni@Mo₂B₂ possesses good OER catalytic activity. Also, it is worth mentioning that Cu@Mo₂B₂ is at the top of both the OER and ORR volcano diagrams, indicating that Cu@Mo₂B₂ possesses outstanding OER/ORR bifunctional catalytic activity. Based on the values of overpotential and the dual volcano plot for the OER and ORR, Ni@Mo₂B₂ exhibits excellent OER (η_OER = 0.52 V) catalytic performance at site I, while Cu@Mo₂B₂ possesses superb catalytic activity for both the OER (η_OER = 0.31 V) and ORR (η_ORR = 0.34 V), which can be applied in fuel cells and metal–air batteries.

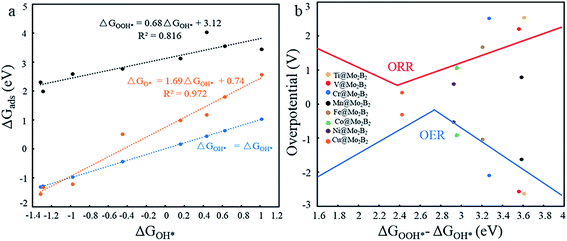Fig. 6 (a) Scaling relationship between the ΔG_OH* and ΔG_O*, ΔG_OOH* at site I. (b) Dual volcano plot for the OER and ORR for TM@Mo₂B₂ at site I.

3.4 HER catalytic activity

Generally, the entire HER process can be formularized by a three-state diagram, which consists of the initial state H⁺ + e⁻, the intermediate state H* and the final product H₂. Herein, we study the HER catalytic activity of TM@Mo₂B₂ at four different sites by calculating the Gibbs free energy difference of the intermediate state H* and the final product H₂ (ΔG_H), which is considered to be the most important descriptor of the HER catalytic activity. Generally, the HER catalytic activity is considered to be high if |ΔG_H| < 0.2 eV. The closer the value of |ΔG_H| is to 0, the higher the HER catalytic activity is. ΔG_H values of all the studied TM@Mo₂B₂ at different sites under 1/16 hydrogen coverage conditions are listed in Table S18†. As shown in Fig. 7, the HER performance of TM@Mo₂B₂ with high OER or ORR catalytic activity (Ni@Mo₂B₂ and Cu@Mo₂B₂) under 1/16 hydrogen coverage conditions was studied. We can conclude that Cu@Mo₂B₂ shows poor HER catalytic activity at site I, site II, site IV and site VII, while Ni@Mo₂B₂ exhibits high HER catalytic activity at site I, site II and site IV. For comparison, we also conducted the HER catalytic activity test of the pristine Mo₂B₂, and its |ΔG_H| is 0.37 eV, indicating that embedding Ni in Mo vacancies of Mo₂B₂ MBenes improves the HER catalytic activity of Mo₂B₂. In addition, we further calculated the ΔG_H of Ni@Mo₂B₂ under different H coverage at site I, as shown in Table S20†. The calculated ΔG_H for Ni@Mo₂B₂ is −0.09 and 0.12 eV for hydrogen coverages of 1/4 and 1/9, respectively, indicating that under higher hydrogen coverages, Ni@Mo₂B₂ still exhibits high HER catalytic activity at site I. Among them, under 1/4 hydrogen coverage conditions, Ni@Mo₂B₂ exhibits high HER catalytic activity compared with Pt (0.09 eV).¹¹ Considering the values of ΔG_H and overpotential, Ni@Mo₂B₂ possesses excellent HER and OER (η_OER = 0.52 V) catalytic activity at site I and can be applied in water splitting.

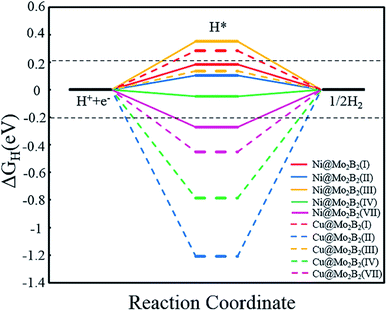Fig. 7 Calculated Gibbs free energy diagram for the HER at different sites for Ni@Mo₂B₂ and Cu@Mo₂B₂ for a hydrogen coverage of 1/16. The two horizontal black dashed lines correspond to |ΔG_H| = 0.2 eV.

Based on the above research, we can conclude that Ni@Mo₂B₂ and Cu@Mo₂B₂ possess high catalytic activity with lower overpotential than the traditional catalysts for a single reaction. In addition, the two electrocatalysts in our work have exhibited extremely high bifunctional catalytic activity so far. For Ni@Mo₂B₂, the overpotential of the HER/OER is −0.09/0.52 V, respectively, indicating better HER/OER catalytic performance than that of Cu₃(HITP)₂ (−0.02/0.75 V)¹⁴ and Mn-anchored C₂N (−0.15/0.67 V).⁵ In particular, the overpotential of the OER/ORR for Cu@Mo₂B₂ (0.31/0.34 V) is much lower than that for Co₃(HITP)₂, Fe₃(HITP)₂, Zn₃(HITP)₂ (0.36/0.73 V, 0.83/0.59 V, and 0.89/0.52 V, respectively),¹⁴ Co-doped g-C₃N₄ (0.53/0.67 V),²⁶ Fe-based covalent organic framework (0.38/0.48 V)⁵⁰ and MoC₂ (0.45/0.47 V).⁹ Therefore, Ni@Mo₂B₂ and Cu@Mo₂B₂ reported in this work are the best HER/OER and OER/ORR bifunctional catalysts so far.

4. Conclusions

In summary, we have demonstrated the feasibility of using TM@Mo₂B₂ as HER/OER and OER/ORR bifunctional electrocatalysts by means of first-principles computations. With good structural stability and metallic conductivity, the OER, ORR and HER catalytic activity of TM@Mo₂B₂ can be tailored by embedding different transition metals. In particular, Ni@Mo₂B₂ is a promising HER/OER bifunctional electrocatalyst for overall water splitting with a low |ΔG_H| (−0.09 eV) for the HER under 1/4 H coverage and overpotential (0.52 V) for the OER. Meanwhile, Cu@Mo₂B₂ has the potential to be an OER/ORR bifunctional electrocatalyst characterized by low overpotentials for the OER and ORR (0.31 and 0.34 V, respectively) and can be compared with the best-known noble electrocatalysts. Our results indicate that TM@Mo₂B₂ MBenes are expected to be economical and efficient candidates for HER/OER and OER/ORR bifunctional electrocatalysts applied in water splitting, fuel cells and metal–air batteries.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Key Research and Development Program of China (No. 2017YFB0701700) and National Natural Science Foundation of China (No. 51871009).

References

1. L. Carrette, K. A. Friedrich and U. Stimming, Fuel Cells, 2001, 1, 5–39.
2. Z. H. Zhao, M. T. Li, L. P. Zhang, L. M. Dai and Z. H. Xia, Adv. Mater., 2015, 27, 6834–6840.
3. T. He, S. K. Matta, G. Will and A. Du, Small Methods, 2019, 3, 1800419.
4. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. B. Chorkendorff, J. K. Norskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
5. X. Zhang, A. Chen, Z. H. Zhang, M. G. Jiao and Z. Zhou, J. Mater. Chem. A, 2018, 6, 11446–11452.
6. J. X. Gu, S. Magagula, J. X. Zhao and Z. F. Chen, Small Methods, 2019, 3, 1800550.
7. Z. P. Cano, D. Banham, S. Y. Ye, A. Hintennach, J. Lu, M. Fowler and Z. W. Chen, Nat. Energy, 2018, 3, 279–289.
8. D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29.
9. Y. Yu, J. Zhou and Z. Sun, Adv. Funct. Mater., 2020, 2000570.
10. M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337.
11. H. X. Xu, D. J. Cheng, D. P. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
12. J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
13. T. Reier, M. Oezaslan and P. Strasser, ACS Catal., 2012, 2, 1765–1772.
14. J. R. Wang, Y. C. Fan, S. Y. Qi, W. F. Li and M. W. Zhao, J. Phys. Chem. C, 2020, 124, 9350–9359.
15. W. F. Chen, C. H. Wang, K. Sasaki, N. Marinkovic, W. Xu, J. T. Muckerman, Y. Zhu and R. R. Adzic, Energy Environ. Sci., 2013, 6, 943–951.
16. L. Liao, S. N. Wang, J. J. Xiao, X. J. Bian, Y. H. Zhang, M. D. Scanlon, X. L. Hu, Y. Tang, B. H. Liu and H. H. Girault, Energy Environ. Sci., 2014, 7, 387–392.
17. Y. Zheng, Y. Jiao, L. H. Li, T. Xing, Y. Chen, M. Jaroniec and S. Z. Qiao, ACS Nano, 2014, 8, 5290–5296.
18. W. F. Chen, J. T. Muckerman and E. Fujita, Chem. Commun., 2013, 49, 8896–8909.
19. B. R. Sathe, X. X. Zou and T. Asefa, Catal. Sci. Technol., 2014, 4, 2023–2030.
20. T. Y. Ma, S. Dai, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2014, 53, 7281–7285.
21. G. L. Tian, M. Q. Zhao, D. S. Yu, X. Y. Kong, J. Q. Huang, Q. Zhang and F. Wei, Small, 2014, 10, 2251–2259.
22. J. Q. Tian, Q. Liu, A. M. Asiri, K. A. Alamry and X. P. Sun, ChemSusChem, 2014, 7, 2125–2130.
23. T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102.
24. R. Miao, B. Dutta, S. Sahoo, J. K. He, W. Zhong, S. A. Cetegen, T. Jiang, S. P. Alpay and S. L. Suib, J. Am. Chem. Soc., 2017, 139, 13604–13607.
25. H. T. Wang, H. W. Lee, Y. Deng, Z. Y. Lu, P. C. Hsu, Y. Y. Liu, D. C. Lin and Y. Cui, Nat. Commun., 2015, 6, 7261.
26. Y. Zheng, Y. Jiao, Y. H. Zhu, Q. R. Cai, A. Vasileff, L. H. Li, Y. Han, Y. Chen and S. Z. Qiao, J. Am. Chem. Soc., 2017, 139, 3336–3339.
27. C. Y. Ling, L. Shi, Y. X. Ouyang, X. C. Zeng and J. L. Wang, Nano Lett., 2017, 17, 5133–5139.
28. B. K. Zhang, J. Zhou, Z. L. Guo, Q. Peng and Z. M. Sun, Appl. Surf. Sci., 2020, 500, 144248.
29. Q. Peng, J. Zhou, J. T. Chen, T. Zhang and Z. M. Sun, J. Mater. Chem. A, 2019, 7, 26062–26070.
30. Z. L. Guo, J. Zhou and Z. M. Sun, J. Mater. Chem. A, 2017, 5, 23530–23535.
31. H. M. Zhang, H. M. Xiang, F. Z. Dai, Z. L. Zhang and Y. C. Zhou, J. Mater. Sci. Technol., 2018, 34, 2022–2026.
32. Z. Jiang, P. Wang, X. Jiang and J. J. Zhao, Nanoscale Horiz., 2018, 3, 335–341.
33. L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833–8840.
34. L. T. Alameda, R. W. Lord, J. A. Barr, P. Moradifar, Z. P. Metzger, B. C. Steimle, C. F. Holder, N. Alem, S. B. Sinnott and R. E. Schaak, J. Am. Chem. Soc., 2019, 141, 10852–10861.
35. J. J. Wang, T. N. Ye, Y. T. Gong, J. Z. Wu, N. X. Miao, T. Tada and H. Hosono, Nat. Commun., 2019, 10, 2284.
36. S. Ji, Y. Chen, X. Wang, Z. Zhang, D. Wang and Y. Li, Chem. Rev., 2020, 120, 11900–11955.
37. F. Huang, Y. C. Deng, Y. L. Chen, X. B. Cai, M. Peng, Z. M. Jia, J. L. Xie, D. Q. Xiao, X. D. Wen, N. Wang, Z. Jiang, H. Y. Liu and D. Ma, Nat. Commun., 2019, 10, 4431.
38. L. B. Wang, W. B. Zhang, S. P. Wang, Z. H. Gao, Z. H. Luo, X. Wang, R. Zeng, A. W. Li, H. L. Li, M. L. Wang, X. S. Zheng, J. F. Zhu, W. H. Zhang, C. Ma, R. Si and J. Zeng, Nat. Commun., 2016, 7, 14036.
39. Y. T. Shi, C. Y. Zhao, H. S. Wei, J. H. Guo, S. X. Liang, A. Q. Wang, T. Zhang, J. Y. Liu and T. L. Ma, Adv. Mater., 2014, 26, 8147–8153.
40. J. Y. Liu, ACS Catal., 2017, 7, 34–59.
41. W. Zhang and W. T. Zheng, Adv. Funct. Mater., 2016, 26, 2988–2993.
42. A. Q. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
43. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
46. D. Le, T. B. Rawal and T. S. Rahman, J. Phys. Chem. C, 2014, 118, 5346–5351.
47. A. A. El-Barbary, R. H. Telling, C. P. Ewels, M. I. Heggie and P. R. Briddon, Phys. Rev. B, 2003, 68, 144107.
48. H. Wu, Z. L. Guo, J. Zhou and Z. M. Sun, Appl. Surf. Sci., 2019, 488, 578–585.
49. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
50. C. Y. Lin, L. P. Zhang, Z. H. Zhao and Z. H. Xia, Adv. Mater., 2017, 29, 1606635.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta08630d

‡ These authors contributed equally.

---