Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The density-based many-body expansion for poly-peptides and proteins†
Johannes R.
Vornweg
 ,
Toni M.
Maier
,
Toni M.
Maier
 and
Christoph R.
Jacob
and
Christoph R.
Jacob
 *
*
Technische Universität Braunschweig, Institute of Physical and Theoretical Chemistry, Gaußstraße 17, 38106 Braunschweig, Germany. E-mail: c.jacob@tu-braunschweig.de
First published on 8th April 2025
Abstract
Fragmentation schemes enable the efficient quantum-chemical treatment of large biomolecular systems, and provide an ideal starting point for the development of accurate machine-learning potentials for proteins. Here, we present a fragment-based method that only uses calculations for single-amino acids and their dimers, and is able to reduce the fragmentation error in total energies to ca. 1 kJ mol−1 per amino acid for polypeptides and proteins across different structural motifs. This is achieved by combining a two-body extension of the molecular fractionation with conjugate caps (MFCC) scheme with the density-based many-body expansion (db-MBE), thus extending the applicability of the db-MBE from molecular clusters to polypeptides and proteins.
1 Introduction
Molecular dynamics simulations make it possible to study the structural dynamics of biomolecules in solution, and provide valuable insights into the emergence and mechanisms of biological function.1,2 Conventionally, such simulations rely on classical force fields to model the potential energy surface of biomolecules such as proteins.3–7 In the past decade, considerable efforts were undertaken to extend the time scales of classical molecular dynamics simulations, which made it possible to directly simulate protein folding processes.8–10However, the accuracy of classical force fields is inherently limited,11,12 and the steep increase in computational effort of more accurate quantum-chemical methods makes them rarely applicable to large biomolecules.13,14 For treating excited state phenomena in biological systems15,16 and to study excited-state dynamics,17–20 quantum-chemical methods are mandatory. Fragmentation methods21–30 provide an avenue to decreasing the computational effort of quantum-chemical calculations and to lower its scaling with system size. This is achieved by replacing a calculation for the full system (e.g., a protein) by many small calculations for its fragments (e.g., single amino acids).
Recently, such quantum-chemical fragmentation schemes have been used as reference for the parametrization of machine-learning potentials for polypeptides and proteins.31–34 These methods hold the promise of enabling molecular dynamics simulations on a highly accurate potential energy surface, possibly matching the accuracy of high-level quantum chemistry, and even allow for extensions to excited state dynamics.35–37 However, any machine learning potential can only be as good as the quantum-chemical reference data on which it has been trained. This includes not only the underlying quantum-chemical methods, but also the accuracy of the fragmentation scheme.
Therefore, the development of quantum-chemical fragmentation schemes remains an important research avenue (for recent efforts, see, e.g., ref. 38–49). Such fragmentation schemes should be (a) versatile in both their applicability to complex chemical systems, including proteins, and in their compatibility with quantum-chemical methods for the fragment calculations, (b) only introduce a small error due to the fragmentation while maintaining a reasonable computational cost, and (c) ideally only use a small number of chemically meaningful fragments. In the past years, our research group has pursued two lines of research towards this goal (see Fig. 1).
First, for systems composed of distinct molecular building blocks such als molecular clusters, we have extended the conventional energy-based many-body expansion (eb-MBE)50–52 by a density-based correction, that is derived by performing a many-body expansion of the electron density, and inserting the resulting total density into the total energy functional of density-functional theory (DFT).53 This density-based many-body expansion (db-MBE) can be considered as an ONIOM-style54,55 multilevel method, in which the high-level is provided by the eb-MBE and the low-level is provided by subsystem-DFT.56,57 Previously, we have demonstrated that for water and ion–water clusters, the db-MBE provides accurate and efficient total and relative energies already at the level of a two-body expansion.58–60
Second, for proteins we have extended the (energy-based) molecular fractionation with conjugate caps (eb-MFCC) method to consistently include two-body (dimer) contributions [eb-MFCC-MBE(2)].61 While our eb-MFCC-MBE(2) scheme can be considered as a special case of more general schemes for energy-based many-body expansions with overlapping fragments,41,62,63 it provided a simple and consistent approach for the quantum-chemical calculation of the energy of proteins and of protein–ligand interaction energies.64 The eb-MFCC and eb-MFCC-MBE(2) schemes are particularly attractive as starting point for the parametrization of machine-learning potentials because they use single amino acids as fragments.31,32
However, our tests showed61,64 that while the inclusion of two-body contributions in the MFCC-MBE(2) scheme dramatically reduced the error in protein energies and protein–ligand interaction energies compared to the MFCC scheme, the remaining errors can still be substantial.
In the present work, we thus combine the eb-MFCC-MBE(2) approach with the db-MBE, thereby extending the scope of the db-MBE from molecular clusters to proteins. We apply the resulting db-MFCC-MBE(2) to various test cases and assess its accuracy for total energies of polypeptides and proteins as well as for relative energies of polypeptide conformers.
2 Computational methodology
2.1 eb-MBE and db-MBE
First, we briefly review the eb-MBE,50–52,65–68 considering a cluster consisting of N molecular fragments. Using an n-body expansion, its total energy is approximated as | (1) |
 | (2) |
 | (3) |
 | (4) |
In the same fashion as the total energy, the electron density can be approximated using a many-body expansion as
 | (5) |
 | (6) |
 | (7) |
 | (8) |
Using such a many-body expansion of the electron density, the nth-order db-MBE is then defined as,58
| E(n)db = E[ρ(n)tot] = E(n)eb + ΔE(n)db-eb, | (9) |
| ΔE(n)db-eb = E[ρ(n)tot] −E(n)eb. | (10) |
| ΔE(n)db-eb[ρi1,ρi1i2,…] = (Vnuc[ρ(n)tot] − V(n)nuc) + (J[ρ(n)tot] − J(n)) + (ENN − E(n)NN) + Tnadd,(n)s[ρi1,ρi1i2,…] + Enadd,(n)xc[ρi1,ρi1i2,…], | (11) |
| Tnadd,(n)s[ρi1,ρi1i2,…] = Ts[ρ(n)tot] − T(n)s | (12) |
| Enadd,(n)xc[ρi1,ρi1i2,…] = Exc[ρ(n)tot] − E(n)xc, | (13) |
2.2 eb-MFCC and eb-MFCC-MBE(2)
The MFCC scheme69–71 has been devised to provide a simple approach for approximating the total energies and electron densities of proteins and to calculate approximate protein–ligand interaction energies.72–76 In its simplest form, the protein is separated into single amino acids by placing cuts across the peptide bonds. The unsaturated bonds are then capped by acetyl (ACE) and N-methylamide groups (NME) (see Fig. 2). Disulfide bridges are similarly cut and capped by methyl sulfide groups.The total energy of a system consisting of N amino acids is then approximated as the sum of all capped fragment energies Efeb from which the sum of all cap molecule energies Eceb is subtracted, leading to the eb-MFCC energy expression
 | (14) |
 is the total energy of the i1-th capped fragment and
is the total energy of the i1-th capped fragment and  is the total energy of the ACE-NME molecule formed from the caps of fragments k1 and k1 + 1. For consistency with the above expressions for the MBE and notational simplicity, we drop the superscript MFCC and refer to the above first-order approximation for the total energy as E(1)eb.
is the total energy of the ACE-NME molecule formed from the caps of fragments k1 and k1 + 1. For consistency with the above expressions for the MBE and notational simplicity, we drop the superscript MFCC and refer to the above first-order approximation for the total energy as E(1)eb.
The most important shortcoming of the MFCC scheme is its neglect of intramolecular interactions. Several extensions of the MFCC scheme have been proposed to alleviate this issue77–81 (see also ref. 61 and references therein). One approach for systematically improving the MFCC scheme is its combination with the many-body expansion. To include pairwise interactions (i.e., two-body contributions), fragment–fragment (ff) interaction energies are calculated akin to the second-order eb-MBE. To take account of the accruing interactions between fragments and caps as well as interactions between caps, one additionally needs to account for fragment–cap (fc) and cap–cap (cc) interactions. The resulting eb-MFCC-MBE(2) energy expression reads,61
| EMFCCtot = E(2)eb = E(1)eb + ΔE(2)eb | (15) |
| ΔE(2)eb = ΔEMFCC-MBE(2)tot = ΔEffeb − ΔEfceb + ΔEcceb | (16) |
 | (17) |
 | (18) |
 | (19) |
 (where
(where  is the total energy of the dimer formed from fragment i1 and cap [k1,k1 + 1]). Note that caps neighboring the capped fragments are excluded from the summation by excluding caps with indices k1 = i1 − 2,…,i1 + 1 due to overlapping caps. Finally, the cap–cap contributions are given by
is the total energy of the dimer formed from fragment i1 and cap [k1,k1 + 1]). Note that caps neighboring the capped fragments are excluded from the summation by excluding caps with indices k1 = i1 − 2,…,i1 + 1 due to overlapping caps. Finally, the cap–cap contributions are given by | (20) |
 . Further details can be found in ref. 61, and an extension of the eb-MFCC-MBE(2) scheme to protein–ligand interaction energies has been presented in ref. 64.
. Further details can be found in ref. 61, and an extension of the eb-MFCC-MBE(2) scheme to protein–ligand interaction energies has been presented in ref. 64.
2.3 db-MFCC and db-MFCC-MBE(2)
The MFCC and MFCC-MBE(2) schemes can straightforwardly be extended to the electron density. At first order, the electron density can be approximated as, | (21) |
| Δρ(2)tot = Δρfftot − Δρfctot + Δρcctot | (22) |
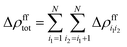 | (23) |
 | (24) |
 | (25) |
By inserting these expansions of the electron density into eqn (9) and (10), we arrive at the energy expressions for the corresponding density-based variants. The db-MFCC energy is given by,
| E(1)db = Edb-MFCCtot = E(1)eb + ΔE(1)db-eb, | (26) |
| E(2)db = Edb-MFCC-MBE(2)tot = E(2)eb + ΔE(2)db-eb. | (27) |
The density-based correction can be evaluated using eqn (11), where for the many-body expansions of the individual energy terms, the more general definition including the contributions of the cap is used. We note that the first-order density-based correction is equivalent to the interaction energy appearing in the generalization of subsystem DFT to the MFCC partitioning.81 Further details are given in Section S1.2 of the ESI.†
2.4 Implementation and computational details
The db-MFCC-MBE(2) method as described above has been implemented in the PyADF scripting framework82 and its PyEmbed module,83 based on the existing implementations of the eb-MFCC-MBE(2) scheme61 and of the db-MBE.53,58 The implementation follows what has been described in our previous publications. The source code of PyADF 1.5, which is suitable for all calculations presented in this work, is available as open source software at ref. 84.The structures of all considered proteins have been obtained from the protein data bank. Hydrogen atoms were added using OpenBabel,85,86 considering a neutral protonation state for each amino acids. In the process of partitioning the proteins, ACE-NME caps are added using the original positions for all cap atoms that are already present in the protein, while the remaining hydrogen atoms of the methyl groups are added using a fixed C–H bond distance of 1.07 Å. Disulfide bridges between amino acids are capped with methylsulfide groups. The resulting dimethyldisulfide cap molecules are treated analogously to the other cap molecules in the many-body corrections.
All quantum-chemical calculations have been performed using density-functional theory (DFT) with the Amsterdam Density Functional (ADF) program87 in the Amsterdam Modeling Suite (AMS)88 with the BP86 exchange-correlation functional89,90 and a DZP basis set.91 In all calculations, we used a Becke integration grid of “normal” accuracy.92 All total energies have been obtained with ADF's total energy implementation.93 These technical settings have previously been tested in the context of the db-MBE.53,58
In the eb-MFCC-MBE(2) and db-MFCC-MBE(2) calculations, a distance cut-off of 4 Å has been used, i.e., calculations for dimers that are further apart than this cutoff are skipped.61 The choice of the cut-off is based on our previous tests in ref. 61. The evaluation of the different terms in the density-based energy correction for db-MFCC and db-MFCC-MBE(2) has been implemented as described in ref. 58. All these terms have been evaluated using the supermolecular numerical integration grid. In the evaluation of the Coulomb contributions, the corrections necessary for ADF's fitted density are included consistently.93,94 Again, these settings have previously shown to be adequate for db-MBE calculation of molecular clusters.53,58 For evaluating the nonadditive exchange–correlation and kinetic energy functionals, the XCFun library95,96 was used, and the BP86 and PW91k97 functionals were applied.
3 Results and discussion
3.1 Alanine polypeptides
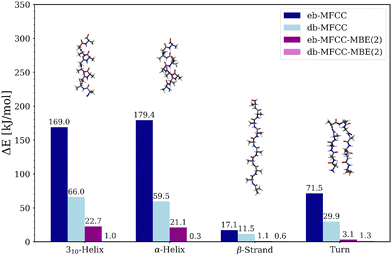
As our initial test case, we consider four alanine polypeptides as idealized models for different secondary structure elements. The test set comprises (Ala)10 in a 310-helix conformation, as an α-helix, and as a β-strand, as well as (Ala)11 featuring a turn between two antiparallel strands, as model of a β-sheet (see insets in Fig. 3). Each of these models was constructed by assuming idealized backbone angles for the respective secondary structure element. These model polypeptides were previously considered in ref. 61.In Fig. 3, the absolute errors in the total energy compared to a supermolecular DFT calculation are plotted for both the eb-MFCC and eb-MFCC-MBE(2) schemes and for the corresponding density-based extensions of these schemes. In all cases, the conventional eb-MFCC scheme leads to rather large errors. For the two helices, the errors of 169 and 179 kJ mol−1 demonstrate the need of accounting for intramolecular interactions. For the turn, the error is smaller because there are fewer intramolecular hydrogen bonds, but with 72 kJ mol−1, it is still substantial. Even for the β-strand, in which no intramolecular hydrogen bonds are present, the error still amounts to 17 kJ mol−1.
Including two-body contributions in the eb-MFCC-MBE(2) reduces these error significantly (see also ref. 61). For the β-strand and the turn, this is sufficient to reduce the errors to 1.1 and 3.1 kJ mol−1, respectively, whereas for the 310-helix and the α-helix, errors of 22.7 and 21.1 kJ mol−1, respectively, remain. In the latter case, each peptide group in the center of the helix is involved in two hydrogen bonds, such that these intramolecular interactions are not fully captured by a two-body approximation.
For both MFCC and MFCC-MBE(2), adding the density-based correction lowers the error significantly. For the db-MFCC scheme, the errors for the 310-helix and the α-helix are reduced to 66 and 60 kJ mol−1, respectively, while for the β-strand and the turn, they are reduced to 12 and 30 kJ mol−1, respectively. When including two-body contributions in the db-MFCC-MBE(2) scheme, the calculations become virtually exact, with errors between 0.3 and 1.3 kJ mol−1 in the total energies. This demonstrates that the density-based correction is able to account for higher-order contributions, that would only appear at third or higher orders in the energy-based expansion.
3.2 Proteins
As a next step, we applied the methods previously tested to a broad range of proteins, which we assembled by considering test cases studied previously with quantum-chemical fragmentation methods73,98,99 as well as a search of the protein data bank for suitable proteins with a size that is still amenable to a supermolecular DFT calculation.Our test set includes human insulin (PDB-code 3I40,100 51 amino acids, 784 atoms), SEM5 SH3 domain (PDB-code 3SEM,101 58 amino acids, 945 atoms), the C-terminal domain of the ribosomal protein L7/L12 (PDB code 1CTF,102 68 amino acids, 1005 atoms), the C-terminal domain of RecA protein (PDB-code 1AA3,103 63 amino acids, 1017 atoms), ubiquitin (PDB-code 1UBQ,104 76 amino acids, 1231 atoms), the FADD (Mort1) death-effector domain (PDB-code 1A1W,105 83 amino acids, 1363 atoms), the immunophilin immunosuppressant complex FKBP-FK506 (PDB code 1FKF,106 107 amino acids, 1662 atoms), the MTCP-1 protein involved in T-cell malignancies (PDB-code 1A1X,107 106 amino acids, 1742 atoms), and the catalytic core domain of FIV integrase (PDB-code 4PA1,108 151 amino acids, 2378 atoms). Of these test cases, 3I40, 3SEM, 1CTF, 1UBQ, 1FKF, and 4PA1 have been used previously by us in ref. 61 to assess the accuracy of the energy-based MFCC and MFCC-MBE(2) schemes, whereas 1AA3, 1A1W, and 1AX1 have been added here.
For this test set of proteins, Fig. 4 plots the absolute errors per amino acid in the total energy compared to supermolecular calculations for the energy-based and density-based MFCC and MFCC-MBE(2) schemes. For better comparison, the errors have been normalized to the number of amino acids in the proteins. The corresponding plot of the unnormalized absolute errors is shown in Fig. S1 in the ESI.†
In agreement with our results for smaller polypeptides, the eb-MFCC scheme leads to unacceptably large errors. For 1AA3 and 1CTF, the error amounts to 42 and 18 kJ mol−1 per amino acid, while for 3I40, 1UBQ, 1A1W, 1FKF, 1A1X, and 4PA1 we find errors between 5 and 14 kJ mol−1 per amino acid. For 3SEM, the error is close to zero, which must be due to fortunate error cancelation in this specific case. As already observed previously,61 the inclusion of two-body contributions in the eb-MFCC-MBE(2) scheme is able to reduce the error significantly, and we find errors between 1.0 and 4.7 kJ mol−1 per amino acid, with the exception of 3SEM, for which the error remains close to zero.
The inclusion of the density-based correction in the db-MFCC scheme is able to reduce the errors substantially compared to the eb-MFCC scheme, resulting in errors per amino acid between 5 and 9 kJ mol−1, again with the exception of 3SEM. While this is a substantial improvement—in particular when considering that no additional fragment calculations are required for evaluation the density-based correction on top of the eb-MFCC—the remaining errors show that the db-MFCC can only partially capture the two-body and higher-order interactions.
However, when including two-body contributions in the db-MFCC-MBE(2) scheme, the errors per amino acid are reduced to below 1.5 kJ mol−1. In most cases, this amounts to a reduction of the error by roughly a factor of two, but in cases such as 1CTF, where the error of the eb-MFCC-MBE(2) was particularly large, even larger reductions are observed. In all cases, the absolute error per amino acid is below the threshold of chemical accuracy (4 kJ mol−1).
Notably, for 3SEM, for which the eb-MFCC-MBE(2) scheme already resulted in an error of close to zero, the error increases when including the density-based correction. This is consistent with the assumption that the excellent performance of the eb-MFCC and eb-MFCC-MBE(2) schemes in this particular case is due to fortunate error cancellation. Finally, we note that for the db-MFCC-MBE(2) scheme, the largest error per amino acid (3.5 kJ mol−1) is found for 3I40, where the error also increases compared to the eb-MFCC-MBE(2) scheme. Again, this seems to be due to fortunate error cancellation in the energy-based expansions. Likely, the inclusion of additional two-body terms (that are neglected due to distance-based screening) and/or of three-body contributions will rectify this.
Overall, we find that the inclusion of the density-based correction on top of the eb-MFCC-MBE(2) scheme, which generally reduces the error in the total energies of the considered proteins, and for most test cases leads to an agreement with full supermolecular calculations within ca. 1 kJ mol−1 per amino acid.
3.3 Relative energies for polypeptides
While the above test cases only consider a single point on the potential energy surface (i.e., a fixed protein structure), molecular dynamics simulations require a balanced description of the low-energy regions of the potential energy surface. This is particularly relevant if quantum-chemical fragmentation methods are to be used for the parametrization of machine learning potentials with the aim to replace classical biomolecular force fields.To assess the accuracy of the considered energy-based and density-based fragmentation schemes across different regions of the potential energy surface, we consider relative energies of three different sets of conformers, specifically (Ala)10 as α-helix, (Ala)11 as a turn (modeling a β-sheet structure), and (Ala)10 as a β-strand. For each set, 11 (for the α-helix and the turn) or 9 (for the β-strand) snapshots extracted from molecular dynamics simulations with a classical force field (see ref. 109 and 110 for details) have been used.
Fig. 5(a) compares the absolute errors in the total energies for eleven conformers of α-helical (Ala)10. The eb-MBFCC and eb-MFCC-MBE(2) schemes lead to large absolute errors that vary widely across the different conformers. With eb-MFCC-MBE(2) we find absolute errors between 35 and 65 kJ mol−1. However, the inclusion of the density-based correction in the db-MFCC-MBE(2) scheme is able to reduce the error consistently, with the largest errors (9.9 and 11.2 kJ mol−1) found for conformers 09 and 10.
The relative energies of the conformers are visualized in Fig. 5(b). Here, it is obvious that neither the eb-MFCC nor the db-MFCC scheme can reproduce the energy pattern correctly. The eb-MFCC-MBE(2) scheme shows a better trend, but still gets many relative energies wrong. The db-MFCC-MBE(2) scheme is able to rectify these shortcomings and closely follows the trend of the single-point reference calculations. Nevertheless, there are still some outliers, in particular for conformers 09 and 10 that also showed the largest absolute errors. Here, it is interesting to note that while for the other schemes there is significant error cancellation when considering the relative energies (i.e., all errors in the total energies have the same sign), this is not the case for the db-MFCC-MBE(2) results, where positive and negative errors in the total energies amplify when comparing relative energies.
For the (Ala)11 turn, the absolute errors in the total energies for eleven conformers are compared in Fig. 6(a). Compared to the α-helical conformers, these absolute errors are significantly smaller, since there are fewer intramolecular interactions. Once two-body contributions are included the absolute errors are below 15 kJ mol−1 for all conformers, both with eb-MFCC-MBE(2) and with db-MFCC-MBE(2). While for some conformers, the density-based scheme is able to reduce the error to close to zero, for other conformers it yields errors comparable to or even slightly worse than the energy-based scheme.
In the plot of the corresponding relative energies of the conformers in Fig. 6(b), we recognize that the eb-MFCC and db-MFCC cannot reproduce the energy ordering of the conformers correctly, even though they partly follow the correct trend. The relative energies from the eb-MFCC-MBE(2) and db-MFCC-MBE(2) schemes both closely follow the supermolecular reference, with a visually better agreement for the energy-based scheme. The db-MFCC-MBE(2) are shifted to higher relative energies, which is to a large part caused by the calculation for the lowest-energy conformer, and shows outliers for conformers 00, 01, and 02.
Finally, Fig. 7 compares the absolute errors in the total energies as well as the relative energies for nine conformers of a (Ala)10 β-strand. Here, the differences in the absolute errors for the eb-MFCC and the db-MFCC scheme are even more pronounced than for the turn structures. The inclusion of two-body contributions reduces the errors substantially in both the energy-based and the density-based schemes. Both eb-MFCC-MBE(2) and db-MFCC-MBE(2) result in similar absolute errors, which fall between 0 and 9 kJ mol−1. While neither eb-MFCC nor db-MFCC are able to reproduce the relative energies correctly, both the eb-MFCC-MBE(2) and db-MFCC-MBE(2) show a good agreement of the overall energy patterns.
Across all three structures, only the db-MFCC-MBE(2) scheme is able to provide consistent relative energies for the different polypeptide conformers. In cases with strong intramolecular interactions, such as those present in the α-helical structures, the inclusion of the density-based correction is essential for an accurate description of these interactions. For the turn and β-strand structures, the intermolecular interactions can largely be captured already with the eb-MFCC-MBE(2) scheme.
4 Conclusions
We have combined the eb-MFCC-MBE(2) scheme, which is a simple fragmentation method for proteins that includes a consistent two-body correction, with the density-based many-body expansion previously developed for molecular clusters. The db-MBE provides a density-based correction to the total energy, which can be calculated from only the electron densities of the considered fragments, i.e., no additional quantum-chemical calculations are required.For the considered test cases, we could demonstrate that the inclusion of such a density-based correction improved the accuracy considerably, while adding little computational overhead. For idealized polypeptide structures, the db-MFCC-MBE(2) scheme is able to bring down the fragmentation errors to ca. 1 kJ mol−1 for all considered secondary structure elements. For proteins, we are able to reach errors below 1 kJ mol−1 per amino acid. However, these still correspond to substantial errors in the total energies of the proteins, even though the db-MFCC-MBE(2) scheme clearly improves upon the corresponding energy-based scheme.
When considering the relative energies of polypeptides, the db-MFCC-MBE(2) scheme is the only method that is able to consistently provide accurate energies across all considered structural motifs. This underlines the potential of the db-MFCC-MBE(2) scheme as starting point for the parametrization of machine-learning potentials for the use in molecular dynamics simulations of ground and excited states.
While in the present work, we only combined the db-MFCC-MBE(2) scheme with DFT calculations, it is not limited to specific quantum-chemical methods. The scheme presented here is straightforward to generalize to highly accurate wavefunction-based methods, such as coupled-cluster theory, as previously demonstrated for molecular clusters.60
Similarly, our density-based approach is not limited to the MFCC-MBE(2) scheme, but can be combined with any energy-based fragmentation method. Therefore, it might be worthwhile to explore the effect of different fragmentation and capping schemes on the fragmentation error.
For further improving the accuracy of the fragmentation method presented here, the combination with a suitable embedding scheme for the fragment calculations seems most promising. Here, we plan to explore both a point-charge embedding as well as the density-based 3-FDE scheme.81 Finally, the extension of the eb-MFCC-MBE and db-MFCC-MBE schemes to higher orders in the many-body expansion is straightforward.
Author contributions
Johannes R. Vornweg: methodology (lead), software (lead), visualization (lead), writing – original draft (lead), writing – review and editing (equal); Toni M. Maier: methodology (supporting), software (supporting), writing – original draft (supporting), writing – review and editing (equal); Christoph R. Jacob: conceptualization (lead), methodology (supporting), software (supporting), writing – review and editing (equal).Data availability
Data for this paper, including PDB files of all considered molecular structures, Jupyter notebooks for data analysis (including all raw data) and for generating all figures, as well as PyADF input scripts to perform the eb-MFCC, db-MFCC, eb-MFCC-MBE(2) and db-MFCC-MBE(2) calculations, are available in Zenodo at https://doi.org/10.5281/zenodo.14884143 (ref. 111).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been conducted within the doctoral programme “Drug Discovery and Cheminformatics for New Anti-Infectives (iCA)” and was financially supported by the Ministry for Science & Culture of the German State of Lower Saxony (MWK no. 21 – 78904-63-5/19).Notes and references
- M. Karplus and J. A. McCammon, Molecular dynamics simulations of biomolecules, Nat. Struct. Biol., 2002, 9, 646–652 Search PubMed.
- R. O. Dror, R. M. Dirks, J. P. Grossman, H. Xu and D. E. Shaw, Biomolecular Simulation: A Computational Microscope for Molecular Biology, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed.
- J. W. Ponder and D. A. Case, Advances in Protein Chemistry, Vol. 66 of Protein Simulations, Academic Press, 2003, pp. 27–85 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 Search PubMed.
- X. Zhu, P. E. M. Lopes and A. D. MacKerell Jr, Recent developments and applications of the CHARMM force fields, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 167–185 Search PubMed.
- P. S. Nerenberg and T. Head-Gordon, New developments in force fields for biomolecular simulations, Curr. Opin. Struct. Biol., 2018, 49, 129–138 Search PubMed.
- O. T. Unke, D. Koner, S. Patra, S. Käser and M. Meuwly, High-dimensional potential energy surfaces for molecular simulations: from empiricism to machine learning, Mach. Learn.: Sci. Technol., 2020, 1, 013001 Search PubMed.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Atomic-Level Characterization of the Structural Dynamics of Proteins, Science, 2010, 330, 341–346 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, How Fast-Folding Proteins Fold, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, Atomic-level description of ubiquitin folding, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5915–5920 Search PubMed.
- S. Piana, J. L. Klepeis and D. E. Shaw, Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations, Curr. Opin. Struct. Biol., 2014, 24, 98–105 CrossRef CAS PubMed.
- P. Dauber-Osguthorpe and A. T. Hagler, Biomolecular force fields: where have we been, where are we now, where do we need to go and how do we get there?, J. Comput.-Aided Mol. Des., 2019, 33, 133–203 CrossRef CAS PubMed.
- K. M. Merz, Using Quantum Mechanical Approaches to Study Biological Systems, Acc. Chem. Res., 2014, 47, 2804–2811 CrossRef CAS PubMed.
- Q. Cui, Perspective: Quantum mechanical methods in biochemistry and biophysics, J. Chem. Phys., 2016, 145, 140901 Search PubMed.
- C. König and J. Neugebauer, Quantum Chemical Description of Absorption Properties and Excited-State Processes in Photosynthetic Systems, ChemPhysChem, 2012, 13, 386–425 CrossRef PubMed.
- C. Curutchet and B. Mennucci, Quantum Chemical Studies of Light Harvesting, Chem. Rev., 2017, 117, 294–343 CrossRef CAS PubMed.
- M. Barbatti, Nonadiabatic dynamics with trajectory surface hopping method, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633 CAS.
- C. M. Marian, Spin–orbit coupling and intersystem crossing in molecules, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- S. Mai, P. Marquetand and L. González, A general method to describe intersystem crossing dynamics in trajectory surface hopping, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin-Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Fragmentation Methods: A Route to Accurate Calculations on Large Systems, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- M. A. Collins, M. W. Cvitkovic and R. P. A. Bettens, The Combined Fragmentation and Systematic Molecular Fragmentation Methods, Acc. Chem. Res., 2014, 47, 2776–2785 CrossRef CAS PubMed.
- S. R. Pruitt, C. Bertoni, K. R. Brorsen and M. S. Gordon, Efficient and Accurate Fragmentation Methods, Acc. Chem. Res., 2014, 47, 2786–2794 CrossRef CAS PubMed.
- N. Sahu and S. R. Gadre, Molecular Tailoring Approach: A Route for ab Initio Treatment of Large Clusters, Acc. Chem. Res., 2014, 47, 2739–2747 CrossRef CAS PubMed.
- K. Raghavachari and A. Saha, Accurate Composite and Fragment-Based Quantum Chemical Models for Large Molecules, Chem. Rev., 2015, 115, 5643–5677 CrossRef CAS PubMed.
- M. A. Collins and R. P. A. Bettens, Energy-Based Molecular Fragmentation Methods, Chem. Rev., 2015, 115, 5607–5642 CrossRef CAS PubMed.
- Fragmentation: Toward Accurate Calculations on Complex Molecular Systems, ed. M. S. Gordon, Wiley, Hoboken, NJ, 1st edn, 2017 Search PubMed.
- D. G. Fedorov, The fragment molecular orbital method: theoretical development, implementation in GAMESS, and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1322 Search PubMed.
- U. Bozkaya and B. Ermis, Linear-Scaling Systematic Molecular Fragmentation Approach for Perturbation Theory and Coupled-Cluster Methods, J. Chem. Theory Comput., 2022, 18, 5349–5359 CrossRef CAS PubMed.
- J. Liu and X. He, Recent advances in quantum fragmentation approaches to complex molecular and condensed-phase systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1650 CAS.
- Y. Han, Z. Wang, Z. Wei, J. Liu and J. Li, Machine learning builds full-QM precision protein force fields in seconds, Briefings Bioinf., 2021, 22, bbab158 CrossRef PubMed.
- Z. Cheng, J. Du, L. Zhang, J. Ma, W. Li and S. Li, Building quantum mechanics quality force fields of proteins with the generalized energy-based fragmentation approach and machine learning, Phys. Chem. Chem. Phys., 2022, 24, 1326–1337 RSC.
- O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel, S. Kashubin, D. Ahlin, M. Gastegger, L. Medrano Sandonas, J. T. Berryman, A. Tkatchenko and K.-R. Müller, Biomolecular dynamics with machine-learned quantum-mechanical force fields trained on diverse chemical fragments, Sci. Adv., 2024, 10, eadn4397 CrossRef CAS PubMed.
- T. Wang, X. He, M. Li, Y. Li, R. Bi, Y. Wang, C. Cheng, X. Shen, J. Meng, H. Zhang, H. Liu, Z. Wang, S. Li, B. Shao and T.-Y. Liu, Ab initio characterization of protein molecular dynamics with AI2BMD, Nature, 2024, 635, 1019–1027 CrossRef CAS PubMed.
- J. Westermayr, M. Gastegger, M. F. S. J. Menger, S. Mai, L. González and P. Marquetand, Machine learning enables long time scale molecular photodynamics simulations, Chem. Sci., 2019, 10, 8100–8107 RSC.
- J. Westermayr and P. Marquetand, Machine learning and excited-state molecular dynamics, Mach. Learn.: Sci. Technol., 2020, 1, 043001 Search PubMed.
- J. Westermayr and P. Marquetand, Machine Learning for Electronically Excited States of Molecules, Chem. Rev., 2021, 121, 9873–9926 CrossRef CAS PubMed.
- S. P. Veccham, J. Lee and M. Head-Gordon, Making many-body interactions nearly pairwise additive: The polarized many-body expansion approach, J. Chem. Phys., 2019, 151, 194101 CrossRef PubMed.
- K.-Y. Liu and J. M. Herbert, Energy-Screened Many-Body Expansion: A Practical Yet Accurate Fragmentation Method for Quantum Chemistry, J. Chem. Theory Comput., 2020, 16, 475–487 CrossRef PubMed.
- T. C. Ricard, A. Kumar and S. S. Iyengar, Embedded, graph-theoretically defined many-body approximations for wavefunction-in-DFT and DFT-in-DFT: Applications to gas- and condensed-phase ab initio molecular dynamics, and potential surfaces for quantum nuclear effects, Int. J. Quantum Chem., 2020, 120, e26244 CrossRef CAS.
- J. Hellmers and C. König, A unified and flexible formulation of molecular fragmentation schemes, J. Chem. Phys., 2021, 155, 164105 CrossRef CAS PubMed.
- J. Hellmers, E. D. Hedegård and C. König, Fragmentation-Based Decomposition of a Metalloenzyme–Substrate Interaction: A Case Study for a Lytic Polysaccharide Monooxygenase, J. Phys. Chem. B, 2022, 126, 5400–5412 CrossRef CAS PubMed.
- S. S. Khire, N. D. Gurav, A. Nandi and S. R. Gadre, Enabling Rapid and Accurate Construction of CCSD(T)-Level Potential Energy Surface of Large Molecules Using Molecular Tailoring Approach, J. Phys. Chem. A, 2022, 126, 1458–1464 CrossRef CAS PubMed.
- D. R. Broderick and J. M. Herbert, Scalable generalized screening for high-order terms in the many-body expansion: Algorithm, open-source implementation, and demonstration, J. Chem. Phys., 2023, 159, 174801 CrossRef CAS PubMed.
- E. Masoumifeshani and T. Korona, AROFRAG-A Systematic Approach for Fragmentation of Aromatic Molecules, J. Chem. Theory Comput., 2024, 20, 1078–1095 CrossRef CAS PubMed.
- S. S. Khire, T. Nakajima and S. R. Gadre, Cluster-in-Cluster Approach for Computing MP2-Level Vibrational Infrared Spectra of Large Molecular Clusters, J. Phys. Chem. A, 2024, 128, 3703–3710 CrossRef CAS PubMed.
- M. P. Hoffman and S. S. Xantheas, The Many-Body Expansion for Aqueous Systems Revisited: IV. Stabilization of Halide–Anion Pairs in Small Water Clusters, J. Phys. Chem. A, 2024, 128, 9876–9892 CrossRef CAS PubMed.
- B. Dehariya, M. B. Ahirwar, A. Shivhare and M. M. Deshmukh, Appraisal of the Fragments-In-Fragments Method for the Energetics of Individual Hydrogen Bonds in Molecular Crystals, J. Comput. Chem., 2025, 46, e70008 Search PubMed.
- P. E. Bowling, D. R. Broderick and J. M. Herbert, Convergent Protocols for Computing Protein–Ligand Interaction Energies Using Fragment-Based Quantum Chemistry, J. Chem. Theory Comput., 2025, 21, 951–966 CrossRef CAS PubMed.
- J. Cui, H. Liu and K. D. Jordan, Theoretical Characterization of the (H2O)21 Cluster: Application of an n-body Decomposition Procedure, J. Phys. Chem. B, 2006, 110, 18872–18878 Search PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, Understanding the many-body expansion for large systems. I. Precision considerations, J. Chem. Phys., 2014, 141, 014108 CrossRef PubMed.
- J. M. Herbert, Fantasy versus reality in fragment-based quantum chemistry, J. Chem. Phys., 2019, 151, 170901 CrossRef PubMed.
- D. Schmitt-Monreal and Ch. R. Jacob, Frozen-density embedding-based many-body expansions, Int. J. Quantum Chem., 2020, 120, e26228 Search PubMed.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, The ONIOM method: its foundation and applications to metalloenzymes and photobiology, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350 CAS.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- Ch. R. Jacob and J. Neugebauer, Subsystem density-functional theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 325–362 CAS.
- Ch. R. Jacob and J. Neugebauer, Subsystem density-functional theory (update), Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1700 CAS.
- D. Schmitt-Monreal and Ch. R. Jacob, Density-Based Many-Body Expansion as an Efficient and Accurate Quantum-Chemical Fragmentation Method: Application to Water Clusters, J. Chem. Theory Comput., 2021, 17, 4144–4156 CrossRef CAS PubMed.
- S. Schürmann, J. R. Vornweg, M. Wolter and Ch. R. Jacob, Accurate quantum-chemical fragmentation calculations for ion–water clusters with the density-based many-body expansion, Phys. Chem. Chem. Phys., 2023, 25, 736–748 RSC.
- K. Focke and Ch. R. Jacob, Coupled-Cluster Density-Based Many-Body Expansion, J. Phys. Chem. A, 2023, 127, 9139–9148 CrossRef CAS PubMed.
- J. R. Vornweg, M. Wolter and Ch. R. Jacob, A simple and consistent quantum-chemical fragmentation scheme for proteins that includes two-body contributions, J. Comput. Chem., 2023, 44, 1634–1644 CrossRef CAS PubMed.
- N. J. Mayhall and K. Raghavachari, Many-Overlapping-Body (MOB) Expansion: A Generalized Many Body Expansion for Nondisjoint Monomers in Molecular Fragmentation Calculations of Covalent Molecules, J. Chem. Theory Comput., 2012, 8, 2669–2675 CrossRef CAS PubMed.
- R. M. Richard and J. M. Herbert, A generalized many-body expansion and a unified view of fragment-based methods in electronic structure theory, J. Chem. Phys., 2012, 137, 064113 CrossRef PubMed.
- J. R. Vornweg and Ch. R. Jacob, Protein–Ligand Interaction Energies from Quantum-Chemical Fragmentation Methods: Upgrading the MFCC-Scheme with Many-Body Contributions, J. Phys. Chem. B, 2024, 128, 11597–11606 CrossRef CAS PubMed.
- H. Stoll and H. Preuß, On the direct calculation of localized HF orbitals in molecule clusters, layers and solids, Theor. Chim. Acta, 1977, 46, 11–21 CrossRef CAS.
- I. G. Kaplan, Theory of molecular interactions, Elsevier, Amsterdam, 1986 Search PubMed.
- K. Rościszewski, B. Paulus, P. Fulde and H. Stoll, Ab initio calculation of ground-state properties of rare-gas crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7905–7910 CrossRef.
- K.-Y. Liu and J. M. Herbert, Understanding the many-body expansion for large systems. III. Critical role of four-body terms, counterpoise corrections, and cutoffs, J. Chem. Phys., 2017, 147, 161729 CrossRef PubMed.
- D. W. Zhang and J. Z. H. Zhang, Molecular fractionation with conjugate caps for full quantum mechanical calculation of protein–molecule interaction energy, J. Chem. Phys., 2003, 119, 3599–3605 CrossRef CAS.
- X. H. Chen, D. W. Zhang and J. Z. H. Zhang, Fractionation of peptide with disulfide bond for quantum mechanical calculation of interaction energy with molecules, J. Chem. Phys., 2004, 120, 839 CrossRef CAS PubMed.
- M. Xu, X. He, T. Zhu and J. Z. H. Zhang, A Fragment Quantum Mechanical Method for Metalloproteins, J. Chem. Theory Comput., 2019, 15, 1430–1439 CrossRef CAS PubMed.
- A. M. Gao, D. W. Zhang, J. Z. H. Zhang and Y. Zhang, An efficient linear scaling method for ab initio calculation of electron density of proteins, Chem. Phys. Lett., 2004, 394, 293–297 CrossRef CAS.
- J. Antony and S. Grimme, Fully ab initio protein-ligand interaction energies with dispersion corrected density functional theory, J. Comput. Chem., 2012, 33, 1730–1739 CrossRef CAS PubMed.
- X. He, T. Zhu, X. Wang, J. Liu and J. Z. H. Zhang, Fragment Quantum Mechanical Calculation of Proteins and Its Applications, Acc. Chem. Res., 2014, 47, 2748–2757 CrossRef CAS PubMed.
- J. Liu, X. Wang, J. Z. H. Zhang and X. He, Calculation of protein–ligand binding affinities based on a fragment quantum mechanical method, RSC Adv., 2015, 5, 107020 RSC.
- J. Liu, T. Zhu, X. He and J. Z. H. Zhang, Fragmentation, John Wiley & Sons, Ltd, 2017, pp. 323–348 Search PubMed.
- X. He and J. Z. H. Zhang, The generalized molecular fractionation with conjugate caps/molecular mechanics method for direct calculation of protein energy, J. Chem. Phys., 2006, 124, 184703 CrossRef PubMed.
- N. Jiang, J. Ma and Y. Jiang, Electrostatic field-adapted molecular fractionation with conjugated caps for energy calculations of charged biomolecules, J. Chem. Phys., 2006, 124, 114112 CrossRef PubMed.
- X. Wang, J. Liu, J. Z. H. Zhang and X. He, Electrostatically Embedded Generalized Molecular Fractionation with Conjugate Caps Method for Full Quantum Mechanical Calculation of Protein Energy, J. Phys. Chem. A, 2013, 117, 7149–7161 CrossRef CAS PubMed.
- J. Liu, T. Zhu, X. Wang, X. He and J. Z. H. Zhang, Quantum Fragment Based ab Initio Molecular Dynamics for Proteins, J. Chem. Theory Comput., 2015, 11, 5897–5905 CrossRef CAS PubMed.
- Ch. R. Jacob and L. Visscher, A subsystem density-functional theory approach for the quantum chemical treatment of proteins, J. Chem. Phys., 2008, 128, 155102 CrossRef PubMed.
- Ch. R. Jacob, S. M. Beyhan, R. E. Bulo, A. S. P. Gomes, A. W. Götz, K. Kiewisch, J. Sikkema and L. Visscher, PyADF—A scripting framework for multiscale quantum chemistry, J. Comput. Chem., 2011, 32, 2328–2338 CrossRef CAS PubMed.
- K. Focke, M. De Santis, M. Wolter, J. A. Martinez B, V. Vallet, A. S. Pereira Gomes, M. Olejniczak and Ch. R. Jacob, Interoperable workflows by exchanging grid-based data between quantum-chemical program packages, J. Chem. Phys., 2024, 160, 162503 CrossRef CAS PubMed.
- Ch. R. Jacob, T. Bergmann, S. M. Beyhan, J. Brüggemann, R. E. Bulo, M. Chekmeneva, T. Dresselhaus, K. Focke, A. S. P. Gomes, A. W. Goetz, M. Handzlik, K. Kiewisch, M. Klammler, L. Ridder, J. Sikkema, L. Visscher, J. Vornweg, M. O. Welzel and M. Wolter, PyADF Version 1.5, 2024 DOI:10.5281/zenodo.13236550, https://github.com/chjacob-tubs/pyadf-releases/.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An open chemical toolbox, J. Cheminf., 2011, 3, 33 Search PubMed.
- The Open Babel package, Version 2.4.1, https://openbabel.org Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- Software for Chemistry and Materials, Version 2021.201, 2021, Ams, Amsterdam Modelling Suite, Amsterdam, https://www.scm.com Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- M. Franchini, P. H. T. Philipsen and L. Visscher, The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- A. W. Götz, S. M. Beyhan and L. Visscher, Performance of Kinetic Energy Functionals for Interaction Energies in a Subsystem Formulation of Density Functional Theory, J. Chem. Theory Comput., 2009, 5, 3161–3174 CrossRef PubMed.
- D. Schlüns, M. Franchini, A. W. Götz, J. Neugebauer, Ch. R. Jacob and L. Visscher, Analytical gradients for subsystem density functional theory within the slater-function-based amsterdam density functional program, J. Comput. Chem., 2017, 38, 238–249 CrossRef PubMed.
- U. Ekström, L. Visscher, R. Bast, A. J. Thorvaldsen and K. Ruud, Arbitrary-Order Density Functional Response Theory from Automatic Differentiation, J. Chem. Theory Comput., 2010, 6, 1971–1980 CrossRef PubMed.
- U. Ekström, R. Bast, R. Di Remigio, Ch. R. Jacob, S. Reine, J. Juselius, E. Rebolini, A. S. P. Gomes, S. R. Jensen, S. Reimann, A. Borgoo, D. H. Friese, L. Frediani, M. Iliaš, Y. Victorovich and J. Furness, XCFun: Exchange-Correlation functionals with arbitrary order derivatives, Version 2.2.1, 2020 DOI:10.5281/zenodo.4269992, https://github.com/dftlibs/xcfun/tree/v2.1.1.
- A. Lembarki and H. Chermette, Obtaining a gradient-corrected kinetic-energy functional from the Perdew-Wang exchange functional, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 5328–5331 CrossRef CAS PubMed.
- Z. Wang, Y. Han, J. Li and X. He, Combining the Fragmentation Approach and Neural Network Potential Energy Surfaces of Fragments for Accurate Calculation of Protein Energy, J. Phys. Chem. B, 2020, 124, 3027–3035 CrossRef CAS PubMed.
- M. Wolter, M. von Looz, H. Meyerhenke and Ch. R. Jacob, Systematic Partitioning of Proteins for Quantum-Chemical Fragmentation Methods Using Graph Algorithms, J. Chem. Theory Comput., 2021, 17, 1355–1367 CrossRef CAS PubMed.
- V. I. Timofeev, R. N. Chuprov-Netochin, V. R. Samigina, V. V. Bezuglov, K. A. Miroshnikov and I. P. Kuranova, X-ray investigation of gene-engineered human insulin crystallized from a solution containing polysialic acid, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2010, 66, 259–263 CrossRef CAS PubMed.
- J. T. Nguyen, C. W. Turck, F. E. Cohen, R. N. Zuckermann and W. A. Lim, Exploiting the Basis of Proline Recognition by SH3 and WW Domains: Design of N-Substituted Inhibitors, Science, 1998, 282, 2088–2092 CrossRef CAS PubMed.
- M. Leijonmarck and A. Liljas, Structure of the C-terminal domain of the ribosomal protein L7L12 from Escherichia coli at 1.7 Å, J. Mol. Biol., 1987, 195, 555–579 CrossRef CAS PubMed.
- H. Aihara, Y. Ito, H. Kurumizaka, T. Terada, S. Yokoyama and T. Shibata, An interaction between a specified surface of the C-terminal domain of RecA protein and double-stranded DNA for homologous pairing1, J. Mol. Biol., 1997, 274, 213–221 CrossRef CAS PubMed.
- S. Vijay-Kumar, C. E. Bugg and W. J. Cook, Structure of ubiquitin refined at 1.8 Å resolution, J. Mol. Biol., 1987, 194, 531–544 CrossRef CAS PubMed.
- M. Eberstadt, B. Huang, Z. Chen, R. P. Meadows, S.-C. Ng, L. Zheng, M. J. Lenardo and S. W. Fesik, NMR structure and mutagenesis of the FADD (Mort1) death-effector domain, Nature, 1998, 392, 941–945 CrossRef CAS PubMed.
- G. D. Van Duyne, R. F. Standaert, P. A. Karplus, S. L. Schreiber and J. Clardy, Atomic Structure of FKBP-FK506, an Immunophilin-Immunosuppressant Complex, Science, 1991, 252, 839–842 CrossRef CAS PubMed.
- Z.-Q. Fu, G. C. Du Bois, S. P. Song, I. Kulikovskaya, L. Virgilio, J. L. Rothstein, C. M. Croce, I. T. Weber and R. W. Harrison, Crystal structure of MTCP-1: Implications for role of TCL-1 and MTCP-1 in T cell malignancies, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 3413–3418 CrossRef CAS PubMed.
- M. Galilee and A. Alian, Identification of Phe187 as a Crucial Dimerization Determinant Facilitates Crystallization of a Monomeric Retroviral Integrase Core Domain, Structure, 2014, 22, 1512–1519 CrossRef CAS PubMed.
- J. Brüggemann, M. Chekmeneva, M. Wolter and Ch. R. Jacob, Structural Dependence of Extended Amide III Vibrations in Two-Dimensional Infrared Spectra, J. Phys. Chem. Lett., 2023, 14, 9257–9264 Search PubMed.
- A. M. van Bodegraven, K. Focke, M. Wolter and Ch Jacob, Benchmarking of Vibrational Exciton Models Against Quantum-Chemical Localized-Mode Calculations, ChemRxiv, 2024, preprint DOI:10.26434/chemrxiv-2024-s2jgl.
- J. R. Vornweg, T. M. Maier and Ch. R. Jacob, Data Set: The density-based many-body expansion for polypeptides and proteins, 2025 DOI:10.5281/zenodo.15118425.
Footnote |
| † Electronic supplementary information (ESI) available: Explicit expressions for the density-based energy correction in the db-MBE, db-MFCC, and db-MFCC-MBE(2) schemes; additional plot of total absolute errors for the protein test set. See DOI: https://doi.org/10.1039/d5cp00727e |
| This journal is © the Owner Societies 2025 |