In silico cooling rate dependent crystallization and glass transition in n-alkanes

Abstract

n-Alkanes (C_nH_2n+2) are linear chain compounds spanning length-scales from small molecules to polymers. Intermediate length alkanes (say, n = 10–20) have attracted much interest as organic phase change materials (PCM) for storing energy as latent heat. The cooling rate (γ) determines both the latent heat and temperature of crystallization. While slow cooling of the liquid leads to the crystalline state, rapid cooling leads to a glassy state (glass transition temperature T_g). Albeit scant theoretical investigations concerning the vitrification processes, the role of molecular conformations therein remains completely unexplored. Our work presents an all-atom molecular dynamics study of (a) cooling intermediate length alkanes (n = 12 and 16) at seven different rates, and (b) rapidly cooling 14 n-alkanes (4 ≤ n ≤ 50) for determining T_g(n). We find that for linear molecules the end-to-end distance (R_ee) is of special relevance: the crystal is composed solely of fully stretched molecules (maximal R_ee). Hence one may define the “degree of crystallization” as the area under the maximal R_ee peak in the R_ee distribution. Other peaks in the distribution represent conformations that existed in the supercooled liquid just before vitrification. A peak for the shortest, hairpin rotamer appears only for n ≥ n₀ = 18, and is also manifested in the minimum of R_g/R_ee(n) for liquid n-alkanes. The dependence of T_g on n is represented as two intersecting Ueberreiter and Kanig equations, intersecting near n₀ = 18. Extrapolation gives the asymptotic n → ∞ limit of T_g, T^∞_g = 250 K, which is probably its most accurate estimate obtained theoretically todate.

---

1 Introduction

Earth's limited energy resources impel scientists to seek out sustainable energy solutions and reuse the waste heat energy. Current research in this direction involves development of phase change materials (PCMs).¹ PCMs have received immense attention in pharmaceutical, automobile, food industry, data storage and energy storage devices.^2–6 For example, NASA used n-dodecane (C12) and n-hexadecane (C16) as thermal energy storage capsules to control the battery temperature in the rover mission.^7,8 The importance of C16 as a PCM is explained by Sgreva et al.⁹ “Two properties make it attractive for experiments dealing with PCMs: its high latent heat and the fact that the temperature at which the phase change takes place is near the room temperature”. Usage of PCMs reduces emission of greenhouse gases, thereby helping in decarbonization of the environment.

Available PCMs can be categorized as inorganic, organic, and a combination of both. Inorganic PCMs suffer from toxicity, thermal stability deficiency, corrosion and decomposition issues, making them less alluring in applications.^9,10 On the other hand, “organic PCMs, e.g. paraffin and fatty acid, have much more stable thermo-physical properties and more suitable phase transition temperatures for a wide range of applications.”⁹ PCMs work by charging/discharging of the absorbed/released latent heat during solid/solid, solid/liquid, liquid/gas or solid/gas phase transitions. Evidently, the transition temperature depends on the PCM and type of the transition. This allows tuning the temperature range of the PCM response. Among the four transitions, the solid to liquid transition is advantageous due to its inexpensiveness and the small volume change involved. n-Alkanes, owing to their high latent heat yet simple chemical formula (C_nH_2n+2, denoted Cn), are considered to be promising candidates for organic PCMs.^5,9–12 Hence, “from the point of view of toxicity and long-term work stability, alkanes seem to be potentially more valuable.”¹⁰

A disadvantage of n-alkanes as PCMs is their low thermal conductivity (∼0.2 W m⁻¹ K⁻¹) which leads to a slow charging/discharging rate.¹³ This limits experimental studies to low cooling/heating rates, γ ≡ −∂T/∂t = 10⁻² to 10² K s⁻¹,^11,14 where T and t are temperature and time. A slow cooling of liquid PCM will lead to crystallization. Major efforts are made nowadays to speed up the thermal conductivity by various methods,^15–18 and then we expect the dependence on cooling rate to become more conspicuous, possibly leading to vitrification (glass formation) rather than crystallization.

In contrast, computational studies can explore the effects of cooling/heating at extremely high rates. Rapid cooling of a liquid to below its melting temperature, T_m, may circumvent the crystallization process, leading to a metastable equilibrium state known as the supercooled liquid (SCL).¹⁹ A recent computational study²⁰ explored the cooling-rate effect on n-eicosane, C20, with γ = 6 × 10⁹ to 6 × 10¹² K min⁻¹. While slow cooling rates led to the crystal state (crystallinity measure close to 1), cooling faster than a threshold rate of 1.2 × 10¹¹ K min⁻¹ resulted predominantly in the SCL state (crystallinity measure close to 0). However, the cooling process studied there did not explore the conditions under which the SCL might undergo a glass transition.

According to a review by Barrat et al.²¹ (Fig. 2 there), two notable results can be obtained from glass transition experiments and simulations of polymers:

(a) The increase of T_g with γ, which may be described by

This result follows²² from the Vogel–Fulcher–Tammann (VFT) structural relaxation time, once equated to 1/γ. In the VFT equation, C is the activation energy for structural relaxation, hence positive. Consequently, for the second term on the rhs to be positive, the second adjustable parameter, D, must obey Dγ < 1.²³ Finally, T⁰_g is the VFT temperature where, formally, the relaxation time diverges and γ → 0 (see Eq. 3 in Soldera and Metatla²⁴).

(b) The increase of T_g with n may be described by the empirical equation first suggested by Fox and Flory (FF) for polystyrene:²⁵

where A is a constant with units of temperature. T^∞_g denotes T_g in the limit of n → ∞. Alternately, this is a dependence of T_g on the molecular mass, M, which is n times the monomeric mass. The motivation of Fox and Flory in constructing eqn (2) was that vitrification (glass formation) occurs when the molecular free volume, V_f, drops below a certain cutoff. Furthermore, they assumed that the main contribution to V_f comes from the two freely rotating monomers at the chain-ends, of which there are 2/n per monomer. Therefore, increasing n decreases V_f and then vitrification occurs at a higher T_g.

There are several alternatives in the literature for the FF equation. Ueberreiter and Kanig (UK) correlated 1/T_g with 1/n, as follows:²⁶

where B is another n-independent constant. Note that the UK and FF equations cannot both be valid over the whole range of n (from 1 to ∞) because then A/B = T_gT^∞_g, and T_g loses its dependence on n. These equations must thus be valid over only part of the n range.

Once polymer data over a wide range of n have accumulated, it became clear that a single equation, be it FF or UK, cannot explain the complete behavior. Cowie²⁷ and others^28,29 suggested that there were actually three regimes. In regime I:

T_g = A_I + B_I log M (4)

(A_I and B_I are constants), and similarly in regime II, whereas in regime III T_g = T^∞_g.

We found only scant discussions in the literature on glass transition of n-alkanes.^30–34 Miller derived n-alkane T_g values from their experimental viscosities using an empirical relationship.³⁰ Extrapolation to n → ∞ gave T^∞_g ≈ 200 K. Otherwise, current n-alkane T_g data comes from simulations using various united-atom approximations.^31–33 Roe³¹ was able to obtain a T_g(n) that confirms eqn (2), with T^∞_g ≈ 215 K. Martín-Betancourt et al.³² obtained T_g(n) for 2 ≤ n ≤ 10 (but high pressures). In this range T_g does not vary smoothly, hence the authors could not compare it with the FF equation. A machine-learning calculation was recently used for extrapolating the dependence to n = 20.³⁴

Considerably more T_g results are available for linear polyethylene, which identifies with n-alkanes in the large n regime. These have been mostly derived from extrapolations e.g., in eqn (1). From these data one could have obtained T^∞_g for n-alkanes, except that there is a huge scatter in the literature values. Davis and Eby³⁵ collected experimental data for polyethylene showing that “temperatures in a rather wide range [140–340 K] have been reported at one time or another as T_g”. Their best estimate for T_g is 231 K. Ramos et al.³³ performed cooling rate MD simulations of C198 (polyethylene) with two different force fields, confirming eqn (1) with T⁰_g of either 187.0 or 214.1 K (Fig. 7 there).

Here we report all atom cooling-rate MD results for n-alkanes in condensed phases in the small to moderate n range (4 ≤ n ≤ 50). This fills the gap between available T_g values for small alkanes (n < 10)³² and T_g of polyethylene.³³ All-atom simulations of larger alkanes become increasingly time consuming, and are not attempted here.

The first part of this work is devoted to crystallization utilizing volumetric analysis, in which we include the temperature dependence of the density (ρ), radius of gyration (R_g) and end-to-end distance (R_ee). For the latter, a recently proposed mathematical model³⁶ is used to explain the simulation data. We introduce the R_ee distribution, showing that it contains information on the dominant conformations existing in the SCL, just before vitrification. The crystal state includes the single conformation of a stretched alkane (maximal R_ee), and the ratio of its probability to that of the rest of the distribution presents a physically-sound definition for the degree of crystallinity, χ.

Moving on to the glass-transition, we present a novel operational definition of T_g from the density data as the intersection point of two second-order polynomials. The conventional definition involving the intersection of two straight lines is applied only to the enthalpy data. Finally, we discuss the T_g(n) dependencies. First, we confirm that T_g(n) = 2T_m(n)/3, where T_m(n) is the melting point. Finally, we show that two FF/UK relations are required for explaining T_g(n), one in the small-n range and another for medium-n.

2 Simulation protocol

The simulations are divided into two groups: detailed study of C12 and C16 for seven cooling rates, and 12 additional n-alkanes that were subject to cooling only at the 3 fastest cooling rates.

2.1 C12 and C16

100 molecules of either C12 or C16 have been randomly placed within a box of dimensions (40 × 40 × 24) ų and (47 × 47 × 22) ų, respectively with the help of the Packmol³⁷ software. No counterions have been added as the charge of each molecule is zero. Topology and parameter files were generated from CHARMM-GUI,³⁸ using the all-atom CHARMM General Force Field (CGenFF), which represents an extension of the CHARMM all-atom additive force field to non-standard molecules.^39,40 This force field has previously been used in modeling alkane-water mixtures.⁴¹ It nevertheless has limitations, because “all-atom models using a 12-6 Lennard-Jones potential [including CHARMM36] show no rotator phase”, in which crystalline molecules can rotate around their long axis.⁴²

The FF is the sum of several interaction terms for bonded and non-bonded atoms.³⁹ The latter include the Coulomb and Lennard-Jones (LJ) interactions, which require cutoffs for their evaluation. At short ranges, the minimum image convention⁴³ was used to compute the LJ interactions, using a spherical cutoff distance of 10 Å and a switching distance of 8 Å (as compared to switching between 10 and 12 Å in ref. 40). This ensures a smooth truncation of the van der Waals potential to zero at the switching distance. Implementation of such long range cutoffs is essential for obtaining accurate densities in MD simulations.⁴⁴ For the long range interactions, the particle–mesh–Ewald method has been implemented.⁴⁵ All the simulations were performed in the NAMD code (ver. 2.14).⁴⁶

Energy minimization was performed with the conjugate gradient method for 50 000 steps at 0 K. To obtain the liquid phase, the temperature was raised from 0 K (minimized structure) to either 310 K for C12, or 370 K for C16. Note that these temperatures are 50–70 K greater than the melting point, which helps in achieving the liquid phase. In both cases, systems were equilibrated for 5 ns under isochoric isothermal (NVT) conditions followed by another 5 ns under isobaric isothermal (NPT) conditions. It is common to use NVT prior to NPT relaxation,^47–49 which leads to fast thermal convergence in the NVT step, followed by pressure relaxation in the NPT step. For example, an MD simulation study on lipid bilayer showed that, in the absence of the NVT step, enormous pressures may develop at the onset of the NPT step, pushing water molecules into non-physical locations.⁴⁸

Subsequently, 100 ns long production trajectories were generated under the NPT conditions. An integration time step of 2 fs was chosen for equilibration, and 1 fs for the production run. Data was saved every 1 ps. The temperature was controlled by the Langevin thermostat, with a friction constant of 1 ps⁻¹, while the pressure was controlled by the Langevin barostat.⁵⁰ Periodic boundary conditions (PBC) were employed on all faces of the simulation box.

The final coordinates obtained after the 100 ns NPT production runs were used as initial coordinates for cooling back to 10 K at seven different cooling rates (Table 1). In order to do that, we have simulated the systems under NPT conditions, decreasing the temperature in steps of 1 K. These cooling protocols provided the time/temperature dependent coordinates forming the basis for most of the analysis presented herein.

Table 1 The rate [in K min⁻¹] and trajectory length [in ns] implemented during the cooling processes for C12 and C16

Rate, γ	Length, C12	Length, C16
6.0 × 10^13	0.3	0.36
6.0 × 10^12	3	3.6
3.0 × 10^12	6	7.2
1.2 × 10^12	15	18
6.0 × 10^11	30	36
3.0 × 10^11	150	180
6.0 × 10^10	300	360

---

2.2 Additional n-alkanes

In addition to the γ dependence, we also investigate the dependence on the chain length, n. Therefore, we have modelled additional 12 n-alkanes namely, n-butane (C4), n-hexane (C6), n-octane (C8), n-decane (C10), n-tetradecane (C14), n-octadecane (C18), n-eicosane (C20), n-docosane (C22), n-tetracosane (C24), n-triacontane (C30), n-tetracontane (C40) and n-pentacontane (C50). For each n-alkane, 100 molecules were heated above its melting point to get a liquid phase. The box dimensions and heating temperatures for all of the 14 alkanes are given in Table S1 of the ESI.†

For each of the additional 12 alkanes, the target temperature had been achieved with sequential increment of temperature through velocity rescaling with a total duration of 1 ns. Then, equilibration was performed for 5 ns in NVT followed by 5 ns under NPT conditions. We observed convergence in the atomic root mean squared deviation (RMSD) within the 10 ns equilibration process, as seen in Fig. S1 of the ESI,† for C4, C16 and C50 (the short alkanes equilibrating faster than the long ones). Subsequently, a 10 ns production run (vs. 100 ns for C12 and C16) was accomplished under NPT conditions. The final coordinates, obtained after the production run, were subjected to cooling at three rates, γ = 6.0 × 10¹³, 6.0 × 10¹² and 3.0 × 10¹² K min⁻¹ (vs. seven rates for C12 and C16). Three trajectories were generated at each of the three rates, and the average of the three trajectories was used for analysis.

3 Results and discussion

3.1 Density

The snapshots of liquid C12 and C16, obtained at the end of the 100 ns NPT production run, are shown in Fig. S2 (ESI†), colored by their end-to-end distances. It is seen that the liquid state is a mixture of different conformers with different R_ee values, and that the shorter alkane tends to have a larger fraction of linear conformers with maximal R_ee.

The densities of each alkane at the temperatures sampled by the cooling process (10–310 K for C12 and 10–370 K for C16), are shown in Fig. S3 (ESI†) (small γ) and Fig. S4 (ESI†) (large γ, all 14 alkanes). To test for finite size effects on ρ, we have created a larger box (60 × 60 × 140 ų) containing 1000 C16 molecules (instead of 100), cooling it at the fastest rate of γ = 6 × 10¹³ K min⁻¹. The comparison in Fig. S5 (ESI†) shows no effect on the density results. We have also tested the dependence on cubical vs. rectangular boxes for C4 in Fig. S6 (ESI†), also with little or no effect.

For small γ (Fig. S3, ESI†), a regime of abrupt increase in ρ with decreasing T is seen, due to the transition from liquid to crystal (TLC), which is a more tightly packed molecular arrangement, whose molar volume is smaller than the liquid. A linear function is fitted in the TLC regime, where the crystallization temperature, T_c, is defined as the middle of this regime. Second and third-order polynomials are fitted in the high-T (HT) and low-T (LT) regimes, respectively (parameters in Table S2, ESI†). These fits are exemplified in Fig. 1.

Fig. 1 Simulated C12 densities (black lines) for two cooling rates (a) slow cooling, 6 × 10¹⁰ and (b) fast cooling, 6 × 10¹³ K min⁻¹. Polynomial fits are shown (a) in the LT (red line), TLC (green) and HT regimes (purple), which are of third-, first- and second-orders, respectively. (b) second-order polynomial fits in the LT (red) and HT (purple) regimes.

For large γ (Fig. S4, ESI†), there is no abrupt change in ρ, only a change of slope. The glass temperature, T_g, is traditionally determined from the intersection point of two straight lines fitted at the LT and HT regimes. This is demonstrated in Fig. S7 (ESI†) for C12. Unfortunately, when the lower limit of T is as low as 10 K, the linearity assumption for ρ(T) breaks down.

Therefore, for large γ we have proceeded as follows (see also Section S1 in the ESI†): first, we performed the conventional linear fits using the intersection point as a tentative glass transition temperature, (Table S3, ESI†). Then, second-order polynomials were fitted below and above (coefficients in Table S4, ESI†). Their intersection point is our final T_g value.

Our polynomial fits are presented in Fig. 2. They can be considered as a high accuracy representation of our simulation data. In addition, available experimental data⁵¹ for C16 are depicted by the magenta line in panel (b). Note that the experimental studies of n-alkanes are performed at orders of magnitude slower cooling rates.^11,14 Presumably, these slow rates are limited by heat conduction, which is essentially instantaneous in the simulations.

Fig. 2 The fitted polynomials to the temperature dependent density, ρ(T) (in units of kg m⁻³), of (a) C12 and (b) C16 at seven cooling rates each. Filled circles indicate the glass transition temperatures, T_g, where a switch in the polynomial occurs.

According to Ehrenfest's characterization of phase transitions,⁵² a discontinuous jump in one of the Gibbs energy (G) first derivatives defines a “first order” phase transition. A liquid to crystal phase transition is of this type. Here V = (∂G/∂P)_T decreases abruptly upon freezing, hence ρ = m/V increases abruptly (m is the mass = xN₀M, where x and N₀ represent number of moles and Avogadro's number). Indeed, the experimental⁵¹ density data for C16 near the crystallization temperature shows such a discontinuity (Fig. 2b, magenta line). It is in nice agreement with our result at the slowest γ, unlike other simulations in which such an agreement has not been observed (compare Fig. 1a in Nazarychev et al.²⁰).

A second-order phase transition according to the Ehrenfest's classification, involves a discontinuity in one of the second derivatives of G (while its first derivatives are continuous). To show that this is the density derivative with respect to T under constant pressure (as in our production run), we note that

α is the coefficient of thermal expansion. Because V (as a first derivative) is continuous in T, a discontinuity in (∂ρ/∂T)_P at T_g means that the mixed 2nd-derivative of G is discontinuous there.

Fig. 3 shows this derivative (of the polynomial fit) for the four largest cooling rates of C12 (or C16 in Fig. S8, ESI†). It indeed shows a discontinuous jump in (∂ρ/∂T)_P at the temperature identified as T_g. Thus formally, by Ehrenfest's definition, T_g represents a 2nd-order phase transition. This, however, is tantamount to applying thermodynamic logic to non-thermodynamic functions, because the glass transition is a dynamic (rather than equilibrium) transition, separating the SCL from glass-like material.

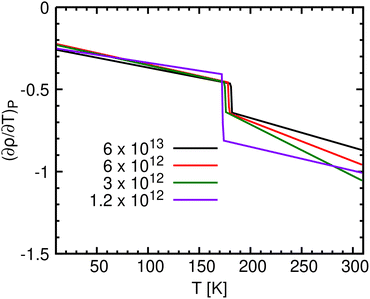Fig. 3 The first partial derivative of ρ with respect to T, (∂ρ/∂T)_P, for C12, obtained by cooling at four different cooling rates, γ [K min⁻¹].

One expects T_g to increase with increasing γ, perhaps obeying eqn (1), as observed both experimentally (for metallic glasses)⁵³ and computationally (e.g., Fig. 5 in Vollmayr et al.⁵⁴). For C12, Fig. 3 shows a minute cooling rate effect on T_g, which is within the error bar of our calculation. However, we show below that for larger n the effect becomes more prominent.

3.2 Radius of gyration and end-to-end distance

Two related measures for distinguishing between crystalline, liquid and glassy phases involve the radius of gyration (R_g) and the end to end distance (R_ee) between the two terminal carbon atoms. Fig. 4a and b show R_g(T) for C12 and C16, respectively, during the seven cooling processes. Similarly, Fig. 4c and d depict R_ee(T) for C12 and C16, respectively. Both R_g and R_ee increase during cooling. They are smallest for the liquid phase, when the alkanes can bend, attaining their maximal length in the crystalline phase, as they elongate along their principal axis to accommodate neighboring molecules in parallel alignment (Table 2).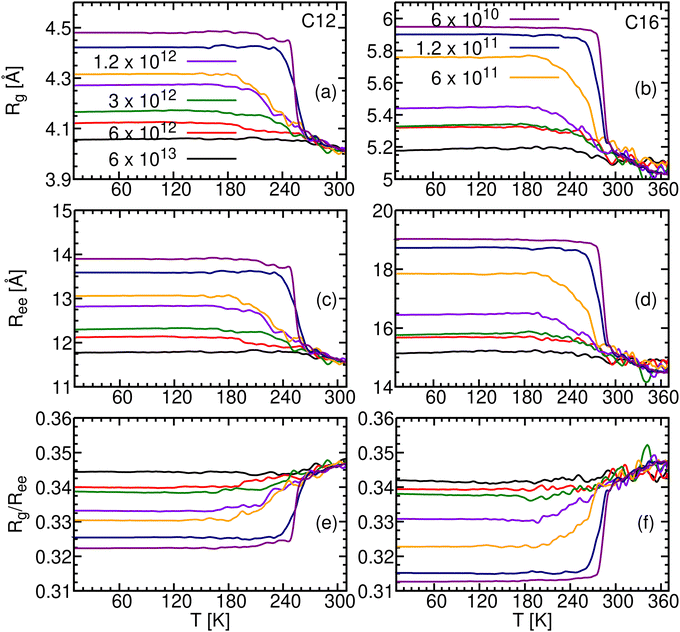

Fig. 4 Radius of gyration, (R_g [Å]) of (a) C12 and (b) C16 and the end to end distance (R_ee [Å]) of (c) C12 and (d) C16, obtained for the seven cooling rates. R_g/R_ee is shown for (e) C12 and (f) C16.

Table 2 The average values of R_ee and R_g for C12 and C16 in their liquid (liq) and crystalline (crys) states. Averaging performed over the 100 ns, NPT production run (liq) and between 10 and 150 K for the slowest γ (crys)

	C12, liq	C12, crys	C16, liq	C16, crys
R g	4.01	4.48	5.01	5.94
R ee	11.55	13.90	14.39	18.96
R g/Ree	0.347	0.322	0.348	0.313

---

In Fig. 4, the increase in R_ee and R_g upon cooling is at first gradual and nearly independent of γ. At the two slowest cooling rates, further cooling results in a discontinuous jump in R_ee and R_g, which we interpret as a first order liquid to crystal phase transition. The crystallization temperature, T_c, is where the slope is maximal (in absolute values). In contrast, the three largest cooling rates (γ ≥ 3 × 10¹² K min⁻¹) produce a continuation of the gradual increase observed above T_c, until it is suddenly arrested at the SCL to glass transition (T_g). This complements the density results from Fig. 2. Finally, the behavior at the two intermediate γ's (1.2 × 10¹² and 6 × 10¹¹ K min⁻¹), could be interpreted as a mixture of the crystalline and the SCL or glassy states.

It is relatively simple to explain R_ee in the crystalline state, if all the n-alkanes achieve the stretched, linear, all-trans configuration. Then, the average distance, l, between consecutive carbon atoms in the chain is

Using the crystal R_ee values from Table 2, we find that l = 1.264 Å for both n = 12 and 16.

This parameter can be obtained from geometric experimental data with the help of Fig. S9 (ESI†), which depicts three consecutive C atoms forming an isosceles triangle. Its two sides are L_CC long (the carbon–carbon covalent bond length). Due to repulsive C⋯C interactions between second nearest-neighbors on the carbon chain, the triangle's head angle α should be slightly larger than the tetrahedral angle of 109.5°. For example, an electron diffraction study of gas-phase C16⁵⁵ measured L_CC = 1.542 Å and α = 114.6°. Then l is half the base of the triangle,

l = L_CC sin(α/2) (8)

This gives l = 1.542 × sin(114.6/2) = 1.298 Å, slightly larger than the value found from eqn (7). For the crystal, R_g is also proportional to the repeat length, l. Biswal and Agmon³⁶ showed that, for even n,

The dependence on l can be eliminated by taking the ratio of R_g and R_ee, which are both proportional to l. Eqn (9) then becomesin which there are no adjustable parameters.

The comparison of this theory with the simulations of Table 2 is shown in Table 3. The agreement between simulation and theory for R_g is truly remarkable, confirming that, at the slowest cooling rate, most of molecules are in the stretched conformation.

Table 3 Radius of gyration and R_g/R_ee of crystalline C12 and C16, simulation vs. theory (with l = 1.298 Å)

R g (Å)	C12	C16	R g/Ree	C12	C16
Simulation	4.48	5.94		0.322	0.313
Theory	4.48	5.98		0.314	0.307

---

For the crystalline alkanes discussed thus far, R_g/R_ee decreases with increasing n, tending to the limiting value of (eqn (10)). In the liquid phase the behavior appears to be quite different (Table 2). We have therefore extended the liquid phase simulations to 14 values of n (Table S1, ESI†).

The results for R_g/R_ee are listed in Table 4 and portrayed graphically by the blue circles in Fig. 5. In the liquid, R_ee is smaller than in the crystal, hence R_g/R_ee is larger. It first decreases with n, remains nearly constant for n between 10 and 20, with two identical minima of R_g/R_ee = 0.347 at n = 12 and 18, thereafter increasing with n. This contrasts with the crystal (green line), in which this ratio decreases monotonically with n. Interestingly, this might be connected with a recently observed transition observed for n-alkanes in the gas-phase.

Table 4 R _g/R_ee for liquid n-alkanes, simulated for 14 values of n at the temperatures listed in Table S1 (ESI)

n	R g/Ree	n	R g/Ree
4	0.4369	18	0.347
6	0.3826	20	0.3474
8	0.3617	22	0.3528
10	0.3533	24	0.3558
12	0.3469	30	0.3612
14	0.3483	40	0.3694
16	0.3487	50	0.3783

---

Fig. 5 R _g/R_ee for liquid n-alkanes, simulated for 14 values of n at the temperatures listed in Table S1 (ESI†) (blue circles; blue line to guide the eye). For comparison, results for the crystal are shown by the green line (eqn (10)) and red circles (C12 and C16 simulations).

3.3 Gas-phase transition at n = 18

Gas-phase n-alkanes were found to undergo a conformational transition from linear (up to n = 16) to a folded “hairpin” conformation (n ≥ 18).^56–59 This transition leads to a huge decrease in R_ee which might even be manifested in the liquid e.g., in a minimum in R_g/R_ee. Let us first discuss this transition in the gas-phase.

For short chains, the linear all-trans conformer is the most stable conformer. For longer chains, it might convert to the hairpin conformer, in which four of the five trans (T) dihedrals in the middle of the chain isomerize to the higher-energy gauche (G) dihedrals, forming a …GGTGG… sequence. The twisting energy of the dihedral angles is compensated by Lennard-Jones (LJ) attraction terms between CH₂ or CH₃ pairs (dashed lines in Fig. S10, ESI†). This “self solvation” effect stabilizes one half-chain via LJ attractions with the other half. Thus, with sufficiently long tails, the LJ attraction wins and the hairpin becomes the most stable gas-phase conformer.

To test whether the CHARMM FF indeed shows a transition from all-trans (…TTTTT…) to hairpin (…GGTGG…), we have constructed the two isolated even isomers with n = 14–20 using gview 6 (e.g., Fig. S10, ESI†, for C16). Each conformer was then subjected to 50 000 steps of energy minimization. The final potential energies for each of the two conformers at each n are summarized in Table 5. Indeed, at small n the all-trans energy is lower, while for large n the hairpin energy is lower. The transition is near n = 16, in good agreement with the literature.

Table 5 Minimized potential energies (in kcal mol⁻¹) for the gas-phase all-trans and hairpin rotamers of linear n-alkanes at four n values, and their difference, ΔE (hairpin minus all-trans)

n	All-trans	Hairpin	ΔE
14	9.5446	10.1894	0.6448
16	9.8138	9.8951	0.0813
18	10.6685	9.8791	−0.7894
20	11.5316	9.9337	−1.5979

---

3.4 Distribution of end-to-end distances

The end-to-end distance distribution is the probability that it has a value between R_ee and R_ee + ΔR. To obtain this distribution for different cooling rates, γ, we count the number of molecules whose length falls within a given interval, using ΔR = 0.1 Å. This is done for all the frames of a given cooling trajectory while 10 < T < 150 K. In this temperature range all nuclear motion is arrested and no conformational change can occur. In addition, we calculate the distribution for the liquid phase, using the 100 ns production runs for C12 and C16, and the 10 ns production runs for C18 and C20.

Fig. 6a compares the R_ee distribution for liquid C12 with glassy C12 obtained using the two largest γ values. A similar graph for C16 is depicted in Fig. S11a (ESI†). Some differences between the two cases (C12 and C16) are discussed in Section S2 (ESI†). The liquid distribution in Fig. 6a (cyan line) has a wide peak near 12 Å, and is otherwise featureless, excepting a small secondary peak at 13.9 Å, which is the R_ee value for a completely stretched C12 (Table 2). The liquid band actually conceals many different conformations, which interconvert rapidly at high temperatures causing their peaks to overlap. The linear isomer is barely seen, because there are many more non-linear isomers that are accessible at high temperatures.

Fig. 6 End-to-end distance distributions and representative conformers for C12. (a) R_ee distributions for liquid C12 (310 K, cyan line), and for glassy C12 obtained by cooling at the rates of 6 × 10¹³ (black line, with some of the peaks marked) and 6 × 10¹² K min⁻¹ (red line). (b) Rotamers of C12 in the fastest cooled sample (6 × 10¹³ K min⁻¹) exhibiting R_ee distances corresponding to the peaks in the R_ee distribution. In comparison, Wallqvist and Covell⁶⁰ in their Fig. 3 have identified some of the conformations of “bent dodecane” in water, characterized (according to them) by R_ee = 14, 12, 10, 8, 6, and 4 Å.

As the liquid is cooled down, fewer conformations are energetically accessible, and peaks for dominant individual conformations become observable. The two distributions for the glass attest that this is indeed the case. Both exhibit the 13.9 Å band, which increases in intensity as γ decreases and more time becomes available for the global minimum energy search. Hence, the linear n-alkane is the lowest energy conformer for n = 12 and 16, which agrees with the gas-phase calculations.⁵⁹ Most likely, there is also a large energetic gap from the other available conformations, which makes the increase in the linear conformer intensity so conspicuous.

Fig. 6b shows some (of the many) C12 rotamers that possess R_ee values corresponding to the peaks observed in panel a. These 5 rotamers, characterized by their n − 3 = 9 dihedral angles being either T or G, are listed in Table 6. While a linear rotamer is obtained when all the dihedrals are T, more G's lead to shorter chains and higher conformeric energies. The glass is thus a wide distribution of conformers, which prevent it from crystallizing.

Table 6 The five rotamers appearing in Fig. 6b (right to left) are characterized by their 9 dihedral angles being either T or G (top to bottom)

R ee, Å	Isomer
13.9	TTTTTTTTT
13.1	TGTTTTTTT
12.1	TTTTGTTTT
11.3	TTTTGTTGT
9.5	TGGTGGTGG

---

The distributions for the slower γ values are given in Fig. 7, showing unmistakably that for n = 12 and 16 the ultimate distribution emerging after slow relaxation contains only a single peak, that of the linear conformer, which dominates the crystal R_ee distributions. For intermediate value of γ, the distributions in Fig. 7 are best interpreted as mixtures of crystal (linear conformer) and glass (the rest).

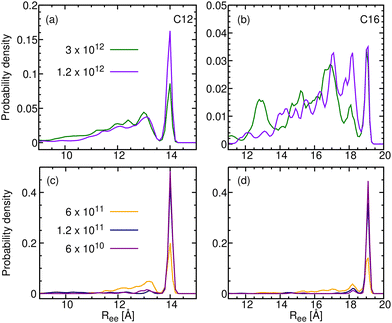Fig. 7 R _ee distributions for frozen C12 (in a and c) and C16 (in b and d) obtained by cooling at rates γ ≤ 3 × 10¹² K min⁻¹.

3.5 Condensed phase transition at n = 18

As discussed above, in the gas phase the lowest energy conformers undergo a transition, from linear (n ≤ 16) to hairpin (n ≥ 18). Is there a hairpin conformation in condensed phases? If so, it should be manifested by a R_ee peak near 4.2 Å (the average R_ee for the hairpin conformer in Fig. S10, ESI†). Fig. S12 (ESI†) shows the distributions for C12 and C16 down to R_ee = 3 Å, in which we find no trace for a 4.2 Å peak. In contrast, Fig. S13 (ESI†) shows that for C18 and C20 (and higher n values) such a peak does indeed appear. Simultaneously, the all-trans peak looses its intensity so it may no longer be the global minimum (or there are several nearly isoenergetic conformations). Fig. S14 (ESI†) depicts one representative snapshot of a hairpin C20, obtained at the fastest γ. Thus, liquid n-alkanes also undergo a transition in the “ground state” rotamer near n = 18, but it is more subtle than in the gas-phase. Hence, it went unnoticed in previous work.

In contrast to the liquid, we do not expect to observe folded chains, such as a hairpins, in the crystal state. Experimentally, at least, such chains were observed only for n ≥ 150.⁶¹ Moreover, mature crystals exhibited strong tendency towards integer folded forms.⁶²

3.6 Degree of crystallinity

Given that n-alkanes with n ≤ 150 crystallize in their extended, all-trans conformation,^61,62 our samples, having n ≤ 50 should all crystallize as all-trans conformers. If, however, the minimum energy principle of Natta and Corradini⁶³ were correct, the crystal would be composed solely of the lowest energy gas-phase conformer, and then n-alkane crystals would be all-trans only up to n = 18. In the present section, we restrict our interest to C12 and C16, so that we may define the “degree of crystallinity”, χ, as the fraction of the lowest energy gas-phase conformer. While intermolecular criteria for crystallinity have been applied before,⁶⁴ the intramolecular criterion suggested here has not been implemented before, so we devote most of the present section to it.

Returning to the example of C12, Fig. 7a and c show its end-to-end distribution for the five slowest cooling rates. In this sequel, the 13.9 Å peak increases in intensity with decreasing γ, whereas the remaining conformers (those with R_ee < 13.7 Å) decrease in intensity, most rapidly at the high energy side (small R_ee). Thus, the 13.9 Å peak is indeed the lowest energy conformer for C12. It is also the conformer found in the crystal state (Table 2). Thus, a physically sound intramolecular definition for χ would be the ratio of its area (i.e., the population of the all-trans conformer) to that of the whole distribution. Fig. 7b and d exhibit similar distributions for C16, with the 19 Å peak originating from the lowest energy conformer. Thus, for C16, any molecule with R_ee > 18.8 Å belongs to a crystalline domain, in agreement with Table 2.

The intramolecular measure of crystallinity for the 7 cooling rates of C12 and C16 is given in Fig. 8a and b. It is compared with an intermolecular measure of crystallinity in Fig. 8c and d (see below). The two measures produce similar results, in spite of being computed differently. Note, however, that we have not tested χ for n ≥ 18. For convenience, the limiting low temperature values of χ(T) (obtained by averaging over the range 10–150 K) are summarized in Table S5 (ESI†).

Fig. 8 Degree of crystallinity, χ [%], obtained from our intramolecular (upper row) and intermolecular criteria (bottom row) for C12 (a) and (c) and C16 (b) and (d).

The interpretation of these results is aided by representative snapshots in Fig. 9 and Fig. S15 (ESI†) for C12 and C16, respectively. The slowest 1–2 cooling rate(s) produce an ordered crystalline phase (χ ≈ 1) in three dimensions, which is composed of linear molecules (colored red). The fastest cooling rate (panel a) produces disordered glass (χ ≈ 0). Here linear molecules are rarely observed, they are isolated, and do not form crystalline domains. Somewhat slower rates produce intermediate χ values, which may be ascribed to an inhomogeneous mixture of the two phases (ordered and disordered) see, for example, panels d and e. Our coloring scheme aids in visualizing this state, as a mixture of the red-colored molecules (ordered/linear) with all other colors (disordered/bent).

Fig. 9 Representative snapshots of C12, as obtained at the end of the cooling process at 10 K. Panels a to g correspond to the seven cooling rates, from fastest to slowest. The five different colors correspond to different R_ee values, as indicated in the inset.

Instead of the intramolecular criterion for χ, one could use an intermolecular criterion. For example, we suggest that two molecules belong to the same crystalline domain if their centers of mass (COM) separation is smaller than the first minimum in the COM radial distribution function, g(r_min) = 6.5 Å, and the angle between their long axes is smaller than 10°.⁶⁴ The resulting χ(T) plots are shown in Fig. 8c and d.

A brief discussion of the COM radial distribution function, g(r), of the crystalline and the glassy phases, is presented in the next section.

3.7 Radial distribution function

The local organization pattern of the COM of the molecules in the different condensed phases considered herein, quantified in terms of g(r), carries information not only about the intermolecular arrangement but also about the intramolecular configuration. For example, we envision the COM's of stretched alkanes approaching each other closely, whereas bending of a linear molecule could prevent another molecule from approaching its COM as closely as in the linear case.

To test this, we have calculated g(r) for the different phases by averaging it over all temperatures for which the phase exists. Thus, g(r) for the crystal was calculated at the slowest cooling rate (of 6 × 10¹⁰ K min⁻¹) for the temperature range 10 K ≤ T ≤ 150 K. For the glass, averaging was performed over trajectories between 150 K and 10 K, while that of the SCL was calculated by averaging between 250 and 210 K for C12, and 270 to 230 K for C16, all at the fastest cooling rate (of 6.0 × 10¹³ K min⁻¹). Finally, in the liquid phase, g(r) has been calculated over the last 50 ns of the NPT production trajectories of C12 at 310 K and C16 at 370 K.

The results are shown in Fig. 10. In the liquid, g(r) shows a broad peak due to the dynamic interchange of structures therein. However, when the molecular movement is arrested (as in the glass or the crystal), more features are seen in g(r). The crystal exhibits a sharp peak near 4.5 Å, which is close to the minimum in the LJ potential. Indeed, in the CHARMM FF

For the CH₂⋯CH₂ interaction, ε = 0.056 kcal mol⁻¹ and r_min = 4.02 Å, where the minimum in V_LJ(r) occurs. It is also close to the average distance between the two tails of the hairpin conformer seen in Fig. S10 (ESI†) (4.25 Å). This indicates that the sharp peak in the COM g(r) of Fig. 10c and d characterizes the repeat distance of the crystal, which consists of stretched molecules separated 4.5 Å from each other).

Fig. 10 Center of mass radial distribution function, g_COM(r) for the glass, SCL and liquid phases are shown for (a) C12 and (b) C16. For the liquid and crystal g_COM(r) is shown for (c) C12 and (d) C16.

For the glass, g(r) follows that of the liquid, on which a series of smaller peaks are superimposed (red lines). One of these peaks (the tallest, in the case of C12) is also near 4.5 Å. In contrast, the tallest SCL peak occurs at a slightly larger distance (5.2 Å) than the tallest crystal peak.

3.8 Enthalpy change during crystallization

The temperature dependence of the enthalpy (H) for the seven cooling rates is depicted in Fig. 11a and b for C12 and C16, respectively. In the liquid phase (T > 270 K for C12 and >290 K for C16), H decreases linearly with decreasing T. Upon further cooling, its temperature dependence deviates from linearity. In particular, for the slowest γ there is a sudden decrease in H, characteristic of a first order phase transition. The vertical drop in H is the heat of crystallization, ΔH_c, which is released to the surrounding at a constant temperature T_c. For larger cooling rates, the enthalpy drops gradually. This is in agreement with the behavior of ρ, discussed above. Upon reheating to the melting temperature, T_m, the solid melts by absorbing heat, ΔH_m, from its surrounding. Typically, T_c < T_m and ΔH_c < ΔH_m, although the differences can be small.⁶⁵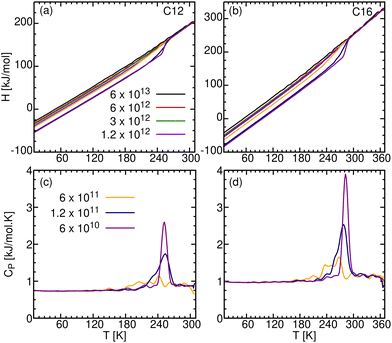

Fig. 11 Enthalpy, H [kJ mol⁻¹], in the top panels, and heat capacity, C_P [kJ mol⁻¹ K⁻¹], in the bottom panels for: (a) and (c) C12 and (b) and (d) C16.

The temperature derivative of the enthalpy is the heat capacity, C_P = (∂H/∂T)_P, which is shown in the bottom panels of Fig. 11. C_P is presented here only for the three slower cooling rates, where we observe a sharp change in H. This corresponds to a spike in C_P, narrower and upshifted for slower γ (compare with Fig. 1b of Nazarychev et al.²⁰ for C20). Its peak location and area are T_c and ΔH_c, respectively. Below T_c, in the crystalline solid phase, C_P is constant, hence H(T) is again linear in T. We find C_P = 0.75 and 1.00 kJ mol⁻¹ K⁻¹ for C12 and C16 respectively. In the literature, the value for C20 is 1.28 kJ mol⁻¹ K⁻¹.²⁰ Hence, C_P is proportional to n (hence also to the mass), which is expected because each monomer contributes the same number of degrees of freedom to the heat capacity.

Our calculated T_c and ΔH_c values are listed in Table 7. To the best of our knowledge, experimental ΔH_c values for C12 or C16 are not available in the literature. Therefore, we compare our simulated ΔH_c values with the averaged ΔH_m from the NIST webbook,⁶⁶ assuming that the difference between them is not very large.⁶⁵

Table 7 The simulated crystallization temperature (T_c) and enthalpy change (ΔH_c) at T_c for C12 and C16 at three cooling rates. Experimental T_m and ΔH_m (last row for each alkane) are the average of the literature values listed in the NIST webbook⁶⁶

Alkane	γ [K min^−1]	T c [K]	ΔHc [kJ mol^−1]
C12
Simul.	6.0 × 10^10	253	26.54
	1.2 × 10^11	253	22.81
	6.0 × 10^11	242	12.9
Exper.	Crystall.	256.65^67	—
	Melting	263.32^66	36.44^66
C16
Simul.	6.0 × 10^10	283	45.37
	1.2 × 10^11	278	42.18
	6.0 × 10^11	268	18.67
Exper.	Crystall.	289.96^12	—
	Melting	291.27^66	51.38^66

---

It is seen that as γ decreases, both T_c and ΔH_c increase, more noticeably for ΔH_c than for T_c. A similar effect was found experimentally by Louanate et al. (Fig. 3),¹⁴ where decreasing the cooling rate from 20 K min⁻¹ to 0.3 K min⁻¹ resulted in a 7.5 K increase in T_c, and 6.5 kJ mol⁻¹ increase in ΔH_c. This similarity is quite remarkable given that our slowest cooling rate is ∼10 orders of magnitude faster than the experimental heating rate. The experimental value of ΔH_m cited in Table 7 is larger than all our simulated values for ΔH_c, as might be expected if these tend to the experimental value as γ → 0. However, the simulations in Table 7 span only one order of magnitude out of 10, so that an extrapolation over such a huge range of γ may not be valid.

3.9 Chain length dependence of T_g

Earlier we presented the temperature dependence of the C12 and C16 densities (Fig. 2), identifying the change of slope as the glass transition temperature T_g, at least for the three fastest cooling rates (γ ≥ 3 × 10¹² K min⁻¹). In order to extend the n (i.e., mass) dependence beyond 16, we repeated the calculation for all 14 alkanes listed in Table S1 (ESI†). Briefly, their simulated ρ(T) shown in Fig. S4 (ESI†) were fitted to 2nd order polynomials, which are reproduced in Fig. 12.

Fig. 12 The fitted polynomials to the temperature-dependent densities, ρ [kg m⁻³], of the 14 alkanes as obtained during cooling at γ = (a) 6 × 10¹³, (b) 6 × 10¹² and (c) 3 × 10¹² K min⁻¹. Filled circles mark T_g.

The 14 simulated T_g values (from the ρ-fits) are listed in Table 8, and presented graphically in Fig. 13a. For a given γ, T_g increases with increasing n. One expects also to observe that, for given n, T_g increases with increasing γ. As Table 8 and Fig. 13a show, this occurs only for n ≥ 20 namely, above the transition at n = 18. Another connection with this transition value is that the T_g(n) curve is not smooth but rather shows a kink at n = 20, very close to the value of 18, where the hairpin rotamer first appears.

Table 8 T _g [K] values calculated from ρ(T) (ρ-fit) and H(T) (H-fit, in parentheses), for the three cooling rates γ = (a) 6.0 × 10¹³, (b) 6.0 × 10¹², and (c) 3.0 × 10¹², and the average values over the 3 cooling rates

n-Alkane	(a)	(b)	(c)	Average
C4	100(100)	90(90)	88(78)	92.66(89.33)
C6	139(150)	117(125)	120(126)	125.33(133.66)
C8	149(156)	149(149)	150(147)	149.33(150.66)
C10	169(154)	158(152)	157(153)	161.33(153)
C12	181(181)	179(179)	175(170)	178.33(176.66)
C14	196(192)	186(186)	177(182)	186.33(186.66)
C16	205(204)	201(200)	201(200)	202.33(201.33)
C18	208(208)	213(218)	199(206)	206.66(210.66)
C20	215(212)	206(204)	189(200)	203.33(205.33)
C22	228(227)	221(219)	215(209)	221.33(218.33)
C24	229(233)	228(230)	219(221)	225.33(228)
C30	233(234)	228(227)	222(224)	227.66(228.33)
C40	241(238)	231(235)	225(227)	232.33(233.33)
C50	242(243)	234(237)	234(234)	236.66(238)

---

Fig. 13 T _g obtained for 14 n-alkanes at three different cooling rates from the (a) ρ-fit and (b) H-fit.

To corroborate the T_g values obtained by the ρ-fits, we have also calculated T_g from the enthalpy data in Fig. 11 and Fig. S16–S18 (ESI†) at the three fastest γ's (hereafter “H-fits”). Here it suffices to fit with two intersecting straight lines, whose equations are listed in Table S6 (ESI†). This requires special care because the changes in slope for H(T) are very small. The H-fit T_g's are presented in Table 8 within parentheses, and graphically in Fig. 13b. We find remarkable similarity in the two sets of T_g results, including the kink at n = 20. Apparently, for the H-fit there is a secondary kink at n = 10. Else, both methods seem to be equivalent for n-alkanes.

The variation of T_g with n is much larger than with the cooling rate, therefore we can utilize the γ dependence of T_g (n, γ) in Table 8 for smoothing the data, by averaging it over the three cooling rates for each n. We have presented these averaged results in Fig. 14a. Previous data in the literature,^30,32,34 based on various approximations, are also shown in the figure. Our T_g values are always higher than the previously reported data.

Fig. 14 Glass transition temperature dependence on the n alkane length. (a) Simulated 14 n-alkane T_g values, obtained from the ρ- and H-fits, and averaged over three cooling rates, are compared with available data in the literature.^30,34 (b) The same, compared with 2/3T_m. (c) The average T_g fitted with two different Ueberreiter and Kanig (UK) equations (four adjustable parameters), plotted as a function of 1/n. (d) The same, for the Fox–Flory (FF) equation.

It is often stated in the literature^68,69 that T_g is a scaled down version of the melting temperature, T_m. Thus

T_g = αT_m (12)

where α < 1. α is often close to 1/2 for a symmetrical polymer and to 2/3 for an unsymmetrical polymer. Taking T_m from ref. 66, Fig. 14b shows that eqn (12) with α = 0.67 depicts quite well the simulated averaged T_g(n) values, except perhaps at large n (where α = 0.64). Since T_m, is measured (elsewhere^66,70) during heating, it is by definition independent of γ. Hence it is reasonable to compare it with the γ-averaged T_g (obtained during cooling).

Since T_m can be obtained, over a wide range of n,⁷⁰ more readily than T_g, one could use our result that α = 0.67 to estimate the limiting value for large n, T^∞_g, on which there are wide disagreements in the literature.³⁵ As Fig. 1 of ref. 70 shows, T^∞_m = 135 °C = 408 K. Therefore, T^∞_g = αT^∞_m = 273 K. This is reasonably close to the “best value” of 231 K suggested by Davis and Eby.³⁵Fig. 14c and d show a fit to the UK and FF equations, from which T^∞_g is either 250 (UK) or 260 K (FF). These values seem reliable because they are intermediate between the two estimates (231 K and 273 K) mentioned above. Thus we have obtained the best theoretical estimate to-date to the glass temperature for very long n-alkanes.

The UK and FF equations suggest a linear dependence of 1/T_g (UK) or T_g (FF) on 1/n. Instead, we find that, in both cases, two linear fits are required, one for n ≥ n₀ (denoted UK1 and FF1) and the other below n₀ (UK2 and FF2). Approximately, n₀ = 20 for the UK equation, and 10 for FF. Interestingly, these values correspond to the two kinks in T_g(n) seen in Fig. 13. Additionally, they are close to the two minima in the liquid-state R_g/R_ee plot in Fig. 5. Finally, the transition at n₀ = 20 (between UK1 and UK2) occurs very close to the hairpin transition discussed in Sections 3.3 and 3.5. Note that although the T_g(n) dependence has previously been represented as two to three intersecting straight lines,²⁸ it was done as a function of n rather than 1/n.

4 Conclusions

When a liquid is cooled slowly, it undergoes a first-order phase transition into an organized crystal. However, when cooling is rapid the liquid has no time to organize, hence an amorphous glassy state is formed by the dynamic arrest of supercooled liquid molecules. Such a dynamic transition behaves as a second-order phase transition. Here we studied, using all-atom MD simulations, the impact of the cooling rate (γ) on the condensed-state phase transitions in n-alkanes, C_nH_2n+2, which have attracted much attention recently as potential phase-change materials (PCMs) for energy storage applications. For each cooling rate, we have calculated the temperature dependence of the density (Fig. 2) and enthalpy (Fig. 11) as a basis for analysis. The slower crystallization process was studied in two n-alkanes, C12 and C16 (i.e., n = 12 and 16), whereas glass formation upon faster cooling was studied for 14 n-alkanes (including 12 and 16), ranging from n = 4 to 50 (n even), in order to elucidate the chain-length effect on the glass transition temperature, T_g.

The T-dependencies of the density (ρ(T)) and enthalpy (H(T)) are useful in characterising a phase-transition. A discontinuity in these functions or their slopes is commensurate with Ehrenfest's nomenclature of first- vs. second-order phase transitions, respectively. Nevertheless, the end-to-end distance (R_ee) is particularly revealing for linear molecules, whose maximal length is R^max_ee = (n − 1)l, where l ≈ 1.264 Å is the length of the repeat unit along the molecular axis. Representative snapshots in Fig. 9 and Fig. S15 (ESI†) (with different conformers colored by their R_ee values) show that crystalline domains are composed solely of R^max_ee conformers, as predicted experimentally for n ≤ 150.⁶¹

A plot of the R_ee distribution, i.e. the number of conformers having a given length (Fig. 6), which is quite featureless in the liquid state (T > 270 K for C12), shows distinct peaks for the glass. These are attributed to conformers existing in the SCL just above T_g. At the slowest γ there is a single peak at R^max_ee, characterizing the crystal. For faster γ, peaks for bent conformations appear at shorter R_ee. Eventually, glasses obtained at the fastest cooling rates capture conformers (rotamers) which existed in the liquid state.

From the distributions we observe that the “most bent”, hairpin conformer exists only for n ≥ 18. Remarkably a linear to hairpin transition was observed experimentally in gas-phase n-alkanes, with the hairpin becoming the most stable conformer for n ≥ 18.⁵⁷ In contrast, in the liquid and glassy states the hairpin population remains tiny even above n = 18. Nevertheless, it may have sufficient impact on reducing the liquid phase R_ee, for R_g/R_ee to show a minimum at n = 18 (Fig. 5).

As a corollary of the R_ee distribution, we have introduced a novel definition for the degree of crystallinity (χ), as the ratio of the number of R^max_ee conformers to all the other, non-linear ones. Thus, a perfect crystal state is characterized by χ = 1, whereas a disordered glass containing only bent molecules is characterized by χ = 0. Intermediate χ values are best interpreted as an inhomogeneous mixture of the two phases.

In order to study the dependence of T_g on n, we have extended our simulations to 14 n-alkanes, with n ranging from 4 to 50. For given n, T_g was calculated as the point of derivative discontinuity in either ρ(T) or H(T), both routes leading to similar results. The only difference between these ρ-fit and H-fit approaches is that in the H-fit the discontinuity is describes by two intersecting lines, whereas in the ρ-fit these are two intersecting parabolas.

As is commonly known, we also find that T_g increases almost monotonically with n, up to the limiting value of T^∞_g. However, at two points, n₀ = 10 and 20, T_g slightly decreases with n, creating the kinks shown in Fig. 13. As a result, the traditional analytical functions, FF and UK, do not fit T_g(n) well. Rather, we find that either two intersecting FF functions or two intersecting UK functions are required (Fig. 14c and d), and then the intersections occur at n₀ = 10 and 20, respectively. In particular, n₀ = 20 is close to 18, the smallest n for which the isolated (gas-phase) chain folds.⁵⁷ For the liquid, we consequently suggest that this length represents the “onset of folding”. While below n = 18, R_ee can only increase with n (ca. 1.3 Å per monomer), above n = 18 this elongation ceases or even reverts due to progressively more folded/bent conformations. As a result, R_g/R_ee shows a minimum at n = 18 and increases thereafter, as revealed by our Fig. 5. In addition, we find that T^∞_g = 250 or 260 K, and this seems by far the most accurate theoretical estimate for this parameter (compare Fig. 14a).

We conclude by returning to the requirements from a good PCM, one of which is the large latent heat of the phase transition (as observed for C16),⁹ see Introduction. Indeed, Table 7 shows that the ΔH of crystallization of C16 is notably larger than for C12, the experimental (equilibrium) ratio being 1.41. This ratio is somewhat larger than the mass ratio, 16/12 = 1.33, whereas equality would be expected if all atoms contributed equally to the latent heat. However, in real PCMs the cooling (and heating) rates are not infinitely slow. Our simulations (Table 7) show that for the two slowest cooling rates the C16 to C12 latent heat ratios increase to 1.71 and 1.85, respectively. Thus, the decrease of ΔH_c with increasing γ is less dramatic for C16 than for C12, making C16 an even better choice for a PCM. Our work suggests a possible explanation for this effect. n = 16 is close to n = 18, where we observed the “hairpin transition”. For n ≥ 18 the chains can fold, so that ΔH_c includes also contributions from unfolding. Thus, understanding the n-alkane conformational behavior can be of technological importance in selecting the most suitable length for a phase-change system.

Author contributions

SS suggested the research topic, performed all of the simulations and some of the analyses, prepared the tables and most of the figures and wrote the first draft of the manuscript. NA guided the research, suggested theoretical interpretations, prepared some of the figures, and edited the final version of the manuscript.

Data availability

Data available upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Daniel Harries and Valeriy Ginzburg for insightful discussions and valuable suggestions. This research was supported by the Israel Science Foundation (ISF) grants number 722/19 and 817/24.

Notes and references

1. J. Leys, B. Duponchel, S. Longuemart, C. Glorieux and J. Thoen, Mater. Renewable Sustainable Energy, 2016, 5, 1–16.
2. I. Shamseddine, F. Pennec, P. Biwole and F. Fardoun, Renewable Sustainable Energy Rev., 2022, 158, 112172.
3. M. Wuttig and N. Yamada, Nat. Mater., 2007, 6, 824–832.
4. R. D. McGillicuddy, S. Thapa, M. B. Wenny, M. I. Gonzalez and J. A. Mason, J. Am. Chem. Soc., 2020, 142, 19170–19180.
5. M. Le and G. G. D. Han, Acc. Mater. Res., 2022, 3, 634–643.
6. S. Wu, Z. Y. Zhang, T. Li, R. Wang and T. Li, ACS Mater. Lett., 2023, 5, 2019–2027.
7. A. S. Fleischer, Thermal Energy Storage Using Phase Change Materials: Fundamentals and Applications, Springer, 2015.
8. T. D. Swanson and G. C. Birur, Appl. Therm. Eng., 2003, 23, 1055–1065.
9. N. R. Sgreva, J. Noel, C. Métivier, P. Marchal, H. Chaynes, M. Isaiev and Y. Jannot, Thermochim. Acta, 2022, 710, 179180.
10. M. Więckowski and M. Królikowski, J. Chem. Eng. Data, 2022, 67, 727–738.
11. A. Abdi, M. Ignatowicz, S. N. Gunasekara, J. N. Chiu and V. Martin, Int. J. Heat Mass Transfer, 2020, 161, 120285.
12. C. Vélez, M. Khayet and J. M. O. de Zárate, Appl. Energy, 2015, 143, 383–394.
13. W. Su, J. Darkwa and G. Kokogiannakis, Renewable Sustainable Energy Rev., 2015, 48, 373–391.
14. A. Louanate, R. El Otmani, K. Kandoussi and M. Boutaous, Phys. Scr., 2020, 95, 105003.
15. X. Du, J. Qiu, S. Deng, Z. Du, X. Cheng and H. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 5695–5703.
16. J. F. Li, W. Lu, Y. B. Zeng and Z. P. Luo, Sol. Energy Mater. Sol. Cells, 2014, 128, 48–51.
17. C. Lin and Z. Rao, Appl. Therm. Eng., 2017, 110, 1411–1419.
18. Y. Cong, L. Cao, M. Cong and M. Fang, J. Energy Storage, 2023, 73, 109135.
19. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267.
20. V. M. Nazarychev, A. D. Glova, S. V. Larin, A. V. Lyulin, S. V. Lyulin and A. A. Gurtovenko, Int. J. Mol. Sci., 2022, 23, 14576.
21. J.-L. Barrat, J. Baschnagel and A. Lyulin, Soft Matter, 2010, 6, 3430–3446.
22. J. Buchholz, W. Paul, F. Varnik and K. Binder, J. Chem. Phys., 2002, 117, 7364–7372.
23. W. Paul and G. D. Smith, Rep. Prog. Phys., 2004, 67, 1117–1185.
24. A. Soldera and N. Metatla, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061803.
25. T. G. Fox, Jr. and P. J. Flory, J. Appl. Phys., 1950, 21, 581–591.
26. K. Ueberreiter and G. Kanig, J. Colloid Sci., 1952, 7, 569–583.
27. J. M. G. Cowie, Eur. Polym. J., 1975, 11, 297–300.
28. J. Hintermeyer, A. Herrmann, R. Kahlau, C. Goiceanu and E. A. Rössler, Macromolecules, 2008, 41, 9335–9344.
29. D. L. Baker, M. Reynolds, R. Masurel, P. D. Olmsted and J. Mattsson, Phys. Rev. X, 2022, 12, 021047.
30. A. A. Miller, J. Polym. Sci., Polym. Phys. Ed., 1968, 6, 249–257.
31. R.-J. Roe, Atomistic Modeling of Physical Properties, Springer-Verlag, Adv. Polymer Sci., 1994, vol. 116, pp. 111–144.
32. M. Martín-Betancourt, J. M. Romero-Enrique and L. F. Rull, Mol. Simul., 2009, 35, 1043–1050.
33. J. Ramos, J. F. Vega and J. Martínez-Salazar, Macromolecules, 2015, 48, 5016–5027.
34. T. Galeazzo and M. Shiraiwa, Environ. Sci. Atm., 2022, 2, 362–374.
35. G. T. Davis and R. K. Eby, J. Appl. Phys., 1973, 44, 4274–4281.
36. S. Biswal and N. Agmon, Biomolecules, 2023, 13, 1744.
37. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
38. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
39. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. MacKerell Jr., J. Comput. Chem., 2010, 31, 671–690.
40. R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and J. Alexander D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273.
41. T. R. Underwood and H. C. Greenwell, Sci. Rep., 2018, 8, 352.
42. S. A. Burrows, I. Korotkin, S. K. Smoukov, E. Boek and S. Karabasov, J. Phys. Chem. B, 2021, 125, 5145–5159.
43. M. P. Allen and D. J. Tildesley, Computer Simulations of Liquids, Clarendon Press, Oxford, UK, 1987.
44. R. E. Isele-Holder, W. Mitchell and A. E. Ismail, J. Chem. Phys., 2012, 137, 174107.
45. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
46. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
47. K. D. Papavasileiou, L. D. Peristeras, A. Bick and I. G. Economou, J. Phys. Chem. B, 2019, 123, 6229–6243.
48. A. Messias, D. E. S. Santos, F. J. S. Pontes, F. S. Lima and T. A. Soares, Molecules, 2020, 25, 5120.
49. A. D. Wade, A. P. Bhati, S. Wan and P. V. Coveney, J. Chem. Theory Comput., 2022, 18, 3972–3987.
50. S. E. Feller, Y. Zhang and R. W. Pastor, J. Chem. Phys., 1995, 103, 4613–4621.
51. W. F. Seyer, R. F. Patterson and J. L. Keays, J. Am. Chem. Soc., 1944, 66, 179–182.
52. G. Jaeger, Arch. Hist. Exact Sci., 1998, 53, 51–81.
53. R. Brüning and K. Samwer, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 11318.
54. K. Vollmayr, W. Kob and K. Binder, J. Chem. Phys., 1996, 105, 4714–4728.
55. S. Fitzwater and L. S. Bartell, J. Am. Chem. Soc., 1976, 98, 8338–8344.
56. J. N. Byrd, R. J. Bartlett and J. A. Montgomery, Jr., J. Phys. Chem. A, 2014, 118, 1706–1712.
57. N. O. B. Lüttschwager and M. A. Suhm, Soft Matter, 2014, 10, 4885–4901.
58. D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 2137–2143.
59. S. Ehlert, S. Grimme and A. Hansen, J. Phys. Chem. A, 2022, 126, 3521–3535.
60. A. Wallqvist and D. G. Covell, J. Phys. Chem., 1995, 99, 13118–13125.
61. G. Ungar, J. Stejny, A. Keller, I. Bidd and M. C. Whiting, Science, 1985, 229, 386–389.
62. G. Ungar and X. Zeng, Chem. Rev., 2001, 101, 4157–4188.
63. G. Natta and P. Corradini, J. Polymer Sci., 1959, 39, 29–46.
64. M. Anwar, F. Turci and T. Schilling, J. Chem. Phys., 2013, 139, 214904.
65. C. Alkan, Thermochim. Acta, 2006, 451, 126–130.
66. J. S. Chickos, Heat of Sublimation Data in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD.
67. K. Zhu, H. Qi, S. Wang, J. Zhou, Y. Zhao, J. Su and X. Yuan, J. Macromol. Sci., Part B: Phys., 2012, 51, 1976–1990.
68. R. F. Boyer, Rubber Chem. Technol., 1963, 36, 1303–1421.
69. W. A. Lee and G. J. Knight, Br. Polym. J., 1970, 2, 73–80.
70. L. Mandelkern, A. Prasad, R. G. Alamo and G. M. Stack, Macromolec., 1990, 23, 3696–3700.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02581d

---