Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Clearance of nanoparticles from blood: effects of hydrodynamic size and surface coatings†
Bingqing
Lu
*,
Jiaqi
Wang
 ,
A. Jan
Hendriks
and
Tom M.
Nolte
,
A. Jan
Hendriks
and
Tom M.
Nolte

Department of Environmental Science, Institute for Biological and Environmental Sciences, Radboud University Nijmegen, Nijmegen, 6500 GL, The Netherlands. E-mail: bingqing.lu@ru.nl
First published on 14th December 2023
Abstract
The distribution of nanoparticles (NPs) in the human body is associated with the development of nano-medicines and nanotoxicity. Physiologically based pharmacokinetic (PBPK) tools can simulate the distribution and elimination of NPs but are primarily dependent on experimental data. Models involving NP size and surface coating as parameters for estimating the clearance of NPs from blood are beneficial to the extension application of PBPK models. To this end, we first collected intravenous kinetic data on the blood distribution of 19 types of NPs for model parameterization and then collected 20 types of NPs for validation. Rate constants for clearance from blood were obtained by fitting the collected data to one- and two-compartment kinetics. A generic model (NP size-based) for estimation of rate constants was developed based on collision and diffusion behavior driven by NP size. NPs with a hydrodynamic diameter of 20 nm have the highest clearance rate constant via penetration and phagocytosis pathways. An extended model (NP size- and surface coating-based) was built to estimate rate constants of various NPs by calculating van der Waals energy between NPs and macrophages. Nearly 3/4 of the validation data are within 95% confidence intervals, indicating that our generic and extended models can be applied to NPs with different sizes and surface modifications.
Environmental significanceThe peer-reviewed literature contains fundamental methods for estimating the bioaccumulation of various nanoparticles based on possible pathways of elimination in the blood, covering particle size and particle surface coating properties. Our study expects to break the bottleneck that the current physiologically based pharmacokinetic model is difficult to extend to other particles, and contribute to the risk assessment of different nanoparticles or development of nanomedicines in humans. |
1. Introduction
Nanoparticles (NPs) have a wide range of applications in various fields due to their unique properties (e.g., small size, large surface area, and surface functionalization). Intentional exposure of organisms to NPs applies to medicine, including drug delivery,1 medical imaging,2 and disease diagnosis.3 For example, NPs can facilitate targeted delivery of pharmaceuticals to tumors4 in the brain by crossing the blood–brain barrier.5 Non-targeted or environmental exposures may occur due to contact between NPs and the human skin6 or respiratory tract.7 NPs have wider biological effects after entering the bloodstream.8 Trapping of NPs by the reticuloendothelial system in the immune system may lead to ineffectiveness of targeted NPs or increase the potential toxicity9 of non-targeted NPs.10,11 Consequently, it is important to quantify the influence of NP properties on the clearance of NPs from blood to optimize biomedical applications of targeted NPs and minimize toxicity of non-targeted NPs.The elimination of NPs in vivo is often predicted using physiologically based pharmacokinetic (PBPK) tools.12 In the last decades, more than 25 different nano-PBPK models have been developed,13,14 covering metallic,15–18 carbon,19 quantum dots (QD),20 liposome,21 polymer22 and crystal NPs.23 Many types of NPs exist. However, the PBPK models have been calibrated on experimental data for a few particles only,24,25 limiting application to broader classes of NPs. As an alternative, statistical methods are applied to estimate parameters of PBPK models22 using the so-called quantitative structure–activity relationships (QSARs).26 Unfortunately, connecting these statistical models to mechanisms is difficult. In addition, overfitting may occur.27 Hence, a generic approach for estimation of PBPK parameters based on NPs and tissue properties is urgently needed.
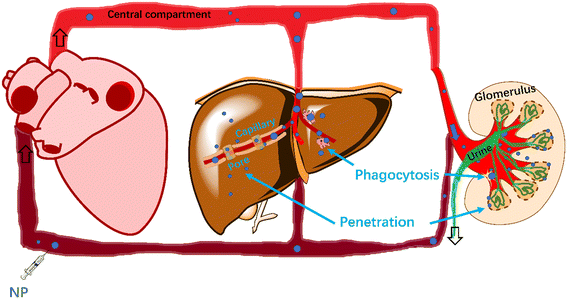
Size influences the behavior of NPs and clearance mechanisms in the blood. Small NPs are widely distributed into different organs by penetration or diffusion from the blood via the endothelial pores.28 Extravasation of NPs into some critical organs (e.g., brain)29 is restricted due to tight junctions formed between the continuous endothelial cells. Pores of the inter-endothelial cell junction openings for non-fenestrated blood capillaries in lungs, skin and intestinal mesentery have sizes of approximately 5 nm.30 NP penetration to the kidney also facilitates their clearance from blood. The glomerular epithelial (fenestrated) filtration slit is 12.1–15 nm in general,31,32 and 5.5 nm (ref. 33) specifically for spherical quantum dots. Pores between sinusoidal endothelial cells (fenestrated) of the liver are larger (upper limit of pore size: 280 nm in rodents and 180 nm in humans),32 permitting hepatocytes34 to take up NPs and excrete NPs into the digestive system.
NPs (d < 1 μm) have various clearance pathways from blood, including permeation through sinusoidal pores (d <150–200 nm),35 phagocytosis35,36 by phagocytes in capillaries and transcytosis by vascular endothelial cells into the interstitium.37 Li et al.38 reported that a NP with a mean diameter of approximately 100 nm shows prolonged blood circulation. Cellular uptake into nonphagocytic cells depends on NP size, with an uptake optimum NP diameter of approximately 50 nm.39 Multipath clearance prevents models from quantitatively describing the effect of NP size on NP clearance. Large NPs with a diameter >1 μm are cleared by the reticuloendothelial system40 or filtered by lungs, liver, or spleen41 from the blood because size-dependent momentum forces increase collision probability with the mononuclear phagocytic system.41 By contrast, if the particle size is within 20 and 1000 nm,41,42 physical clearance mechanisms are minimized, and circulation time is prolonged.
Surface coatings moderate the effects of size on clearance. The circulation time of NPs in the blood can be prolonged by hydrophilic modification. Polyethylene glycol (PEG) and analogues43 were used as coatings of NPs to prevent interactions with plasma proteins44 or the reticuloendothelial system. The absence of ‘sufficient’ chain density of PEG, i.e., decreased hydrophilicity, aids opsonins to bind to the NP surface.45 However, excessively high PEG density limits mobility and produces steric hindrance effects.41,46 The length and surface density of PEG chains for ‘shielding’ depend on dosing requirements. Hoshyar et al.47 showed that pegylation of small NPs increases their half-lives in blood. The mixed effects of NP size and surface coating on NP clearance behavior need to be considered.
Whereas the aforementioned studies shed valuable qualitative insight into biodistribution pathways and kinetics of NPs within the body, quantitative predictions are still lacking. This hampers the parameterization of PBPK models to be applied to many different NP types. In the present study, we aimed to quantify the clearance of NPs from blood involving two pathways: 1) NP penetration through capillary pores and 2) phagocytosis by macrophages located in capillaries between blood and tissues. The easily accessible parameter-size was used to build a generic model based on penetration and phagocytosis for estimating rate constants of clearance. The interactions between NPs and capillary pores/macrophages were modelled based on physical diffusion and collision. In addition, we expanded the phagocytosis-based model by adding surface coatings of NPs as parameters, detailing the interaction of NPs with macrophages, and expect to estimate the rate constants for clearance of various NPs in blood.
2. Methods
2.1. Data collection and analysis
We conducted an extensive literature search on Web of Science by using ‘nanoparticles distribution in blood’, ‘biodistribution of nanoparticles in vivo’, ‘intravenous’, ‘nanoparticles’ and ‘physiologically based pharmacokinetic (PBPK)’ as keywords to first obtain blood clearance kinetics of 19 data points for model parameterization and then collected 20 data points for model validation (16 data points for validating the generic model and four data points for validating the extended model). The data were to meet the following criteria: 1) spherical NPs are injected intravenously into different rats or mice as a single dose. 2) For parameterization we only used hydrodynamic sizes (measured by dynamic light scattering (DLS)), whereas for validation we used both TEM (transmission electron microscopy) sizes and hydrodynamic sizes. 3) NPs are coated by the same chain of compounds instead of multiple chains with compounds (i.e., mixed coatings). 4) At least four data points of NP concentration were measured over time. 5) Rate constants for clearance of NPs from blood were obtained with statistical significance (p < 0.05). The sources (studies), materials, properties and conditions of test animals of all data for parameterization and validation are shown in Table 1. All NP diameters range from 2 to 220 nm.| NP-core-coatings | Sizes (nm) | Zeta potential (mV) | Animal/health |
|---|---|---|---|
| a Denotes pore sizes of AuNPs without coating. b Denotes hydrodynamic diameter based on DLS. c Denotes diameters based on TEM. d Denotes (i.e., 2-S-(4-isothiocyanatobenzyl)-1,4,7-triacetic acid) and FSHR-mAb-SH. e Denotes (fluorescence dye)-human/murine chimeric IgG1 monoclonal antibody (TRC105). NPs used in the extended model are marked in bold. | |||
| Data for parameterization | |||
| QDPEG5000/2000 (ref. 49) | 15.5b | — | Mice |
| QD-CdTe/CdS25 | 4.2b | — | Mice |
| PAMAM CND50 | 5b | +2.5 | Mice with melanoma |
| PAMAM CND50 | 11b | −20 | Mice with melanoma |
| Cu2−xSe NP51 | 5.6b | — | Mice |
| CdTe-QD52 | 4.0b | — | Mice |
| AuNP53 | 2.0b | — | Mice |
| ZnO18 | 10b | −27.1 | Mice |
| ZnO18 | 71b | −19.3 | Mice |
| IONPs-PEG2000 (ref. 54) | 26.5b | — | Mice |
| IONPs-PEG5000 (ref. 54) | 34.2b | — | Mice |
| IONPs- PEG5000 (ref. 54) | 81b | — | Mice |
| PLGA-mPEG256-5000 (ref. 55) | 114.8b | −6.2 | Mice |
| PLGA-mPEG153-5000 (ref. 55) | 97.4b | −5.9 | Mice |
| PLGA-mPEG61-5000 (ref. 55) | 79b | −4.7 | Mice |
| PLGA-mPEG34-5000 (ref. 55) | 67b | −5.2 | Mice |
| PAA(Polyacrylamide) 56 | 31b | — | Rat |
| PAA-PEG 56 | 35b | — | Rat |
| Nanocrystal 23 | 203b | — | Rat |
| Data for validation | |||
| AuNP-PEG5000 (ref. 57) | 4a,c | — | Mice |
| AuNP-PEG5000 (ref. 57) | 13a,c | — | Mice |
| QD705-PEG5000 (ref. 58) | 13c | — | Mice |
| QD705-PEG5000 (ref. 58) | 18.5c | — | Mice |
| AuNP-PEG59 | 88.9b | −27.1 | Tumor-bearing mice |
| AuNP-PEG60 | 38b | −10.5 | Mice |
| AuNP-Trimethylammonium groups and sulfonic groups60 | 20b | −9.8 | Mice |
| AuNP-Citric acid-PEG-Thioctic acid61 | 45.4b | −7.4 | Mice |
| AuNP-Citric acid-PEG-Thioctic acid61 | 60b | −7.4 | Mice |
| AuNP-Citric acid-PEG-Thioctic acid61 | 89.3b | −9.4 | Mice |
| AuNP-Dextran62 | 46b | — | Athymic nude mice |
| Graphene oxide-PEG-NH2,p-SCN-Bn-NOTAd63 | 220b | +4 | Mice bearing cbgLuc-MDA-MB-231 tumor nodules in lungs |
| 64Cu-multifunctional mesoporous silica NP-800CWe64 | 175.3b | −3.3 | Tumor-bearing mice |
| 64Cu-NOTA-hollow mesoporous silica NP-ZW800-PEG-TRC105 (ref. 65) | 194b | −5.1 | Tumor-bearing mice |
| Cy5 dye-encapsulating core–shell silica NP66 | 7b | — | Athymic nude mice with human melanoma |
| IONPs-N-(trimethoxysilylpropyl)ethylenediaminetriacetate trisodium salt67 | 29b | −39 | Mouse with blood–brain barrier disruption and under magnetic targeting |
| DL-Poly(L-lactide) NP68 | 187.7b | −37.7 | Mice |
| PEG-Poly(L-lactide)-PEG NP68 | 171.5b | −2.2 | Mice |
| Methoxy-PEG-poly(lactide-co-glycolide)-PEG-Methoxy (PELGE)69 | 100c | — | Mice |
| Yb2O3-Silanated m-PEG70 | 175c | −0.9 | Mice |
All pharmacokinetic data were fitted to one-compartment (C(t) = C(0)·e−kt + C(∞)) and two-compartment pharmacokinetic models (C(t) = Cc(0)·e−kct + Cp(0)·e−kpt). The two-compartment kinetic model assumed that the distribution of NPs in the central compartment (arterial blood and highly perfused tissues including kidneys and liver) is practically instantaneous compared to the distribution of NPs in the peripheral compartment (poorly perfused tissues such as muscles). Results for kinetic fits are given in Fig. S1 and Table S1 in the ESI.† 95% confidence intervals of all models were calculated as described previously.48
2.2. Prediction of rate constants for clearance of NPs from blood
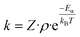 | (1) |
 | (2) |
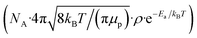 and filling θ in eqn (1) and (2), rate constants for clearance based on penetration pathways (kpenetration) could be
and filling θ in eqn (1) and (2), rate constants for clearance based on penetration pathways (kpenetration) could be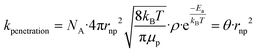 | (3) |
Clearance of NPs by the reticuloendothelial system depends on interaction between NPs and phagocytes (i.e., macrophages). Encounters between NPs and the macrophages may trap NPs, influencing clearance rates of NPs in the blood. According to collision theory, the frequency of encounters between NPs and macrophages (Zm, s−1) in aqueous solutions is78
| Zm = 4πRDr | (4) |
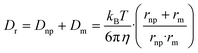 | (5) |
 | (6) |
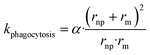 | (7) |
To our knowledge, there are no experimentally derived values for θ and α published in the literature. However, the relationship between the rate constant k and radius of NPs allows extracting the universal θ and α for all collected NP datasets. NPs can be eliminated by different pathways, resulting in total clearance of NPs from blood. The total rate constant k for clearance of NPs from blood can be obtained by assuming that underling mechanisms (penetration and phagocytosis) operate in parallel (ESI† Methods 1.1 and Fig. S2). The total rate constant k for clearance is thus 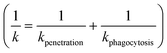 described generically as:
described generically as:
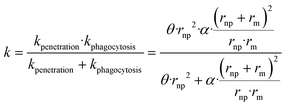 | (8) |
| ln(kc) = ln(Zm) + ln(ρ) + δ·ΔGLW(h) | (9) |
| Symbol | Description | Unit | Typical or default value |
|---|---|---|---|
| C 0 | Initial concentration of NP | μ(n)g g−1(mL−1) | — |
| C c | Initial concentration of NP in central compartment | μ(n)g g−1(mL−1) | — |
| C p | Initial concentration of NP in peripheral compartment | μ(n)g g−1(mL−1) | — |
| d | Diameter | nm | — |
| D m | Diffusion constant of monocyte/macrophage | m2 s−1 | — |
| D np | Diffusion constant of NP | m2 s−1 | — |
| D r | Relative diffusion constant between NP and macrophage | m2 s−1 | — |
| E a | Activation energy | J | — |
| h | Separation distance between the interacting surfaces | nm | 0.157 |
| k | Rate constant for clearance in one-compartment | h−1 | — |
| k B | Boltzmann constant | J K−1 | 1.38 × 1023 |
| k c | Rate constant for clearance in central compartment | h−1 | — |
| k p | Rate constant for clearance in peripheral compartment | h−1 | — |
| k penetration | Rate constant for penetration | s−1 | — |
| k phagocytosis | Rate constant for phagocytosis | s−1 | — |
| N A | Avogadro constant | mol−1 | 6.02 × 1023 |
| R | The sum of rnp and rm | nm | — |
| r m | Radius of macrophage | μm | 10.5 |
| r np | Radius of NP | nm | — |
| T | Temperature | K | — |
| Z | Collision frequency in general | s−1 | — |
| Z m | Collision frequency between NP and macrophage | s−1 | — |
| Z p | Collision frequency between NP and pore | s−1 | — |
| ΔGLW(h) | van der Waals interaction energy | J | — |
| η | Dynamic viscosity of blood | m2 s−1 | — |
| μ p | Reduced mass of NP | kg | — |
| ρ | Steric factor | Unitless | — |
| σ p | Interaction cross section | nm2 | — |
| γ np LW | van der Waals free energies of NP coatings | J m−2 | — |
| γ m LW | van der Waals free energies of macrophage | J m−2 | 30 |
3. Results and discussion
3.1. Fits for clearance rate constants of NPs in blood
All fitting profiles and results based on one- and two-compartment kinetics for 19 data with different NP types (on blood clearance) are shown in Fig. S1 and Table S1,† respectively. Most NPs fitted well into the one-compartment model. An exception was noted for PLGA-mPEG153–5000 (p = 0.14). Besides, the statistical significance of three two-compartment fittings could not be calculated (two PAMAM CNDs and one CdTe-QD) because the number of data points is too small for a two-compartment kinetics with four parameters. Some two-compartment fittings (QDPEG5000/2000, QD CdTe/CdS, IONPs-PEG2000, PLGA-mPEG256-5000 and PLGA-mPEG61-5000) showed increasing blood concentrations over time due to equilibration or redistribution of NPs between tissues and the vascular system,49 which is not captured by our model.Fig. 2 shows all rate constants for clearance based on one- and two-compartment kinetics as a function of NP diameter. Most one-compartment rate constants k for clearance vary between the rate constants kc and kp based on two-compartment kinetics (kp < k < kc). The one-compartment parameter k (in black) seems to increase with NP size and then to decrease with increasing NP size. The distribution of kc (in red) relative to the NP size is more variable than k, indicating that size is not the only factor affecting kc. All two-compartment fittings show that the rate constants for clearance of the central compartment are greater than those of the peripheral compartment (kc ≥ kp). The rate constants kp (in blue) for clearance of the peripheral compartment for all NPs are close to zero.
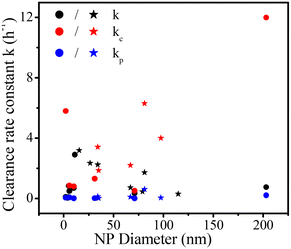 | ||
| Fig. 2 Rate constants for clearance based on one- (k) and two-compartment (kc and kp) kinetics for pegylated NPs (stars) and non-pegylated NPs (dots) versus NP diameter. | ||
Non-pegylated NPs (ZnO NP, 10 nm) have the lowest rate constant kp (0.002) for clearance in the peripheral compartment, and the corresponding half-life is 346 hours. The most extended half-life is obtained for one non-pegylated NP (ZnO NP), opposite to the idea that pegylated NPs usually have long half-lives as the low surface hydrophobicity evades opsonin modification and reduces reticuloendothelial system capture.45 Chen et al.18 reported that a considerable number of ZnO NPs are captured by lung macrophages, increasing NP circulation time in pulmonary circulation. NPs that enter the lungs may travel from the interstitium to the lymphatic system8 where they are likely re-released into the blood. These complex mechanisms may cause prolonged NP circulation time in blood. Besides, the solubility of ZnO NPs may also increase their blood circulation time because researchers took the concentration of (ref. 65) Zn as the concentration of ZnO NPs.18
3.2. Rate constants k for clearance (obtained from one-compartment kinetics) as a function of NP size
19 rate constants (Table 1) based on one-compartment were used to parameterize the generic model in Fig. 3 (black symbols). The generic model (NP size-based, obtained from eqn (8)) following penetration and phagocytosis mechanisms is shown in Fig. 3 (red curve). The rate constants k for clearance based on one-compartment kinetics were statistically significant related to the radius of NPs reflecting pore penetration and phagocytosis, proving that taking size as the only parameter could be used to estimate the rate constants k for clearance of NPs from blood.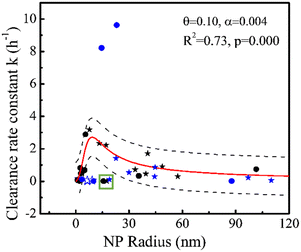 | ||
| Fig. 3 Rate constant k (h−1) for clearance based on one-compartment kinetics versus radius (nm) of NPs for pore penetration and phagocytosis with data on pegylated NPs (stars) and non-pegylated NPs (dots) for hydrodynamic size (solid) and TEM size (open). Black symbols denote 19 data points for parameterization and blue symbols denote 16 data points for validation. All symbols denote experimental data and the red curve was obtained using eqn (8). The dashed black lines show 95% confidence intervals of the model. The green square marks two overestimated outliers (black symbols) we did not involve in the regression. | ||
Fig. 3 shows that rate constants k for clearance increase with increasing NP size when the NP's hydrodynamic diameter is smaller than ∼20 nm, consistent with the penetration mechanism where kpenetration increases with increasing NP size (kpenetration ∼ rnp2, eqn (3)). Our modeling is similar to the ratio (∼rnp2) of distribution of a solute between a pore and solutions.85 By contrast, Fig. 3 also shows that rate constants k for clearance decrease with increasing NP size when the NP's hydrodynamic diameter is larger than ∼20 nm, consistent with the phagocytosis mechanism where kphagocytosis decreases with increasing NP size (kphagocytosis ∼ rnp−1, eqn (7)). According to the Stokes–Einstein relation, larger NPs are expected to be less mobile (the diffusion coefficient Dnp is inversely proportional to the size, see Methods eqn (5)), resulting in fewer encounters between NPs and macrophages, and reducing phagocytosis.
The clearance of NPs from blood is the result of the dual action of penetration25 and phagocytosis,86 which is also the result of mutual restriction of NP collision and diffusion ability. The increased phase (NP from 0 to ∼20 nm) of rate constants k with increasing NP size illustrates that penetration might contribute more than phagocytosis. At the same time, the slope changes from positive to negative as the particle size increases, which seems to indicate that phagocytosis becomes more dominant following the increase of NP size. Penetration might contribute more than phagocytosis for clearance of smaller NPs for several reasons. Small NPs (for example, d = 18 nm) with strongly curved surfaces lead to protein interactions distinct from larger NPs (for example, d > 78 nm). Reduced opsonin attachment41 increases pore penetration of small NPs and reduces recognition by macrophages.87
The highest rate constant k for clearance from blood occurs when the hydrodynamic diameter of the NP is around ∼20 nm, which may imply that NP–pore/macrophage interactions via collision and diffusion are beneficial to each other. At this time, kpenetration might equal kphagocytosis. Generally, the clearance of NPs from blood includes the distribution of NPs from blood to organs and clearance of NPs from blood to urine (outside of the body) by glomerular filtration. We call the latter absolute clearance, since it is impossible for NPs to return from the urine to blood. Sizes of 10–20 nm (ref. 37 and 88) can rapidly be taken up by the liver and sizes of less than 5–15 (ref. 33 and 89) nm are more easily excreted through glomerular filtration,31 which increase the clearance of NPs from blood. By contrast, NPs with sizes of 20–200 nm (ref. 41) can remain in circulation for an extended period, as confirmed by our modeling. The decreasing slope in Fig. 3 might not apply when the model covers larger NP sizes (to include micron sizes) due to other factors like gravitational pull,41 which can be ignored for NPs. NP aggregation could also take place to increase cellular uptake,90 which is not covered by our generic modeling and can be carried out in the future.
Clearly, our model is not perfect (R2 = 0.73) as penetration and phagocytosis are the only pathways considered. To validate the model, we used 16 rate constants from studies not used for parameterization (four NPs with TEM size marked as open blue symbols and 12 NPs with hydrodynamic size marked as solid blue symbols in Fig. 3). Three of the four data points with only core size and TEM size (marked as open blue symbols in Fig. 3) are out of the generic model due to lack of well-defined hydrodynamic sizes. Their hydrodynamic behavior may render their penetrative capacity uncertain. Hydrodynamic sizes are usually larger than primary size due to hydration layers, electric double layers, and aggregation.91 Besides, 8 of the 12 data points marked in solid blue symbols (Fig. 3) can be predicted well by our generic model because they are within 95% confidence intervals (dashed line in Fig. 3), which support that the generic model could provide generic prediction of various NPs. The model based on one parameter (radius of NPs) allows one to avoid overfitting. Two of the 12 data points (46 nm AuNP-Dextran and 29 nm IONPs) were greatly underestimated (k ∼ 8–10 h−1) and 2 of the 12 data points (38 nm AuNP-PEG and 20 nm AuNP-mixed groups) were overestimated by our model. The two overestimated data points came from the same study,60 which might reflect specific conditions not covered by the model. The two underestimations (Fig. 3) were obtained from immunodeficient mice or mice with blood–brain barrier disruption under magnetic targeting, whereas 17 of the 19 data points for model parameterization were obtained from healthy animals. Although some studies reported that tumor-bearing does not significantly affect the overall biodistribution of NPs,92,93 the influence of the disease on NP clearance from blood needs further research. In addition, surface charge44 could influence NP behavior (e.g., 29 nm IONPs are highly negative). The two data points (PAA-coated NP and PAA-PEG-coated NP, marked by a green square in Fig. 3) out of 95% confidence intervals confirm that other factors exist (e.g., surface coatings, discussed in the later section). Other pathways not considered by our generic model could influence NP clearance behavior, causing prediction error, e.g., clathrin-mediated internalization by endothelial cells.94
3.3. Rate constants kc for clearance (obtained from two-compartment kinetics) as a function of NP size and surface coating
In our extended phagocytosis-based model (2.2.4), the van der Waals interaction energy (ΔGLW(h)) between NPs and macrophages was used to predict the rate constants kc for clearance (eqn (9)). Seven out of the 19 data points for parameterization were used to build the extended model because of available information on surface coatings in Fig. 4 (black symbols). The linear regression (red line, eqn (9)) between van der Waals interaction energy ΔGLW(h) and ln(kc) − ln(Zm) is shown in Fig. 4. The regression is statistically significant with a high R2 (0.95) and low p-value ((<0.0001)), indicating that interaction between macrophages and NPs drives the clearance of NPs in the well-perfused compartment (kc). After involving properties of surface coatings, outliers in the generic model (marked in a green square in Fig. 3) fitted well to the extended model (Fig. 4), indicating that the behavior of some NPs in the blood can be affected by both NP size and surface coating.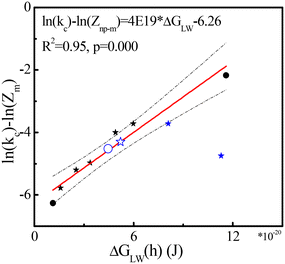 | ||
| Fig. 4 ln(kc) − ln(Zm) as a function of van der Waals interaction energy ΔGLW(h) (J) for pegylated NPs (stars) and non-pegylated NPs (dots) with hydrodynamic size (solid) and TEM size (open). All symbols denote experimental data and the red line was obtained with eqn (9). The dashed black lines show 95% confidence intervals of the model. Blue symbols denote four tested data points (Table 1) from studies not used for parameterization.68–70 | ||
Four independent data points are added (Tables S1 and S2†) to test the extended model and Fig. 4 shows that three out of the four data points are within the 95% confidence intervals (dashed line in Fig. 4). The prediction of NP coated by mPEG-PLA (Poly(L-lactide))-mPEG (PELE) copolymers with 30% PEG68 is deeply lower than our estimation (Fig. 4). The surficial structure of PELE copolymers with 30% PEG was not reported in the original study, and the structure from work in ref. 95 was used, which may have caused deviations. Our current modeling does not consider the proportion of coatings, which might cause prediction errors. In addition, deviations in rate constants for clearance may be introduced by multiple interlaced data point lines in the original image. Interestingly, two tested data points with TEM size (170–190 nm) can be estimated well, illustrating that the function of size might be diluted by the effects of surface coatings in some scales. As the number of data is limited, more data is needed to increase the accuracy and precision of the model.
van der Waals energies explain the clearance kinetics of NPs in blood, via phagocytosis, as shown in Fig. 4. Indeed, van der Waals energies appear especially relevant for opsonin/macrophage interaction.96 Particle/pathogen uptake involves macrophage polarization97 and van der Waals energies are essential forces from induced dipoles: forces from polarization.98 In addition, the coatings we used in current model show neutral or negative charges (Table 1). Surface charge44 and targeting ligands99 may affect opsonin adsorption as well, in turn affecting the clearance of NPs by phagocytosis. Our model might be extended in the future to include more interaction energies, such as electrostatic energy100 and binding energy of ligands and receptors,101 to explore the effect of net positive surface charges and ligand modification on NP accumulation102 or clearance in the body. In addition, the clearance of NPs in peripheral compartments (e.g., muscles) involves complex mechanisms, and the rate constants kp for clearance cannot be estimated accurately.
3.4. Recommendations
The rate constants for clearance calculated in our study may be applied in PBPK models for nanomedicine research and NP risk assessment. To increase the application domain for more NPs, we explored options for linking clearance to NP size and surface coating. Nevertheless, several limitations should be noted in the present study. First, our study did not consider aggregation and protein modification. Secondly, our generic model only involved size as the only variable, while the expanded model requires specific information on single types of surface coatings. Characterization of NPs with mixed coatings60 need more methods to define in the future. Thirdly, the model application to soluble NPs (e.g., ZnO and AgNPs)103 requires combining properties of NPs and ions. Fourthly, our dataset only included spherical NPs with administration by intravenous injection due to limited data. Lastly, we limited ourselves to NPs because data on microparticles (MPs) are lacking and theories on NPs may not apply to MPs due to the greater gravity or resistance.41 In the future, we will therefore focus on addressing these limitations.4. Conclusions
The data on clearance of NPs from blood after intravenous injection generally fit one- and two-compartment kinetics. The generic model (NP size-based) was used to estimate rate constants for clearance obtained by one-compartment kinetics following pore penetration and phagocytosis pathways. Hydrodynamic diameter ∼20 nm is reported as the optimal size for fast clearance of NPs from blood in the current dataset. The effect of surface coatings on clearance rate constants kc based on two-compartment kinetics can be explained by an extended model (NP size- and surface coating-based), combining properties of NPs (size and surface coatings) and macrophages. These models may provide basic approaches to increase the application domain of PBPK models for the design of NPs in drug delivery or assessing the biological hazards of NPs.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We would like to express our gratitude to the China Scholarship Council for the support of the first author at Radboud University Nijmegen.References
- R. Lopez-Cabeza, M. Kah, R. Grillo, M. Koutny, J. Salac, Z. Bilkova, M. Eghbalinejad and J. Hofman, Tebuconazole and terbuthylazine encapsulated in nanocarriers: preparation, characterization and release kinetics, Environ. Sci.: Nano, 2022, 9, 1427–1438 RSC.
- D. Peng, Y. Du, Y. W. Shi, D. Mao, X. H. Jia, H. Li, Y. K. Zhu, K. Wang and J. Tian, Precise diagnosis in different scenarios using photoacoustic and fluorescence imaging with dual-modality nanoparticles, Nanoscale, 2016, 8, 14480–14488 RSC.
- M. Goel, Y. Mackeyev and S. Krishnan, Radiolabeled nanomaterial for cancer diagnostics and therapeutics: principles and concepts, Cancer Nanotechnol., 2023, 14, 15 CrossRef.
- J. J. Shi, P. W. Kantoff, R. Wooster and O. C. Farokhzad, Cancer nanomedicine: progress, challenges and opportunities, Nat. Rev. Cancer, 2017, 17, 20–37 CrossRef CAS PubMed.
- A. Truskewycz, H. Yin, N. Halberg, D. T. H. Lai, A. S. Ball, V. K. Truong, A. M. Rybicka and I. Cole, Carbon Dot Therapeutic Platforms: Administration, Distribution, Metabolism, Excretion, Toxicity, and Therapeutic Potential, Small, 2022, 18, e2106342 CrossRef PubMed.
- P. Kocbek, K. Teskac, M. E. Kreft and J. Kristl, Toxicological Aspects of Long-Term Treatment of Keratinocytes with ZnO and TiO2 Nanoparticles, Small, 2010, 6, 1908–1917 CrossRef CAS.
- A. S. Anand, K. Jain, A. Chauhan, D. N. Prasad and E. Kohli, Zinc oxide nanoparticles trigger dysfunction of mitochondrial respiratory complexes and repair dynamics in human alveolar cells, Toxicol. Ind. Health, 2023, 39, 127–137 CrossRef CAS.
- A. Shimada, N. Kawamura, M. Okajima, T. Kaewamatawong, H. Inoue and T. Morita, Translocation pathway of the intratracheally instilled ultrafine particles from the lung into the blood circulation in the mouse, Toxicol. Pathol., 2006, 34, 949–957 CrossRef.
- Y. Pan, S. Neuss, A. Leifert, M. Fischler, F. Wen, U. Simon, G. Schmid, W. Brandau and W. Jahnen-Dechent, Size-dependent cytotoxicity of gold nanoparticles, Small, 2007, 3, 1941–1949 CrossRef CAS.
- W. H. De Jong and P. J. A. Borm, Drug delivery and nanoparticles: Applications and hazards, Int. J. Nanomed., 2008, 3, 133–149 CrossRef CAS PubMed.
- M. W. Wang, P. Zhang, Z. Y. Li, Y. Yan, X. Cheng, G. Wang and X. S. Yang, Different cellular mechanisms from low- and high-dose zinc oxide nanoparticles-induced heart tube malformation during embryogenesis, Nanotoxicology, 2022, 16, 580–596 CrossRef CAS PubMed.
- F. A. Monikh, M. G. Vijver, R. Kortet, I. Lynch and W. Peijnenburg, Emerging investigator series: perspectives on toxicokinetics of nanoscale plastic debris in organisms, Environ. Sci.: Nano, 2022, 9, 1566–1577 RSC.
- M. Kumar, P. Kulkarni, S. F. Liu, N. Chemuturi and D. K. Shah, Nanoparticle biodistribution coefficients: A quantitative approach for understanding the tissue distribution of nanoparticles, Adv. Drug Delivery Rev., 2023, 194, 114708 CrossRef CAS.
- D. P. K. Lankveld, A. G. Oomen, P. Krystek, A. Neigh, A. Troost-de Jong, C. W. Noorlander, J. C. H. Van Eijkeren, R. E. Geertsma and W. H. De Jong, The kinetics of the tissue distribution of silver nanoparticles of different sizes, Biomaterials, 2010, 31, 8350–8361 CrossRef CAS.
- Z. M. Lin, N. A. Monteiro-Riviere and J. E. Riviere, A physiologically based pharmacokinetic model for polyethylene glycol-coated gold nanoparticles of different sizes in adult mice, Nanotoxicology, 2016, 10, 162–172 CAS.
- V. V. Kasyanova and I. N. Bazhukova, Modeling of cerium oxide nanoparticles pharmacokinetics, AIP Conf. Proc., 2020, 2313, 080015 CrossRef CAS.
- G. Bachler, N. von Goetz and K. Hungerbuhler, Using physiologically based pharmacokinetic (PBPK) modeling for dietary risk assessment of titanium dioxide (TiO2) nanoparticles, Nanotoxicology, 2015, 9, 373–380 CrossRef CAS PubMed.
- W. Y. Chen, Y. H. Cheng, N. H. Hsieh, B. C. Wu, W. C. Chou, C. C. Ho, J. K. Chen, C. M. Liao and P. Lin, Physiologically based pharmacokinetic modeling of zinc oxide nanoparticles and zinc nitrate in mice, Int. J. Nanomed., 2015, 10, 6277–6292 CAS.
- A. R. R. Pery, C. Brochot, P. H. M. Hoet, A. Nemmar and F. Y. Bois, Development of a physiologically based kinetic model for 99m-Technetium-labelled carbon nanoparticles inhaled by humans, Inhalation Toxicol., 2009, 21, 1099–1107 CrossRef PubMed.
- H. A. Lee, T. L. Leavens, S. E. Mason, N. A. Monteiro-Riviere and J. E. Riviere, Comparison of Quantum Dot Biodistribution with a Blood-Flow-Limited Physiologically Based Pharmacokinetic Model, Nano Lett., 2009, 9, 794–799 CrossRef CAS.
- L. Kagan, P. Gershkovich, K. M. Wasan and D. E. Mager, Dual Physiologically Based Pharmacokinetic Model of Liposomal and Nonliposomal Amphotericin B Disposition, Pharm. Res., 2014, 31, 35–45 CrossRef CAS PubMed.
- M. G. Li, Z. Panagi, K. Avgoustakis and J. Reineke, Physiologically based pharmacokinetic modeling of PLGA nanoparticles with varied mPEG content, Int. J. Nanomed., 2012, 7, 1345–1356 CAS.
- D. Dong, X. Wang, H. L. Wang, X. W. Zhang, Y. F. Wang and B. J. Wu, Elucidating the in vivo fate of nanocrystals using a physiologically based pharmacokinetic model: a case study with the anticancer agent SNX-2112, Int. J. Nanomed., 2015, 10, 2521–2535 CAS.
- D. S. Li, G. Johanson, C. Emond, U. Carlander, M. Philbert and O. Jolliet, Physiologically based pharmacokinetic modeling of polyethylene glycol-coated polyacrylamide nanoparticles in rats, Nanotoxicology, 2014, 8, 128–137 CrossRef CAS.
- X. W. Liang, H. L. Wang, J. E. Grice, L. Li, X. Liu, Z. P. Xu and M. S. Roberts, Physiologically Based Pharmacokinetic Model for Long-Circulating Inorganic Nanoparticles, Nano Lett., 2016, 16, 939–945 CrossRef CAS PubMed.
- W. C. Chou, Y. H. Cheng, J. E. Riviere, N. A. Monteiro-Riviere, W. G. Kreyling and Z. M. Lin, Development of a multi-route physiologically based pharmacokinetic (PBPK) model for nanomaterials: a comparison between a traditional versus a new route-specific approach using gold nanoparticles in rats, Part. Fibre Toxicol., 2022, 19, 47 CrossRef CAS.
- B. Q. Lu, A. J. Hendriks and T. M. Nolte, A generic model based on the properties of nanoparticles and cells for predicting cellular uptake, Colloids Surf., B, 2022, 209, 112155 CrossRef CAS.
- A. Nacev, C. Beni, O. Bruno and B. Shapiro, The behaviors of ferromagnetic nano-particles in and around blood vessels under applied magnetic fields, J. Magn. Magn. Mater., 2011, 323, 651–668 CrossRef CAS PubMed.
- S. Seo, H. Kim, J. H. Sung, N. Choi, K. Lee and H. N. Kim, Microphysiological systems for recapitulating physiology and function of blood-brain barrier, Biomaterials, 2020, 232, 119732 CrossRef CAS PubMed.
- Y. H. Kim, K. J. Kim, D. Z. D'Argenio and E. D. Crandall, Characteristics of Passive Solute Transport across Primary Rat Alveolar Epithelial Cell Monolayers, Membranes, 2021, 11, 331 CrossRef CAS.
- E. Gagliardini, S. Conti, A. Benigni, G. Remuzzi and A. Remuzzi, Imaging of the Porous Ultrastructure of the Glomerular Epithelial Filtration Slit, J. Am. Soc. Nephrol., 2010, 21, 2081–2089 CrossRef.
- H. Sarin, Physiologic upper limits of pore size of different blood capillary types and another perspective on the dual pore theory of microvascular permeability, Vasc. Cell, 2010, 2, 14 Search PubMed.
- S. M. Moghimi, A. C. Hunter and T. L. Andresen, Factors Controlling Nanoparticle Pharmacokinetics: An Integrated Analysis and Perspective, Annu. Rev. Pharmacol. Toxicol., 2012, 52, 481–503 CrossRef CAS.
- W. Poon, Y. N. Zhang, B. Ouyang, B. R. Kingston, J. L. Y. Wu, S. Wilhelm and W. C. W. Chan, Elimination Pathways of Nanoparticles, ACS Nano, 2019, 13, 5785–5798 CrossRef CAS.
- Y. Liu, W. Huang, C. F. Xiong, Y. X. Huang, B. J. Chen, L. Racioppi, N. Chao and T. Vo-Dinh, Biodistribution and sensitive tracking of immune cells with plasmonic gold nanostars, Int. J. Nanomed., 2019, 14, 3403–3411 CrossRef CAS.
- T. M. Nolte, B. Q. Lu and A. J. Hendriks, Nanoparticles in bodily tissues: predicting their equilibrium distributions, Environ. Sci.: Nano, 2023, 10, 424–439 RSC.
- B. Wang, X. He, Z. Y. Zhang, Y. L. Zhao and W. Y. Feng, Metabolism of Nanomaterials in Vivo: Blood Circulation and Organ Clearance, Acc. Chem. Res., 2013, 46, 761–769 CrossRef CAS.
- S. D. Li and L. Huang, Pharmacokinetics and biodistribution of nanoparticles, Mol. Pharmaceutics, 2008, 5, 496–504 CrossRef CAS.
- K. Kettler, K. Veltman, D. van de Meent, A. van Wezel and A. J. Hendriks, Cellular uptake of nanoparticles as determined by particle properties, experimental conditions, and cell type, Environ. Toxicol. Chem., 2014, 33, 481–492 CrossRef CAS.
- J. Malaczewska, Impact of noble metal nanoparticles on the immune system of animals, Med. Weter., 2014, 70, 204–208 Search PubMed.
- X. P. Duan and Y. P. Li, Physicochemical Characteristics of Nanoparticles Affect Circulation, Biodistribution, Cellular Internalization, and Trafficking, Small, 2013, 9, 1521–1532 CrossRef CAS PubMed.
- P. Decuzzi, B. Godin, T. Tanaka, S. Y. Lee, C. Chiappini, X. Liu and M. Ferrari, Size and shape effects in the biodistribution of intravascularly injected particles, J. Controlled Release, 2010, 141, 320–327 CrossRef CAS.
- H. L. Qian, K. Wang, M. T. Lv, C. S. Zhao, H. Wang, S. C. Wen, D. C. Huang, W. Chen and Y. A. Zhong, Recent advances on next generation of polyzwitterion-based nano-vectors for targeted drug delivery, J. Controlled Release, 2022, 343, 492–505 CrossRef CAS.
- P. Aggarwal, J. B. Hall, C. B. McLeland, M. A. Dobrovolskaia and S. E. McNeil, Nanoparticle interaction with plasma proteins as it relates to particle biodistribution, biocompatibility and therapeutic efficacy, Adv. Drug Delivery Rev., 2009, 61, 428–437 CrossRef CAS.
- D. E. Owens and N. A. Peppas, Opsonization, biodistribution, and pharmacokinetics of polymeric nanoparticles, Int. J. Pharm., 2006, 307, 93–102 CrossRef CAS.
- G. Storm, S. O. Belliot, T. Daemen and D. D. Lasic, Surface modification of nanoparticles to oppose uptake by the mononuclear phagocyte system, Adv. Drug Delivery Rev., 1995, 17, 31–48 CrossRef CAS.
- N. Hoshyar, S. Gray, H. B. Han and G. Bao, The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction, Nanomedicine, 2016, 11, 673–692 CrossRef CAS PubMed.
- B. Q. Lu, J. Q. Wang, P. T. J. Scheepers, A. J. Hendriks and T. M. Nolte, Generic prediction of exocytosis rate constants by size-based surface energies of nanoparticles and cells, Sci. Rep., 2022, 12, 17813 CrossRef CAS PubMed.
- E. Yaghini, E. Tacconi, A. Pilling, P. Rahman, J. Broughton, I. Naasani, M. R. S. Keshtgar, A. J. MacRobert and O. Della Pasqua, Population pharmacokinetic modelling of indium-based quantum dot nanoparticles: preclinical in vivo studies, Eur. J. Pharm. Sci., 2021, 157, 105639 CrossRef CAS PubMed.
- D. E. Mager, V. Mody, C. Xu, A. Forrest, W. G. Lesniak, S. S. Nigavekar, M. T. Kariapper, L. Minc, M. K. Khan and L. P. Balogh, Physiologically Based Pharmacokinetic Model for Composite Nanodevices: Effect of Charge and Size on In Vivo Disposition, Pharm. Res., 2012, 29, 2534–2542 CrossRef CAS.
- Y. B. Han, T. T. Wang, H. H. Liu, S. H. Zhang, H. Zhang, M. T. Li, Q. Sun and Z. Li, The release and detection of copper ions from ultrasmall theranostic Cu2-xSe nanoparticles, Nanoscale, 2019, 11, 11819–11829 RSC.
- K. C. Nguyen, Y. Zhang, J. Todd, K. Kittle, D. Patry, D. Caldwell, M. Lalande, S. Smith, D. Parks, M. Navarro, A. Massarsky, T. W. Moon, W. G. Willmore and A. F. Tayabali, Biodistribution and Systemic Effects in Mice Following Intravenous Administration of Cadmium Telluride Quantum Dot Nanoparticles, Chem. Res. Toxicol., 2019, 32, 1491–1503 Search PubMed.
- F. Naz, V. Koul, A. Srivastava, Y. K. Gupta and A. K. Dinda, Biokinetics of ultrafine gold nanoparticles (AuNPs) relating to redistribution and urinary excretion: a long-term in vivo study, J. Drug Targeting, 2016, 24, 720–729 CrossRef CAS.
- W. M. Xue, Y. Y. Liu, N. Zhang, Y. D. Yao, P. Ma, H. Y. Wen, S. P. Huang, Y. N. Luo and H. M. Fan, Effects of core size and PEG coating layer of iron oxide nanoparticles on the distribution and metabolism in mice, Int. J. Nanomed., 2018, 13, 5719–5731 CrossRef CAS.
- K. Avgoustakis, A. Beletsi, Z. Panagi, P. Klepetsanis, E. Livaniou, G. Evangelatos and D. S. Ithakissios, Effect of copolymer composition on the physicochemical characteristics, in vitro stability, and biodistribution of PLGA-mPEG nanoparticles, Int. J. Pharm., 2003, 259, 115–127 CrossRef CAS PubMed.
- Y. Wenger, R. J. Schneider, G. R. Reddy, R. Kopelman, O. Jolliet and M. A. Philbert, Tissue distribution and pharmacokinetics of stable polyacrylamide nanoparticles following intravenous injection in the rat, Toxicol. Appl. Pharmacol., 2011, 251, 181–190 CrossRef CAS PubMed.
- W. S. Cho, M. Cho, J. Jeong, M. Choi, B. S. Han, H. S. Shin, J. Hong, B. H. Chung, J. Jeong and M. H. Cho, Size-dependent tissue kinetics of PEG-coated gold nanoparticles, Toxicol. Appl. Pharmacol., 2010, 245, 116–123 CrossRef CAS.
- R. H. Yang, L. W. Chang, J. P. Wu, M. H. Tsai, H. J. Wang, Y. C. Kuo, T. K. Yeh, C. S. Yang and P. Lin, Persistent tissue kinetics and redistribution of nanoparticles, quantum dot 705, in mice: ICP-MS quantitative assessment, Environ. Health Perspect., 2007, 115, 1339–1343 CrossRef CAS PubMed.
- Arnida, M. M. Janát-Amsbury, A. Ray, C. M. Peterson and H. Ghandehari, Geometry and surface characteristics of gold nanoparticles influence their biodistribution and uptake by macrophages, Eur. J. Pharm. Biopharm., 2011, 77, 417–423 CrossRef CAS PubMed.
- X. S. Liu, H. Li, Y. J. Chen, Q. Jin, K. F. Ren and J. Ji, Mixed-Charge Nanoparticles for Long Circulation, Low Reticuloendothelial System Clearance, and High Tumor Accumulation, Adv. Healthcare Mater., 2014, 3, 1439–1447 CrossRef CAS PubMed.
- G. D. Zhang, Z. Yang, W. Lu, R. Zhang, Q. Huang, M. Tian, L. Li, D. Liang and C. Li, Influence of anchoring ligands and particle size on the colloidal stability and in vivo biodistribution of polyethylene glycol-coated gold nanoparticles in tumor-xenografted mice, Biomaterials, 2009, 30, 1928–1936 CrossRef CAS.
- A. L. Bailly, F. Correard, A. Popov, G. Tselikov, F. Chaspoul, R. Appay, A. Al-Kattan, A. V. Kabashin, D. Braguer and M. A. Esteve, In vivo evaluation of safety, biodistribution and pharmacokinetics of laser-synthesized gold nanoparticles, Sci. Rep., 2019, 9, 12890 CrossRef.
- D. Z. Yang, L. Z. Feng, C. A. Dougherty, K. E. Luker, D. Q. Chen, M. A. Cauble, M. M. B. Holl, G. D. Luker, B. D. Ross, Z. Liu and H. Hong, In vivo targeting of metastatic breast cancer via tumor vasculature-specific nano-graphene oxide, Biomaterials, 2016, 104, 361–371 CrossRef CAS PubMed.
- F. Chen, T. R. Nayak, S. Goel, H. F. Valdovinos, H. Hong, C. P. Theuer, T. E. Barnhart and W. B. Cai, In Vivo Tumor Vasculature Targeted PET/NIRF Imaging with TRC105(Fab)-Conjugated, Dual-Labeled Mesoporous Silica Nanoparticles, Mol. Pharmaceutics, 2014, 11, 4007–4014 CrossRef CAS.
- F. Chen, H. Hong, S. X. Shi, S. Goel, H. F. Valdovinos, R. Hernandez, C. P. Theuer, T. E. Barnhart and W. B. Cai, Engineering of Hollow Mesoporous Silica Nanoparticles for Remarkably Enhanced Tumor Active Targeting Efficacy, Sci. Rep., 2014, 4, 5080 CrossRef CAS PubMed.
- M. Benezra, O. Penate-Medina, P. B. Zanzonico, D. Schaer, H. Ow, A. Burns, E. DeStanchina, V. Longo, E. Herz, S. Iyer, J. Wolchok, S. M. Larson, U. Wiesner and M. S. Bradbury, Multimodal silica nanoparticles are effective cancer-targeted probes in a model of human melanoma, J. Clin. Invest., 2011, 121, 2768–2780 CrossRef CAS PubMed.
- Z. Z. Sun, M. Worden, J. A. Thliveris, S. Hombach-Klonisch, T. Klonisch, J. van Lierop, T. Hegmann and D. W. Miller, Biodistribution of negatively charged iron oxide nanoparticles (IONPs) in mice and enhanced brain delivery using lysophosphatidic acid (LPA), Nanomedicine, 2016, 12, 1775–1784 CrossRef CAS PubMed.
- X. Q. Shan, C. S. Liu, Y. Yuan, F. Xu, X. Y. Tao, Y. Sheng and H. J. Zhou, In vitro macrophage uptake and in vivo biodistribution of long-circulation nanoparticles with poly(ethylene-glycol)-modified PLA (BAB type) triblock copolymer, Colloids Surf., B, 2009, 72, 303–311 CrossRef CAS PubMed.
- Y. R. Duan, J. P. Xu, Y. Z. Lin, H. Yu, T. Gong, Y. G. Li and Z. R. Zhang, A preliminary study on MeO-PEG-PLGA-PEG-OMe nanoparticles as intravenous carriers, J. Biomed. Mater. Res., Part A, 2008, 87, 515–523 CrossRef.
- Z. Liu, Z. H. Li, J. H. Liu, S. Gu, Q. H. Yuan, J. S. Ren and X. G. Qu, Long-circulating Er3+-doped Yb2O3 up-conversion nanoparticle as an in vivo X-Ray CT imaging contrast agent, Biomaterials, 2012, 33, 6748–6757 CrossRef CAS.
- M. G. Vijver, Y. J. Zhai, Z. Wang and W. Peijnenburg, Emerging investigator series: the dynamics of particle size distributions need to be accounted for in bioavailability modelling of nanoparticles, Environ. Sci.: Nano, 2018, 5, 2473–2481 RSC.
- C. Y. Loo, E. L. Siew, P. M. Young, D. Traini and W. H. Lee, Toxicity of curcumin nanoparticles towards alveolar macrophage: Effects of surface charges, Food Chem. Toxicol., 2022, 163, 112976 CrossRef CAS PubMed.
- Z. L. Chen and Z. J. You, New expression for collision efficiency of spherical nanoparticles in Brownian coagulation, J. Appl. Math. Mech., 2010, 31, 851–860 CrossRef.
- M. L. Eggersdorfer and S. E. Pratsinis, Agglomerates and aggregates of nanoparticles made in the gas phase, Adv. Powder Technol., 2014, 25, 71–90 CrossRef CAS.
- R. Arvidsson, S. Molander, B. A. Sandén and M. Hassellöv, Challenges in Exposure Modeling of Nanoparticles in Aquatic Environments, Hum. Ecol. Risk Assess., 2011, 17, 245–262 CrossRef CAS.
- M. Farshbaf, H. Valizadeh, Y. Panahi, Y. Fatahi, M. W. Chen, A. Zarebkohan and H. L. Gao, The impact of protein corona on the biological behavior of targeting nanomedicines, Int. J. Pharm., 2022, 614, 121458 CrossRef CAS.
- https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/06%3A_Modeling_Reaction_Kinetics/6.01%3A_Collision_Theory/6.1.06%3A_The_Collision_Theory, 2013.
- M. Smoluchowski, Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen, Phys. Z., 1916, 17, 557–585 Search PubMed.
- K. Cui, C. L. Ardell, N. P. Podolnikova and V. P. Yakubenko, Distinct Migratory Properties of M1, M2, and Resident Macrophages Are Regulated by alpha(D)beta(2) and alpha(M)beta(2) Integrin-Mediated Adhesion, Front. Immunol., 2018, 9, 2650 CrossRef.
- B. B. Hong and A. Z. Panagiotopoulos, Molecular Dynamics Simulations of Silica Nanoparticles Grafted with Poly(ethylene oxide) Oligomer Chains, J. Phys. Chem. B, 2012, 116, 2385–2395 CrossRef CAS.
- A. Darras, J. Fiscina, N. Vandewalle and G. Lumay, Relating Brownian motion to diffusion with superparamagnetic colloids, Am. J. Phys., 2017, 85, 265–270 CrossRef CAS.
- Y. Q. Qie, H. F. Yuan, C. A. von Roemeling, Y. X. Chen, X. J. Liu, K. D. Shih, J. A. Knight, H. W. Tun, R. E. Wharen, W. Jiang and B. Y. S. Kim, Surface modification of nanoparticles enables selective evasion of phagocytic clearance by distinct macrophage phenotypes, Sci. Rep., 2016, 6, 26269 CrossRef CAS PubMed.
- S. A. MacParland, K. M. Tsoi, B. Ouyang, X. Z. Ma, J. Manuel, A. Fawaz, M. A. Ostrowski, B. A. Alman, A. Zilman, W. C. W. Chan and I. D. McGilvray, Phenotype Determines Nanoparticle Uptake by Human Macrophages from Liver and Blood, ACS Nano, 2017, 11, 2428–2443 CrossRef CAS.
- C. J. C. Van Oss, M. K. Chaudhury and R. J. Good, Interfacial Lifshitz-van der Waals and Polar Interactions in Macroscopic Systems, Chem. Rev., 1988, 88, 927–941 CrossRef CAS.
- R. E. Beck and J. S. Schultz, Hindrance of solute diffusion within membranes as measured with microporous membranes of known pore geometry, Biochim. Biophys. Acta, 1972, 255, 273–303 CrossRef CAS PubMed.
- C. D. Walkey, J. B. Olsen, H. B. Guo, A. Emili and W. C. W. Chan, Nanoparticle Size and Surface Chemistry Determine Serum Protein Adsorption and Macrophage Uptake, J. Am. Chem. Soc., 2012, 134, 2139–2147 CrossRef CAS.
- H. L. Gao and Q. He, The interaction of nanoparticles with plasma proteins and the consequent influence on nanoparticles behavior, Expert Opin. Drug Delivery, 2014, 11, 409–420 CrossRef CAS.
- M. Longmire, P. L. Choyke and H. Kobayashi, Clearance properties of nano-sized particles and molecules as imaging agents: considerations and caveats, Nanomedicine, 2008, 3, 703–717 CrossRef CAS.
- H. S. Choi, W. Liu, P. Misra, E. Tanaka, J. P. Zimmer, B. I. Ipe, M. G. Bawendi and J. V. Frangioni, Renal clearance of quantum dots, Nat. Biotechnol., 2007, 25, 1165–1170 CrossRef CAS PubMed.
- P. Nativo, I. A. Prior and M. Brust, Uptake and intracellular fate of surface-modified gold nanoparticles, ACS Nano, 2008, 2, 1639–1644 CrossRef CAS.
- M. Kaasalainen, V. Aseyev, E. von Haartman, D. S. Karaman, E. Makila, H. Tenhu, J. Rosenholm and J. Salonen, Size, Stability, and Porosity of Mesoporous Nanoparticles Characterized with Light Scattering, Nanoscale Res. Lett., 2017, 12, 74 CrossRef.
- V. M. Weiss, H. Lucas, T. Mueller, P. Chytil, T. Etrych, T. Naolou, J. Kressler and K. Mäder, Intended and Unintended Targeting of Polymeric Nanocarriers: The Case of Modified Poly(glycerol adipate) Nanoparticles, Macromol. Biosci., 2018, 18, 1700240 CrossRef.
- M. Lindén, Chapter Seven - Biodistribution and Excretion of Intravenously Injected Mesoporous Silica Nanoparticles: Implications for Drug Delivery Efficiency and Safety, Enzymes, 2018, 43, 155–180 Search PubMed.
- D. Ye, M. N. Raghnaill, M. Bramini, E. Mahon, C. Aberg, A. Salvati and K. A. Dawson, Nanoparticle accumulation and transcytosis in brain endothelial cell layers, Nanoscale, 2013, 5, 11153–11165 RSC.
- F. Li, S. M. Li, A. El Ghzaoui, H. Nouailhas and R. X. Zhuo, Synthesis and gelation properties of PEG-PLA-PEG triblock copolymers obtained by coupling monohydroxylated PEG-PLA with adipoyl chloride, Langmuir, 2007, 23, 2778–2783 CrossRef CAS PubMed.
- N. Kotagiri, J. Sakon, H. Han, V. P. Zharov and J. W. Kim, Fluorescent ampicillin analogues as multifunctional disguising agents against opsonization, Nanoscale, 2016, 8, 12658–12667 RSC.
- Y. T. Konttinen, J. Pajarinen, Y. Takakubo, J. Gallo, C. Nich, M. Takagi and S. B. Goodman, Macrophage Polarization and Activation in Response to Implant Debris: Influence by “Particle Disease” and “Ion Disease”, J. Long-Term Eff. Med. Implants, 2014, 24, 267–281 CrossRef PubMed.
- M. W. Cole and D. Velegol, Van der Waals energy of a 1-dimensional lattice, Mol. Phys., 2008, 106, 1587–1596 CrossRef CAS.
- V. N. Shukla, A. K. Mehata, A. Setia, P. Kumari, S. K. Mahto, M. S. Muthu and S. K. Mishra, Rational design of surface engineered albumin nanoparticles of asiatic acid for EGFR targeted delivery to lung cancer: Formulation development and pharmacokinetics, Colloids Surf., A, 2023, 676, 132188 CrossRef CAS.
- L. Wang, N. Hartel, K. X. Ren, N. A. Graham and N. Malmstadt, Effect of protein corona on nanoparticle-plasma membrane and nanoparticle-biomimetic membrane interactions, Environ. Sci.: Nano, 2020, 7, 963–974 RSC.
- S. H. Wang and E. E. Dormidontova, Selectivity of Ligand-Receptor Interactions between Nanoparticle and Cell Surfaces, Phys. Rev. Lett., 2012, 109, 238102 CrossRef PubMed.
- C. Schleh, M. Semmler-Behnke, J. Lipka, A. Wenk, S. Hirn, M. Schaffler, G. Schmid, U. Simon and W. G. Kreyling, Size and surface charge of gold nanoparticles determine absorption across intestinal barriers and accumulation in secondary target organs after oral administration, Nanotoxicology, 2012, 6, 36–46 CrossRef CAS PubMed.
- L. Yang, H. J. Kuang, W. Y. Zhang, Z. P. Aguilar, H. Wei and H. Y. Xu, Comparisons of the biodistribution and toxicological examinations after repeated intravenous administration of silver and gold nanoparticles in mice, Sci. Rep., 2017, 7, 3303 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3en00812f |
| This journal is © The Royal Society of Chemistry 2024 |