Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Helium nanodroplets as an efficient tool to investigate hydrogen attachment to alkali cations†
Siegfried
Kollotzek
 *a,
José
Campos-Martínez
*a,
José
Campos-Martínez
 *b,
Massimiliano
Bartolomei
*b,
Massimiliano
Bartolomei
 b,
Fernando
Pirani
b,
Fernando
Pirani
 c,
Lukas
Tiefenthaler
a,
Marta I.
Hernández
c,
Lukas
Tiefenthaler
a,
Marta I.
Hernández
 b,
Teresa
Lázaro
b,
Eva
Zunzunegui-Bru
b,
Teresa
Lázaro
b,
Eva
Zunzunegui-Bru
 b,
Tomás
González-Lezana
b,
Tomás
González-Lezana
 b,
José
Bretón
d,
Javier
Hernández-Rojas
b,
José
Bretón
d,
Javier
Hernández-Rojas
 d,
Olof
Echt
d,
Olof
Echt
 ae and
Paul
Scheier
ae and
Paul
Scheier
 a
a
aUniversity of Innsbruck, Institute for Ion Physics and Applied Physics, Innsbruck, Austria. E-mail: siegfried.kollotzek@uibk.ac.at
bInstituto de Física Fundamental, C.S.I.C., Madrid, Spain. E-mail: jcm@iff.csic.es
cDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, Perugia, Italy
dDepartamento de Física and IUdEA, Universidad de La Laguna, La Laguna, Tenerife, Spain
eDepartment of Physics, University of New Hampshire, Durham, NH 03824, USA
First published on 17th November 2022
Abstract
We report a novel method to reversibly attach and detach hydrogen molecules to positively charged sodium clusters formed inside a helium nanodroplet host matrix. It is based on the controlled production of multiply charged helium droplets which, after picking up sodium atoms and exposure to H2 vapor, lead to the formation of Nam+(H2)n clusters, whose population was accurately measured using a time-of-flight mass spectrometer. The mass spectra reveal particularly favorable Na+(H2)n and Na2+(H2)n clusters for specific “magic” numbers of attached hydrogen molecules. The energies and structures of these clusters have been investigated by means of quantum-mechanical calculations employing analytical interaction potentials based on ab initio electronic structure calculations. A good agreement is found between the experimental and the theoretical magic numbers.
1. Introduction
In the ample search for suitable materials for hydrogen storage leading to more sustainable and green energy and fuels, the important role that nanoporous materials might play in the near future1,2 and the relevance of metal decoration in improving the performance of such materials have been recognized.3–5 Studies have proved that the adsorption of molecular hydrogen gas on graphite, graphene, carbon nanotubes, layers of fullerenes, and other polycyclic aromatic hydrocarbon (PAH) materials is significantly improved by doping the complex with alkali atoms.6 Sodium is already well known for being a promising candidate for increasing the efficiency of hydrogen attachment in multiple storage systems and a good alternative to more scarce elements like lithium.7,8Therefore the investigation and characterization of the hydrogen–sodium interaction are important to the H2 energy community, driven by the need to develop fundamentally new ways to store hydrogen in low-weight environments with high storage density.9 The physisorption energy of H2 in pristine carbon-based materials is only around 40–50 meV and ∼30 meV in coronene,10 so the goal of doped complexes would be to raise the adsorption energies sufficiently to allow for efficient storage at moderate pressures near ambient temperatures.11,12 In line with this, the characterization of the isolated cation sites and their ability to attach H2 molecules13 are very important since it allows us to very accurately determine the structures and interactions intervening in the hydrogen storage on nanoporous materials.
Along with a high number of already established methods of investigating this process,14 this work opens up a new approach using a well-tested technique in laboratory astrochemical investigations.15–18 Superfluid helium droplets provide a powerful and flexible environment for investigations of hydrogen interactions with single molecules and dopants. With this different approach, complete knowledge of the most stable structures and configurations can be obtained. Laimer et al. reported in 2019 on the production and stability of highly charged droplets of superfluid helium.19 The potential of these multiply charged helium droplets led to the construction of a new experiment, which enables a more intense and controlled investigation of processes including the nucleation of dopant cluster ions as well as their decoration with helium or molecular hydrogen20 inside of these superfluid helium nanodroplets at a temperature of 0.37 K.21 This experimental setup allows accurate and reproducible control of the number of the attached hydrogen molecules. The resulting charged sodium/hydrogen complexes are analyzed using time-of-flight mass spectrometry and shell closures for the attachment of hydrogen are determined via local maxima in the ion yield of these species.
In this work, we present experimental as well as theoretical data showing the relative ion abundance of up to 15 hydrogen molecules attached to either a monomer or sodium dimer cations. They are investigated in consideration of their ability to reversibly bind molecular hydrogen. The relative ion abundances of Na+(H2)n and Na2+(H2)n from mass spectra obtained by sequential pickup of sodium and molecular hydrogen into multiply charged helium nanodroplets are compared with quantum mechanical calculations. The computational results provide detailed information about the binding energy and structure of a specific number of H2 molecules attached to a positively charged sodium atom or dimer. The structure of the paper is as follows: Section 2 outlines the methods employed, both experimental and theoretical; in Section 3 we analyze the experimental data and present the theoretical results; Section 4 is devoted to conclusions.
2. Methods
2.1. Experimental
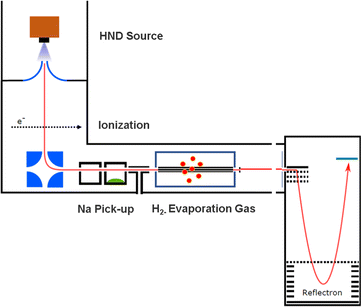
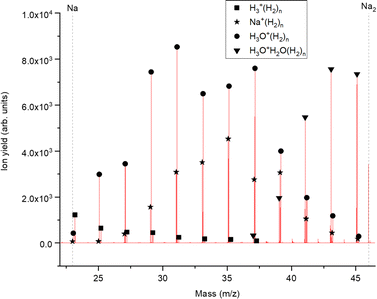
The experimental setup utilized in this work has been explained in detail elsewhere,22 but a brief description is given below. Helium nanodroplets (HNDs) are produced via supersonic expansion of ultrapure helium (Messer, purity 99.9999%) with a stagnation pressure of 20 bar through a 5 μm pinhole nozzle into ultrahigh vacuum. The nozzle was cooled with a closed-cycle cryocooler (Sumitomo Heavy industries) and counter-heated with an ohmic resistor operated with a PID controller (Lakeshore Model331) to 8.8 K. Under the present conditions the pressure in the source chamber increases from 0.01 mPa to 53 mPa. According to Gomez et al.23 and Laimer et al.19 the resulting average droplet size is calculated to be 5 × 106 He atoms under the present conditions. To prevent the destruction of HNDs by collisions with shock fronts, the resulting jet of He was then passed through a 0.5 mm skimmer (Beam Dynamics, Inc) located 10 mm after the nozzle. HNDs are ionized by a Nier-type electron impact ionization unit directly after the skimmer. The ion source was operated at an electron energy of 65 eV and an electron current of 350 mA. Under these conditions most HNDs are hit by multiple electrons that can directly ionize helium atoms; the positively charged He+ moves to the center of the droplet and, after several steps, ends forming He2+. This ion is subsequently solvated by neighboring He atoms leading to tight He3+ structures.24 The tree atoms ionic core then forms the so-called Atkins snowball.25,26 Mutual repulsion of these Hen+ charge centers into minimum energy configurations distributes them uniformly close to the surface of HNDs.27 This results in a mean charge state of the selected HNDs of z = 15. Charged droplets, consisting of 3 × 105 He atoms per charge were then mass-per-charge filtered by an electrostatic quadrupole bender. Subsequent guiding of the charged HNDs through sodium vapor leads to the pick-up of single atoms. Due to the heliophobic nature of sodium atoms, they stay unsubmerged on the surface of the HNDs until a certain limit is reached.28 The polarizability of captured sodium is much higher than that of He and therefore, ion-induced dipole interaction attracts dopants to the charge centers also sitting close to the surface of the droplet. Charge transfer from Hen+ to the first dopant leads to a Na+ charge center and the excess energy due to the difference in the ionization energies will be dissipated into the HNDs and leads to the evaporation of 1600 He atoms per eV. Further dopants will simply attach to an already existing ionic core and the binding energy will be transferred to the surrounding He, leading to the evaporation of additional He atoms from the surface of the HND. Subsequent collisions with room temperature H2 vapor first replaces He atoms surrounding the sodium ions with hydrogen molecules and upon consecutive collisions with H2 the droplet shrinks below the critical size for the given charge state and a hydrogen solvated sodium cation is ejected from the droplet. In the next section, we will compare binding energies for the cluster interactions in the cases of He and H2, and the easy replacement of the first by the second species will then be easily understood. With increasing hydrogen pressure in this evaporation cell (see Fig. 1) the amount of H2 molecules solvating the sodium ions can be reduced appropriately to enhance the visibilty of intensity anomalies and shell closures. This effect can be readily noticed in the ESI,† Fig. S1, where several pressures of hydrogen can be seen and its influence in the population of different sodium clusters. The hydrogen solvated sodium ions are analyzed using a time-of-flight mass spectrometer (Q-TOF Ultima Waters/Micromass).Fig. 2 displays a section of mass spectrum obtained by the method described above. A larger range of masses (m/z) that can be reached in the experiment can be found in the ESI,† Fig. S2. Important mass peaks are the bare sodium monomer (m/z = 23) and dimer (m/z = 46) cations, followed by mass peaks due to Na1,2+(H2)n. In the mass spectrum sodium cluster ions Nam+ up to sizes of n = 13 can be identified and the corresponding mass peaks are indicated in Fig. 2 by the dashed vertical lines (as well as in Fig. S2 in the ESI†). Under the present conditions, where sodium cluster ions are solvated by hydrogen molecules, the cluster size distribution of Nam+ does not exhibit the well-known intensity anomalies often reported for cationic alkali clusters,29,30 however, several Nam+(H2)n cluster size distributions exhibit clear intensity anomalies as a function of the number of hydrogen molecules n. The mass spectra for different pressures in the evaporation cell were measured to confirm the magic numbers of the Na+(H2) and Na2+(H2)n cluster size distributions shown in the results.
The setup is easily adjustable and in order to rule out pick up effects, experiments with H2 predoping and helium as an evaporation gas where performed. This alternative sequence leads to the same cluster products and similar relative ion abundances as the previous pick up sequence. To probe the possible underlying mechanism in the alternative pick up sequence, we carried out high level ab initio calculations. When sodium is picked up first, as in the regular sequence, the main pathway would follow a charge transfer from the HND to sodium (Na+) with subsequent addition of molecular hydrogen, resulting in the mass spectrum shown in Fig. 2. On the other hand, with a reversed pickup sequence in which H2 doping is achieved first, charge transfer leads to H2+ and via pickup of additional hydrogen molecules to H3+ as the first charge carrier (see ref. 20 for an explanation leading to this triatomic species), this species can further encounter Na with two possible outcomes,
| H3+ + Na → NaH + H2+ Δ(E) = 4.628 eV | (1) |
| H3+ + Na → Na+ + H2 + H Δ(E) = −4.053 eV | (2) |
It can be seen that the theoretical electronic energy difference (obtained from reactants and products optimizations at the MP2/aug-cc-pVTZ level of theory) clearly favors the second pathway, thus suggesting an explanation of why both pick up sequences lead to the same results. Since NaH+ is not a chemical species but rather an aggregate and H in eqn (2) is more weakly attached to the Na+ cation than the corresponding diatomic, H2, it is preferentially removed from the cluster upon collision induced activation. This explains the low abundance of the Na1,2+(H2)nH peak series. It is also worth noting that for similar clusters of Cs+(H2)n formed in HNDs, no CsH+ species were detected.31 A mass spectrum corroborating this fact can be found in the ESI,† Fig. S3.
2.2. Theoretical methods
We have taken for the total interaction potential a sum of two-body (2B) terms and thus we write for (H2)nNam+
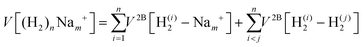 | (3) |
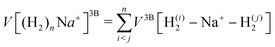 .
.
The different contributions are represented by suitable functional forms,31,32 whose parameters are optimized on accurate quantum ab initio estimations33–35 for both interaction energies and monomer properties. A full account of the procedure and parameters to describe the complete force field is given in the ESI.†
An important point to be emphasized is the different representation of the long range in Na+(H2)n and Na2+(H2)n clusters stability which is controlled by the induction attraction. In particular, while Na+ is a charge point,36–38 Na2+ is a strongly polarizable and elongated ionic diatom39,40 showing an equilibrium distance, Re, of 3.71 Å and a strongly anisotropic charge distribution, as suggested by its high electric quadrupole moment (see the ESI†). Therefore, the radial dependence of the induction attraction for configurations involving Na2+ aligned along the intermolecular distance (see configurations L and Tb in the Potential Energy Surfaces section of the ESI†) assumes the canonical R−4 dependence (such as that for Na+) only asymptotically (R![[double greater-than, compressed]](https://www.rsc.org/images/entities/char_2aa2.gif) Re), while in the region of interest for cluster stability (R ∼ Re) the R−6 dependence, typical of a dipole, is found to be more appropriate (see Fig. S4 in the ESI†).
Re), while in the region of interest for cluster stability (R ∼ Re) the R−6 dependence, typical of a dipole, is found to be more appropriate (see Fig. S4 in the ESI†).
The expressions of the different terms in eqn (3) as well as a full account of the procedure and parameters to describe the complete force field is given in the ESI.†
In the PIMC, hydrogen molecules will be treated as pseudoatoms.41,42 In this method43 the analogy in the partition function for a system composed of N classical ring polymers, each having M beads with the corresponding quantum system of the N particles is exploited to obtain the energy and structures of the clusters. We have used the thermodynamic estimator,44 and classical minimization procedures such as Evolutionary Algorithm and a Basin-Hoping technique45,46 to start sampling the initial configuration. Details of the method and parameters of interest are given in the ESI.†
The DMC method47,48 computes the ground state of the cluster by means of a transformation of the time-dependent Schrödinger equation into a diffusion equation by changing the variable time, t, to imaginary time, τ = it. The ground state of the system is then achieved as a lasting term in the (imaginary time) propagation of the diffusion equation. In this method, the wavefunction is represented by a set of replicas describing different configurations of the particles of the system and, at each time step Δτ, the particles randomly move according to the kinetic energy term in the Hamiltonian and the replicas multiply or disappear with a probability depending on the value of the potential energy term.47,48 We have used the implementation for rigid bodies due to Buch and collaborators49–51 and a classical Monte Carlo (MC) method to obtain the initial configurations for the DMC calculations. The working parameters and details on the calculations can be found in the ESI.† We have used for all the calculations 1.007825 amu and 22.98977 amu for the masses of H and Na atoms, respectively.
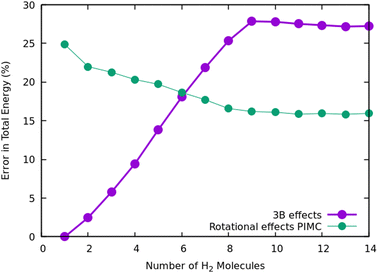
Once we have briefly described the theoretical methods, we present in Fig. 3 the percentage of differences found in the cluster total energy when we use a pseudo-atom approach or we just take the 2B terms in the potential interaction for the case of Na+(H2)n. A comparison is made with the rigid-rotor DMC approach including the 3B terms considered as the “exact” result. We can see that the error in total energy stabilizes very quickly and for n ≥ 8 it becomes practically constant. These differences correspond to the total energy but, actually, when we consider energy differences known as evaporation energies, shown in Fig. 4, it can be appreciated that the main features regarding peaks, plateaus and slopes remain unchanged, and would lead to similar structures or magic numbers. In particular it can be observed that the 3B effects are more noticeable and that a pseudoatom approach, except for the smaller hydrogen clusters, brings no significant differences. This could be anticipated from Fig. 3 where the differences remain almost constant with a very small slope, for the pseudoatom approach.
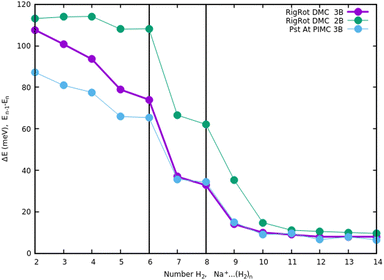 | ||
| Fig. 4 Evaporation energies, for Na+(H2)n, within several approaches, DMC with a rigid rotor model, 2B and 3B interaction potential and PIMC with a 3B potential. | ||
Therefore our rather thorough analysis indicates that for larger clusters a simpler treatment (2B interactions only, or considering a system composed of pseudo atoms) can still yield accurate predictions, regarding structure and stabilities. For analysis of the results and comparison with the experiment in the next section, we will use DMC within the rigid rotor model and the 3B interaction potential for a sodium monomer, while a 2B interaction model will be used for the sodium dimer clusters.
At this point it is also useful to stress that dissociation energies computed in this work E0 = −112.28 meV for Na+H2 and E0 = −38.86 meV for Na2+H2 dimers, are larger than those previously found for Na+He (E0 = 32.61 meV in the harmonic approximation in ref. 52) and Na2+He (E0 = −6.1 meV,53,54E0 = −7.0 meV55), of about a factor of 3 and 6, respectively. These differences result in the easy replacement of He by H2 in the evaporation cell and are mostly due to the higher polarizability of H2 compared with He, even if the electrostatic contribution which is absent for adducts involving He plays a non-negligible role.
3. Data analysis and results
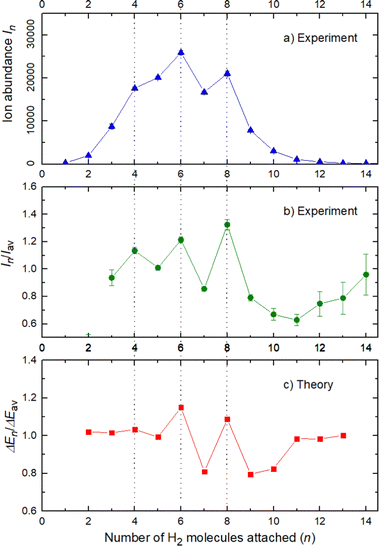
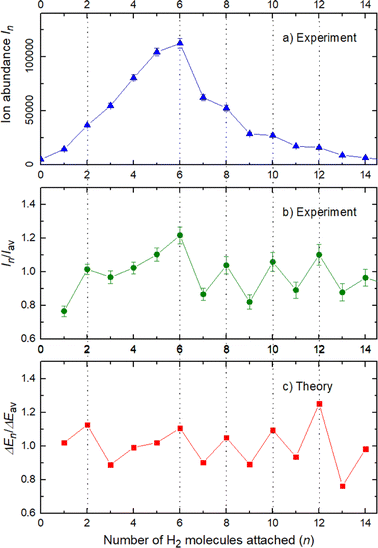
The experimental ion abundance In is plotted versus the number of the attached H2 molecules, n, in Fig. 5a and Fig. 6a for Na+(H2)n and Na2+(H2)n, respectively. The data shown in these figures are extracted from the mass spectra shown in Fig. 2. The ion abundances feature local anomalies which suggest similar local effects in the evaporation energies ΔEn, for example at n = 6 and 8 for Na+(H2)n. Several procedures have been proposed in the literature in order to establish a quantitative relationship between anomalies in In and ΔEn; their applicability depends on the experimental conditions. For the present data we adopt an approach that was first proposed by Leidlmair et al.,56 and justified in more detail in ref. 57 and 58. It asserts that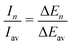 | (4) |
The left and right-hand sides of eqn (4) are plotted in Fig. 5b and c, respectively, for Na+(H2)n. The local averages Iav and ΔEav were obtained by averaging over adjacent sizes with weights computed from a Gaussian with a standard deviation σ = 1 (the results did not change significantly if σ = 2 was chosen). The similarity of the data in Fig. 5b and c is excellent. Cluster ions with n = 6 and 8 clearly form magic numbers, although the local maximum at n = 4 in the experimental data is not completely supported by the theory. Likewise, experimental and theoretical data for Na2+(H2)n are plotted in Fig. 6b and c, respectively. Again, the two data sets are very similar; they feature local maxima at n = 2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6,
6,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8,
8,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and 12.
10, and 12.
These evaluations are also performed for different H2 pressures in order to exclude anomalies due to size distribution effects and the results for nearly all pressures are similar to the ones previously shown and in fact the survival of the higher ion yield at several pressures is also an indication of larger stability, or in other words, magic numbers.
The appearance of exceptionally stable structures or “magic numbers” with agreement between theory and experiment deserves some comments, specially concerning the differences and similarities between the sodium monomer and dimer and their interactions with the H2 molecules.
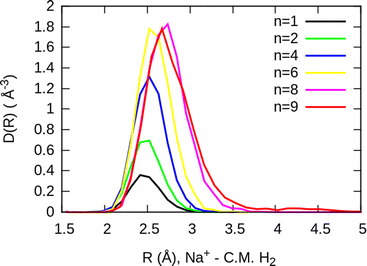
The simplest case corresponds to the sodium monomer, in which three clear islands of stability are apparent, for hydrogen sizes, n = 4, 6, and 8, as shown in the bottom of Fig. 5. In Fig. 7 we show the theoretical radial distribution, D(R), for several compositions of these clusters. The distributions are normalized to the number of H2 contained within. It can be seen that up to n = 8 the distributions vanish between 3–3.5 Å while for n = 9, there is a small recurrence between 4–4.6 Å that corresponds to the beginning of a new shell around the Na+ cation. These results are very similar to those found for Li+Hen,41 where also a close resemblance can be found in the second energy differences for that system, and the one we show at the bottom of Fig. 5. This result is a consequence of the interactions brought into play in both cases, with similar equilibrium distances and well depths between the cation and the other component of the cluster (He/H2) that, in turn, have a small interaction between them.
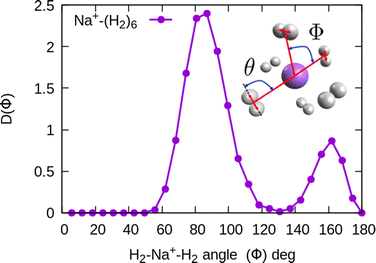
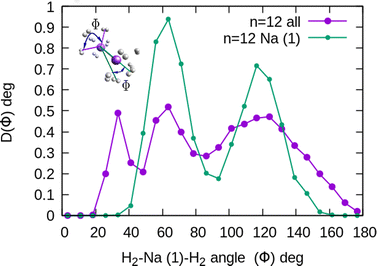
In the structure two angles are relevant, that we will call (θ, Φ). The angles θ in a given cluster are those formed between the vector defining the bond in a particular H2 molecule, and the vector from its center of mass to the cation. More interesting for the geometry are the Φ angles, which are those formed between two vectors that are directed from the sodium atom, to the center of mass of two different H2 units. These angles can be better seen in the ESI,† where we have plotted the minimum energy structures obtained with classical MC simulations, in the case of Na+(H2)6 and Na2+(H2)12 for the sodium monomer and dimer, respectively. They have also been included as insets, in some of the next figures.
In the case of the sodium monomer, the structure is nearly rigid, the H2 molecules orient with their bond perpendicularly to the vector joining each molecular center of mass to the cation, angle θ = 90°, with a narrow distribution around this value. On the other hand, how the different monomers are arranged surrounding the cation, is better defined by the angle Φ and the distribution for the cluster Na+(H2)6 is shown in Fig. 8. As can be seen, this distribution, D(Φ), shows two predominant peaks with maxima at angles around 90 and 160 degrees and with little dispersion, certainly signaling a clear structure corresponding to an octahedron, that was also found previously in other clusters.41,61 This structure is close to the classical one, which is included as an inset in the figure. Similar tight structures can be found for n = 4 and 8, with geometries corresponding to a tetrahedron and square antiprism, respectively. Barbati et al.62 reported structures obtained from ab initio calculations up to n = 7 and the same structures were found for n = 2, 3, 4, and 6.
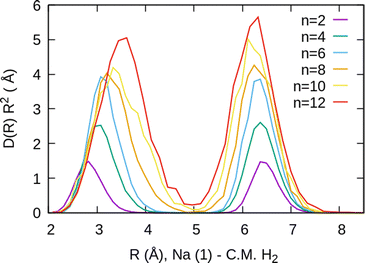
For the case of the sodium dimer clusters, Na2+(H2)n, we present in Fig. 9 the radial distributions of H2 molecules with respect to one of the sodium atoms composing the dimer (Na(1) in Fig. S3 in the ESI†). It can be seen that there are some H2 monomers around Na(1), leading to one peak, and at longer distances, the rest of the monomers are more directly joined to the other atom, Na(2), leading to the second peak. The plot indicates that there is a preference for H2 to evenly cover each Na atom. This feature has been checked by integration of the distributions of Fig. 9 up to the middle of the two peaks (around 5 Å), and it was found that the number of diatomic molecules around each Na is, in general terms, half the total number of them. This is the origin of the relatively large stability of the clusters with an even number of H2 molecules observed both in the calculations as well as in the measurements of Fig. 6.
The existence of a bond in Na2+, leading to a more anisotropic and weaker interaction with H2 as compared with Na+, also makes the distribution more prone to forming caps around each alkaline atom, rather than a spherical distribution around a single sodium cation. This effect can be seen in Fig. 10 for n = 12, in which we plot (similarly as in Fig. 8) the distribution of angles Φ formed between two vectors connecting one of the sodium atoms, Na(1), and the center of mass of any two hydrogen molecules. The peak around Φ = 30° corresponds to H2 diatoms which are around the other Na atom, Na(2). If we discard the H2 monomers surrounding that atom (equivalent to eliminating the peak on the right of Fig. 9), we get a bimodal distribution (green curve in Fig. 10 whose central angles correspond to six molecules forming the cap of an icosahedron (for comparison, see ref. 31 for the icosahedral structure found for Cs+(H2)12). This structure is close to the classical one, shown as an inset in Fig. 10.
4. Conclusions
In conclusion, this work shows an important mechanism for the future understanding of how molecular hydrogen binds to single sodium atoms. The good agreement between the experimental and theoretical data supports the idea of favored structures, where the attachment of 4, 6 and 8 hydrogen molecules is especially strong for the sodium monomer Fig. 5. The dimer complexes show agreement between theory and experiment regarding the special stability of complexes with 2, 6, 8, 10 and 12 molecules, since both Na atoms behave as quasi-independent attractors for H2 molecules, each of them showing the same number of stable molecule attachments. This symmetric hydrogen attachment to each side of the sodium dimer leads to two-step-plateaus (5,6–7,8–9,10–11,12) for ion yields, shown at the top of Fig. 6, that can also be observed in evaporation energies. Our calculations, concerning the energy difference of every possible pathway for the generation of the cluster complexes due to the experimental setup and its pick up sequence, conclusively explain the ion abundances observed. These calculations also indicate that protonation of single sodium atoms is very unlikely and that the binding energy of a hydrogen molecule is higher than the one of a single H atom, what explains the low abundance of sodium cluster ion complexes with an odd number of hydrogen atoms.The theoretical calculations confirm and support these conclusions and explain the behavior of the monomer versus the sodium dimer. The present results are expected to be of relevance for organic materials containing alkali atoms, where electron transfer to the organic component leads to positively charged alkali ions that act as attractors for hydrogen molecules in novel hydrogen storage materials.6
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Author contributions
S. Kollotzek, S. Tiefenthaler, and P. Scheier carried out the experiments. J. Campos-Martnez, M. Bartolomei, F. Pirani, M. I. Hernández, T. Lázaro, E. Zunzunegui-Bru, T. González-Lezana, J. Bretón, and J. Hernández-Rojas worked on the theoretical results. O. Echt participated in the experiments and the comparison with the theoretical results.Conflicts of interest
We declare no conflicts of interest.Acknowledgements
This work was supported by the Austrian Science Fund, FWF (project number P31149) and the Spanish MICINN with Grants FIS2016-79596-P and PID2019-105225GB-I00 (JB, JHR); PID2020-114654GB-I00/AEI/10.13039/501100011033, 2021-2024 (TGL,MB) and PID2020-114957GB-I00/AEI/10.13039/501100011033 (JCM, MIH). Collaboration has also been supported by the CSIC under i-Link+ program LINKB20041. Allocation of computing time by CESGA (Spain) is also acknowledged.Notes and references
- Z. Chen, P. Li, R. Anderson, X. Wang, X. Zhang, L. Robison, L. R. Redfern, S. Moribe, T. Islamoglu, D. A. Gómez-Gualdrón, T. Yildirim, J. F. Stoddart and O. K. Farha, Science, 2020, 368, 297–303 CrossRef CAS PubMed.
- A. Olabi, M. A. Abdelkareem, T. Wilberforce and E. T. Sayed, Renewable Sustainable Energy Rev., 2021, 135, 110026 CrossRef CAS.
- R. K. Sahoo, B. Chakraborty and S. Sahu, Int. J. Hydrogen Energy, 2021, 46, 40251–40261 CrossRef CAS.
- C. Wang, C. Tang and L. Fu, Int. J. Hydrogen Energy, 2020, 45, 25054–25064 CrossRef CAS.
- V. Jain and B. Kandasubramanian, J. Mater. Sci., 2020, 55, 1865–1903 CrossRef CAS.
- H. Tachikawa and T. Iyama, J. Phys. Chem. C, 2019, 123, 8709–8716 CrossRef CAS.
- H. Tachikawa, H. Yi, T. Iyama, S. Yamasaki and K. Azumi, Hydrogen, 2022, 3, 43–52 CrossRef CAS.
- R. K. Sahoo, B. Chakraborty and S. Sahu, Int. J. Hydrogen Energy, 2021, 46, 40251–40261 CrossRef CAS.
- L. Schlapbach and A. Züttel, Materials for sustainable energy: a collection of peer-reviewed research and review articles from nature publishing group, World Scientific, 2011, pp. 265–270 Search PubMed.
- M. Bartolomei, R. Pérez de Tudela, K. Arteaga, T. González-Lezana, M. I. Hernández, J. Campos-Martínez, P. Villarreal, J. Hernández-Rojas, J. Bretón and F. Pirani, Phys. Chem. Chem. Phys., 2017, 19, 26358–26368 RSC.
- P. Mauron, A. Remhof, A. Bliersbach, A. Borgschulte, A. Züttel, D. Sheptyakov, M. Gaboardi, M. Choucair, D. Pontiroli and M. Aramini, et al. , Int. J. Hydrogen Energy, 2012, 37, 14307–14314 CrossRef CAS.
- H. Lee, J. Ihm, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115412 CrossRef.
- I. Savchenko, B. Gu, T. Heine, J. Jakouwski and S. Garashchuk, Chem. Phys. Lett., 2017, 670, 64–70 CrossRef CAS.
- V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954–14965 RSC.
- A. Kaiser, J. Postler, M. Ončák, M. Kuhn, M. Renzler, S. Spieler, M. Simpson, M. Gatchell, M. K. Beyer, R. Wester, F. A. Gianturco, P. Scheier, F. Calvo and E. Yurtsever, J. Phys. Chem. Lett., 2018, 9, 1237–1242 CrossRef CAS PubMed.
- M. Meyer, P. Martini, A. Schiller, F. Zappa, S. A. Krasnokutski and P. Scheier, Astrophys. J., 2021, 913, 136 CrossRef CAS.
- A. Kaiser, M. Renzler, L. Kranabetter, M. Schwärzler, R. Parajuli, O. Echt and P. Scheier, Int. J. Hydrogen Energy, 2017, 42, 3078–3086 CrossRef CAS.
- S. Spieler, M. Kuhn, J. Postler, M. Simpson, R. Wester, P. Scheier, W. Ubachs, X. Bacalla, J. Bouwman and H. Linnartz, Astrophys. J., 2017, 846, 168 CrossRef.
- F. Laimer, L. Kranabetter, L. Tiefenthaler, S. Albertini, F. Zappa, A. M. Ellis, M. Gatchell and P. Scheier, Phys. Rev. Lett., 2019, 123, 165301 CrossRef CAS PubMed.
- L. Tiefenthaler, S. Kollotzek, A. M. Ellis, P. Scheier and O. Echt, Phys. Chem. Chem. Phys., 2020, 22, 28165–28172 RSC.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed.
- L. Tiefenthaler, J. Ameixa, P. Martini, S. Albertini, L. Ballauf, M. Zankl, M. Goulart, F. Laimer, K. von Haeften and F. Zappa, et al. , Rev. Sci. Instrum., 2020, 91, 033315 CrossRef CAS PubMed.
- L. F. Gomez, E. Loginov, R. Sliter and A. F. Vilesov, J. Chem. Phys., 2011, 135, 154201 CrossRef PubMed.
- S. Albertini, E. Gruber, F. Zappa, S. Krasnokutski, F. Laimer and P. Scheier, Mass Spectrom. Rev., 2022, 41, 529–567 CrossRef CAS PubMed.
- K. R. Atkins, Phys. Rev., 1959, 116, 1339–1343 CrossRef CAS.
- D. Mateo, F. Gonzalez and J. Eloranta, J. Phys. Chem. A, 2015, 119, 2262–2270 CrossRef CAS PubMed.
- A. J. Feinberg, F. Laimer, R. M. P. Tanyag, B. Senfftleben, Y. Ovcharenko, S. Dold, M. Gatchell, S. M. O. O'Connell-Lopez, S. Erukala, C. A. Saladrigas, B. W. Toulson, A. Hoffmann, B. Kamerin, R. Boll, A. De Fanis, P. Grychtol, T. Mazza, J. Montano, K. Setoodehnia, D. Lomidze, R. Hartmann, P. Schmidt, A. Ulmer, A. Colombo, M. Meyer, T. Möller, D. Rupp, O. Gessner, P. Scheier and A. F. Vilesov, Phys. Rev. Research, 2022, 4, L022063 Search PubMed.
- L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, R. Jochum, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, J. Chem. Phys., 2011, 135, 044309 CrossRef PubMed.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143 CrossRef CAS.
- L. An der Lan, P. Bartl, C. Leidlmair, H. Schöbel, R. Jochum, S. Denifl, T. D. Märk, A. M. Ellis and P. Scheier, J. Chem. Phys., 2011, 135, 044309 CrossRef PubMed.
- J. Ortiz de Zárate, M. Bartolomei, T. González-Lezana, J. Campos-Martínez, M. I. Hernández, R. Pérez de Tudela, J. Hernández-Rojas, J. Bretón, F. Pirani, L. Kranabetter, P. Martini, M. Kuhn, F. Laimer and P. Scheier, Phys. Chem. Chem. Phys., 2019, 21, 15662–15668 RSC.
- F. Pirani, M. Albertí, A. Castro, M. M. Teixidor and D. Cappelletti, Chem. Phys. Lett., 2004, 394, 37–44 CrossRef CAS.
- D. Cappelletti, F. Pirani, B. Bussery-Honvault, L. Gómez and M. Bartolomei, Phys. Chem. Chem. Phys., 2008, 10, 4281 RSC.
- Q. Hong, Q. Sun, F. Pirani, M. A. Valentín-Rodríguez, R. Hernández-Lamoneda, C. Coletti, M. I. Hernández and M. Bartolomei, J. Chem. Phys., 2021, 154, 064304 CrossRef CAS PubMed.
- F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- T. N. Olney, N. M. Cann, G. Cooper and C. E. Brion, Chem. Phys., 1997, 223, 59–98 CrossRef CAS.
- M. M. Liu, M. S. Wu, H. L. Han and T. Y. Shi, J. Chem. Phys., 2016, 145, 034304 CrossRef PubMed.
- M. Rastogi, C. Leidlmair, L. An der Lan, J. Ortiz de Zárate, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, J. Hernández-Rojas, J. Bretón, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576 RSC.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez and R. Hernández-Lamoneda, J. Comput. Chem., 2011, 32, 279–290 CrossRef CAS PubMed.
- M. Bartolomei, T. González-Lezana, J. Campos-Martínez, M. I. Hernández and F. Pirani, J. Phys. Chem. A, 2019, 123, 8397–8405 CrossRef CAS PubMed.
- M. Rastogi, C. Leidlmair, L. An der Lan, J. Ortiz de Zárate, R. Pérez de Tudela, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, J. Hernández-Rojas, J. Bretón, P. Scheier and M. Gatchell, Phys. Chem. Chem. Phys., 2018, 20, 25569–25576 RSC.
- R. Pérez de Tudela, P. Martini, M. Goulart, P. Scheier, F. Pirani, J. Hernández-Rojas, J. Bretón, J. Ortiz de Zárate, M. Bartolomei, T. González-Lezana, M. I. Hernández, J. Campos-Martínez and P. Villarreal, J. Chem. Phys., 2019, 150, 154304 CrossRef PubMed.
- R. Rodríguez-Cantano, T. González-Lezana and P. Villarreal, Int. Rev. Phys. Chem., 2016, 35, 37–68 Search PubMed.
- J. A. Barker, J. Chem. Phys., 1979, 70, 2914 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- J. Hernández-Rojas and D. J. Wales, J. Chem. Phys., 2003, 119, 7800–7804 CrossRef.
- J. B. Anderson, J. Chem. Phys., 1975, 63, 1499–1503 CrossRef CAS.
- M. A. Suhm and R. O. Watts, Phys. Rep., 1991, 204(293), 329 Search PubMed.
- V. Buch, J. Chem. Phys., 1992, 97, 726–729 CrossRef CAS.
- P. Sandler, V. Buch and J. Sadlej, J. Chem. Phys., 1996, 105, 10387–10397 CrossRef CAS.
- P. Sandler and V. Buch, General purpose QCLUSTER program for Rigid Body Diffusion Monte Carlo simulation of an arbitrary molecular cluster, (private communication), 1999.
- N. Issaoui, K. Abdessalem, H. Ghalla, S. J. Yaghmour, F. Calvo and B. Oujia, J. Chem. Phys., 2014, 141, 174316 CrossRef PubMed.
- E. Bodo, E. Yurtsever, M. Yurtsever and F. A. Gianturco, J. Chem. Phys., 2006, 124, 074320 CrossRef CAS PubMed.
- F. Marinetti, L. Uranga-Piña, E. Coccia, D. López-Durán, E. Bodo and F. A. Gianturco, J. Phys. Chem. A, 2007, 111, 12289–12294 CrossRef CAS PubMed.
- N. Alharzali, H. Berriche, P. Villarreal and R. Prosmiti, J. Phys. Chem. A, 2019, 123, 7814–7821 CrossRef CAS PubMed.
- C. Leidlmair, Y. Wang, P. Bartl, H. Schöbel, S. Denifl, M. Probst, M. Alcamí, F. Martín, H. Zettergren, K. Hansen, O. Echt and P. Scheier, Phys. Rev. Lett., 2012, 108, 076101 CrossRef PubMed.
- L. An der Lan, P. Bartl, C. Leidlmair, R. Jochum, S. Denifl, O. Echt and P. Scheier, Chem. – Eur. J., 2012, 18, 4411 CrossRef CAS PubMed.
- T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez and P. Scheier, Int. Rev. Phys. Chem., 2020, 39, 465–516 Search PubMed.
- J. Gspann, Physics of Electronic and Atomic Collisions, North-Holland, Amsterdam (The Netherlands), 1982, pp. 79–96 Search PubMed.
- K. Hansen, Springer Series on Atomic, Optical and Plasma Physics, 2nd edn, 2019, p. 231 Search PubMed.
- A. Ponzi, F. Marinetti and F. A. Gianturco, Phys. Chem. Chem. Phys., 2009, 11, 3868–3874 RSC.
- M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Chem. Phys., 2001, 114, 2213–2218 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03841b |
| This journal is © the Owner Societies 2023 |