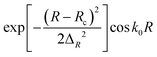A neural network potential energy surface and quantum dynamics studies for the Ca+(2S) + H2 → CaH+ + H reaction†
Received
15th June 2022
, Accepted 25th July 2022
First published on 26th July 2022
Abstract
Reactive collisions of Ca+ ions with H2 molecules play a crucial role in ultracold chemistry, quantum information and other cutting-edge fields, and have been widely studied experimentally, but the corresponding theoretical studies have not been reported due to the lack of an applicable potential energy surface (PES). Herein, a globally accurate PES of the ground-state CaH2+ is constructed using the permutation invariant polynomial neural network method based on 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points calculated at the multi-reference configuration interaction level. On the new PES, the quantum time-dependent wave packet calculations are performed to study the dynamics mechanisms of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction. The calculated results suggest that the reaction follows a direct abstraction process when the collision energy is below 5.0 eV. The dynamics results would have a great reference significance for the experimental research of this reactive system at a finer level, and further dynamics studies, such as the effects of isotope substitution and rovibrational excitations of the reactant molecule, could be carried out on this newly constructed PES.
780 ab initio points calculated at the multi-reference configuration interaction level. On the new PES, the quantum time-dependent wave packet calculations are performed to study the dynamics mechanisms of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction. The calculated results suggest that the reaction follows a direct abstraction process when the collision energy is below 5.0 eV. The dynamics results would have a great reference significance for the experimental research of this reactive system at a finer level, and further dynamics studies, such as the effects of isotope substitution and rovibrational excitations of the reactant molecule, could be carried out on this newly constructed PES.
1 Introduction
Reactive collisions between alkaline earth metal ions and neutral molecules have a great significance in the fields of ultracold chemistry,1–5 astrophysics6–8 and quantum information science.9–12 Among them, the reactions of calcium ions with hydrogen and its isotopic variations have received particular attention in recent years. An important reason is that the CaH+ product molecule has been considered as a promising candidate to determine the time dependence of mp/me,13,14 in which mp and me are the masses of protons and electrons, respectively. This is because the vibrational frequency w and mp/me follow the relationship of d(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (w))/dt = −1/2d(ln
(w))/dt = −1/2d(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (mp/me))dt,13 and the measurement of the pure vibrational transition frequency of CaH+ can reach within the uncertainty of 10−16. In addition, CaH+ is also an astrophysically important molecular ion,15–17 thus understanding its formation plays a crucial role in the evolution of interstellar clouds.
(mp/me))dt,13 and the measurement of the pure vibrational transition frequency of CaH+ can reach within the uncertainty of 10−16. In addition, CaH+ is also an astrophysically important molecular ion,15–17 thus understanding its formation plays a crucial role in the evolution of interstellar clouds.
A variety of experimental studies have been carried out on the Ca+ + H2 reactive system. Georgiadis and Armentrout used the guided ion beam mass spectrometry device to examine the kinetic energy dependence of the reactions of Ca+(2S) with H2, D2 and HD.18 The ground-state reaction proceeds along a single adiabatic surface with an energy threshold of about 2.5 eV due to the considerably stronger bond energy of the H2 molecule than the CaH+ molecule. There is a strong intramolecular isotope effect on the Ca+(2S) + HD reaction that the ratio of CaH+ to CaD+ is about a factor of 4 in the energy range of 3–4.5 eV, suggesting that a direct abstraction process dominates this reaction. This is because the center of mass of the HD molecule is close to that of the D atom, resulting in the H end sweeping out a larger volume than the D end and the CaH+ product is preferentially formed when the reaction proceeds preferentially through a H-abstraction path. Hansen et al. reported the single-ion recycling reactions in which the laser-cooled and trapped Ca+(2P1/2) ions reacted repeatedly with a gas mixture of HD (83%) and H2 (17%).19 A total of 87 single-ion reaction events were recorded, and the fractional CaD+ product was found to be around 0.56. Different from the ground-state reactions, the collisions of excited Ca+ with HD/H2 need to go through a non-adiabatic transition. This preference for forming CaD+ implies that the product is generated by the dissociation of an intermediate complex, and it can be explained that the forces acting on both H and D ends are the same but the ejection of the lighter H atom would be preferred for a complex-forming reaction. Chou et al.1 developed a general technique for optical pumping and preparation of the target molecular ions into a pure initial state based on quantum-logic spectroscopy to prepare and non-destructively detect quantum states in CaH+. In their experiments, CaH+ molecular ions are formed by a laser-induced reaction of the trapped Ca+ ions in a harmonic ion trap with H2 molecules in an ultrahigh vacuum at room temperature. This experimental study presents great importance to the development such as precision control of molecular dynamics, rigorous tests of fundamental physics, quantum computing and other cutting-edge fields.
However, for the theoretical aspect, the dynamics calculations of the Ca+ + H2 reactive system have not been performed, so the inherent dynamics characteristics have not been understood completely. Theoretical study of reaction dynamics at the state-resolved level is necessary for gaining insight into reaction mechanisms and ultimately controlling the reactivity. A reliable potential energy surface (PES) is an important prerequisite for obtaining detailed dynamics information theoretically. The only PES20 of the CaH2+ system was constructed by Czuchaj et al. in 1999. In their work, the ab initio points are calculated at the internally contracted multi-reference configuration interaction (MRCI) level with the contracted Cartesian Gaussian basis set for Ca and the correlation consistent valence quintuple zeta (V5Z) basis set for H. The Ca+–H2 complexes of the ground and first excited states were studied for C∞v and C2v configurations, and the calculated results show that the C2v geometry is the most stable structure for both the two electronic states. This PES is reasonably accurate for analyzing the triatomic complex, but it cannot be used to study the dynamics of the Ca+ + H2 reaction since the product channel and some regions where the reaction can access are not included. Therefore, a globally accurate PES is required for further understanding the microscopic dynamics mechanisms of this important reactive system.
In this study, a high-fidelity global PES of the ground-state (12A′) CaH2+ is structured using the permutation invariant polynomial-neural network (PIP-NN) method21,22 based on a large number of high-level ab initio points. Furthermore, the state-to-state quantum dynamics studies for the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction are performed using the time-dependent wave packet (TDWP)23–26 calculations on this new PES. The remainder of this paper is organized as follows: Section 2 gives the computational details and the topographic characteristics of the ground-state CaH2+ PES. A brief description of the TDWP method and detailed dynamics discussion are given in Section 3 and Section 4 concludes this article.
2 Potential energy surface
2.1
Ab initio calculations
The ab initio calculations are performed using the internally contracted MRCI method27,28 with the molecular orbitals optimized by the complete active space self-consistent field (CASSCF) calculations,29,30 and the Davidson correction is used to compensate for the effect of higher-order correlation. In the CASSCF calculations, three valence electrons are included in eleven active orbitals (8a′ + 3a′′), and three electronic states 12A′′, 22A′ and 12A′′ of CaH2+ with the weights of 0.8, 0.1 and 0.1 are included in the state-averaged calculations, respectively. The V5Z basis set31 and the QZVP basis set32 are adopted for H and Ca, respectively. A large number of configurations within Cs symmetry over a large range of space are chosen in the Jacobi coordinates, with the reactant region being defined by 0.8 ≤ RHH/a0 ≤ 20, 0.1 ≤ RCa+–HH/a0 ≤ 25, 0 ≤ θ/degree ≤ 90, and the product region by 2.0 ≤ RCaH+/a0 ≤ 20, 0.1 ≤ RH–CaH+/a0 ≤ 25, 0 ≤ θ′/degree ≤ 180. All the electronic structure calculations are implemented in the Molpro 2012 package.33
2.2 PIP-NN fitting
The global CaH2+ PES consists of two-body and three-body terms, written as follows:| | 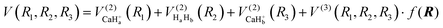 | (1) |
where R1, R2 and R3 represent the internuclear distances of Ca+–Ha, Ha–Hb and Ca+–Hb, respectively. f(R) is a switch function to enhance the description of the reactant and product asymptotic regions, and its form can be written as:| | 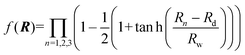 | (2) |
where Rd is the central position of f(R), and Rw expresses the switch strength constant.
The two-body terms are fitted by the back-propagation NN model, and the NN structure includes two hidden layers with 5–6 neurons. A total of 82 and 68 ab initio points are calculated to determine the analytical potential energy curves (PECs) of HH and CaH+, and the fitting root mean square error (RMSE) are 0.239 and 0.137 meV, respectively. As shown in Fig. 1, the fitting PECs of the ground state H2(X1Σg+) and CaH+(X1Σg) are in good agreement with the original ab initio data. To make further comparison, the molecular constants of the two diatomic molecules are displayed in Table 1. The equilibrium bond length Re, dissociation energy De, vibrational frequencies ωe, and anharmonicity constants ωexe of H2(X1Σg+) are in good agreement with the experimental values.34 In the case of CaH+(X1Σg), the theoretical estimates of spectroscopic constants calculated at the (EOM)-CCSDT/V5Z level35 (De was calculated at the CCSD(T)/CV5Z for Ca and V5Z for the H level36) are listed for comparison since the corresponding experimental data have not been determined. It can be seen that the spectroscopic data obtained from the fitting CaH+ PEC are in good agreement with the high-level ab initio results, and the small deviation could be caused by the different selection of basis function of the Ca atom. Thus, fitting two-body potentials are sufficiently accurate for describing the rovibrational energy levels of the reactant and product molecules.
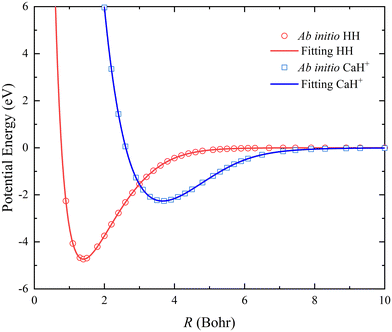 |
| | Fig. 1 Comparison between ab initio data and the fitting results for the PECs of H2(X1Σg+) and CaH+(X1Σg). | |
Table 1 Molecular constants of H2(X1Σg+) and CaH+(X1Σ+)
|
|
R
e (Bohr) |
D
e (eV) |
ω
e (cm−1) |
ω
e
x
e (cm−1) |
|
Obtained from the PIP-NN PES.
Exp. corresponds to ref. 34.
Theo. corresponds to ref. 35.
Theo. corresponds to ref. 36.
|
| H2(X1Σg+) |
| This worka |
1.401 |
4.735 |
4400.1 |
123.7 |
| Experimental datab |
1.401 |
4.747 |
4401.2 |
121.3 |
| CaH+(X1Σ+) |
| This worka |
3.662 |
2.264 |
1512.1 |
16.6 |
|
Ab initio calculations |
3.573c |
2.246d |
1507.1c |
20.1c |
The global PES of the ground state CaH2+ is constructed by the PIP-NN scheme,21,22 which can strictly ensure the exchange symmetry of the fitting PES about the two identical H atoms, and this method has been successfully applied to a wide range of reactive systems, including triatomic,37–41 polyatomic42–46 and diabatic PESs.47–51 The primary invariants are written as:
| | Pi = exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−0.2Ri) (i =1, 2, 3) (−0.2Ri) (i =1, 2, 3) | (3) |
And then, the symmetrized polynomial vector G = {Gi} can be structured as:
Finally, the vector G is given normalized treatment as:
| | 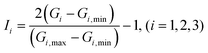 | (7) |
in which
Gi,min and
Gi,max are the minimum and maximum values of
Gi, respectively.
The NN that is used to construct the global CaH2+ PES includes two hidden layers with 14 neurons. The hyperbolic tangent function and simple linear function are selected as the transfer functions φ in the 1–2, 2–3 layers, and 3–4 layers, respectively. The final analytical expansion of the total PES can be presented as:
| | 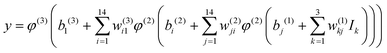 | (8) |
where
w is the connecting weight between two neurons of the adjacent two layers, and
b is the corresponding bias of a certain neuron and
y represents the normalized energy. The mean squared error (MSE) serves as the cost function optimized by the Levenberg–Marquardt algorithm,
52 and
w and
b are iteratively updated until the fitting MSE decreases to a small enough value.
Here, to ensure the fitting PES can accurately describe each region, a total of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points are selected to participate in the PIP-NN fitting, and these points are divided randomly into the training set (90%), testing set (5%), and validation set (5%) for effectively avoiding the over-fitting behavior. Fig. 2 shows the distribution of the NN fitting errors defined by the difference between the fitting values and ab initio data, and the energy values of the horizontal axis are relative to the triatomic dissociation limit of Ca+–H–H. It is clear that the PIP-NN PES keeps a very small predictive error in the whole energy region, and the percentage of points with an absolute error less than 5 meV is 98.1%. The overall RMSE of the final PES is only 1.64 meV. Therefore, the fitting PIP-NN PES is accurate enough for dynamics calculations of the CaH2+ reactive system.
780 ab initio points are selected to participate in the PIP-NN fitting, and these points are divided randomly into the training set (90%), testing set (5%), and validation set (5%) for effectively avoiding the over-fitting behavior. Fig. 2 shows the distribution of the NN fitting errors defined by the difference between the fitting values and ab initio data, and the energy values of the horizontal axis are relative to the triatomic dissociation limit of Ca+–H–H. It is clear that the PIP-NN PES keeps a very small predictive error in the whole energy region, and the percentage of points with an absolute error less than 5 meV is 98.1%. The overall RMSE of the final PES is only 1.64 meV. Therefore, the fitting PIP-NN PES is accurate enough for dynamics calculations of the CaH2+ reactive system.
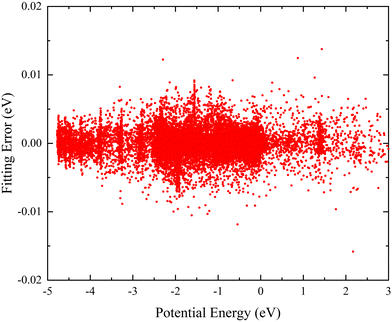 |
| | Fig. 2 Distribution of the fitting errors defined by the difference between the PIP-NN fitting values and ab initio data. | |
2.3 Topographic features of PES
The contour maps of the ground-state CaH2+ PES at four different fixed bond lengths or bond angles are shown in Fig. 3, and the energy is set as zero at the Ca+ + H2 dissociation limit. Panels (a) and (b) describe the topographies of the PIP-NN PES with the bending angle between R1 and R3 of 90° and 180°, respectively. Excellent exchange symmetry of the PES is displayed, and there is a saddle point structure at R1 = R3 = 4.01 a0 for each bond angle. Moreover, the topography shows little change as the bending angle increases under this configuration. The global minimum energy of the CaH2+ PES corresponds to C2v symmetry and it is located at R2 = 1.41a0, RCa+–HH = 6.28a0 with the energy of −0.04 eV, as shown in Fig. 3 (c). The location and the corresponding potential energy obtained from the new PES are consistent with the previous Czuchaj PES.20 When the collision energy is slightly larger than the threshold, the Ca+ ion collides with the H2 molecule along its midperpendicular with the slight elongation of the HH bond. Fig. 3 (d) presents the collinear topography of the PES with a Ca+–H–H angle of 180°. In this plot, the bottom and left valleys correspond to the Ca+(2S) + H2 and CaH+ + H channels, respectively. The corresponding energy value of the left channel is much larger than the value of the bottom valley, suggesting that the title reaction is highly endothermic. There is a saddle point at R1 = 3.71 a0, R2 = 3.44 a0, and it corresponds to a higher potential energy than the product channel, implying that the larger extra energy is required for the title reaction when the Ca+ ion approaches the H2 molecule by the collinear path.
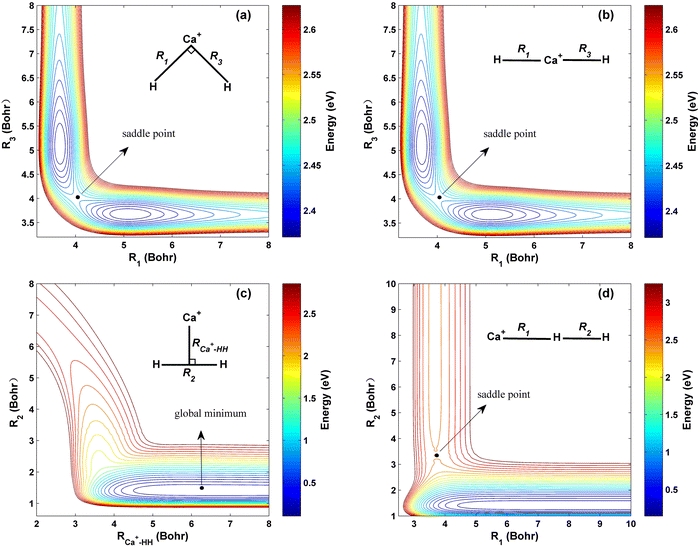 |
| | Fig. 3 Contour plots of the PIP-NN PES (a) for the bending angle between R1 and R3 fixed at 90°, (b) for the bending angle between R1 and R3 fixed at 180°, (c) for the C2v symmetry and (d) for the Ca+–H–H angle fixed at 180°. | |
Table 2 summarizes the geometries, energies and harmonic frequencies of all stationary points on the ground-state CaH2+ PES. Only the theoretical results of the global minimum in the previous studies are listed for comparison since the computational values of other stationary points and the experimental data haven’t been reported. It can be seen that the results of the equilibrium structure obtained are basically consistent with that corresponding to the data obtained on Czuchaj PES20 and ab initio values,53 and the small deviation comes from the different computational methods and basis sets. In this work, the PIP-NN PES is constructed by a large number of high-level ab initio points, and the fitting error is extremely small, thus it can accurately describe the characteristics of all stationary points.
Table 2 Geometries, energies and harmonic frequencies of stationary points for the ground-state CaH2+. The energy values are relative to the Ca+ + H2 dissociation limit
|
|
R
1 (a0) |
R
2 (a0) |
R
3 (a0) |
E (eV) |
w
1 (cm−1) |
w
2 (cm−1) |
w
3 (cm−1) |
|
Obtained from the PIP-NN PES.
Ref. 20.
Ref. 53.
|
| Global minimum (C2v) |
| This worka |
6.32 |
1.41 |
6.32 |
−0.04 |
64.4 |
325.8 |
4339.5 |
| Czuchaj PESb |
6.31 |
1.41 |
6.31 |
−0.07 |
— |
— |
— |
| CCSD(T)c |
6.24 |
1.41 |
6.24 |
−0.04 |
103 |
330 |
4359 |
| Saddle point 1 (C2v) |
| This worka |
4.01 |
5.67 |
4.01 |
2.44 |
26.4i |
387.7 |
1496.1 |
| Saddle point 2 (D∝h) |
| This worka |
4.01 |
8.02 |
4.01 |
2.46 |
653.2i |
119.2 |
1072.7 |
| Saddle point 3 (C∝ν) |
| This worka |
3.71 |
3.44 |
7.15 |
2.52 |
3318.7i |
60.3 |
1038.8 |
To more clearly present the characteristics of the title reaction on this new PES, the global minimum energy path (MEP) and the MEPs of the Ca+(2S) + H2 → CaH+ + H reaction at five different Ca+–H–H angles (60°, 90°, 120°, 150° and 180°) are shown in Fig. 4, which are determined by scanning the PIP-NN PES with small step lengths (ΔR = 0.01 a0, Δ∠Ca+–H–H = 1°) at different coordinates (RHH–RCaH+) to find the minimum energy. The global MEP includes a shallow well with a depth of 0.04 eV, and it is also the global minimum in the C2v geometry shown in Fig. 3 (c). Although the global MEP includes a well, the CaH2+ complex could not be formed since the depth of the well is too shallow. There are no obvious well or barrier for the approach angles of 60°and 90°, suggesting that the product CaH+ molecule is formed by a direct abstraction process of the reactants. A small barrier appears at the product channel of the reactive path when the Ca+–H–H angle increases to 120°, and the height of the barrier increases slowly as the approach angle becomes larger. In addition, the reaction paths of the approach angles at 150° and 180° almost overlap, implying that the topographic characteristics of the CaH2+ PES change a little at a large Ca+–H–H angle. When the vibrational zero-point energies of H2 and CaH+ molecules are included, the endothermicity of the title reaction is 2.29 eV, which is in good agreement with the experimental estimation.18 As shown in Table 2, the ground-state CaH2+ PES has three saddle points, which are corresponding to three transient states (TSs), but they are not presented in the global MEP. To clearly describe the role of these TSs, the intrinsic reaction coordinate (IRC)54 analysis is performed on each TS, as shown in Fig. S1 (ESI†). The results of IRC calculations suggest the TS1 and TS2 exist in two different H-exchange path of the Ha + CaHb+ → Hb + CaHa+ reaction, and the TS3 exist in the collinear H-abstraction path of the Ca+(2S) + H2 → CaH+ + H reaction.
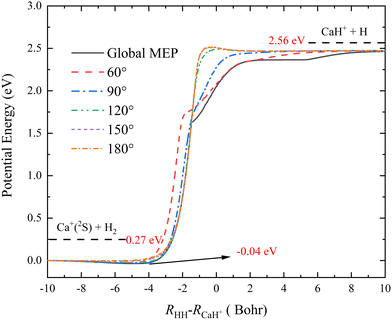 |
| | Fig. 4 Global MEP and the MEPs of the Ca+(2S) + H2 → CaH+ + H reaction at five Ca+–H–H angles (60°, 90°, 120°, 150° and 180°) calculated on the PIP-NN PES. | |
For the PES constructed by the NN model, the risk of over-fitting would significantly increase when the fitting error decreases to a very small value, especially for the long-range potential. However, the long-range interaction of the reactant channel is very crucial for calculating reaction dynamics, and its minor change may cause distinct dynamics behaviors. In addition, there still is interaction between the charged species and a neutral molecule in the long-range part for some ion-molecule reactions, such as the recently reported NH2− + H2 reaction.44Fig. 5 presents a comparison between the long-range potential energy values obtained on the new PES and the corresponding ab initio data along the radial coordinate at four selected Jacobi angles θ = 2°, 30°, 60° and 90°, where the bond length of HH is fixed at its equilibrium distance (1.401 a0). To examine the interaction of this reactive system and ensure the PIP-NN PES is globally reliable, the distance of RCa+–HH is calculated up to 40 Bohr. It can be seen that the fitting potentials are very smooth and are in good agreement with the original ab initio calculations for each angle, and there is no interaction between the Ca+ ion and H2 molecule at the long-range part. The difference between the fitting value and the ab initio data is 0.001 eV when the potential energy value stops changing, and this small deviation nearly has no effect on the dynamics of the title reaction. Therefore, no over-fitting occurs during the PIP-NN fitting and the PESs are accurate enough for describing the long-range potential.
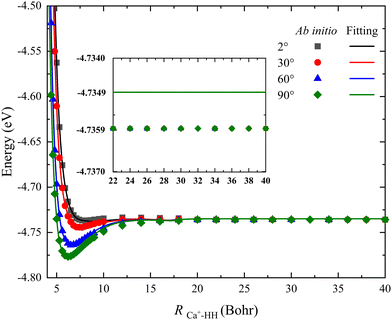 |
| | Fig. 5 Comparison of ab initio data and the corresponding values obtained on the PIP-NN PES in a long range of the reactant channel as a function of RCa+–HH at four Jacobi angles (θ = 2°, 30°, 60° and 90°) for the bond length of HH fixed at 1.401 a0. | |
3 Quantum dynamics calculations
Theoretically, the most reliable scheme for obtaining accurate dynamics data to study the collision mechanisms of a chemical reaction is to perform the dynamics calculations using the quantum mechanical method on a globally accurate PES. For the triatomic reactive systems, the TDWP method23–26 is an efficient and powerful tool for studying reaction dynamics. Based on the newly constructed ground-state CaH2+ PES, the quantum dynamics calculations of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction are carried out by the TDWP method to study the state-to-state dynamics. Here, an abbreviated outline of the TDWP calculations is displayed. In the body-fixed representation, the Hamiltonian of the reactive system is expressed as follows:| | 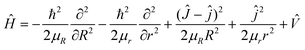 | (9) |
in which μR and μr are the reduced masses associated with R and r coordinates. J is the total angular momentum of CaH2+ and j is the rotational angular momentum of the H2 molecule. ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) expresses the potential energy values obtained from the PIP-NN PES. Herein, the state-to-state S-matrix is extracted by the reactant coordinate-based method,55,56 and the second-order split operator method57 is used to evaluate the wave packet. It is worth mentioning that the TDWP method considers the symmetry for the studied reaction once the adoptive PES satisfies the exchange symmetry of the same atom, but the symmetry could not be completely included for more complex reactive systems with high symmetry in the conventional TDWP calculations, such as H + CH458 and H + NH3.59,60 The state-to-state reaction probability can be calculated as:
expresses the potential energy values obtained from the PIP-NN PES. Herein, the state-to-state S-matrix is extracted by the reactant coordinate-based method,55,56 and the second-order split operator method57 is used to evaluate the wave packet. It is worth mentioning that the TDWP method considers the symmetry for the studied reaction once the adoptive PES satisfies the exchange symmetry of the same atom, but the symmetry could not be completely included for more complex reactive systems with high symmetry in the conventional TDWP calculations, such as H + CH458 and H + NH3.59,60 The state-to-state reaction probability can be calculated as:| | 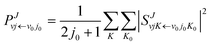 | (10) |
The state-to-state integral cross sections (ICSs) are obtained by adding the reaction probabilities of different J values:
| | 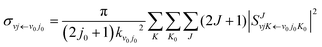 | (11) |
where
kν0j0 represents the momenta in the entrance channel. The state-resolved differential cross sections (DCSs) can be calculated by
| | 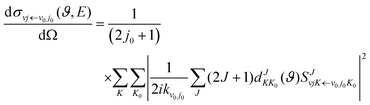 | (12) |
where
ϑ is the scattering angle, and
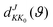
expresses the element of reduced Wigner rotation matrix.
The initial rovibrational state of the H2 molecule is set as (ν0 = 0, j0 = 0), and the J value is calculated up to 98 for obtaining convergent ICS up to 5.0 eV. The main numerical parameters used in the TDWP calculations determined by numerous convergence tests are listed in Table 3.
Table 3 Main numerical parameters in the TDWP calculations
| Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H |
| Grid/basis range and size |
R (Bohr) ∈ [0.1, 25.0], NtotR = 299, NintR = 189 |
|
r (Bohr) ∈ [0.01, 20.0], Ntotr = 199, Nasyr = 79 |
|
N
j
= 119 |
| Initial wave packet |
R
c = 16.0 Bohr |
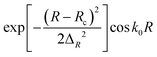
|
ΔR = 0.20 Bohr |
|
k
0 = (2E0μR)1/2 with E0 = 4.0 eV |
| Total propagation time |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. 000 a.u. |
The collision energy dependence of the total ICS of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction is displayed in Fig. 6. The energy threshold is consistent with the endothermicity determined by the PIP-NN PES because there is no barrier on the global MEP. The total ICS curve first rises with the increase of collision energy and then falls at Ec = 4.37 eV, showing a typical feature of the endothermic reactions. The main reason for the declining ICSs is that the more repulsive regions of the PES become available at high collision energy. On the other hand, the more collision energy is used to efficiently excite the product molecule to the higher vibrational or rotational energy levels, thus the cross-section begins to descend. The previous experimental study18 also presented the same variation tendency of the ICS with collision energy. Furthermore, there exist oscillations near 5.0 eV, which is because high enough collision energy opens the dissociation channel of Ca+(2S) + H2 → Ca+ + H + H, resulting in the formation of oscillations on the total ICS curve. Similar oscillation structures at high collision energy have also been presented in other ion-molecule reactive systems, such as Au+ +HD61 and Pr+ + HD.62
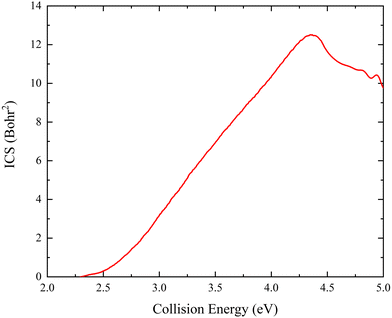 |
| | Fig. 6 Total ICS as a function of collision energy of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction calculated by the TDWP method on the PIP-NN PES. | |
The (2J + 1) weighted opacity functions of the title reaction at four collision energies (Ec = 2.5, 3.0, 4.0 and 5.0 eV) are plotted in Fig. 7, which can clearly show the contribution of each partial wave J on the total ICS. It can be seen that the maximum of available J value can reach J = 40 at Ec = 2.5 eV. The participation of many partial waves is consistent with the barrierless nature, as shown in the global MEP, suggesting that the reactive scattering proceeds in a large range of impact parameters. The opacity functions of the O + OH reaction63 also has a similar feature. More partial waves are available as the collision energy increases, and the maximum shifts to a larger J value. In addition, the contributions of higher-order partial waves (J > 50) become significantly obvious as the collision energy increases.
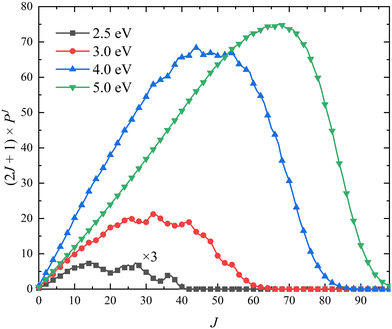 |
| | Fig. 7 Opacity functions of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at four collision energies (Ec = 2.5, 3.0, 4.0 and 5.0 eV) calculated by the TDWP method on the PIP-NN PES. | |
To further understand the dynamics mechanisms of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at the state-to-state level, the rovibrational state-resolved ICSs of the product molecule at the collision energies of 2.5, 3.0, 4.0 and 5.0 eV are displayed in Fig. 8. For Ec = 2.5 eV, only the lowest two vibrational states are available, whereas the rotational quantum number can reach j′ = 18 at ν′ = 0, and the maximum of ICS is located at j′ = 14 at ν′ = 0. As the collision energy increases, more rovibrational states are opened, and the population inversion of vibrational states becomes more obvious. The product CaH+ can be excited to very high rovibrational states when the collision energy increases to 5.0 eV, and the peak value is populated at v′ = 10, j′ = 28. This is because the title reaction proceeds along a direct abstraction path, and the collision energy is mainly transferred to the internal energies of the CaH+ molecule. In addition, the product prefers to distribute at high vibrational states and relatively low rotational states for high collision energy, which is because the interval of two adjacent vibrational energy levels becomes smaller with the increase of ν′, whereas it is the opposite for the rotational energy levels.
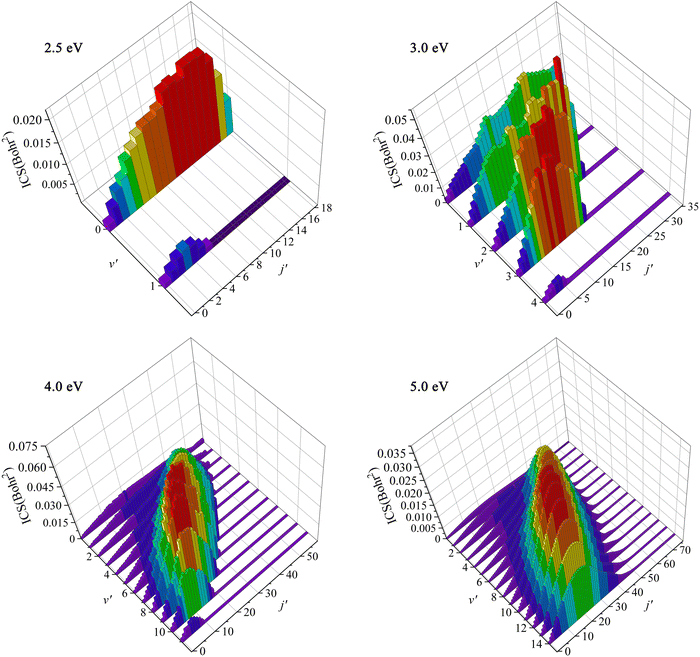 |
| | Fig. 8 Rovibrationally state-resolved ICSs of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at four collision energies (Ec = 2.5, 3.0, 4.0 and 5.0 eV) calculated by the TDWP method on the PIP-NN PES. | |
DCSs can describe the scattering features in greater detail by giving the product angular distribution of a reaction. The three-dimensional plot of the total DCSs as a function of collision energy and scattering angle for the title reaction is presented in Fig. 9. It can be seen that the peaks of the angular distribution appear at two extreme angles and the forward scattering is more obvious when the collision energy is closed to the reactive threshold. Although there exists a small backward peak at relatively low collision energy, it cannot conclude that the title reaction is dominated by a complex-forming mechanism due to the observably forward–backward asymmetric DCSs. As the collision energy increases, the backward scattering peak gradually decreases and eventually disappears, while the forward scattering completely dominates this reaction, displaying a distinctly non-statistical behavior. The DCS results further demonstrate that the title reaction follows the direct abstraction mechanism in the selected collision energy range.
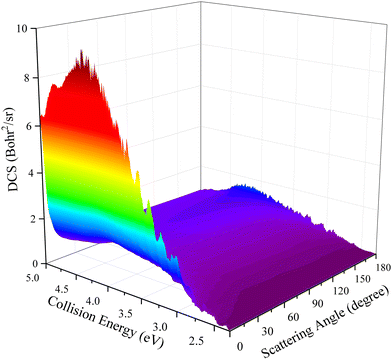 |
| | Fig. 9 Total DCS as a function of collision energy and scattering angle for the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction calculated by the TDWP method on the PIP-NN PES. | |
4 Conclusions
In this work, we report a globally accurate PES of the ground-state CaH2+ by using the PIP-NN method. The energy points are calculated at the internally contracted MRCI level with the Davidson correction, and the V5Z basis set and the QZVP basis set are adopted for H and Ca, respectively. A total of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points are selected to represent the global PES, and the fitting RMSE is only 1.64 meV. The equilibrium structure of this system corresponds to C2v symmetry, and there are multiple saddle points on the PES. The state-to-state quantum dynamics calculations of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at the collision energy below 5.0 eV is performed by the TDWP method based on this new PES to analyze the microscopic mechanisms in detail. The dynamics results of rovibrational state-resolved ICSs and DCSs can conclude that the title reaction follows a direct abstraction process in the studied collision energy range. The calculated dynamics data in this work would have great reference significance on the experimental studies at the finer level. Furthermore, this newly constructed PES can be used to further study the reaction dynamics of this system, such as the effects of isotopic substitution and rovibrational excitations of the reactant molecules.
780 ab initio points are selected to represent the global PES, and the fitting RMSE is only 1.64 meV. The equilibrium structure of this system corresponds to C2v symmetry, and there are multiple saddle points on the PES. The state-to-state quantum dynamics calculations of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at the collision energy below 5.0 eV is performed by the TDWP method based on this new PES to analyze the microscopic mechanisms in detail. The dynamics results of rovibrational state-resolved ICSs and DCSs can conclude that the title reaction follows a direct abstraction process in the studied collision energy range. The calculated dynamics data in this work would have great reference significance on the experimental studies at the finer level. Furthermore, this newly constructed PES can be used to further study the reaction dynamics of this system, such as the effects of isotopic substitution and rovibrational excitations of the reactant molecules.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant no. 11774043).
References
- C. W. Chou, C. Kurz, D. B. Hume, P. N. Plessow, D. R. Leibrandt and D. Leibfried, Nature, 2017, 545, 203–204 CrossRef CAS PubMed.
- B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem., 2021, 5, 125–140 CrossRef CAS.
- P. F. Staanum, K. Hojbjerre, R. Wester and M. Drewsen, Phys. Rev. Lett., 2008, 100, 243003 CrossRef PubMed.
- S. Willitsch, M. T. Bell, A. D. Gingell, S. R. Procter and T. P. Softley, Phys. Rev. Lett., 2008, 100, 043203 CrossRef PubMed.
- T. G. Yang, A. Y. Li, G. K. Chen, C. J. Xie, A. G. Suits, W. C. Campbell, H. Guo and E. R. Hudson, J. Phys. Chem. Lett., 2018, 9, 3555–3560 CrossRef CAS PubMed.
- M. Agundez and V. Wakelam, Chem. Rev., 2013, 113, 8710–8737 CrossRef CAS PubMed.
- M. Singh, Astrophys. Space Sci., 1988, 140, 421–427 CrossRef CAS.
- A. J. Sauval and J. B. Tatum, Astrophys. J., Suppl. Ser., 1984, 56, 193–209 CrossRef CAS.
- B. C. Sawyer, J. G. Bohnet, J. W. Britton and J. J. Bollinger, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 011401 CrossRef.
- M. McAneny, B. Yoshimura and J. K. Freericks, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 043434 CrossRef.
- B. J. McMahon and B. C. Sawyer, Phys. Rev. Appl., 2022, 17, 014005 CrossRef CAS.
- C. J. Ballance, T. P. Harty, N. M. Linke, M. A. Sepiol and D. M. Lucas, Phys. Rev. Lett., 2016, 117, 060504 CrossRef CAS PubMed.
- M. Kajita, M. Abe, M. Hada and Y. Moriwaki, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 025402 CrossRef.
- M. Abe, M. Kajita, M. Hada and Y. Moriwaki, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 245102 CrossRef.
- K. Sinha, Proc. - Astron. Soc. Aust., 1991, 9, 32–36 CrossRef CAS.
- K. Sinha, B. M. Tripathi, R. M. Atalla and P. D. Singh, Sol. Phys., 1988, 115, 221–227 CrossRef CAS.
- S. Canuto, M. A. Castro and K. Sinha, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 2461–2463 CrossRef CAS PubMed.
- R. Georgiadis and P. B. Armentrout, J. Phys. Chem., 1988, 92, 7060–7067 CrossRef CAS.
- A. K. Hansen, M. A. Sorensen, P. F. Staanum and M. Drewsen, Angew. Chem., Int. Ed., 2012, 51, 7960–7962 CrossRef CAS PubMed.
- E. Czuchaj, M. Krosnicki and H. Stoll, Mol. Phys., 2000, 98, 419–427 CrossRef CAS.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- Z. G. Sun, S. Y. Lee, H. Guo and D. H. Zhang, J. Chem. Phys., 2009, 130, 174102 CrossRef PubMed.
- Z. G. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef PubMed.
- B. Buren, M. D. Chen, Z. G. Sun and H. Guo, J. Phys. Chem. A, 2021, 125, 10111–10120 CrossRef CAS PubMed.
- J. Y. Huang, S. Liu, D. H. Zhang and R. V. Krems, Phys. Rev. Lett., 2018, 120, 143401 CrossRef CAS PubMed.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- T. Leininger, A. Nicklass, W. Küchle, H. Stoll, M. Dolg and A. Bergner, Chem. Phys. Lett., 1996, 255, 274–280 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
-
K. P. Huber and G. Herzberf, Constants of Diatomic Molecules, Springer, 1979 Search PubMed.
- J. Condoluci, S. Janardan, A. T. Calvin, R. Rugango, G. Shu, C. D. Sherrill and K. R. Brown, J. Chem. Phys., 2017, 147, 214309 CrossRef CAS PubMed.
- M. Abe, Y. Moriwaki, M. Hada and M. Kajita, Chem. Phys. Lett., 2012, 521, 31–35 CrossRef CAS.
- J. C. Yuan, D. He and M. D. Chen, Phys. Chem. Chem. Phys., 2015, 17, 11732–11739 RSC.
- B. Kolb, B. Zhao, J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2016, 144, 224103 CrossRef PubMed.
- K. M. Thompson, Y. D. Gao, P. Marshall, H. Wang, L. S. Zhou, Y. L. Li and H. Guo, J. Chem. Phys., 2017, 147, 134302 CrossRef PubMed.
- Z. J. Yang, S. F. Wang, J. C. Yuan and M. D. Chen, Phys. Chem. Chem. Phys., 2019, 21, 22203–22214 RSC.
- W. T. Li, D. He and Z. G. Sun, J. Chem. Phys., 2019, 151, 185102 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS PubMed.
- J. Li, S. Carter, J. M. Bowman, R. Dawes, D. Q. Xie and H. Guo, J. Phys. Chem. Lett., 2014, 5, 2364–2369 CrossRef CAS PubMed.
- K. S. Song, H. W. Song and J. Li, Phys. Chem. Chem. Phys., 2022, 24, 10160–10167 RSC.
- J. X. Zuo, J. F. E. Croft, Q. Yao, N. Balakrishnan and H. Guo, J. Chem. Theory Comput., 2021, 17, 6747–6756 CrossRef CAS PubMed.
- S. Manzhos and T. Carrington, Chem. Rev., 2021, 121, 10187–10217 CrossRef CAS PubMed.
- Y. F. Guan, C. J. Xie, D. R. Yarkony and H. Guo, Phys. Chem. Chem. Phys., 2021, 23, 24962–24983 RSC.
- C. J. Xie, X. L. Zhu, D. R. Yarkony and H. Guo, J. Chem. Phys., 2018, 149, 144107 CrossRef PubMed.
- Y. N. Shu, Z. Varga, A. G. S. De Oliveira and D. G. Truhlar, J. Chem. Theory Comput., 2021, 17, 1106–1116 CrossRef CAS PubMed.
- Z. J. Yang, J. C. Yuan, S. F. Wang and M. D. Chen, RSC Adv., 2018, 8, 22823–22834 RSC.
- J. C. Yuan, D. He, S. F. Wang, M. D. Chen and K. L. Han, Phys. Chem. Chem. Phys., 2018, 20, 6638–6647 RSC.
- M. T. Hagan and M. B. Menhaj, IEEE Int. Conf. Neural Networks, 1994, 5, 989–993 CrossRef CAS PubMed.
- K. Sen, S. Pakhira, C. Sahu and A. K. Das, Mol. Phys., 2014, 112, 182–188 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- Z. G. Sun, X. Lin, S. Y. Lee and D. H. Zhang, J. Phys. Chem. A, 2009, 113, 4145–4154 CrossRef CAS PubMed.
- S. Gómez-Carrasco and O. Roncero, J. Chem. Phys., 2006, 125, 054102 CrossRef PubMed.
- M. D. Feit, J. A. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
- J. Li, J. Chen, Z. Q. Zhao, D. Q. Xie, D. H. Zhang and H. Guo, J. Chem. Phys., 2015, 142, 204302 CrossRef PubMed.
- J. Li and H. Guo, Phys. Chem. Chem. Phys., 2014, 16, 6753–6763 RSC.
- H. W. Song, M. H. Yang and H. Guo, J. Chem. Phys., 2016, 145, 131101 CrossRef PubMed.
- F. X. Li, C. S. Hinton, M. Citir, F. Y. Liu and P. B. Armentrout, J. Chem. Phys., 2011, 134, 024310 CrossRef PubMed.
- M. Ghiassee, J. Ewigleben and P. B. Armentrout, J. Chem. Phys., 2020, 153, 144304 CrossRef CAS PubMed.
- S. Y. Lin, H. Guo, P. Honvault, C. X. Xu and D. Q. Xie, J. Chem. Phys., 2008, 128, 014303 CrossRef PubMed.
|
| This journal is © the Owner Societies 2022 |
 ,
Hanghang
Chen
,
Ye
Mao
and
Maodu
Chen
,
Hanghang
Chen
,
Ye
Mao
and
Maodu
Chen
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points calculated at the multi-reference configuration interaction level. On the new PES, the quantum time-dependent wave packet calculations are performed to study the dynamics mechanisms of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction. The calculated results suggest that the reaction follows a direct abstraction process when the collision energy is below 5.0 eV. The dynamics results would have a great reference significance for the experimental research of this reactive system at a finer level, and further dynamics studies, such as the effects of isotope substitution and rovibrational excitations of the reactant molecule, could be carried out on this newly constructed PES.
780 ab initio points calculated at the multi-reference configuration interaction level. On the new PES, the quantum time-dependent wave packet calculations are performed to study the dynamics mechanisms of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction. The calculated results suggest that the reaction follows a direct abstraction process when the collision energy is below 5.0 eV. The dynamics results would have a great reference significance for the experimental research of this reactive system at a finer level, and further dynamics studies, such as the effects of isotope substitution and rovibrational excitations of the reactant molecule, could be carried out on this newly constructed PES.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (w))/dt = −1/2d(ln
(w))/dt = −1/2d(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (mp/me))dt,13 and the measurement of the pure vibrational transition frequency of CaH+ can reach within the uncertainty of 10−16. In addition, CaH+ is also an astrophysically important molecular ion,15–17 thus understanding its formation plays a crucial role in the evolution of interstellar clouds.
(mp/me))dt,13 and the measurement of the pure vibrational transition frequency of CaH+ can reach within the uncertainty of 10−16. In addition, CaH+ is also an astrophysically important molecular ion,15–17 thus understanding its formation plays a crucial role in the evolution of interstellar clouds.
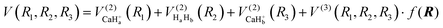
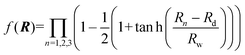

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−0.2Ri) (i =1, 2, 3)
(−0.2Ri) (i =1, 2, 3)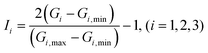
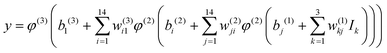
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points are selected to participate in the PIP-NN fitting, and these points are divided randomly into the training set (90%), testing set (5%), and validation set (5%) for effectively avoiding the over-fitting behavior. Fig. 2 shows the distribution of the NN fitting errors defined by the difference between the fitting values and ab initio data, and the energy values of the horizontal axis are relative to the triatomic dissociation limit of Ca+–H–H. It is clear that the PIP-NN PES keeps a very small predictive error in the whole energy region, and the percentage of points with an absolute error less than 5 meV is 98.1%. The overall RMSE of the final PES is only 1.64 meV. Therefore, the fitting PIP-NN PES is accurate enough for dynamics calculations of the CaH2+ reactive system.
780 ab initio points are selected to participate in the PIP-NN fitting, and these points are divided randomly into the training set (90%), testing set (5%), and validation set (5%) for effectively avoiding the over-fitting behavior. Fig. 2 shows the distribution of the NN fitting errors defined by the difference between the fitting values and ab initio data, and the energy values of the horizontal axis are relative to the triatomic dissociation limit of Ca+–H–H. It is clear that the PIP-NN PES keeps a very small predictive error in the whole energy region, and the percentage of points with an absolute error less than 5 meV is 98.1%. The overall RMSE of the final PES is only 1.64 meV. Therefore, the fitting PIP-NN PES is accurate enough for dynamics calculations of the CaH2+ reactive system.

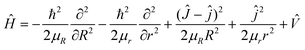
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) expresses the potential energy values obtained from the PIP-NN PES. Herein, the state-to-state S-matrix is extracted by the reactant coordinate-based method,55,56 and the second-order split operator method57 is used to evaluate the wave packet. It is worth mentioning that the TDWP method considers the symmetry for the studied reaction once the adoptive PES satisfies the exchange symmetry of the same atom, but the symmetry could not be completely included for more complex reactive systems with high symmetry in the conventional TDWP calculations, such as H + CH458 and H + NH3.59,60 The state-to-state reaction probability can be calculated as:
expresses the potential energy values obtained from the PIP-NN PES. Herein, the state-to-state S-matrix is extracted by the reactant coordinate-based method,55,56 and the second-order split operator method57 is used to evaluate the wave packet. It is worth mentioning that the TDWP method considers the symmetry for the studied reaction once the adoptive PES satisfies the exchange symmetry of the same atom, but the symmetry could not be completely included for more complex reactive systems with high symmetry in the conventional TDWP calculations, such as H + CH458 and H + NH3.59,60 The state-to-state reaction probability can be calculated as: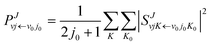
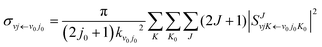
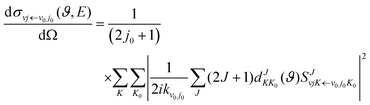
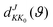 expresses the element of reduced Wigner rotation matrix.
expresses the element of reduced Wigner rotation matrix.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 ab initio points are selected to represent the global PES, and the fitting RMSE is only 1.64 meV. The equilibrium structure of this system corresponds to C2v symmetry, and there are multiple saddle points on the PES. The state-to-state quantum dynamics calculations of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at the collision energy below 5.0 eV is performed by the TDWP method based on this new PES to analyze the microscopic mechanisms in detail. The dynamics results of rovibrational state-resolved ICSs and DCSs can conclude that the title reaction follows a direct abstraction process in the studied collision energy range. The calculated dynamics data in this work would have great reference significance on the experimental studies at the finer level. Furthermore, this newly constructed PES can be used to further study the reaction dynamics of this system, such as the effects of isotopic substitution and rovibrational excitations of the reactant molecules.
780 ab initio points are selected to represent the global PES, and the fitting RMSE is only 1.64 meV. The equilibrium structure of this system corresponds to C2v symmetry, and there are multiple saddle points on the PES. The state-to-state quantum dynamics calculations of the Ca+(2S) + H2(ν0 = 0, j0 = 0) → CaH+ + H reaction at the collision energy below 5.0 eV is performed by the TDWP method based on this new PES to analyze the microscopic mechanisms in detail. The dynamics results of rovibrational state-resolved ICSs and DCSs can conclude that the title reaction follows a direct abstraction process in the studied collision energy range. The calculated dynamics data in this work would have great reference significance on the experimental studies at the finer level. Furthermore, this newly constructed PES can be used to further study the reaction dynamics of this system, such as the effects of isotopic substitution and rovibrational excitations of the reactant molecules.