Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Suppressing non-radiative decay of photochromic organic molecular systems in the strong coupling regime†
Rafael C.
Couto
 * and
Markus
Kowalewski
* and
Markus
Kowalewski
 *
*
Department of Physics, Stockholm University, Albanova University Center, SE-106 91 Stockholm, Sweden. E-mail: rafael.carvalho@fysik.su.se; markus.kowalewski@fysik.su.se
First published on 14th July 2022
Abstract
The lifetimes of electronic excited states have a strong influence on the efficiency of organic solar cells. However, in some molecular systems a given excited state lifetime is reduced due to the non-radiative decay through conical intersections. Several strategies may be used to suppress this decay channel. The use of the strong light-matter coupling provided in optical nano-cavities is the focus of this paper. Here, we consider the meso–tert-butyl-4,4-difluoro-4-bora-3a,4a-diaza-s-indacene molecule (meso–tert-butyl-BODIPY) as a showcase of how strong and ultrastrong coupling might help in the development of organic solar cells. The meso–tert-butyl-BODIPY is known for its low fluorescence yield caused by the non-radiative decay through a conical intersection. However, we show here that, by considering this system within a cavity, the strong coupling can lead to significant changes in the multidimensional landscape of the potential energy surfaces of meso–tert-butyl-BODIPY, suppressing almost completely the decay of the excited state wave packet back to the ground state. By means of multi configuration electronic structure calculations and nuclear wave packet dynamics, the coupling with the cavity is analyzed in-depth to provide further insight of the interaction. By fine-tuning the cavity field strength and resonance frequency, we show that one can change the nuclear dynamics in the excited state, and control the non-radiative decay. This may lead to a faster and more efficient population transfer or the suppression of it.
1 Introduction
The understanding of how a molecule in an electronic excited state behaves is one of the key components of the production of high efficient light harvesting photovoltaic cells. This can be related to spectral shape, range of absorption/emission, and the excited state lifetime, to name a few.1,2 A long-lived excited state in a photon acceptor molecule leads to a more efficient charge transfer for the energy conversion in solar cells. However, in some systems an ultrafast non-radiative decay from the electronically excited state, caused by the presence of a conical intersection (CoIn), is observed.3 There are several approaches to quench the non-radiative decay due to molecular dynamics in the excited state, which includes chemical substitutions, the use of high density or highly interactive solvents, to cite a few.4–6 Nonetheless, in the past years, it has been found that a potential energy surface's (PES) landscape might change significantly when a molecule is placed in an optical nano-cavity and strongly coupled to the quantized light field.7–14 This interaction creates polaritonic states, which are a combination of the PES of the bare molecule and the cavity field. By tuning the cavity properties, one can drastically change the wave packet evolution in such polaritonic PES.In this paper, we demonstrate theoretically how one can suppress the non-radiative decay of the wave packet in an electronic excited state when a molecule is coupled strongly to a cavity, by means of multi configuration electronic structure calculations and quantum nuclear wave packet simulations. The showcase system chosen is a derivative of the 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (also referred as BODIPY). This molecular system has being widely studied due to its optical properties with applications in organic solar cells.15–20 As presented in Fig. 1a, the core BODIPY structure has different substitution sites, covering various options to create derivatives with widely different properties. One very important aspect of BODIPY is the presence of a conical intersection in the HOMO–LUMO excited state (π → π* transition) which leads to a non-radiative decay of the excited state wave packet back to the ground electronic state. The essence of the excited state nuclear dynamics involves the bending of the central structure and the raise of the group at the position 8. In the case of the core BODIPY structure (Fig. 1a), there is a significant barrier between the Franck–Condon (FC) region and CoIn (around 2.9 eV), which makes the non-radiative decay irrelevant and the fluorescence yield of this system in around 0.99.21 However, different substitution groups may change drastically the fluorescence yield of the system. An example of this is the meso–tert-butyl-BODIPY (MTBB), depicted in Fig. 2b, which fluorescence yield is reported to be 0.04, due to the strong nuclear dynamics in the S1 electronic excited state.6,22,23
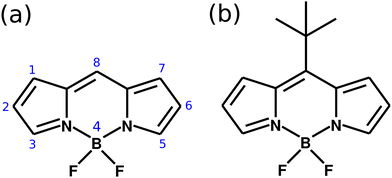 | ||
| Fig. 1 (a) Molecular structure of the BODIPY core, with the numbering showing the different substitution sites. (b) Structure of the meso–tert-butyl-BODIPY (MTBB). | ||
The low fluorescence yield of the MTBB molecule is the main motivation of the study presented here, with our goal being to direct the nuclear dynamics in the excited state in order to suppress the non-radiative decay of the wave packet back to the electronic ground state, creating a long-lived electronic excited state. To do so, this system is studied under the influence of strong light-matter coupling in a nano-cavity. We demonstrate that the cavity strong and ultrastrong coupling leads to a significant change in the PES landscape where the wave packet is trapped in the excited state due to the Rabi splitting between the polaritonic states, and the non-radiative decay is almost fully suppressed. There have been several experimental studies related to BODIPY in cavities, involving hybridization between the excitonic transitions,24 radiative pumping of polaritons,25 polariton condensation,26 polariton Lasing,27 anti-Stokes fluorescence28 and general optical properties.29 The main focus of this paper is on the suppression of the non-radiative decay of the wave packet in the excited electronic state.
2 Theory and model
2.1 MTBB structure and reaction coordinates
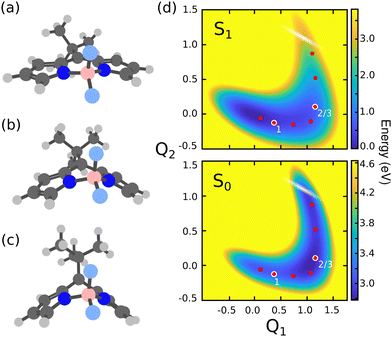
There are several possible derivatives of the BODIPY molecule, considering different substitution sites (Fig. 1a) present in the core structure. As the main goal of this paper is to understand the effects of a cavity in the excited state dynamics of BODIPY, a structure which presents a very low fluorescence yield, the MTBB (Fig. 1b and 2), was chosen. This molecule has been the subject of theoretical and experimental studies6,22,23 due to its characteristic low fluorescence yield related to strong non-adiabatic dynamics in the electronic excited state, leading to the non-radiative decay to the ground state through conical intersections.The MTBB molecule possesses 99 nuclear degrees of freedom. To be able to treat this system with a full quantum wave packet description, a careful selection of the degrees of freedom has to be made. Through geometry optimization and gradient analysis of the ground and excited state, three critical structures were identified, which are presented in Fig. 2. The first one is the ground state equilibrium geometry (Seq0), which shows a relatively planar core structure, with the tert-butyl group rotated (Fig. 2a). The second structure (Fig. 2b) is the S1 excited state minimum (Seq1), characterized by a bent structure and the tert-butyl group rotated and symmetric to the molecule. The third important structure was identified at the point of the CoIn (Fig. 2c), displaying a more pronounced bent structure and the tert-butyl group with a ∼120° angle relative to the core of the molecule. Experimental and theoretical evidence6,22,23 shows that the low fluorescence yield is mainly caused by the non-radiative decay through the CoIn. Thus, the most probable reaction pathway of MTBB in the excited state involves the three molecular structures in Fig. 2a–c. Following this idea, the multidimensional MTBB system can be reduced to a 2D problem, with the reaction coordinates Q1 and Q2 defined as the difference between the Cartesian coordinates x of these molecular structures:
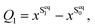 | (1) |
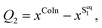 | (2) |
2.2 Hamiltonian
A full quantum wave packet dynamics approach is used to understand the behavior of MTBB in the strong coupling regime. The Hamiltonian describing the light-matter interaction is defined as| ĤMC = ĤM + ĤC + ĤI, | (3) |
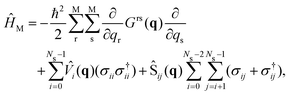 | (4) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) i the ith PES of the electronic states considered in the dynamics Ns, Ŝij the non-adiabatic coupling between electronic states Si and Sj (here we consider S0 and S1 electronic states only) and σij = |i〉〈j| and σ†ij = |j〉〈i| are the electronic excitation creation and annihilation operators, respectively. The reaction coordinates are represented by q = (Q1, Q2)T. The G-matrix elements Grs in eqn (4) take the form
i the ith PES of the electronic states considered in the dynamics Ns, Ŝij the non-adiabatic coupling between electronic states Si and Sj (here we consider S0 and S1 electronic states only) and σij = |i〉〈j| and σ†ij = |j〉〈i| are the electronic excitation creation and annihilation operators, respectively. The reaction coordinates are represented by q = (Q1, Q2)T. The G-matrix elements Grs in eqn (4) take the form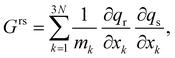 | (5) |
The cavity Hamiltonian (eqn (3)) is defined as
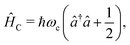 | (6) |
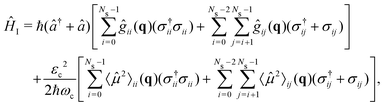 | (7) |
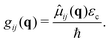 | (8) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ij are the permanent (i = j) and transition (i ≠ j) dipole moments.〈
ij are the permanent (i = j) and transition (i ≠ j) dipole moments.〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 2〉ij = 〈i|
2〉ij = 〈i|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 2|j〉 is the squared dipole operator, describing the influence of the dipole self-energy interaction.38
2|j〉 is the squared dipole operator, describing the influence of the dipole self-energy interaction.38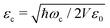 is the cavity vacuum electric field strength with cavity mode volume V. Note that in eqn (7), the first term represents the electronic gij and vibrational gii cavity couplings, while the second term (dependent on 〈
is the cavity vacuum electric field strength with cavity mode volume V. Note that in eqn (7), the first term represents the electronic gij and vibrational gii cavity couplings, while the second term (dependent on 〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 2〉ij) relates to the dipole self-energy interaction. The latter has shown to be important in the description of the light-matter interaction in complex systems.37,39–41
2〉ij) relates to the dipole self-energy interaction. The latter has shown to be important in the description of the light-matter interaction in complex systems.37,39–41
In order to treat the studied system in a numerical efficient way, we use photon displacement coordinates to describe the cavity mode (6) and (7).9,37,42 This is done by expressing the cavity mode's ladder operator as
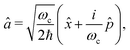 | (9) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and the conjugate momentum
and the conjugate momentum 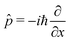 . Therefore, the cavity Hamiltonian (6) reads
. Therefore, the cavity Hamiltonian (6) reads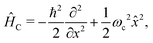 | (10) |
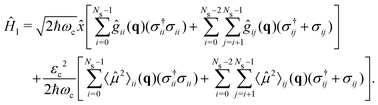 | (11) |
3 Computational details
3.1 Electronic structure
The S1/S0 CoIn is responsible for the non-radiative decay back to the ground state. Thus, one could consider only the first two states in the quantum dynamics simulations. However, under the influence of ultrastrong coupling, higher lying electronic states may start to mix with the S0 and S1 and influence in the change in the PES landscape. Due to this, we considered in our simulations three upper electronic excited states, S2, S3 and S4 (see Fig. S2–S4 of ESI†). Higher lying states were neglected due to small transition dipole moment and large excitaton energies.The PESs presented in Fig. 2d, and higher electronic states (see Fig. S2–S4 of ESI†), were computed with the state-average complete-active-space self-consistent-field (SA-CASSCF) method,43–45 with the cc-pVDZ basis set.46 The active space chosen consists of 12 electrons distributed over 11 orbitals, CAS(12,11), corresponding to the full set of the ππ* molecular orbitals (see Fig. S1 of ESI†). The molecular structures of the S0 and S1 minima (Fig. 2a and b) were obtained through geometry optimization with the OpenMolcas software,47 using the active space and basis set described above. The molecular structure at the CoIn (Fig. 2c) was obtained by the conical intersection optimization procedure implemented in the MOLPRO-2019 program package,48,49 with the same active space but the 6-311G* basis set.50 The transition dipole moments between all involved electronic states were computed in the velocity gauge with the restricted-active-space state-interaction approach51,52 and the non-adiabatic couplings between S0 and S1 were computed analytically,53 both implemented in the OpenMolcas software.
The analytical non-adiabatic couplings computed with OpenMolcas47,53 are represented by a 3N matrix (N is the number of atoms), related to the Cartesian coordinates of the atoms. It takes the form 〈ψi|∂/∂xkψj〉, where ψn represents the wave function of the corresponding electronic state and xk the Cartesian coordinate (x, y, z) for atom k. To convert the non-adiabatic coupling matrix from Cartesian coordinates to the reaction coordinates Q1 and Q2, the following transformation is used:54
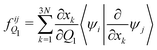 | (12) |
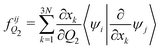 | (13) |
The PES of all electronic states (Fig. 2d and Fig. S2–S4, ESI†), as well as all other properties (permanent and transition dipole moments, non-adiabatic coupling and G-matrix elements) were computed on a 43 × 33 (Q1, Q2) grid, which later were interpolated with a polyharmonic spline procedure55 to a 256 × 256 grid, with Q1 ranging from −1.0 to 1.75 and Q2 from −0.5 to 1.5. The permanent and transition dipole moments, G-matrix elements and non-adiabatic couplings used in the wave packet propagation are presented in Fig. S5–S22 of the ESI.†
3.2 Quantum nuclear wave packet dynamics
The excited state dynamics of MTBB was simulated with the quantum nuclear wave packet propagation method, where the time-dependent Schrödinger equation is solved numerically, considering the total Hamiltonian (3), which includes eqn (4), (10) and (11). The wave packet propagation is done by using the Chebychev method,56 implemented in our in-house code (QDng), with a maximum propagation time of 450 fs and a time step of 0.3 fs. Due to the use of photon displacement coordinate![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (see eqn (10) and (11)), the dynamics were run on a 3D grid (256 × 256 × 32). Here, the last coordinate corresponds to the photon displacement coordinate
(see eqn (10) and (11)), the dynamics were run on a 3D grid (256 × 256 × 32). Here, the last coordinate corresponds to the photon displacement coordinate ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . The excited state dynamics is initiated by placing the ground state ν0 vibrational wave function on the S1 PES at the Franck–Condon region (Q1 = Q2 = 0.0) The vibrational ground state has been obtained by the imaginary time propagation method,57 also implemented in QDng.
. The excited state dynamics is initiated by placing the ground state ν0 vibrational wave function on the S1 PES at the Franck–Condon region (Q1 = Q2 = 0.0) The vibrational ground state has been obtained by the imaginary time propagation method,57 also implemented in QDng.
Note that in eqn (11), we considered the interaction between all states involved, i.e., the transition dipole moments between all electronic states: ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 01,
01,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 12,
12,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 34…, with a total of 9 terms. The expectation value of the squared dipole operator 〈
34…, with a total of 9 terms. The expectation value of the squared dipole operator 〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 2〉ij(q) is computed by using the resolution of identity37,41
2〉ij(q) is computed by using the resolution of identity37,41
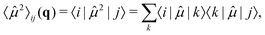 | (14) |
The dynamics in presence of the cavity was simulated by considering two main external parameters, the cavity vacuum electric field strength εc and the cavity's resonance frequency ωc. To obtain an extended picture of the effect of the cavity coupling on the excited state dynamics, the chosen εc ranges from 0.005 to 2.06 GV m−1. The resonance frequency ωc was set as the energy difference between the S0 and S1 PES at different points, following the excited state reaction coordinate which corresponds to the minimum energy pathway from the FC position to the CoIn in the S1 PES (see red dots in Fig. 2d). Therefore, ωc ranges from 3.02 to 0.45 eV.
4 Results
4.1 Potential energy surfaces
The use of reactive coordinates requires a careful selection of the degrees of freedom considered in our simulations. Experimental evidence shows a fluorescence yield of around 0.04,6 meaning that almost all S1 population decays non-radiatively to the S0 PES. Our simulations for the bare molecule show a decay of ∼27% of the S1 wave packet through the CoIn. To understand this difference, a closer look into the wave packet propagation and the PES of MTBB (Fig. 2d) is required. In the excited state dynamics, the wave packet in the S1 PES would travel from the FC region (Q1 = Q2 = 0.0) along the Q1 coordinate until Q1 ∼ 1, which takes around 120 fs. Here, part of the wave packet returns to the FC region due to the presence of barrier at around Q1 = 0.5 (Q2 = 0.0), of about 0.025 eV. Even though this barrier is relatively small, the wave packet does not have enough momentum to fully overcome it and only part of it reaches Q1 ∼ 1. Furthermore, after ∼120 fs, the wave packet continues along the Q2 coordinate, reaching the CoIn region at t ∼ 200 fs. Here, the presence of another barrier (Q1 ∼ 1, Q2 ∼ 0.5), of about 0.13 eV, slows down the wave packet. The appearance of these two barriers and the fact that the wave packet propagation is limited to 500 fs are the main factors that lead to a ∼27% non-radiative decay.The two small barriers seen in the S1 PES can be understood through the geometry optimization of the Seq1 and CoIn structures (Fig. 2b and c), which roughly shows the minimum energy pathway to get to these structures. Starting from the Seq0, it was observed that the MTBB molecule bends the core first and then rotates the tert-butyl group (Fig. 2b), which would lead to a barrier less potential. However, in our selected reaction coordinate Q1, the bending and rotation processes happen simultaneously, and a small barrier is observed. The same can be said about the CoIn structure (Fig. 2c), where our simulations show a sequential movement of the bending the core and raising the tert-butyl group, while the Q2 represents this motion concurrently.
We acknowledge the difference between the experimental results and our simulations in fluorescence yield and focus on the relative changes that occur in the presence of the cavity.
4.2 Dynamics in the strong coupling regime
The cavity quantum dynamics of the MTBB excited state was simulated and the field strength εc and the resonance frequency ωc have been varied. The results are presented in the form of a 2D map in Fig. 3, which shows the total population in the electronic excited state at 400 fs. This propagation time was chosen as it represents the maximum population decay (within our simulations), whereas after this point the wave packet travels back and forth in the PES. Alongside the population, a contour map of the coupling strength (gij/ωc) is shown. It is assumed that the ultrastrong coupling regime is when gij/ωc > 0.158–60 is reached, as indicated in Fig. 3.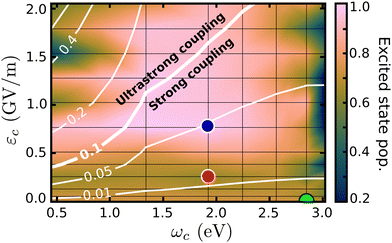 | ||
| Fig. 3 Population in the excited state, at 400 fs, as a function of the cavity resonance frequency ωc and field strength εc. The coupling strength (gij/ωc) is shown by the contour lines. The colored dots mark the position of the cases considered in Fig. 4 and in the discussion. | ||
The wave packet propagates exclusively in the S1 and S0 PESs for cavity coupling strengths gij/wc < 0.1. However, in the ultrastrong coupling region, a small portion of the population (up to 10% in the region with gij/wc > 0.4) is projected to higher excited states (S2, S3 and S4). Due to this mixing, the time evolution of the populations presented in this paper is related to the total population in the excited states and includes S1 to S4. The 2D map shows significant changes in the final excited state populations when varying εc and ωc, from suppression to increase of the non-radiative decay. On the right-most side of Fig. 3, the resonance frequency is set to the FC region, with leads to strong Rabi oscillations (see Fig. S8 in the ESI†), where at 400 fs shows population around 0.2. When considering the extreme case, with the smallest ωc = 0.45 eV and εc > 1.3, the excited state population is transferred almost completely to the electronic S0 ground state. Moreover, let us focus on the region within the extremes and analyze three cases that illustrate the major effects of the strong coupling in the excited state dynamics of MTBB.
Fig. 3 presents three main regions related to the influence of the strong coupling. The first region represents the weak cavity field interaction, close to εc = 0.0, where the excited state population remains at around 73%, as for the bare molecule. With the increase of the field strength (εc ∼ 0.25 GV m−1), a decrease of the final excited state population of up to 62% is observed. The third region relates to the suppression of the non-radiative decay, observed at approximately εc > 0.8 GV m−1. In all three regions, it is also observed that the cavity resonance frequency plays an important role in the excited state dynamics. The intricacies of these different effects will be discussed in the following.
In Fig. 4 are presented three cases that represent the major cavity effects in the excited state nuclear dynamics. The time-dependent excited state population for case (1), ωc = 2.85 eV, εc = 0.005 GV m−1 (representing the minimum cavity effect), case (2), ωc = 1.93 eV, εc = 0.26 GV m−1 (representing the well in Fig. 3), and case (3) – ωc = 1.93 eV, εc = 0.77 GV m−1 (illustrating the suppression of the non-radiative decay). All three cases are marked in Fig. 4 with color-coded circles. The results for the bare molecule (εc = 0.00) are shown for comparison and the positions of the resonance frequency in the PES are shown in Fig. 2b. In case (1), the cavity's resonance frequency is set close the FC region (Q1 ≈ −0.1 Q2 ≈ 0.4 – Fig. 2d), while the field strength is set to its lowest value considered here (εc = 0.005 GV m−1). This results in a minimum change of the population transfer to the ground state when compared to the bare molecule (green and black curves in Fig. 4, respectively). Case (2): by increasing the field strength and setting the resonance frequency at the barrier along Q2 of the S1 PES (Q1 ≈ 1.1, Q2 ≈ 0.1; Fig. 2d), an increase of the non-radiative decay can be seen (Fig. 4 red curve), with the excited state population reaching 0.62 at 400 fs. This constitutes a change of about 15% when compared to the bare molecule. In the third scenario, case (3), an interesting behavior is observed. As seen in the blue curve in Fig. 4, the beginning of the propagation is dominated by large Rabi oscillations, due to the strong coupled field strength considered (εc = 0.77 GV m−1), leading to a direct transfer of about 3% of excited state population to the ground state. After around 100 fs, a rapid decay to S0 is observed, with the excited state population reaching ∼0.75. However, at 200 fs, the population is transferred back to excited state, which at the end of the propagation (400 fs) is 0.95.
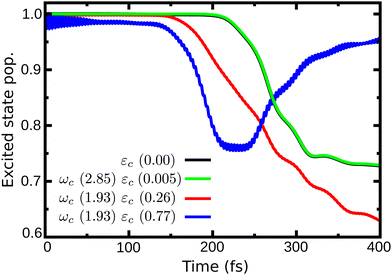 | ||
| Fig. 4 Time dependent population in the excited state for case (1) (ωc = 2.85 eV, εc = 0.005 GV m−1), case (2) (ωc = 1.93 eV, εc = 0.26 GV m−1) and case (3) (ωc = 1.93 eV, εc = 0.77 GV m−1). | ||
To shed light on how the cavity strong coupling changes the PESs landscape, we analyze the approximate 1D cuts of the polaritonics surfaces along the S1 reaction coordinate (Fig. 5a). The 1D reaction coordinate was chosen by considering the minimum energy pathway of the wave packet in the S1 PES, namely the S1 reaction coordinate (S1,RC). These 1D cuts show the main features of the S1 PES (Fig. 5): the FC region at position S1,RC = 0.0, the barrier along the Q1 coordinate (S1,RC ≈ 0.5), the S1 minimum (S1,RC = 1.0), the barrier along Q2 (S1,RC ≈ 1.5), and the CoIn (S1,RC ≈ 2.0). The 1D polaritonic potential energy curves (PEC) were obtained by the diagonalization of the Hamiltonian in the basis of the Fock states (Fig. 5b–d), and considering |S0|0〉 to |S4|0〉, and S0 and S1 with up to three photon modes, i.e., |S0|1〉, |S0|2〉, |S0|3〉…. Note that we have neglected the counter-rotating terms in the diagonalization, and the 1D polaritonic surfaces presented here are used for a qualitative understanding of the dynamics. All results presented in the paper were obtained from the full PES as described in Section 2.
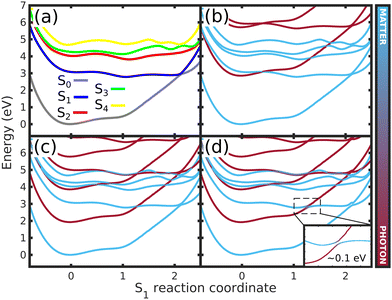 | ||
| Fig. 5 Potential energy curves along the S1 reaction coordinate (S1,RC) for (a) the bare molecule, (b) case (1) (ωc = 2.85 eV, εc = 0.005 GV m−1), (c) case (2) (ωc = 1.93 eV, εc = 0.26 GV m−1) and (d) case (3) (ωc = 1.93 eV, εc = 0.77 GV m−1) – (Fig. 3 and 4). In (a), the curves represents the 1D cuts of the 2D PES (Fig. 2d and Fig. S2–S4, ESI†) of all electronic states. (b)–(d) shows the approximate polaritonic potential energy curves obtained from the diagonalization of the Hamiltonian (3) in the basis of the Fock states, considering |S0|0〉 to |S4|0〉 and up to three photons for S0 and S1 electronic states (|S0|1〉,|S0|2〉,|S0|3〉, …). The insert in (d) shows the Rabi splitting between upper and lower polaritons. The color bar represents the photon-matter interaction of the UP and LP states. | ||
Comparing the polaritonic 1D curves for case (1) (ωc = 2.85 eV, εc = 0.005 GV m−1 – Fig. 5b) with the bare molecule (Fig. 5a), it becomes clear why the wave packet dynamics results are very similar. The strong coupling between the upper (UP) and lower (LP) polaritons can be seen close to the FC region, mainly related to |S0|1〉, as higher photon polaritons are above 6 eV. It leads to a free movement of the wave packet on the LP towards the CoIn through a merely altered PES, when compared to the S1 PEC of the bare molecule. For case (2), (Fig. 5c) the difference is more striking. Now, the crossing between UP and LP PECs appears at S1,RC ≈ 1.3, which leads to a significant change in the dynamics. The excited state wave packet has to overcome two barriers (along Q1 and Q2) in order to reach the CoIn, slowing it down and even trapping it in certain regions of the PES. Moreover, by tuning the cavity resonance frequency in these regions and using moderate field strengths, the wave packet may overcome these barriers more easily, leading to an increase of the population transfer to the ground state PES. Case (2) (Fig. 5c), is an example that illustrates these phenomena, as the crossing between UP and LP appears in the region close to the barrier at S1,RC ≈ 1.3. As in case (1), the potentials are mostly affected by |S0|1〉. A larger non-radiative decay is observed compared to the bare molecule and case (1). In Fig. 6 the time-dependent wave packet is shown in both S0 and S1 electronic states' PES along with the expectation value of the interaction Hamiltonian (eqn (7)) and the excited state population, for the three cases presented in Fig. 4 and 5. The wave packet |Ψ(Q1,Q2)〉 was obtained from the full 3D quantum dynamics, where the wave packet has been integrated over the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) coordinate:
coordinate: 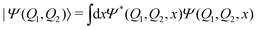 . By comparing the panels (a) and (b) of Fig. 6, a similar wave packet propagation behavior can be observed: only part of the wave packet reaches the CoIn, while the majority is trapped close the FC region (Q1 ≈ 0.1/Q2 ≈ 0.0). However, case (2) (Fig. 6b) shows that, due to the strong cavity coupling close the barrier along Q2 of the S1 PES (Q1 ≈ 1.1/Q2 ≈ 0.1 or S1,RC ≈ 1.3 in Fig. 5), the wave packet has a more direct pathway to reach the CoIn, leading to a bigger population transfer to S0 (increase of around 62%). Another striking feature is the significant increase in the cavity coupling strength (〈HI〉), of about three order of magnitude from case (1) (Fig. 5a) to case 2 (Fig. 5b). The case (2) (ωc = 1.93 eV/εc = 0.26 GV m−1) represents the behavior throughout the lower population valley of Fig. 3, where in each case, the cavity's resonance frequency and field strength couples the regions of the PES related to the barrier along the Q1 coordinate (S1,RC ≈ 0.5 of Fig. 5a), the S1 minimum (S1,RC = 1.0), and the barrier along Q2 (S1,RC ≈ 1.5), which facilitates the wave packet reaching to the CoIn region, leading to a bigger population transfer to S0.
. By comparing the panels (a) and (b) of Fig. 6, a similar wave packet propagation behavior can be observed: only part of the wave packet reaches the CoIn, while the majority is trapped close the FC region (Q1 ≈ 0.1/Q2 ≈ 0.0). However, case (2) (Fig. 6b) shows that, due to the strong cavity coupling close the barrier along Q2 of the S1 PES (Q1 ≈ 1.1/Q2 ≈ 0.1 or S1,RC ≈ 1.3 in Fig. 5), the wave packet has a more direct pathway to reach the CoIn, leading to a bigger population transfer to S0 (increase of around 62%). Another striking feature is the significant increase in the cavity coupling strength (〈HI〉), of about three order of magnitude from case (1) (Fig. 5a) to case 2 (Fig. 5b). The case (2) (ωc = 1.93 eV/εc = 0.26 GV m−1) represents the behavior throughout the lower population valley of Fig. 3, where in each case, the cavity's resonance frequency and field strength couples the regions of the PES related to the barrier along the Q1 coordinate (S1,RC ≈ 0.5 of Fig. 5a), the S1 minimum (S1,RC = 1.0), and the barrier along Q2 (S1,RC ≈ 1.5), which facilitates the wave packet reaching to the CoIn region, leading to a bigger population transfer to S0.
 | ||
| Fig. 6 Time-dependent wave packet |Ψ(Q1,Q2)〉 in the S0 and S1 PES for the dynamics considering (a) case (1) – ωc = 2.85 eV, εc = 0.005 GV m−1, (b) case (2) – ωc = 1.93 eV, εc = 0.26 GV m−1 and (c) case (3) – ωc = 1.93 eV, εc = 0.77 GV m−1. The bottom panels show the time-dependent excited state population and expectation value of the interaction Hamiltonian 〈HI〉 (eqn (7)). The dashed lines indicate correspondent time of the wave packet plots, 150, 240 and 330 fs. | ||
Moving on to the last case of this analysis, with ωc = 1.93 eV/εc = 0.77 GV m−1 (case 3), which represents the strong suppression of the non-radiative decay of MTBB excited state dynamics. The time-dependent excited state population (Fig. 4) shows an oscillatory behavior in the population between the excited states and S0. The polaritonic curves for this study case (Fig. 5d) shows a significant Rabi splitting (∼0.1 eV) between UP and LP PECs of low photon modes (S0|1〉), however, a population exchange still occurs between the two states. Let us analyze the time-dependent wave packet presented in Fig. 6c. First, the strong cavity coupling led to the most significant changes in the PES, as the wave packet does not reach the CoIn region, even though the same ωc from case (2) is considered. At t = 150 fs, when the excited state population begins to decrease, the wave packet reaches the region where the UP and LP are close together. This also reduces the Rabi oscillation observed in the coupling strength 〈HI〉 (Fig. 6). However, due to the large Rabi splitting (≈0.1 eV) between the UP and LP PESs (Fig. 5d), the wave packet is never actually transferred to the S0 state. When the wave packet reaches this region and slows down (t = 240 fs), the large cavity coupling strength strongly couples the wave packet in both excited and ground electronic states. (Fig. 6c). Moreover, when the wave packet starts moving back on the PES (t = 330 fs), no significant population is actually transferred to the S0 electronic state and the wave packet is trapped in the excited state, suppressing the non-radiative decay. These phenomena can be seen throughout the region where the excited state population is greater than 0.80 (Fig. 3), with the main difference being the smaller coupling strength which leads to a less pronounced population change (see Fig. S8 in the ESI†).
The strong coupling with the cavity drastically changes the excited state nuclear dynamics, leading to the minimization of the non-radiative decay. The interaction Hamiltonian HI (eqn (11)) is governed by the two terms that describe the electronic and vibrational cavity coupling, dependent on gij, and the dipole self-energy, which depends on 〈μ2〉ij. In addition, each of these terms connects the transition and permanent dipole moments of the studied system. Thus, to have a better understanding of the importance of these terms, the cavity-coupled dynamics was simulated by using three modified versions of the Hamiltonian ĤI(11):
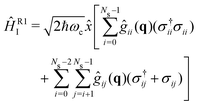 | (15) |
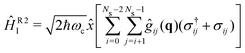 | (16) |
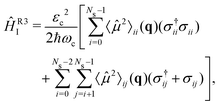 | (17) |
The first Hamiltonian (15) comprehends just the electronic ĝij and vibrational ĝii cavity coupling terms. In the second Hamiltonian (16), only the electronic states coupling ĝij is included. In the third Hamiltonian (17), the electronic and vibrational cavity coupling is neglected and only the dipole self-energy, dependent on 〈μ2〉ij, are considered. For this analysis, three values for the cavity field strength were chosen, εc = 0.26, 0.51 and 1.54 GV m−1, and three different resonant frequencies ωc, 2.56, 1.92 and 0.45 eV. In Fig. 7 is presented the time-dependent excited state population for the full interaction Hamiltonian (11) and the three reduced versions (eqn (15)–(17)), along with the bare molecule results for comparison. For the smaller field strength 0.26 and 0.51 GV m−1, it is observed that the main coupled dynamics behavior is related to the electronic states coupling term ĝij, as small changes in time-dependent population is seeing when comparing the results from ĤI, ĤR1I and ĤR2I. It is also observed that self-dipole terms have small influence in the dynamics, becoming more significant for smaller resonance frequencies (ωc = 0.45 eV). For the case with the strongest coupling (εc = 1.54 GV m−1), the effect of the different terms of Hi is quite evident, specially for ωc = 0.45 eV. In this case, the self-dipole terms shown to be quite important, as pointed out by other authors.37,39–41
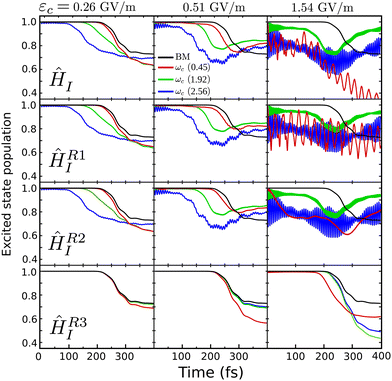 | ||
| Fig. 7 Influence of different terms of the interaction Hamiltonian ĤI in the cavity coupled quantum dynamics. It is presented the results for εc = 0.26, 0.51 and 1.54 GV m−1, and ωc = 0.45, 1.92 and 2.56 eV, as well as the bare molecule (BM). The time-dependent excited state population is shown for, from top to bottom, the full ĤI Hamiltonian (11), the reduced ĤR1I(15), ĤR2I(16) and ĤR3I(17). | ||
There are a few aspects that were not considered in the simulations of the excited state dynamics of MTBB in nano-cavities that should be addressed. The first one relates to the collective light-matter coupling, which has been shown to influence the excited state dynamics.61–65 The collective effects in molecular assembly have shown to have a significant effect on the photo dissociation mechanism, however, the size of the considered system can change drastically with this effect.64 On a molecular system, it was observed that the collective coupling effects are sensitive to the cavity resonance frequency when going from the FC to the CoIn,65 but also shown to be system dependent. Nevertheless, this effect might strongly influence the excited state dynamics of MTBB and to have a more complete description of the cavity effects in the non-radiative decay suppression, such terms would be needed to be taken into account.
The effects of a finite photon life on the dynamics have been neglected in this study. It should be noted that these effects can be quite significant for short-lived cavity modes and affect the dynamics in non-trivial ways.30,60,66–69 However, the size and type of the numerical Hamiltonian does not permit the use of Lindblad equation or the use of a simple non-Hermitian term. The results in this study thus need to be interpreted in the context of strong coupling with low photon loss rates. MTBB in lossy cavities will be the subject of future study.
5 Conclusions
The excited state nuclear dynamics of MTBB under the influence of strong and ultrastrong coupling has been simulated by means of multiconfigurational electronic structure calculation and quantum dynamical wave packet simulations. Through a careful selection of the reaction coordinates that represent the MTBB dynamics in the excited state, the multidimensional system was reduced to a 2D problem. This allowed for a full description of the light-matter interaction of MTBB in a strong coupling regime.The 2D MTBB PES exhibits two barriers that act as a trap and/or slow the wave packet, making it less likely to reach the conical intersection. However, tuning of the cavity resonance frequency and field strength leads to significant changes in the potential energy landscape, effectively removing the barriers, and increasing the population transfer from the excited electronic state to the electronic ground state. This effect can be understood by analysis of the polaritonic potentials and the visualization of the time-dependent wave packets. This interesting feature might be used to identify transition states in multidimensional molecular systems, by monitoring the population change through the scan with different cavity parameters. When a faster decay is observed, it could indicate that the cavity is coupled to a region where a barrier is present, which can be directly related to a transition state structure.
We demonstrated that, by tuning the cavity parameters, population transfer between the electronic states can be increased or decreased. Considering the possibility of suppressing the non-radiative decay of the excited state, we have shown that the interplay between the cavity's resonance frequency and field strength is crucial. This can be done by carefully tuning both parameters, while reaching the ultrastrong coupling regime. In the cases where the non-radiative decay suppression is observed, the coupling is so strong that the wave packet is briefly projected onto the ground state PESs, even though the Rabi splitting between the upper and lower polaritons was ∼0.1 eV. With the focus in the suppression of the non-radiative decay, an optimal region is clearly observed, as the increase of the coupling strength led to a reduction of this effect, as well as tuning the cavity frequency to the FC region.
Other aspects of the strong coupled nuclear dynamics were analyzed, such as the influence of the different terms of the interaction Hamiltonian ĤI. It was shown that not only the electronic and vibrational coupling terms are important, but the dipole self-energy interaction terms are important for the suppression of the non-radiative decay.
Strong and ultrastrong coupling via nanostructures can be considered a tool for optimizing photochromic organic molecular systems for solar cell applications. By considering the showcased BODIPY structure, it was shown that ultrastrong coupling can drastically increase the fluorescence yield of such systems. This might open the field for the application of simpler and cheaper organic molecules in solar cell manufacturing, where the extension of the excited state lifetimes can be done using strongly coupled nano-cavities. This paper was focused on this one aspect, however, other important factors might be considered in the future, such as a shift in absorption and emission bands, efficiency of the charge transfer, as well as molecular design and optimization.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 852286).Notes and references
- H. Hoppe and N. S. Sariciftci, J. Mater. Res., 2004, 19, 1924–1945 CrossRef CAS
.
- T. J. Kucharski, Y. Tian, S. Akbulatov and R. Boulatov, Energy Environ. Sci., 2011, 4, 4449–4472 RSC
.
- R. Long, O. V. Prezhdo and W. Fang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1305 Search PubMed
.
- A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS PubMed
.
- J. Bañuelos, I. J. Arroyo-Córdoba, I. Valois-Escamilla, A. Alvarez-Hernández, E. Peña-Cabrera, R. Hu, B. Zhong Tang, I. Esnal, V. Martínez and I. López Arbeloa, RSC Adv., 2011, 1, 677–684 RSC
.
- L. Jiao, C. Yu, J. Wang, E. A. Briggs, N. A. Besley, D. Robinson, M. J. Ruedas-Rama, A. Orte, L. Crovetto, E. M. Talavera, J. M. Alvarez-Pez, M. Van der Auweraer and N. Boens, RSC Adv., 2015, 5, 89375–89388 RSC
.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., 2012, 51, 1592–1596 CrossRef CAS PubMed
.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Phys. Rev. X, 2015, 5, 041022 Search PubMed
.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Phys. Chem. Lett., 2016, 7, 2050–2054 CrossRef CAS PubMed
.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Chem. Phys., 2016, 144, 054309 CrossRef PubMed
.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Nat. Commun., 2016, 7, 13841 CrossRef CAS PubMed
.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Phys. Rev. Lett., 2017, 119, 136001 CrossRef PubMed
.
- J. Feist, J. Galego and F. J. Garcia-Vidal, ACS Photonics, 2018, 5, 205–216 CrossRef CAS
.
- B. Gu and S. Mukamel, Chem. Sci., 2020, 11, 1290–1298 RSC
.
- T. Rousseau, A. Cravino, T. Bura, G. Ulrich, R. Ziessel and J. Roncali, Chem. Commun., 2009, 1673–1675 RSC
.
- C. Y. Lee and J. T. Hupp, Langmuir, 2010, 26, 3760–3765 CrossRef CAS PubMed
.
- S. Kolemen, O. A. Bozdemir, Y. Cakmak, G. Barin, S. Erten-Ela, M. Marszalek, J.-H. Yum, S. M. Zakeeruddin, M. K. Nazeeruddin, M. Grätzel and E. U. Akkaya, Chem. Sci., 2011, 2, 949–954 RSC
.
- T. Mueller, R. Gresser, K. Leo and M. Riede, Sol. Energy Mater. Sol. Cells, 2012, 99, 176–181 CrossRef CAS
.
- T. Jadhav, R. Misra, S. Biswas and G. D. Sharma, Phys. Chem. Chem. Phys., 2015, 17, 26580–26588 RSC
.
- D. Madrid-Úsuga, A. G. Mora-León, A. M. Cabrera-Espinoza, B. Insuasty and A. Ortiz, Comput. Theor. Chem., 2021, 1197, 113165 CrossRef
.
- M. Buyuktemiz, S. Duman and Y. Dede, J. Phys. Chem. A, 2013, 117, 1665–1669 CrossRef CAS PubMed
.
- A. Prlj, L. Vannay and C. Corminboeuf, Helv. Chim. Acta, 2017, 100, e1700093 CrossRef
.
- Z. Lin, A. W. Kohn and T. Van Voorhis, J. Phys. Chem. C, 2020, 124, 3925–3938 CrossRef CAS
.
- K. Georgiou, P. Michetti, L. Gai, M. Cavazzini, Z. Shen and D. G. Lidzey, ACS Photonics, 2018, 5, 258–266 CrossRef CAS
.
- R. T. Grant, P. Michetti, A. J. Musser, P. Gregoire, T. Virgili, E. Vella, M. Cavazzini, K. Georgiou, F. Galeotti, C. Clark, J. Clark, C. Silva and D. G. Lidzey, Adv. Opt. Mater., 2016, 4, 1615–1623 CrossRef CAS
.
- T. Cookson, K. Georgiou, A. Zasedatelev, R. T. Grant, T. Virgili, M. Cavazzini, F. Galeotti, C. Clark, N. G. Berloff, D. G. Lidzey and P. G. Lagoudakis, Adv. Opt. Mater., 2017, 5, 1700203 CrossRef
.
- D. Sannikov, T. Yagafarov, K. Georgiou, A. Zasedatelev, A. Baranikov, L. Gai, Z. Shen, D. Lidzey and P. Lagoudakis, Adv. Opt. Mater., 2019, 7, 1900163 CrossRef
.
- K. Georgiou, R. Jayaprakash, A. Askitopoulos, D. M. Coles, P. G. Lagoudakis and D. G. Lidzey, ACS Photonics, 2018, 5, 4343–4351 CrossRef CAS
.
- C. Schäfer, J. Mony, T. Olsson and K. Börjesson, Chem. – Eur. J., 2020, 26, 14295–14299 CrossRef PubMed
.
- S. Felicetti, J. Fregoni, T. Schnappinger, S. Reiter, R. de Vivie-Riedle and J. Feist, J. Phys. Chem. Lett., 2020, 11, 8810–8818 CrossRef CAS PubMed
.
- E. B. Wilson, J. C. Decius, P. C. Cross and B. R. Sundheim, J. Electrochem. Soc., 1955, 102, 235C CrossRef
.
- J. Stare and G. G. Balint-Kurti, J. Phys. Chem. A, 2003, 107, 7204–7214 CrossRef CAS
.
- M. Kowalewski, J. Mikosch, R. Wester and R. de Vivie-Riedle, J. Phys. Chem. A, 2014, 118, 4661–4669 CrossRef CAS PubMed
.
- J. C. Kromann, Calculate Root-Mean-Square Deviation (RMSD) of Two Molecules Using Rotation, 2013, https://github.com/charnley/rmsd/commit/cd8af49, accessed: Aug. 2020.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922–923 CrossRef
.
- C. Eckart, Phys. Rev., 1935, 47, 552–558 CrossRef CAS
.
- M. Gudem and M. Kowalewski, J. Phys. Chem. A, 2021, 125, 1142–1151 CrossRef CAS PubMed
.
- J. Flick, H. Appel, M. Ruggenthaler and A. Rubio, J. Chem. Theory Comput., 2017, 13, 1616–1625 CrossRef CAS PubMed
.
- V. Rokaj, D. M. Welakuh, M. Ruggenthaler and A. Rubio, J. Phys. B: At. Mol. Phys., 2018, 51, 034005 CrossRef
.
- C. Schäfer, M. Ruggenthaler and A. Rubio, Phys. Rev. A, 2018, 98, 043801 CrossRef
.
- A. Mandal, T. D. Krauss and P. Huo, J. Phys. Chem. B, 2020, 124, 6321–6340 CrossRef CAS PubMed
.
- C. Schäfer, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4883–4892 CrossRef PubMed
.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS
.
- B. O. Roos, Int. J. Quantum
Chem., 1980, 18, 175–189 CrossRef
.
-
B. O. Roos, The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations, John Wiley Sons, Ltd, 1987, pp. 399–445 Search PubMed
.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS
.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovacevic, E. Kallman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed
.
-
H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2019.2, a package of ab initio programs, 2019 Search PubMed
.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS
.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS
.
- P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS
.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS
.
- I. F. Galván, M. G. Delcey, T. B. Pedersen, F. Aquilante and R. Lindh, J. Chem. Theory Comput., 2016, 12, 3636–3653 CrossRef PubMed
.
- A. M. Mebel, A. Yahalom, R. Englman and M. Baer, J. Chem. Phys., 2001, 115, 3673–3689 CrossRef CAS
.
-
G. E. Fasshauer, Meshfree Approximation Methods with Matlab, World Scientific, 2007 Search PubMed
.
- H. Tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967–3971 CrossRef CAS
.
- R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230 CrossRef CAS
.
- A. Frisk Kockum, A. Miranowicz, S. De Liberato, S. Savasta and F. Nori, Nat. Rev. Phys., 2019, 1, 19–40 CrossRef
.
- D. G. Baranov, B. Munkhbat, E. Zhukova, A. Bisht, A. Canales, B. Rousseaux, G. Johansson, T. J. Antosiewicz and T. Shegai, Nat. Commun., 2020, 11, 2715 CrossRef CAS PubMed
.
- E. Davidsson and M. Kowalewski, J. Chem. Phys., 2020, 153, 234304 CrossRef CAS PubMed
.
- J. Flick, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3026–3034 CrossRef CAS PubMed
.
- O. Vendrell, Phys. Rev. Lett., 2018, 121, 253001 CrossRef CAS PubMed
.
- I. S. Ulusoy, J. A. Gomez and O. Vendrell, J. Phys. Chem. A, 2019, 123, 8832–8844 CrossRef CAS PubMed
.
- E. Davidsson and M. Kowalewski, J. Phys. Chem. A, 2020, 124, 4672–4677 CrossRef CAS PubMed
.
- J. B. Pérez-Sánchez and J. Yuen-Zhou, J. Phys. Chem. Lett., 2020, 11, 152–159 CrossRef PubMed
.
- I. S. Ulusoy and O. Vendrell, J. Chem. Phys., 2020, 153, 044108 CrossRef CAS PubMed
.
- P. Antoniou, F. Suchanek, J. F. Varner and J. J. Foley, J. Phys. Chem. Lett., 2020, 11, 9063–9069 CrossRef CAS PubMed
.
- J. Fregoni, S. Corni, M. Persico and G. Granucci, J. Comput. Chem., 2020, 41, 2033–2044 CrossRef CAS PubMed
.
- J. Torres-Sánchez and J. Feist, J. Chem. Phys., 2021, 154, 014303 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Molecular orbitals, cartesian coordinates, surfaces of the properties used in simulations and extra analysis. See DOI: https://doi.org/10.1039/d2cp00774f |
| This journal is © the Owner Societies 2022 |