How does evolution design functional free energy landscapes of proteins? A case study on the emergence of regulation in the Cyclin Dependent Kinase family†
Zahra
Shamsi
a and
Diwakar
Shukla
 *abcdef
*abcdef
aDepartment of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA. E-mail: diwakar@illinois.edu
bCenter for Biophysics and Quantitative Biology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
cNational Center for Supercomputing Applications, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
dDepartment of Plant Biology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
eNIH Center for Macromolecular Modeling and Bioinformatics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
fBeckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
First published on 20th December 2019
Abstract
Evolution has altered the free energy landscapes of protein kinases to introduce different regulatory switches and modify their catalytic functions. In this work, we demonstrate how cyclin dependency has emerged in cyclin-dependent kinases (CDKs) by reconstructing their closest experimentally characterized cyclin-independent ancestor, CMGI, using molecular dynamics simulations. Four hypotheses are formulated to describe why CDKs require an additional regulatory switch, i.e. cyclin binding to adopt an active state. Each hypothesis is tested using all-atom molecular dynamics simulations of CDK2 and the ancestor. In both systems, the K33–E51 hydrogen bond and the alignment of regulatory-spine residues have similar stabilities. However, auto-inhibition due to a helical turn in the A-loop is observed to be less favorable in the ancestor. Unlike the ancestor, the aspartate of the DFG motif does not form a bidentate bond with a Mg2+ ion in CDK2. These results explain the experimental observation of cyclin independency of the ancestor. Our findings provide a mechanistic rationale for how evolution has added a new regulatory switch to CDKs to tightly regulate the signalling pathways. This approach is directly applicable to other proteins to study the emergence of different types of regulatory mechanisms.
Design, System, ApplicationDesign of free energy landscapes associated with protein conformational ensembles determines the functional attributes of proteins. Uncovering the link between protein function, sequence, and structure is the first step in this design problem. Ancestral sequence reconstruction (ASR) is a natural approach to study the protein function, sequence, and structure relationship. In this study, we computationally reconstructed a protein ancestor using large-scale molecular dynamics simulations to shed light on how protein structure and dynamics have evolved to allow conformational regulation for the case of protein kinases. Protein kinases are a large family of proteins involved in cell growth. They organize the cell cycle by switching between active and inactive states, considered as ON/OFF states. Kinase activation is a complex dynamic process that involves multiple conformational switches. In cyclin-dependent kinases (CDKs), association of another protein (cyclin) is required for the switches to stay in the ON state. A better understanding of kinase activation offers opportunities for the rational design of novel kinase inhibitors and an informed perspective on how evolution solves the protein design problem for a given task. Finally, this computational study of ancestral proteins presents the first example of computational ancestral sequence reconstruction to shed light on the design of regulatory mechanisms in proteins. |
1 Introduction
Protein kinases are proteins involved in a variety of cellular signaling pathways that control cell growth. They coordinate the cell cycle by switching between active and inactive states, considered as ON/OFF states. Active kinase phosphorylates target proteins to turn “ON” downstream pathways for signal transduction. Kinase activation is a complex dynamic process, which involves multiple intra- and intermolecular switches that regulate kinase conformational preferences. For example, phosphorylation of the activation loop is one of the most common intramolecular switches regulating the activity of kinases.1 These switches are identified using X-ray crystallography, site-directed mutagenesis and computational approaches.1–8 The ability of kinases to transfer phosphate groups to a substrate also depends on an electrostatic network of molecular switches spread across the catalytic domain (kinase structure is shown in Fig. 1). The interaction between two fully conserved residues, glutamate (E) in the αC-helix and lysine (K) in the N-terminal lobe, is a key switch controlling phosphotransfer.9 An aspartate situated in the C-terminal lobe, referred to as a catalytic base, needs to be accessible to the substrate to facilitate the extraction of protons from the hydroxyl side chains (serine, threonine, and tyrosine) of the substrate.10 Four hydrophobic residues (Leu66, Leu55, Phe146, and His125, all residue numbers are based on CDK2's crystal structure (PDB ID: 1FIN11)) in the core of the kinase called the regulatory spine (R-spine) align during activation and coordinate the movement of the two lobes.12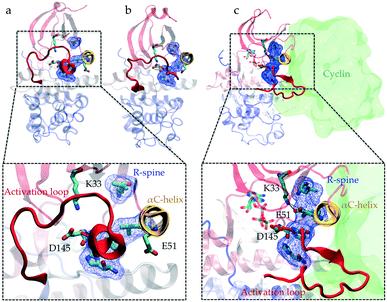 | ||
| Fig. 1 Conformational differences between the active and inactive crystal structures of CDK2. Comparison of the (a and b) inactive (PDB IDs: 3PXF25 and 4GCJ26) and (c) active crystal structures (PDB ID: 1FIN11) highlights the conformational changes associated with the activation process: the activation loop (A-loop) in red adopts different folded conformations, αC-helix in yellow rotates, electrostatic network formed between Lys33, Glu51 and Asp145 switches and alignment of residues Leu66, Leu55, Phe146, and His125 known as the regulatory spine (R-spine) (shown in licorice and blue surface representations) alters. In the active crystal structure (c), cyclin is also shown (with a green surface representation) in its bound position next to the αC-helix. | ||
In addition to the common intramolecular regulatory switches, which can control kinase activation, a variety of intermolecular switches modulate kinase activity via protein–protein interaction. In cyclin-dependent kinases (CDKs), the association of another protein (cyclin) is required for activation. In different cell phases, cyclin can activate CDKs to specifically stimulate distinct signaling pathways.13 Similarly, other kinases such as the Src family kinases are also regulated via intermolecular interactions through the SH2 and SH3 domains.14 Considering a domino model for the conformational changes in molecular switches that can lead to kinase activation, a series of molecular switches have to become conformationally active along the pathway connecting the inactive and active states of the kinase domain.15–19 If a single switch remains in the “OFF” state, it prevents the overall activation of the kinase. In the past few decades, substantial studies have been carried out to elucidate protein kinase switches and how they are triggered. However, the question of how different switches work in tandem to regulate the conformational preferences of kinases remains unanswered except for a few well-studied human kinases. Furthermore, it is not clear how these molecular switches have evolved to regulate conformational switching between active and inactive states of kinases.
Understanding the relationship between sequence, structure, and function of proteins during evolution using large-scale molecular dynamics simulations can shed light on how protein structure and dynamics have evolved to allow conformational regulation.19 A common way of studying this question is called horizontal analysis, which involves swapping sequences of extant protein and checking the functionality to find the underlying structure–function relationship. Hence, we can investigate the effect of changes in each residue, or groups of residues, on the protein function. In practice, horizontal analysis of extant proteins has a major problem: as the number of suspected residues in the sequence increases, the number of required experiments increases combinatorially. Due to the highly complex nature of protein structure and function, this type of method also experiences a high frequency of failures in finding sequence, structure and function relationships. For example, Src and Abl are two protein kinases with ∼47% sequence identity and a highly conserved three-dimensional structure.20 Despite this, they exhibit very different affinities for the cancer drug, imatinib.21 Seeliger et al. tried sequence swapping experiments to identify the key residues responsible for the high affinity in Abl or low affinity in Src. Despite the high sequence identity between Src and Abl, they performed multiple single residue swapping experiments and still could not identify any distinct set of mutations, which could significantly change the Src's affinity toward imatinib.22
Recently, due to advances in sequencing technologies, whole genome sequences for over 1000 species has become available, which makes it possible to reconstruct the phylogeny of modern proteins. This technique, called vertical analysis, makes it possible to follow the changes in residues along evolutionary paths encoding different functional or conformational preferences. Wilson et al. applied vertical analysis to answer the challenging question of imatinib selectivity between Src and Abl.23 They reconstructed common ancestors of Abl and Src from predicted sequences and tested the drug affinity for each one of them. They also obtained an X-ray crystal structure for one of the ancestors and identified the mechanism of drug selectivity. Another example of successfully finding the sequence–function relationship using vertical analysis is the study of substrate specificity in the CMGC kinase family by Howard et al.24 They reconstructed CMGI, the common ancestor of the CMGC family, and tested peptide specificity differences between CMGI and the extant proteins in the family, mainly comprising CDKs (Fig. S1†). They observed no co-expression between CMGI and any cyclin or cyclin-like protein even though CMGI was active, which suggests that CMGI, unlike CDKs, is not cyclin-dependent. Their observation demonstrates that evolution introduced new regulatory switches in CDKs to make their function more specific. However, the exact set of residues and structural mechanisms responsible for the emergence of cyclin dependence remains elusive.
In this study, we address the question of how cyclin dependency emerged in the CDK family using computational ancestral reconstruction of a CMGC family kinase. We study the activation process in CDK2 and the closest common ancestor (concestor) in the CMGC family (named CMGI), which is experimentally proven to be active without co-expression with any cyclin protein.23 Potential mechanistic differences between CDK2 and CMGI were extracted from available crystal structures and tested using all-atom molecular dynamics simulations. Then, we compare their activation mechanisms in atomistic detail to find the differences and similarities to explain how the cyclin dependency emerged and influenced their activation mechanism. For the sake of specificity and considering a significant number of available crystal structures of CDK2, we focus our study on the differences between the modern kinase, CDK2, and CMGI (Fig. S2†). We identified two molecular switches involved in the activation mechanism that have different free energy landscapes between these proteins.
2 Results
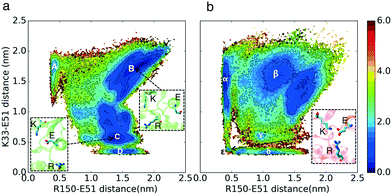
We hypothesize that in the absence of cyclin, at least one regulatory switch in CDK2 is “OFF” while constitutively remaining “ON” in CMGI. To find suitable candidate regulatory switches, all available crystal structures of CDK2 were curated and well-known characteristics of active and inactive kinases were measured (Fig. S3–S7†). We obtained four possible molecular switches that could explain the activity in CDK2 crystal structures. Based on these switches, four hypotheses are presented below.Cyclin binds to CDKs by forming an interface with the αC-helix and pushing it inward, as observed in the active crystal structure (PDB ID: 1FIN11). The most intuitive mechanism likely responsible for cyclin dependence is the rotation/inward motion of the αC-helix, which can be characterized by hydrogen bonds between Lys33 and Glu51 (K–E) and Glu51 and Arg150 (E–R). The K–E hydrogen bond is essential for providing an electrostatic network required for the process of phosphotransfer, while the E–R hydrogen bond facilitates rotation of the αC-helix27 (shown in Fig. 1c). We found that the available crystal structures of CDK2 either have formed E–R and broken K–E bonds or vice versa (Fig. S3†). Therefore, our first hypothesis is that CDK2 and its ancestor, CMGI, have different equilibrium probabilities of forming and breaking the K–E and E–R bonds. A higher probability of forming the K–E bond in CMGI would explain its catalytic activity in the absence of cyclin.
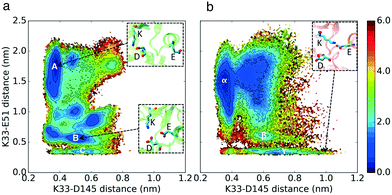
Crystal structures of CDK2 in the inactive conformation exhibit misaligned regulatory-spine (R-spine) residues (Leu66, Leu55, Phe146, and His125) (Fig. 1a and b), suggesting the potential relevance of another regulatory switch (Fig. S4†). Cyclin pushes the αC-helix inward which leads to the alignment of the R-spine residues (Fig. 1c). Therefore, the second hypothesis is that CDK2 and CMGI have different equilibrium probabilities of R-spine alignment. A higher probability of R-spine alignment in CMGI would lead to activity in the absence of cyclin.
The formation of a helical region at the beginning of the activation loop (A-loop) is another characteristic of inactive CDK structures, which prevents binding of the substrate protein (PDB ID: 3PXR and 3PXF25). The helical turn pushes the αC-helix out, thereby acting as a molecular switch that could alter the cyclin dependence of CDKs (Fig. 1). This auto-inhibitory mechanism is observed in several kinases such as CDKs, Src, and Abl.28 Crystal structure analysis shows high degrees of correlation between the presence of a helical turn and the existence of the K–E bond (Fig. S5†). Therefore, the third hypothesis is that the helical turn is more stable in CDK2 as compared to that in CMGI in the absence of cyclin. The helical turn blocks binding of the substrate protein which would lead to the lower activity of CDK2.
The precise orientation and positioning of the triad of highly conserved residues, Lys33 (K33), Glu51 (E51) and Asp145 (D145), are crucial for catalysis and phosphotransfer processes in kinases.11,29 The orientation of Asp145 in the well-known DFG (Asp145, Phe146 and Gly147) motif (Fig. 1) is particularly critical due to its interaction with Mg2+ ions, serving as a shuttle for cations to the ATP phosphate groups.11,29 Even though the exact catalytic role of Asp145 is not well understood, some crystal structures of cAMP-dependent protein kinases (another family of kinases) captured the intermediates in the phosphoryl transfer process. These crystal structures show that Asp145 forms a bidentate bond with one of the Mg2+ ions to enable the phosphotransfer reaction. Previous quantum mechanical calculations also show that Asp145 forms a bidentate bond with a Mg2+ ion in its active structure.30 Therefore, the formation of the Asp145–Mg2+ interaction could serve as another regulatory switch in protein kinases31 (see Fig. S9†). As there are no Mg2+ ions in the majority of the crystal structures, the availability of Asp145 is measured by calculating the Asp145–Lys33 distance in crystal structures of CDK2, which suggests the existence of two distinct states (Fig. S6†). Cyclin binding/unbinding can alter the orientation, accessibility and hydrogen bonds formed by Asp145 (ref. 13) in CDK2, while in CMGI, they may become aligned without cyclin binding. Therefore, the fourth hypothesis is that Asp145 in CDK2 does not form a bidentate bond with a Mg2+ ion in the absence of cyclin, whereas in CMGI, it does. In this study, we test each hypothesis by investigating the dynamic behavior of the switches in CDK2 and CMGI via large timescale unbiased molecular simulations (see Materials and methods).
K–E hydrogen bond is equally stable in CMGI and CDK2
The free energy landscapes in Fig. 2 show that the relative free energies of being in the active-like states where the K–E bond is formed are comparable between CDK2 and CMGI (Fig. 2 regions D and δ). The similar stabilities of regions D and δ refute our first hypothesis. The interaction between Arg150 (residue in the A-loop) and Glu51 (E–R) is a competitor for the Lys33–Glu51 (K–E) bond. The presence of an intermediate state with both the K–E and R–E bonds formed (Fig. 2 region ε, with K–E < 0.5 nm and E–R < 0.5 nm) in CMGI reveals an alternative activation pathway where an intermediate state, with triplet Lys33, Glu51, and Arg150 interacting, facilitates the formation of the K–E bond. The triplet interaction of residues corresponding to Lys33, Glu51, and Arg150 is conserved in the crystal structures of CDK1 (PDB ID: 4Y72, 4YC3, 5HQ0, 6GU2, 6GU3, 6GU4) and CDK4 (PDB ID: 2W9F, 2W9Z, 2W96, 2W99). This facilitation process has also been observed in other kinases, including other CDKs.27,32 In the free energy landscape of CDK2, the K–E bond forms only when the E–R bond is broken consistently with the lack of evidence for a triple interaction in CDK2. The mechanism of K–E bond formation is different, but the stability difference between the two end-states is the same. The E–R bond also seems to be a universal characteristic of multiple inactive kinase structures, as it's observed in multiple cyclin-dependent kinases, such as CDK2 (PDB ID: 2DS1, 5OO3, 5OSJ, 6GUK, 6Q3B, 6Q3C, 6Q4E, 6Q4F, 6Q4G, 6Q4H, 6Q4I, 6Q4J, 6Q48, 6Q49), CDK1 (PDB ID: 4YC6, 6GU6), CIPK (PDB ID: 4D28), and pfpk5 (PDB ID: 1OB3, 1V0P).R-spine acts similarly in CMGI and CDK2
The conformational landscape of CDK2 in Fig. 3 does not display any considerable barrier for alignment or misalignment of the R-spine (there is no high energy region to move along the x-direction in Fig. 3). In both conformational landscapes, the R-spine can form or break easily when the K–E bond is broken (when K–E is larger than 0.5 nm, the RMSD of the R-spine can be either high or low), whereas when the K–E bond is formed, the R-spine does not break (when K–E is less than 0.5 nm, the RMSD of the R-spine with respect to the active structure is always low). This observation is consistent with previous studies on kinases.4 The similar dynamic behavior between the R-spines of CMGI and CDK2 disqualifies our second hypothesis. In this analysis, the K–E bond is used as the Y axis to control the preference of the R-spine. Therefore, the first and second hypotheses are still independent.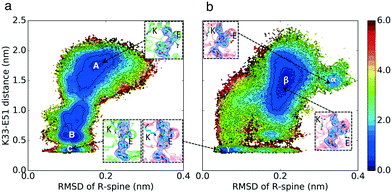 | ||
| Fig. 3 Effect of evolution on the prevalence of the active-like state with the aligned R-spine. Comparison of MSM-weighted free energy plots projected onto the R-spine RMSD and K–E distances between (a) CDK2 and (b) CMGI. Corresponding regions between CDK2 and CMGI show similar stabilities in these free energy landscapes (ΔΔGB–C ∼ ΔΔGβ–γ). The R-spine RMSDs were calculated with respect to the active crystal structure of CDK2 (PDB ID: 1FIN11) in CDK2 simulations and an active structure of CMGI obtained from the simulations. Colors show the free energy in kcal mol−1. | ||
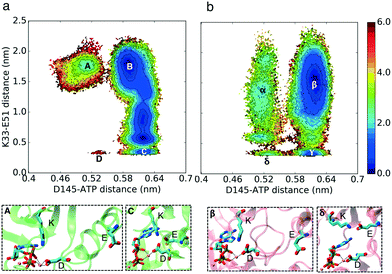
Auto-inhibition due to the helical turn in the A-loop is less probable in CMGI compared to CDK2
The simulation results projected onto the two dimensional conformational landscape of K–E distance versus RMSD of helical turn at the beginning of the A-loop with respect to an inactive structure (PBD ID: 3XPR25) reveal a barrier of ∼6 kcal mol–1 for unfolding of the helical turn in CDK2, whereas this barrier is not observed in CMGI due to a stable intermediate state. In Fig. 4, region β shows the intermediate state in CMGI, with its relatively low free energy facilitating the transition from the inactive state, region α, to the active-like state, region δ. The region corresponding to β in CDK2's landscape is B, which is less stable. The low stability of B leads to a barrier of ∼6 kcal mol−1 for the transition from the inactive state, region A, to the active-like state, region D. This intermediate state is not observed in any of CDK2's crystal structures, while it exists in CDK6 (PDB ID: 1BLX) and CDK4 (PDB ID: 3G33).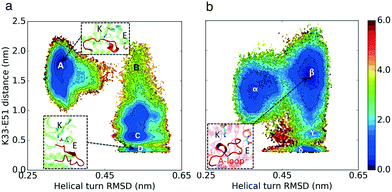 | ||
| Fig. 4 Effect of evolution on the prevalence of the intermediate state with the helical turn in the A-loop. Comparison of MSM-weighted free energy plots projected onto the RMSD of the helical turn in the A-loop and K–E distances between (a) CDK2 and (b) CMGI. The intermediate state with the helical turn in the A-loop is more stable in CMGI (region β) compared to that in CDK2 (region B). Colors show the free energy in kcal mol−1. Helical turn RMSDs are calculated with respect to an inactive crystal structure of CDK2 (PDB ID: 3PXR25). | ||
The helical secondary structure moves from the beginning of the A-loop toward its end in the intermediate state in CMGI (Fig. 4b, region β), which allows the A-loop to fully unfold with a relatively lower barrier. These free energy landscapes support our third hypothesis that differences in the stability of the A-loop helical turn between CDK2 and CMGI is one of the main factors responsible for the cyclin dependence of CDK2. However, the molecular origin of the difference in helical turn stability remains unclear.
Analysis of the available crystal structures of CDKs reveals that there is a salt bridge between His161 in the A-loop and Glu12 in the P-loop which is observed in all inactive CDK2 crystal structures with a helical turn (Fig. S7†). This ionic interaction stabilizes the “upward” (when the A-loop is closer to the N-terminal lobe, shown in Fig. S7†) conformation of the A-loop, which provides enough space for the formation of the helical turns. His161 in CDK2 is substituted with Glu161 in the ancestor. Repulsion between Glu12 and Glu161 destabilizes the “upward” conformation of the A-loop and consequently prevents the formation of the helical turn (Fig. S8†), even though the sequence analysis of the helical turn region shows a similar helical propensity between CDK2 and CMGI.33 The free energy landscape of K33–E51 versus E12–H161 shows that the ∼3 kcal mol−1 barrier for the unfolding of the helical turn in CDK2 is due to E12–H161 bond breaking.
The aspartate in the DFG motif does not form a bidentate bond with Mg2+ in CDK2
In our simulations, Asp145 can interact with a Mg2+ ion with two different bond types: it can form a bidentate bond with its two carboxyl oxygen atoms and Mg2+ or a single bond between one of its carboxyl oxygen atoms and a Mg2+ ion (Fig. 6 and 5). Based on the simulation results, CDK2 without cyclin bound has a very low probability of forming the K–E bond and bidentate D145–Mg2+ bonds at the same time, which is the key difference between the active and inactive structures of CDK2 (Fig. 6 region D). In contrast, CMGI has access to low free energy state δ (Fig. 6) that has both bidentate D145–Mg2+ and K–E bond interactions. In the two systems, D145 can form both types of interactions with Mg2+ while the K–E bond is broken.In order to determine which type of Asp145–Mg2+ bond is formed by cyclin-bound CDK2, additional ∼2 μs simulations of CDK2 bound to cyclin with ATP and two Mg2+ ions were performed. In these simulations, the Asp145–Mg2+ bidentate bond is stable while all other switches are in the “ON” conformation as well. This shows a significantly different stability profile for the Asp145–ATP distance between cyclin-bound and cyclin-free CDK2. Unlike the CDK2 monomer, the CDK2–cyclin dimer demonstrates no barrier for switching between the two bond types, which is similar to CMGI. Cyclin binding changes the electrostatic network of the residues in a way that makes the Asp145–Mg2+ bidentate bond more stable (see Fig. S10†).
Activation pathways are different between CDK2 and CMGI
Apart from the hypotheses explaining the cyclin dependent nature of CDK2 activation, we studied the activation pathways of the modern and ancient kinases. Simulations were analyzed using Markov state models34 and the activation pathways were estimated using transition path theory (TPT).35 TPT is a way to extract the highest-flux pathways of a system from an estimated MSM (Fig. S17 and S18†).In the activation pathway of CDK2, the presence of intermediate states with a stable helical turn in the A-loop and a well aligned R-spine reduces the activation rate (Fig. S17, 2–7†). In these intermediate states, the stable well aligned R-spine prevents the αC-helix from rotating and the K–E bond from forming. Similar conformations have also been observed in the crystal structures of CDK2 (PDB ID: 5OSM, 6Q3F, 6Q4A, 6Q4B, 6Q4C, 6Q4D, 6Q4K), G/CDK (PDB ID: 3GBZ), and pfpk5 (PDB ID: 1V0B) where a K–D bond is formed but not K–E, the A-loop forms the helical turn and the R-spine residues are aligned. Based on the TPT analysis, as the helical turn unfolds, Glu51 finds enough space to move and push the αC-helix inward and rotate it to form the K–E bond (Fig. S17, 8†). Unlike in CDK2, in CMGI, the helical turn unfolds first and then the R-spine forms simultaneously as the K–E bond (Fig. S18†). K–D bond breakage has a lower free energy barrier in CMGI. As the bidentate bond Asp145–Mg2+ in CDK2 is not stable, in the TPT calculations, the Asp145–Mg2+ bond was disregarded and the focus of our study was on the other regulatory switches.
3 Discussion
Homogeneous active versus heterogeneous inactive states are observed in kinases. While a defined active conformation is needed to guarantee a catalytically competent active site and specific interaction with downstream partners, deactivation of a protein kinase can be accomplished by a shift to any conformation other than the active structure. The intrinsically entropic nature of the inactive state may not be a limitation in the efficiency of the conformational transition, but rather provides an advantage. Modern proteins have evolved mechanisms for enhanced regulation. Evolution has significantly changed the features of free energy landscapes and created more complex landscapes by introducing multiple new minima (Fig. 5).A visual inspection of the kinetic plots (Fig. 2–6) suggests that thermal fluctuations toggle all the molecular switches via a concerted mechanism, where molecular switches are triggered cooperatively. However, looking at the conformational landscape of molecular switches reveals a different, more sequential view of CDK activation, where some molecular switches are turned ON/OFF before other switches change their conformation. This observation is directly related to a prominent debate about conformational change mechanisms in general, comparing a sequential “domino brick effect” to the “Monod–Wyman–Changeux” type of concerted action allostery.36–39 Therefore, the mechanism of global conformational change associated with CDK2 kinase activation lies between a sequential and cooperative mode of molecular switching so that the system is “functionally concerted”. One-dimensional and two-dimensional probability density maps for each of the metrics are shown in Fig. S11–S16.†
Our study raises several interesting questions about the evolution of protein structure and function. (1) How does a network of protein conformations evolve to acquire a specific function or integrate an external signal in the form of binding partners such as ligands and other proteins? (2) How do the conformational network properties change during the evolution? These properties include a network connectivity, i.e. the number of connections per state and robustness, i.e. how many states and edges (connections between states) could be removed without altering the overall function. (3) Are modern signaling proteins more efficient than ancestral proteins in terms of energy dissipated during functional dynamics? (4) Finally, how are functional free energy and folding free energy landscapes designed during evolution to enable protein conformational change while keeping it in the folded state? The process could be elucidated by investigating ancestral proteins along the evolutionary trajectory. However, the large computational time requirements would make such an investigation intractable, which calls for the development of more efficient computational approaches40,41 to enable computational ancestral protein reconstruction of evolutionary pathways.
4 Methods
To enhance the sampling process, accelerated molecular dynamics (aMD) simulations were performed prior to the unbiased simulations. aMD simulations were initiated from the crystal structures of CDK2 and homology models of CMGI. These simulations uncovered multiple starting structures for the unbiased simulations. In the next step, the unbiased simulations were performed using the adaptive sampling technique, and Markov state models (MSMs) were built using the unbiased simulated data.Generation of initial structures using Modeller and accelerated molecular dynamics simulations
One active (PDB ID: 1FIN11) and three different inactive (PDB IDs: 3PX,254GCJ26 and 3PXF25) X-ray crystal structures of human CDK2 kinase were used as starting structures for CDK2 simulations. CMGI simulations were initiated from homology models. One active (PDB ID: 1FIN11) and three different inactive (PDB IDs: 3PXR,254GCJ26 and 3PXF25) X-ray crystal structures of human CDK2 kinase were used as template structures for homology modelling. The sequence alignment of CDK2 and CMGI shows 51.6% identity in 289 residue overlap, with a score of 721.0 and gap frequency of 2.1%.42 The software Modeller43 was used to build the homology models. In order to evaluate the relevance of the homology models, discrete optimized protein energy (DOPE)44 and GA341 (ref. 45) scores were estimated. The DOPE score is a statistical potential used to assess homology models in protein structure prediction. The GA341 score combines a Z-score calculated with a statistical potential function, target-template sequence identity and a measure of structural compactness. This score always ranges from 0.0 (worst) to 1.0 (native-like). All the homology models used as initial structures are native-like based on the GA341 score and have comparable DOPE scores with the CDK2 native structure as shown in Table 1. The lower the DOPE score, the better the model.In each system, all molecules except CDK2 (or CMGI) were removed. Phosphate on Thr160 and an ATP molecule with two magnesium ions bound, taken from previous simulations,6 were inserted into the binding pocket. The starting structures were solvated in water boxes, with dimensions of approximately 85 Å × 70 Å × 60 Å with TIP3P model molecules.46 Sodium and chloride ions were added to neutralize the charge of all systems and bring the salt concentration to approximately 150 mM. All systems were subjected to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of energy minimization and were equilibrated for 2–4 ns in an NPT ensemble at 300 K and 1 atm. Simulations were performed using a 2 fs time step, periodic boundary conditions, and constraints of hydrogen-containing bonds using the SHAKE algorithm.47,48
000 steps of energy minimization and were equilibrated for 2–4 ns in an NPT ensemble at 300 K and 1 atm. Simulations were performed using a 2 fs time step, periodic boundary conditions, and constraints of hydrogen-containing bonds using the SHAKE algorithm.47,48
Equilibrated structures were simulated (5 μs for each system) using aMD to obtain starting structures for the production unbiased MD runs49,50 (see the ESI† for the aMD parameters). Starting structures for the first round of unbiased production run were chosen randomly from landscapes covered by aMD. Unbiased production ran in multiple rounds, where the starting structures for each round were selected based on the adaptive sampling technique. At the end of the production run, Markov state models were used to analyze the simulations.
All simulations ran on the CUDA version of AMBER 14,51 using the AMBER14 force field ff14SB for proteins52 and general AMBER force field (GAFF)53 for ATP on a Blue Waters supercomputer. Total aggregated unbiased MD simulations of 76 μs for CDK2 and 42 μs for CMGI were performed.
MSM construction and hyper-parameter selection
Markov state models are kinetic models used to model randomly changing systems like protein dynamics.54 An MSM represents protein dynamics as a Markov chain on discretized conformational space achieved by clustering of protein conformations in MD trajectories. Transitions between discretized states in MD trajectories are counted and a transition probability matrix is estimated using the maximum likelihood method. If vector p(t0) denotes the probability of being in any of the states at time t0, the probabilities at time t0 + kτ are given by:| p(t0 + kτ) = p(t0)T(τ)k |
Adaptive sampling is a computational technique used to enhance the simulation of biomolecular functions and folding.40,41,57 Adaptive sampling involves iteratively running short simulations, clustering on a relevant metric, and seeding new simulations from clusters based on some criterion. Adaptive sampling has been shown to sample configurational space more efficiently than the simulated tempering method for simulation of an RNA hairpin.58 MSMs importantly estimate the equilibrium populations of states from trajectories sampled from non-equilibrium distributions and generate unbiased transition probabilities, allowing for the accurate characterization of both kinetics and thermodynamics.
In order to build MSMs, the system's dynamics should be discretized into a relevant metric. We calculated the root mean square fluctuations (RMSFs) of all residues to identify residues with higher fluctuations, which show that they participate more in the kinase dynamics (Fig. S19 and S20†) (residues 31 to 83 and 145 to 177 in CDK2 and 31 to 100 and 145 to 180 in CMGI). Based on the literature, we knew that residues in the C-lobe are not participating in the activation process, so we did not include them even with high RMSF values. The dihedral angles (ϕ and ψ) of these residues were considered as raw features. Time-structure independent component analysis (tICA) was used to reduce the dimension of the high dimensional dihedral angle metric space by projecting onto the slowest subspace.59,60 To build optimal MSMs, we varied the numbers of clusters along with numbers of tICA components to project onto in order to build our MSMs. The generalized matrix Rayleigh quotient (GMRQ)61 score and percentage of the data used were calculated for each MSM and parameter, which gave the higher GMRQ score with the higher data usage being picked as the best sets (see Fig. S21 and S22†) (1000 clusters with 10 tICA components for CDK2 and 300 clusters with 6 tICA components for CMGI were picked as the best sets). To find the best lag time, series of MSMs with different lag times were built and the implied timescales were calculated to find a region where the spectrum of implied timescales was relatively insensitive to lag time. A lag time of 14 ns was found to be suitable for both systems (Fig. S23 and S24†). All MSM analysis in this study was conducted using the MSMBuilder 3.8.0 package.62
Transition path theory
Transition path theory (TPT) is a rare event sampling method allowing for the determination of the likelihood of transition along with the pathways in the Markov random field between two states. We used the MSMBuilder implementation of TPT in order to identify top pathways from the net flux matrix. For a detailed overview of TPT, we refer the reader to a review by Metzner et al.355 Conclusions
Our simulations confirm the experimental observation that the CDK ancestor, CMGI, can become activated in the absence of cyclin, unlike modern CDK2. A set of four regulatory switches was tested to identify the origin of activation differences between the two kinases. All of CMGI's regulatory switches can be in the “ON” mode at the same time independent of any intermolecular interactions, whereas two of CDK2’s regulatory switches cannot be in the “ON” mode, simultaneously. First, the stable helical turn in CDK2's A-loop blocks the binding of the substrate protein and leads to the auto-inhibition and lower activity of CDK2. Moreover, the critically important conserved Asp145 residue displayed different behavior in the CDK2 monomer compared to that in the CDK2–cyclin dimer and CMGI. The Asp145 in the CDK2 monomer is tightly bound to Lys33, which not only makes the residue less accessible to the substrate but also prevents the formation of a bidentate bond with a Mg2+ ion, thereby reducing kinase activity.This computational study of ancestral proteins presents the first example of computational ancestral sequence reconstruction to shed light on the design of regulatory mechanisms in proteins by evolution. We need to understand design principles from evolution before these principles can be leveraged for design. Moreover, protein kinases are major targets for cancer drugs and a better understanding of kinase activation offers opportunities for the rational design of novel drugs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. S. is supported by a NSF Early Career Award, NSF MCB 18-45606. This research is part of the Blue Waters sustained petascale computing project, which is supported by the National Science Foundation (awards OCI-0725070 and ACI-1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana-Champaign and its National Center for Supercomputing Applications.References
- A. A. Russo, P. D. Jeffrey and N. P. Pavletich, Nat. Struct. Biol., 1996, 3, 696–700 CrossRef CAS PubMed.
- J. Lennartsson, P. Blume-Jensen, M. Hermanson, E. Pontén, M. Carlberg and L. Rönnstrand, Oncogene, 1999, 18, 5546–5553 CrossRef CAS PubMed.
- K. A. James and G. M. Verkhivker, PLoS One, 2014, 9, e113488 CrossRef PubMed.
- D. Shukla, Y. Meng, B. Roux and V. S. Pande, Nat. Commun., 2014, 5, 3397 CrossRef PubMed.
- S. Wan and P. V. Coveney, J. Comput. Chem., 2011, 32, 2843–2852 CrossRef CAS PubMed.
- A. S. Moffett, K. W. Bender, S. C. Huber and D. Shukla, J. Biol. Chem., 2017, 292, 12643–12652 CrossRef CAS PubMed.
- A. S. Moffett, K. W. Bender, S. C. Huber and D. Shukla, Biophys. J., 2017, 113, 2354–2363 CrossRef CAS PubMed.
- A. S. Moffett and D. Shukla, Biochem. J., 2018, 475, 905–921 CrossRef CAS PubMed.
- E. Ozkirimli, S. S. Yadav, W. T. Miller and C. B. Post, Protein Sci., 2008, 17, 1871–1880 CrossRef CAS PubMed.
- A. Krupa, G. Preethi and N. Srinivasan, J. Mol. Biol., 2004, 339, 1025–1039 CrossRef CAS PubMed.
- P. D. Jeffrey, A. A. Russo, K. Polyak, E. Gibbs, J. Hurwitz, J. Massagué and N. P. Pavletich, Nature, 1995, 376, 313–320 CrossRef CAS PubMed.
- R. Robinson, PLoS Biol., 2013, 11, e1001681 CrossRef CAS PubMed.
- H. L. D. Bondt, J. Rosenblatt, J. Jancarik, H. D. Jones, D. O. Morgant and S.-H. Kim, Nature, 1993, 363, 595–602 CrossRef PubMed.
- S. S. Yadav and W. T. Miller, Cancer Lett., 2007, 257, 116–123 CrossRef CAS PubMed.
- D. Shukla, A. Peck and V. S. Pande, Nat. Commun., 2016, 7, 10910 CrossRef CAS PubMed.
- Y. Meng, D. Shukla, V. S. Pande and B. Roux, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9193–9198 CrossRef CAS PubMed.
- D. K. Vanatta, D. Shukla, M. Lawrenz and V. S. Pande, Nat. Commun., 2015, 6, 7283 CrossRef PubMed.
- K. J. Kohlhoff, D. Shukla, M. Lawrenz, G. R. Bowman, D. E. Konerding, D. Belov, R. B. Altman and V. S. Pande, Nat. Chem., 2013, 6, 15–21 CrossRef PubMed.
- B. Selvam, Z. Shamsi and D. Shukla, Angew. Chem., 2018, 130, 3102–3107 CrossRef.
- M. Deininger, E. Buchdunger and B. J. Druker, Blood, 2005, 105, 2640–2653 CrossRef CAS PubMed.
- R. Capdeville, E. Buchdunger, J. Zimmermann and A. Matter, Nat. Rev. Drug Discovery, 2002, 1, 493–502 CrossRef CAS PubMed.
- M. A. Seeliger, B. Nagar, F. Frank, X. Cao, M. N. Henderson and J. Kuriyan, Structure, 2007, 15, 299–311 CrossRef CAS PubMed.
- C. Wilson, R. V. Agafonov, M. Hoemberger, S. Kutter, A. Zorba, J. Halpin, V. Buosi, R. Otten, D. Waterman, D. L. Theobald and D. Kern, Science, 2015, 347, 882–886 CrossRef CAS PubMed.
- C. J. Howard, V. Hanson-Smith, K. J. Kennedy, C. J. Miller, H. J. Lou, A. D. Johnson, B. E. Turk and L. J. Holt, eLife, 2014, 3, e04126 CrossRef PubMed.
- S. Betzi, R. Alam, M. Martin, D. J. Lubbers, H. Han, S. R. Jakkaraj, G. I. Georg and E. Schonbrunn, ACS Chem. Biol., 2011, 6, 492–501 CrossRef CAS PubMed.
- E. Schonbrunn, S. Betzi, R. Alam, M. P. Martin, A. Becker, H. Han, R. Francis, R. Chakrasali, S. Jakkaraj, A. Kazi, S. M. Sebti, C. L. Cubitt, A. W. Gebhard, L. A. Hazlehurst, J. S. Tash and G. I. Georg, J. Med. Chem., 2013, 56, 3768–3782 CrossRef CAS PubMed.
- A. Berteotti, A. Cavalli, D. Branduardi, F. L. Gervasio, M. Recanatini and M. Parrinello, J. Am. Chem. Soc., 2009, 131, 244–250 CrossRef CAS PubMed.
- N. Dolker, M. W. Gorna, L. Sutto, A. S. Torralba, G. Superti-Furga and F. L. Gervasio, PLoS Comput. Biol., 2014, 10, e1003863 CrossRef PubMed.
- D. M. Jacobsen, Z.-Q. Bao, P. O'Brien, C. L. Brooks and M. A. Young, J. Am. Chem. Soc., 2012, 134, 15357–15370 CrossRef CAS PubMed.
- A. Pérez-Gallegos, M. Garcia-Viloca, À. González-Lafont and J. M. Lluch, Phys. Chem. Chem. Phys., 2015, 17, 3497–3511 RSC.
- J. A. Adams, Chem. Rev., 2001, 101, 2271–2290 CrossRef CAS PubMed.
- W. Gan, S. Yang and B. Roux, Biophys. J., 2009, 97, L8–L10 CrossRef PubMed.
- E. Lacroix, A. R. Viguera and L. Serrano, J. Mol. Biol., 1998, 284, 173–191 CrossRef CAS PubMed.
- V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed.
- P. Metzner, C. Schütte and E. Vanden-Eijnden, Multiscale Model. Simul., 2009, 7, 1192–1219 CrossRef CAS.
- D. E. Koshland, G. Nmethy and D. Filmer, Biochemistry, 1966, 5, 365–385 CrossRef CAS PubMed.
- J.-P. Changeux and S. J. Edelstein, Science, 2005, 308, 1424–1428 CrossRef CAS PubMed.
- T. Kenakin, Trends Pharmacol. Sci., 2004, 25, 186–192 CrossRef CAS PubMed.
- J. Monod, J. Wyman and J.-P. Changeux, J. Mol. Biol., 1965, 12, 88–118 CrossRef CAS PubMed.
- Z. Shamsi, K. J. Cheng and D. Shukla, J. Phys. Chem. B, 2018, 122, 8386–8395 CrossRef CAS PubMed.
- Z. Shamsi, A. S. Moffett and D. Shukla, Sci. Rep., 2017, 7, 12700 CrossRef PubMed.
- P. Artimo, M. Jonnalagedda, K. Arnold, D. Baratin, G. Csardi, E. de Castro, S. Duvaud, V. Flegel, A. Fortier, E. Gasteiger, A. Grosdidier, C. Hernandez, V. Ioannidis, D. Kuznetsov, R. Liechti, S. Moretti, K. Mostaguir, N. Redaschi, G. Rossier, I. Xenarios and H. Stockinger, Nucleic Acids Res., 2012, 40, W597–W603 CrossRef CAS PubMed.
- B. Webb and A. Sali, Protein Structure Prediction, 2014, pp. 1–15 Search PubMed.
- M.-Y. Shen and A. Sali, Protein Sci., 2006, 15, 2507–2524 CrossRef CAS PubMed.
- B. John, Nucleic Acids Res., 2003, 31, 3982–3992 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- N. Eswar, D. Eramian, B. Webb, M.-Y. Shen and A. Sali, Structural proteomics: high-throughput methods, 2008, pp. 145–159 Search PubMed.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, Amber 14, University of California, San Francisco, 2014 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882–5895 CrossRef CAS PubMed.
- D. Shukla, C. X. Hernández, J. K. Weber and V. S. Pande, Acc. Chem. Res., 2015, 48, 414–422 CrossRef CAS PubMed.
- F. Noe, C. Schutte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19011–19016 CrossRef CAS PubMed.
- J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144 CrossRef CAS PubMed.
- G. R. Bowman, D. L. Ensign and V. S. Pande, J. Chem. Theory Comput., 2010, 6, 787–794 CrossRef CAS PubMed.
- X. Huang, G. R. Bowman, S. Bacallado and V. S. Pande, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19765–19769 CrossRef CAS PubMed.
- G. Pérez-Hernández, F. Paul, T. Giorgino, G. D. Fabritiis and F. Noé, J. Chem. Phys., 2013, 139, 015102 CrossRef PubMed.
- C. R. Schwantes, D. Shukla and V. S. Pande, Biophys. J., 2016, 110, 1716–1719 CrossRef CAS PubMed.
- R. T. McGibbon and V. S. Pande, J. Chem. Phys., 2015, 142, 124105 CrossRef PubMed.
- M. P. Harrigan, M. M. Sultan, C. X. Hernández, B. E. Husic, P. Eastman, C. R. Schwantes, K. A. Beauchamp, R. T. McGibbon and V. S. Pande, Biophys. J., 2017, 112, 10–15 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00097f |
| This journal is © The Royal Society of Chemistry 2020 |