Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural considerations for physical hydrogels based on polymer–nanoparticle interactions†
Anthony C.
Yu
 ,
Anton A. A.
Smith
and
Eric A.
Appel
,
Anton A. A.
Smith
and
Eric A.
Appel
 *
*
Department of Materials Science & Engineering, Stanford University, Stanford, CA 94305, USA. E-mail: eappel@stanford.edu
First published on 9th January 2020
Abstract
Designing supramolecular hydrogels for complex translational applications requires the ability to engineer viscoelasticity and flow behaviour at the bulk scale as well as the network structure at the nano and micro scales. Here we examine supramolecular hydrogels formed by polymer–nanoparticle interactions between hydrophobically-modified biopolymers and polymeric nanoparticles. Crosslinking in these systems is driven by dynamic and multivalent interactions between the biopolymers and the nanoparticles. We demonstrate control over viscoelasticity and microstructure by altering the hydrophobicity of pendant groups along the polymer backbone. Increasing the pendant group hydrophobicity creates larger polymer corona heights and, once a critical interparticle distance is spanned, induces a jammed microstructure that reinforces bridging based crosslinking. These studies suggest that design considerations for polymer–nanoparticle hydrogels are analogous to those of jammed soft glasses and provide an engineering handle to tune microstructure and viscoelasticity through chemical modifications to the polymer backbone. These materials are expected to be useful for applications that require injection, spraying, and control over cargo release kinetics.
Design, System, ApplicationThe ability of hydrogels to dramatically shear-thin for injection or spraying, rapidly self-heal, and have appropriate viscoelastic properties has found utility in diverse biomedical applications ranging from tissue engineering to drug delivery and regenerative medicine. In these applications, supramolecular hydrogels are particularly attractive due to the versatility and modularity of the physical interactions that make up the crosslinks. Design criteria of new supramolecular hydrogels are often constrained by function-critical properties, such as injectability, self-healing, biodegradability, cargo release kinetics, and biocompatibility, which necessitate more deliberate microstructural engineering. Here, we use a supramolecular hydrogel crosslinked by polymer–nanoparticle interactions and elucidate how increasing hydrophobicity of the polymers affects the gel microstructure and viscoelasticity. The increasing hydrophobicity leads to larger polymer coronas surrounding each particle, which induces a jammed microstructure and correspondingly increases shear moduli and relative elasticity of the gels. These engineering principles will guide future polymer–nanoparticle hydrogel designs for control over bulk mechanics and microstructure. |
1. Introduction
Supramolecular hydrogels have shown potential for applications in drug delivery, cell delivery, biomaterials, and 3D printing.1–10 The utility of these materials is largely due to function-critical properties, such as injectability, self-healing, biodegradability, and biocompatibility, which are largely enabled by the transient physical interactions that crosslink the hydrogels.8,9,11–15 Moreover, the abundance of available physical interactions (e.g., host–guest, ionic, hydrogen bonding, peptide, and hydrophobic interactions) offers a broad chemical space to design new materials.6–8,16–18Among these crosslinking motifs are polymer–nanoparticle (PNP) interactions, which consist of multivalent physical bonds between polymers and the surface of nanoparticles that imbue materials with complex flow behavior and enhanced elasticity.19–22 These PNP interactions are highly modular and tunable, and provide a simple strategy for self-assembly without the need to design specific small-molecule binding partners.19–21,23 PNP hydrogels form when addition of nanoparticles to polymers results in crosslinking and corresponding enhancements in elasticity, which is commonly experimentally observed as an increase in the shear storage modulus (G′), an increase of relative elasticity (i.e., a decrease in tan(δ), as defined as the ratio between the shear loss and storage moduli, G′′/G′), longer bulk relaxation times (τ), and the emergence of a functional yield stress (σy).24 The origins of these changes can be attributed to two main contributions:24–26 (1) The formation of transient networks which are driven by energetically favourable polymer–nanoparticle interactions leading chains to bridge between particles, and (2) jamming of polymer–nanoparticle unit components (defined here as a particle and the locally bound polymer corona). Although this generalization is useful for broad discussions of PNP hydrogels, the relative contribution of each mechanism is highly dependent on formulation variables such as particle size, polymer molecular weight and hydrodynamic size, PNP interaction strength, concentration of each component, and total occupied volume fraction.
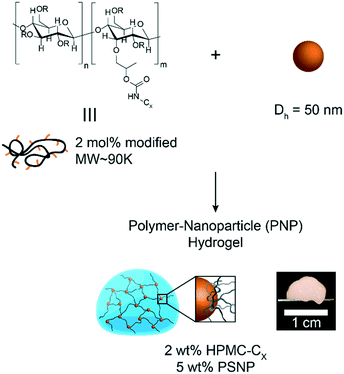
Recently we developed a PNP hydrogel platform and demonstrated its injectability, two-stage release of therapeutic cargo, enhanced cell viability after injection, and efficacy in preventing post-surgical adhesions.21,22,27,28 In these applications, the underpinning functionality is made possible by the intricate combination of viscoelasticity, flow properties, yield stress, and microstructure characteristic of PNP hydrogels.21,22,27,28 These hydrogels are formed as nanoparticles are added to hydroxypropylmethylcellulose (HPMC) solutions, and the robustness of gelation can be tuned by attaching different hydrophobic pendant groups onto the HPMC chains. This tunability creates a useful handle to modulate bulk properties crucial for each application, such as modulus, relative elasticity, and flow behaviour. In this work, we use this tunability to elucidate how the pendant group hydrophobicity of HPMC chains affects bulk properties and microstructure of the resulting PNP hydrogels. We demonstrate that increasing the pendant group hydrophobicity increases polymer corona heights around the nanoparticles after adsorbing to the nanoparticle surface, thereby reducing the interparticle distance between polymer–particle unit components. Once a critical interparticle distance is spanned by the majority of polymer corona populations, a jammed microstructure is formed. These results clarify molecular architectural origins of elasticity in these PNP hydrogels and propose engineering criteria for tuning viscoelasticity and microstructure in future designs for applications such as drug delivery, 3D printing, and sprayable materials. For example, when engineering materials for drug delivery, microstructure design is critical for controlling solute diffusivity and release kinetics, while control over viscoelasticity is important for creating an injectable material that remains cohesive under physiological stresses.27–29
2. Experimental section
2.1 Materials
Hydroxypropylmethylcellulose (USP grade; MW ∼ 90 kDa; HPMC), hexyl isocyanate, dodecyl isocyanate, N,N-diisopropylethylamine (DIPEA), acetone, and anhydrous N-methyl-2-pyrrolidone (NMP) were obtained from Sigma-Aldrich. Polystyrene nanoparticles (PSNP; 50 nm diameter) were obtained from Phosphorex Inc. Phosphate buffered saline without calcium or magnesium (PBS) was obtained from Corning.2.2 Concentrating polystyrene nanoparticles (PSNP)
PSNP were isolated from a stock solution (10 mg mL−1) by centrifugal filtration using an Amicon Ultra-15 (10 kDa nominal molecular weight limit) filter tube and centrifugation for 30–40 minutes at 3000 RCF. The concentrated PSNP solution was then transferred to a separate vial and diluted to 75 mg mL−1 with PBS. Dynamic light scattering determined the PSNPs to have a hydrodynamic diameter of ∼57 nm (PD = 0.035).2.3 Modified hydroxypropylmethylcellulose (HPMC-Cx) synthesis
HPMC (1 g) was dissolved in NMP (40 mL) at 60 °C while stirring. Hexyl isocyanate or dodecyl isocyanate (15 wt%) was dissolved in NMP (5 mL) and then added dropwise to the HPMC solution at room temperature with stirring. DIPEA (3–4 drops) was added and the reaction was left stirring for ∼16 hours (overnight). The modified polymer was then precipitated from acetone, collected by filtration, re-dissolved in water, dialyzed in a Spectra/Por 3 dialysis membrane for 3–4 days, and then isolated by lyophilization as a white solid. The HPMC-Cx (x = C6 or C12) was then dissolved in PBS at 6 wt%. HPMC-Cx were characterized by 1H-NMR (Inova 500 MHz) using D2O as a solvent for HPMC and DMSO-d6 for HPMC-Cx (Fig. S1†). Final modification amounts were ∼2 mol%, corresponding to 1 pendant group every 50 glucose units.2.4 Polymer–nanoparticle (PNP) hydrogel formation
Gels were formed at 2 wt% of HPMC-Cx and 5 wt% of PSNP by mixing the two components followed by centrifugation to remove bubbles.2.5 Dynamic rheometry
All rheometry experiments were performed on a torque-controlled Discovery HR-2 Rheometer (TA Instruments). Dynamic measurements on materials were performed using a 20 mm sandblasted parallel plate (Peltier plate steel) geometry and a sandblasted (Peltier plate steel) plate bottom. Amplitude sweeps were performed at 10 rad s−1 from 1 to 100–850% strain. Frequency sweeps were performed at 0.75 μN m torque from 0.1 to 100 rad s−1.2.6 Flow rheometry
Step shear measurements were performed using a 20 mm sandblasted parallel plate (Peltier plate steel) geometry and a sandblasted (Peltier plate steel) plate bottom. Low shear regions were at a shear rate of 0.1 rad s−1 and held for 30 seconds and high shear regions were at a shear rate of 10 rad s−1 and held for 120 seconds. The pre-shear protocol was a 30 second step at 10 rad s−1 followed by holding the shear rate at 0.1 rad s−1 until viscosity was recovered (∼50 seconds).2.7 Dynamic light scattering (DLS)
All DLS experiments were performed at 25 °C on a DynaPro® Plate Reader II. All solutions were prepared using phosphate buffered saline. While stirring, PSNP were added to a ∼0.005 mg mL−1 solution of HPMC-Cx until a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 HPMC-Cx
5 HPMC-Cx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSNP ratio was achieved. 3 samples of each formulation was made, corresponding to n = 3 calculations for diameters and polydispersity indices. DLS sample acquisition time was set at 1 second and 10 acquisitions were taken per 45 μL sample in a black 384 well plate. Corona heights were calculated by subtracting the hydrodynamic diameter of the PSNP control from the hydrodynamic diameter values of the PNP combinations (Table S1†). Corona height probability distributions were calculated using the measured polydispersity indices and by assuming a normal distribution.
PSNP ratio was achieved. 3 samples of each formulation was made, corresponding to n = 3 calculations for diameters and polydispersity indices. DLS sample acquisition time was set at 1 second and 10 acquisitions were taken per 45 μL sample in a black 384 well plate. Corona heights were calculated by subtracting the hydrodynamic diameter of the PSNP control from the hydrodynamic diameter values of the PNP combinations (Table S1†). Corona height probability distributions were calculated using the measured polydispersity indices and by assuming a normal distribution.
2.8 Interparticle spacing calculation
The interparticle spacing (IPS) was calculated by assuming close random packing and the following equation:30IPS = 2r((ϕm/ϕ)1/3−1) where ϕm is 0.63, ϕ is the particle volume fraction, and r is the radius of the particle.3. Results and discussion
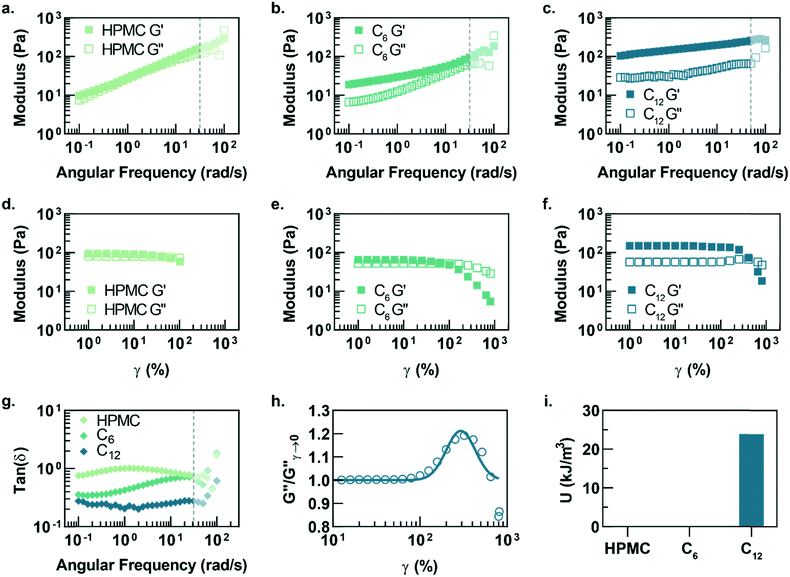
In this study, hydrophobically-modified HPMC and polystyrene nanoparticles (DH ∼ 50 nm) were used to generate model PNP hydrogels to investigate the role of microstructure on materials properties (Fig. 1). HPMC (MW ∼ 90 kDa) was chosen due to its previous demonstration in the generation of PNP hydrogels and its translational relevance as a biocompatible, high molecular weight polymer.31 Furthermore, the high molecular weight and rigidity of the polymer results in large hydrodynamic sizes, increasing the probability for chains to bridge between nanoparticles and inducing a higher degree of crosslinking, as well as increasing the probability of jamming interactions between polymer–nanoparticle units. The hydrophobicity of HPMC was tuned by attaching either hexyl (C6) or dodecyl (C12) pendant groups at ∼2 mol% (Fig. 1 and S1†). Simple mixing of the HPMC-Cx (2 wt%) polymers and PSNPs (5 wt%) produces an opaque, mouldable hydrogel (Fig. 1).Oscillatory shear rheometry illustrates that increasing the hydrophobicity of HPMC pendant groups increases the stiffness and solid-like nature of the resulting PNP gels (Fig. 2a–g). Furthermore, it is apparent that the addition of PSNPs is necessary to form a gel with a tan(δ) < 1 in the frequency range tested (Fig. S2a–f and S3a–f†). PNP gels comprising unmodified HPMC exhibit moduli with strong frequency dependence (G′ ∼ ω0.43) and a tan(δ) ∼ 1 for the frequency range measured (Fig. 2a and g). This frequency dependence is close to Rouse behaviour of pure polymer matrices (G′ ∼ ω0.5) and suggests minimal influence of PNP interactions on the rheological properties.32 These materials are relatively soft and predominately liquid-like, overall barely forming a gel. On the other hand, PNP gels made with HPMC-C6 display a dampened frequency dependence of G′ (G′ ∼ ω0.19) at low angular frequencies and, consequently, a significantly lower tan(δ) consistent with solid-like relaxation behaviour24 (Fig. 2b and g). Similarly, PNP gels made with HPMC-C12 exhibited low frequency dependence of G′ (G′ ∼ ω0.14) and G′′, as well as a nearly constant tan(δ) of ∼0.2, indicating robust solid-like relaxation behaviour24 (Fig. 2c and g). This relatively rapid relaxation behaviour is also demonstrated in step-shear experiments, which measure the rate at which viscosity is recovered after high shear (Fig. S4†). Although all formulations recovered their structure after high shear within 120 seconds, the HPMC-C12 formulation recovers the fastest (Fig. S4a–c†). Furthermore, HPMC-C12-based gels exhibited markedly greater moduli values, with G′ values an order of magnitude greater than HPMC-C6 gels. These rheometry measurements demonstrate that HPMC-C12 gels are much stiffer, prominently more solid-like, and more cohesive when deformed.
Amplitude sweeps of each material provide a microstructural explanation for the enhancement in viscoelasticity for gels comprising HPMC-C12 (Fig. 2d–f). While the terminal strain amplitude of the linear viscoelastic region (LVER) is approximately the same for gels made with HPMC and HPMC-C6, gels made with HPMC-C12 display an order of magnitude extension of the LVER. More importantly, however, the G′′ curve for gels made with HPMC-C12 exhibit a peak that aligns with the crossover of G′ and G′′ (Fig. 2f). This characteristic G′′ maximum is commonly seen in a variety of soft glassy materials (e.g., pastes, emulsions, and soft particle glasses) and, in the case of polymer–nanoparticle composites, has been attributed to the local yielding (“uncaging”) of jammed particles.25,33–38 Analogously, in the PNP hydrogels, uncaging occurs when jammed polymer–nanoparticle units locally yield and dissipate stress. The area under the G′′ peak can be estimated as the energy dissipated per unit volume for these uncaging events.25,38 The existence of a G′′ peak in gels comprising HPMC-C12, and not in those comprising HPMC or HPMC-C6, implies the increased hydrophobicity of C12 pendant groups induce a jamming transition. This G′′ peak can be normalized and fit to a log-normal curve to calculate an energy of uncaging (U) of ∼24 kJ m−3 (Fig. 2h and i).
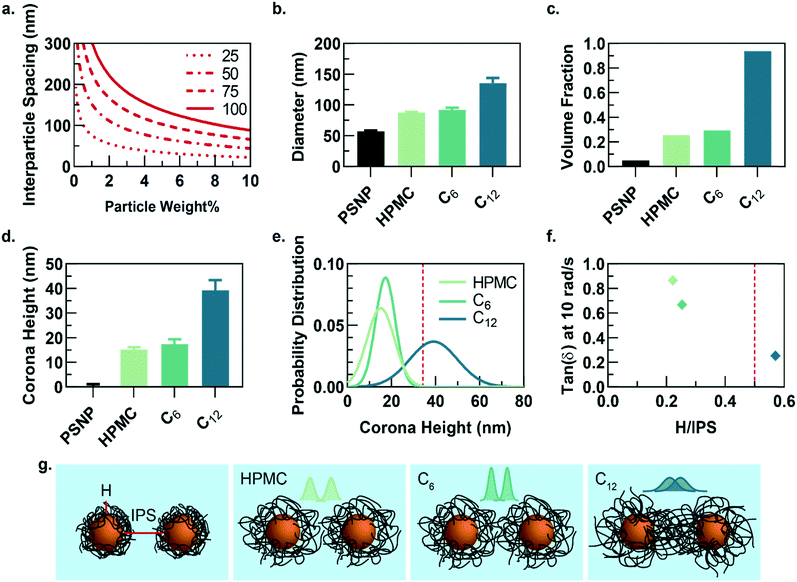
While the PNP gel formulations have the same weight percent of solids in solution (2 wt% polymer, 5 wt% PSNP), the observed strain-amplitude dependent rheology suggests an important microstructural difference between materials comprising HPMC-C12 and the other formulations, which prompted us to further explore the architectural reasons for this difference (Fig. 3a–g). A calculation of the interparticle spacing (IPS) between the surfaces of two particles in a homogeneous dispersion shows that for 50 nm diameter particles at 5 wt% loading, the IPS is ∼69 nm (Fig. 3a).30 Consequently, the adsorbed polymer corona must span at least half the ∼69 nm IPS (∼34.5 nm in height) before overlapping with another particle-corona unit (assuming random dense packing and no net interactions between units). This height requirement scales linearly with particle diameter at a given wt% loading of particles, implying that smaller particles should enable more overlap of polymer coronas as the IPS is reduced (Fig. 3a).
Dilute solutions of each gel formulation were analysed using dynamic light scattering (DLS) to characterize the hydrodynamic diameter of the structural unit component of the gel, which is defined as a single particle and the polymer corona adsorbed on the NP surface (Fig. 3b and S5†). As the hydrophobicity of the pendant group increases, the diameter of the unit component increases. Compared to HPMC-C6 gels, the increased hydrophobicity of the dodecyl groups on the HPMC-C12 chains led to the formation of larger polymer coronas. Correspondingly, these unit component sizes can be used to calculate the volume fraction occupied by these units if they are assumed to be solid spheres (Fig. 3c). Notably, this analysis highlights that the volume fraction occupied by PNP units comprising HPMC-C12 polymers (ϕ ∼ 0.94) exceeds the theoretical ϕ = 0.58 value at which non-interacting hard spheres jam, while PNP units comprising non-modified HPMC (ϕ ∼ 0.25) and HPMC-C6 (ϕ ∼ 0.29) do not.39 This analysis supports the increased viscoelasticity and caging seen in PNP gels comprising HPMC-C12 in bulk rheometry experiments and agrees with previous work on polymer–nanoparticle composites.24,40 Examining the corona heights (H) and the distribution of heights offers further insight as it is apparent most of the corona population in gels comprising HPMC-C12 are larger than the ∼34.5 nm threshold established in IPS calculations (Fig. 3d–f and h). On the other hand, gels made with unmodified HPMC and HPMC-C6 have essentially no corona heights that extend past this critical threshold (Fig. 3d, e and h). In these cases, enhanced elasticity is most likely still apparent due to bridging of HPMC polymers between nanoparticles caused by attractive PNP interactions and a decrease in mobility for chains adsorbed onto or near particles. Since the diameter of gyration of unbound HPMC polymers (∼74 nm, calculated using a persistence length of 10 nm (ref. 41 and 42)) is on the order of the IPS (∼69 nm) at these concentrations, bridging chains are possible in each of the formulations investigated here. Favourable energies of adsorption can therefore yield crosslinking interactions in each system investigated. Plotting the tan(δ) versus the ratio of corona height to the IPS illustrates that gels made with HPMC-C12 are the only formulation where the 0.5 H/IPS threshold is surpassed to achieve corona overlap, and this formulation exhibits lowest tan(δ) values (Fig. 3f). These results demonstrate that the extent of corona overlap is highly correlative to the generation of PNP hydrogels with caged polymer–particle units, which in turn leads to higher moduli and relative elasticity. It is important to note that this characterization does not rule out contributions from bridging polymer chains and greater corona heights should lead to higher propensity of bridging chains.26 Furthermore, we hypothesize that the increased hydrophobicity of dodecyl pendant groups on the HPMC-C12 polymers may also lead to stronger PNP interactions, which increase immobilization of chains proximate to particle surfaces and increase the energetic gain of forming an interparticle bridge.
Conclusions
Overall, we demonstrate that increasing the hydrophobicity of the modifications on HPMC increases the modulus and relative elasticity of the resulting PNP hydrogels. These enhanced properties are driven by increased overlap between polymer chains adsorbed onto the nanoparticle surfaces as the corona height distributions shift to higher values. A threshold interparticle spacing must be spanned by polymer coronas before robust elasticity and caging are manifested. Unmodified HPMC and HPMC-C6 do not span the interparticle distance when bound to the nanoparticle surface, and correlatively exhibit relatively fluid-like material properties and do not exhibit a G′′ peak in the strain-dependent rheology that is indicative of caging. These materials are most likely primarily formed through bridging polymer chains and reduced chain mobility near particle surfaces. HPMC-C12 polymers form a corona height population that mostly spans the IPS distance, leading to higher G′ values, lower tan(δ), and evidence of PNP unit caging. These results demonstrate how molecular level changes of the polymer backbone lead to microstructural changes of the PNP network architecture that ultimately impact bulk-scale viscoelasticity, stiffness, and yield behaviour critical for translational functionality.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Professor Andy Spakowitz and Quinn MacPherson for helpful discussion. This work was supported by a Kodak Fellowship (A. C. Y.) and the Center for Human Systems Immunology with Bill & Melinda Gates Foundation (OPP1113682). A. A. A. S. was funded by grant NNF18OC0030896 from the Novo Nordisk Foundation and the Stanford Bio-X Program. A part of this work was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under award ECCS-1542152.References
- M. J. Webber, E. A. Appel, E. W. Meijer and R. Langer, Nat. Mater., 2016, 15, 13–26 CrossRef CAS PubMed.
- P. S. Kowalski, C. Bhattacharya, S. Afewerki and R. Langer, ACS Biomater. Sci. Eng., 2018, 4, 3809–3817 CrossRef CAS.
- D. Seliktar, Science, 2012, 336, 1124–1128 CrossRef CAS PubMed.
- M. J. Webber and R. Langer, Chem. Soc. Rev., 2017, 46, 6600–6620 RSC.
- P. M. Kharkar, K. L. Kiick and A. M. Kloxin, Chem. Soc. Rev., 2013, 42, 7335–7372 RSC.
- S. M. Mantooth, B. G. Munoz-Robles and M. J. Webber, Macromol. Biosci., 2019, 19 Search PubMed.
- E. A. Appel, J. del Barrio, X. J. Loh and O. A. Scherman, Chem. Soc. Rev., 2012, 41, 6195–6214 RSC.
- J. L. Mann, A. C. Yu, G. Agmon and E. A. Appel, Biomater. Sci., 2017, 6, 10–37 RSC.
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 16071 CrossRef CAS PubMed.
- K. Dubbin, Y. Hori, K. K. Lewis and S. C. Heilshorn, Adv. Healthcare Mater., 2016, 5, 2488–2492 CrossRef CAS PubMed.
- S. J. Buwalda, T. Vermonden and W. E. Hennink, Biomacromolecules, 2016, 18(2), 316–330 CrossRef PubMed.
- S. Mitragotri, P. A. Burke and R. Langer, Nat. Rev. Drug Discovery, 2014, 13, 655–672 CrossRef CAS PubMed.
- C. B. Rodell, A. L. Kaminski and J. A. Burdick, Biomacromolecules, 2013, 14, 4125–4134 CrossRef CAS PubMed.
- D. E. Clarke, E. T. Pashuck, S. Bertazzo, J. V. M. Weaver and M. M. Stevens, J. Am. Chem. Soc., 2017, 139, 7250–7255 CrossRef CAS PubMed.
- J. R. McKee, E. A. Appel, J. Seitsonen, E. Kontturi, O. A. Scherman and O. Ikkala, Adv. Funct. Mater., 2014, 24, 2706–2713 CrossRef CAS.
- H. G. Cui, M. J. Webber and S. I. Stupp, Biopolymers, 2010, 94, 1–18 CrossRef CAS PubMed.
- M. J. Rowland, E. A. Appel, R. J. Coulston and O. A. Scherman, J. Mater. Chem. B, 2013, 1, 2904–2910 RSC.
- C. Chassenieux and C. Tsitsilianis, Soft Matter, 2016, 12, 1344–1359 RSC.
- S. Rose, A. Prevoteau, P. Elziere, D. Hourdet, A. Marcellan and L. Leibler, Nature, 2014, 505, 382–385 CrossRef CAS PubMed.
- E. A. Appel, M. W. Tibbitt, J. M. Greer, O. S. Fenton, K. Kreuels, D. G. Anderson and R. Langer, ACS Macro Lett., 2015, 4, 848–852 CrossRef CAS.
- E. A. Appel, M. W. Tibbitt, M. J. Webber, B. A. Mattix, O. Veiseh and R. Langer, Nat. Commun., 2015, 6, 6295 CrossRef CAS PubMed.
- L. M. Stapleton, A. N. Steele, H. Wang, H. Lopez Hernandez, A. C. Yu, M. J. Paulsen, A. A. A. Smith, G. A. Roth, A. D. Thakore, H. J. Lucian, K. P. Totherow, S. W. Baker, Y. Tada, J. M. Farry, A. Eskandari, C. E. Hironaka, K. J. Jaatinen, K. M. Williams, H. Bergamasco, C. Marschel, B. Chadwick, F. Grady, M. Ma, E. A. Appel and Y. J. Woo, Nat. Biomed. Eng., 2019, 3, 611–620 CrossRef CAS PubMed.
- A. C. Yu, H. X. Chen, D. Chan, G. Agmon, L. M. Stapleton, A. M. Sevit, M. W. Tibbitt, J. D. Acosta, T. Zhang, P. W. Franzia, R. Langer and E. A. Appel, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14255–14260 CrossRef CAS PubMed.
- V. Pryamitsyn and V. Ganesan, Macromolecules, 2006, 39, 844–856 CrossRef CAS.
- A. Agrawal, H. Y. Yu, A. Sagar, S. Choudhury and L. A. Archer, Macromolecules, 2016, 49, 8738–8747 CrossRef CAS.
- M. Surve, V. Pryamitsyn and V. Ganesan, Langmuir, 2006, 22, 969–981 CrossRef CAS PubMed.
- H. L. Hernandez, A. K. Grosskopf, L. M. Stapleton, G. Agmon and E. A. Appel, Macromol. Biosci., 2019, 19, 1800275 CrossRef PubMed.
- A. K. Grosskopf, G. A. Roth, A. A. A. Smith, E. C. Gale, H. L. Hernandez and E. A. Appel, Bioeng. Transl. Med., 2019, e10147 Search PubMed.
- E. Axpe, D. Chan, G. S. Offeddu, Y. Chang, D. Merida, H. L. Hernandez and E. A. Appel, Macromolecules, 2019, 52, 6889–6897 CrossRef CAS PubMed.
- T. Hao and R. E. Riman, J. Colloid Interface Sci., 2006, 297, 374–377 CrossRef CAS PubMed.
- E. Doelker, in Hydrogels in Medicine and Pharmacy, ed. N. A. Peppas, CRC Press, Boca Raton, 1986, vol. 2, pp. 115–160 Search PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, UK, 1986 Search PubMed.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC.
- K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, P. N. Pusey and W. C. K. Poon, Europhys. Lett., 2006, 75, 624–630 CrossRef CAS.
- H. M. Wyss, K. Miyazaki, J. Mattsson, Z. B. Hu, D. R. Reichman and D. A. Weitz, Phys. Rev. Lett., 2007, 98, 238303 CrossRef PubMed.
- P. Sollich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 738–759 CrossRef CAS.
- P. Agarwal and L. A. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041402 CrossRef PubMed.
- P. Agarwal, H. B. Qi and L. A. Archer, Nano Lett., 2010, 10, 111–115 CrossRef CAS PubMed.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2770–2773 CrossRef CAS PubMed.
- Y. N. Pandey, G. J. Papakonstantopoulos and M. Doxastakis, Macromolecules, 2013, 46, 5097–5106 CrossRef CAS.
- C. Roschinski and W. M. Kulicke, Macromol. Chem. Phys., 2000, 201, 2031–2040 CrossRef CAS.
- T. R. Patel, G. A. Morris, J. G. de la Torre, A. Ortega, P. Mischnick and S. E. Harding, Macromol. Biosci., 2008, 8, 1108–1115 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00120d |
| This journal is © The Royal Society of Chemistry 2020 |