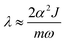DOI:
10.1039/D0RA08200G
(Paper)
RSC Adv., 2020,
10, 41891-41900
Anomalous boron isotope effects on electronic structure and lattice dynamics of CuB2O4†‡
Received
25th September 2020
, Accepted 9th November 2020
First published on 17th November 2020
Abstract
Copper metaborate had a unique crystal structure and exhibited noteworthy magnetic phase transitions at 21 and 10 K. The electronic structure and lattice dynamics of copper metaborate Cu11B2O4 single crystals were investigated and compared with the optical properties of CuB2O4, to assess the boron isotope effect. The optical absorption spectrum at room temperature revealed two charge-transfer bands at approximately 4.30 and 5.21 eV with an extrapolated direct optical band gap of 3.16 ± 0.07 eV. Compared with the data on CuB2O4, the electronic transitions were shifted to lower energies upon the replacement of a heavier boron isotope. The band gap was also determined to be lower in Cu11B2O4. Anomalies in the temperature dependence of the optical band gap were observed below 21 K. Furthermore, 38 Raman-active phonon modes were identified in the room-temperature Raman scattering spectrum of Cu11B2O4, which were also observed in CuB2O4 with a shift to lower frequencies. No broadening caused by isotopic changes was observed. As the temperature decreased, phonon frequencies shifted to higher wavenumbers and the linewidth decreased. Anomalous softening in the Raman peaks below 21 K was also revealed.
I. Introduction
Isotopes are atoms with the same number of protons and electrons but a different number of neutrons. Isotopes differ in mass but are chemically identical. Early theoretical works have established that only properties dependent on nuclear mass are altered in isotopes. The most obvious instance of such dependence is the mass-dependent effect on the harmonic lattice vibrational frequency, which is represented as 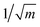 . Isotope-dependent properties also include properties that are affected by changes in unit cell volume, atomic hopping mobility, and anharmonicities—for example, thermal conductivity, thermal expansion, melting temperature, nuclear magnetic resonance, and superconducting phase transition temperature. The electronic band structures were once believed to remain identical in isotopes under such changes. However, this belief has been justified only by atomic-spectra data. Evidence has revealed that in the case of molecular spectra, the effect of mass involves differences between isotopes through the mechanism of electron–phonon coupling.1,2 The presence of an isotope effect is an effective indicator of phonon-mediated superconductivity in materials and constitutes support for the Bardeen–Cooper–Schrieffer (BSC) theory of superconductivity.3–5
. Isotope-dependent properties also include properties that are affected by changes in unit cell volume, atomic hopping mobility, and anharmonicities—for example, thermal conductivity, thermal expansion, melting temperature, nuclear magnetic resonance, and superconducting phase transition temperature. The electronic band structures were once believed to remain identical in isotopes under such changes. However, this belief has been justified only by atomic-spectra data. Evidence has revealed that in the case of molecular spectra, the effect of mass involves differences between isotopes through the mechanism of electron–phonon coupling.1,2 The presence of an isotope effect is an effective indicator of phonon-mediated superconductivity in materials and constitutes support for the Bardeen–Cooper–Schrieffer (BSC) theory of superconductivity.3–5
Studies on the isotope effects of different materials are crucial in clarifying these materials' properties, especially when investigating phonons and their interactions. For instance, isotope labeling in the study of graphene provided direct evidence that the growth mechanism is substrate dependent.6 Furthermore, isotopic substitution in diamond (12C and 13C) and in diamond-type semiconductors (Si and Ge) was noted to increase the indirect electronic energy gap because of isotopically induced changes in lattice volume and electron–phonon interaction.7,8 Isotopic shifts in the superconducting gap and binding energy of high Tc superconductors were used to analyze the nature of the electron–lattice coupling and elucidate the electron pairing mechanism in high Tc superconductors.3,9,10 Isotope shifts were demonstrated to be an essential test of superconductivity.
BCS superconductors with electron–phonon coupling are expected to have a total isotope effect coefficient of 0.5. The isotope effect coefficient α, is defined as α = −d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc/d
Tc/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M where M is the atomic mass. The coefficient α was measured in the superconductor MgB2. An analysis of the magnetization data revealed a large boron isotope effect, which indicated superconductivity in this material. The extrapolated Tc exhibited at least 1 K difference between the 11B and 10B samples. The isotope effects from Mg were small compared with the boron isotope effects, which clearly indicated that phonons associated with boron vibrations are crucial in superconductivity. The findings further revealed superconductivity in transition metal diborides (i.e. NbB2) and borocarbides (e.g., YNi2B2C and LiNi2B2C).4,11 The natural abundance of stable boron isotopes facilitated the assessment of isotopic effects, despite a lack of suitable isotopes for the other elements.
M where M is the atomic mass. The coefficient α was measured in the superconductor MgB2. An analysis of the magnetization data revealed a large boron isotope effect, which indicated superconductivity in this material. The extrapolated Tc exhibited at least 1 K difference between the 11B and 10B samples. The isotope effects from Mg were small compared with the boron isotope effects, which clearly indicated that phonons associated with boron vibrations are crucial in superconductivity. The findings further revealed superconductivity in transition metal diborides (i.e. NbB2) and borocarbides (e.g., YNi2B2C and LiNi2B2C).4,11 The natural abundance of stable boron isotopes facilitated the assessment of isotopic effects, despite a lack of suitable isotopes for the other elements.
Although isotopic effects are well studied in high Tc superconductors, research on isotopic shifts in phase transition of magnetic materials is scarce. Copper metaborate, CuB2O4 exhibited complex magnetic properties that have been extensively investigated. Canted antiferromagnetic ordering occurred below 21 K followed by a commensurate-to-incommensurate magnetic structure at 10 K.12,13 CuB2O4 crystallizes in a unique noncentrosymmetric I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d structure which contains BO4 tetrahedrons with Cu2+ ions between them. These Cu2+ ions are located in two inequivalent crystallographic positions (see ESI Fig. 1‡). Various studies reported that CuB2O4 exhibited the unusual magnetoelectric properties and complex magnetic, electric and optical coupling phenomenon.14–17 Notably, CuB2O4 containing 11B and 10B isotopes exhibited no significant shifts in the phase transition temperatures, as demonstrated by the nearly identical magnetic susceptibility illustrated in Fig. 1. This finding contrasted with the large isotope effects identified in high Tc superconductors. Studies on antiferromagnetic cuprates have also revealed negligible oxygen isotope effects in the magnetic phase transition temperatures.18,19
2d structure which contains BO4 tetrahedrons with Cu2+ ions between them. These Cu2+ ions are located in two inequivalent crystallographic positions (see ESI Fig. 1‡). Various studies reported that CuB2O4 exhibited the unusual magnetoelectric properties and complex magnetic, electric and optical coupling phenomenon.14–17 Notably, CuB2O4 containing 11B and 10B isotopes exhibited no significant shifts in the phase transition temperatures, as demonstrated by the nearly identical magnetic susceptibility illustrated in Fig. 1. This finding contrasted with the large isotope effects identified in high Tc superconductors. Studies on antiferromagnetic cuprates have also revealed negligible oxygen isotope effects in the magnetic phase transition temperatures.18,19
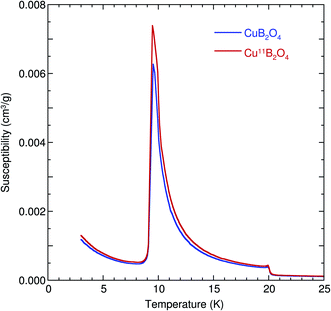 |
| | Fig. 1 The temperature dependence of magnetic susceptibility measured in an applied magnetic field of 50 Oe for H ⊥[001] of single-crystal Cu11B2O4 and CuB2O4. | |
The optical features of antiferromagnetic copper metaborate under isotopic substitution remain unexplored. In this paper, the boron isotope effects in copper metaborate were optically and vibrationally investigated. We analyzed the dependence of the electronic transition energy on the boron isotope mass as obtained from spectroscopic ellipsometry. Our measurements revealed notable isotope effects in the charge-transfer excitation energies and the direct band gap. The Raman isotopic shifts accorded with the calculated shifts because of changes in isotopic mass, which enabled the identification of the boron-related vibrations. Anomalies in the band gap, the peak energy of charge-transfer bands, and Raman-active phonon modes of Cu11B2O4 were observed at 21 K, confirming the spin–charge–lattice interaction in this material. These results elucidate the intricate lattice dynamics and the influence of the isotope effects on the electronic states, which are vital for the isotope engineering of optoelectronic and photonic devices.
II. Experimental details
The flux method was used to grow Cu11B2O4 single crystals.20 The crystals with a (110) surface used in this study had approximate dimensions of 3 × 3 × 2 mm3. For each batch, crystals were characterized using X-ray powder diffraction (see ESI Fig. 2 and 3‡) and magnetization measurements (Fig. 1). The X-ray powder diffraction profile, the Rietveld refinement pattern, and the difference pattern for Cu11B2O4 confirmed the formation of a single crystal. The lattice constants and the sample's crystallographic data, obtained from the Rietveld refinement, accorded with those reported in the literature on CuB2O4.20 The magnetization data revealed low-temperature magnetic phase transitions at 21 and 10 K. Above 21 K, Cu11B2O4 exhibited paramagnetism. Between 21 and 10 K, the material revealed commensurate antiferromagnetism. Below 10 K, the material transitioned to incommensurate antiferromagnetism. The spectroscopic ellipsometry measurements were performed under angles of incidence of 60°–75° using a J. A. Woollam Co. M-2000U ellipsometer over a spectral range of 0.73–6.42 eV. For temperature-dependent measurements between 4.5 and 300 K, the ellipsometer was equipped with a Janis ST-400 ultrahigh-vacuum cryostat. Only a single angle of incidence was possible because of the 70° angle of the two cryostat windows.21 The micro-Raman scattering spectra were measured in a backscattering configuration using a laser with an excitation wavelength of 488 nm and a SENTERRA spectrometer with a 1024-pixel-wide charge-coupled detector. The spectral resolution using this spectrometer was typically lower than 0.5 cm−1, and the laser power was lower than 4.0 mW to avoid heating effects. The polarized Raman scattering spectra were obtained in backscattering geometry with incident and scattered lights parallel to the [110] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] directions, denoted as Y′ and
0] directions, denoted as Y′ and  , respectively. Three scattering configurations were thus obtained:
, respectively. Three scattering configurations were thus obtained: 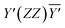 ,
, 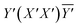 , and
, and 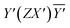 . In this Porto notation, the direction parallel to the crystallographic (c) axis was labelled as Z, whereas the [
. In this Porto notation, the direction parallel to the crystallographic (c) axis was labelled as Z, whereas the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] crystal direction was labelled as X′. The sample was placed in a continuous-flow helium cryostat, which enabled measurements in the temperature range of 10–300 K.21
10] crystal direction was labelled as X′. The sample was placed in a continuous-flow helium cryostat, which enabled measurements in the temperature range of 10–300 K.21
III. Results and discussion
A. Electronic excitations
The room-temperature optical absorption spectrum of Cu11B2O4 is displayed in Fig. 2. The bands display different features as compared to the absorption spectrum of CuB2O4. We fitted the absorption spectrum using the Lorentz oscillators, as illustrated by the dashed lines. The spectrum displayed two peaks approximately at 4.30 and 5.21 eV. These peaks originated from the electronic transitions from the 2p states of the oxygen ions to the 3d states of the copper ions.22,23 The direct band gap Eg of Cu11B2O4, estimated from the absorption coefficient α(E), was determined to be 3.16 ± 0.07 eV, as displayed in the inset of Fig. 2. The band gap of a normal solid, which holds contributions from direct and indirect transitions, can be estimated from the absorption coefficient α(E) as follows:24| | |
α(E) = A(E − Eg,dir)0.5 + B(E − Eg,indir ∓ Eph)2,
| (1) |
where Eg,dir and Eg,indir are the magnitudes of direct and indirect gaps, respectively; Eph is the emitted (absorbed) phonon energy, and A and B are constants.
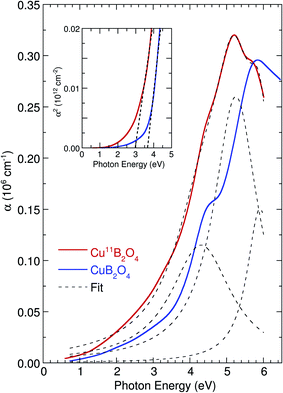 |
| | Fig. 2 Optical absorption spectra of Cu11B2O4 and CuB2O4 at room temperature. The dashed lines illustrate the best fit with the Lorentz function. Inset illustrates the direct band gap analysis of Cu11B2O4 and CuB2O4 at 300 K. | |
The temperature-dependent optical absorption spectra of Cu11B2O4 are displayed in Fig. 3. As the temperature decreased, the absorption peaks displayed a gradual increase in their intensity and peak position, whereas the linewidth narrowed. The temperature-dependent band gap is displayed in the inset of Fig. 3. The band gap decreased as the temperature decreased consistent with the anomalous behavior of CuB2O4. We find 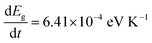 which is a little lower compared to CuB2O4 but still in the same order of magnitude with those found for MAPbI3.25 Below 21 K, the band gap exhibited a gradual increase as the temperature decreased. This anomaly and discontinuity were correlated with the magnetic ordering at this temperature point. These findings demonstrate that the shifts were caused by spin–charge interactions, rather than changes induced by thermal contraction or alterations in the unit cell volume.
which is a little lower compared to CuB2O4 but still in the same order of magnitude with those found for MAPbI3.25 Below 21 K, the band gap exhibited a gradual increase as the temperature decreased. This anomaly and discontinuity were correlated with the magnetic ordering at this temperature point. These findings demonstrate that the shifts were caused by spin–charge interactions, rather than changes induced by thermal contraction or alterations in the unit cell volume.
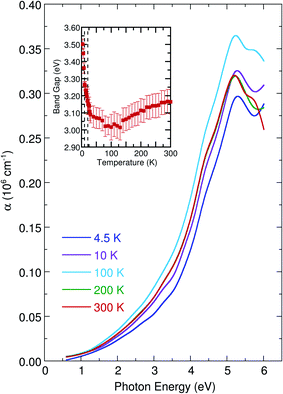 |
| | Fig. 3 Temperature-dependent optical absorption spectra of Cu11B2O4. Inset illustrates the temperature-dependent band gap energy. The vertical dashed lines denote the magnetic phase transition temperatures at 10 and 21 K. | |
We examined the peak energy, linewidth, and normalized intensity of the fitted Lorentzian peaks displayed in Fig. 4. Above 21 K, the energy peak and linewidth exhibited minimal temperature variation, whereas the peak intensity increased as the temperature decreased. Anomalies near the magnetic phase transition temperature were evident in Cu11B2O4. Below 21 K, the peak position shifted to higher energies and the linewidth decreased for two absorption peaks. These phenomena were similar to those observed in CuB2O4. The temperature dependences of Cu11B2O4 and CuB2O4 were somewhat similar. The hardening as well as damping and intensity changes of the absorption bands below 21 K were approximately of the same magnitude in both samples. A notable isotope effect was indicated by the shift of the absorption band toward lower energies in Cu11B2O4 (4.30 and 5.21 eV) compared with CuB2O4 (4.49 and 5.83), as illustrated in Fig. 2. This isotopic shift has an opposite sign with the generally established behavior.9,26,27 Moreover, the extrapolated band gap was determined to be lower in Cu11B2O4 with a difference of ∼0.6 eV, as illustrated in the inset of Fig. 3. The replacement of a light isotope with a heavy isotope caused an increase in the energy gap in superconducting LiH and in most semiconductors – such as Si, Ge, and diamond (13C and 12C).7–9,26–29 Exception to this behavior has been observed in isotopic shifts in the energy gap of CuCl and other Cu salts. The dependence of the semiconductors band gap on the isotopic composition at constant temperature is governed mainly by two contributions expressed as:30
| |
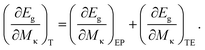 | (2) |
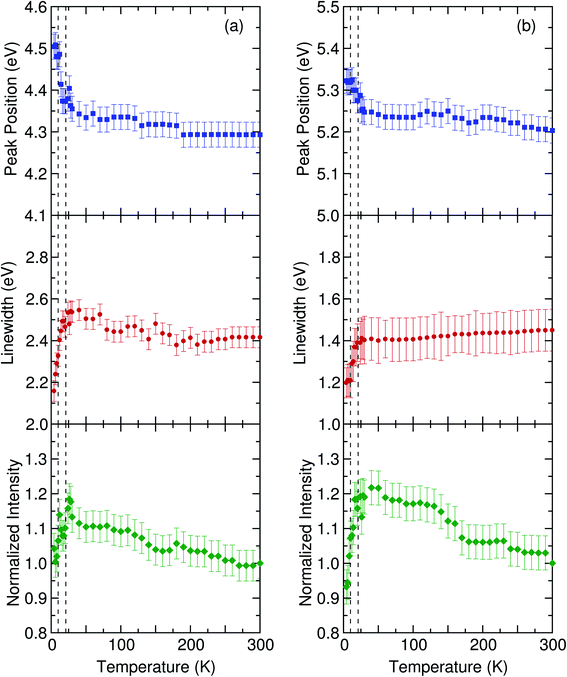 |
| | Fig. 4 Temperature dependence of the peak energy, linewidth, and normalized intensity of the (a) 4.30 and (b) 5.21 eV optical transitions. The vertical dashed lines denote the magnetic phase transition temperatures at 10 and 21 K. | |
The first term is a contribution from the electron–phonon interaction (EP). The second term stems from lattice constant changes and is labeled as TE since it has similar behavior with thermal lattice expansion. Moreover, the second term can be extended in terms of the isotopic mass. The changes in isotopic mass translate to the changes in pressure within the crystal structure and a relative change in the lattice constants. We have observed the negligible changes in the X-ray powder diffraction profiles of CuB2O4 and Cu11B2O4 (see ESI Fig. 2‡), and thus ruled out the contributions from the second term. We speculate that the negative isotope effect in Cu11B2O4 may arise from the changes in the electronic band structures induced by the d-electron–phonon interactions.9,27 The degeneracy of the d states of the Cu ions in the upper valence band was partially lifted and mixed with the p states of B ions under a crystal field. This p–d hybridization was verified in CuB2O4 and accounted for its magnetoelectric properties.17 Substitution of a heavier B isotope in Cu11B2O4 may enhance the p–d hybridization through the electron–phonon interactions and raise the maximum of the valence band, resulting in a decrease of the band gap. Similar phenomenon has been confirmed in energy band transition studies on other Cu containing compounds such as CuCl, CuBr, and CuInS2.30,31 Further theoretical calculations of the electronic band structures of Cu11B2O4 and CuB2O4 are needed to clarify the origin of this negative isotope effect.
B. Vibrational properties
Fig. 5 displays the room-temperature unpolarized Raman scattering spectrum of Cu11B2O4. The phonon peaks were fitted using a standard Lorentzian profile. The spectrum comprised 38 first-order Raman-active phonon modes, which is the same number of phonon modes observed in CuB2O4. We previously identified 12A1, 12B2, and 14E modes in polarized Raman scattering measurements of CuB2O4. The inset of Fig. 5 illustrates the polarized Raman scattering spectra of Cu11B2O4 in different configurations. The peaks that appeared in the 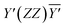 ,
, 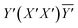 , and
, and 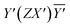 polarizations were identical to those observed in CuB2O4 in the same configurations. The phonon peaks and their assigned symmetries are summarized in Table 1. We assigned the phonon peaks of Cu11B2O4 to the same atomic vibrations assigned to CuB2O4. Low-frequency modes below 200 cm−1 were rotational vibrations of Cu ions. Peaks higher than 200 cm−1 but lower than 400 cm−1 were modes associated with changes in the bond angles that tilted and bent the BO4 tetrahedra. These phonon peaks were coupled to the Cu–O vibrations, which were distributed over the entire frequency range. The highest vibrations from Cu–O stretching modes were observed in the range of 400–900 cm−1. The Cu–O stretching modes in the range 700–900 cm−1 were mixed with the B–O vibrations, whereas modes above 900 cm−1 were considered to have occurred mainly from B–O stretching vibrations. Our experimental results of the phonon modes demonstrated good agreement with the theoretical ab initio calculations by Pisarev et al.32 The data on the isotope boron effects, summarized in Table 1, elucidates the coupling involved in the phonon vibrations occurring primarily between Cu and B.
polarizations were identical to those observed in CuB2O4 in the same configurations. The phonon peaks and their assigned symmetries are summarized in Table 1. We assigned the phonon peaks of Cu11B2O4 to the same atomic vibrations assigned to CuB2O4. Low-frequency modes below 200 cm−1 were rotational vibrations of Cu ions. Peaks higher than 200 cm−1 but lower than 400 cm−1 were modes associated with changes in the bond angles that tilted and bent the BO4 tetrahedra. These phonon peaks were coupled to the Cu–O vibrations, which were distributed over the entire frequency range. The highest vibrations from Cu–O stretching modes were observed in the range of 400–900 cm−1. The Cu–O stretching modes in the range 700–900 cm−1 were mixed with the B–O vibrations, whereas modes above 900 cm−1 were considered to have occurred mainly from B–O stretching vibrations. Our experimental results of the phonon modes demonstrated good agreement with the theoretical ab initio calculations by Pisarev et al.32 The data on the isotope boron effects, summarized in Table 1, elucidates the coupling involved in the phonon vibrations occurring primarily between Cu and B.
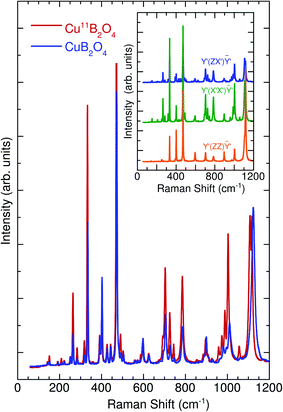 |
| | Fig. 5 Unpolarized room-temperature Raman scattering spectrum of Cu11B2O4 and CuB2O4. Inset illustrates the polarized Raman scattering spectra of Cu11B2O4. | |
Table 1 Raman peaks observed at room temperature for Cu11B2O4
| Phonon frequency (cm−1) |
Symmetry |
Δω (cm−1) (ω10B − ω11B) |
ω11B/ω10B |
Assignment |
| ω1 |
142 |
E |
1 |
0.990 |
Cu atom oscillations |
| ω2 |
151 |
B2 |
1 |
0.993 |
| ω3 |
192 |
E |
2 |
0.992 |
| ω4 |
209 |
B2 |
2 |
0.993 |
| ω5 |
222 |
E |
1 |
0.994 |
BO4 tetrahedron tilting and bending coupled to Cu–O vibrations |
| ω6 |
250 |
A1 |
2 |
0.993 |
| ω7 |
264 |
B2 |
1 |
0.995 |
| ω8 |
284 |
B2 |
1 |
0.995 |
| ω9 |
318 |
B2 |
2 |
0.995 |
| ω10 |
333 |
A1 |
2 |
0.994 |
| ω11 |
391 |
E |
1 |
0.997 |
| ω12 |
401 |
A1 |
1 |
0.997 |
Cu–O stretching/Jahn–Teller modes |
| ω13 |
426 |
B2 |
1 |
0.997 |
| ω14 |
443 |
E |
2 |
0.997 |
| ω15 |
471 |
A1 |
2 |
0.997 |
| ω16 |
491 |
B2 |
1 |
0.998 |
| ω17 |
505 |
E |
1 |
0.998 |
| ω18 |
559 |
E |
3 |
0.995 |
| ω19 |
572 |
E |
2 |
0.997 |
| ω20 |
587 |
B2 |
2 |
0.996 |
| ω21 |
596 |
A1 |
2 |
0.997 |
| ω22 |
625 |
E |
2 |
0.997 |
| ω23 |
677 |
E |
3 |
0.995 |
| ω24 |
692 |
B2 |
4 |
0.995 |
| ω25 |
704 |
A1 |
2 |
0.997 |
| ω26 |
726 |
A1 |
2 |
0.997 |
| ω27 |
744 |
B2 |
3 |
0.996 |
Mixed Cu–O, B–O vibrations |
| ω28 |
785 |
A1 |
2 |
0.998 |
| ω29 |
885 |
E |
3 |
0.996 |
| ω30 |
896 |
A1 |
4 |
0.996 |
| ω31 |
907 |
E |
4 |
0.995 |
Pure B–O stretching |
| ω32 |
926 |
B2 |
39 |
0.959 |
| ω33 |
959 |
E |
23 |
0.977 |
| ω34 |
974 |
E |
21 |
0.979 |
| ω35 |
988 |
A1 |
23 |
0.977 |
| ω36 |
1004 |
B2 |
59 |
0.944 |
| ω37 |
1057 |
A1 |
58 |
0.948 |
| ω38 |
1107 |
A1 |
16 |
0.985 |
The Raman scattering spectrum of Cu11B2O4 was shifted to lower frequencies by at least one wavenumber compared with the Raman scattering spectrum of CuB2O4, as illustrated in Fig. 5. The softening of the frequencies of the heavier isotope mass was expected based on the simple harmonic model. In this case, Cu11B2O4 contains the heavier 11B isotope compared with the 10B isotope in CuB2O4. The simple harmonic model is expressed as follows:
| |
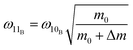 | (3) |
where
ω11B represents the Raman frequency of the
11B enriched sample,
ω10B represents the frequency of the
10B sample,
m0 is the mass of the
10B, and Δ
m is the mass difference between the
11B and
10B isotopes. Using this model, we calculated a ratio of
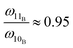
which accords with the observed redshift in the high-frequency Raman modes (
Table 1). For frequencies below 900 cm
−1, we obtained
ω11B/
ω10B ratio of approximately 0.99. For frequencies above 900 cm
−1, the ratio was approximately 0.95 for
ω36 and
ω37, with the largest possible shift of 59 cm
−1. These modes are thus confirmed to be pure B vibrations. Modes below 200 cm
−1 exhibited the smallest shift in frequency because these peaks mostly originated from the Cu atom vibrations. The shifts in frequency, which were 200–900 cm
−1, exhibited differences of approximately 1–2 cm
−1. This finding indicates that the boron atoms influence these vibrational modes. High-frequency peaks above 900 cm
−1 exhibited more obvious softening in the phonon frequencies shifting by at least 16 cm
−1. We observed a clear double peak constituted by
ω37 (1057 cm
−1) and
ω38 (1107 cm
−1) because of the nonuniform shift in the peaks, which contrasted with the overlapping peaks observed in CuB
2O
4. The phonon frequency
ω38 most likely resulted from oxygen stretching vibrations. We surmise this because it is not heavily shifted with isotopic substitution, similar to other phonon modes in this range.
The temperature-dependent unpolarized Raman scattering spectra of Cu11B2O4 are displayed in Fig. 6. For normal anharmonic solids, the phonon frequency should increase and the linewidth should decrease as the temperature decreased. The Raman scattering spectrum at 10 K was fitted with 38 Lorentz oscillators (inset of Fig. 6). The phonon modes of the 11B enriched sample were redshifted. However, no significant changes in the linewidth were observed, and temperature-dependent behavior was similar to that of CuB2O4. An examination of the intense peak at 333 and 443 cm−1 is displayed in Fig. 7. Data for all other phonon modes were reported in ESI Fig. 4.‡ Above 21 K, the peak frequencies and linewidth behaved according to the anharmonic model represented by the thin solid lines in Fig. 7. The anharmonic model is expressed as follows:33
| |
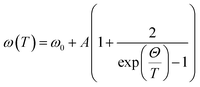 | (4) |
| |
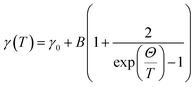 | (5) |
where
ω0 is the intrinsic frequency of the optical phonon mode,
γ0 is the linewidth broadening caused by defects,
Θ is the Debye temperature, and
A and
B are the anharmonic coefficients. The values of the fitting parameters are summarized in
Table 2. Negative values of
A indicate that the phonon frequency increased as the temperature decreased, whereas positive values of
B for the linewidth indicates the contrary. The Debye temperature obtained for different phonon frequencies was within 400–600 K in the same range obtained for CuB
2O
4. The anharmonic model revealed that the Raman phonon modes were mostly temperature independent at low temperature. Below the magnetic ordering temperature (21 K), deviations from the anharmonic model remained evident for all intense peaks. A gradual softening of up to 0.3 cm
−1 was observed in Cu
11B
2O
4.
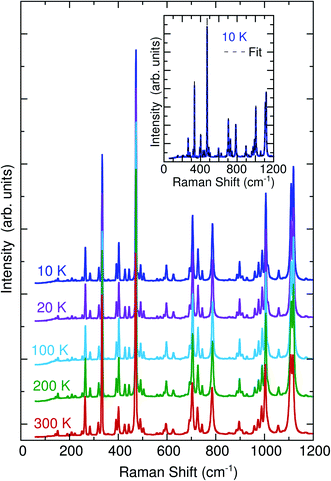 |
| | Fig. 6 Temperature-dependent unpolarized Raman scattering spectra of Cu11B2O4. Inset illustrates the results of fitting the spectrum obtained at 10 K using the Lorentzian model. | |
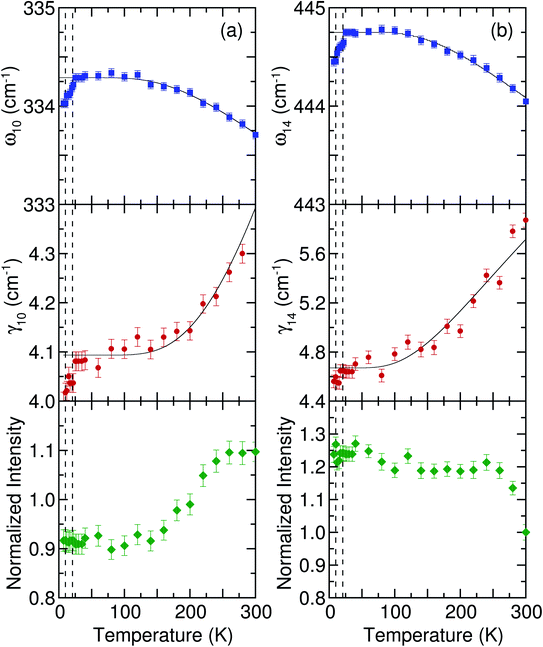 |
| | Fig. 7 Temperature dependence of the frequency, linewidth, and normalized intensity of (a) 333 and (b) 443 cm−1 phonon modes. Thin solid lines are the fitting results obtained with the anharmonic model. The vertical dashed lines denote the magnetic phase transition temperatures at 10 and 21 K. | |
Table 2 Values of parameters obtained from fitting temperature dependence of the phonon frequencies and linewidth based on the anharmonic model expressed in eqn (4) and (5)
| |
ω0 (cm−1) |
γ0 (cm−1) |
A (cm−1) |
B (cm−1) |
Θ (K) |
| ω10 |
338 |
4.20 |
−3.06 |
0.89 |
498 |
| ω11 |
396 |
3.21 |
−2.49 |
2.20 |
554 |
| ω12 |
406 |
3.50 |
−3.68 |
1.61 |
611 |
| ω14 |
448 |
4.96 |
−3.41 |
1.02 |
560 |
| ω15 |
478 |
3.02 |
−4.02 |
1.87 |
528 |
| ω21 |
605 |
3.80 |
−5.98 |
3.79 |
551 |
| ω25 |
710 |
2.68 |
−4.24 |
3.84 |
551 |
| ω28 |
788 |
3.09 |
−1.96 |
0.56 |
543 |
Softening in the phonon peaks at the magnetic phase transition temperature usually indicates the spin–phonon interactions. The sensitivity of the phonon frequency to correlations of spins of nearest-neighbor pairs can be expressed as follows:34
where
λ is the spin–phonon coupling constant and 〈
Si ×
Sj〉 is the nearest neighbor spin correlation. The 〈
Si ×
Sj〉 can be estimated from
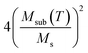
where
Msub(
T) is the sublattice magnetization per magnetic ion and
Ms is the saturation magnetization. The factor of 4 was based on the number of nearest neighbors.
34 As displayed in
Fig. 8, the sublattice magnetization data
13 obtained from a prior study scaled well with the shift in phonon frequency. Using this correlation, we extracted the spin–phonon coupling constant
λ for Cu–O stretching phonon modes tabulated in
Table 3.
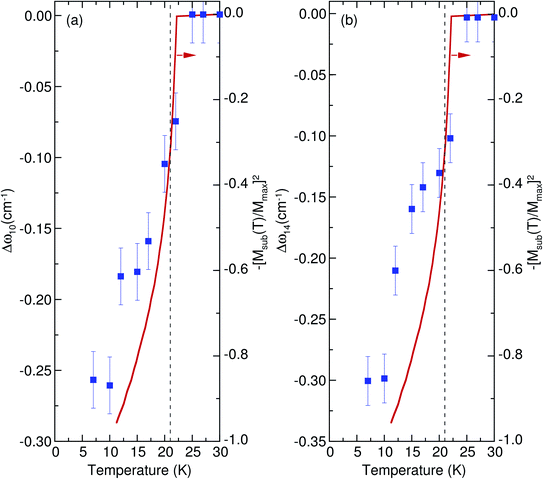 |
| | Fig. 8 Temperature dependence of the shift in the phonon frequency of (a) 333 and (b) 443 cm−1 modes plotted against the normalized square of the magnetic susceptibility.13 The vertical dashed line denotes the magnetic phase transition temperatures at 21 K. | |
Table 3 Spin–phonon coupling constant of Cu11B2O4 obtained for Cu–O stretching related modes
| Mode frequency (cm−1) |
λ (cm−1) |
| ω10 |
333 |
0.032 |
| ω11 |
391 |
0.035 |
| ω12 |
401 |
0.038 |
| ω14 |
443 |
0.038 |
| ω15 |
471 |
0.032 |
| ω21 |
596 |
0.030 |
| ω25 |
704 |
0.030 |
| ω28 |
785 |
0.030 |
| ω30 |
896 |
0.030 |
A slightly higher value of the spin–phonon coupling constant was obtained for Cu11B2O4 compared with the values obtained for CuB2O4. This slight difference coincides with the quantitative estimate of the spin–phonon coupling λ using a simplified lattice model proposed by Sushkov et al.,35 which can be calculated as follows:
| |
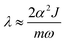 | (7) |
where
m is the mass of the magnetic ion,
ω is the mode frequency,
J is the nearest neighbor exchange coupling constant, and
α can be calculated using
α = 2
z/3
aB (
aB is the Bohr radius and
z is the nearest neighbor coordination number).
Eqn (7) is inversely related to the phonon frequencies. The phonon frequencies of Cu
11B
2O
4 were redshifted from those of CuB
2O
4, which causes the spin–phonon coupling to increase. Considering only the nearest neighbors (
z = 4), we obtained
α = 5.04 Å
−1. Moreover, we estimated the exchange coupling constant using
35where
kB is the Boltzmann constant,
Θcw is the Currie–Weiss temperature, and
S is the spin angular moment. We used
z = 4,
S = 1/2, and
Θcw = 21 K to get
J = 0.95 meV.
13 Therefore, we obtained a quantitative spin–phonon coupling constant
λ ≈ 0.037 cm
−1 which is slightly higher than the values obtained for CuB
2O
4 (
λ ≈ 0.035 cm
−1) and scales well with the empirical spin–phonon coupling
λ tabulated in
Table 3.
IV. Summary
We used spectroscopic ellipsometry and Raman scattering spectroscopy to study the electronic structure and lattice dynamics of Cu11B2O4 single crystals. We assessed the boron isotope effects by comparing the results obtained with the results for CuB2O4. The room-temperature optical absorption spectrum of Cu11B2O4 revealed the occurrence of charge-transfer transitions from the 2p states of O to the 3d states of Cu at approximately 4.30 and 5.21 eV, which were lower than the values measured for CuB2O4. The direct optical band gap was determined to lower in Cu11B2O4 (extrapolated at 3.16 ± 0.07 eV). The temperature-dependent band gap and the peak energy of charge-transfer bands exhibited anomalies through the canted antiferromagnetic ordering temperature at 21 K. The Raman frequencies of Cu11B2O4 shifted lower, whereas the linewidth exhibited no significant change. The extent of the isotopic shift in frequencies accorded with the inverse square root dependence of the mean atomic mass. The temperature dependence of the phonon frequency, linewidth, and normalized intensity exhibited anomalies near 21 K. The temperature dependence of the Cu–O stretching modes also exhibited an anomalous softening at a temperature of less than 21 K. The spin–phonon coupling constant, λ, were slightly higher than CuB2O4, estimated to be 0.030–0.038 cm−1.
Author contributions
H. L. L. conceived the research and was responsible for the experimental design. R. D. M. conducted the experiments. C. H. L. and C. H. D. were responsible for the sample preparation. R. D. M. and H. L. L. drafted the paper. All contributing authors have discussed the results and provided the comments regarding the manuscript.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
H. L. L. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 109-2112-M-003-016. C. H. D. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 108-2112-M-032-007.
References
- E. E. Haller, Isotopically engineered semiconductors, J. Appl. Phys., 1995, 77, 2857–2878 CrossRef CAS.
- R. S. Mulliken, The isotope effect in band spectra, part I, Phys. Rev., 1925, 25, 119–138 CrossRef CAS.
- G.-H. Gweon, T. Sasagawa, S. Y. Zhou, J. Graf, H. Takagi, D.-H. Lee and A. Lanzara, An unusual isotope effect in a high-transition-temperature superconductor, Nature, 2004, 430, 187–190 CrossRef CAS.
- S. L. Bud'ko, G. Lapertot, C. Petrovic, C. E. Cunningham, N. Anderson and P. C. Canfield, Boron isotope effect in superconducting MgB2, Phys. Rev. Lett., 2001, 86, 1877–1880 CrossRef.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Theory of superconductivity, Phys. Rev., 1957, 108, 1175 CrossRef CAS.
- B. R. Carvalho, Y. Hao, A. Righi, J. F. Rodriguez-Nieva, L. Colombo, R. S. Ruoff, M. A. Pimenta and C. Fantini, Probing carbon isotope effects on the Raman spectra of graphene with different 13C concentrations, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125406 CrossRef.
- S. Zollner, M. Cardona and S. Gopalan, Isotope and temperature shifts of direct and indirect band gaps in diamond-type semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 3376–3385 CrossRef CAS.
- A. T. Collins, S. C. Lawson, G. Davies and H. Kanda, Indirect energy gap of 13C diamond, Phys. Rev. Lett., 1990, 65, 891–894 CrossRef CAS.
- V. G. Plekhanov, Isotopic and disorder effects in large exciton spectroscopy, Usp. Fiz. Nauk, 1997, 167, 577 CrossRef CAS.
- G. H. Gweon, T. Sasagawa, S. Y. Zhou, J. Graf, H. Takagi, D. H. Lee and A. Lanzara, An unusual isotope effect in a high-transition-temperature superconductor, Nature, 2004, 430, 187–190 CrossRef CAS.
- D. G. Hinks, H. Claus and J. D. Jorgensen, The complex nature of superconductivity in MgB2 as revealed by the reduced total isotope effect, Nature, 2001, 411, 457–460 CrossRef CAS.
- G. A. Petrakovskiǐ, A. I. Pankrats, M. A. Popov, A. D. Balaev, D. A. Velikanov, A. M. Vorotynov, K. A. Sablina, B. Roessli, J. Schefer, A. Amato, U. Staub, M. Boehm and B. Ouladdiaf, Magnetic properties of copper metaborate CuB2O4, Low Temp. Phys., 2002, 28, 606–612 CrossRef.
- M. Boehm, B. Roessli, J. Schefer, A. S. Wills, B. Ouladdiaf, E. Lelièvre-Berna, U. Staub and G. A. Petrakovskii, Complex magnetic ground state of CuB2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024405 CrossRef.
- M. Saito, K. Taniguchi and T. H. Arima, Gigantic optical magnetoelectric effect in CuB2O4, J. Phys. Soc. Jpn., 2008, 77, 1–4 CrossRef.
- K. N. Boldyrev, R. V. Pisarev, L. N. Bezmaternykh and M. N. Popova, Antiferromagnetic dichroism and Davydov splitting of 3d-excitons in a complex multisublattice magnetoelectric CuB2O4, Phys. Rev. Lett., 2014, 114, 247210 CrossRef.
- M. Saito, K. Ishikawa, K. Taniguchi and T. Arima, Magnetic control of crystal chirality and the existence of a large magneto-optical dichroism effect in CuB2O4, Phys. Rev. Lett., 2008, 101, 1–4 Search PubMed.
- N. D. Khanh, N. Abe, K. Kubo, M. Akaki, M. Tokunaga, T. Sasaki and T. Arima, Magnetic control of electric polarization in the noncentrosymmetric compound (Cu,Ni)B2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–5 CrossRef.
- G. Zhao, K. K. Singh and D. E. Morris, Oxygen isotope effect on Néel temperature in various antiferromagnetic cuprates, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 4112–4117 CrossRef CAS.
- E. Amit, A. Keren, J. S. Lord and P. King, A precise measurement of the oxygen isotope effect on the Néel temperature in cuprates, Adv. Condens. Matter Phys., 2011, 2011, 1–5 CrossRef.
- G. A. Petrakovskii, K. A. Sablina, D. A. Velikanov, A. M. Vorotynov, N. V. Volkov and A. F. Bovina, Synthesis and magnetic properties of copper metaborate single crystals CuB2O4, Crystallogr. Rep., 2000, 45, 853–856 CrossRef.
- R. D. Mero, K. Ogawa, S. Yamada and H. L. Liu, Optical study of the electronic structure and lattice dynamics of NdBaMn2O6 single crystals, Sci. Rep., 2019, 9, 18164 CrossRef CAS.
- R. V. Pisarev, A. M. Kalashnikova, O. Schöps and L. N. Bezmaternykh, Electronic transitions and genuine crystal-field parameters in copper metaborate CuB2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–11 CrossRef.
- A. D. Molchanova, M. A. Prosnikov, R. M. Dubrovin, V. Y. Davydov, A. N. Smirnov, R. V. Pisarev, K. N. Boldyrev and M. N. Popova, Lattice dynamics and electronic transitions in a structurally complex layered copper borate Cu3(BO3)2, Phys. Rev. B, 2017, 96, 1–11 CrossRef.
- J. I. Pankove and D. A. Kiewit, Optical processes in semiconductors, J. Electrochem. Soc., 1972, 119, 156C CrossRef.
- S. Singh, C. Li, F. Panzer, K. L. Narasimhan, A. Graeser, T. P. Gujar, A. Köhler, M. Thelakkat, S. Huettner and D. Kabra, Effect of thermal and structural disorder on the electronic structure of hybrid perovskite semiconductor CH3NH3PbI3, J. Phys. Chem. Lett., 2016, 7, 3014–3021 CrossRef CAS.
- V. G. Plekhanov, Wannier-Mott excitons in isotope-disordered crystals, Rep. Prog. Phys., 1998, 61, 1045–1097 CrossRef CAS.
- V. G. Plekhanov, Fundamentals and applications of isotope effect in solids, Prog. Mater. Sci., 2006, 51, 287–426 CrossRef CAS.
- G. Davies, E. C. Lightowlers, T. S. Hui, V. Ozhogin, K. M. Itoh, W. L. Hansen and E. E. Haller, Isotope dependence of the lowest direct energy gap in crystalline germanium, Semicond. Sci. Technol., 1993, 8, 2201 CrossRef CAS.
- D. Rönnow, L. F. Lastras-Martínez and M. Cardona, Isotope effects on the electronic critical points of germanium: ellipsometric investigation of the E1 and E1+Δ1 transitions, Eur. Phys. J. B, 1998, 5, 29–35 CrossRef.
- A. Göbel, T. Ruf, M. Cardona, C. T. Lin, J. Wrzesinski, M. Steube, K. Reimann, J.-C. Merle and M. Joucla, Effects of the isotopic composition on the fundamental gap of CuCl, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 15183–15190 CrossRef.
- T. M. Hsu and J. H. Lin, Anomalous temperature-dependent band gaps in CuInS2 studied by surface-barrier electroreflectance, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 4106–4110 CrossRef CAS.
- R. V. Pisarev, K. N. Boldyrev, M. N. Popova, A. N. Smirnov, V. Y. Davydov, L. N. Bezmaternykh, M. B. Smirnov and V. Y. Kazimirov, Lattice dynamics of piezoelectric copper metaborate CuB2O4, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 1–15 CrossRef.
- M. Balkanski, R. F. Wallis and E. Haro, Anharmonic effects in light scattering due to optical phonons in silicon, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1928–1934 CrossRef CAS.
- E. Granado, A. García, J. A. Sanjurjo, C. Rettori, I. Torriani, F. Prado, R. D. Sánchez, A. Caneiro and S. B. Oseroff, Magnetic ordering effects in the Raman spectra of La1-xMn1-xO3, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11879–11882 CrossRef CAS.
- A. B. Sushkov, O. Tchernyshyov, W. Ratcliff II, S. W. Cheong and H. D. Drew, Probing spin correlations with phonons in the strongly frustrated magnet ZnCr2O4, Phys. Rev. Lett., 2005, 94, 137202 CrossRef CAS.
Footnotes |
| † PACS numbers: 31.30.Gs, 71.27.+a, 78.20.−e, 78.30.−j. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08200g |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Chun-Hao Laib,
Chao-Hung Du
a,
Chun-Hao Laib,
Chao-Hung Du b and
Hsiang-Lin Liu
b and
Hsiang-Lin Liu *a
*a
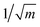 . Isotope-dependent properties also include properties that are affected by changes in unit cell volume, atomic hopping mobility, and anharmonicities—for example, thermal conductivity, thermal expansion, melting temperature, nuclear magnetic resonance, and superconducting phase transition temperature. The electronic band structures were once believed to remain identical in isotopes under such changes. However, this belief has been justified only by atomic-spectra data. Evidence has revealed that in the case of molecular spectra, the effect of mass involves differences between isotopes through the mechanism of electron–phonon coupling.1,2 The presence of an isotope effect is an effective indicator of phonon-mediated superconductivity in materials and constitutes support for the Bardeen–Cooper–Schrieffer (BSC) theory of superconductivity.3–5
. Isotope-dependent properties also include properties that are affected by changes in unit cell volume, atomic hopping mobility, and anharmonicities—for example, thermal conductivity, thermal expansion, melting temperature, nuclear magnetic resonance, and superconducting phase transition temperature. The electronic band structures were once believed to remain identical in isotopes under such changes. However, this belief has been justified only by atomic-spectra data. Evidence has revealed that in the case of molecular spectra, the effect of mass involves differences between isotopes through the mechanism of electron–phonon coupling.1,2 The presence of an isotope effect is an effective indicator of phonon-mediated superconductivity in materials and constitutes support for the Bardeen–Cooper–Schrieffer (BSC) theory of superconductivity.3–5
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tc/d
Tc/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M where M is the atomic mass. The coefficient α was measured in the superconductor MgB2. An analysis of the magnetization data revealed a large boron isotope effect, which indicated superconductivity in this material. The extrapolated Tc exhibited at least 1 K difference between the 11B and 10B samples. The isotope effects from Mg were small compared with the boron isotope effects, which clearly indicated that phonons associated with boron vibrations are crucial in superconductivity. The findings further revealed superconductivity in transition metal diborides (i.e. NbB2) and borocarbides (e.g., YNi2B2C and LiNi2B2C).4,11 The natural abundance of stable boron isotopes facilitated the assessment of isotopic effects, despite a lack of suitable isotopes for the other elements.
M where M is the atomic mass. The coefficient α was measured in the superconductor MgB2. An analysis of the magnetization data revealed a large boron isotope effect, which indicated superconductivity in this material. The extrapolated Tc exhibited at least 1 K difference between the 11B and 10B samples. The isotope effects from Mg were small compared with the boron isotope effects, which clearly indicated that phonons associated with boron vibrations are crucial in superconductivity. The findings further revealed superconductivity in transition metal diborides (i.e. NbB2) and borocarbides (e.g., YNi2B2C and LiNi2B2C).4,11 The natural abundance of stable boron isotopes facilitated the assessment of isotopic effects, despite a lack of suitable isotopes for the other elements.![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d structure which contains BO4 tetrahedrons with Cu2+ ions between them. These Cu2+ ions are located in two inequivalent crystallographic positions (see ESI Fig. 1‡). Various studies reported that CuB2O4 exhibited the unusual magnetoelectric properties and complex magnetic, electric and optical coupling phenomenon.14–17 Notably, CuB2O4 containing 11B and 10B isotopes exhibited no significant shifts in the phase transition temperatures, as demonstrated by the nearly identical magnetic susceptibility illustrated in Fig. 1. This finding contrasted with the large isotope effects identified in high Tc superconductors. Studies on antiferromagnetic cuprates have also revealed negligible oxygen isotope effects in the magnetic phase transition temperatures.18,19
2d structure which contains BO4 tetrahedrons with Cu2+ ions between them. These Cu2+ ions are located in two inequivalent crystallographic positions (see ESI Fig. 1‡). Various studies reported that CuB2O4 exhibited the unusual magnetoelectric properties and complex magnetic, electric and optical coupling phenomenon.14–17 Notably, CuB2O4 containing 11B and 10B isotopes exhibited no significant shifts in the phase transition temperatures, as demonstrated by the nearly identical magnetic susceptibility illustrated in Fig. 1. This finding contrasted with the large isotope effects identified in high Tc superconductors. Studies on antiferromagnetic cuprates have also revealed negligible oxygen isotope effects in the magnetic phase transition temperatures.18,19
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] directions, denoted as Y′ and
0] directions, denoted as Y′ and 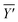 , respectively. Three scattering configurations were thus obtained:
, respectively. Three scattering configurations were thus obtained: 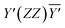 ,
, 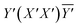 , and
, and 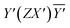 . In this Porto notation, the direction parallel to the crystallographic (c) axis was labelled as Z, whereas the [
. In this Porto notation, the direction parallel to the crystallographic (c) axis was labelled as Z, whereas the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] crystal direction was labelled as X′. The sample was placed in a continuous-flow helium cryostat, which enabled measurements in the temperature range of 10–300 K.21
10] crystal direction was labelled as X′. The sample was placed in a continuous-flow helium cryostat, which enabled measurements in the temperature range of 10–300 K.21
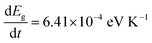 which is a little lower compared to CuB2O4 but still in the same order of magnitude with those found for MAPbI3.25 Below 21 K, the band gap exhibited a gradual increase as the temperature decreased. This anomaly and discontinuity were correlated with the magnetic ordering at this temperature point. These findings demonstrate that the shifts were caused by spin–charge interactions, rather than changes induced by thermal contraction or alterations in the unit cell volume.
which is a little lower compared to CuB2O4 but still in the same order of magnitude with those found for MAPbI3.25 Below 21 K, the band gap exhibited a gradual increase as the temperature decreased. This anomaly and discontinuity were correlated with the magnetic ordering at this temperature point. These findings demonstrate that the shifts were caused by spin–charge interactions, rather than changes induced by thermal contraction or alterations in the unit cell volume.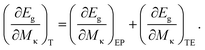
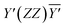 ,
, 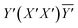 , and
, and 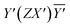 polarizations were identical to those observed in CuB2O4 in the same configurations. The phonon peaks and their assigned symmetries are summarized in Table 1. We assigned the phonon peaks of Cu11B2O4 to the same atomic vibrations assigned to CuB2O4. Low-frequency modes below 200 cm−1 were rotational vibrations of Cu ions. Peaks higher than 200 cm−1 but lower than 400 cm−1 were modes associated with changes in the bond angles that tilted and bent the BO4 tetrahedra. These phonon peaks were coupled to the Cu–O vibrations, which were distributed over the entire frequency range. The highest vibrations from Cu–O stretching modes were observed in the range of 400–900 cm−1. The Cu–O stretching modes in the range 700–900 cm−1 were mixed with the B–O vibrations, whereas modes above 900 cm−1 were considered to have occurred mainly from B–O stretching vibrations. Our experimental results of the phonon modes demonstrated good agreement with the theoretical ab initio calculations by Pisarev et al.32 The data on the isotope boron effects, summarized in Table 1, elucidates the coupling involved in the phonon vibrations occurring primarily between Cu and B.
polarizations were identical to those observed in CuB2O4 in the same configurations. The phonon peaks and their assigned symmetries are summarized in Table 1. We assigned the phonon peaks of Cu11B2O4 to the same atomic vibrations assigned to CuB2O4. Low-frequency modes below 200 cm−1 were rotational vibrations of Cu ions. Peaks higher than 200 cm−1 but lower than 400 cm−1 were modes associated with changes in the bond angles that tilted and bent the BO4 tetrahedra. These phonon peaks were coupled to the Cu–O vibrations, which were distributed over the entire frequency range. The highest vibrations from Cu–O stretching modes were observed in the range of 400–900 cm−1. The Cu–O stretching modes in the range 700–900 cm−1 were mixed with the B–O vibrations, whereas modes above 900 cm−1 were considered to have occurred mainly from B–O stretching vibrations. Our experimental results of the phonon modes demonstrated good agreement with the theoretical ab initio calculations by Pisarev et al.32 The data on the isotope boron effects, summarized in Table 1, elucidates the coupling involved in the phonon vibrations occurring primarily between Cu and B.

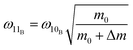
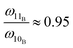 which accords with the observed redshift in the high-frequency Raman modes (Table 1). For frequencies below 900 cm−1, we obtained ω11B/ω10B ratio of approximately 0.99. For frequencies above 900 cm−1, the ratio was approximately 0.95 for ω36 and ω37, with the largest possible shift of 59 cm−1. These modes are thus confirmed to be pure B vibrations. Modes below 200 cm−1 exhibited the smallest shift in frequency because these peaks mostly originated from the Cu atom vibrations. The shifts in frequency, which were 200–900 cm−1, exhibited differences of approximately 1–2 cm−1. This finding indicates that the boron atoms influence these vibrational modes. High-frequency peaks above 900 cm−1 exhibited more obvious softening in the phonon frequencies shifting by at least 16 cm−1. We observed a clear double peak constituted by ω37 (1057 cm−1) and ω38 (1107 cm−1) because of the nonuniform shift in the peaks, which contrasted with the overlapping peaks observed in CuB2O4. The phonon frequency ω38 most likely resulted from oxygen stretching vibrations. We surmise this because it is not heavily shifted with isotopic substitution, similar to other phonon modes in this range.
which accords with the observed redshift in the high-frequency Raman modes (Table 1). For frequencies below 900 cm−1, we obtained ω11B/ω10B ratio of approximately 0.99. For frequencies above 900 cm−1, the ratio was approximately 0.95 for ω36 and ω37, with the largest possible shift of 59 cm−1. These modes are thus confirmed to be pure B vibrations. Modes below 200 cm−1 exhibited the smallest shift in frequency because these peaks mostly originated from the Cu atom vibrations. The shifts in frequency, which were 200–900 cm−1, exhibited differences of approximately 1–2 cm−1. This finding indicates that the boron atoms influence these vibrational modes. High-frequency peaks above 900 cm−1 exhibited more obvious softening in the phonon frequencies shifting by at least 16 cm−1. We observed a clear double peak constituted by ω37 (1057 cm−1) and ω38 (1107 cm−1) because of the nonuniform shift in the peaks, which contrasted with the overlapping peaks observed in CuB2O4. The phonon frequency ω38 most likely resulted from oxygen stretching vibrations. We surmise this because it is not heavily shifted with isotopic substitution, similar to other phonon modes in this range.
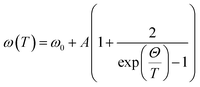
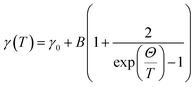

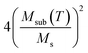 where Msub(T) is the sublattice magnetization per magnetic ion and Ms is the saturation magnetization. The factor of 4 was based on the number of nearest neighbors.34 As displayed in Fig. 8, the sublattice magnetization data13 obtained from a prior study scaled well with the shift in phonon frequency. Using this correlation, we extracted the spin–phonon coupling constant λ for Cu–O stretching phonon modes tabulated in Table 3.
where Msub(T) is the sublattice magnetization per magnetic ion and Ms is the saturation magnetization. The factor of 4 was based on the number of nearest neighbors.34 As displayed in Fig. 8, the sublattice magnetization data13 obtained from a prior study scaled well with the shift in phonon frequency. Using this correlation, we extracted the spin–phonon coupling constant λ for Cu–O stretching phonon modes tabulated in Table 3.