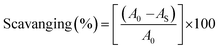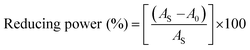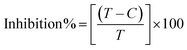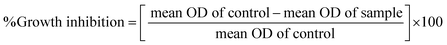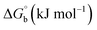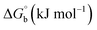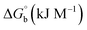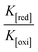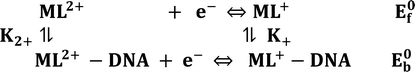DOI:
10.1039/C8RA09218D
(Paper)
RSC Adv., 2019,
9, 14220-14241
Spectro-electrochemical assessments of DNA/BSA interactions, cytotoxicity, radical scavenging and pharmacological implications of biosensitive and biologically active morpholine-based metal(II) complexes: a combined experimental and computational investigation†
Received
8th November 2018
, Accepted 7th April 2019
First published on 7th May 2019
Abstract
Biosensitive and biologically active morpholine-based transition metal(II) complexes (1–5) were constructed as [MII(L) AcO]·nH2O {where M = Cu (1) n = 1; Co (2), Mn (3), Ni (4), n = 4 and Zn (5) n = 2}, which were synthesized from 2-(-(2-morpholinoethylimino) methyl)-4-bromophenol ligand (HL) and structurally characterized by various analytical and spectroscopic techniques, which proposed a square planar and tetrahedral geometry around the central metal ion with lattice water molecules. The gel electrophoresis results revealed that complexes 1 and 5 had more potent DNA cleavage efficacy in the presence of an oxidizing agent (H2O2) as compared to the others. The observed DNA binding results for all the compounds as determined by spectro-electrochemical and hydrodynamic techniques were in the order 3.36 (1) > 3.06 (2) > 2.73 (4) > 2.61 (5) > 1.84 (3) > 1.00 (HL) × 104 M−1. The obtained bovine serum albumin (BSA) protein binding constant (Kb) results put forward the following order 2.38 (1) > 2.21 (2) > 2.18 (5) > 1.76 (4) > 1.40 (3) > 1.26 (HL) × 104 M−1. Also, the biothermodynamic parameters (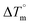 ,
, 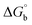 , ΔH° and ΔS°) and binding results divulged that all the complexes (1–5) could bind to DNA via intercalation in a spontaneous manner. Density functional theory calculations were employed to optimize the structure of ligand (HL) and its complexes (1–5) to gain insights into their electronic structures. Molecular docking analysis was carried out to identify the preferential binding modes of these complexes toward DNA and BSA protein. The theoretical observations of all cases were found to be very close to the experimental observations. Among the radical scavenging activity results for all the cases toward DPPH, hydroxyl radical, superoxide, nitric oxide and ferric reducing agents, complex (1) revealed a superior scavenging potency over the other compounds. In the screened antimicrobial reports against 10 different selected pathogenic species, although all the complexes (1–5) exhibited a greater significant inhibitory effect than the free ligand, complexes 4 and 5 achieved the best potency over standard drugs. The observed percentage of growth inhibition for all the compounds against the A549, HepG2, MCF-7 and NHDF cell lines suggested that complex 1 had enhanced growth-inhibitory potency over the other compounds and slightly affected normal cells as compared to the standard drug cisplatin, which may lead to its investigation as a promising anticancer agent in future research.
, ΔH° and ΔS°) and binding results divulged that all the complexes (1–5) could bind to DNA via intercalation in a spontaneous manner. Density functional theory calculations were employed to optimize the structure of ligand (HL) and its complexes (1–5) to gain insights into their electronic structures. Molecular docking analysis was carried out to identify the preferential binding modes of these complexes toward DNA and BSA protein. The theoretical observations of all cases were found to be very close to the experimental observations. Among the radical scavenging activity results for all the cases toward DPPH, hydroxyl radical, superoxide, nitric oxide and ferric reducing agents, complex (1) revealed a superior scavenging potency over the other compounds. In the screened antimicrobial reports against 10 different selected pathogenic species, although all the complexes (1–5) exhibited a greater significant inhibitory effect than the free ligand, complexes 4 and 5 achieved the best potency over standard drugs. The observed percentage of growth inhibition for all the compounds against the A549, HepG2, MCF-7 and NHDF cell lines suggested that complex 1 had enhanced growth-inhibitory potency over the other compounds and slightly affected normal cells as compared to the standard drug cisplatin, which may lead to its investigation as a promising anticancer agent in future research.
Introduction
Cancer is one of humanity's greatest health challenges today as it is the second leading cause of death globally behind cardiovascular diseases, accounting for the deaths of more than 9.6 million people from an estimated 18.1 million cancer cases around the world in 2018, with 9.5 million of these cases being in men and 8.6 million in women.1 According to WHO estimates, this number is expected to increase to over 14.5 million deaths from an estimated 24 million cancer cases by 2035.2,3 That is nearly 1 in 6 of global deaths due to cancer, with approximately 70% of cancer deaths occurring in poor and less developed countries. For instance, one woman dies by cervical cancer every 8 min and one woman dies for every two women newly diagnosed with breast cancer in India.4 As per the most recent globally estimated reports in 2018, nearly 400 types of cancers were recorded, with 28 types mostly seen as a problematic burden every day. In particular, lung (2.09 million), breast (2.09 M), colorectal (1.80 M), prostate (1.28 M), non-melanoma skin (1.04 M) and stomach (1.03 M) cancers are the top 5 deadliest cancers in the world.1,5,6 Despite the majority of anticancer drugs currently available for the conventional chemotherapeutic treatments of human cancers being platinum based, there is still no standard amicable scientific solution to date because of the poor efficacy, non-selectivity and high toxicity of such drugs, which results in many inherent limitations, like neurotoxicity, nephrotoxicity, ototoxicity, tissue toxicity, peripheral neuropathy, thrombocytopenia, neutropenia, nausea, emetogenesis and myelosuppression due to their interaction with DNA via covalent binding.7,8 As a result, people are continuously affected with heavy mental stress and strain across the world. Researchers are thus accelerating their efforts to invent novel synthetic roots to address the many challenges involved in the “war on cancer”. In today's critical situation, there is an indispensable need to replace current drugs with appropriate alternatives to resolve the current limitations and to further the development and screening of potential anticancer agents with innovative strategies for the synthesis of less toxic alternatives, and to further identify potent and target specific drugs, which may preferably include non-covalent interactions.9
Nowadays, novel cancer treatment approaches, like immunotherapy, have significantly raised hope among the various treatments.10 According to the concept and its mechanism reported by the 2018 Nobel laureates James P. Allison and Tasuku Honjo, human immune cells have checkpoints proteins, such as cytotoxic T-lymphocyte-associated antigen 4 receptors (CTLA-4 protein) and programmed cell death protein 1 (PD-1/PD-L1/PD-L2), which are negative regulators and function as a brake on the immune system. They also help to conserve the T cells from attacking foreign/other cells. Hence, the proliferation of cancer cells may be controlled/prevented by stimulating the inherent ability of the checkpoint proteins of our immune T cells. The activated T cells can penetrate into the tumour environment and release the cytotoxins after binding with the recognised cancer cells, which helps to induce apoptosis in their target cancer cells. Several immune checkpoint inhibitors, including radiolabelled or chemolabelled (chemo drug/anticancer active metal complex incorporated antibodies) monoclonal specific and bispecific antibodies, can be used in targeted therapy to block abnormal protein in cancer cells and to induce T cell immunity. Also, immune checkpoint therapy has revealed a great deal of promise for reducing side effects and such therapy is currently undergoing clinical trials.11,12 Hence, much research work has been performed in this field, which has also recommended that Schiff base/metal complex-labelled antibodies can be used in cancer treatment for chemolabelled immunotherapy in the future.
Moreover, biosensitive and biologically active morpholine-based gefitinib and linezolid possess significant cytotoxic and antibiotic potencies, respectively. The derivatives inhibit the growth of tumour cells, while the effect on normal cells was considerably lower due to them having cell selective effects, specifically in terms of inhibiting the proliferation of cancer cells at low concentration. The morpholine-based ligands and their metal complexes also possess enhanced biological potencies, such as anticancer, anticonvulsant, antiproliferative, antiinflammatory, antimicrobial and antidiabetic.13,14 Numerous literature survey reports have reported transition metal complexes utilized in the probes for DNA structure and as chemotherapeutic agents. DNA and proteins are the foremost cellular targets for cytotoxicity due to the interaction between small molecules and DNA, which can cause DNA damage in cancer cells by blocking the division of cancer cells, resulting in cell death.15 Bovine serum albumin (BSA) is one of the key components of blood plasma, and possesses 76% sequence homology similarities with human serum albumin (HSA). Each BSA molecule contains two tryptophan (Trp) residues with a self-fluorescence emission nature and it is widely used as a model protein to predict the interaction features of suitable anticancer drugs.16 Some enzymatic endogenous and non-enzymatic exogenous antioxidants are essential biocatalysts and play a protective role as body cellular constituents to protect against the oxidative stress/damage generated by reactive oxygen (ROS) and reactive nitrogen species (RNS) in normal and different pathological conditions, whereby they convert the dangerous oxidative product into a harmless molecule by donation of a hydrogen or electron to the free radicals.17 When the production of highly reactive free radicals and oxygen species exceed the scavenging capacity of the cell's endogenous systems in the respiration and cell-mediated immune functions of the metabolic process, the free radicals can attack specific biomolecules, such as proteins, lipids and DNA, for stabilizing themselves through electron pairing. The pairing of free radicals with biomolecules can result in the induction of lipid peroxidation and prolonged oxidative stress, which could eventually lead to many chronic diseases. Hence, the number of antioxidant studies seeking to overcome such diseases has accelerated recently.18 Molecular docking analysis has gained special attention for understanding the nature of stabilizing interactions, the active site environment and the binding modes of DFT-optimized chemical entities towards DNA and BSA protein and plays a vital role in rational drug design.19,20 In this report, the copper complex (1) demonstrated superior biological potency as compared to the other complexes, and it may have potential as an anticancer leading agent in future research.
Experimental
Materials and methods
All the required chemicals and other reagents were procured from Sigma Aldrich Company. The ligand (HL) and its complexes (1–5) were characterized using a Bruker 300 MHz 1H NMR spectrometer, Bruker Avance III HD Nanobay 400 MHz 13C NMR, Shimadzu FT-IR spectrometer, Shimadzu UV Vis 1800, Varian E112 EPR spectrometer. More detail are given in our previous report.21
Synthesis of the Schiff base ligand (HL) and its complexes (1–5)
Details of the synthesized ligand (HL) and its complexes (1–5) together with information from the various structural characterization studies are enclosed in the ESI† (Scheme 1).
 |
| | Scheme 1 The proposed structure of complexes 1–5 [MII(L) AcO]·nH2O. | |
DNA/BSA interaction studies
Nuclease activity by gel electrophoresis. Agar-gel electrophoresis experiments were carried out for all the compounds with CT-DNA in the presence of H2O2 in Tris–HCl buffer solution (pH 7.2) (Fig. 1). Finally, the gel layer was isolated from the tank solution and snapped under a UV transilluminator. The migrated band lanes were clearly analyzed and compared with the control (DNA + H2O2).22
 |
| | Fig. 1 Gel electrophoresis showing the chemical nuclease activity of CT-DNA by the synthesized ligand (HL) and its complexes (1–5) in the presence of hydrogen peroxide. Lane 1: DNA alone + H2O2; lane 2: ligand [HL] + DNA + H2O2; lane 3: complex (1) + DNA + H2O2; lane 4: complex (2) + DNA + H2O2: lane 5: complex (3) + DNA + H2O2; lane 6: complex (4) + DNA + H2O2; lane 7: complex (5) + DNA + H2O2. | |
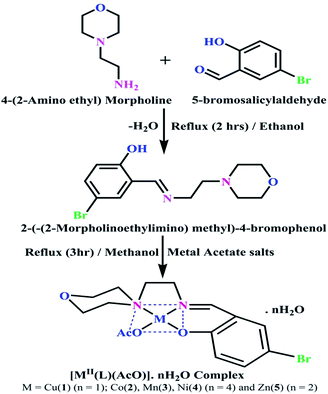
DNA binding properties by absorption titrations. Electronic absorption titrations were carried out at a fixed complex concentration (10−4 M/100 μM) in aqueous media at 25 °C by varying the concentration of DNA (0–150 μM) and the DNA purity, with its concentration checked in Tris–HCl buffer (5 mM Tris–HCl/50 mM NaCl, pH = 7.2) solution. The ratio of the absorbance at 260 and 280 nm was about 1.8–1.9, which indicates that the DNA was sufficiently free from the protein. Also, the DNA concentration per nucleotide and polynucleotide was determined with the help of the molar extinction coefficient (6600 M−1 cm−1) at 260 nm.23 With increasing the concentration of DNA in the complexes (1–5) solution, the decrease in absorbance was carefully monitored until full binding was achieved (Fig. 2 and S12†), with the results listed in Table 1.
 |
| | Fig. 2 Absorption spectra of the ligand (HL) and its complexes (1–5) in Tris–HCl buffer pH = 7.2 at 25 °C in the presence of an increasing amount of CT-DNA. Arrow indicates the changes in absorbance upon increasing the CT-DNA concentration. | |
Table 1 Absorption spectral parameters of the ligand (HL) and its complexes (1–5) bound to CT-DNAa
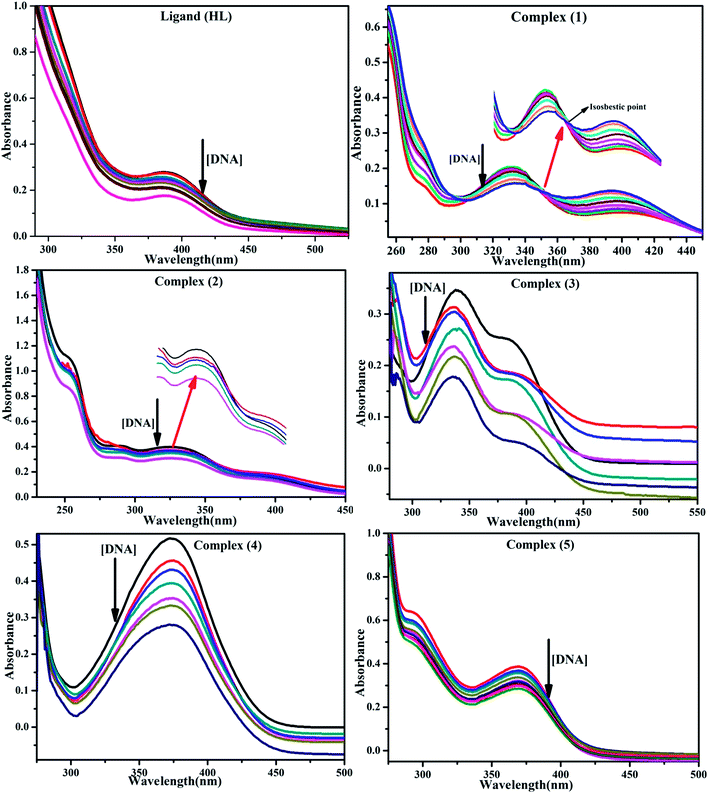
BSA binding assay by absorption titrations. Electronic absorption titrations were carried out at a fixed bovine serum albumin (BSA) concentration (10−4 M/100 μM) in aqueous media (pH = 7.2) at 25 °C by varying the concentration of ligand (HL) and its complexes (1–5) (0–100 μM). BSA is characterized by a strong absorption band in the UV region at 278 nm (Fig. 3 and Table 2). Here, the addition of the respective compound led to a gradual increase in the BSA absorption band, and the observed hyperchromism with a blue-shift designated that structural changes had occurred due to non-covalent interactions of the compound with BSA.24
 |
| | Fig. 3 Absorption spectra of BSA alone and in the presence of increasing amounts of the ligand (HL) and its complexes (1–5) in Tris–HCl buffer pH = 7.2 at 25 °C. Arrow indicates the changes in absorbance upon increasing the compound concentration. Inset: Benesi–Hildebrand linear plot [(A∞ − A0)/(Ax − A0)] versus 1/[compound] determining the binding constant for the ligand (HL) and its complexes (1–5) – DNA at 298 K. | |
Table 2 Absorption spectral parameters of the ligand (HL) and its complexes (1–5) bound to BSAa
DNA thermal denaturation properties by absorption titrations. The thermal denaturation properties can provide strong evidence for interactions between complexes and the DNA double helix. DNA denaturation is the separation of a double strand into two single strands at elevated temperature, where, Tm demonstrates the transition between double-stranded and single-stranded nucleic acid. Tm also denotes that 50% of DNA is in a denaturalized single-stranded state and the other 50% of DNA is in a native double-stranded state.25 The denaturation of proteins and nucleic acids directly depends on Tm, pH and the nonphysiological concentrations of the salt, organic solvents and other chemical agents, etc. When the temperature or pH increases, the DNA double helix splits into two single strands, which is attributed to the breaking of hydrophobic stacking attractions as well as the breaking of hydrogen bonds between the DNA bases due to the hydroxide ions (OH− ions) pulling the hydrogen ions (H+) from the DNA base pairs. This leads to increasing the absorbance (i.e. a hyperchromic shift) at 260 nm. The rate of increase in absorbance is directly proportional to the rate of denaturation, while the viscosity is inversely proportional to the rate of denaturation. On the other hand, a low salt concentration could also denature DNA double-strands by removing ions that stabilize the negative charges on the two strands from each other. Here, the experiments were carried out in the absence and presence of the compounds using a Shimadzu UV-Vis spectrophotometer 1800 unit equipped with a temperature-controlled sample cell holder. The ligand (HL) and its complexes (1–5) were incubated with CT-DNA at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio {[DNA]/[complex] = (R)1} in 5 mM Tris–HCl/50 mM NaCl buffer (pH = 7.2) solution and the solution was heated from 25 °C to 100 °C at a temperature rate of 2 °C per minute and the absorbance changes at 260 nm continuously monitored26 (Fig. S13† and Table 3). A decrease in DNA absorbance was observed in the presence of the metal complexes (1–5) due to strong intercalation in the DNA–complex adducts.
1 ratio {[DNA]/[complex] = (R)1} in 5 mM Tris–HCl/50 mM NaCl buffer (pH = 7.2) solution and the solution was heated from 25 °C to 100 °C at a temperature rate of 2 °C per minute and the absorbance changes at 260 nm continuously monitored26 (Fig. S13† and Table 3). A decrease in DNA absorbance was observed in the presence of the metal complexes (1–5) due to strong intercalation in the DNA–complex adducts.
Table 3 Thermodynamic profiles of the electronic absorption spectra for the binding of the ligand (HL) and its complexes (1–5) to CT-DNAa
| Compounds |
Tm (K) |
ΔTm (K) |
Binding constant Kr at 298 K × 104 (M−1) |
Binding constant Km at Tm K × 103 (M−1) |
ΔH° (kcal mol−1) |
ΔS° (cal mol−1) |
ΔG° (kcal mol−1) |
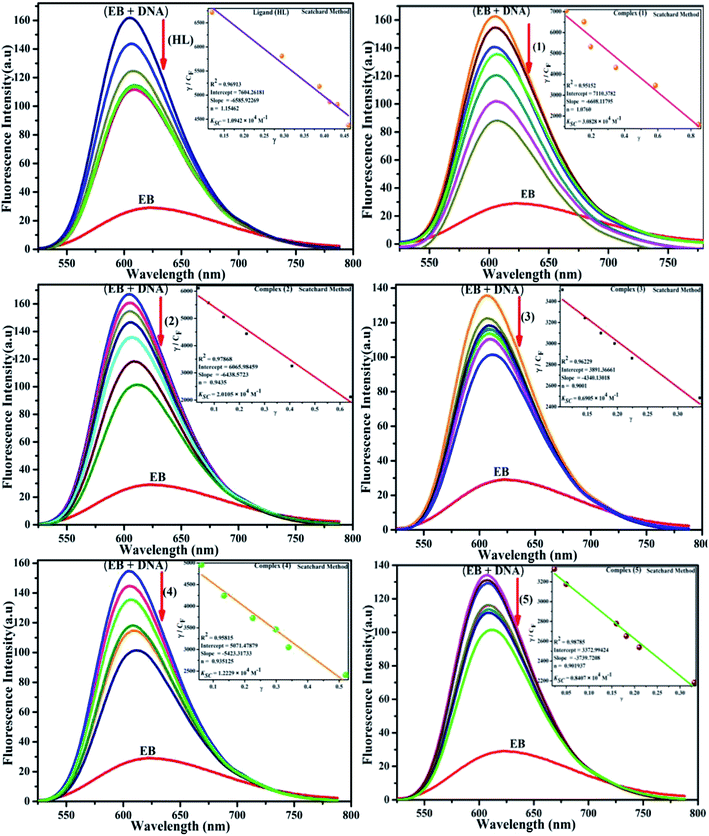
CT-DNA melting temperature (Tm) = 337 K; ΔTm = melting temperature changes between complexes and DNA alone in the thermal denaturation experiments; enthalpy change 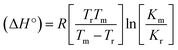 , Tr = 298 K, Tm = DNA melting temperature of compounds, R = universal gas constant = 1.987 cal K−1 mol−1; Gibb's free energy (ΔG°) = −RTm , Tr = 298 K, Tm = DNA melting temperature of compounds, R = universal gas constant = 1.987 cal K−1 mol−1; Gibb's free energy (ΔG°) = −RTm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Km; entropy change Km; entropy change 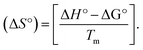 |
| (HL) |
341 |
277 |
1.0038 |
2.1254 |
−7.2270 |
−5.9697 |
−5.1913 |
| (1) |
351 |
287 |
3.4297 |
4.8152 |
−7.6988 |
−0.5100 |
−7.5198 |
| (2) |
348 |
284 |
3.0619 |
4.2021 |
−8.1848 |
−2.3660 |
−7.3614 |
| (3) |
344 |
280 |
1.8469 |
3.0542 |
−7.9686 |
−2.6455 |
−7.0586 |
| (4) |
346 |
282 |
2.7349 |
4.1488 |
−8.0493 |
−2.1358 |
−7.3103 |
| (5) |
347 |
283 |
2.6126 |
3.9249 |
−7.9486 |
−1.8891 |
−7.2931 |
DNA binding study by viscometry titration. Hydrodynamic volume measurements afforded information about the interaction modes between the complex and DNA. However, it did not provide conclusive evidence of the precise mode of binding. The titrations were executed for the ligand (HL), complexes (1–5) and ethidium bromide (control) at different concentrations of 20, 40, 60, 80, 100 μM (10−4 M), with each compound blended with the CT-DNA solution (10−4 M/100 μM) in an Ostwald viscometer (Fig. 4 and Table S7†). The average flow time was measured by a digital stopwatch with an accuracy of 0.01 s. The classical intercalative mode causes a considerable increase in viscosity of DNA solution due to an enhancement of the overall contour length of DNA during the separation of base pairs at intercalation sites. In general, if the compounds bind with DNA base pairs through major/minor grooves, they may cause a less positive/negative or even no change in viscosity.27 It is well-known that the viscosity of DNA increases when it interacts with metal complexes (e.g. complexes 1–5) via intercalation.
 |
| | Fig. 4 Relative specific viscosities of CT-DNA in the presence of increasing amounts of the ligand (HL), its complexes (1–5) and ethidium bromide (EB) at 25 °C in 5 mM Tris–HCl buffer at pH = 7.2. | |
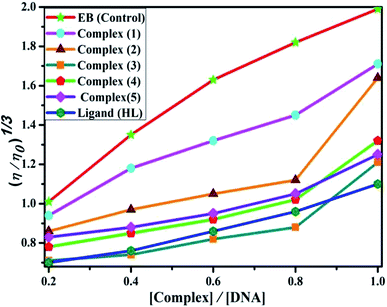
Competitive binding assay by fluorescence spectra. The fluorescence spectral titration was performed using a JASCO FP-6300 spectrofluorometer in the range 200–800 nm to further confirm the binding mode of the complexes (1–5) to DNA. Ethidium bromide (EB) was used as a reference to determine the relative DNA binding properties of the complex to CT-DNA in 50 mM Tris–HCl/1 mM NaCl buffer (pH 7.2) solution. The intensity changes for the initial emission and excitation of ethidium bromide were carefully monitored from 610 nm to 510 nm in the absences and presence of DNA (100 μM) (Fig. 5, S14† and Table 4). EB is a conjugate planar molecule and its fluorescence intensity is very weak, but it is greatly raised when EB is intercalated with DNA base pairs. When the concentrations of the test compounds increased (0–120 μM), the intensity of the EB–DNA system decreased due to the quenching effect of DNA by static quenching. This can also be attributed to the formation of the ground-state DNA–complex adduct due to the cationic metal complexes binding with the negatively charged oxygen of the phosphodiester of DNA, where the contraction of DNA drives a few EB molecules out of the DNA base pairs.28
 |
| | Fig. 5 Fluorescence quenching curve of EB-bound DNA in the presence of the ligand (HL) and its complexes (1–5). [DNA] = 100 μM, [complex] = 0–120 μM. Inset: Scatchard plot determining the association of the binding constant and the number of binding sites for the ligand (HL) and its complexes (1–5) to DNA. | |
Table 4 Binding constants and binding sites for the interaction of the ligand (HL) and its complexes (1–5) with EB–DNA at pH = 7.4 from ethidium bromide displacement assay by fluorescence spectral titrationa
DNA binding parameters by electrochemical analysis. Cyclic voltammetry is an essential tool to investigate the electron-transfer reactions of complexes. A CHI 620C electrochemical analyzer with a three-electrode system comprising a glassy carbon (working electrode), Ag/AgCl (reference electrode) and platinum wire (counter/auxiliary) electrode was used to monitor the change of peak current and peak potential during the interaction between the complexes and DNA at a scan rate of 0.1 V. The changes of peak current and peak potential also provide information on the binding constant and mode of interaction for the complex–DNA adduct. The cyclic voltammetric titrations for all the complexes were performed at room temperature in the absence and presence of CT-DNA in single-compartment cells of 5–15 mL and the solutions were deoxygenated by passing through N2 prior to the measurements (Fig. S15†). The experiments for the free complexes were carried out at 10 μM concentration in the presence of 5 mM Tris–HCl/50 mM NaCl (pH = 7.2) buffer solution. When the concentration of CT-DNA increased from 2 to 10 μM into each solution of the complexes (1–5), the changes of the anodic and cathodic peak current and potential shifts were recorded29 and the observed results are listed in Table 5.
Table 5 Redox potential profiles for the interaction of CT-DNA with complexes 1–5a
| Complex |
ΔEP (V) |
E1/2 (V) |
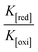
|
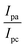
|
D0 × 10−4 cm2 s−1 |
Kb × 104 M−1 |
S (bp) |
| Free |
Bound |
Free |
Bound |
Free |
Bound |
I |
II |
| ΔEP = peak-to-peak separation = (EPa − EPc), E° (or) E1/2 = formal electrode potential = ½(EPa + EPc), D0 = diffusion coefficient of the M(II)/M(I) couple in the free and bound forms, respectively, Ipa = anodic peak current, Ipc = cathodic peak current, K+ = binding constant of reduction process, K2+ = binding constant of oxidation process, S = binding site size (base pairs, bp), scan rate = 100 mV s−1, I = method-I for the plot of Ip2 vs. (Ipo2 − Ip2)/[DNA], II = method-II for the plot of of Cp/Cf vs. [DNA]. |
| (1) |
−0.799 |
−0.218 |
0.550 |
0.545 |
0.823 |
0.980 |
1.951 |
1.760 |
6.805 |
2.098 |
1.068 |
| (2) |
−0.212 |
−0.144 |
0.138 |
0.136 |
0.925 |
0.815 |
1.920 |
1.882 |
5.247 |
1.585 |
1.295 |
| (3) |
−0.333 |
−0.244 |
0.231 |
0.228 |
0.889 |
1.007 |
2.127 |
2.026 |
4.890 |
1.166 |
1.088 |
| (4) |
−0.247 |
−0.460 |
0.282 |
0.277 |
0.823 |
0.985 |
1.233 |
1.153 |
6.759 |
1.241 |
1.503 |
| (5) |
−0.029 |
−0.038 |
0.170 |
0.164 |
0.792 |
0.912 |
2.495 |
2.266 |
3.183 |
1.181 |
1.255 |
Molecular modelling studies. Gaussian 09 software was used to optimize the ligand (HL) and the synthesized complexes (1–5). As reported in the literature, the B3LYP/6-31g(d) level was used for the geometry optimization. During geometry optimization, the metal atoms were treated at the LANL2DZ level, while H, C, N, O and Br atoms were treated at the 6-31g(d) level.30 The optimized geometries are given in Fig. 6. No imaginary frequencies in the frequency analysis were obtained, which confirmed that the optimized geometries were at their ground state. It is well known that the chemical reactivity and stability can be understood from Frontier molecular orbitals (FMO) analysis and hence FMO analysis was performed here on the optimized geometries (Fig. S16 and S17†).31,32 The crystal structure of the duplex DNA d(CGCGAATTCGCG)2 dodecamer (PDB:355D) and the structure of bovine serum albumin (BSA) protein (PDB ID:4F5S) were extracted from the Protein Data Bank (PDB).33,34 The Auto Dock Vina program was used for the molecular docking analysis.35 A grid box with a size of 60, 60 and 60 along the X-, Y- and Z-axes was used for the molecular docking.
 |
| | Fig. 6 DFT optimized geometry of the ligand (HL) and its complexes (1–5). | |
In vitro antioxidant assay. The scavenging activities at different concentrations of 4, 8, 12, 16, 20, 25 × 10−5 M of ligand (HL) and complexes (1–5) were evaluated by an absorption technique. The IC50 values of ligand (HL) and complexes (1–5) were compared with standard ascorbic acid (Fig. 9a–e and a1–e1) and the results are summarized in Table S8(a–e).† The antioxidant studies for DPPH, hydroxyl, superoxide, nitric oxide radical scavenging and ferric reducing antioxidant power (FRAP) assay were carried out with careful monitoring of the absorbance at 517, 230, 590, 546 and 700 nm, respectively.21
In vitro antimicrobial assay. Antimicrobial activities of all the compounds were screened against seven selected different pathogenic bacteria and three different fungi species by the Kirby–Bauer agar disc diffusion method36 (Table 6). According to this method, Mueller–Hinton nutrient agar was prepared from the following constituents: beef infusion (300 g), acid hydrolysate of casein (17.5 g), starch (1.5 g) and agar (17 g) dissolved in one litre distilled water. The resulting mixture was warmed on a water bath till the agar dissolved and was then sterilized in an autoclave at 15 lb pressure and 121 °C for 15 min. Generally, the agar medium should be maintained at pH 7.2 at room temperature after gelling. If the pH is too low, certain drugs/complexes may lose or exceed potency. If the pH is too high, the opposite effects may occur. 20 mL of autoclaved Mueller–Hinton nutrient agar medium was poured up to an approximately 4 mm depth onto 100 mm flat-bottomed sterilized glass/plastic Petri plates while still molten and swabbed uniformly across a culture plate, allowing them to solidify on a plane table. The agar medium was placed in a refrigerator (2 °C to 8 °C) for 24 h. The Petri plates containing 20 mL Mueller–Hinton medium were seeded/streaked with 24 h culture of bacterial and fungal strains. Filter paper discs approximately 6 mm in diameter were impregnated with a specific 20 μL of the test compounds (100 μM) and placed on the dried surface of the agar medium inoculated with the target microorganisms by the spread plate method. The test compounds diffuse from the filter paper into the agar. Each disc was pressed down to ensure complete contact with the agar surface and the sealed packages of plates were stored in an incubator at 37 °C for the bacteria and 22 °C for the fungal strains. The diameter of clear zone inhibition was measured under the bottom of the plate with the help of a ruler after 48 h incubation for the bacteria and 7 days for the fungal strains (Fig. S18 and S19†) and the results are listed in Table 6. The observed clearance zone results also were compared with standard antibacterial drugs amikacin, streptomycin and antifungal drugs ketokonazole, amphotericin B.
Table 6 Evaluation of the antimicrobial activities (diameter of clear zone inhibition in mm) (inhibition%) of the ligand (HL) and its complexes (1–5)a
| S. no. |
Compounds |
Antibacterial activity |
Antifungal activity |
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
| A = (−) Escherichia coli, B = (−)Salmonella enteric serovar typhi, C = (−)Chromobacterium violaceum, D = (−)Pseudomonas aeruginosa, E = (−)Shigella flexneri, F = (+)Staphylococcus aureus, G = (+)Bacillus cereus, H = Aspergillus niger, I = Candida albicans, J = Mucor indicus. Standard drugs for bacterial strains: amikacin & streptomycin. Standard drugs for fungal strains: ketokonazole & amphotericin B [control (DMSO) = 6 mm]. |
| 1 |
Ligand (HL) |
14 (57) |
12 (50) |
12 (50) |
12 (50) |
17 (65) |
10 (40) |
10 (40) |
25 (76) |
12 (50) |
17 (65) |
| 2 |
Complex (1) |
18 (67) |
16 (63) |
14 (57) |
17 (65) |
22 (73) |
18 (67) |
14 (57) |
26 (77) |
14 (57) |
19 (68) |
| 3 |
Complex (2) |
17 (65) |
13 (54) |
16 (63) |
13 (54) |
17 (65) |
15 (60) |
15 (60) |
20 (70) |
10 (40) |
15 (60) |
| 4 |
Complex (3) |
19 (68) |
16 (63) |
17 (65) |
15 (60) |
20 (70) |
13 (54) |
17 (65) |
26 (77) |
16 (63) |
12 (50) |
| 5 |
Complex (4) |
29 (79) |
28 (78) |
16 (63) |
19 (68) |
27 (78) |
22 (73) |
23 (74) |
28 (78) |
25 (76) |
26 (77) |
| 6 |
Complex (5) |
28 (78) |
24 (75) |
15 (60) |
17 (65) |
29 (80) |
19 (68) |
26 (77) |
30 (80) |
27 (78) |
29 (79) |
| Amikacin |
22 (73) |
22 (73) |
24 (75) |
20 (70) |
20 (70) |
20 (70) |
20 (70) |
— |
— |
— |
| Streptomycin |
24 (75) |
26 (77) |
24 (75) |
21 (71) |
25 (76) |
21 (71) |
21 (71) |
— |
— |
— |
| Ketokonazole |
— |
— |
— |
— |
— |
— |
— |
16 (63) |
18 (67) |
18 (67) |
| Amphotericin B |
— |
— |
— |
— |
— |
— |
— |
15 (60) |
17 (65) |
17 (65) |
In vitro anticancer study by MTT assay. The in vitro anticancer profiles were determined for the ligand (HL) and its complexes (1–5) against A549, HepG2, MCF-7 and NHDF cell lines by MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) assay37 (Table 7). The MTT assay is a quantitative, sensitive and consistent enzyme-based colorimetric technique that is generally used for assessing the viability, cytotoxicity and proliferation of cells. Axenic cancer cells were seeded in a 96-well plate at a concentration of 1 × 105 cells per well and were incubated at 37 °C under a humidified atmosphere containing 5% CO2 for 24 h and then the cells were further incubated in media containing various concentrations of the test compounds (10–100 μg mL−1 of the ligand (HL) and complexes (1–5) in DMSO). After one day, the cell medium was removed and washed with sterile phosphate buffer saline (PBS), 190 mL RPMI-1640 sodium bicarbonate buffer system [Roswell Park Memorial Institute medium containing biotin, vitamin B12 and p-aminobenzoic acid], which was used to maintain the physiological pH, and 10 mL of the tetrazolium dye (5 mg mL−1) solution was then added to each well and the cells were incubated for an additional 4 h at 37 °C. This meant that the viable cells contained NAD(P)H-dependent oxidoreductase enzymes (nicotinamide adenine dinucleotide phosphate oxidase enzyme complex), which reduce the water-soluble yellow MTT tetrazolium salt into water-insoluble purple-blue-coloured stable formazan crystals. When the cells die, they lose their reducing ability, thus the colour formation serves as a useful and convenient marker of the viable cells. Subsequently, the medium was removed and 100 μL of DMSO was added. After shaking slowly twice for 5 s, the absorbance of the purple blue formazan dye produced by the cells was measured using an ELISA plate reader at 570 nm. The absorbance directly correlates with the number of viable cells. The obtained results (mean OD ± SD) from triplicate wells were used in the calculations to determine the half-maximum inhibitory concentration (IC50) by means of the percentage cell viability/growth inhibition of the test samples and the results were compared with the standard anticancer drug (cisplatin).21,38
Table 7 Cytotoxicity of the ligand (HL), its complexes (1–5) and the standard drug cisplatin against axenic cancer and normal cell linesa
| Compounds |
IC50a (μg mL−1) |
| A549 |
R2 |
HepG2 |
R2 |
MCF-7 |
R2 |
NHDF |
R2 |
| Average IC50 values from at least three independent experiments for drug concentration in μg mL−1 of 50% cell death following 72 h exposure. |
| Cisplatin |
09.62 |
0.9870 |
06.94 |
0.9869 |
06.11 |
0.9834 |
08.08 |
0.9916 |
| (1) |
21.42 |
0.9847 |
22.68 |
0.9912 |
20.47 |
0.9824 |
58.43 |
0.9972 |
| (2) |
22.67 |
0.9846 |
23.21 |
0.9875 |
23.82 |
0.9892 |
58.17 |
0.9987 |
| (3) |
26.24 |
0.9871 |
25.27 |
0.9902 |
26.11 |
0.9892 |
61.15 |
0.9887 |
| (4) |
24.46 |
0.9902 |
24.26 |
0.9781 |
24.08 |
0.9672 |
59.16 |
0.9891 |
| (5) |
30.45 |
0.9884 |
33.53 |
0.9612 |
35.72 |
0.9848 |
66.45 |
0.9951 |
| (HL) |
31.74 |
0.9943 |
27.48 |
0.9882 |
26.67 |
0.9841 |
66.72 |
0.9843 |
Results and discussions
The synthesized Schiff base ligand (HL) and its complexes (1–5) were intensely coloured with a slightly hygroscopic nature at room temperature and were soluble in methanol, ethanol, CHCl3 and DMSO. The results and discussions of the structural characterization of all cases are provided in the ESI.†
DNA/BSA interaction studies
In general, tumour cells can be destroyed by preventing the replication of the affected DNA. Using the complexes in particular, DNA could be damaged by either following a binding or cleavage approach.
DNA nuclease activity by gel electrophoresis
The DNA cleavage process plays a vital role in all living systems. In particular, helicases and topoisomerase enzymes have nuclease activity and resolve the topological problems of DNA in replication, transcription and other cellular transactions by breaking the hydrogen bonds between DNA double helix nucleotides. When the enzyme dissociates from the DNA strands, the phosphodiester bond reforms due to it being a reversible process. The negative charge of the phosphodiester bond in DNA is highly inert towards hydrolysis through nucleophilic attack under physiological conditions. However, metal ions accelerate nucleophilic attack by water/hydroxide on the phosphate group. Most anticancer drugs depend on their ability to do extended damage to the DNA in the cells. There are also available some classical DNA-cleaving agents, like esperamicin, calicheamicin, dynemicin and neocarzinostatin.39 In general, three different types of DNA cleavage can be distinguished: hydrolytic cleavage (DNA hydrolysis), oxidative cleavage and photochemical cleavage. Oxidative cleavage is generally mediated by H2O2 additives/photostimulated DNA-cleaving agents. The oxidative cleavage mechanism proceeds in three ways, which can take place both at the carbohydrate level and at the nucleic base level by hydrogen abstraction, addition and electron transfer. Hydroxyl radical species (·OH) are generally involved in this oxidative cleavage40 and the redox potential of the metal complex is an imperative parameter for the generation of hydroxyl (·OH) and peroxide radicals (·OOH) under the experimental conditions. Generally, if the redox potentials of the metal ions are low enough in a complex, the metal ions can be easily oxidized to their higher valences, as in the case of the Fenton reaction. The observed DNA cleavage efficiencies of complexes (1–5) were compared with DNA alone (control) and the free ligand. The control (lane 1; DNA + H2O2) did not exhibit significant cleavage even with a longer exposure time, while the ligand (HL) alone (lane 2) was found to be inactive in the presence of H2O2. Lane 3 represented complex 1 and exhibited superior DNA cleavage efficacy compared to the other complexes (2–5) and the ligand (HL), while the disappearance of the band in lane 3 was also displayed in the agarose gel. Lane 7 labelled with complex 5 demonstrated a partial DNA-cleavage potency, while lanes 4–6 with complexes (2–4) showed no significant cleavage efficiency in the series of complexes (Fig. 1). Complex 1 caused vigorous damage to CT-DNA in the presence of diffusible hydroxyl free radicals (·OH), generated by the oxidation of H2O2. According to the Fenton/Haber–Weiss mechanism,41,42 it can be clearly understood that complex 1 acted as a catalyst for the generation of hydroxyl free radicals from H2O2. In addition, the hydroxyl free radical abstracts the hydrogen atom from the sugar moiety of DNA to form a sugar radical, which leads to the hydrolytic cleavage at the sugar–phosphate backbone to discharge specific residues, but it also depends on the position from which the hydrogen atom is being removed. During the gel agarose electrophoresis, the observed fastest migration of DNA with partial cleavage may be attributed to the conversion of the open circular form into linear form, and so the results were also compared with DNA binding results from various spectro-electrochemical analyses. In this case, it could be concluded that complex 1 exhibited better DNA cleavage efficacy than the other complexes.
| MI–L + H2O2 → MII–L + OH− + ·OH |
| ·OH + CT-DNA → DNA fragments |
where L = ligand, M = Cu(II) (1), Co(II) (2), Mn(II) (3), Ni(II) (4) and Zn(II) (5)
DNA binding assay by absorption titration
Electronic absorption titrations for ligand (HL) and its complexes (1–5) were carried out in buffer pH = 7.2 at 25 °C in the absence and presence of CT-DNA (Fig. 2 and S12†). In the absorption spectra, complexes (1–5) exposed two intense absorption bands at about 260 nm and 324–386 nm, corresponding to π–π* transitions of aromatic chromophores and metal-to-ligand charge-transfer bands (MLCT), respectively. Upon increasing the concentration of DNA to each compound, changes of both the intensity and wavelength of the intraligand charge-transfer bands were clearly recorded. The observed results of the ligand (HL) and its complexes (1–5) revealed 30.14–35.06% hypochromism with 4–8 nm bathochromic shifts due to the decreasing π–π* transition energy and the partially filled electrons of coupling orbitals, which lead to an intercalation binding mode between the compounds and DNA base pairs. On other hand, if hyperchromism with a hypsochromic shift would occur in the complex–DNA adduct, electrostatic interactions may become feasible. The intrinsic binding constants (Kb) for the ligand (HL) and its complexes (1–5) were calculated from the Wolfe–Shimmer (eqn (1))43 and Benesi–Hildebrand equations (eqn (2)).44| |
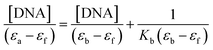 | (1) |
| |
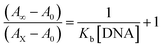 | (2) |
where [DNA] is the concentration of DNA in the base pairs; εa is the apparent extinction coefficient for the MLCT absorption band at the given DNA concentration, as obtained by calculating Abs/[complex]; and εf and εb correspond to the extinction coefficient of the complex free and fully bound to DNA. Further, b = ∞, f = 0, a = x, A = εc, [A = εcl, l = 1], ΔAmax = (A∞ − A0); ΔA = (Ax − A0), A0 is the absorbance of the free complex, Ax is the absorbance of the intermediate form of the complex with DNA, and A∞ is the absorbance of the fully bound form of the complex with DNA. The Wolfe–Shimmer binding constant (Kb) can be obtained from the ratio of the slope to the intercept in the linear plots of [DNA]/(εa − εf) vs. [DNA] M and the Benesi–Hildebrand binding constant (Kb) can be calculated from the ratio of the intercept to the slope in the linear plot of [(A∞ − A0)/(Ax − A0)] versus {1/[DNA]} M−1. The standard Gibb's free energy change 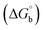 for DNA binding can be determined using the van't Hoff equation (eqn (3)), while the percentage of chromaticity for all the compounds was determined from eqn (4).
for DNA binding can be determined using the van't Hoff equation (eqn (3)), while the percentage of chromaticity for all the compounds was determined from eqn (4).| |
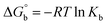 | (3) |
| |
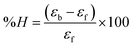 | (4) |
The observed binding constant (Kb) values for all the compounds by the Wolfe–Shimmer and Benesi–Hildebrand methods were found to follow the order (1) > (2) > (4) ≈ (5) > (3) > (HL). The Gibb's free energy change 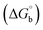 was observed from −22.84 to −25.94 kJ mol−1 (Table 1). Among the binding results in all the cases, complex 1 had the strongest binding potency with DNA base pairs, which was also confirmed by the gel electrophoresis technique. It is suggested that this may be due to the co-planarity of the morpholine-based ligand and acetate moiety, which induce the smooth penetration of the complex within DNA base pairs. The appearance of the isosbestic point at 351 nm suggests that equilibrium was established between the DNA and complex 1. It was clearly concluded that complexes (1–5) could bind to DNA via intercalation in a spontaneous manner.
was observed from −22.84 to −25.94 kJ mol−1 (Table 1). Among the binding results in all the cases, complex 1 had the strongest binding potency with DNA base pairs, which was also confirmed by the gel electrophoresis technique. It is suggested that this may be due to the co-planarity of the morpholine-based ligand and acetate moiety, which induce the smooth penetration of the complex within DNA base pairs. The appearance of the isosbestic point at 351 nm suggests that equilibrium was established between the DNA and complex 1. It was clearly concluded that complexes (1–5) could bind to DNA via intercalation in a spontaneous manner.
BSA binding assay
Electronic absorption spectroscopy is a dynamic tool to investigate the structural changes and the type of quenching of BSA by drug molecules. Absorption titrations were performed for BSA in the absence and presence of complexes (1–5) at physiological pH (7.2) (Fig. 3 and Table 2). Generally, quenching may happen either by a dynamic or static mode. The static quenching process represents the formation of a fluorophore (BSA)-quencher (compound) in the ground state; whereas in the dynamic quenching process, the fluorophore and the quencher come into contact during the temporary existence of the excited state. Moreover, the dynamic quenching process influences only the excited state while it has no function on the absorption spectrum.45 Here, it was clearly demonstrated that the absorption intensity of BSA appeared in the range 273–280 nm. When the concentration of complexes (1–5) was increased, the absorbance also increased along with a blue-shift (2–7 nm). This indicated that a static interaction occurred between BSA and the complexes in the ground state. The hyperchromism was found in the range from 34.27% to 74.13% for all compounds. The results further clearly showed that structural changes may occur due to the non-covalent interactions, such as by electrostatic and hydrogen bonding attraction between the complexes (1–5) and BSA.46 The value of the binding constant was measured by the Benesi–Hildebrand method (eqn (5)).| |
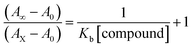 | (5) |
where ΔAmax = (A∞ − A0), ΔA = (Ax − A0), A0 is the absorbance of BSA alone, Ax is the absorbance of BSA upon the addition of different concentrations of compound, and A∞ is absorbance of the fully bound form of BSA with the complex. The binding constants (Kapp) values for the ligand (HL) and its complexes (1–5) were calculated from the ratio of the intercept to the slope in the linear plot of [(A∞ − A0)/(Ax − A0)] versus {1/[compound]} M−1. The observed BSA binding constant (Kb) values for all the compounds were found in the following order 2.38 (1) > 2.21 (2) > 2.18 (5) > 1.76 (4) > 1.40 (3) > 1.26 (HL) × 104 M−1 with 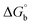 values from −23.41 to −24.98 kJ mol−1. It was clear that complex 1 had the best binding potency with BSA in a spontaneous manner.
values from −23.41 to −24.98 kJ mol−1. It was clear that complex 1 had the best binding potency with BSA in a spontaneous manner.
Evaluation of the biothermodynamic parameters
Many chronic diseases are caused by DNA denaturation, which leads to DNA repair deficiency disorder, genetic disorders and can eventually reduce the functionality of DNA repair. The DNA repair defects and its mutations can cause both an increased risk of cancer and accelerated aging diseases, like blood syndrome, Fanconi's anemia and xeroderma pigmentosum. Thermal denaturation studies can help determine the stabilization ability of double-stranded DNA. The observed melting temperatures of the complexes bound to DNA were higher than DNA alone, because the complex bound to DNA is more difficult to melt than the unlabelled DNA due to the involvement of strong binding to DNA via intercalation. The biothermodynamic parameters were calculated by the van't Hoff (eqn (6)) and Gibb's Helmholtz equations (eqn (7)), and the results are summarized in Table 3.| |
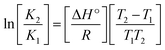 | (6) |
| |
ΔG° = –RTm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Km = ΔH° − TmΔS° Km = ΔH° − TmΔS°
| (7) |
where K2 (Km) is the binding constant at T2 (DNA melting temperature of compounds – TmK), K1 is the binding constant at T1 (room temperature – Tr = 298 K), R is the universal gas constant = 1.987 cal K−1 mol−1, ΔG° is the Gibb's free energy, ΔH° is the enthalpy change, and ΔS° is the entropy change. Numerous literature reports have depicted that there are four general types of classical interacting agents that play important roles among the group of small molecules and macromolecules in drug design, namely alkylators, intercalators, groove binders and DNA-cleaving agents (e.g. bleomycin, tirapazamine, anthracycline and enediyne). Alkylating agents are strong electrophilic compounds that react chemically with nucleophilic groups on DNA to form covalent bonds. The resulting alkylator–DNA adducts are irreversible and non-specific inhibitors of transcription and translation. A few classical alkylators, like cyclophosphamide, chlormethine, uramustine, chlorambucil, ifosfamide, busulfan, cisplatin, oxaliplatin, nedaplatin and carboplatin,47 have resistance and can cause numerous undesirable side effects, like severe kidney problems, allergic reactions, decreased immunity to infections, gastrointestinal disorders, haemorrhage and hearing loss, especially in younger patients.48 Moreover, the reversible non-covalent interactions of drug–DNA have attained an essential role in controlling certain diseases with fewer limitations. However, the interaction models in DNA–drug systems are not feasible since there is no formal active site in DNA, unlike with enzymes/proteins. Certain base sequences are dependent on the chemical, structural and conformational characteristics of the DNA double helix and are involved in three primary ways: (i) through exterior electrostatic interactions with the negatively charged phosphate of the DNA base: here, the energetics of DNA recognition is not fully understood at a molecular level due to the nonspecific electrostatic interactions prevalent in the whole system;49 (ii) through interior surface binding interactions at the edges of base-pairs in the minor/major grooves of nucleic acids due to hydrogen bonding/van der Waals force attraction: here, most of the major and minor groove-binding drugs bind to guanine–cytosine- and adenosine–thymine-rich sequences, respectively,50 and the groove binding of crescent-shaped molecules does not induce large conformational changes in DNA and may be considered similar to standard lock-and-key models for compound–DNA adducts. Some examples for classical groove binders include netropsin, distamycin, berenil, Hoechst 33258, etc.;51 (iii) through interior surface insertion binding interactions by intercalation of planar aromatic ring systems between DNA base-pairs due to hydrophobic forces, stabilized by π–π stacking interactions. The intercalators show strong structural perturbations in DNA due to interactions with the preferential N-7 position of quinine and N-3 of adenine and prevent DNA replication and transcription by interfering with the action of topoisomerases due to the miscoding of DNA. Some examples of classical intercalators include ethidium bromide, actinomycin, adriamycin, anthracyclines, doxorubicin, mitoxantrone, daunorubicin, quinacrine, proflavin and propidium, etc.40 The necessary information on the binding constants and the corresponding free energy, entropy, enthalpy changes on complex–DNA adduct formation can be obtained from thermal denaturation studies. Here, the observed melting temperature of DNA alone was 64 ± 2 °C under the same set of experimental conditions, while the observed melting temperature of DNA–compound adducts were in the following order 78 °C (1) > 75 °C (2) > 74 °C (5) > 73 °C (4) > 71 °C (3) > 68 °C (HL) and the change of melting temperature (ΔTm °C) was 14 (1) > 11 (2) > 10 (5) > 9 (4) > 7 (3) > 4 (HL). The thermodynamic parameters were also favourable for the intercalation binding mode between DNA and the complexes. The observed negative binding free energy of the complex–DNA adduct was lower than the sum of the binding energies of the free complex and DNA (Fig. S13† and Table 3). This also indicates that the complexes (1–5) bind to DNA via intercalation in a spontaneous manner. Generally, the driving forces between the compound and DNA depend on the nature of the reaction. When enthalpy is favourable, the driving forces are responsible for the van der Waals interactions, hydrogen bonding and electrostatic interactions. When entropy is favourable, binding is driven by hydrophobic interactions, whereas unfavourable entropic changes are due to the loss of conformational degrees of freedom. Moreover, Ross and co-workers reported that the enthalpy changes (ΔH°) and entropy changes (ΔS°) occurred in the following order: (a) hydrophobic forces → ΔH° > 0 and ΔS° > 0, (b) van der Waals interaction and hydrogen bonding → ΔH° < 0 and ΔS° < 0, (c) electrostatic interactions → H° < 0 or ΔH° ≈ 0 and ΔS° > 0.21,52 The observed results ΔH° < 0 and ΔS° < 0 clearly described that the interactions between complexes (1–5) and DNA could be attributed to van der Waals forces and hydrogen bonding. However, the loss of translational and rotational degrees of freedom and the interaction of counter ions along with hydrophobic forces in the complex–DNA adduct could provide for negative entropy and enthalpy changes with an exothermic effect. Moreover, it is strongly put forward that hydration and hydrophobic interactions are the main forces in the complex–DNA adduct formation during the counter ion release process. As a result, the overall complex–DNA interaction generates large negative enthalpy and entropy changes.53 According to the mechanism for protein/DNA–complex interactions proposed by Ross and Subramanian, it could be concluded that the planar phenyl ring system linked with the morpholine moiety in the complexes may intercalate between DNA base pairs due to π–π stacking interactions. In addition, according to the polyelectrolyte theory proposed by Manning and Record, if the complex is positively charged, once the complex involves stacking interactions, the various non-covalent molecular interactions, like dipole–dipole, van der Waals force, hydrogen bonding and electrostatic forces, may prevail in the complex–DNA adduct.
Evaluation of DNA binding affinity by viscosity titration measurements
The nature of interactions between the test compounds and CT-DNA was further verified by hydrodynamic volume measurements, which are sensitive to DNA length change and can be observed as the least ambiguous and the most critical test of binding. When the concentration of the ligand (HL) and its complexes (1–5) was gradually raised with a fixed DNA concentration, the relative viscosity of the resulting solution also steadily increased due to increasing the overall double-helix contour length of DNA by the intercalation binding mode54 (Fig. 4). However, the groove binding, electrostatic, partial and non-classical binding did not change the viscosity of DNA solution, even with the incremental increase in the concentration of the complexes. The relative specific viscosity (η/η0) was plotted against [complex]/[DNA]. The relative specific viscosity of DNA either in the presence or absence of the complexes was determined from eqn (8).| |
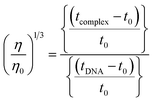 | (8) |
Data were analyzed as (η/η0)1/3 vs. [complex]/[DNA], where, η is the specific viscosity of DNA in the presence of the complex, η0 is the specific viscosity of DNA alone; t0 is the average flow time of Tris–HCl buffer solution, tDNA is the average flow time of DNA alone, and tcomplex is the average flow time of DNA with the complex. In this case, the observed relative viscosity of DNA for the ligand (HL) and its complexes (1–5) increases the binding affinity and also increases the slopes. The binding affinity and their slopes were depicted as per the following the order (EB) (1.215) > (1) (0.905) > (2) (0.855) > (4) (0.625) > (5) (0.505) > (3) (0.570) > (HL) (0.500) (Fig. 4 and Table S7†). The increase in viscosity of CT-DNA upon the addition of complex 1 was much higher than for the other complexes (2–5) and for the ligand (HL) and also slightly lower than that of the classical intercalator (ethidium bromide). This suggested that complexes (1–5) can bind strongly to DNA via intercalation due to the presence of a morpholine-based aromatic ring planar system in the complexes. The observed results also agreed well with the obtained results from the electronic absorption, fluorescence and electrochemical titration studies.
Competitive binding assay by fluorescence titration
Fluorescence measurements are widely used to differentiate the binding modes of a metal complex with CT-DNA. Here, the complexes did not exhibit any fluorescence in the presence of CT-DNA at room temperature in Tris–HCl buffer solution (at pH = 7.2). Fluorescence titration experiments were carried out using the strongly fluorescent-active substance ethidium bromide (EB), which is a very weak fluorescent molecule in Tris–HCl buffer solution. When ethidium bromide binds with CT-DNA, the EB fluorophore emits very intense fluorescence at around 610 nm due to the strong intercalation with CT-DNA.55 In the experiment, increasing the concentration of the compounds (0–120 μM) in the CT-DNA–EB mixture in solution caused a considerable reduction in emission intensity at 610 nm (Fig. 5). The decrease in the fluorescence intensity indicated that the complexes compete with EB for binding with DNA, displacing EB from DNA due to strong intercalation. The occurrence of quenching in the fluorescence of the compounds by DNA might be due to the photoelectron transfer from the guanine base of DNA to the excited states. The Stern–Volmer binding constant (KSV), bimolecular quenching rate constant (Kq) and number of binding sites were calculated from the classical Stern–Volmer equations (eqn (9) and (10)).| |
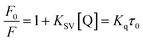 | (9) |
where F0 and F are the fluorescence intensities in the absence and in the presence of the quencher (complex) at concentration [Q]. The Stern–Volmer binding constant (KSV) was determined from the ratio of the slope to the intercept of the straight line obtained from the plot F0/F vs. [Q]. Kq is the bimolecular quenching rate constant or Stern–Volmer dynamic quenching rate constant. The average lifetime of biomolecular quenching (τ0) in the absence of a quencher (complex) was 10−8 S. The association binding constant (Kass) and number of binding sites (n) were calculated from the following Stern–Volmer equation29 (eqn (10)). The apparent binding constant (Kapp) was calculated from eqn (11).| |
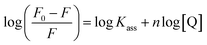 | (10) |
| | |
KEB[EB] = Kapp[compound]
| (11) |
where Kass is the association binding constant, which was calculated from the linear plot of log(F0 − F)/F vs. log[Q]; n is the number of binding sites; Kapp is the apparent binding constant, which can be determined from eqn (11); and KEB = 107 M−1 at the concentration of 50 μM EB.56 The IC50 value of complex concentration was measured at a 50% reduction of the fluorescence intensity of EB. The measurements were further extended to confirm the binding affinities by Lineweaver–Burk (eqn (12)) and Scatchard analysis (eqn (13))57,58 and compared with the obtained results from the Stern–Volmer method.| |
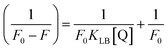 | (12) |
where ΔF = (F0 − F), and where the modified Stern–Volmer equation is called the Lineweaver–Burk equation (eqn (12)). The Lineweaver–Burk binding constant (KLB) was determined from the ratio of the intercept to the slope of the linear plot of 1/(F0 − F) vs. 1/[Q].| |
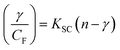 | (13) |
where γ = (F0 − F)/F0, CF is the concentration of the free compound, and where the Scatchard binding constant (KSC) and the number of binding sites (n) were calculated from eqn (13) and ratio of the intercept to the slope of the linear plot of (γ/CF) vs. γ, respectively. All the observed binding constant values (KSV, Kass, Kapp, KLB and KSC) were found to occur in the following order (1) > (2) > (4) > (5) ≈ (3) > (HL) × 104 M−1. The number of binding sites (n) was in the range from 0.9016 to 1.1546 for all compounds (Fig. 5 and S14† and Table 4). Among the experimental results in all cases, complex 1 revealed the best binding affinity compared to the free ligand and the other complexes (2–5). The ratio of the fluorescence quantum efficiency (P) of the DNA–complexes adducts was also observed to be in the range 0.3267–0.4535. The observed binding constant values from the fluorescence technique were in good agreement with the obtained values from the electronic absorption and viscosity titration measurements.
Determination of DNA binding parameters by electrochemical analysis
Cyclic voltammetry is one of the key techniques for exploring the binding mode of DNA–complex adducts. The electrochemical behaviours of complexes (1–5) in the absence and presence of CT-DNA were determined within the potential range +2 to −2 at a scan rate of 0.1 V in Tris–HCl (5 mM)/NaCl (50 mM) (pH 7.2) buffer solution. The complexes exhibited one anodic and one cathodic peak responsible for the M(II)/M(I) redox couple. The (Ipa/Ipc) ratio values for the redox couple were approximately unity, which indicated that the reaction of the complex on the glassy carbon electrode surface was a quasi-reversible one-step one-electron redox process27 (Fig. S15† and Table 5). Upon the addition of CT-DNA to the complexes (1–5), the redox couples reduced the formal electrode potential (E1/2) and anodic/cathodic peak currents due to a decrease in the apparent diffusion coefficient (D0). It could thus be clearly concluded that the observed results of the diffusion coefficient (D0) of the DNA-bound complexes (1–5) were lower than for the free complex. Generally, a shift of the peak potential towards the positive direction indicates the compounds interact with DNA via intercalation. If the shift of the peak potential is towards the negative direction, the compounds interact with DNA via minor/major groove binding or electrostatic binding. Owing to the continuous shift in the positive direction with the successive addition of DNA, the mode of binding is termed as predominantly intercalation in the DNA–complex adduct and also it could be attributed to the presence of a morpholine-based aromatic planar group in the metal complex, which is able to establish insertion via intercalation due to π–π stacking interactions and hydrophobic forces in the DNA base pairs. This was further evidenced by electronic absorption, fluorescence quenching titration, viscosity measurements and biothermodynamic studies. In general, if the value of the equilibrium binding constant ratio {[K+/K2+] = 1} is equal to unity, it indicates groove binding or electrostatic binding interaction in the DNA–complex adduct, while if the value is less than unity {[K+/K2+] < 1}, it reveals that the intercalation binding mode may occur in the DNA–complex adduct due to hydrophobic forces. The later observation was found in the complexes (1–5)–DNA adduct. Also, the binding constants, number of binding sites, the diffusion coefficient (D0) and binding constant ratio for the reduction and oxidation process were calculated with the help of the following equations (eqn (14)–(17)).59,60| |
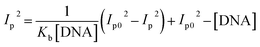 | (14) |
| |
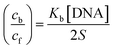 | (15) |
| |
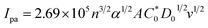 | (16) |
| |
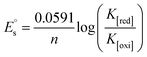 | (17) |
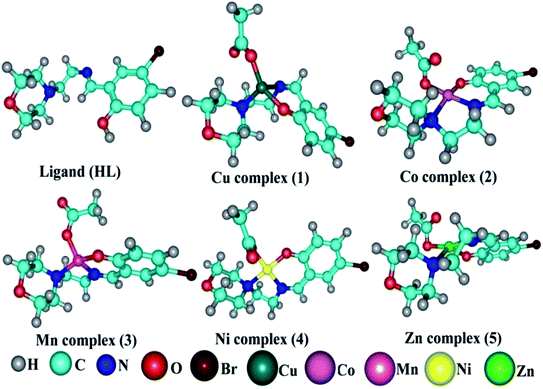
In eqn (14), Ipo and Ip are the peak currents of complexes 1–5 in the absence and presence of DNA, and the binding constant (Kb) was obtained from the straight line of the plot of Ip2 vs. (Ipo2 – Ip2)/[DNA] and the slope was equal to the reciprocal of Kb. In eqn (15), 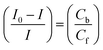 , where I0 and I represent the peak currents of the complex in the absence and presence of DNA. [DNA] is the concentration of the base pairs, Cf and Cb denote the concentration of the free complex and DNA-bound complex, respectively, Kb was further determined from slope of the linear plot of Cp/Cf vs. [DNA], and S is the binding site size in terms of the base pairs (bp). The observed binding constant values from methods I and II followed the order (1) > (2) > (4) > (3) ≳ (5) and the observed binding site size was in the range 1.068–1.503 bp (Table 5). Among the observed binding results from both methods, complex 1 revealed a higher binding efficacy than the others. In the quasi-reversible Randles–Sevcik equation (eqn (16)),61 Ipa is the anodic peak current in amperes; n is the number of electrons involved in the redox process (n = 1); α is the activation coefficient or charge transfer coefficient = 0.5, which is a reasonable and commonly-used approximation for many quasi-reversible systems and can be calculated from the Bard–Faulkner relation [α = 47.7/(EP – EP/2)];61 A is the cross-sectional area of the glassy carbon electrode in cm2 (≈0.07 cm2);
, where I0 and I represent the peak currents of the complex in the absence and presence of DNA. [DNA] is the concentration of the base pairs, Cf and Cb denote the concentration of the free complex and DNA-bound complex, respectively, Kb was further determined from slope of the linear plot of Cp/Cf vs. [DNA], and S is the binding site size in terms of the base pairs (bp). The observed binding constant values from methods I and II followed the order (1) > (2) > (4) > (3) ≳ (5) and the observed binding site size was in the range 1.068–1.503 bp (Table 5). Among the observed binding results from both methods, complex 1 revealed a higher binding efficacy than the others. In the quasi-reversible Randles–Sevcik equation (eqn (16)),61 Ipa is the anodic peak current in amperes; n is the number of electrons involved in the redox process (n = 1); α is the activation coefficient or charge transfer coefficient = 0.5, which is a reasonable and commonly-used approximation for many quasi-reversible systems and can be calculated from the Bard–Faulkner relation [α = 47.7/(EP – EP/2)];61 A is the cross-sectional area of the glassy carbon electrode in cm2 (≈0.07 cm2); 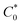 is the bulk concentration of the electroactive species in mol cm−3, D0 is the diffusion coefficient of the analyte (complex) in cm2 s−1 and v is the potential scan rate at 0.1 volt S−1. In the Nernst equation62 (eqn (17)) for the electrochemical cell,
is the bulk concentration of the electroactive species in mol cm−3, D0 is the diffusion coefficient of the analyte (complex) in cm2 s−1 and v is the potential scan rate at 0.1 volt S−1. In the Nernst equation62 (eqn (17)) for the electrochemical cell, 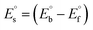 , E1/2 or
, E1/2 or 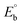 and
and 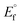 are the formal electrode potential of the M(II)/M(I) couple in the free and bound forms, respectively, and K+ and K2+ are the corresponding binding constants for the binding of the +1 and +2 species to DNA, respectively. The electrochemical possible mechanisms for the DNA–complexes adduct are given below.
are the formal electrode potential of the M(II)/M(I) couple in the free and bound forms, respectively, and K+ and K2+ are the corresponding binding constants for the binding of the +1 and +2 species to DNA, respectively. The electrochemical possible mechanisms for the DNA–complexes adduct are given below.
Molecular modelling and docking studies
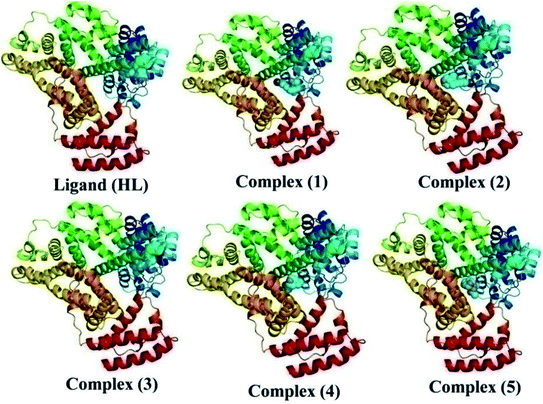
The nature of binding modes and the active site environment of the protein-compounds as obtained from molecular docking are often helpful to understand the mechanism of drug action.63 Therefore, in this present work, a detailed molecular docking analysis was carried out to understand how these metal complexes and free ligand bind into the BSA protein and DNA. The ligand (HL) and its complexes (1–5) were optimized at the B3LYP level and their optimized geometries are given in Fig. 6. From the optimized geometry, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are drawn (Fig. S16†). It can be seen that the HOMO of the free ligand spreads over the entire molecule, while the LUMO is concentrated on the phenolic moiety. The morpholine moiety does not contribute either to the HOMO or LUMO of the metal complexes. It is also interesting to note that the bromine atom is not involved in the stabilization of the LUMOs of the metal complexes and free ligand. However, the bromine atom is involved in the stabilization of the HOMO in all the complexes, except for the Mn complex (3). Overall, the Frontier molecular orbitals (HOMOs and LUMOs) indicate that these metal complexes are expected to have π–π* transitions, while the free ligand is expected to show intra-molecular charge transfer along with π–π* transitions. Molecular docking analysis was performed using the DFT optimized geometries and both DNA and the BSA protein were considered for the docking. The results show that the free ligand binds to the DNA with a binding energy of 5.8 kcal mol−1 and the metal complexes (1–5) bind to the DNA with a higher binding affinity (>5.8 kcal mol−1) than the free ligand. Fig. 8 clearly portrays the nature of binding of these metal complexes to the DNA double helix. It is important to note that the metal complexes preferentially bind to DNA in an intercalation fashion, which is in good agreement with the experiment results. The results of molecular docking of these metal complexes and ligand to BSA protein are given in Fig. 7 and the active site environments are collected in Fig. S17.† The results reveal that the ligand establishes a hydrogen bond with Tyr160 inside the active site of BSA protein and the other neighbouring residues are Leu115, Tyr137 and Arg185. Moreover, the observed binding energies of the ligand (HL) and its metal complexes (1–5) bound with DNA were in the following order 7.0 (1) > 6.6 (4) > 6.1 (2) > 6.0 (5) ≈ 6.0 (3) > 5.8 (HL) kcal mol−1. The binding pocket of the BSA–Cu complex (1) consists of the following residues: Asp108, Ser109, Pro110, Asp111, Leu112, Lys114, Arg144, His145, Leu189, Glu424, Ser192 and Arg458. It should be noted that the Cu-complex (1) showed three hydrogen bonding interactions with Asp111, Leu112 and His145, while the Co-complex (2) showed only one hydrogen bonding interaction with Ser192. The binding pocket of the BSA–Mn complex (3) consisted of the following amino acid residues: Leu115, Pro117, Leu122, Lys136, Tyr137, Ile141, Glu140, Arg144, His145, Tyr160, Arg185, Val188, Leu189 and Ser192, while the BSA–Zn complex (5) had His145, Leu189, Thr190, Ser192, Ala193, Arg196,Ser428, Arg435, Leu454, Ile455 and Arg458 residues in its active site. It is important to note that the oxygen of the morpholine group in the Ni complex (4) and in the Zn complex (5) was found to show a hydrogen bond interaction with Arg435 of BSA. These two metal complexes were found to have 7.6 and 7.4 kcal mol−1 binding energies towards BSA. These binding energies indicate that the metal complexes (1–5) demonstrate a higher binding affinity towards DNA and BSA protein as compared to that of the free ligand. Compared to DNA, these metal complexes also showed slightly greater binding affinity towards BSA. For instance, Cu-complex (1) and Ni-complex (4) bind to the BSA with 7.3 and 7.6 kcal mol−1, which are 0.3 and 1.0 kcal mol−1 higher than their binding energies toward DNA. Overall, the ligand and its metal complexes are stabilized inside the active site of BSA through hydrogen bonding and other non-covalent interactions. In summary, DFT calculations in conjunction with molecular docking analysis helped us understand the binding modes and binding affinities of these synthesized chemical species towards DNA and BSA.
 |
| | Fig. 7 The best possible binding pose of the ligand (HL) and its complexes (1–5) into the BSA. | |
 |
| | Fig. 8 The preferred binding mode of the ligand (HL) and its complexes (1–5) towards DNA. | |
Antioxidant assay
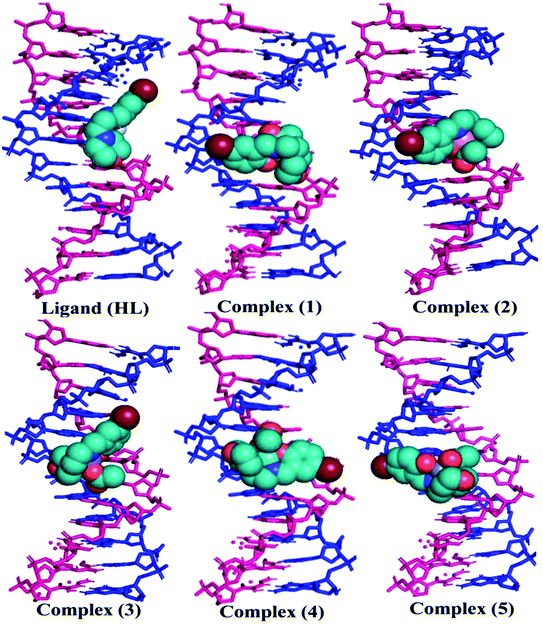
An antioxidant is any substance that has the ability to prevent/delay oxidation of the substrate or free radical formation. Oxidizable substrates, like proteins, lipids, DNA and carbohydrates, are found in all living cells and protect biological systems against potential harmful effects caused by excessive oxidation. Recently, antioxidant studies have gained an important role in the control of cancer-related diseases. Antioxidants donate a hydrogen or electron to the free radicals to convert them into harmless/water molecules, which may decrease the energy of the free radicals or suppress radical formation or break chain propagation of lipid oxidation at the initiation step.64 Moreover, the radical scavenging abilities can be measured by various methods, like hydrogen atom transfer (HAT), single electron transfer (ET), singlet oxygen quenching, reducing power and metal ion chelation. However, many factors influence the antioxidant activities of complexes, such as the oxidation potential of the central metal atom, spin electron density on the metal ion, planarity, band angle between chelated rings, steric effects, intramolecular hydrogen bonding, bond dissociation energy (BDE) and dipole moment. The observed antioxidant values of complex 1 in all cases were higher than for the others due to its high spin electron density. The IC50 (maximum inhibitory concentration) values for DPPH, hydroxyl radical, superoxide, nitric oxide and the ferric reducing antioxidant power assay are shown in Fig. 9(a–e and a1–e1). The percentage of scavenging activity and reducing power of all the compounds were measured from the following equations (eqn (18) and (19)).| |
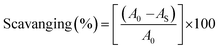 | (18) |
| |
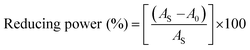 | (19) |
where A0 is the absorbance of the control or (DPPH alone in ethanol) and AS is the absorbance of the sample or (mixture of DPPH and compounds in ethanol).
 |
| | Fig. 9 (a–e) Plots of antioxidant properties (% inhibition) of DPPH, hydroxyl, superoxide, nitric oxide and ferric reducing power scavenging assay for the ligand (HL), its complexes (1–5) and standard ascorbic acid; (a1–e1) absorption spectra of DPPH, hydroxyl radical, superoxide, nitric oxide and ferric reducing power scavenging activities with various concentrations (40, 80, 120, 160, 200, 240 μM) of complex 1. | |
DPPH radical scavenging assay
The DPPH assay is a simple and sensitive method, which can be influenced by several factors, including the type and amount of solvent, concentration of hydrogen, metal ions and freshness of the DPPH reagent, for assessing the antioxidant activity depending on the electron-donating capacity/reducing power. In this method, a blank DPPH solution without the sample was used for the baseline correction and a strong absorption maximum at 517 nm (ε = 8320 M−1 cm−1) was found. DPPH is a stable chromogen-free radical at room temperature and readily reacts with an antioxidant complex due to accepting a hydrogen or electron from the donor groups, which also involves a colour change from deep purple to light yellow in an aqueous or methanol solution. Here, when the concentration of the compounds was increased from 40 to 240 μM, a decrease in absorbance for each sample was carefully noted at 517 nm.65 The increasing concentration of compounds led to enhanced radical inhibition. The observed maximum inhibition percentage (%) of all the compounds at 240 μM followed the order: ascorbic acid (AA) (82.75) > (1) (74.89) > (2) (70.11) > (5) (61.15) > (4) (55.63) > (3) (53.52) > (HL) (50.64), while the observed half-maximum inhibitory concentration (IC50) values of standard ascorbic acid and complex 1 were 80 μM and 160 μM, respectively (Fig. 9 a, a1 and Table S8a†).
Hydroxyl radical scavenging assay
Hydrogen peroxide is an essential reactive oxygen species in biological systems. The uncontrolled accumulation of H2O2 leads to the conversion of hydroxyl/oxygen free radicals, which can cause harmful effects in living cells due to immense damage of the cell membrane. The antioxidant compounds donate electrons to hydrogen peroxide and neutralize it into a water molecule. The hydroxyl radical scavenging activity was measured from the percentage inhibition for the ligand (HL) and its complexes (1–5) at 230 nm. As per the observed results of the maximum inhibition percentage of all compounds at 240 μM followed the order (AA) (78.83) > (1) (56.07) > (2) (55.66) > (4) (55.40) > (5) (54.60) > (3) (52.21) > (HL) (51.78), while the observed IC50 values of standard ascorbic acid and complex (1) were 160 μM and 240 μM, respectively (Fig. 9b, b1 and Table S8b†).
Superoxide scavenging assay
The superoxide is an anion radical (O2˙−) that can generate an uncharged hydroperoxyl radical (HOO˙) in aqueous media due to protonation and it is generally a better reducing agent than oxidizing agent. Several pieces of evidence support that the superoxide does not cross lipid membranes readily and is permitted in cells and tissues due to it being relatively unreactive towards most biological molecules at low level.66 However, an increased level of superoxide radicals could damage DNA and proteins in living cells. Superoxide dismutase (SOD) is an essential enzymatic catalyst in the body's antioxidant defence system. It has high affinities for superoxide and it readily reduces cellular damage and toxicity due to conversion of the superoxide into harmless molecules/water molecules. The percentage of inhibition for the superoxide radical quenching ability of the ligand (HL) and its complexes (1–5) was measured at 590 nm and the results followed the order (AA) (84.85) > (1) (71.60) > (2) (65.34) > (4) (60.57) > (5) (55.53) > (3) (53.84) > (HL) (50.62). The observed IC50 values of standard ascorbic acid and complex 1 were 120 μM and 200 μM, respectively (Fig. 9c, c1 and Table S8c†).
Nitric oxide scavenging assay
Nitric oxide (NO˙) is a diffusible free radical and important chemical mediator generated from amino acid L-arginine by enzymes in the vascular endothelial cells, macrophages, phagocytes and certain neuronal cells. They are synthesized by three isoforms of the enzyme nitric oxide synthase (NOS), namely endothelial NOS, neuronal NOS and inducible NOS, which are involved in the regulation of diverse physiological processes. Also, chronic exposure to nitric oxide radicals is associated with various types of carcinomas, inflammatory conditions, including juvenile diabetes, ulcerative colitis, multiple sclerosis, neuronal messenger, vasodilatation (blood vessels dilatation), antimicrobial, AIDS, cancer, Alzheimer's and arthritis by cytotoxic effects. Also, DNA fragmentation, cell damage and neuronal cell death occur due to the toxicity from the overproduction of NO˙. The toxicity of NO˙ increases greatly when it reacts with the superoxide radical, forming the highly reactive peroxynitrite anion (ONOO−).18 Hence, the nitric oxide scavenging assay is very supportive to overcome such diseases. The free radical scavenging potentials of the ligand (HL) and its complexes (1–5) were further determined by the nitric oxide scavenging assay at 546 nm. The nitric oxide radical scavenging effect depended on the concentration of the compounds. When the concentration of the test compounds was increased, the nitric oxide radical scavenging ability also increased. The observed percentage of inhibition for the nitric oxide radical quenching ability of the ligand (HL) and its complexes (1–5) was observed to follow the order (AA) (72.73) > (1) (64.16) > (2) (58.54) > (4) (56.53) > (5) (52.35) > (3) (51.98) > (HL) (50.20), while the observed IC50 values of standard ascorbic acid and complex 1 were 200 μM and 240 μM, respectively (Fig. 9d, d1 and Table S8d†).
Ferric reducing antioxidant power (FRAP) assay
The FRAP assay is a simple, rapid and inexpensive method for measuring antioxidant activity. The increase in absorbance was monitored at 700 nm. The reducing capacity of the ligand (HL) and its complexes (1–5) was analyzed by the conversion from Fe3+ to Fe2+. The Fe2+ concentration is proportional to the reducing power of the antioxidant. The higher electronic absorbance was observed at 700 nm when the concentration of the complexes was increased, which indicated a higher reducing power. Fig. 9e, e1 and Table S8e† illustrate the percentage reduction potential of complexes (1–5) was comparable with that of standard ascorbic acid. The observed percentage ferric reducing scavenging ability of all the compounds was measured using eqn (19) and the results were found to follow the order (AA) (88.67) > (1) (66.6) > (2) (61.76) > (4) (58.53) > (5) (56.43) > (3) (55.48) > (HL) (54.29), while the observed IC50 values of the standard ascorbic acid and complex 1 were 160 μM and 200 μM, respectively. The simplified scheme for these two reactions is given below.67
| Antioxidant + Fe3+ ⇄ Fe2+ + oxidized antioxidant |
| Fe2+ + Fe(CN)63− ⇄ Fe[Fe(CN)6]− |
(or)
| Antioxidants + Fe(CN)63− ⇄ Fe(CN)64− + oxidized antioxidant |
| Fe(CN)64− + Fe3+ ⇄ Fe[Fe(CN)6]− |
Antimicrobial assay
The results of the clear zone inhibition values (mm) for the ligand (HL) and its complexes (1–5) were obtained using the Kirby–Bauer agar disc diffusion method. The results also indicated that the complexes (1–5) exhibited significantly greater antimicrobial activity than the free ligand. However, complexes 4 and 5 possessed higher antimicrobial potency than the standard drugs amikacin and streptomycin for bacteria and ketoconazole and amphotericin B for fungi strains (Table 6 and Fig. S18 and S19†). This can be explained on the basis of Overtone's concept and Tweedy's chelation theory.68 According to the chelation theory, the polarity of the metal ion will be reduced to a large level due to an overlap of the ligand orbital and partial sharing of the positive charge of the metal centre with donor groups. This increases the delocalization of π and d electrons over the whole chelated ring system and increases the lipophilicity of the metal complexes, which further induces the cell permeability into lipid membranes and breakdown of the cell wall synthesis in the enzymes of the microorganisms, thus retarding the normal cell processes. Generally, antimicrobial drugs may either kill microorganisms outright or simply prevent their cell growth by way of inhibiting cell-wall/protein/nucleic acid synthesis, folate metabolism and the cytoplasmic membrane. Furthermore, the mode of action of the test compounds may involve the formation of a hydrogen bond through the morpholine-linked iminic group with the active centre of the cell constituents and disturb the respiration process of the cell, thus preventing the further growth of the organism. It could be clearly concluded that the influences of other factors, like the steric function, electronic, pharmakinetic, solubility, conductivity and bond length between the metal and ligand, may contribute to the enhanced antimicrobial activity. The percentage of inhibition of all the test compounds was calculated using eqn (20).69| |
 | (20) |
where T is the diameter of microbial growth on the test plate and C is the diameter of microbial growth on the control plate (6 mm).
In vitro anticancer study by MTT assay
The MTT assay is a sensitive and reliable technique for measuring the cellular viability or metabolic activity. The observed results of DNA binding, DNA cleavage and antimicrobial properties of the ligand (HL) and complexes (1–5) encouraged us to assess their cytotoxicity against human lung cancer (A549), liver cancer (HepG2), breast (MCF-7) and normal human dermal fibroblast (NHDF) cell lines. The half-maximum inhibitory concentration (IC50) of the ligand (HL) and its complexes (1–5) was measured by way of the percentage cell viability/growth inhibition. Although the complexes (1–5) exhibited higher activity than the free ligand against the axenic cancer cell lines, they only slightly affected the human normal cell line (NHDF) as compared to cisplatin (Fig. S20†). However, complex 1 exhibited superior anticancer potency compared to the others,70 with the observed results summarized in Table 7. The cytotoxic potency was also found to follow the order: Cisplatin > (1) > (2) > (4) > (3) > (5) > (HL). The anticancer activities were not only directly proportional to the concentration of the test compounds and incubation time exposure but also to the structure–activity relationship and modes of binding with DNA. According to Tweedy's chelation theory, the coordination between the ligands and metal ion reduces their polarity through charge equilibration. The reduced polarity induces the penetration ability of the complexes through the lipid layer of the cell membrane. Thereby, it prevents the cell-wall/protein/nucleic acid synthesis. The percentage of growth inhibition was calculated using eqn (21).| |
 | (21) |
Although the copper complex (1) exhibited better biological potency than the others in all cases, some essential factors, like solubility, conductivity, metal–ligand bond length, charge, Lewis acid character, electron density, dipole moment influenced by the metal ions, intermolecular hydrogen bonding and proton transfer equilibria, may attribute to the enhanced biological activities. However, the Cu+ ion has a peculiar character among the transition metals due to its size and d10 electronic configuration as well as a soft character and flexible nature in distorted coordination geometric arrangements. The Cu+ reduced form influences the shape, symmetry and functionality of the complexes and leads to an enhanced biological potency. Meanwhile, Zn2+ is also a d10 ion, but is harder in character than Cu+, which can be minimized as an interfering species based on the ligand donor choice. In reality, copper complexes could act as a double-edged sword by inducing DNA damage and also by inhibiting their repair. A number of copper complexes have been reported that have revealed excellent cytotoxic efficacy through cell apoptosis or enzyme inhibition.
Conclusion
Synthesized Cu(II) (1), Co(II) (2), Mn(II) (3), Ni(II) (4) and Zn(II) (5) monomeric complexes were structurally characterized by elemental analysis, magnetic susceptibility, LC-MS Mass, 1H NMR, FT-IR, UV-Vis, TGA and EPR spectral techniques. The observed analytical and spectral results proposed square planar and tetrahedral geometry around a central metal ion. All the compounds were found to be non-electrolytes due to their low electrical conductance. The obtained DNA/BSA binding properties of the ligand (HL) and its complexes (1–5) as determined by various spectro-electrochemical and viscosity measurement techniques suggest that all the complexes could interact with DNA via intercalation. Electronic structure information of these compounds was obtained from DFT calculations, while molecular docking analysis provided information on the binding affinity of these compounds towards DNA and BSA protein. The observed results exposed that the metal complexes bind more readily with non-covalent interactions towards DNA and BSA protein than that the free ligand does. It was found that the theoretical observations of all compounds were in good agreement with the experimental observations. Among the gel electrophoresis investigation results, complex 1 revealed excellent metallonucleases efficacy in the presence of H2O2. The antimicrobial activity results against certain pathogenic species disclosed that the complexes (1–5) all possessed a more significant inhibition potency than the free ligand. However, complexes 4 and 5 exhibited higher antimicrobial activity than the standard drugs tested. The various antioxidant properties revealed that complex 1 had superior radical scavenging ability than the free ligand and the other complexes (2–5). The in vitro screening of complexes (1–5) against the panel of cell-lines showed that complex 1 had greater anticancer efficacy than the others but its affect on normal cells was found to be lower than the standard drug cisplatin. As a result, complex 1 may have potential as a novel class of anticancer agent in the future.
Conflicts of interest
The authors declare that there are no conflicts of interest in this work.
Acknowledgements
The authors acknowledge the DST – SERB, Govt of India, New Delhi for the financial support granted with the Project ref. no. SR/FT/CS – 117/2011 dated 29.06.2012 and we would like to express our sincere and heartfelt thanks of gratitude to the Managing Board, Dean, Principal and Chemistry Research Centre MSEC, Kilakarai for providing lab facilities. RVS thanks DST India for the financial support in the form of early career research award (DST-SERB-ECR/2017/001147).
References
- F. Bray, J. Ferlay, I. Soerjomataram, R. L. Siegel, L. A. Torre and A. Jemal, Ca-Cancer J. Clin., 2018, 0, 1–31 Search PubMed.
- K. S. Reddy, Lancet, 2016, 388, 1448–1449 CrossRef.
- H. W. Liu, L. Chen, C. Xu, Z. Li, H. Zhang, X. B. Zhang and W. Tan, Chem. Soc. Rev., 2018, 47, 7140–7180 RSC.
- F. Bray, J. S. Ren, E. Masuyer and J. Ferlay, Int. J. Cancer, 2012, 132, 1133–1145 CrossRef.
- GBD 2015 Maternal Mortality Collaborators, Obstet. Gynecol. Surv., 2017, 72, 11–13 CrossRef.
- M. K. M. Subarkhan and R. Ramesh, Inorg. Chem. Front., 2016, 3, 1245–1255 RSC.
- M. S. Mohamed Kasim, S. Sundar and R. Rengan, Inorg. Chem. Front., 2018, 5, 585–596 RSC.
- W. Ma, Z. Tian, S. Zhang, X. He, J. Li, X. Xia, X. Chen and Z. Liu, Inorg. Chem. Front., 2018, 1–15, 10.1039/c8qi00620b.
- Y. Zhang, Q. Luo, W. Zheng, Z. Wang, Y. Lin, E. Zhang, S. Lü, J. Xiang, Y. Zhao and F. Wang, Inorg. Chem. Front., 2018, 5, 413–424 RSC.
- C. Fitzmaurice, C. Allen, R. M. Barber, L. Barregard, Z. A. Bhutta, H. Brenner, D. J. Dicker, O. Chimed-Orchir, R. Dandona, L. Dandona, T. Fleming and M. Naghavi, JAMA Oncol., 2017, 3, 524 CrossRef.
- G. J. Freeman, A. J. Long, Y. Iwai, K. Bourque, T. Chernova, H. Nishimura, L. J. Fitz, N. Malenkovich, T. Okazaki, M. C. Byrne, H. F. Horton, L. Fouser, L. Carter, V. Ling, M. R. Bowman, B. M. Carreno, M. Collins, C. R. Wood and T. Honjo, J. Exp. Med., 2000, 192, 1027–1034 CrossRef CAS.
- J. A. Seidel, A. Otsuka and K. Kabashima, Front. Oncol., 2018, 8, 1–14 CrossRef PubMed.
- A. Carella, V. Roviello, R. Iannitti, R. Palumbo, S. La Manna, D. Marasco, M. Trifuoggi, R. Diana and G. N. Roviello, J. Biol. Macromol., 2019, 121, 77–88 CrossRef CAS.
- S. Y. Ebrahimipour, I. Sheikhshoaie, J. Castro, M. Dušek, Z. Tohidiyan, V. Eigner and M. Khaleghi, RSC Adv., 2015, 5, 95104–95117 RSC.
- P. Kalaivani, R. Prabhakaran, E. Vaishnavi, T. Rueffer, H. Lang, P. Poornima, R. Renganathan, V. Vijaya Padma and K. Natarajan, Inorg. Chem. Front., 2014, 1, 311–324 RSC.
- P. Sevilla, J. M. Rivas, F. García-Blanco, J. V. García-Ramos and S. Sanchez-Cortés, Biochim. Biophys. Acta, Proteins Proteomics, 2007, 1774, 1359–1369 CrossRef CAS.
- K. Karami, Z. Mehri Lighvan, H. Farrokhpour, M. Dehdashti Jahromi and A. A. Momtazi-borojeni, J. Biomol. Struct. Dyn., 2017, 1–17, DOI:10.1080/07391102.2017.1391125.
- K. Divya, V. Smitha and M. S. Jisha, Int. J. Biol. Macromol., 2018, 114, 572–577 CrossRef CAS PubMed.
- J. Lakshmipraba, S. Arunachalam, R. V. Solomon, P. Venuvanalingam, A. Riyasdeen, R. Dhivya and M. A. Akbarsha, J. Biomol. Struct. Dyn., 2014, 33, 877–891 CrossRef PubMed.
- J. de Ruyck, G. Brysbaert, R. Blossey and M. Lensink, Adv. Appl. Bioinf. Chem., 2016, 9, 1–11 Search PubMed.
- K. Sakthikumar, J. Dhaveethu Raja, S. Rajadurai Vijay and M. Sankarganesh, J. Biomol. Struct. Dyn., 2018, 1–17, DOI:10.1080/07391102.2018.1492970.
- P. R. Reddy, A. Shilpa, N. Raju and P. Raghavaiah, J. Inorg. Biochem., 2011, 105, 1603–1612 CrossRef CAS PubMed.
- K. Sakthikumar, J. D. Raja, M. Sankarganesh and J. Rajesh, Indian J. Pharm. Sci., 2018, 80, 723–738 Search PubMed.
- A. M. Pyle, J. P. Rehmann, R. Meshoyrer, C. V. Kumar, N. J. Turro and J. K. Barton, J. Am. Chem. Soc., 1989, 111, 3051–3058 CrossRef CAS.
- K. Nagaraj, K. S. Murugan, P. Thangamuniyandi and S. Sakthinathan, RSC Adv., 2014, 4, 56084–56094 RSC.
- P. Uma Maheswari and M. Palaniandavar, J. Inorg. Biochem., 2004, 98, 219–230 CrossRef CAS PubMed.
- N. Pravin and N. Raman, Eur. J. Med. Chem., 2014, 85, 675–687 CrossRef CAS PubMed.
- M. M. V. Ramana, R. Betkar, A. Nimkar, P. Ranade, B. Mundhe and S. Pardeshi, Spectrochim. Acta, Part A, 2016, 152, 165–171 CrossRef CAS PubMed.
- R. Arif, P. S. Nayab, I. A. Ansari, M. Shahid, M. Irfan, S. Alam, M. Abid and R. Uddin, J. Mol. Struct., 2018, 1160, 142–153 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef.
- R. V. Solomon, P. Veerapandian, S. A. Vedha and P. Venuvanalingam, J. Phys. Chem. A, 2012, 116, 4667–4677 CrossRef CAS.
- R. V. Solomon, R. Jagadeesan, S. A. Vedha and P. Venuvanalingam, Dyes Pigm., 2014, 100, 261–268 CrossRef CAS.
- P. W. Rose, A. Prlić, C. Bi, W. F. Bluhm, C. H. Christie, S. Dutta, R. K. Green, D. S. Goodsell, J. D. Westbrook, J. Woo, J. Young, C. Zardecki, H. M. Berman, P. E. Bourne and S. K. Burley, Nucleic Acids Res., 2014, 43, D345–D356 CrossRef.
- A. Bujacz, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2012, 68, 1278–1289 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2009, 31, 455–461 Search PubMed.
- S. Shujah, N. Khalid and S. Ali, Russ. J. Gen. Chem., 2017, 87, 515–522 CrossRef CAS.
- I. Ali, W. A. Wani, K. Saleem and M. F. Hsieh, RSC Adv., 2014, 4(56), 29629–29641 RSC.
- R. J. Ruch, S. Cheng and J. E. Klaunig, Carcinogenesis, 1989, 10, 1003–1008 CrossRef CAS PubMed.
- P. A. Wender, R. C. Kelly, S. Beckham and B. L. Miller, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 8835–8839 CrossRef CAS PubMed.
- C. N. Sudhamani, H. S. Bhojya Naik, K. R. S. Gowda, M. Giridhar, D. Girija and P. N. P. Kumar, Med. Chem. Res., 2017, 26, 1160–1169 CrossRef CAS.
- H. J. H. Fenton, J. Chem. Soc., Trans., 1894, 65, 899–910 RSC.
- C. A. Detmer, F. V. Pamatong and J. R. Bocarsly, Inorg. Chem., 1996, 35, 6292–6298 CrossRef CAS.
- A. K. Patra, M. Nethaji and A. R. Chakravarty, J. Inorg. Biochem., 2007, 101, 233–244 CrossRef CAS.
- H. A. Benesi and J. H. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703–2707 CrossRef CAS.
- S. Kathiresan, S. Mugesh, M. Murugan, F. Ahamed and J. Annaraj, RSC Adv., 2016, 6, 1810–1825 RSC.
- M. Idowu, E. Lamprecht and T. Nyokong, J. Photochem. Photobiol., A, 2008, 198, 7–12 CrossRef CAS.
- M. Shimada, H. Itamochi and J. Kigawa, Cancer Manage. Res., 2013, 5, 67–76 CrossRef CAS PubMed.
- S. Dasari and P. Bernard Tchounwou, Eur. J. Pharmacol., 2014, 740, 364–378 CrossRef CAS.
- B. Jayaram, K. McConnell, S. B. Dixit, A. Das and D. L. Beveridge, J. Comput. Chem., 2001, 23, 1–14 CrossRef.
- S. A. Shaikh, S. R. Ahmed and B. Jayaram, Arch. Biochem. Biophys., 2004, 429, 81–99 CrossRef CAS.
- I. Haq, Arch. Biochem. Biophys., 2002, 403, 1–15 CrossRef CAS.
- M. Gellert, C. E. Smith, D. Neville and G. Felsenfeld, J. Mol. Biol., 1965, 11, 445–457 CrossRef CAS PubMed.
- N. Shahabadi, N. Fatahi, M. Mahdavi, Z. K. Nejad and M. Pourfoulad, Spectrochim. Acta, Part A, 2011, 83, 420–424 CrossRef CAS PubMed.
- S. Parveen and F. Arjmand, Spectrochim. Acta, Part A, 2012, 85, 53–60 CrossRef CAS PubMed.
- W. J. Lian, X. T. Wang, C. Z. Xie, H. Tian, X. Q. Song, H. T. Pan, X. Qiao and J. Y. Xu, Dalton Trans., 2016, 45, 9073–9087 RSC.
- K. Dhara, J. Ratha, M. Manassero, X. Y. Wang, S. Gao and P. Banerjee, J. Inorg. Biochem., 2007, 101, 95–103 CrossRef CAS PubMed.
- A. Ray, B. Koley Seth, U. Pal and S. Basu, Spectrochim. Acta, Part A, 2012, 92, 164–174 CrossRef CAS PubMed.
- Q. Feng, N. Q. Li and Y. Y. Jiang, Anal. Chim. Acta, 1997, 344, 97–104 CrossRef CAS.
- N. Arshad, U. Yunus, S. Razzque, M. Khan, S. Saleem, B. Mirza and N. Rashid, Eur. J. Med. Chem., 2012, 47, 452–461 CrossRef CAS PubMed.
- R. A. Hussain, A. Badshah and K. Akbar, Russ. J. Electrochem., 2015, 51, 198–208 CrossRef CAS.
- M. Iqbal, S. Ali and M. N. Tahir, J. Coord. Chem., 2018, 71, 991–1002 CrossRef CAS.
- I. Somasundaram and M. Palaniandavar, J. Inorg. Biochem., 1994, 53, 95–107 CrossRef CAS.
- X. Y. Meng, H. X. Zhang, M. Mezei and M. Cui, Curr. Comput.-Aided Drug Des., 2011, 7, 146–157 CrossRef CAS PubMed.
- J. Javanmardi, Food Chem., 2003, 83, 547–550 CrossRef CAS.
- F. Liu, K. A. Meadows and D. R. McMillin, J. Am. Chem. Soc., 1993, 115, 6699–6704 CrossRef CAS.
- J. P. Kehrer, J. D. Robertson and C. V. Smith, Compr. Toxicol., 2010, 0, 277–307 Search PubMed.
- K. Isil Berker, K. Guclu, I. Tor, B. Demirata and R. Apak, Food Analyt. Method., 2009, 3, 154–168 CrossRef.
- K. N. Thimmaiah, W. D. Lloyd and G. T. Chandrappa, Inorg. Chim. Acta, 1985, 106, 81–83 CrossRef CAS.
- I. H. Bhat and S. Tabassum, Spectrochim. Acta, Part A, 2009, 72, 1026–1033 CrossRef PubMed.
- G. Kumaravel, P. U. Ponnukalai, D. Mahendiran and N. Raman, Int. J. Biol. Macromol., 2018, 126, 1303–1317 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09218d |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Rajadurai Vijay Solomon
a,
Rajadurai Vijay Solomon b and
Jeyaraj Dhaveethu Raja
b and
Jeyaraj Dhaveethu Raja *c
*c
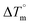 ,
, 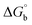 , ΔH° and ΔS°) and binding results divulged that all the complexes (1–5) could bind to DNA via intercalation in a spontaneous manner. Density functional theory calculations were employed to optimize the structure of ligand (HL) and its complexes (1–5) to gain insights into their electronic structures. Molecular docking analysis was carried out to identify the preferential binding modes of these complexes toward DNA and BSA protein. The theoretical observations of all cases were found to be very close to the experimental observations. Among the radical scavenging activity results for all the cases toward DPPH, hydroxyl radical, superoxide, nitric oxide and ferric reducing agents, complex (1) revealed a superior scavenging potency over the other compounds. In the screened antimicrobial reports against 10 different selected pathogenic species, although all the complexes (1–5) exhibited a greater significant inhibitory effect than the free ligand, complexes 4 and 5 achieved the best potency over standard drugs. The observed percentage of growth inhibition for all the compounds against the A549, HepG2, MCF-7 and NHDF cell lines suggested that complex 1 had enhanced growth-inhibitory potency over the other compounds and slightly affected normal cells as compared to the standard drug cisplatin, which may lead to its investigation as a promising anticancer agent in future research.
, ΔH° and ΔS°) and binding results divulged that all the complexes (1–5) could bind to DNA via intercalation in a spontaneous manner. Density functional theory calculations were employed to optimize the structure of ligand (HL) and its complexes (1–5) to gain insights into their electronic structures. Molecular docking analysis was carried out to identify the preferential binding modes of these complexes toward DNA and BSA protein. The theoretical observations of all cases were found to be very close to the experimental observations. Among the radical scavenging activity results for all the cases toward DPPH, hydroxyl radical, superoxide, nitric oxide and ferric reducing agents, complex (1) revealed a superior scavenging potency over the other compounds. In the screened antimicrobial reports against 10 different selected pathogenic species, although all the complexes (1–5) exhibited a greater significant inhibitory effect than the free ligand, complexes 4 and 5 achieved the best potency over standard drugs. The observed percentage of growth inhibition for all the compounds against the A549, HepG2, MCF-7 and NHDF cell lines suggested that complex 1 had enhanced growth-inhibitory potency over the other compounds and slightly affected normal cells as compared to the standard drug cisplatin, which may lead to its investigation as a promising anticancer agent in future research.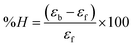 ; εf = the extinction coefficient of free complex and εb = the extinction coefficient of the complex fully bound to DNA, Gibb's free energy change
; εf = the extinction coefficient of free complex and εb = the extinction coefficient of the complex fully bound to DNA, Gibb's free energy change 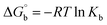 , Kb = intrinsic DNA binding constant determined from the UV-Vis absorption spectral titration, R = universal gas constant = 1.987 cal K−1 mol−1 (or) 8.314 J K−1 mol−1, T = 298 K, error limit ± 2.5, WS = Wolfe–Shimmer method, BH = Benesi–Hildebrand method.
, Kb = intrinsic DNA binding constant determined from the UV-Vis absorption spectral titration, R = universal gas constant = 1.987 cal K−1 mol−1 (or) 8.314 J K−1 mol−1, T = 298 K, error limit ± 2.5, WS = Wolfe–Shimmer method, BH = Benesi–Hildebrand method.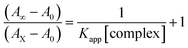 ; hyperchromism
; hyperchromism 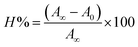 ; A0 = absorbance of BSA alone at 278 nm, A∞ = absorbance of the fully bound form of BSA with the complex or ligand and Ax = absorbance of BSA upon the addition of different concentrations of complex or ligand, Gibb's free energy change
; A0 = absorbance of BSA alone at 278 nm, A∞ = absorbance of the fully bound form of BSA with the complex or ligand and Ax = absorbance of BSA upon the addition of different concentrations of complex or ligand, Gibb's free energy change 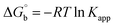 ; Kapp = apparent binding constant determined from the UV-Vis absorption spectral titration, error limit ± 2.5.
; Kapp = apparent binding constant determined from the UV-Vis absorption spectral titration, error limit ± 2.5.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio {[DNA]/[complex] = (R)1} in 5 mM Tris–HCl/50 mM NaCl buffer (pH = 7.2) solution and the solution was heated from 25 °C to 100 °C at a temperature rate of 2 °C per minute and the absorbance changes at 260 nm continuously monitored26 (Fig. S13† and Table 3). A decrease in DNA absorbance was observed in the presence of the metal complexes (1–5) due to strong intercalation in the DNA–complex adducts.
1 ratio {[DNA]/[complex] = (R)1} in 5 mM Tris–HCl/50 mM NaCl buffer (pH = 7.2) solution and the solution was heated from 25 °C to 100 °C at a temperature rate of 2 °C per minute and the absorbance changes at 260 nm continuously monitored26 (Fig. S13† and Table 3). A decrease in DNA absorbance was observed in the presence of the metal complexes (1–5) due to strong intercalation in the DNA–complex adducts.
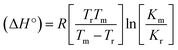 , Tr = 298 K, Tm = DNA melting temperature of compounds, R = universal gas constant = 1.987 cal K−1 mol−1; Gibb's free energy (ΔG°) = −RTm
, Tr = 298 K, Tm = DNA melting temperature of compounds, R = universal gas constant = 1.987 cal K−1 mol−1; Gibb's free energy (ΔG°) = −RTm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Km; entropy change
Km; entropy change 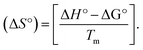
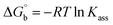 ; Kq = bimolecular quenching rate constant or Stern–Volmer dynamic quenching rate constant
; Kq = bimolecular quenching rate constant or Stern–Volmer dynamic quenching rate constant 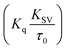 , average lifetime of biomolecular quenching in the absence of a quencher (τ0) = 10−8 S; KLB = Lineweaver–Burk binding constant; KSC = Scatchard binding constant; Kapp = apparent binding constant; n = the number of binding sites; P = ratio of fluorescence quantum efficiency of DNA bound and free complex
, average lifetime of biomolecular quenching in the absence of a quencher (τ0) = 10−8 S; KLB = Lineweaver–Burk binding constant; KSC = Scatchard binding constant; Kapp = apparent binding constant; n = the number of binding sites; P = ratio of fluorescence quantum efficiency of DNA bound and free complex 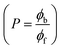 , obtained as the intercept from the plot F/F0 vs. 1/[DNA]. Error limit ± 2.5.
, obtained as the intercept from the plot F/F0 vs. 1/[DNA]. Error limit ± 2.5.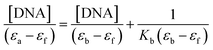
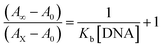
 for DNA binding can be determined using the van't Hoff equation (eqn (3)), while the percentage of chromaticity for all the compounds was determined from eqn (4).
for DNA binding can be determined using the van't Hoff equation (eqn (3)), while the percentage of chromaticity for all the compounds was determined from eqn (4).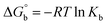
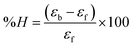
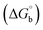 was observed from −22.84 to −25.94 kJ mol−1 (Table 1). Among the binding results in all the cases, complex 1 had the strongest binding potency with DNA base pairs, which was also confirmed by the gel electrophoresis technique. It is suggested that this may be due to the co-planarity of the morpholine-based ligand and acetate moiety, which induce the smooth penetration of the complex within DNA base pairs. The appearance of the isosbestic point at 351 nm suggests that equilibrium was established between the DNA and complex 1. It was clearly concluded that complexes (1–5) could bind to DNA via intercalation in a spontaneous manner.
was observed from −22.84 to −25.94 kJ mol−1 (Table 1). Among the binding results in all the cases, complex 1 had the strongest binding potency with DNA base pairs, which was also confirmed by the gel electrophoresis technique. It is suggested that this may be due to the co-planarity of the morpholine-based ligand and acetate moiety, which induce the smooth penetration of the complex within DNA base pairs. The appearance of the isosbestic point at 351 nm suggests that equilibrium was established between the DNA and complex 1. It was clearly concluded that complexes (1–5) could bind to DNA via intercalation in a spontaneous manner.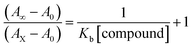
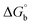 values from −23.41 to −24.98 kJ mol−1. It was clear that complex 1 had the best binding potency with BSA in a spontaneous manner.
values from −23.41 to −24.98 kJ mol−1. It was clear that complex 1 had the best binding potency with BSA in a spontaneous manner.
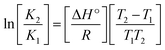
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Km = ΔH° − TmΔS°
Km = ΔH° − TmΔS°

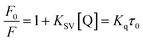
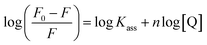
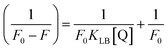
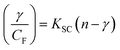
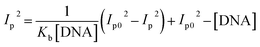
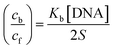
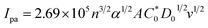
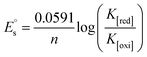
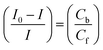 , where I0 and I represent the peak currents of the complex in the absence and presence of DNA. [DNA] is the concentration of the base pairs, Cf and Cb denote the concentration of the free complex and DNA-bound complex, respectively, Kb was further determined from slope of the linear plot of Cp/Cf vs. [DNA], and S is the binding site size in terms of the base pairs (bp). The observed binding constant values from methods I and II followed the order (1) > (2) > (4) > (3) ≳ (5) and the observed binding site size was in the range 1.068–1.503 bp (Table 5). Among the observed binding results from both methods, complex 1 revealed a higher binding efficacy than the others. In the quasi-reversible Randles–Sevcik equation (eqn (16)),61 Ipa is the anodic peak current in amperes; n is the number of electrons involved in the redox process (n = 1); α is the activation coefficient or charge transfer coefficient = 0.5, which is a reasonable and commonly-used approximation for many quasi-reversible systems and can be calculated from the Bard–Faulkner relation [α = 47.7/(EP – EP/2)];61 A is the cross-sectional area of the glassy carbon electrode in cm2 (≈0.07 cm2);
, where I0 and I represent the peak currents of the complex in the absence and presence of DNA. [DNA] is the concentration of the base pairs, Cf and Cb denote the concentration of the free complex and DNA-bound complex, respectively, Kb was further determined from slope of the linear plot of Cp/Cf vs. [DNA], and S is the binding site size in terms of the base pairs (bp). The observed binding constant values from methods I and II followed the order (1) > (2) > (4) > (3) ≳ (5) and the observed binding site size was in the range 1.068–1.503 bp (Table 5). Among the observed binding results from both methods, complex 1 revealed a higher binding efficacy than the others. In the quasi-reversible Randles–Sevcik equation (eqn (16)),61 Ipa is the anodic peak current in amperes; n is the number of electrons involved in the redox process (n = 1); α is the activation coefficient or charge transfer coefficient = 0.5, which is a reasonable and commonly-used approximation for many quasi-reversible systems and can be calculated from the Bard–Faulkner relation [α = 47.7/(EP – EP/2)];61 A is the cross-sectional area of the glassy carbon electrode in cm2 (≈0.07 cm2);  is the bulk concentration of the electroactive species in mol cm−3, D0 is the diffusion coefficient of the analyte (complex) in cm2 s−1 and v is the potential scan rate at 0.1 volt S−1. In the Nernst equation62 (eqn (17)) for the electrochemical cell,
is the bulk concentration of the electroactive species in mol cm−3, D0 is the diffusion coefficient of the analyte (complex) in cm2 s−1 and v is the potential scan rate at 0.1 volt S−1. In the Nernst equation62 (eqn (17)) for the electrochemical cell, 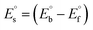 , E1/2 or
, E1/2 or 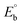 and
and 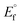 are the formal electrode potential of the M(II)/M(I) couple in the free and bound forms, respectively, and K+ and K2+ are the corresponding binding constants for the binding of the +1 and +2 species to DNA, respectively. The electrochemical possible mechanisms for the DNA–complexes adduct are given below.
are the formal electrode potential of the M(II)/M(I) couple in the free and bound forms, respectively, and K+ and K2+ are the corresponding binding constants for the binding of the +1 and +2 species to DNA, respectively. The electrochemical possible mechanisms for the DNA–complexes adduct are given below.