A multi-state supramolecular switch realized via a [π⋯π] dimer

Abstract

Supramolecular assemblies have attracted great attention in the latest studies of molecular electronic devices for their superiorities. Here, we design a non-covalent [π⋯π] dimer made of DCV4Ts (two-terminally dicyanovinyl-substituted quaterthiophenes), and five typical conformations of this dimer are specifically focused on. Based on density-functional theory calculations and the non-equilibrium Green's function technique, electron transport properties through the dimer are mainly investigated in molecular junctions. It is revealed that four distinct states of conductance can be observed through these five conformations, with the maximal ON/OFF ratio over 400 and the minimal one around 10. The multiple states of conductance basically stem from the destructive quantum interference and the spatial overlap of the two DCV4T monomers. To implement the above-indicated molecular switch in experiments, it is essential to mechanically stretch or compress the designed dimer, probably using the piezo-modulated scanning tunneling microscope based break-junction technique.

---

1 Introduction

Electrical molecular switches, especially the non-volatile ones, have advantages in power consumption and footprint areas, and thus they are expected to be basic building blocks for future integrated circuits. To achieve such molecular devices, single-molecule junctions are primarily constructed,^1–5 and an individual molecule is utilized as the functional unit. Potential molecules for the switching unit possess at least two switchable molecular configurations in response to external stimuli. One configuration leads to high conductance and is conventionally referred to as the ON state, while the other results in low conductance and is referred to as the OFF state. Nevertheless, this variety of molecules is limited,^6,7 and typical examples include spin crossover complexes,^8–10 fullerene derivatives with foreign structures embedded into the cages^11,12 and some particular complexes with switchable conformations.^13–17 Moreover, the switching performances of these complexes in single-molecule junctions are generally far below the criteria for practical applications and it is also hard to make crucial improvements to them, in spite of many advances reached. Therefore, exploring new molecular architectures as switching units is emerging and burgeoning in recent years.^18,19

For new molecular architectures, supramolecular assemblies attracted great attention in the latest studies of molecular electronic devices,^18,19 and they are commonly a class of complexes with two or more molecules bonded non-covalently. When an individual supramolecular assembly is utilized as the functional unit in a molecular junction, the junction is normally named a single-supramolecule junction or SSJ, and the related conductance can be impacted by the relative positioning and orientation of monomers in the supramolecular assembly,^20–24 indicating that the intermolecular non-covalent interactions are a key factor for the charge transport properties of SSJs. As for non-covalent interactions, the [π⋯π] one is widely used in studies of SSJs, which is mainly because (i) charges can be conducted efficiently through such an interaction;^25–27 (ii) this interaction is strong enough to sustain electrical currents;^28,29 and (iii) the conductances can be manipulated in a more precise way by adjusting the overlap of the monomeric π-backbones.^21,30,31 For these reasons, we also try to achieve the conductance switching by means of shaping the [π⋯π] interaction in SSJs. On this topic, some achievements have been made,^32–34 but it is still necessary to continue expanding the number of candidates of [π⋯π] supramolecular assemblies for such electronic devices, and novel transport properties and related mechanisms could be disclosed simultaneously.

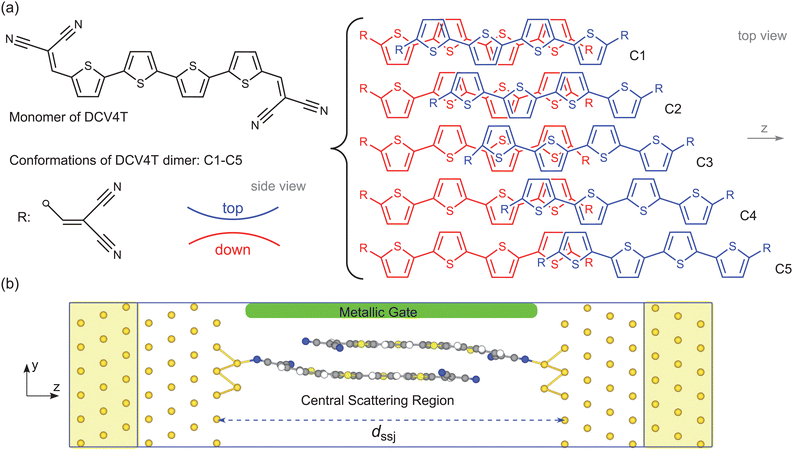
In the present study, the adopted supramolecular assembly is made up of two-terminally dicyanovinyl-substituted quaterthiophenes (DCV4Ts),³⁵ called the DCV4T dimer. Two or more conformations are possibly stabilized by the [π⋯π] interaction for this dimer, which favors a molecular switch of multiple states. This study is based on density-functional theory (DFT) calculations and the DFT plus non-equilibrium Green's function technique (DFT+NEGF) is used for the investigation of charge transport. The mainly focused upon questions are (1) typical conformations of the DCV4T dimer that are stabilized by the [π⋯π] interaction, including the most favorable one in energy; (2) charge transport properties of these conformations in SSJs and the switching performance; and (3) mechanisms for the featured charge transport properties.

2 Models and computational details

Our designed [π⋯π] dimer is composed of two DCV4T monomers, as shown in Fig. 1a, and all possible conformations are optimized at the PBE-D2/def2-SVP level using the Gaussian 16 package.³⁶ PBE implies that the exchange–correlation potential takes the generalized gradient approximation (GGA) with the form proposed by Perdew, Burke, and Ernzerhof.^37,38 D2 implies that a long-range dispersion correction is taken into account in DFT calculations, and it was developed by Grimme et al.³⁹ The stability is checked by the frequency calculations. To quantitatively characterize the non-covalent interaction between the two monomers, the energy decomposition analysis (EDA) is performed at the PBE-D2/def2-TZVP level with the counterpoise corrections, using the Q-Chem package.^40–43

Fig. 1 (a) Schematic graphs for the monomer and the dimer of DCV4T considered in this study. For clarity, dicyanovinyl groups are symbolized by R, and the dimer is made of the blue-top and red-bottom monomers in the side view. In the top view, the relative position and orientation of the monomers can be clearly seen, which are generated by analyzing optimized conformations of the dimer. (b) A representative SSJ model with one conformation of the dimer in (a). The yellow shadows marks the semi-infinite Au(111) electrode in the left/right side, and the rest corresponds to the central scattering region, including the metallic gate. d_ssj is the distance between two electrode surfaces, also called the width of the supramolecular junction.

The charge transport through the [π⋯π] dimer is explored using the QuantumATK package⁴⁴ and the SSJ model in Fig. 1b. The SSJ model can be divided into three parts, namely, the semi-infinite Au(111) electrode in the left/right side (marked by yellow shadows) and the central scattering region. The central scattering region includes a single [π⋯π] dimer, two tips of three Au atoms, several screening Au(111) layers, and the metallic gate. In the metallic gate, no specific atoms are present and its effect on charge transport is considered just by setting certain electrostatic potentials in designated zones. The width of the SSJ, represented by d_ssj in Fig. 1b, is crucial for the conformation of the [π⋯π] dimer, and the desired conformation can be obtained by adjusting this width. Before performing calculations for charge transport, the geometries of all SSJs are relaxed by using the rigid-optimization method. Details of structural relaxations for SSJ models and d_ssj can be seen in the ESI.† When constructing the SSJ model, the initial geometry of the dimer takes the one optimized by using the Gaussian package.

For calculations conducted by using the QuantumATK package, the FHI pseudopotential together with the double-ζ plus polarization (DZP) basis set is used for electrode atoms for efficiency. The PseudoDojo pseudopotential together with the medium basis set⁴⁵ is used for other atoms. The cutoff energy for defining the real-space grid is 200 Rydberg. The exchange–correlation potential takes the PBE form with the Grimme's D2 dispersion correction, consistent with the Gaussian calculations. In addition, when calculating charge transport properties, the k-grids of 1 × 1 × 100 and 1 × 1 × 1 are used for the electrodes and the central scattering region. The temperature-dependent conductance G is studied and obtained using the following formula:²³

where G₀ = 2e²/h is the quantum conductance (e: the charge of the electron; h: the Planck's constant), f(E) = 1/[1 + e^{(E−E_F)/k_BT}] is the Fermi–Dirac distribution function (E_F: the Fermi level of a molecular junction; k_B the Boltzmann constant; T the temperature, equal to 300 K); and T(E) is the transmission coefficient. Electronic structures of the dimer in the SSJ model are analyzed using the molecular projected self-consistent Hamiltonian (MPSH) method with effects of surrounding electrodes taken into consideration.⁴⁶

3 Results and discussion

Five typical conformations are mainly studied and discussed for the DCV4T dimer, i.e. C1–C5 provided in Fig. 1a. They are stabilized by the intermolecular interactions and exhibit no imaginary frequencies. C1 is the most energetically favorable conformation among all possible ones, and C2–C5 are attained by gradually decreasing the contact interface of the two monomers. The top monomer rotates by 180 degrees around the z axis relative to the bottom monomer in all conformations. Interactions between the two monomers in C1–C5 are confirmed to be non-covalent from the EDA study.^41–43 Specifically, the total interaction energy (ΔE_tot) between the top and bottom monomers is divided into four distinct energy terms in the EDA study, i.e. the electrostatic interaction energy (ΔE_elstat), the Pauli repulsion energy (ΔE_Pauli), the dispersion interaction energy (ΔE_disp) and the orbital or through-bond interaction energy (ΔE_orb), as shown by eqn (2). Negative (positive) values of energy in Fig. 2 means that the corresponding interactions favor (disfavor) the stabilization of the DCV4T dimer. Obviously, the dispersion interaction plays a critical role in stabilizing C1–C5 for the largest negative values of energy. The electrostatic interaction favors the stabilization of the dimer as well, but its effect is less than that of the dispersion interaction. The through-bond interaction is almost invariable and is notably weaker than the dispersion interaction for C1–C5. The Pauli interactions are repulsive, as a result of which the DCV4T dimer is destabilized. In a word, the negative value of ΔE_tot or stabilization of the DCV4T dimer is crucially dominated by the dispersion interaction, which proves the non-covalent nature of interaction between the monomers.

ΔE_tot = ΔE_elstat + ΔE_Pauli + ΔE_disp + ΔE_orb (2)

Fig. 2 Energy decomposition analysis (EDA) of the interaction between DCV4T monomers for C1–C5 in Fig. 1a.

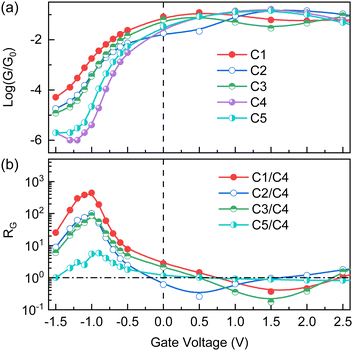
Next, electron transport properties are demonstrated and discussed. The gate effect on electron transport is taken into account here by applying various voltages to the metallic gate, which is a widely used technique for molecular electronic devices. With the gate effect, the device performance could be optimized by shifting the molecular energy levels relative to the electrode's Fermi level.^47–51 As shown in Fig. 3a, the conductances through C1–C5 decrease by several orders of magnitude when applying negative voltages to the gate, in comparison to the zero-voltage ones. Nonetheless, the relationship of conductance is robust among different conformations, and the deviations of conductance are apparent as well. In detail, the conductance through C1 is always the highest, and that through C4 is the lowest. C2 and C3 result in nearly identical conductances, which is the second highest. The conductance through C5 is lower than that through C2 or C3, but higher than that through C4. To highlight differences of conductance, R_G is defined and equals the ratio of conductance through other conformations to that through C4. R_G universally reaches the maximum when the voltage of −1.0 V is applied to the gate. R_G(C1/C4) is over 400 at this voltage, and even R_G(C5/C4) is close to 10. Clearly, four distinct states of conductance can be realized as the conformation extends from C1 to C5 under a certain negative gate voltage. When applying positive voltages to the gate, the relationship of conductance is affected by these voltages. For example, when the voltage is 0.5 V the lowest conductance is generated by C2, but it induced by C3 when the voltage increases to 1.5 V. Besides, magnitudes of conductance are roughly between 0.01G₀ and 0.1G₀ for C1–C5, and R_G is correspondingly less than one order of magnitude. Positive gate voltages are obviously unfavorable for the optimal performance of our designed SSJ.

Fig. 3 (a) Gate-dependent conductances G through different conformations of the DCV4T dimer. G₀ is the quantum conductance. (b) Conductance ratios R_G of other conformations to C4 under gate voltages. Dashed lines mark the zero voltage applied to the gate, and R_G = 1 is marked by a dashed–dotted line.

To understand conductances of different conformations, it is first necessary to analyze the transmission spectra and energy levels of frontier molecular orbitals (FMOs). Several transmission peaks appear above the Fermi level for C1–C5 in Fig. 4. These are generated by electron tunneling through the lowest unoccupied molecular orbitals of the dimer, labelled as LUMO, LUMO+1, … in Table 1. LUMO and LUMO+1 are nearly degenerate in energy for C2, C4 and C5, and thus related transmission peaks almost overlap. The transmission peaks below the Fermi level are associated with the highest occupied molecular orbitals of the dimer, labelled as HOMO and HOMO−1 in Table 1. Since the transmission peaks associated with LUMO and LUMO+1 are positioned near Fermi levels of SSJs, they potentially make crucial contributions to the conductance. A transmission dip is surprisingly witnessed at the Fermi level for C4, inducing smallest transmission coefficients closely below the Fermi level. This contrasts significantly with the scenarios observed for other conformations and could substantially impact the conductance of C4, especially under negative gate voltages.

Fig. 4 Transmission spectra of SSJs with different conformations of the dimer: (a) for C1–C3 and (b) for C3–C5. Dash-dotted lines mark the Fermi levels of SSJs. The yellow shadows highlight the energy interval from −0.13 to 0.13 eV, which is crucial for the conductance at room temperature (T = 300 K). These spectra are calculated without voltages applied to the metallic gate.

Table 1 Energy levels of FMOs relative to Fermi levels of SSJs for C1–C5 (in units of eV). The data are calculated using the MPSH method

FMO	C1	C2	C3	C4	C5
LUMO+3	0.58	0.61	0.55	0.54	0.52
LUMO+2	0.35	0.35	0.45	0.39	0.38
LUMO+1	0.19	0.09	0.22	0.09	0.11
LUMO	0.02	0.07	0.03	0.07	0.06
HOMO	−1.09	−1.14	−1.13	−1.04	−1.12
HOMO−1	−1.27	−1.18	−1.18	−1.27	−1.27

---

According to eqn (1), the conductance G is primarily governed by transmission coefficients in a certain energy window from E_F − 5k_BT to E_F + 5k_BT (k_B), which is marked by the yellow color in Fig. 4 and referred to as the TEW. When no voltages are applied to the gate, the LUMO-related transmission peak is invariably present in the TEW for all considered conformations. This is the reason why conductances of different conformations are close to each other and the maximum of R_G is less than 3 at zero voltage (Fig. 3b). For C4, although the transmission dip is within the TEW, the conductance is dominated by larger transmission coefficients, similar to the fact that (1 + 10⁻⁶) is nearly equal to 1. Concerning positive voltages applied to the gate, the transmission spectra generally shift down in energy, relative to the zero-voltage ones in Fig. 4. For example, the transmission peak of C1 related to LUMO could appear below the Fermi level in this case, and that related to LUMO+1 becomes closer to the Fermi level. Since the applied voltage is moderate (from 0.0 to 2.5 V), the transmission peaks associated with the LUMO and LUMO+1 are still closer to Fermi levels of SSJs than others (see the ESI†). On the other hand, differences between the LUMO and LUMO+1 are maximally 0.19 for C1–C5 in energy, less than the energy width of the TEW (10k_BT ≈ 0.26 eV at room temperature). The two facts imply that at least one of these two transmission peaks is located in the TEW under positive voltages. Hence, the conductance shows minor variations as the dimer extends from C1 to C5, with R_G being less than one order of magnitude at most, similar to the zero-voltage case.

For negative voltages applied to the gate, the transmission spectra shift up in energy, contrary to the case of positive gate voltages. The HOMO-related transmission peaks tend to approach the Fermi level, but due to deep positions in energy, they are out of the TEW and contribute little to the charge transport, especially for voltages from 0.0 to −1.5 V. The LUMO-related transmission peaks drift away from the Fermi level as the negative gate voltage increases, potentially moving beyond the TEW. In such a circumstance, transmission coefficients in the TEW are generally determined by tails of the LUMO-related transmission peaks. Meanwhile, the impact of the C4-related transmission dip becomes increasingly significant, and its maximum effect can be reached at a specific negative gate voltage. These are the reasons why conductances of C1–C5 decrease under negative gate voltages and R_G reaches the largest value at −1.0 V. When the negative voltage further increases in magnitude, this transmission dip tends to be disrupted, leading to the conductance increase for C4 and the reduction of R_G at higher voltages.

The C4-related transmission dip is a key factor for the device performance R_G. This dip is originated from the destructive quantum interference (DQI) effect. As reported previously,^52–56 the DQI effect can be predicted by the following equation:

Here, T_i,j(E) is the transmission coefficient of an electron with energy E from site i to j; s_n = φⁿ_iφⁿ_j and φⁿ_i is the amplitude of the nth molecular orbital on site i; ε_n is the corresponding energy of the molecular orbital; η is an infinitesimal constant. The right side of eqn (3) is actually the approximation for |g_i,j(E)|² and g_i,j(E) is the Green's function of the molecule. The sign of s_n is a key factor for the DQI effect and it is dependent on the orbital phases of sites i and j. If the orbital phases of sites i and j are the same in a molecular orbital, a symmetrical (S) pattern is attained and s_n is positive. Conversely, if the orbital phases of sites i and j are opposite, an anti-symmetrical (AS) pattern is attained and s_n is negative.

To unfold the DQI effect inherent in C4 using eqn (3), (i) ε_1,2,3 is artificially set to be −1.0, 0.5 and 1.0 eV just for clarity, and n = 1, 2, 3 correspond to the HOMO, LUMO and LUMO+1 of the dimer; (ii) sites i and j denote the end groups of the dimer; (iii) s₁ and s₂ are set to be positive, while s₃ is set to be negative, according to the calculated orbital phase patterns (OPPs) of the end group for C4. After applying these settings, a DQI-related transmission dip naturally appears between HOMO (n = 1) and LUMO (n = 2) in Fig. 5b, consistent with the transmission data of C4 in Fig. 4b. If the OPP of the LUMO is different from those of the HOMO and LUMO+1, like C1 and C2 cases, the signs of s₁ and s₃ should be opposite to that of s₂. As a consequence, the transmission dip completely disappears near the same energy position (see Fig. 5c), in agreement with the transmission data of C1–C3 and C5 in Fig. 4. From the perspective of quantum interference, the OPPs of the three FMOs in C1–C3 and C5 physically lead to the constructive quantum interference (CQI) effect,⁵⁶ which basically governs the transmission between the HOMO and LUMO.

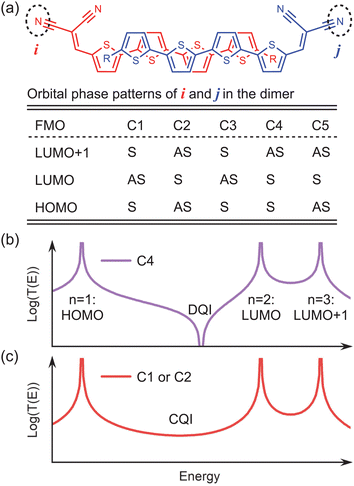Fig. 5 (a) Orbital phase patterns (OPPs) of the end groups in C1–C5. The end groups are marked by dashed circles, and named i and j. S (AS) means that the orbital phase of site i is the same as (opposite to) that of site j. The patterns are obtained by analyzing related FMOs calculated by the MPSH method (see the ESI†). (b)–(c) Schematic graphs for the quantum interference generated by specific OPPs using eqn (3).

R _G(C1/C4) > R_G(C3/C4) > R_G(C5/C4) around the gate voltage of −1.0 V can be understood by the transmission below the Fermi level in Fig. 4, specifically by T(E,C1) > T(E,C3) > T(E,C5). More basically, the spatial overlap between the monomers plays a critical role in these two results. In Fig. 1a, the spatial overlap is the greatest for C1 and the least for C5, while that for C3 is intermediate. The greater overlap between monomers is present in space, the higher transmission can be achieved through the dimer. For R_G(C2/C4) ≈ R_G(C3/C4), the main reason is that the LUMO of C3 is energetically lower than that of C2 in Table 1 and a higher transmission tail is generated below the Fermi level for C3. This effect compensates for the reduced spatial overlap between monomers in the electron transport of C3.

Finally, the underlying mechanism is illustrated for the formation of the OPPs of the end group in the dimer. The illustration is based on three factors: (i) the OPPs of the free monomer; (ii) the bonding and anti-bonding interactions between the FMOs of the monomer when forming the FMOs of the dimer; and (iii) the geometries of different conformations. By analyzing the FMOs of the free DCV4T, they are seen to be primarily composed of p_z orbitals of carbon and nitrogen atoms (see Fig. S5-b in the ESI†). To illustrate the mechanism clearly and simply, the OPPs in Fig. 6a are constructed from the two FMOs of the free monomer with some simplifications. The p_z orbitals of C and N atoms, crucially contributing to the second factor, are included in the shown OPPs of the free monomer. During dimer formation, possible interactions between FMOs of the monomers are bonding and anti-bonding. The bonding interaction between the HOMOs (LUMOs) of the monomers leads to the HOMO−1 (LUMO) of the dimer, while the anti-bonding interaction between the HOMOs (LUMOs) of the monomers leads to the HOMO (LUMO+1) of the dimer (see Fig. 6b). As for geometries of conformations, two points need to be emphasized. Firstly, before forming the considered conformations C1–C5, one of monomers rotates by 180 degrees around the z axis relative to the other monomer (vide supra). Thus the HOMOs and LUMOs of the two (top and bottom) monomers initially have opposite OPPs (see Fig. 6c). The second is the relative position of the top and bottom monomers in real geometries of conformations.

Fig. 6 (a) Orbital phase patterns (OPPs) in the HOMO and LUMO of the free monomer. For simplicity and clarity, p_z orbitals are shown only for N1, N2 and C1–C10. (b) The relationship between the FMOs of the monomers and those of the dimer when considering the bonding and anti-bonding interactions. The FMOs of the monomer are denoted as m.HOMO and m.LUMO, and those of the dimer as d.HOMO, d.LUMO, etc. (c) The OPPs in the HOMOs and LUMOs of the top and bottom monomers before forming the dimer. (d) Representative OPPs formed in the FMOs of C3 and C4. Vertical dashed lines mark positions of S1 of the top monomer relative to the bottom one. Red/green p_z orbitals mark the ones that make crucial contributions to the anti-bonding/bonding interaction between the FMOs of the monomers in the dimer.

Here, C3 and C4 are taken as representative examples to illustrate the OPPs of the end groups in some typical FMOs of the dimer. Combining the above three factors, a symmetrical OPP of the end groups (marked by i and j) is derived in the HOMO due to the anti-bonding interaction (see Fig. 6d), while the bonding interaction favors an anti-symmetrical OPP of the end groups in the HOMO−1 for C4. For C3, an anti-symmetrical OPP of the end groups is required by the bonding interaction in the LUMO, but the anti-bonding interaction causes a symmetrical OPP of the end groups in LUMO+1. These results are consistent with those in Fig. 5a. For the FMOs of other conformations, the OPPs of the end groups can be explained in similar ways. As a general rule, reversed OPPs of the end groups will be generated in the LUMO and LUMO+1 (or HOMO−1 and HOMO) of the dimer, but the OPPs of the end groups in the HOMO and LUMO of the dimer can vary and are not definitively determined.

To implement our proposed supramolecular switch experimentally, the piezo-modulated STM-BJ technique reported recently by Zhou et al.²³ could be utilized to mechanically stretch and compress the [π⋯π] dimer, thereby accessing its four distinct conductance states. According to this work, the movement distance of the electrode is related to the voltage applied to the piezoelectric ceramic, and the required displacement amplitude of 2–11 Å (Table S1 in ESI†) can be achieved easily for our switching device. Besides, the experiment conducted by Li et al.²⁹ indicates that long molecules at high concentrations favor the formation of the corresponding dimer in the device environment, which is also helpful for realizing the proposed device. We note that similar [π⋯π] dimers are studied for their electron transport properties in ref. 29. However, our advances are (i) five typical conformations are explicitly identified for the considered dimer, which are stabilized by the intermolecular [π⋯π] interaction without imaginary frequencies; (ii) these five conformations exhibit four distinct conductance states, which are valuable for the future development of multi-state molecular switches; and (iii) the involved DQI effect is confirmed through careful investigations (see Section S5 of the ESI†), and the underlying mechanism is illustrated as well. The proposed molecular switching device finally needs to be validated in further experiments, especially its performance and robustness.

4 Conclusions

In this study, a non-covalent [π⋯π] dimer is designed using DCV4T, and its electron transport properties are mainly investigated and discussed through DFT calculations and the NEGF technique. Here, for this dimer, five crucial conformations C1–C5 are taken into account. The non-covalent interactions between the involved monomers are confirmed via EDA studies in these conformations. Importantly, it is discovered that these five conformations can lead to four distinct conductance states. The presence of multiple conductance states is attributed to the DQI effect and the spatial overlap of the two DCV4T monomers. Hence, a multi-state molecular switch is revealed based on this [π⋯π] dimer, and it has the potential to operate at room temperature.²⁹

Data availability

The data supporting this article have been included as parts of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Start-Up Funding of Hangzhou Normal University under Grant No. 4245C50222204105 and the National Natural Science Foundation of China under Grant No. 11934355.

Notes and references

1. M. del Valle, R. Gutiérrez, C. Tejedor and G. Cuniberti, Nat. Nanotechnol., 2007, 2, 176–179.
2. C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445.
3. L. Gerhard, K. Edelmann, J. Homberg, M. Valášek, S. G. Bahoosh, M. Lukas, F. Pauly, M. Mayor and W. Wulfhekel, Nat. Commun., 2017, 8, 14672.
4. Z.-Y. Cai, Z.-W. Ma, W.-K. Wu, J.-D. Lin, L.-Q. Pei, J.-Z. Wang, T.-R. Wu, S. Jin, D.-Y. Wu and Z.-Q. Tian, J. Phys. Chem. Lett., 2023, 14, 9539–9547.
5. R. Wang, A. Tang, Z. Li, Y. Li, D. Qu and H. Li, CCS Chem., 2024, 6, 465–472.
6. J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022.
7. W. Si, J. Li, G. Li, C. Jia and X. Guo, J. Mater. Chem. C, 2024, 12, 751–764.
8. V. Meded, A. Bagrets, K. Fink, R. Chandrasekar, M. Ruben, F. Evers, A. Bernand-Mantel, J. S. Seldenthuis, A. Beukman and H. S. J. van der Zant, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 245415.
9. T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938.
10. J. Huang, R. Xie, W. Wang, Q. Li and J. Yang, Nanoscale, 2016, 8, 609–616.
11. K. Zhang, C. Wang, M. Zhang, Z. Bai, F. F. Xie, Y. Z. Tan, Y. Guo, K. J. Hu, L. Cao, S. Zhang, X. Tu, D. Pan, L. Kang, J. Chen, P. Wu, X. Wang, J. Wang, J. Liu, Y. Song, G. Wang, F. Song, W. Ji, S. Y. Xie, S. F. Shi, M. A. Reed and B. Wang, Nat. Nanotechnol., 2020, 15, 1019–1024.
12. J. Li, S. Hou, Y.-R. Yao, C. Zhang, Q. Wu, H.-C. Wang, H. Zhang, X. Liu, C. Tang, M. Wei, W. Xu, Y. Wang, J. Zheng, Z. Pan, L. Kang, J. Liu, J. Shi, Y. Yang, C. J. Lambert, S.-Y. Xie and W. Hong, Nat. Mater., 2022, 21, 917–923.
13. C. P. Collier, G. Mattersteig, E. W. Wong, Y. Luo, K. Beverly, J. Sampaio, F. M. Raymo, J. F. Stoddart and J. R. Heath, Science, 2000, 289, 1172–1175.
14. P. Liljeroth, J. Repp and G. Meyer, Science, 2007, 317, 1203–1206.
15. T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7, 215–220.
16. C. Wu, D. Bates, S. Sangtarash, N. Ferri, A. Thomas, S. J. Higgins, C. M. Robertson, R. J. Nichols, H. Sadeghi and A. Vezzoli, Nano Lett., 2020, 20, 7980–7986.
17. L.-Q. Pei, J. R. Horsley, J.-W. Seng, X. Liu, Y. Q. Yeoh, M.-X. Yu, X.-H. Wu, A. D. Abell, J.-F. Zheng, X.-S. Zhou, J. Yu and S. Jin, ACS Appl. Mater. Interfaces, 2021, 13, 57646–57653.
18. H. Chen and J. F. Stoddart, Nat. Rev. Mater., 2021, 6, 804–828.
19. X. Li, W. Ge, S. Guo, J. Bai and W. Hong, Angew. Chem., Int. Ed., 2023, 62, e202216819.
20. K. Yoshida, I. V. Pobelov, D. Z. Manrique, T. Pope, G. Mészáros, M. Gulcur, M. R. Bryce, C. J. Lambert and T. Wandlowski, Sci. Rep., 2015, 5, 9002.
21. R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099–1104.
22. A. Magyarkuti, O. Adak, A. Halbritter and L. Venkataraman, Nanoscale, 2018, 10, 3362–3368.
23. P. Li, S. Hou, B. Alharbi, Q. Wu, Y. Chen, L. Zhou, T. Gao, R. Li, L. Yang, X. Chang, G. Dong, X. Liu, S. Decurtins, S.-X. Liu, W. Hong, C. J. Lambert, C. Jia and X. Guo, J. Am. Chem. Soc., 2022, 144, 15689–15697.
24. A. Feng, Y. Zhou, M. A. Y. Al-Shebami, L. Chen, Z. Pan, W. Xu, S. Zhao, B. Zeng, Z. Xiao, Y. Yang and W. Hong, Nat. Chem., 2022, 14, 1158–1164.
25. S. T. Schneebeli, M. Kamenetska, Z. Cheng, R. Skouta, R. A. Friesner, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2011, 133, 2136–2139.
26. M. Carini, M. P. Ruiz, I. Usabiaga, J. A. Fernández, E. J. Cocinero, M. Melle-Franco, I. Diez-Perez and A. Mateo-Alonso, Nat. Commun., 2017, 8, 15195.
27. D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988.
28. S. Wu, M. T. González, R. Huber, S. Grunder, M. Mayor, C. Schönenberger and M. Calame, Nat. Nanotechnol., 2008, 3, 569–574.
29. X. Li, Q. Wu, J. Bai, S. Hou, W. Jiang, C. Tang, H. Song, X. Huang, J. Zheng, Y. Yang, J. Liu, Y. Hu, J. Shi, Z. Liu, C. J. Lambert, D. Zhang and W. Hong, Angew. Chem., Int. Ed., 2020, 59, 3280–3286.
30. G. C. Solomon, J. Vura-Weis, C. Herrmann, M. R. Wasielewski and M. A. Ratner, J. Phys. Chem. B, 2010, 114, 14735–14744.
31. S. Caneva, P. Gehring, V. M. García-Suárez, A. García-Fuente, D. Stefani, I. J. Olavarria-Contreras, J. Ferrer, C. Dekker and H. S. J. van der Zant, Nat. Nanotechnol., 2018, 13, 1126–1131.
32. Y. Han, C. Nickle, Z. Zhang, H. P. A. G. Astier, T. J. Duffin, D. Qi, Z. Wang, E. del Barco, D. Thompson and C. A. Nijhuis, Nat. Mater., 2020, 19, 843–848.
33. P. Zhou, Y. Fu, M. Wang, R. Qiu, Y. Wang, J. F. Stoddart, Y. Wang and H. Chen, J. Am. Chem. Soc., 2023, 145, 18800–18811.
34. X. Li, Y. Zheng, Y. Zhou, Z. Zhu, J. Wu, W. Ge, Y. Zhang, Y. Ye, L. Chen, J. Shi, J. Liu, J. Bai, Z. Liu and W. Hong, J. Am. Chem. Soc., 2023, 145, 21679–21686.
35. R. Fitzner, E. Reinold, A. Mishra, E. Mena-Osteritz, H. Ziehlke, C. Körner, K. Leo, M. Riede, M. Weil, O. Tsaryova, A. Weiß, C. Uhrich, M. Pfeiffer and P. Bäuerle, Adv. Funct. Mater., 2011, 21, 897–910.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.02, Gaussian Inc., Wallingford CT, 2019.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
39. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
40. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
41. R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753–8765.
42. P. R. Horn, E. J. Sundstrom, T. A. Baker and M. Head-Gordon, J. Chem. Phys., 2013, 138, 134119.
43. P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107.
44. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov and U. G. Vej-Hansen, et al. , J. Phys.: Condens. Matter, 2020, 32, 015901.
45. M. Van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
46. K. Stokbro, J. Taylor, M. Brandbyge, J.-L. Mozos and P. Ordejón, Comput. Mater. Sci., 2003, 27, 151–160.
47. N. J. Tao, Nat. Nanotechnol., 2006, 1, 173–181.
48. Z. Li, M. Smeu, A. Rives, V. Maraval, R. Chauvin, M. A. Ratner and E. Borguet, Nat. Commun., 2015, 6, 6321.
49. N. Xin, X. Li, C. Jia, Y. Gong, M. Li, S. Wang, G. Zhang, J. Yang and X. Guo, Angew. Chem., Int. Ed., 2018, 57, 14026–14031.
50. Y. Li, M. Buerkle, G. Li, A. Rostamian, H. Wang, Z. Wang, D. R. Bowler, T. Miyazaki, L. Xiang, Y. Asai, G. Zhou and N. Tao, Nat. Mater., 2019, 18, 357–363.
51. P. Zhou, J. Zheng, T. Han, L. Chen, W. Cao, Y. Zhu, D. Zhou, R. Li, Y. Tian, Z. Liu, J. Liu and W. Hong, Nanoscale, 2021, 13, 7600–7605.
52. T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265.
53. K. Yoshizawa, Acc. Chem. Res., 2012, 45, 1612–1621.
54. X. Zhao, V. Geskin and R. Stadler, J. Chem. Phys., 2017, 146, 092308.
55. C. J. Lambert and S. Liu, Chem. – Eur. J., 2018, 24, 4193–4201.
56. H. Chen, S. Hou, Q. Wu, F. Jiang, P. Zhou, L. Zhang, Y. Jiao, B. Song, Q.-H. Guo, X.-Y. Chen, W. Hong, C. J. Lambert and J. F. Stoddart, Matter, 2021, 4, 3662–3676.

---

Footnote

† Electronic supplementary information (ESI) available: Details of supramolecular junction geometries, transmission spectra at non-zero gate voltages, frontier molecular orbitals in supramolecular junctions, etc. See DOI: https://doi.org/10.1039/d4cp03131h

---