αnhm-GeSe: a multifunctional semiconductor combining auxeticity and piezoelectricity†
Jiajun
Zhu
 a,
Heyun
Zhao
a,
Heyun
Zhao
 a and
Wanbiao
Hu
a and
Wanbiao
Hu
 *abcd
*abcd
aYunnan Key Laboratory of Electromagnetic Materials and Devices, National Center for International Research on Photoelectric and Energy Materials, School of Materials and Energy, Yunnan University, Kunming, 650091, P. R. China. E-mail: huwanbiao@ynu.edu.cn
bElectron Microscopy Center, Yunnan University, Kunming 650091, P. R. China
cSouthwest United Graduate School, Kunming 650092, P. R. China
dSchool of Engineering, Yunnan University, Kunming 650091, P. R. China
First published on 6th December 2024
Abstract
Multifunctional materials with outstanding performance have enormous potential applications in the next generation of nanodevices. Using first principles calculations, we design a series of multifunctional two-dimensional materials in monolayer αnhm-GeSe (n, m = 1, 2) that combine auxeticity and piezoelectricity. Due to the similar local structures of α-GeSe and h-GeSe, monolayer αnhm-GeSe can be designed through the combination of these two materials. Elastic constants and phonon dispersion curves confirm that all the structures are mechanically and dynamically stable. Monolayer αnhm-GeSe exhibits auxetic properties with an in-plane negative Poisson's ratio along the diagonal direction. An out-of-plane negative Poisson's ratio effect can be observed by applying tensile strain in the x-direction, which is beneficial for mechanical devices. Only a few materials are both in-plane and out-of-plane auxetic. In addition, monolayer αnhm-GeSe can exhibit electric polarization because of the breaking of the central symmetry, demonstrating in-plane piezoelectric properties with strong anisotropy. The above results make monolayer αnhm-GeSe an interesting multifunctional material and provide a candidate material for a nanoscale device.
Introduction
Two-dimensional materials exhibit excellent performance in various fields, such as ferroelectricity, ferromagnetism, mechanics, optics, catalysis, electrochemistry, etc.1–3 Multifunctional two-dimensional materials have attracted considerable attention due to their highly integrated and distinct properties, which hold even greater promise to become the next generation of nanodevices.4 Auxeticity corresponds to the situation in which the induced strain in an orthogonal direction to the applied strain has the same sign as the applied strain. Usually, when tensile strain is applied in one direction the material is compressed in the other directions. The Poisson ratio is then defined to be positive. In an auxetic material, the Poisson ratio is negative.5 This unique phenomenon can enhance mechanical properties, such as shear modulus, indentation resistance and fracture toughness.6,7 As a result, the auxetic materials have been extensively applied in foam, cubic metals and α-cristobalite.8,9 Until today, only a few materials exhibit auxetic properties, such as BI, Be5C2, Ag2S and δ-phosphorene, which implies that exploring 2D auxetic materials is meaningful.10–12The linear coupling between mechanical deformation and electric fields manifests as the piezoelectric effect, which plays a crucial role in the application of miniaturized and high-performance devices.13 Two-dimensional piezoelectric materials can endure much higher strain than brittle traditional piezoelectrics, enabling a broader range of applications such as sensors and nanoelectromechanical systems.14 Recently, various types of monolayer or few-layer two-dimensional piezoelectric materials have been successively reported, including CuInP2S6, transition metal dichalcogenides (TMDs), group III–IV materials, and group IV monochalcogenides (MXs, where M = Ge, Sn, and X = S, Se).15–17 Due to their exceptional mechanical and piezoelectric properties, group-IV monochalcogenides have garnered significant attention among these piezoelectric candidate materials.18–20
Over the past few years, a considerable number of GeSe allotropes have been theoretically discovered, and some have since been successfully synthesized experimentally.21,22 The most stable phase, α-GeSe, exhibits a puckered structure similar to black phosphorene, displaying both in-plane ferroelectricity and out-of-plane NPR.23 The second synthesized allotrope, β-GeSe, is transformed from α-GeSe under high pressure.24 This allotrope also exhibits outstanding piezoelectric and thermoelectric properties.25 Recently, a hexagonal allotrope of group-IV monochalcogenides, named γ-GeSe, has been synthesized on a SiO2 substrate.26 The synthesis of these allotropes has not only broadened the possibilities of diverse metastable allotropes but also stimulated the research and development of novel GeSe materials with intriguing attributes like mechanical and piezoelectric properties. Additionally, various other allotropes like δ-GeSe, T-GeSe, h-GeSe, etc., have been theoretically predicted using density functional theory (DFT), and these monolayers exhibit semiconductor and piezoelectric properties.27–29
Here, in this work, we design a series of group-IV monochalcogenide hybrid αnhm-GeSe by combining the α-GeSe and h-GeSe structures through DFT theoretical predictions, in order to achieve coupled auxeticity and piezoelectricity with the following considerations.26 Firstly, GeSe has various phases with intriguing piezoelectric and mechanical properties.24,30–34 Secondly, two α-GeSe and h-GeSe phases share the same structural motif of threefold-coordinated Ge/Se atoms surrounded by the nearest neighbors Se/Ge atoms in a tetrahedral arrangement and this tetrahedral arrangement can even be maintained in specific intra-layer connections of different structures, which exhibit great potential to be combined with individual blocks to design new allotropes. Thirdly, the breaking of the symmetry of αnhm-GeSe leads to the existence of electric polarization and the puckered structure is much more flexible (softer), so that it is possible to have a negative Poisson ratio.
The phonon dispersion and molecular dynamics simulation results reveal that monolayer αnhm-GeSe is structurally stable. The puckered structure of αnhm-GeSe results in its NPR properties along both in-plane and out-of-plane directions. The underlying physics of out-of-plane NPR is related to the competition between two strain responses: the response of strain along the x-direction to the z-direction and the response of strain along the y-direction to the z-direction. Moreover, monolayer αnhm-GeSe displays strong in-plane anisotropy in the piezoelectricity properties. Our results demonstrate that monolayer αnhm-GeSe is a novel multifunctional material that holds great potential applications in mechanics and optoelectronic devices.
Method
First-principles calculations were performed based on density functional theory as implemented in the Vienna ab initio simulation package (VASP).35–37 The electron–electron interactions were treated within a generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE) for the exchange–correlation functional.38,39 We take the energy cutoff 450 eV and the thickness of 15 Å for vacuum. The criteria were set to 10−8 eV and 10−5 eV Å−1 for energy and force with the 18× 6 × 1 Monkhorst–Pack sampling for self-consistent calculations, respectively. For better evaluation of electronic and optical properties, the hybrid functional (HSE06) was adopted.40 Besides, the phonon dispersion is performed based on density functional perturbation theory (DFPT) as embedded in the Phonopy program.41 The phonon dispersion using a 4 × 4 × 1 supercell.Results and discussion
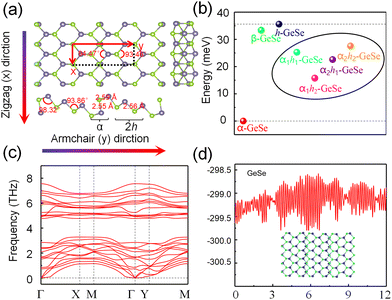
Fig. 1(a) shows monolayer α-GeSe with a layer-puckered structure that can be obtained by exfoliating from the lower symmetry bulk phase along the (100) plane, similar to black phosphorus. The unit cell of α-GeSe has an in-plane Ge–Se bond length of 2.63 Å, which is longer than the out-of-plane bond length (2.54 Å). The in-plane Se–Ge–Se bond angle is 96.46°, and the dihedral angle Se–Ge–Se is 97.39°. Fig. 1(b) shows the periodic structure of monolayer h-GeSe, whose unit cell consists of two atoms, similar to blue phosphorus. To better fit with monolayer α-GeSe, we reconstructed the unit cell of monolayer h-GeSe to be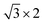 , which comprises four atoms in a unit cell. This structure consists of two chains: one chain is composed of germanium and selenium (Ge–Se–Ge), and the other consists of selenium and germanium (Se–Ge–Se). The bond length and angle in monolayer h-GeSe are 2.57 Å and 91.27°, respectively, similar to α-GeSe. Considering the local similarity of the two structures, we propose assembling them together. Specifically, we use the α unit cell of α-GeSe and the chain (Se–Ge–Se, Ge–Se–Ge) of h-GeSe as building blocks denoted by α and h. Fig. 1(c) demonstrates the potential to design a range of GeSe materials by combining nα and mh, forming what we refer to as αnhm-GeSe.
, which comprises four atoms in a unit cell. This structure consists of two chains: one chain is composed of germanium and selenium (Ge–Se–Ge), and the other consists of selenium and germanium (Se–Ge–Se). The bond length and angle in monolayer h-GeSe are 2.57 Å and 91.27°, respectively, similar to α-GeSe. Considering the local similarity of the two structures, we propose assembling them together. Specifically, we use the α unit cell of α-GeSe and the chain (Se–Ge–Se, Ge–Se–Ge) of h-GeSe as building blocks denoted by α and h. Fig. 1(c) demonstrates the potential to design a range of GeSe materials by combining nα and mh, forming what we refer to as αnhm-GeSe.
 | ||
| Fig. 1 Design of the αnhm-GeSe structures by two blocks. Top and side views of α-GeSe (a) and h-GeSe (b); (c) diagram of nα and mh assembly called αnhm-GeSe. | ||
To confirm our idea, through first principles calculations, we predicted αnhm-GeSe (n, m = 1, 2) structures. The study primarily examines the structure of α1h2-GeSe (Fig. 2(a)), comprising four atomic layers with each Ge atom bonded to its three nearest Se atoms through sp3 hybridization. Fig. 2(a) illustrates that the Ge–Se bond lengths in the α1h2-GeSe range from 2.55 to 2.59 Å, resembling those of α-GeSe (2.54 Å) and h-GeSe (2.57 Å). The in-plane bond angle and dihedral angle of Se–Ge–Se are 94.47° and 93.46°, respectively, which closely resemble those of α-GeSe (96.46°, 97.39°) and γ-GeSe (91.27°). Therefore, the local coordination environment of α1h2-GeSe resembles that of monolayer α- and h-GeSe. Additionally, the α1h2-GeSe structure combines one unit cell of α-GeSe with two unit chains of h-GeSe. Consequently, this results in an increased layer thickness of α1h2-GeSe to 3.78 Å, exceeding the layer thicknesses of α-GeSe and h-GeSe at 2.6 Å and 1.45 Å, respectively. Additional structures are depicted in Fig. S1 of the ESI.†
In order to compare the energy differences between these allotropes, we calculated the total energy of αnhm-GeSe and the two parent phases. The results of the calculations are shown in Table 1, with the monolayer α-GeSe taken as the zero energy reference point. We notice that the total energy of α-GeSe is the most stable phase. The total energy of αnhm-GeSe is ∼30 meV per atom higher than that of α-GeSe, while its energy is less than that of h-GeSe, as shown in Fig. 2(b). The above results show that the total energy of the mixed phase αnhm-GeSe lies between those of the two sub-phases (α-GeSe and h-GeSe), indicating that the mixed phase is a metastable phase.
| Allotrope | a | b | t | ΔE |
|---|---|---|---|---|
| α-GeSe | 3.98 | 4.26 | 2.60 | 0 |
| h-GeSe | 3.66 | 3.66 | 1.45 | 35.6 |
| β-GeSe | 3.67 | 5.89 | 1.78 | 33.4 |
| α1h1-GeSe | 3.79 | 14.57 | 3.48 | 27.8 |
| α1h2-GeSe | 3.79 | 10.48 | 3.78 | 15.8 |
| α2h1-GeSe | 3.79 | 22.77 | 4.01 | 23.4 |
| α2h2-GeSe | 3.79 | 14.74 | 4.72 | 29.7 |
To assess the structural stability, we calculated the phonon dispersion and conducted molecular dynamics simulations. The phonon dispersion of the monolayer α1h2-GeSe is shown in Fig. 2(c), demonstrating no imaginary frequencies throughout the Brillouin zone, confirming the structural stability at 0 K. Additionally, the thermal stability of the monolayer α1h2-GeSe is confirmed by the results of an AIMD simulation, as shown in Fig. 2(d), illustrating that the structure remains stable for at least 12 ps at a temperature of 300 K. The phonon dispersions of the α1h2-, α1h2- and α1h2-GeSe structures are illustrated in Fig. S2 (ESI†). On the other hand, α1h2-GeSe belongs to space group Pmm2 (no. 25) within the orthorhombic system. For bulk materials, following Voigt notation conventions, the elastic modulus matrix can be expressed as follows:
 | (1) |
For 2D materials, we ignore the c-direction component, so the elastic modulus matrix become a second-order tensor, and can be written as follows:
 | (2) |
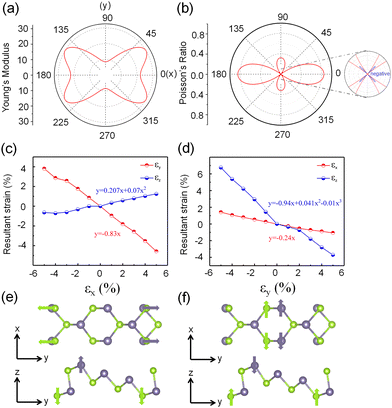
In light of its distinct puckered configuration, α1h2-GeSe is anticipated to display intriguing mechanical characteristics. In order to examine its mechanical behavior, we evaluated the Young's modulus Y(θ) and Poisson's ratio υ(θ) via the following expressions:43
 | (3) |
 | (4) |
Previous studies have reported that α-groupV exhibits out-of-plane NPR.44 The presence of a partial α phase structure exists in the mixed phase α1h2-GeSe structure; it is worthwhile to investigate whether α1h2-GeSe also possesses out-of-plane NPR. For studying the out-of-plane response mechanism, strain (ε) is defined as εi = (li − li0)/li0, where i refers to x, y, z directions, and li and li0 denote the lattice parameter along the i-direction with and without strain, respectively. The Poisson's ratio can be determined by fitting ε = −υ1εi + υ2εi2 + υ3εi3, where ε and υ1 represent the resultant strain and Poisson's ratio, respectively. This study examines the strain response of α1h2-GeSe ranging from −5% to +5%, as illustrated in Fig. 3(c) and (d). Under y-direction tension, εz decreases, leading to a reduction in the z-direction thickness of α1h2-GeSe with increasing εy strain, as denoted by the PPR value of υz = 0.24. Conversely, when subjected to x-direction tension, εz increases, causing an augmentation in the z-direction thickness of α1h2-GeSe with increasing εx strain, as shown by the NPR value of υz = −0.207, which is higher than that of α-phosphorene (−0.027)45 and SnSe (−0.17),46 but less than that of δ-GeSe (−0.32)47 and Ag2S (−0.52)12Table 2.
To enhance our understanding of the NPR effect in the z-direction, we propose that the Poisson's ratio of monolayer α1h2-GeSe in the z-direction results from the superposition of changes in strain εz caused by strain εx in the x-direction and changes in strain εz caused by strain εy in the y-direction. The tensile strain in the x-direction leads to the compression of the material along the y- and z-directions, whereas tensile strain in the y-direction additionally influences the compression strain in the z-direction. Hence, the z-direction strain can be expressed as εz = εz1 + εz2 = −Aεx − Bεy = −Cεx (A, B, C > 0). When there is tension strain (εx > 0) along the x-direction (refer to Fig. 3(e)), α1h2-GeSe will experience compression along the y-direction (εy < 0). Taking into account the impact of Poisson's ratio, when A > B × υyx, εz = −Cεx with C being positive. This results in a z-direction thickness decrease with increasing x-direction tension strain, resulting in a positive Poisson's ratio (PPR). Conversely, under tensile strain (εy > 0) along the y-direction (refer to Fig. 3(f)), α1h2-GeSe will undergo compression in the x-direction (εx < 0). If the A < B × υyx, thus εz = −Cεy and C < 0. This results in a z-direction thickness increase with increasing y-direction tension strain, results in NPR. In this context, we can calculate the values of A and B utilizing density functional theory (DFT). By applying strain εx/εy in the x/y-direction and eliminating the Poisson effect along the y/x-direction, the strain response coefficients for A and B in the z-direction are approximately 0.97 and 1.11.
To evaluate the electronic structure of α1h2-GeSe more accurately, we performed band structure calculations at the HSE06 level. Our results, depicted in Fig. 4(a), show that a monolayer of α1h2-GeSe is a semiconductor with a bandgap of 2.306 eV. The valence band maximum (VBM) is at the Γ point along the Γ M path, while the conduction band minimum (CBM) is at the M point.
 | ||
| Fig. 4 Electronic structure and light absorption. The band structure (a) and light absorption (b) of α1h2-GeSe at the HSE06 level. Here, the 0 means the Fermi level for the band structure. | ||
In general, the dielectric function is divided into a real part εr and an imaginary part εi. Without considering electron–hole or exciton effects, we calculate it based on the independent particle approximation.51 The imaginary part εi is obtained through VASP calculations, while the real part εr is derived using the Kramers–Kronig relation. The formula below establishes a direct relationship between light absorption w and the dielectric function:
 | (5) |
Fig. 4(b) presents the optical absorption spectra of α1h2-GeSe, which reveals a strong light absorption between the in-plane wx and wy absorption coefficients near the ultraviolet range, reaching a maximum value of 22.5% near 280 nm and 19% near 230 nm for the wx and wy directions, respectively. We compared the absorption of α1h2-GeSe to other transition metal dichalcogenides, such as α-GeSe and δ-GeS and found that α1h2-GeSe has a greater absorption in the ultraviolet range (23%), indicating its potential for use in ultraviolet applications.
By applying stress or strain to a non-centrosymmetric material, the piezoelectric effect can be induced. A third-rank piezoelectric stress tensors eijk and strain tensor dijk can be used to describe the piezoelectric response of a material. The relaxed piezoelectric tensor (eijk and dijk) include the electronic and ionic contributions,
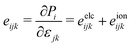 | (6) |
 | (7) |
 | (8) |
Due to the difference in electronegativity and the broken symmetry, monolayer α2h1-GeSe has in-plane electric polarization, akin to the characteristics of α-GeSe. Other hybrid phases also do not possess center inversion symmetry and can exhibit piezoelectricity by applying in-plane strain. Here the two independent d22(y) and d21 can be expressed as follows:
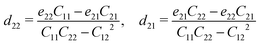 | (9) |
| Clamped-ion | Relaxed-ion | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Materials | C 11 | C 22 | C 12 | C 66 | e elc22 | e elc21 | d elc22 | d elc21 | e ion22 | e ion21 | d ion22 | d ion21 |
| α1h1-GeSe | 37.7 | 11.0 | 13.5 | 13.0 | 0.82 | 0.15 | 12.4 | −4.0 | 2.18 | 0.25 | 33.9 | −11.4 |
| α1h2-GeSe | 30.4 | 11.6 | 9.8 | 12.6 | 1.22 | 0.06 | 14.2 | −4.3 | 3.18 | 0.14 | 37.1 | −11.5 |
| α2h1-GeSe | 39.6 | 11.3 | 14.7 | 16.0 | 0.78 | 0.17 | 12.2 | −4.1 | 2.22 | 0.43 | 35.2 | −12.0 |
| α2h2-GeSe | 32.2 | 8.4 | 9.0 | 12.9 | 0.66 | 0.06 | 10.9 | −2.8 | 1.84 | 0.15 | 30.5 | −8.0 |
Summary
In conclusion, we design a new class of stable αnhm-GeSe (n, m = 1, 2), which are characterized by combining with α- and h-GeSe structures. These materials have thermodynamic, kinetic and mechanical stability. α1h2-GeSe demonstrates auxetic properties, with both in-plane and out-of-plane negative Poisson's ratios (NPR). The underlying physics for out-of-plane NPR is related to the competition of two the responses i.e. εz to εx and εy. Moreover, α1h2-GeSe also exhibits a strong anisotropy in mechanical and piezoelectric properties due to its unique structure. These findings suggest that α1h2-GeSe may have potential applications in mechanics and optoelectronics.Data availability
The data that support the findings of this study are available with the corresponding author and can be obtained upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China (Grant No. 22175150 and U2002217).References
- A. Carvalho, M. Wang, X. Zhu, A. S. Rodin, H. Su and A. H. Castro Neto, Nat. Rev. Mater., 2016, 1, 1–16 CrossRef.
- N. Youngblood, C. Chen, S. J. Koester and M. Li, Nat. Photon., 2015, 9, 247–252 CrossRef CAS.
- A. Chandrasekaran, A. Mishra and A. K. Singh, Nano Lett., 2017, 17, 3290–3296 CrossRef CAS.
- M. Sun and U. Schwingenschlögl, Phys. Rev. Appl., 2020, 14, 044015 CrossRef CAS.
- X. Kong, J. Deng, L. Li, Y. Liu, X. Ding, J. Sun and J. Z. Liu, Phys. Rev. B, 2018, 98, 184104 CrossRef.
- J. Choi and R. Lakes, Int. J. Fract., 1996, 80, 73–83 CrossRef.
- J. Choi and R. Lakes, J. Mater. Sci., 1992, 27, 5375–5381 CrossRef CAS.
- R. Lakes and K. Elms, J. Compos. Mater., 1993, 27, 1193–1202 CrossRef.
- F. Scarpa, IEEE Sig. Proc. Magaz., 2008, 25, 126–128 Search PubMed.
- S. Shen, Q. Wu, Y. Liang, B. Huang, Y. Dai and Y. Ma, Phys. Rev. Appl., 2021, 15, 014027 CrossRef CAS.
- Y. Wang, F. Li, Y. Li and Z. Chen, Nat. Commun., 2016, 7, 11488 CrossRef CAS.
- R. Peng, Y. Ma, Z. He, B. Huang, L. Kou and Y. Dai, Nano Lett., 2019, 19, 1227–1233 CrossRef CAS.
- S. Lee, H.-R. Kim, W. Jiang, Y.-K. Kwon and T. Low, Phys. Rev. B, 2024, 109, 195429 CrossRef CAS.
- T. Jia, L. Yang, J. Zhang, H. Kimura, H. Zhao, Q. Guo and Z. Cheng, Nanomaterials, 2023, 13, 2504 CrossRef CAS PubMed.
- J. A. Brehm, S. M. Neumayer, L. Tao, A. O. Hara, M. Chyasnavichus, M. A. Susner, M. A. McGuire, S. V. Kalinin, S. Jesse and P. Ganesh, et al. , Nat. Mater., 2020, 19, 43–48 CrossRef CAS PubMed.
- L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B, 2015, 92, 214103 CrossRef.
- Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han and M. C. Downer, et al. , Nano Lett., 2017, 17, 5508–5513 CrossRef CAS.
- Z. Guan, H. Hu, X. Shen, P. Xiang, N. Zhong, J. Chu and C. Duan, Adv. Electron. Mater., 2020, 6, 1900818 CrossRef CAS.
- L. Li, Z. Chen, Y. Hu, X. Wang, T. Zhang, W. Chen and Q. Wang, J. Am. Chem. Soc., 2013, 135, 1213–1216 CrossRef CAS.
- Y. J. Park and J. K. Kim, Adv. Mater. Sci. Eng., 2013, 2013 Search PubMed.
- A. S. Sarkar and E. Stratakis, Adv. Sci., 2020, 7, 2001655 CrossRef CAS.
- R. Fei, W. Kang and L. Yang, Phys. Rev. Lett., 2016, 117, 097601 CrossRef PubMed.
- Y. Xu, H. Zhang, H. Shao, G. Ni, J. Li, H. Lu, R. Zhang, B. Peng, Y. Zhu, H. Zhu and C. M. Soukoulis, Phys. Rev. B, 2017, 96, 245421 CrossRef.
- F. O. Von Rohr, H. Ji, F. A. Cevallos, T. Gao, N. P. Ong and R. J. Cava, J. Am. Chem. Soc., 2017, 139, 2771–2777 CrossRef CAS.
- S. Guan, C. Liu, Y. Lu, Y. Yao and S. A. Yang, Phys. Rev. B, 2018, 97, 144104 CrossRef.
- S. Lee, J.-E. Jung, H.-G. Kim, Y. Lee, J. M. Park, J. Jang, S. Yoon, A. Ghosh, M. Kim and J. Kim, et al. , Nano Lett., 2021, 21, 4305–4313 CrossRef CAS.
- Z. Li, Y. Gu, C. He and X. Zou, Phys. Rev. B, 2022, 106, 035426 CrossRef CAS.
- H. Lei, T. Ouyang, C. He, J. Li and C. Tang, Appl. Phys. Lette., 2023, 122, 062903 CrossRef CAS.
- C. Liu, S. Guan, H. Yin, W. Wan, Y. Wang and Y. Zhang, Appl. Phys. Lett., 2019, 115, 252904 CrossRef.
- S. Guan, C. Liu, Y. Lu, Y. Yao and S. A. Yang, Phys. Rev. B, 2018, 97, 144104 CrossRef.
- Z. Shu, B. Wang, X. Cui, X. Yan, H. Yan, H. Jia and Y. Cai, Chem. Enj. J., 2023, 454, 140242 CrossRef CAS.
- C. Huan, Y. Cai, D. R. Kripalani, K. Zhou and Q. Ke, Nanoscale Horiz., 2023, 8, 404–411 RSC.
- F. Chen, H. Xu, J. Wang, Z. Wang, X. Liu, Y. Lu and L. Wang, J. Appl. Phys., 2019, 125, 214303 CrossRef.
- J. Jang, J. Kim, D. Sung, J. H. Kim, J.-E. Jung, S. Lee, J. Park, C. Lee, H. Bae and S. Im, et al. , Nano Lett., 2023, 23, 3144–3151 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- G. Kresse and J. Furthmüller, Comp. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- D. Alfè, Comp. Phys. Commun., 2009, 180, 2622–2633 CrossRef.
- Z.-j Wu, E.-j Zhao, H.-p Xiang, X.-f Hao, X.-j Liu and J. Meng, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- X. Rong, Y. Li, S. Han, P. Cao, Y. Zeng, W. Xu, M. Fang, W. Liu, D. Zhu and Y. Lu, Phys. Chem. Chem. Phys., 2020, 22, 8739–8744 RSC.
- G. Qin, Q.-B. Yan, Z. Qin, S.-Y. Yue, H.-J. Cui, Q.-R. Zheng and G. Su, Sci. Rep., 2014, 4, 1–11 Search PubMed.
- L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Sci. Rep., 2016, 6, 1–9 CrossRef.
- Z. Li, Y. Gu, C. He and X. Zou, Phys. Rev. B, 2022, 106, 035426 CrossRef CAS.
- J.-W. Jiang and H. S. Park, Nat. Commun., 2014, 5, 4727 CrossRef CAS.
- J. Han, J. Xie, Z. Zhang, D. Yang, M. Si and D. Xue, Appl. Phys. Express, 2015, 8, 041801 CrossRef.
- B. Liu, M. Niu, J. Fu, Z. Xi, M. Lei and R. Quhe, Phys. Rev. Mater., 2019, 3, 054002 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- G.-J. Lee, M.-K. Lee, J.-J. Park, D. Y. Hyeon, C. K. Jeong and K.-I. Park, ACS Appl. Mater. Interfaces, 2019, 11, 37920–37926 CrossRef CAS.
- W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao and T. F. Heinz, et al. , Nature, 2014, 514, 470–474 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04045g |
| This journal is © the Owner Societies 2025 |