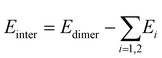Enantioselective interactions of aminonitrile dimers

Abstract

Enantioenrichment of amino acids is essential during the early chemical evolution leading to the origin of life. However, the detailed molecular mechanisms remain unsolved. Dimerization of enantiomers is the first molecular process in the nucleation of deposition and crystallization, which are both essential for enantioenrichment. Here, we report the enantioselective interactions of dimers of chiral intermediates, i.e., aminonitriles, in both gas and water environments based on density functional theory (DFT) and more accurate coupled-cluster (CC) calculations. We show that all the aminonitriles stabilize the homochiral dimer preferentially to the heterochiral dimer in the gas phase, while this trend was not observed in water. The energies of the enantioselective interactions in aminonitriles are substantially lower compared to those in amino acids, especially isovaline. These results suggest that prebiotic enhancements of enantiomeric excess are more likely to occur in amino acids than in the aminonitrile intermediates.

---

1. Introduction

All living things on Earth are made up of specific biomolecules such as amino acids, sugars, and nucleotides, and a unique property of these biomolecules is their chirality. Although all amino acids, except glycine, can exist in two chiral forms (L- and D-forms), the L-form amino acids are predominantly used by life on Earth. This means that all the molecular chirality must have been selected before the emergence of life. However, the mechanisms underlying chiral selection are still not fully clarified. The process of acquiring chirality would provide clear insights into early prebiotic reactions.

To achieve definitive homochirality, at least two processes are required.^1,2 The first one is chiral symmetry breaking, which can be induced by circularly polarized light or spin-polarized electrons.^3–5 Chiral symmetry breaking can contribute to produce enantiomeric excesses of up to a few percent.^5,6 The second process is a further chiral amplification performed by physical or chemical processes.^1,7 This process is essential to enhance the small enantiomeric excess, and it ultimately reaches a high enantiomeric excess. From the Murchison meteorite, excesses of L-enantiomers up to ∼60% have been reported for some amino acids.^6,8,9 Among the wide variety of amino acids detected in meteorites, the enantiomeric excess of isovaline has been intensively analyzed, as isovaline is rare in the terrestrial biosphere and external contamination can be minimized. Excesses of L-enantiomers vary within certain meteorites and across carbonaceous meteorite groups.¹⁰ The observations of large enantiomeric excesses suggest a strong correlation with aqueous alteration. Even in aqueous alteration, many contributing factors exist, such as selective crystallization, metal content, and interactions with other chiral materials. However, detailed molecular mechanisms of these influential processes have not been fully defined. In our previous studies, we theoretically demonstrated that isovaline has an inherent property, which preferentially stabilizes the homochiral dimer over the heterochiral dimer, in contrast to alanine.¹¹ This result is qualitatively consistent with the molecular properties that isovaline forms conglomerate crystals, while alanine forms racemic crystals.² We also demonstrated that aminonitriles, one of the chiral intermediates before hydrolysis in the Strecker synthesis (Fig. 1(a)), are more easily rendered homochiral compared to amino acids by the absorption of circularly polarized light in the Lyman-α wavelength around 10.2 eV, where the intensive Lyman-α line is irradiated during the early stage of galaxy formation.^12,13 We also showed that aminonitrile is stable compared to amino acids based on the minimum energy principle.¹⁴ Therefore, evaluating the enantioselective properties of aminonitriles is important as they are one of the key chiral intermediates leading to amino acids.

Fig. 1 (a) Aminonitrile (AN) is a precursor of an amino acid (AA) before hydrolysis in the Strecker synthesis. (b) Molecular structures of four aminonitriles in the L-form. Chiral carbon atoms are marked with asterisk (*) symbols.

In both the chiral amplification processes of deposition and crystallization, molecules aggregate into nanoparticles and subsequently crystallize.¹⁵ In crystal structures of amino acids, such as valine and norvaline, dimer units are observed as basic structural motifs, and these small oligomers have been analyzed.^16–18

In the present study, we investigated the dimers of aminonitriles in gas and water phases by using first-principles calculations within density functional theory (DFT) and ab initio calculations of coupled-cluster singles and doubles with perturbative triples [CCSD(T)].¹⁹ We performed a complete conformation search based on our developed algorithm, the random sampling (RS) method, to obtain the most stable conformation of the aminonitrile dimers.¹¹ Four aminonitriles, i.e., 2-aminopropionitrile, 2-aminobutanenitrile, 2-amino-3-methylbutanenitrile, and 2-amino-2-methylbutanenitrile, were investigated (Fig. 1(b)). These molecules correspond to the aminonitrile precursors of amino acids: alanine (Ala), aminobutyric acid (Aba), valine (Val), and isovaline (Iva), which are detected in meteorites. Hereafter, we refer to these aminonitriles (AN) as Ala_AN, Aba_AN, Val_AN, and Iva_AN, respectively.

2. Method

Conformational sampling was performed by using the RS method.¹⁴ The RS method employs three different theoretical methods for structural optimizations to search over a broad conformational space for a target molecule and to find out the most stable conformation. The detailed procedure has already been described in our previous studies.^12,14 The first optimizations were performed under a simple force field (FF) level from randomly distributed atomic positions for a selected aminonitrile dimer. We used a custom Python program for generation of the initial geometries and the rough FF optimization. Second optimizations were carried out under the PM7 semiempirical molecular orbital method. For the solvated calculation, a conductor-like screening model (COSMO) was adapted. We used the MOPAC2016 package for the PM7 optimization.²⁰ The third optimization was performed under the density functional theory with B3LYP-D3//6-311++G**.^21–24 For the solvated calculations, a polarizable continuum model (PCM) was applied. We used the Gaussian 16 program package for the DFT calculations.²⁵ We generated 2000 conformational samplings for each molecule to search for a global minimum conformation. We checked that the most stable conformations were duplicated for more than five times after the sampling. The generated aminonitrile dimers are classified by the chirality into LL- or LD-forms with the same enantiomers or different ones, respectively. Relative energies were calculated including the zero-point vibrational energy (ZPE) correction at the theoretical level of the B3LYP-D3//6-311++G** and the basis set superposition errors (BSSE) estimated by using the counterpoise method.²⁶ In the present study, entropy contributions are not included because of the low temperature environments at interstellar space (T = 10 K). Solvation effects were included by adapting the PCM model.²⁷ We also examined the solvation effects with the SMD solvation model, however, the interaction energies were qualitatively unchanged (Table S1, ESI†). Therefore, in the present study, we discuss the solvation effects based on the results with the PCM model. The DFT energies were further validated by domain-based local pair natural orbital coupled cluster theory with single-, double-, and perturbative triple excitations [DLPNO-CCSD(T)/aug-cc-pVTZ] calculations^28,29 on the DFT optimized structures using the ORCA 5.0 program package.³⁰ The molecular structures shown in the figures were drawn using the VMD program.³¹

3. Results and discussion

3.1. Aminonitrile dimers in the gas phase

The most stable conformers of the four aminonitrile dimers in the gas phase calculated at the B3LYP-D3//6-311++G** level are shown in Fig. 2(a). Dimers with LL- and LD-enantiomers are shown in the upper and lower panels of Fig. 2, respectively. For all these aminonitriles, the LL-aminonitriles of the most stable conformations are lower in energy compared to the corresponding LD-enantiomers by less than 0.6 kcal mol⁻¹. The evaluated chirodiastaltic energies (ΔE_chir) defined as the energy difference between homo- and hetero chiral pairs (ΔE_chir = E_LL − E_LD) are −0.17, −0.55, −0.38, and −0.16 kcal mol⁻¹ for Ala_AN, Aba_AN, Val_AN, and Iva_AN, respectively. The more accurate DLPNO-CCSD(T)/aug-cc-pVTZ results in the most stable conformations are −0.11, −0.24, −0.18 and 0.07 kcal mol⁻¹, respectively as shown in Table 1. The DLPNO-CCSD(T) results are much smaller in absolute value than the DFT energies. Using the same RS approach, we have previously shown that ΔE_chir values for Ala and Iva are −0.08 (−0.17) and −0.67 (−0.81) kcal mol⁻¹, respectively, where the values in parentheses are the DLPNO-CCSD(T)/cc-pVTZ results.¹¹ These reference ΔE_chir values are corrected to −0.03 and −0.68 kcal mol⁻¹ by removing BSSE. Ala and Iva crystalize as a racemic mixture and a conglomerate, respectively. These results indicate that the aminonitriles do not have preferred properties to take conglomerate crystals.

Fig. 2 (a) The most stable conformations of aminonitrile dimers in the gas phase and (b) the second stable ones in the gas phase. The dashed red and blue lines represent the molecular interactions with their atomic distances in Å. Long distances with few interactions are depicted by dashed green lines. Enantiomeric forms (L or D) and relative energies (kcal mol⁻¹) to each of the most stable conformations are given in parenthesis. CPK colour scheme was used for the elements (hydrogen (H) = white, carbon (C) = gray, nitrogen (N) = blue).

Table 1 Interaction energies (E_inter/kcal mol⁻¹) of aminonitrile dimers in the most stable conformations^a

	In gas				In water
	Ala_AN	Aba_AN	Val_AN	Iva_AN	Ala_AN	Aba_AN	Val_AN	Iva_AN
a Calculated at the B3LYP-D3//6-311++G**. Values in parentheses are calculated at DLPNO-CCSD(T)/aug-cc-pVTZ. Zero-point vibrational energy (ZPE) corrections at the B3LYP-D3//6-311++G** and basis set superposition error (BSSE) corrections at each theoretical level are included for all results. Solvation effects were accounted through the PCM. b ΔEchir = Einter(LL) − Einter(LD).
LL	−8.87 (−8.25)	−9.27 (−8.39)	−9.66 (−8.88)	−9.24 (−8.32)	−3.77 (−1.98)	−4.55 (−2.98)	−4.27 (−2.42)	−4.39 (−2.68)
LD	−8.70 (−8.14)	−8.72 (−8.15)	−9.28 (−8.70)	−9.08 (−8.39)	−3.86 (−2.09)	−4.16 (−2.47)	−4.47 (−2.62)	−4.23 (−2.60)
ΔEchir^b	−0.17 (−0.11)	−0.55 (−0.24)	−0.38 (−0.18)	−0.16 (0.07)	0.09 (0.10)	−0.39 (−0.51)	0.20 (0.20)	−0.17 (−0.08)

---

The aminonitriles of LL-dimers are nearly arranged with a C₂ symmetry, while the LD-dimers are almost oriented with a central symmetry. Intermolecular interactions are depicted by the dotted lines in Fig. 2. In these intermolecular interactions, there are two different types of distances. Shorter distances are in the range of 2.2–2.3 Å, while the longer ones are in the range of 2.7–2.9 Å. The former is between the N atom of the nitrile group and the H atom of the amine group. The latter is between the N atom of the nitrile group and the H atom of a hydrocarbon in the side chain or an α-H atom. Compared to these distances between LL- and LD-dimers, the LL-dimers tend to have slightly shorter distances compared to the corresponding ones in LD-dimers.

The second most stable conformers are shown in Fig. 2(b). All the conformations in Fig. 2 possess two shorter interactions, and the longer interactions tend to be disrupted in the higher energy conformations.

The head-to-tail arrangements in Fig. 2 were also observed in the crystal structures of valine^16,17 and in the calculations of the amino acid dimers in the zwitterionic form,¹⁴ where two amino acids are oriented toward each other through interactions of the carboxyl group and amino group in another amino acid. As the carboxyl group (COO⁻) in one amino acid has two O atoms, one of the O atoms can become close to a H atom of the other side-chain, and another O atom is close to a H atom of the other amino group. The N atoms of the nitrile groups in aminonitriles tend to have longer distances to the H atoms of the side-chains, 2.76–2.88 Å, compared to the ones in the amino acids, 2.62–2.69 Å. This may be attributed to the lower electronegative charges on the N atoms of the nitrile groups.

3.2. Aminonitrile dimers in water

The most stable conformations of the four aminonitriles in water are shown in Fig. 3. In water, the most stable conformations are predominantly head-to-head, forming a hydrogen bond between the amino groups, except for the LL of the Aba_AN dimer, which is head-to-tail. The calculated chirodiastaltic energies in water are 0.09 (0.10), −0.39 (−0.51), 0.20 (0.20), and −0.17 (−0.08) kcal mol⁻¹ for Ala_AN, Aba_AN, Val_AN, and Iva_AN, respectively. The values in parentheses are the DLPNO-CCSD(T)/aug-cc-pVTZ results. The chirodiastaltic energies of Ala_AN and Val_AN changed from negative to positive ones in water, while the values of Aba_AN and Iva_AN remained negative. Among these calculated aminonitriles, Aba_AN has the strongest enantioenrichment properties, and these aminonitriles including Iva_AN have weaker enantioenrichment properties compared to Iva (ΔE_chir(Iva) = −0.68 kcal mol⁻¹). These results also indicate that aminonitriles are not preferable chemical species for achieving homochirality.

Fig. 3 The most stable conformations of the aminonitrile dimers in water. The dashed red and blue lines represent the molecular interactions with their atomic distances in Å. Enantiomeric forms (L or D) and relative energies (kcal mol⁻¹) to each of the most stable conformations are given in parenthesis. CPK colour scheme was used for the elements (hydrogen (H) = white, carbon (C) = gray, nitrogen (N) = blue).

In the most stable dimer of the head-to-head conformation, the nearest hydrogen bond distances are 2.12–2.15 Å, and the second nearest atomic distances are 2.66–2.78 Å, which are formed between the N atom of the nitrile group and the H atom of α-H or the side chain aliphatic hydrocarbons. The latter interactions are expected to be very weak, because the angles of the hydrogen bonds are far from the standard values (θ > 150°), such as 90.2°, 81.7° and 88.5° for Ala_AN(LL), Val_AN(LL) and Iva_AN(LL), respectively. The most stable conformation of the LL-dimer of Aba_AN in water was the same head-to-tail conformation as obtained under gas conditions. This conformation is preferred as the dimer is aggregated using their hydrophobic side chains.

3.3. Interaction energies

The interaction energies (E_inter) were evaluated by using the supramolecular energy decomposition scheme,
where E_dimer and E_i are the energies of the dimer and each monomer i in the most stable conformation, respectively. The calculated E_inter energies for Ala_AN, Aba_AN, Val_AN, and Iva_AN in the LL forms in the gas are −8.87, −9.27, −9.66, and −9.24 kcal mol⁻¹, respectively, at the B3LYP-D3//6-311++G** theoretical level. The E_inter energies in water are further smaller as −3.77, −4.55, −4.27, and −4.39 kcal mol⁻¹ in the same order. These values are less than one-fourth of the values of the amino acids in water, i.e., −15.73 and −16.73 kcal mol⁻¹ for Ala(LL) and Iva(LL), respectively, where these values are all BSSE corrected. These results suggest that the crystallizations are easier for amino acids compared to aminonitriles.

3.4. Relative stability between Val_AN and Iva_AN

Val_AN and Iva_AN are structural isomers with the same chemical formula, but with a different connectivity. In this case, the energies can be compared to each other. The energy difference between Val_AN and Iva_AN (ΔE_{Iva_AN} = E_{Iva_AN} − E_{val_AN}) at the B3LYP-D3//6-311++G** theoretical level is −1.83 and −1.47 kcal mol⁻¹ in the gas and water, respectively. Molecular structures in the gas phase are shown in Fig. 4A and B. These results suggest that Iva_AN is more thermodynamically stable than Val_AN in the various environments.

Fig. 4 The most stable conformations of aminonitriles in the gas phase: (A) valine aminonitrile (Val_AN) and (B) isovaline aminonitrile (Iva_AN), and amino acids in water: (C) valine (Val) and (D) isovaline (Iva). CPK colour scheme was used for the elements (hydrogen (H) = white, carbon (C) = gray, nitrogen (N) = blue).

We also investigated the relative stability of their amino acid forms: Val and Iva. In water, the energy difference was calculated to be ΔE_Iva = E_Iva − E_val = −1.58 kcal mol⁻¹ at the B3LYP-D3//6-311++G** theoretical level, where the molecular structures in water are shown in Fig. 4C and D. This means that Iva is still stable and can be formed more easily than Val. These similar energy differences indicate the intrinsic energy difference between the α-methyl and α-H isomers.

3.5. Electrostatic surface potential (ESP) analysis

Aminonitriles in the monomer and dimer forms are characterized by the electronic static potential (ESP) analysis. We compared them with the amino acid in the same condition, thus we selected the most stable conformation in water at the theoretical level of B3LYP-D3//6-311++G**. As shown in Fig. 5(A), Ala_AN has negative atomic charges on the nitrile N atom and amine N atom, and positive atomic charges can be seen for the H atoms in the amine group and side chain. The corresponding amino acid, Ala, has higher atomic charges, i.e., higher negative charges (colored red) on the carboxyl O atoms and higher positive charges (colored blue) on the H atoms of the amino group. In the dimers, these positive and negative charged atoms are closed forming the molecular interactions (Fig. 5(B)). It is notable that the uniform charge distribution of aminonitrile is consistent with the smaller interaction energy and smaller chirodiastaltic energy. The ESP surface and the ESP atomic charges suggest that the aminonitrile form with nitrile and amino groups is not superior to the amino acid form for chiral recognition.

Fig. 5 (A) Electrostatic surface potential (ESP) and the ESP atomic charges of alanine aminonitrile (Ala_AN) and alanine (Ala) in monomer and (B) in dimer. Positive and negative potentials are colored blue and red, respectively. CPK colour scheme was used for the elements (hydrogen (H) = white, carbon (C) = gray, nitrogen (N) = blue, oxygen (O) = red).

4. Conclusions

In the present study, we investigated aminonitriles as characteristic chiral intermediates formed before the hydrolysis of amino acids in the Strecker reaction. The dimerization process is the first molecular process in both the nucleation of deposition and crystallization. The most stable conformations are found by using the RS method, and the interaction energies of the aminonitrile dimers are evaluated at the theoretical levels of DFT and DLPNO-CCSD(T).

Negatively large values of chirodiastaltic energy among the aminonitriles were obtained for Aba_AN (ΔE_chir = −0.55 (−0.24) kcal mol⁻¹) and Val_AN (ΔE_chir = −0.38 (−0.18) kcal mol⁻¹) in the gas phase, where the values in parentheses are the DLPNO-CCSD(T)/aug-cc-pVTZ results. These values are still smaller than that of Iva (ΔE_chir = −0.68 kcal mol⁻¹). Chirodiastaltic energies of Aba_AN (ΔE_chir = −0.39 (−0.51) kcal mol⁻¹) and Iva_AN (ΔE_chir = −0.17 (−0.08) kcal mol⁻¹) in water are negatively smaller than the value of Iva. The four calculated aminonitriles have a unique feature that chirodiastaltic energies are all negative in the gas phase, while they are not maintained in water. This feature is reversed in amino acids. The correlation between aqueous alteration in meteorites and the large enantiomeric excesses does not match with the above-mentioned feature of the aminonitriles. Among the calculated four aminonitriles, Aba_AN is the most promising candidate to contribute to enantioenrichment, and we were able to show that the aminonitrile species do not contribute to the enantioenrichment any more than amino acids.

T. Kawasaki and colleagues reported that a chiral amino acid, α-(p-tolyl)glycine, induces the formation of an enantioenriched conglomerate of the aminonitrile intermediate.^32,33 Amplification of the enantiomeric excess can be achieved at the aminonitrile formation through heating and cooling cycles. These experiments demonstrate that the actual feedback loop of molecular chirality started from the aminonitrile and the acquired chirality is preserved in the amino acid. ^32,33 However, further studies are required to determine whether such aminonitrile derivatives can be formed abundantly in prebiotic reactions, and other chiral molecules including minerals and non-biological molecules may also contribute to the enantioenrichment of amino acids through a surrounding environmental effect. More detailed chemical evolution processes leading to amino acids will also provide deeper insights into the origin of the homochirality of biomolecules on Earth.

Data availability

The data supporting this article have been included as part of the ESI:† (1) interaction energies with the SMD solvation model, (2) interaction energies of Iva_AN dimers in the low-lying states calculated, (3) interaction energies of aminonitrile dimers in the most stable conformations at different theoretical methods, (4) energy contributions of interaction energies, (5) energy contributions of Iva_AN in the low-lying states, (6) molecular structures of low-lying states of Iva_AN(LL) and Iva_AN(LD), and (7) optimized structures of aminonitriles in the xyz format.

Conflicts of interest

No competing financial interests exist.

Acknowledgements

This research was supported by JSPS KAKENHI grant numbers JP22H00347, JP22H04916, JP23K04660, and JP24KJ0486. N. W. is grateful for a research fellowship from Institute for Quantum Chemical Exploration. Computational resources were supported by the Multidisciplinary Cooperative Research Program (MCRP) in CCS, University of Tsukuba.

References

1. D. G. Blackmond, Cold Spring Harb. Perspect. Biol., 2019, 11, a032540.
2. D. P. Glavin, A. S. Burton and J. E. Elsila, et al. , Chem. Rev., 2020, 120, 4660–4689.
3. C. Meinert, A. D. Garcia and J. Topin, et al. , Nat. Commun., 2022, 13, 502.
4. C. Meinert, J. H. Bredehöft and J.-J. Filippi, et al. , Angew. Chem., Int. Ed., 2012, 51, 4484–4487.
5. C. Meinert, S. V. Hoffmann and P. C. Chenaï, et al. , Angew. Chem., Int. Ed., 2014, 53, 210–214.
6. J. E. Elsila, J. C. Aponte and D. G. Blackmond, et al. , ACS Cent. Sci., 2016, 2, 370–379.
7. K. Soai, T. Shibata and H. Morioka, et al. , Nature, 1995, 378, 767–768.
8. M. H. Engel and B. Nagy, Nature, 1982, 296, 837.
9. M. H. Engel and S. A. Macko, Nature, 1997, 389, 265–268.
10. D. P. Glavin, H. L. Mclain and J. P. Dworkin, et al. , Meteorit. Planet. Sci., 2020, 9, 1979–2006.
11. N. Watanabe, M. Shoji and K. Miyagawa, et al. , Phys. Chem. Chem. Phys., 2023, 25, 15023–15029.
12. A. Sato, M. Shoji and N. Watanabe, et al. , Astrobiology, 2023, 23, 1019–1026.
13. M. Shoji, K. Kitazawa and A. Sato, et al. , J. Phys. Chem. Lett., 2023, 14, 3243–3248.
14. M. Shoji, N. Watanabe and Y. Hori, et al. , Astrobiology, 2022, 22, 1129–1142.
15. D. Gebauer, M. Kellermeier and J. D. Gale, et al. , Chem. Soc. Rev., 2014, 43, 2348–2371.
16. A. I. Isakov, H. Lorenz, A. A. ZolotarevJr and E. N. Kotelnikova, CrystEngComm, 2020, 22, 986–997.
17. M. Mallikarjunan and S. T. Rao, Acta Cryst., 1969, 25, 296–303.
18. B. Dalhus and C. H. Gorbitz, Acta Cryst., 1999, 55, 1547–1555.
19. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157(6), 479–483.
20. J. J. P. Stewart, MOPAC2016, Stewart Computational Chemistry, Colorado Springs, USA, 2016, available at https://www.OpenMOPAC.net.
21. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
22. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
23. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
24. T. Clark, J. Chandrasekhar, S. Jayaraman, W. Günther and R. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
25. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 16 revision C.01, Gaussian Inc., Willingford CT, 2019.
26. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–556.
27. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
28. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
29. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
30. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
31. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
32. T. Kawasaki, N. Takamatsu, S. Aiba and Y. Tokunaga, Chem. Commun., 2015, 51, 14377–14380.
33. S. Aiba, N. Takamatsu and T. Sasai, et al. , Chem. Commun., 2016, 52, 10834–10837.

---

Footnote

† Electronic supplementary information (ESI) available: Interaction energies with the SMD solvation model, interaction energies of Iva_AN dimers in the low-lying states calculated, interaction energies of aminonitrile dimers in the most stable conformations at different theoretical methods, energy contributions of interaction energies, energy contributions of Iva_AN in the low-lying states, molecular structures of low-lying states of Iva_AN(LL) and Iva_AN(LD), and optimized structures of aminonitriles in the xyz format. See DOI: https://doi.org/10.1039/d4cp02579b

---