Anisotropic fluid flows in black phosphorus nanochannels†
Ruda
Jian
a,
Shiwen
Wu
a,
Siyu
Tian
a,
Amirarsalan
Mashhadian
a,
Zhihao
Xu
 b,
Stefano
Leonardi
a,
Tengfei
Luo
b,
Stefano
Leonardi
a,
Tengfei
Luo
 *b and
Guoping
Xiong
*b and
Guoping
Xiong
 *a
*a
aDepartment of Mechanical Engineering, The University of Texas at Dallas, Richardson, Texas 75080, USA. E-mail: Guoping.Xiong@utdallas.edu
bDepartment of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, Indiana 46556, USA. E-mail: tluo@nd.edu
First published on 8th January 2024
Abstract
With the development of advanced micro/nanoscale technologies, two-dimensional materials have emerged from laboratories and have been applied in practice. To investigate the mechanisms of solid–liquid interactions in potential applications, molecular dynamics simulations are employed to study the flow behavior of n-dodecane (C12) molecules confined in black phosphorus (BP) nanochannels. Under the same external conditions, a significant difference in the velocity profiles of fluid molecules is observed when flowing along the armchair and zigzag directions of the BP walls. The average velocity of C12 molecules flowing along the zigzag direction is 9-fold higher than that along the armchair direction. The friction factor at the interface between C12 molecules and BP nanochannels and the orientations of C12 molecules near the BP walls are analyzed to explain the differences in velocity profiles under various flow directions, external driving forces, and nanochannel widths. The result shows that most C12 molecules are oriented parallel to the flow direction along the zigzag direction, leading to a relatively smaller friction factor hence a higher average velocity. In contrast, along the armchair direction, most C12 molecules are oriented perpendicular to the flow direction, leading to a relatively larger friction factor and thus a lower average velocity. This work provides important insights into understanding the anisotropic liquid flows in nanochannels.
1. Introduction
With the fast development of micro/nanoscale technologies, an increasing number of two-dimensional (2D) nanomaterials have been developed in laboratories and used in practical applications.1–4 As a typical 2D nanomaterial, black phosphorus (BP) has attracted enormous attention because of its direct bandgap,5 high carrier mobility,6 and anisotropic properties.7 The outstanding physical,8 electronic,9 and optical properties10 of BP have driven the development of micro/nanofluidic devices11 based on the material. However, current research on BP-based micro/nanofluidic devices is still at the exploratory stage, focusing on fluid flow characteristics in nanochannels12,13 and solid–liquid interface mechanisms.14,15 The interaction mechanisms at the solid–liquid interface in BP nanochannels remain elusive. Therefore, unveiling the interplay between the BP-based nanochannel and fluids is crucial to understanding the transport properties of fluids in such nanochannels for practical applications.In recent years, molecular dynamics (MD) simulations have emerged as a widely-used tool to investigate fluid transport at the molecular scale and have been extensively applied to study the pressure-driven flow of liquid hydrocarbons in nanochannels.7,16–28 The liquid molecules confined in a nanochannel behave differently compared to the bulk state because of the more dominant role of interaction between the molecules and confined nanochannel walls.29–31 The flow behavior of molecules in BP nanochannels becomes more complicated because of the solid–liquid interaction with the anisotropic lattice structure of BP.32 In a recent study, water flowing in BP nanochannels exhibited a discrepancy (maximum 2 times) of flow velocity along the zigzag/armchair directions.7 However, whether the simulation results in water as liquid phase can be generalized to other liquids (e.g., hydrocarbons) is not clear. Particularly, the flow behavior of long-chain hydrocarbons in nanochannels is highly related to their molecular orientation.28 Therefore, investigating the flow behavior of hydrocarbon molecules confined in BP nanochannels with anisotropy is warranted.
In this paper, MD simulations are conducted to investigate the anisotropic flow behavior of liquid oil confined in BP nanochannels. As a representative oil model n-dodecane (C12) is employed in the simulations. The velocity profiles of oil molecules are analyzed by changing the external driving force and nanochannel width. The average velocities of C12 molecules flowing along the armchair and zigzag directions differ by a factor of ∼9 under the same conditions due to the anisotropic lattice nature of BP, which is significantly higher compared to the reported water flow in BP channels with a velocity difference of 2 times along the armchair and zigzag directions. Furthermore, we investigate the friction factor at the interface between the nanochannel and C12 molecules and the orientation of the C12 molecules near the BP walls. Results show that oil flow along the armchair and zigzag exhibit a large velocity discrepancy, which can be influenced by the external driving force and width of the nanochannels. These findings provide a better understanding of the transport properties of the C12 molecules in BP nanochannels under different conditions.
2. Methods and simulation model
In this work, all simulations are performed using Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)33 and visualized by Open Visualization Tool (OVITO).34Fig. 1a shows a schematic of the simulation setup. Two BP layers with a dimension of ∼5 nm (x) × 5.5 nm (z) are used as the nanochannel walls with 180 C12 molecules sandwiched between the two parallel BP walls while the atoms number of different conditions is listed in Table S1 (ESI†). Periodic boundary conditions are applied along the x and z directions. The time step size is set to 1 fs. The cutoff distance is set to 12 Å. The C12 molecules are modeled using the polymer consistent force field (PCFF).35 The BP molecules are modeled using the Stillinger–Weber (SW) potential.7 The non-bond interactions are described by the Lennard-Jones (L-J) potential,36,37 which has included the impact of van der Waals interactions:36 | (1) |
 | (2) |
| Atom | ε (kcal mol−1) | σ (Å) | |
|---|---|---|---|
| BP | P | 0.367 | 3.438 |
| C12 | C | 0.54 | 4.01 |
| H | 0.02 | 2.995 |
The system is relaxed by the following processes: first, the system is run in the microcanonical ensemble (i.e., NVE) for 10 ps. Then, a canonical ensemble (i.e., NVT) is applied at a temperature of 300 K for 2 ns. Subsequently, the system is equilibrated by applying an isobaric-isothermal ensemble (i.e., NPT) for 10 ns at 1 atm with one of the BP nanochannel walls fixed by a spring force of 2 × 10−2 kcal mol−1 Å−1 while the other is free to move. Finally, a following NVT for 5 ns is applied. The density profiles of C12 molecules along the y direction are collected and averaged during the last 5 ns of the NVT process. As shown in Fig. 1b, the average density of C12 in the middle region of the BP nanochannels is calculated to be 0.708 g cm−3, which is within 94.53% to the experimental density data of its bulk phase (0.749 g cm−3)41 at the same pressure and temperature. The density of C12 is calculated with the same relaxed process without BP wall as shown in Fig. S3 (ESI†).
The flow behavior of C12 molecules confined in the BP nanochannel is studied by nonequilibrium molecular dynamics (NEMD). During the simulations, both BP nanochannel walls are fixed, and constant external driving forces along the z direction (i.e., armchair direction) or x direction (i.e., zigzag direction) are applied to all the C12 molecules in the BP nanochannel to mimic the flowing behavior of C12 under constant pressure conditions. The NEMD simulation based on the previous condition continues for 20 ns with the Nosé–Hoover thermostat applied along the directions perpendicular to the C12 molecules flow28,42–44 since employing the velocity perpendicular to the flow direction and subtracting the center of mass velocity help accurately control the temperature. The interactions between BP nanochannel and C12 molecules under different conditions are quantitatively analyzed using the group force computation method (Table S1, ESI†).
3. Results and discussion
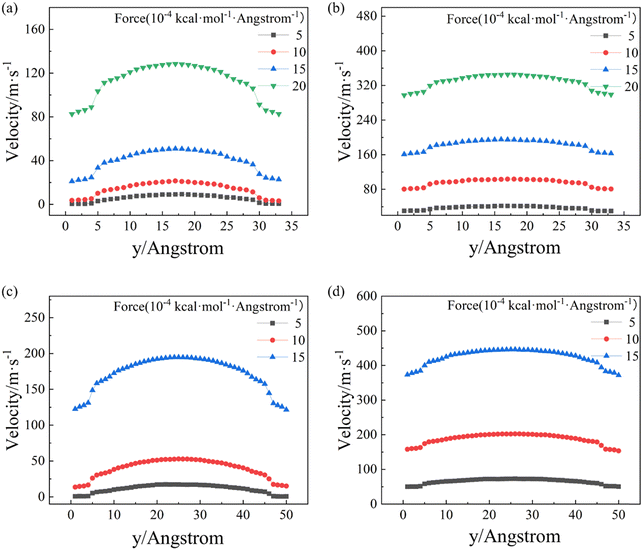
For the simulated model (Fig. 1a), the zigzag direction of the BP is in the x direction, and the armchair direction is along the z direction. External driving forces ranging from 5 × 10−4 kcal mol−1 Å−1 to 2 × 10−3 kcal mol−1 Å−1 are applied to each atom in the C12 molecules along either armchair or zigzag direction of the BP nanochannel. The group force computation method applied to calculate the interaction between BP nanochannel and C12 molecules. This interaction influences the pressure gradience (Table S1, ESI†) and velocity profile of the C12 molecules under various conditions. The velocity profiles of C12 molecules in the relaxed system along the y direction are averaged every 20,000 time steps (i.e., 2 × 10−2 ns) based on the data from the last 10 ns of NVT. Fig. 2 shows the velocity profiles of C12 molecules confined in the BP nanochannels when the C12 molecules are flowing along the armchair (Fig. 2a) and zigzag (Fig. 2b) directions under different driving forces. Under the same external driving force, the average velocity of C12 molecules flowing along the armchair direction is much lower than that flowing along the zigzag direction. When C12 molecules are flowing along the zigzag direction of a 2-nm nanochannel under an external driving force of 5 × 10−4 kcal mol−1 Å−1, the average velocity of C12 molecules is 9 times higher than that flowing along the armchair direction. Moreover, the velocity profiles of C12 molecules flowing along the armchair direction exhibit larger curvatures than those along the zigzag direction, which can be attributed to the larger friction32 between BP walls and C12 molecules along the armchair direction. This can also explain why the average velocity along the armchair direction is smaller than that along the zigzag direction. In addition, with the increase of the external driving force, the average velocity change along the armchair direction is higher than that along the zigzag direction (Fig. S1, ESI†). It can be inferred that the friction between the C12 molecules and the BP walls changes as the external driving force increases. | ||
| Fig. 2 Velocity profiles of the C12 molecules flowing along the (a) armchair direction and (b) zigzag direction under different external driving forces in a 2-nm BP nanochannel. | ||
To further explain the different flow behaviors of the C12 molecules along the armchair and zigzag directions, the Darcy–Weisbach friction factor is calculated based on the data collected from the MD simulations by the following formula:45–47
 | (3) |
Fig. 3 depicts the calculated friction factors at the interfaces between C12 molecules and BP nanochannels with a width of 2 nm under different external driving forces. The magnitude friction factor varies from 1 to 104, which agrees well with the simulation results of other nanochannels in prior work.46,47 Results show that the friction factor along the zigzag direction is consistently smaller than that along the armchair direction. On the other hand, the friction factor decreases as the external driving force increases along both directions. Consequently, the disparity between friction factor along the armchair and zigzag directions reduces as the external driving force increases (Fig. S2, ESI†). The friction factor results are consistent with the velocity profile results shown in Fig. 2.
 | ||
| Fig. 3 The logarithm of the friction factor between C12 molecules and BP nanochannels under external driving forces ranging from 5 × 10−4 to 2 × 10−3 kcal mol−1 Å−1. | ||
To further elucidate the mechanisms of the drastically different flow behaviors along the armchair and zigzag directions, the orientation of the C12 molecules near the BP wall is investigated because it can affect the molecules flowing at the interface.28 The orientation parameter (S) of each C12 molecule is calculated by:48,49
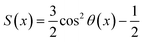 | (4) |
 | (5) |
Fig. 4a exhibits the x–z cross-sectional view of the one-layered oil molecular structure close to the BP wall. The chain-like C12 molecules are parallel to the BP wall and aligned in different directions. As Fig. 4b shows, under an external driving force of 1 × 10−3 kcal mol−1 Å−1, the orientation parameter S of C12 molecules flowing along the zigzag direction is higher than that along the armchair direction under the same external force. The result implies that along the zigzag direction, most C12 molecules are oriented parallel to the flow direction. On the contrary, most C12 molecules are oriented perpendicular to the flow direction along the armchair direction.
As such, when the C12 molecules flow along the zigzag direction, the friction between the C12 molecules near the BP walls is low, leading to a high average velocity. In contrast, when the C12 molecules flow along the armchair direction, the molecules in the neighboring layers need to overcome the corrugated landscape, resulting in a lower average velocity. Therefore, we can conclude that for C12 molecules flowing along armchair and zigzag directions, the alignment of oil molecules near the wall is different, leading to substantial divergences in the friction factor and average velocities.
Additionally, Fig. 5 and Fig. S4 (ESI†) illustrate that as the width of the nanochannel increases, the velocity profiles along both the armchair and zigzag directions retain their high-curvature and low-curvature configurations, respectively,32 indicating that the friction between the BP walls and C12 molecules flowing along the armchair direction is consistently higher than that along the zigzag direction.32 The mechanism of the different velocity profiles will be analyzed by following the friction factor and orientation data with different width of nanochannels.
The comparison between Fig. 5a and b with Fig. 5c and d and further results (Fig. S4, ESI†) demonstrate that the curvature of the velocity profiles declines as the width of the nanochannel increases. This suggests that the velocity difference between C12 molecules in the middle region and the near-wall region of the nanochannel is gradually decreasing because the relative importance of the friction from the BP walls is progressively diminishing. As the width of the nanochannel increases, the interaction between the BP walls and the C12 molecules in the middle region of nanochannels gradually weakens. On the other hand, when the nanochannel widens, the velocity gradient difference along the y direction decreases due to the increase in the total number of atoms, making the velocity profiles appear smoother.
In Fig. 6a and b, we present the logarithm of friction factor at the interface between BP nanochannel surface and C12 molecules versus external forces for BP nanochannels with widths of ∼4 nm and ∼6 nm. Similar to the results for the 2-nm-wide nanochannel, the friction factors along the armchair direction are significantly higher than those along the zigzag direction. As the external driving force increases, the friction factors along both directions decrease. Similarly, the friction factors along the zigzag direction experience a smaller reduction than along the armchair direction with the increment of the external driving force. This reduces the disparity between the friction factors along the two directions in each nanochannel, and these findings are consistent with the velocity distribution results. Moreover, the friction factors along different directions decrease as the width of the nanochannel increases under identical driving forces. For instance, under the same external driving force of 5 × 10−4 kcal mol−1 Å−1, the friction factor of the 4-nm-wide nanochannel (Fig. 6a) is 2 times higher than that of the 6-nm-wide nanochannel (Fig. 6b). The discrepancy between the friction factors along different directions diminishes when the width of the nanochannel increase.
 | ||
| Fig. 6 The logarithm of the friction factor between C12 molecules and BP nanochannels for BP nanochannels with widths of (a) 4 nm and (b) 6 nm. | ||
To further reveal the influence of nanochannel width on the flow behavior, we calculate the orientation parameters of the C12 molecules close to the BP walls in 4-nm and 6-nm nanochannels under identical external driving forces. Fig. 7a and b shows that the orientation parameters S calculated from eqn (5) along the zigzag direction are larger than those along the armchair direction in the 4-nm and 6-nm nanochannels. This implies that along the zigzag direction, most C12 molecules are oriented parallel to the flow direction, whereas along the armchair direction, most C12 molecules are oriented perpendicular to the flow direction. This can also explain why the frictional resistance along the zigzag direction is lower than that along the armchair direction under the same conditions. By comparing the orientation parameters of C12 molecular in 4-nm (Fig. 7a) to 6-nm (Fig. 7b) nanochannels, the difference gradually diminishes between the orientation parameters S along the armchair and zigzag directions. This indicates that the disparity in molecular orientations of the C12 one-layered structure near the BP wall along the direction of motion is decreasing along different directions, which is consistent with the results of the friction factor and velocity distribution differences.
 | ||
| Fig. 7 S values of one-layered C12 molecules close to the BP wall along the armchair and zigzag directions in (a) 4-nm and (b) 6-nm nanochannels. | ||
4. Conclusion
systematic molecular dynamics simulations have been performed to study the flow behavior of C12 molecules in BP nanochannels. Average velocities of C12 molecules along armchair and zigzag directions of BP walls under different conditions were calculated and compared. Results show that the C12 molecules exhibit prominent anisotropic flow behavior in the BP nanochannels. When C12 molecules are flowing along the zigzag direction of a 2-nm nanochannel under an external driving force of 5 × 10−4 kcal mol−1 Å−1, the average velocity of C12 molecules is 9 times higher than that flowing along the armchair direction. The difference in average velocities of oil flowing along armchair and zigzag directions depends on the external driving force applied to the C12 molecules and the flow resistance, while the difference in friction is related to the orientation of C12 molecules in the near-wall region. Along the zigzag flow direction, most C12 molecules in the layered structure are aligned parallel to the flow direction, resulting in smaller friction and higher velocities. In contrast, along the armchair flow direction, most C12 molecules in the one-layered structure are aligned perpendicularly to the flow direction, leading to larger friction and therefore lower velocities. Moreover, the molecular orientation also explains the velocity profiles of the C12 molecules in the BP nanochannels under varying width of nanochannels. These findings facilitate a better understanding of the flow behavior of fluid molecules under nanoconfinement in BP nanochannels and may shed light on the solid–liquid interactions in nanochannels.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. X. thanks the University of Texas at Dallas startup fund and NSF (Grant No. CBET-1949962). T. L. thanks the support from the NSF (Grant No. CBET-1949910). S. L. acknowledge support from the NSF (Grant No. CBET – 2202710) The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing high-performance computing (HPC) resources that have contributed to the research results reported within this paper. URL: https://www.tacc.utexas.edu.References
- N. R. Glavin, R. Rao, V. Varshney, E. Bianco, A. Apte, A. Roy, E. Ringe and P. M. Ajayan, Adv. Mater., 2020, 32, 1904302 CrossRef CAS PubMed
.
- J. T. Paul, A. K. Singh, Z. Dong, H. Zhuang, B. C. Revard, B. Rijal, M. Ashton, A. Linscheid, M. Blonsky, D. Gluhovic, J. Guo and R. G. Hennig, J. Phys.: Condens. Matter, 2017, 29, 473001 CrossRef CAS PubMed
.
- G. G. Naumis, S. Barraza-Lopez, M. Oliva-Leyva and H. Terrones, Rep. Prog. Phys., 2017, 80, 096501 CrossRef PubMed
.
- N. C. Keim and P. E. Arratia, Phys. Rev. Lett., 2014, 112, 028302 CrossRef PubMed
.
- H. Huang, B. Jiang, X. Zou, X. Zhao and L. Liao, Sci. Bull., 2019, 64, 1067–1079 CrossRef CAS PubMed
.
- R. F. Service, Science, 2015, 348, 490–492 CrossRef CAS PubMed
.
- Z.-Q. Zhang, H.-L. Liu, Z. Liu, Z. Zhang, G.-G. Cheng, X.-D. Wang and J.-N. Ding, Appl. Surf. Sci., 2019, 475, 857–862 CrossRef CAS
.
- X. Mu, J. Wang and M. Sun, Mater. Today Phys., 2019, 8, 92–111 CrossRef
.
- A. Zaoui and F. E. H. Hassan, J. Phys.: Condens. Matter, 2001, 13, 253 CrossRef CAS
.
- C. Wang, G. Zhang, S. Huang, Y. Xie and H. Yan, Adv. Opt. Mater., 2020, 8, 1900996 CrossRef CAS
.
- Z. Li, C. Cheng, H. Gong, Q. Liu and C. Huang, J. Mol. Liq., 2020, 309, 113023 CrossRef CAS
.
- F. D. Sofos, T. E. Karakasidis and A. Liakopoulos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 026305 CrossRef PubMed
.
- C. Y. Soong, T. H. Yen and P. Y. Tzeng, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 036303 CrossRef CAS PubMed
.
- S. Balasubramanian and C. J. Mundy, Bull. Mater. Sci., 1999, 22, 873–876 CrossRef CAS
.
- V. Turlo, O. Politano and F. Baras, Acta Mater., 2015, 99, 363–372 CrossRef CAS
.
- S. Yao, J. Wang and X. Liu, Int. J. Heat Mass Transfer, 2021, 176, 121441 CrossRef CAS
.
- P. Alipour, D. Toghraie, A. Karimipour and M. Hajian, J. Mol. Liq., 2019, 275, 192–203 CrossRef CAS
.
- Z. Cao, H. Jiang, J. Zeng, H. Saibi, T. Lu, X. Xie, Y. Zhang, G. Zhou, K. Wu and J. Guo, J. Chem. Eng., 2021, 420, 127578 CrossRef CAS
.
- L. S. de Lara, M. F. Michelon and C. R. Miranda, J. Phys. Chem. B, 2012, 116, 14667–14676 CrossRef CAS PubMed
.
- S. Wang, F. Javadpour and Q. Feng, Fuel, 2016, 171, 74–86 CrossRef CAS
.
- S. Zhan, Y. Su, Z. Jin, W. Wang and L. Li, Fuel, 2020, 262, 116560 CrossRef CAS
.
- Z. Li, Y. Jun and J. Kou, J. Phys. Chem. Lett., 2019, 10, 4291–4296 CrossRef CAS PubMed
.
- J. Liu, Y. Zhao, Y. Yang, Q. Mei, S. Yang and C. Wang, Energies, 2020, 13, 3815 CrossRef CAS
.
- W. Cui, Z. Shen, J. Yang and S. Wu, Case Stud. Therm. Eng., 2015, 5, 114–121 CrossRef
.
- J. Liu, Y. Yang, S. Sun, J. Yao and J. Kou, Chem. Eng. J., 2022, 434, 134682 CrossRef CAS
.
- H. Zheng, Y. Du, Q. Xue, L. Zhu, X. Li, S. Lu and Y. Jin, Nanoscale Res. Lett., 2017, 12, 1–9 CrossRef PubMed
.
- X. Wang, S. Xiao, Z. Zhang and J. He, Environ. Sci.: Nano, 2019, 6, 2810–2819 RSC
.
- S. Wu, Z. Xu, R. Jian, S. Tian, L. Zhou, T. Luo and G. Xiong, J. Phys. Chem. B, 2023, 127, 6184–6190 CrossRef CAS PubMed
.
- B. Liu, R. Wu, J. A. Baimova, H. Wu, A. W.-K. Law, S. V. Dmitriev and K. Zhou, Phys. Chem. Chem. Phys., 2016, 18, 1886–1896 RSC
.
- H. Lu, Y. Xu, C. Duan, P. Jiang and R. Xu, Energy Fuels, 2022, 36, 5267–5275 CrossRef CAS
.
- S. Mozaffari, P. Tchoukov, A. Mozaffari, J. Atias, J. Czarnecki and N. Nazemifard, Colloids Surf., A, 2017, 513, 178–187 CrossRef CAS
.
- B. Chen, H. Jiang, X. Liu and X. Hu, J. Phys. Chem. C, 2017, 121, 1321–1328 CrossRef CAS
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef
.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS
.
- S. Wu, Z. Xu, S. Tian, T. Luo and G. Xiong, J. Mol. Liq., 2022, 360, 119410 CrossRef CAS
.
- D. Huang, S. Wu, G. Xiong and T. Luo, J. Appl. Phys., 2022, 132, 015104 CrossRef CAS
.
- S. Tian, Z. Xu, S. Wu, T. Luo and G. Xiong, Int. J. Heat Mass Transfer, 2022, 195, 123134 CrossRef CAS
.
- S. Tian, D. Huang, Z. Xu, S. Wu, T. Luo and G. Xiong, Int. J. Heat Mass Transfer, 2022, 183, 122188 CrossRef CAS
.
- Y. Pang, J. Zhang, R. Ma, Z. Qu, E. Lee and T. Luo, ACS Energy Lett., 2020, 5, 437–456 CrossRef CAS
.
-
W. M. Haynes, CRC handb. chem. phys., CRC press, 2016 Search PubMed
.
- X. Sui, H. Ding, Z. Yuan, C. F. Leong, K. Goh, W. Li, N. Yang, D. M. D'Alessandro and Y. Chen, Carbon, 2019, 148, 277–289 CrossRef CAS
.
- D. Bahamon and L. F. Vega, Mol. Phys., 2019, 117, 3703–3714 CrossRef CAS
.
- Z. Xu, S. Wu, S. Tian, D. Huang, G. Xiong and T. Luo, J. Phys. Chem. C, 2023, 127, 3671–3681 CrossRef CAS
.
- A. Shadloo-Jahromi and M. K.-K. O. Bavi, Molecular Dynamic Study of Friction Factor of Water Flowing Through Nanochannels with Different Wall Hydrophobicity, 8th International Conference on Nanostructures, Tehran, 2020.
- A. Shadloo-Jahromi, M. Kharati-Koopaee and O. Bavi, Int. Commun. Heat Mass Transfer, 2021, 124, 105278 CrossRef CAS
.
- A. Liakopoulos, F. Sofos and T. E. Karakasidis, Microfluid. Nanofluid., 2016, 20, 24 CrossRef
.
- H. Sui, F. Zhang, Z. Wang, D. Wang and Y. Wang, J. Mol. Liq., 2020, 305, 112745 CrossRef CAS
.
- W. Zhang, Q. Feng, Z. Jin, X. Xing and S. Wang, Chem. Eng. J., 2021, 245, 116948 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04736a |
| This journal is © the Owner Societies 2024 |