Open Access Article
Open Access ArticleAccessing the triplet state of perylenediimide by radical-enhanced intersystem crossing†
Maximilian
Mayländer
 a,
Oliver
Nolden
a,
Oliver
Nolden
 b,
Michael
Franz
b,
Michael
Franz
 a,
Su
Chen
a,
Su
Chen
 c,
Laura
Bancroft
c,
Laura
Bancroft
 c,
Yunfan
Qiu
c,
Michael R.
Wasielewski
c,
Yunfan
Qiu
c,
Michael R.
Wasielewski
 c,
Peter
Gilch
c,
Peter
Gilch
 b and
Sabine
Richert
b and
Sabine
Richert
 *a
*a
aInstitute of Physical Chemistry, University of Freiburg, Albertstraße 21, 79104 Freiburg, Germany. E-mail: sabine.richert@physchem.uni-freiburg.de
bInstitute of Physical Chemistry, Heinrich Heine University Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany
cDepartment of Chemistry, Center for Molecular Quantum Transduction, Institute for Sustainability and Energy at Northwestern, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208-3113, USA
First published on 11th May 2022
Abstract
Owing to their exceptional photophysical properties and high photostability, perylene diimide (PDI) chromophores have found various applications as building blocks of materials for organic electronics. In many light-induced processes in PDI derivatives, chromophore excited states with high spin multiplicities, such as triplet or quintet states, have been revealed as key intermediates. The exploration of their properties and formation conditions is thus expected to provide invaluable insight into their underlying photophysics and promises to reveal strategies for increasing the performance of optoelectronic devices. However, accessing these high-multiplicity excited states of PDI to increase our mechanistic understanding remains a difficult task, due to the fact that the lowest excited singlet state of PDI decays with near-unity quantum yield to its ground state. Here we make use of radical-enhanced intersystem crossing (EISC) to generate the PDI triplet state in high yield. One or two 2,2,6,6-tetramethylpiperidinyloxyl (TEMPO) stable radicals were covalently attached to the imide position of PDI chromophores with and without p-tert-butylphenoxy core substituents. By combining femtosecond UV-vis transient absorption and transient electron paramagnetic resonance spectroscopies, we demonstrate strong magnetic exchange coupling between the PDI triplet state and TEMPO, resulting in the formation of excited quartet or quintet states. Important differences in the S1 state deactivation rate constants and triplet yields are observed for compounds bearing PDI moieties with different core substitution patterns. We show that these differences can be rationalized by considering the varying importance of competitive excited state decay processes, such as electron and excitation energy transfer. The comparison of the results obtained for different PDI–TEMPO derivatives leads us to propose design guidelines for optimizing the efficiency of triplet sensitization in molecular assemblies by EISC.
Introduction
Excited states of organic chromophores with high spin multiplicities (S ≥ 1), such as triplet or quintet states, play a major role as reaction intermediates in a number of photophysical processes of technological relevance, including singlet fission (SF), photodynamic therapy, and triplet–triplet annihilation photon up-conversion (TTA).1–7 For instance, the performance of many optoelectronic devices, such as OLEDs, may be significantly improved if we know how to control (maximize or avoid) triplet formation and the subsequent regeneration of emissive singlet states (i.e., triplet harvesting). Recent reports have shown that the spin properties of the molecules may be crucial for the efficiency of these processes and thus the performance of optoelectronic devices relying on them.8–13Due to their exceptional photostability, low production cost, high molar absorption coefficients, and tunable energy levels,14–16 perylenediimide (PDI, see Fig. 1a) chromophores have been suggested as alternatives to fullerene acceptors in organic solar cells and photovoltaics.17 They have photophysical and redox properties that overcome some of the limitations of commonly employed organic solar cell materials, making them promising candidates for organic energy conversion applications, as demonstrated by the wealth of literature available on the topic. In a number of studies, PDIs have been shown to undergo singlet fission,18,19 which is promising for enhancing solar cell performance by creating two triplet excitons from a singlet exciton.8,20,21 Recent reports on PDI dimers, trimers, and tetramers22–25 show that even unsubstituted PDI has suitable energetic properties to undergo SF and that geometric arrangements for efficient SF can be found. However, it is likely that the device performance may still be considerably enhanced if we manage to understand (and control) the optical and magnetic properties of the PDI chromophores in their excited triplet or even quintet states, and optimize the covalent linkage mediating the electronic and spin communication between the PDI subunits.
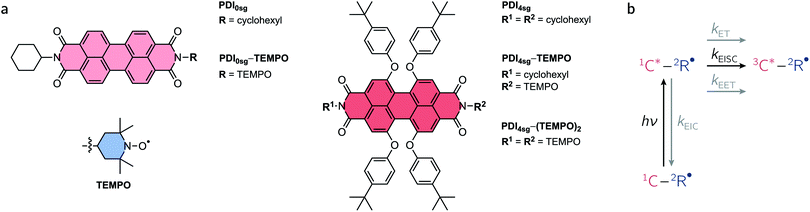
While it seems evident that an investigation into the properties and formation conditions of the high-multiplicity excited states of PDI will increase our understanding, accessing these states is not straightforward due to the near-unity fluorescence quantum yield of PDI.26 Most approaches to access the PDI excited triplet state that have been presented so far have relied on bimolecular excitation energy transfer, radical pair recombination, or core substitution with groups bearing heavy atoms.27–32 However, more recently it has been shown that the PDI excited triplet state can also be sensitized efficiently by covalent attachment of a stable radical to the chromophore,33–36 making use of the process of radical-enhanced intersystem crossing (EISC). By varying the attachment position of the linker, linker type, and radical type, the interaction between chromophore and radical can in principle be tuned to optimize the triplet yield. However, guidelines for a rational design of such chromophore–radical systems still remain to be established.37 Apart from the magnitude of the exchange interaction between chromophore triplet and radical (JTR), the excited state energies may also play an important role and may limit the overall yield of EISC, e.g. by favoring other excited state decay pathways.
An overview of the relevant photophysical processes is shown in Fig. 1b. Possible excited state processes are excitation energy transfer (EET), electron transfer (ET), and enhanced internal conversion (EIC), which may effectively compete with EISC and limit its yield. In the presence of the stable radical, the chromophore triplet state is generated and may further interact with the stable radical, whereby the type of interaction depends primarily on the magnitude of the exchange interaction between chromophore triplet and radical, JTR.4,34,38–41 When referring to the different accessible spin states in such systems, we will adopt the Gouterman nomenclature42 in which the first part denotes the spin multiplicity of the chromophore and the second part the overall spin multiplicity of the chromophore – radical system. By spin coupling, (excited trip-doublet and) trip-quartet states may be formed in chromophore – radical systems, while, when a second radical is attached to the chromophore, overall quintet spin states may become accessible if JTR is larger than any other magnetic interactions in the system.43–46
Here, we use a systematic approach to explore the optical and magnetic properties of the excited singlet and triplet states of PDI chromophores with and without p-tert-butylphenoxy side groups on the PDI core. The chosen side groups can be synthetically introduced in a straightforward manner and improve the solubility of the compounds considerably. The respective chromophores are referred to as PDI0sg and PDI4sg and their structures are shown in Fig. 1a. Making use of radical-enhanced intersystem crossing, we show that the PDI excited triplet state can be sensitized efficiently by covalent attachment of either one or two 2,2,6,6-tetramethylpiperidinyloxyl (TEMPO) stable radicals to the imide position(s) of the PDI chromophores. These PDI–TEMPO compounds are shown in Fig. 1a and are referred to as PDI0sg–TEMPO, PDI4sg–TEMPO, and PDI4sg–(TEMPO)2. Using transient electron paramagnetic resonance experiments (EPR), we demonstrate, that the interaction between chromophore triplet and radical falls within the strong coupling regime, where trip-quartet or trip-quintet states are formed. Femtosecond UV-vis transient absorption spectroscopy (fsTA) reveals important differences in the EISC rate constants and yields between the different PDI–TEMPO compounds with and without side groups on the PDI core. It becomes evident that faster EISC does not necessarily guarantee a higher EISC yield, highlighting the need to consider the excited state energies of the reaction partners and the varying yields of competing excited state processes for a complete description of the interaction between chromophore triplet and radical. The critical discussion and comparison of the results, leads us to propose strategies to optimize the yields of EISC in molecular three-spin systems.
Experimental
Steady state absorption and fluorescence spectroscopy
Steady-state absorption measurements of the samples in toluene were carried out on a Shimadzu UV-1601 UV-vis spectrometer. For all fluorescence measurements, the samples were diluted substantially, corresponding to absorbances <0.1 at the excitation wavelengths. Steady-state fluorescence spectra were recorded on a FluoroMax-4 fluorimeter from Horiba. The raw spectra were corrected for the spectral sensitivity of the instrument and fluctuations of the excitation light source.Fluorescence quantum yields and lifetimes
Fluorescence quantum yields were determined using a C11347 absolute photoluminescence quantum yield spectrometer from Hamamatsu Photonics K. K., Japan. The same solutions as prepared for the fluorescence measurements were used. Wavelengths of 480 nm or 520 nm, for compounds based on PDI0sg or PDI4sg, respectively, were chosen for excitation of the samples and the analysis was performed using the tools provided with the data acquisition software. Fluorescence lifetime measurements were carried out using a FluoTime 100 fluorescence lifetime spectrometer from Picoquant GmbH, Germany. The samples were excited at 470 nm and the scattering light from the excitation source was cut off with the help of a long-pass filter placed in the detection path. The instrument response function was collected (without any filters) using a solution of LUDOX® (colloidal silica) in distilled water. To obtain the fluorescence decay times, iterative re-convolution of the instrument response function with a monoexponential decay function was performed in MATLAB. The model decay function was fit to the experimental data using a least-squares fitting approach (minimization of the residuals using a built-in trust-region-reflective algorithm).Femtosecond transient absorption
The setup has been described in more detail elsewhere.47–50 In brief, a Ti:sapphire laser amplifier system (Coherent Libra) with a repetition rate of 1 kHz, a pulse duration of 100 fs and a wavelength of 800 nm was used as the pulse source. Part of its output was used to pump a TOPAS-White non-collinear optical parametric amplifier tuned to deliver pulses peaking at 530 nm. The pump power at the sample position amounted to 1 mW (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μJ per pulse). For probing (330–740
μJ per pulse). For probing (330–740![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm), a supercontinuum was generated in a CaF2 plate. The pump beam diameter at the sample was 160
nm), a supercontinuum was generated in a CaF2 plate. The pump beam diameter at the sample was 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm (FWHM), while the diameter of the probe beam was 100
μm (FWHM), while the diameter of the probe beam was 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. The relative polarization of pump and probe beams was set to the magic angle and the instrumental response time was ∼180 fs (FWHM).
μm. The relative polarization of pump and probe beams was set to the magic angle and the instrumental response time was ∼180 fs (FWHM).
Femtosecond transient UV-vis absorption (fsTA) spectra were recorded at 139 different time delays, where 50 linear time steps between −1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ps were followed by linear steps on a logarithmic scale up to roughly 4 ns. A total of 2000 spectra were acquired per time point and averaged over four successive scans. The chopper in the probe beam path was set to a frequency of 500 Hz, while that in the pump path was set to 250 Hz. For every time point, four different sets of data were collected: (i) only the white light (probe) reaches the sample, (ii) pump and probe both blocked, (iii) pump and probe both reach the sample, (iv) only the pump reaches the sample. Signals (i) and (iii) are used for the calculation of ΔA, while signals (ii) and (iv) are needed to account for dark signals and pump light scattering. The chirp of the white light was measured in a separate (optical Kerr effect, OKE) experiment and accounted for in the processing of the TA data. In addition, solvent spectra were recorded separately under identical conditions as the samples and subtracted from the sample data following the procedure detailed in ref. 51.
ps were followed by linear steps on a logarithmic scale up to roughly 4 ns. A total of 2000 spectra were acquired per time point and averaged over four successive scans. The chopper in the probe beam path was set to a frequency of 500 Hz, while that in the pump path was set to 250 Hz. For every time point, four different sets of data were collected: (i) only the white light (probe) reaches the sample, (ii) pump and probe both blocked, (iii) pump and probe both reach the sample, (iv) only the pump reaches the sample. Signals (i) and (iii) are used for the calculation of ΔA, while signals (ii) and (iv) are needed to account for dark signals and pump light scattering. The chirp of the white light was measured in a separate (optical Kerr effect, OKE) experiment and accounted for in the processing of the TA data. In addition, solvent spectra were recorded separately under identical conditions as the samples and subtracted from the sample data following the procedure detailed in ref. 51.
The TA data were analyzed using home-written MATLAB routines. After subtraction of the suitably scaled solvent background, the data were chirp-corrected by interpolation in the time domain using a function of the form 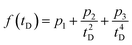 , where tD is the instrumental delay time and the parameters pn are obtained by fitting the temporal peaks of the OKE response as a function of wavelength.
, where tD is the instrumental delay time and the parameters pn are obtained by fitting the temporal peaks of the OKE response as a function of wavelength.
For the room temperature fsTA experiments the samples were prepared in toluene solutions with an absorbance between 0.1 and 0.4 at the excitation wavelength of 530 nm in a 1 mm cuvette. During the experiments, the sample solutions (∼2 mL) were flown continuously. In addition, UV-vis spectra were taken before and after the measurements to verify the sample absorbances and confirm the absence of sample degradation during the measurement.
Electron paramagnetic resonance
For all transient EPR measurements, the samples were prepared with an absorbance of roughly 0.3 at the excitation wavelength of 535 nm, measured in a 2 mm cuvette. For the measurements at Q-band frequencies (34.0 GHz), the samples in toluene were transferred into quartz EPR tubes with an outer diameter of 1.6 mm (inner diameter of 1 mm). The solutions were rapidly frozen in liquid nitrogen before insertion into the EPR resonator for the measurements.Transient EPR measurements were carried out on a Bruker ELEXSYS E580 spectrometer operated at the Q-band and equipped with a Bruker EN 5107D2 resonator. During the measurement, the sample was kept at a constant temperature of 80 K using an Oxford Instruments nitrogen gas-flow cryostat (CF 935). The samples were excited through the top of the sample holder with depolarized light at 535 nm using an optical fiber. The excitation energy was 0.5 mJ at a repetition rate of 50 Hz (pulse duration ∼5 ns).
Echo-detected field-swept EPR spectra were recorded using the sequence 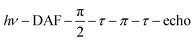 with a delay-after-flash (DAF) of 9 μs, τ = 140 ns and a π pulse length of 40 ns. The DAF value was chosen to maximize the signal intensity. The repetition rate of the experiment is determined by that of the laser.
with a delay-after-flash (DAF) of 9 μs, τ = 140 ns and a π pulse length of 40 ns. The DAF value was chosen to maximize the signal intensity. The repetition rate of the experiment is determined by that of the laser.
Transient nutation measurements used the sequence hν − DAF − ζ − τ − π − τ − echo where the flip angle ζ was gradually increased by increasing the corresponding microwave pulse length in steps of 2 ns, starting at 20 ns, i.e.,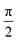 . At every magnetic field position within the region of the transient spectrum, the integrated echo intensity was then recorded as a function of this pulse length. The magnetic field step size was set to 0.1 mT (field scan range of 70 mT, 701 points). The whole data set was background corrected using a polynomial background function. The (cross-term averaged) Fourier transform was then calculated after dead-time reconstruction, windowing using a Hamming window, and zero filling to 2048 data points. The frequency spectra were normalized by division of the frequency axis by the reference frequency ω0 obtained for the same sample in the dark (doublet multiplicity).
. At every magnetic field position within the region of the transient spectrum, the integrated echo intensity was then recorded as a function of this pulse length. The magnetic field step size was set to 0.1 mT (field scan range of 70 mT, 701 points). The whole data set was background corrected using a polynomial background function. The (cross-term averaged) Fourier transform was then calculated after dead-time reconstruction, windowing using a Hamming window, and zero filling to 2048 data points. The frequency spectra were normalized by division of the frequency axis by the reference frequency ω0 obtained for the same sample in the dark (doublet multiplicity).
Results and discussion
UV-vis characterization
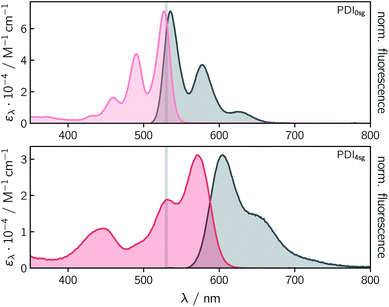
Fig. 2 shows the UV-vis absorption and steady state fluorescence spectra of the two PDI chromophores, PDI0sg and PDI4sg, measured in toluene solution at room temperature. It can be seen that the UV-vis absorption spectrum of PDI4sg is considerably red-shifted due to the presence of the four p-tert-butylphenoxy side groups on the PDI core, as also predicted by TD-DFT calculations presented in the ESI.† The strongest absorption peak of the S0 → S1 transition shifts from 527 nm in PDI0sg to 571 nm in PDI4sg. Compared to the UV-vis absorption spectrum of PDI0sg, the transitions in the spectrum of PDI4sg appear to be significantly broadened, potentially indicating a larger conformational space or a stronger solute–solvent interaction. As known from the literature15,16 and confirmed by DFT, the presence of the side groups also induces a significant twist of the PDI core.Both PDI chromophores are highly fluorescent with fluorescence quantum yields of 0.97 measured for PDI0sg and 0.92 for PDI4sg. The maximum of the fluorescence spectrum is located at 535 nm for PDI0sg and 604 nm for PDI4sg, which corresponds to Stokes shifts of 284 cm−1 and 957 cm−1, respectively.
Although PDI4sg has a lower fluorescence quantum yield, its fluorescence lifetime, measured by time-correlated single photon counting, is significantly increased compared to that of PDI0sg. A monoexponential fit to the data in toluene (Fig. S2†) yielded values of 3.95 ± 0.05 ns for PDI0sg and 5.94 ± 0.05 ns for PDI4sg. Literature data are available for PDI0sg and agree very well with the photophysical characterization presented here.27,52
The fluorescence lifetimes measured for the two PDI chromophores are also consistent with the values obtained from a Strickler-Berg analysis.53,54 The analysis, presented in the ESI,† resulted in fluorescence lifetimes of τSBF = 3.9 ns for PDI0sg and 7.9 ns for PDI4sg, assuming molar absorption coefficients of 7.1 × 104 M−1 cm−1 for PDI0sg52 and 3.1 × 104 M−1 cm−1 for PDI4sg at the maximum of the respective absorption spectrum in the visible region. The latter value determined here for PDI4sg in toluene, is in good agreement with data published previously for similar PDIs.14,55
For PDI0sg, the calculated fluorescence lifetime is very close to the experimentally measured value of 3.95 ns, indicating that the assumptions implicit in the Strickler-Berg analysis are well satisfied and that the absorbing and emitting electronic states are the same. For PDI4sg, the trend is predicted correctly but the agreement between the experimental (5.94 ns) and calculated (7.0 ns) values is less satisfying. A possible reason for this could be a relatively large geometry change in the excited state (i.e., Condon approximation only partially fulfilled), which would be consistent with the significantly increased Stokes shift in PDI4sg as compared to PDI0sg.
Due to the low molar absorption coefficient of TEMPO (ε470nm = 10.5 M−1 cm−1)56 compared to PDI, the UV-vis absorption spectrum of PDI0sg–TEMPO is virtually identical to that of its parent compound PDI0sg. In the case of PDI4sg–TEMPO and PDI4sg–(TEMPO)2 we observe a slight red-shift of the absorption bands compared to the spectrum of PDI4sg (see Fig. S1†). Although the absorption of TEMPO itself does not contribute to the spectral shape, the presence of the TEMPO radical substituents may influence the solute–solvent interactions which may result in the observed spectral red-shift of up to 6 nm for PDI4sg–(TEMPO)2 in toluene.
While the fluorescence quantum yields of the parent PDI chromophores are similar, the fluorescence quantum yields ΦF of the three PDI–TEMPO compounds differ significantly. PDI4sg–TEMPO has a relatively high fluorescence quantum yield of 0.23 (23%). In contrast, that of PDI0sg–TEMPO is roughly a factor of ten lower (∼0.02). The attachment of a second nitroxide radical to the second imide position of PDI in PDI4sg–(TEMPO)2 also has a major effect on the fluorescence quantum yield, which from 0.23 in PDI4sg–TEMPO to 0.04 in PDI4sg–(TEMPO)2 (see also Table 1).
| Compound | Φ F | τ S1/ps | Φ EISC | k EISC/s−1 |
|---|---|---|---|---|
| PDI0sg | 0.97 | 4.0 × 103 | — | — |
| PDI0sg–TEMPO | 0.02 | 27 | 0.55 | 2.0 × 1010 |
| PDI4sg | 0.92 | 5.9 × 103 | — | — |
| PDI4sg–TEMPO | 0.23 | 1.1 × 102 | 0.51 | 4.6 × 109 |
| PDI4sg–(TEMPO)2 | 0.04 | 47 | 0.57 | 1.2 × 1010 |
In line with the fluorescence quantum yields, also the fluorescence lifetimes of the PDI–TEMPO compounds are reduced significantly with respect to those of their parent chromophores. The fluorescence lifetimes correspond to the S1 state deactivation time constants and will be discussed in more detail further below. They reflect the same trend as observed for the fluorescence quantum yields.
Femtosecond transient UV-vis absorption
To characterize and compare the excited state kinetics of the different PDI systems, fsTA experiments were carried out for all compounds in toluene solution at room temperature. Contour plots of the data obtained for PDI0sg and PDI0sg–TEMPO are shown in Fig. 3, while the data for all remaining compounds can be found in the ESI (Fig. S4).†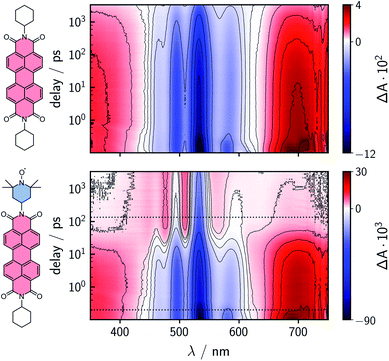 | ||
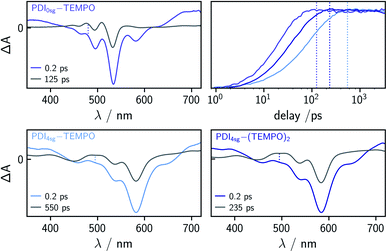
| Fig. 3 Contour plots of the fsTA data of PDI0sg (top) and PDI0sg–TEMPO (bottom) recorded at room temperature in toluene. The red and blue color coding represents positive and negative signals, respectively. The horizontal black dotted lines in the contour plot of PDI0sg–TEMPO indicate the time delays corresponding to the spectra in Fig. 4. | ||
The photophysics of PDI derivatives is well-known and has been studied extensively.28,34,57–60 In agreement with previous results for unsubstituted PDIs, we observe an intense ground state bleach between ∼400 and 550 nm for PDI0sg. In the center of the spectrum (∼530 nm), the ground state bleach overlaps with stimulated emission extending from 500 to ∼660 nm, in line with the fluorescence spectrum of PDI0sg shown in Fig. 2. Ground state bleach and stimulated emission are accompanied by a broad excited state absorption extending almost over the entire visible range. The ground state bleach recovers only partially within the detection time window of ∼3 ns, corresponding to an S1 state decay in the nanosecond range, in agreement with the measured fluorescence lifetime of 4.0 ns.
When a TEMPO radical is attached to the imide position of the PDI in PDI0sg–TEMPO, the decay of the excited singlet state is found to be markedly accelerated. After about ∼60 ps, the features corresponding to the S1 state have disappeared and we observe the formation of new excited state absorption signals at 480 and 510 nm, which can be attributed to the excited triplet state of PDI.27,28 Furthermore, the stimulated emission signal has vanished, indicating the depletion of the S1 state. The signals present after ∼60 ps are long-lived and do not decay within the detection time window, indicating an excited state lifetime of microseconds (or longer).
We can thus confirm that the PDI excited triplet state is formed rapidly in PDI0sg–TEMPO after photoexcitation by enhanced intersystem crossing in the presence of the covalently attached TEMPO radical. A similar observation is made for PDI4sg–TEMPO and PDI4sg–(TEMPO)2 as shown in Fig. S4.†
To determine the time constants of the excited state deactivation, a global kinetic analysis of the fsTA data of the PDI–TEMPO compounds was carried out and the results (including the decay associated spectra) are presented and discussed in the ESI.† We found that three time constants were necessary in all cases to reproduce the experimental data satisfactorily. The third time constant, representing the triplet state decay, was fixed to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μs in the analysis of the spectra while the first two time constants, attributed to (i) vibrational relaxation in the S1 state and (ii) deactivation of the S1 state, were left to vary freely. In the case of PDI0sg–TEMPO, we obtained an S1 state deactivation time constant of 27 ps, while time constants of 110 ps and 47 ps were obtained for PDI4sg–TEMPO and PDI4sg–(TEMPO)2, respectively.
μs in the analysis of the spectra while the first two time constants, attributed to (i) vibrational relaxation in the S1 state and (ii) deactivation of the S1 state, were left to vary freely. In the case of PDI0sg–TEMPO, we obtained an S1 state deactivation time constant of 27 ps, while time constants of 110 ps and 47 ps were obtained for PDI4sg–TEMPO and PDI4sg–(TEMPO)2, respectively.
Compared to PDI4sg–TEMPO, the fsTA data of which was already published previously,36 the deactivation of the excited singlet state is found to be faster in PDI0sg–TEMPO by a factor of about four. The S1 state deactivation is also accelerated (by a factor of roughly two) when attaching a second TEMPO radical to the system in PDI4sg–(TEMPO)2.
When carefully analyzing the recovery of the ground state bleach, it is possible to determine the triplet/EISC yield from the fsTA data of the different PDI–TEMPO systems37 as illustrated in Fig. S7 in the ESI† using PDI0sg–TEMPO as an example. We accounted for the contribution of stimulated emission to the apparent amplitude of the ground state bleach by considering the shapes of the steady state UV-vis absorption and fluorescence spectra. For the determination of the amplitude of the ground state bleach, the contribution from stimulated emission was subtracted from the spectra. The yields were then determined by considering the amplitude of the ground state bleach directly after photoexcitation (0.2 ps) and comparing this value to the amplitude of the ground state bleach after complete deactivation of the S1 state, accounting also for partial overlap with excited state absorption signals. The deactivation of the S1 state was considered to be complete at a time delay corresponding to 5 × τS1. The spectra used for this determination of the triplet yields are shown in Fig. 4 together with a visual comparison of the kinetics of triplet state formation for PDI0sg–TEMPO, PDI4sg–TEMPO, and PDI4sg–(TEMPO)2. It can be seen that while triplet state formation is much faster in PDI0sg–TEMPO, the triplet yield is comparable to that of PDI4sg–TEMPO and PDI4sg–(TEMPO)2. The corresponding calculated yields for the three compounds in toluene are listed in Table 1.
Discussion of the triplet state formation yields
The latter finding, that the triplet yield is not significantly higher in PDI0sg–TEMPO despite a much faster deactivation of the S1 state, is unexpected and demands an explanation. As illustrated in Fig. 1b, different competitive decay processes are possible in the excited state and may limit the triplet state formation yield. In particular, we will need to consider the likelihood of electron and excitation energy transfer in the excited state and possible differences between PDI0sg–TEMPO and PDI4sg–TEMPO that may have an impact on the yield of these decay processes.In a previous study on a similar PDI–TEMPO compound with two phenoxy sidegroups,33 PDI2sg–TEMPO, electron transfer was found to occur in tetrahydrofuran solution at room temperature with a time constant of 1.2 ps, followed by a fast decay of the excited state absorption to the ground state with a time constant of 86 ps (i.e., no triplet formation). In toluene, on the other hand, triplet formation by enhanced intersystem crossing was found to occur with a time constant of 45 ps, well in line with the observations made here for PDI0sg–TEMPO and PDI4sg–TEMPO. The absence of electron transfer in toluene was rationalized by the stabilization of the ion pair state in polar solvents.
To determine whether electron transfer is possible in PDI0sg–TEMPO, PDI4sg–TEMPO, and PDI4sg–(TEMPO)2 we investigated the influence of the solvent polarity on the excited state reaction rate constants and yields. To this end, room temperature fsTA data were also recorded using 2-methyltetrahydrofuran as the solvent, which has a significantly higher dielectric constant than toluene (εr = 7.0 vs. 2.4).61 The corresponding data are shown in Fig. S8† and the spectra and kinetics of the three compounds are compared in Fig. S9.†
The formation of the PDI anion by photoinduced electron transfer should be detectable in fsTA experiments, since the corresponding signatures are well known. The radical anion of PDI0sg (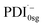 ) has its first absorption peak near ∼710 nm,62,63 while
) has its first absorption peak near ∼710 nm,62,63 while 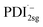 absorbs around ∼725
absorbs around ∼725![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm.64 In
nm.64 In 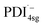 this peak is further red-shifted to ∼780 nm.58
this peak is further red-shifted to ∼780 nm.58
If electron transfer occurred for PDI0sg–TEMPO and was followed by recombination to the ground state, the sharp anion absorption band around 710 nm should be clearly visible in the spectra. For PDI4sg–TEMPO, the maximum of the PDI anion absorption peak at 780 nm is outside the standard detection window of our UV-vis fsTA setup. For this reason, we acquired additional fsTA data using a setup with an extended detection window. These data for PDI4sg–TEMPO were already published earlier36 but are shown again in Fig. S12† for completeness. When comparing the shapes of the spectra of the two PDI–TEMPO compounds, recorded a few picoseconds after photoexcitation, with those of their parent chromophores,58 no significant differences are observed in either of the two solvents. In addition, no clear spectral signatures indicating electron transfer could be discerned.
The short time constant of photoinduced electron transfer observed previously for PDI2sg–TEMPO in tetrahydrofuran33 is in contrast to the absence of any PDI anion signatures in the fsTA spectra of both PDI0sg–TEMPO and PDI4sg–TEMPO. In search for an explanation, we calculated the free energies (driving forces for electron transfer, −ΔG0) of the hypothetical charge separated states of the three different PDI–TEMPO compounds (including PDI2sg–TEMPO) and considered also the reorganization energies in our detailed discussion in the ESI.† It is found that the driving forces for charge separation are higher in 2-methyltetrahydrofuran by about 0.5 eV as compared to toluene, but this larger driving force is roughly compensated by the larger outer sphere reorganization energy so that the electron transfer reaction could theoretically proceed almost barrierless −ΔG0 ≃ λ in both solvents.
When considering all λ- and ΔG0-dependent terms in the expression of the Marcus rate equation for photoinduced electron transfer65,66 it seems that electron transfer should be fast and equally feasible for all three considered PDI chromophores (PDI0sg, PDI2sg, and PDI4sg). Although these types of calculations necessarily rely on many assumptions and estimated values, it is puzzling why electron transfer does not seem to occur for any of the PDI–TEMPO compounds investigated here.
Two different explanations for this apparent inconsistency could be invoked. (i) The rate constant for electron transfer further depends on the square of the coupling matrix element |HAB|2 (see eqn S12 in the ESI†), describing the coupling between the electron donor and acceptor states.67,68 The value of HAB is difficult to estimate reliably but could be responsible for a considerably smaller rate constant than would be expected based on our considerations of the reorganization energies and driving forces. Considering the short distance between electron donor and acceptor, there is no obvious reason to assume that HAB should be particularly small in our PDI–TEMPO systems. However, the saturated carbon atoms of the TEMPO radical will exponentially reduce the coupling between the nitroxide group and PDI. In addition, an inspection of the HOMO and LUMO orbitals of PDI0sg and PDI4sg, as shown in the ESI in Fig. S16,† reveals that a nodal plane runs through the axis connecting the two imide nitrogen atoms in PDI where the TEMPO radical is attached, potentially significantly reducing |HAB|. However, this argument cannot explain the observations made previously for PDI2sg–TEMPO in tetrahydrofuran,33 since |HAB| should be affected in a similar way.
(ii) An alternative explanation for the absence of any clearly identifiable PDI radical anion signatures in the spectra of both PDI0sg–TEMPO and PDI4sg–TEMPO could be that electron transfer does indeed occur for all PDI–TEMPO systems, as predicted, with a rate constant of ∼kEISC but is directly followed by fast charge recombination (CR) with kCR ≥ 2–3 × kEISC to the chromophore triplet state, so-called “inverted” kinetics. Based on the spectroscopic S1 state energies, the driving forces for charge recombination (i.e. energies of the charge-transfer, CT, states) computed from experimental redox potentials, and the calculated vertical triplet energies obtained from TD-DFT calculations (see the ESI†), the charge recombination to the chromophore triplet state should be exergonic. For PDI0sg–TEMPO, for instance, these energies amount to ES1 = 2.33 eV, ECT = 1.80 eV, and ET1 = 1.45 eV. Triplet formation via charge recombination thus seems to be a viable option which will be discussed in more detail further below.
Apart from electron transfer, another possible excited state decay mechanism to be considered here is excitation energy transfer (EET). In this context, two different mechanisms are frequently invoked, referred to as Förster-type and Dexter-type excitation energy transfer.69–71 Both mechanisms require spectral overlap of the fluorescence spectrum of the energy donor (PDI) and the absorption spectrum of the energy acceptor (TEMPO). While Dexter-type energy transfer is based on an exchange mechanism, Förster-type energy transfer relies on a dipolar mechanism. The rate constants for Dexter energy transfer are difficult to predict, but the Förster excitation energy transfer rate constants can be calculated in a straightforward manner, assuming the validity of the point-dipole approximation.69 Although the calculated rate constants are likely not accurate because the center-to-center distance between chromophore and radical is short compared to their individual molecular sizes, a good estimate of the feasibility and importance of excitation energy transfer can be gained. The calculation is shown in the ESI† and reveals that the contribution from excitation energy transfer can become significant, even though the TEMPO radical absorbs only weakly in the visible range. Assuming a collinear orientation of the transition dipole moments (κ2 = 4), the results further show that energy transfer could still be competitive for PDI0sg–TEMPO with an approximated Förster time constant of 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ps, while the energy transfer quenching efficiency significantly drops for PDI4sg, associated with a Förster time constant of 1.5 ns. The latter is a consequence of the red-shifted fluorescence spectrum of PDI4sg, significantly reducing the spectral overlap of the TEMPO absorption and PDI emission as illustrated in Fig. S3.†
ps, while the energy transfer quenching efficiency significantly drops for PDI4sg, associated with a Förster time constant of 1.5 ns. The latter is a consequence of the red-shifted fluorescence spectrum of PDI4sg, significantly reducing the spectral overlap of the TEMPO absorption and PDI emission as illustrated in Fig. S3.†
In a previous study,37 the occurrence of EET could be confirmed by the observation of the excited state absorption signatures and corresponding ground state bleach of the radical in fsTA experiments. Unfortunately, this is not possible in the present case, since the excited state absorption of the TEMPO radical, potentially buried underneath the intense PDI signatures, is too weak to be detected. However, the Förster time constants calculated for the two PDI–TEMPO compounds strongly suggest that excitation energy transfer cannot be neglected for PDI0sg–TEMPO: it might be a major excited state deactivation channel and could account for the much smaller S1 state deactivation time constant and lower fluorescence quantum yield as compared to PDI4sg–TEMPO.
Finally, apart from ET and EET, enhanced internal conversion (EIC) certainly is a viable deactivation pathway for all of the investigated PDI–TEMPO systems. It can be assumed that the yield of EIC is given as ΦEIC = 1 − (ΦEISC + ΦET + ΦEET).
Transient EPR spectroscopy
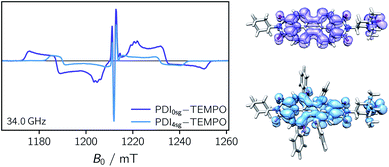
Transient EPR spectroscopy was employed to characterize the magnetic properties of the photogenerated spin states and the coupling strengths between chromophore triplet and radical in the three PDI–TEMPO compounds. Fig. 5 shows a comparison of the field-swept echo-detected EPR spectra recorded for PDI0sg–TEMPO and PDI4sg–TEMPO in frozen toluene solution at the Q-band after light irradiation at 535 nm. PDI4sg–TEMPO was previously characterized by pulse EPR spectroscopy36 and its transient EPR spectrum could be assigned to the trip-quartet state of PDI4sg–TEMPO by transient nutation experiments. The rather unusual, complex central feature was shown to arise from an additional splitting of the quartet sublevels by the hyperfine interaction of the 14N nucleus of the TEMPO moiety. When including the nitrogen hyperfine coupling in a simulation of the EPR spectrum using a spin Hamiltonian approach and assuming the magnetic interaction parameters (g tensor, hyperfine coupling tensor) expected for a quartet state, the spectral shape could be qualitatively reproduced, confirming the assignment of the transient spectrum to a pure quartet state. Since the spectral features of the transient EPR spectra shown in Fig. 5 are very similar, it can be assumed that trip-quartet states are also formed in PDI0sg–TEMPO. The interaction between the PDI excited triplet state and the TEMPO radical thus falls within the strong coupling regime, indicating that the exchange interaction between the two spin centers is larger than any other magnetic interactions in the system.When analyzing the shape of the trip-quartet spectra recorded for PDI0sg–TEMPO and PDI4sg–TEMPO, one notices that the outer wings of both EPR spectra (multiplet polarization) show the same sequence of absorptive (a) and emissive (e) transitions: on going from low to high field, an aeeaae multiplet polarization pattern is observed in both cases. This spin polarization pattern is rather unusual since it cannot be obtained by “normal” (i.e., spin–orbit coupling induced) intersystem crossing, suggesting a triplet state formation mechanism involving more than one step. In the case of triplet states, the aeeaae polarization pattern is indicative for a selective population of the high-field triplet |T0〉 state for each canonical orientation,72 and was previously observed for triplet states resulting from singlet fission but also for triplets formed by radical ion pair recombination.2,73–76 In the case of quartet states, an aeeaae multiplet polarization pattern indicates a selective population of the high-field quartet levels with 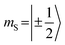 which could be consistent with the hypothesis that electron transfer occurs in these PDI–TEMPO systems and is followed by rapid charge recombination to the chromophore triplet state. We propose the following mechanism: (i) electron transfer occurs from 2TEMPO˙ to 1*PDI leaving 2PDI˙− and the diamagnetic 1TEMPO+; (ii) charge recombination yields 3PDI and 2TEMPO˙ in an overall trip-doublet state as a result of the spin–orbit charge transfer intersystem crossing (SOCT–ISC) mechanism;77 (iii) due to the exchange interaction JTR between chromophore triplet and radical, the trip-doublet and trip-quartet states are split in energy; (iv) the trip-quartet state is populated from the trip-doublet state via a spin-exchange mechanism78,79 and spin conservation will lead to an overpopulation of the quartet sublevels with
which could be consistent with the hypothesis that electron transfer occurs in these PDI–TEMPO systems and is followed by rapid charge recombination to the chromophore triplet state. We propose the following mechanism: (i) electron transfer occurs from 2TEMPO˙ to 1*PDI leaving 2PDI˙− and the diamagnetic 1TEMPO+; (ii) charge recombination yields 3PDI and 2TEMPO˙ in an overall trip-doublet state as a result of the spin–orbit charge transfer intersystem crossing (SOCT–ISC) mechanism;77 (iii) due to the exchange interaction JTR between chromophore triplet and radical, the trip-doublet and trip-quartet states are split in energy; (iv) the trip-quartet state is populated from the trip-doublet state via a spin-exchange mechanism78,79 and spin conservation will lead to an overpopulation of the quartet sublevels with 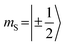 .
.
Compared to the light-induced EPR spectrum of PDI4sg–TEMPO, the width of the spectrum of PDI0sg–TEMPO is markedly increased due to an increased localization of the trip-quartet state wavefunction in the absence of the four side groups on the PDI core. This difference in the spin density distribution is also confirmed by DFT calculations as shown in the ESI† and graphically illustrated in Fig. 5, where it can be seen that the oxygen atom of the phenoxy linker still carries significant spin density. The spectral widths amount to 78 mT and 58 mT for PDI0sg–TEMPO and PDI4sg–TEMPO, respectively. Since the spectral width of a quartet state is given as 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |DQ|, this corresponds to experimental zero-field splitting |DQ| values of 545 MHz and 405 MHz.
|DQ|, this corresponds to experimental zero-field splitting |DQ| values of 545 MHz and 405 MHz.
From the D value of the trip-quartet state, the interaction strength between chromophore triplet and radical (DTR) can, in principle, be calculated from the relation 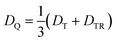 .80 For a PDI without any core substituents, the triplet |D| value has been determined before and amounts to 45.5 mT, i.e., 1275 MHz,81 which would result in |DTR| = 3 |DQ| − |DT| = 360 MHz.
.80 For a PDI without any core substituents, the triplet |D| value has been determined before and amounts to 45.5 mT, i.e., 1275 MHz,81 which would result in |DTR| = 3 |DQ| − |DT| = 360 MHz.
From a DFT model of the structures (see the ESI†), a center-to-center distance between PDI and TEMPO of ∼0.99 nm was obtained. However, the effective coupling distance between the two spin centers is likely to be considerably shorter than the center-to-center distance, due to a significant delocalization of both the radical and triplet spin densities.
A calculation, based on a simple point-dipole model, of the coupling between triplet and radical (DTR) yields DTR = −80 MHz for a distance of rTR = 0.99 nm, according to
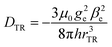 | (1) |
For a PDI chromophore with two phenoxy side groups on the PDI core, PDI2sg, an experimental triplet |DT| value of 40 mT was determined.82 Based on this and the knowledge of the value for PDI0sg, we estimate the experimental |DT| value for PDI4sg to be roughly 35 mT, i.e., 981 MHz. This consideration would yield DTR = −234 MHz, corresponding to rTR = 0.69 nm. A slightly stronger effective coupling can thus be assumed for PDI0sg–TEMPO.
Regarding the PDI compound with two nitroxide radicals, PDI4sg–(TEMPO)2, we would expect an overall quintet spin state to be formed upon photoexcitation in the case of strong coupling between the two radicals and the PDI triplet state. However, before interpreting the excited state behavior of the molecule, we first needed to verify the absence of significant through-bond (exchange) coupling between the two nitroxides in the ground state. To this end, a double electron–electron resonance experiment was carried out in frozen toluene solution at 80 K. The experimental details are given in the ESI† and the data are shown in Fig. S15.† A model-free analysis of the obtained dipolar evolution trace based on Tikhonov regularization using the program DeerAnalysis83,84 yielded a narrow distance distribution centered at 2.08 nm. This value is in very good agreement with the distance that would be expected based on a DFT model of the structure (2.10 nm, see the ESI†), confirming the structural model and indicating that any significant contribution of exchange coupling can likely be excluded. Any weak exchange coupling between the two nitroxides, of the order of the dipolar coupling, would alter the detected modulation frequency and corresponding Pake pattern of the trace.85–88 The fact that the obtained distance distribution is relatively narrow further points towards a high rigidity of the molecular structure.
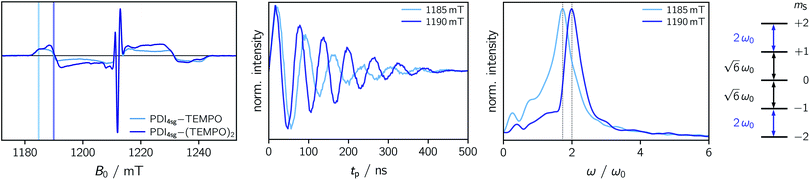
To explore whether overall quintet spin states are formed after photoexcitation of PDI4sg–(TEMPO)2, transient nutation experiments were performed in frozen toluene solution at 80 K as a function of field, spanning the entire width of the transient EPR spectrum, as detailed in the ESI.† The frequency axis obtained after Fourier transform of the measured time traces was normalized by the reference frequency ω0 obtained for the radical (doublet state) in the dark. The complete frequency map is shown in the ESI (Fig. S14†), while two selected time traces and their Fourier transform are shown in Fig. 6.
As can be seen from Fig. 6, the EPR spectrum of PDI4sg–(TEMPO)2 measured after photoexcitation, has a close resemblance with that of PDI4sg–TEMPO. Since the quintet state EPR spectrum is expected to have a reduced spectral width and smaller nitrogen hyperfine coupling constants leading to a narrower feature in the center of the spectrum, this observation suggests that most of the observed spectral features can be attributed to the trip-quartet state, rather than the trip-quintet state. In particular, the prominent central feature can clearly be attributed to a quartet state as revealed by the transient nutation frequency map shown in Fig. S14.† Although quartet state features seem to dominate the appearance of the transient EPR spectrum of PDI4sg–(TEMPO)2, small differences in the spectral shape are observed between PDI4sg–TEMPO and PDI4sg–(TEMPO)2 that are likely due to quintet formation. To confirm the formation of quintet states, we focused on the magnetic field position showing the largest spectral difference and compared the transient nutation data to those obtained at a field position where only quartet state signals are expected (outer wings).
According to 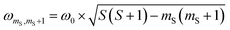 ,43,89,90 frequencies of
,43,89,90 frequencies of 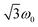 and 2ω0 would be expected for the quartet
and 2ω0 would be expected for the quartet 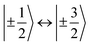 and
and 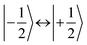 transitions, respectively, while, for a quintet state, the nutation frequency should amount to 2ω0 for the quintet |± 1〉 ↔ |± 2〉 transitions and
transitions, respectively, while, for a quintet state, the nutation frequency should amount to 2ω0 for the quintet |± 1〉 ↔ |± 2〉 transitions and 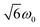 for the quintet |0〉 ↔ |± 1〉 transitions. The chosen magnetic field positions shown in Fig. 6 correspond to the
for the quintet |0〉 ↔ |± 1〉 transitions. The chosen magnetic field positions shown in Fig. 6 correspond to the 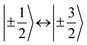 transition of the quartet state and the |± 1〉 ↔ |± 2〉 transition of the quintet state, so a frequency of
transition of the quartet state and the |± 1〉 ↔ |± 2〉 transition of the quintet state, so a frequency of 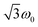 would be expected for a quartet state, while a quintet state would be characterized by a frequency of 2ω0. These frequencies are also indicated in the frequency plot in Fig. 6. The good agreement between the measured and expected frequencies confirms quintet state formation in PDI4sg–(TEMPO)2. However, the quintet formation yield appears to be relatively low for reasons that could not be revealed with the available methods. This observation will require further investigation in the future. Assuming that the sample is pure, as suggested by thin-layer chromatography and quantitative EPR experiments, it might be that only certain conformations of the molecule (i.e., mutual orientations of the TEMPO moieties) lead to quintet formation. Alternatively, although the presence of two TEMPO radicals per PDI unit is consistent with quantitative EPR as shown in Fig. S13,† a small amount of sample degradation cannot be excluded and might also be responsible for the residual quartet signal observed here for PDI4sg–(TEMPO)2, keeping in mind that the signal intensities of spin polarized species are not proportional to concentration.
would be expected for a quartet state, while a quintet state would be characterized by a frequency of 2ω0. These frequencies are also indicated in the frequency plot in Fig. 6. The good agreement between the measured and expected frequencies confirms quintet state formation in PDI4sg–(TEMPO)2. However, the quintet formation yield appears to be relatively low for reasons that could not be revealed with the available methods. This observation will require further investigation in the future. Assuming that the sample is pure, as suggested by thin-layer chromatography and quantitative EPR experiments, it might be that only certain conformations of the molecule (i.e., mutual orientations of the TEMPO moieties) lead to quintet formation. Alternatively, although the presence of two TEMPO radicals per PDI unit is consistent with quantitative EPR as shown in Fig. S13,† a small amount of sample degradation cannot be excluded and might also be responsible for the residual quartet signal observed here for PDI4sg–(TEMPO)2, keeping in mind that the signal intensities of spin polarized species are not proportional to concentration.
Conclusions
In conclusion, the excited state kinetics and yields as well as the magnetic properties of three PDI–TEMPO compounds have been investigated by optical and transient EPR spectroscopies. The TEMPO radical was directly attached to the imide position of the PDI in all cases, but the structures differ with respect to the number of p-tert-butylphenoxy side groups (none vs. four) and the number of TEMPO substituents (one vs. two). We could show that the PDI excited triplet state, difficult to access by other methods, can be efficiently sensitized after photoexcitation of the compounds in the presence of the TEMPO radical. The triplet yields were determined by femtosecond UV-vis transient absorption spectroscopy, while transient EPR experiments revealed strong coupling between the PDI excited triplet state and the TEMPO radical, leading to the formation of trip-quartet (or trip-quintet) states.The presence of the side groups on PDI induces a core twist and enhances exciton delocalization, reflected by a red-shift in the UV-vis absorption spectrum and the narrowing of the transient EPR spectrum of the trip-quartet state of PDI4sg–TEMPO compared to PDI0sg–TEMPO. Interestingly, the excited state reaction kinetics were found to be influenced considerably by this core substitution: triplet formation is about four times slower in PDI4sg–TEMPO as compared to PDI0sg–TEMPO. However, the triplet yield was shown to be almost identical. When the experiments were performed in 2-methyltetrahydrofuran solution instead of toluene, the S1 state deactivation rate constants were found to be smaller and the triplet yields are considerably reduced.
Calculations of the electron transfer rate based on driving forces and reorganization energies suggest that electron transfer should be fast and equally feasible for all investigated PDI–TEMPO compounds both in toluene and 2-methyltetrahydrofuran. Nevertheless, no PDI anion signatures were observed in the fsTA spectra, which led us to propose that electron transfer in these systems is followed by rapid charge recombination to the chromophore triplet state. The latter hypothesis is also supported by the unusual polarization pattern observed in the transient EPR spectra of the corresponding trip-quartet states, clearly suggesting a multi-step process. This new triplet formation mechanism proposed here, referred to as “sequential EISC”, will need to be further explored and experimentally confirmed in future studies by investigating different triplet–radical systems.
Calculations of the rate constants of Förster-type excitation energy transfer suggest that energy transfer is competitive with EISC for PDI0sg–TEMPO, while such a contribution can virtually be excluded for PDI4sg–TEMPO. Energy transfer as an additional excited state deactivation channel in PDI0sg–TEMPO might account for the faster S1 state deactivation and much lower fluorescence quantum yield of PDI0sg–TEMPO as compared to PDI4sg–TEMPO.
The presence of a second TEMPO substituent, attached to the second imide position of the PDI chromophore, was shown to enhance the deactivation of the excited singlet state by a factor of about two, accompanied by an increase of the triplet yield and considerable decrease of the fluorescence quantum yield in toluene. DEER experiments showed that the exchange coupling between the two radicals in PDI4sg–(TEMPO)2 is close to zero in the ground state. However, upon photoexcitation, a trip-quintet state is formed as revealed by transient nutation experiments in frozen toluene solution.
The present study shows that faster triplet formation in photoexcited chromophore–radical compounds does not guarantee a higher triplet yield, since competing deactivation processes, like excitation energy transfer or electron transfer, if they can occur, are often faster. As the choice of easily functionalizable stable radicals is limited, most effort to suppress these unwanted deactivation processes will need to be directed at the identification of suitable chromophores. Electron transfer can be suppressed, to a large extent, by tuning the redox potentials of the chromophore by core substitution. Core substitution, especially with electron donating groups, can also result in a considerable red-shift of the UV-vis absorption spectrum of the chromophore and may reveal as an important strategy to limit the yield of excitation energy transfer by reducing the spectral overlap between chromophore emission and radical absorption.
This and a previous study37 suggest that excitation energy transfer is often the main factor limiting the yield of EISC in strongly-coupled photogenerated multi-spin systems. Consequently, regarding the design of novel chromophore–radical systems with high triplet yields, we believe that it will be essential to reflect on strategies to limit EET as a possible deactivation pathway. Apart from core substitution with ethers or amines, another strategy could be to add the linker in a position that is perpendicular to the orientation of the transition dipole moment of the chromophore. For PDI chromophores, this would imply connecting the linker to the core of the PDI, rather than the imide position.
Our results further indicate that fast electron transfer may also be beneficial for triplet formation in chromophore–radical compounds if charge recombination is fast and an energetically low-lying triplet state of the chromophore is available. This strategy termed “sequential EISC” will be further explored by us in the near future.
In general, we believe that modular chromophore–radical compounds are ideal model compounds for the study of spin-dependent light-induced processes. As demonstrated here, they provide access to excited states with high spin multiplicities, like triplet and quintet states, which are key intermediates in photophysical processes for solar energy conversion, such as singlet fission or triplet–triplet annihilation photon upconversion. Future studies will reveal whether the study of the properties of these states, enabled by EISC, can provide new insight into the mechanisms underlying these processes.
Data availability
The data supporting the findings of this study are available within the article and in the ESI.†Author contributions
Spectroscopic characterization of the compounds, EPR data acquisition and analysis, fsTA data analysis, draft editing and data visualization M. M.; FsTA data acquisition and analysis, draft editing O. N.; quantum chemical calculations M. F.; synthesis and characterization of the compounds S. C., L. B., Y. Q.; Supervision of the synthesis, funding acquisition, review and editing of the manuscript M. R. W.; supervision of the fsTA experiments, funding acquisition, review and editing of the manuscript P. G.; conceptualization, project administration, funding acquisition, supervision of the optical and EPR experiments, original draft writing S. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project numbers 417643975 (S. R.) and 396890929 (GRK 2482, P. G.). Work at Northwestern University was supported by the Center for Molecular Quantum Transduction, and Energy Frontier Research Center funded by DOE, Office of Science, BES under Award #DE-SC0021314 (M. R. W.). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant number INST 40/575-1 FUGG (JUSTUS2 cluster).Notes and references
- M. J. Y. Tayebjee, S. N. Sanders, E. Kumarasamy, L. M. Campos, M. Y. Sfeir and D. R. McCamey, Nat. Phys., 2017, 13, 182–189 Search PubMed.
- L. R. Weiss, F. Bayliss, S. L. Kraffert, K. J. Thorley, J. E. Anthony, R. Bittl, R. H. Friend, A. Rao, N. C. Greenham and J. Behrends, Nat. Phys., 2017, 13, 176–182 Search PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, B. T. Phelan, M. D. Krzyaniak, S. R. Reddy, P. B. Coto, N. E. Horwitz, R. M. Young, F. J. White, F. Hampel, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Nat. Commun., 2017, 8, 15171 Search PubMed.
- Y. Teki, Chem. –Eur. J., 2020, 26, 980–996 CrossRef CAS PubMed.
- Z. Wang, Y. Gao, M. Hussain, S. Kundu, V. Rane, M. Hayvali, E. A. Yildiz, J. Zhao, H. G. Yaglioglu, R. Das, L. Luo and J. Li, Chem. –Eur. J., 2018, 24, 18663–18675 CrossRef CAS PubMed.
- Z. Wang, J. Zhao, A. Barbon, A. Toffoletti, Y. Liu, Y. An, L. Xu, A. Karatay, H. G. Yaglioglu, E. A. Yildiz and M. Hayvali, J. Am. Chem. Soc., 2017, 139, 7831–7842 CrossRef CAS PubMed.
- J. Han, Y. Jiang, A. Obolda, P. Duan, F. Li and M. Liu, J. Phys. Chem. Lett., 2017, 8, 5865–5870 CrossRef CAS PubMed.
- A. Rao and R. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS.
- A. J. Gillett, A. Privitera, R. Dilmurat, A. Karki, D. Qian, A. Pershin, G. Londi, W. K. Myers, J. Lee, J. Yuan, S.-J. Ko, M. K. Riede, F. Gao, G. C. Bazan, A. Rao, T.-Q. Nguyen, D. Beljonne and R. H. Friend, Nature, 2021, 597, 666–671 CrossRef CAS PubMed.
- R. Ieuji, K. Goushi and C. Adachi, Nat. Commun., 2019, 10, 5283 CrossRef PubMed.
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS.
- A. Köhler and H. Bässler, Mater. Sci. Eng., R, 2009, 66, 71–109 CrossRef.
- Y. Shao and Y. Yang, Adv. Mater., 2005, 17, 2841–2844 CrossRef CAS.
- F. Würthner, Chem. Commun., 2004, 1564–1579 RSC.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052 CrossRef PubMed.
- A. Nowak-Król and F. Würthner, Org. Chem. Front., 2019, 6, 1272–1318 RSC.
- A. Nowak-Król, K. Shoyama, M. Stolte and F. Würthner, Chem. Commun., 2018, 54, 13763–13772 RSC.
- S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135, 14701–14712 CrossRef CAS PubMed.
- N. Renaud and F. C. Grozema, J. Phys. Chem. Lett., 2015, 6, 360–365 CrossRef CAS PubMed.
- M. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- M. H. Farag and A. I. Krylov, J. Phys. Chem. C, 2018, 122, 25753–25763 CrossRef CAS.
- A. K. Le, J. A. Bender, D. H. Arias, D. E. Cotton, J. C. Johnson and S. T. Roberts, J. Am. Chem. Soc., 2018, 140, 814–826 CrossRef CAS PubMed.
- B. Carlotti, I. K. Madu, H. Kim, Z. Cai, H. Jiang, A. K. Muthike, L. Yu, P. M. Zimmerman and T. Goodson III, Chem. Sci., 2020, 11, 8757–8770 RSC.
- A. K. Muthike, B. Carlotti, I. K. Madu, H. Jiang, H. Kim, Q. Wu, L. Yu, P. M. Zimmerman and T. Goodson III, J. Phys. Chem. B, 2021, 125, 5114–5131 CrossRef CAS PubMed.
- H. Weissman, E. Shirman, T. Ben-Moshe, R. Cohen, G. Leitus, L. J. W. Shimon and B. Rybtchinski, Inorg. Chem., 2007, 46, 4790–4792 CrossRef CAS PubMed.
- W. E. Ford and P. V. Kamat, J. Phys. Chem., 1987, 91, 6373–6380 CrossRef CAS.
- A. A. Rachford, S. Goeb and F. N. Castellano, J. Am. Chem. Soc., 2008, 130, 2766–2767 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- M. R. Wasielewski, J. Org. Chem., 2006, 71, 5051–5066 CrossRef CAS PubMed.
- A. Prodi, C. Chiorboli, F. Scandola, E. Iengo, E. Alessio, F. Dobrawa and R. Würthner, J. Am. Chem. Soc., 2005, 127, 1454–1462 CrossRef CAS PubMed.
- E. O. Danilov, A. A. Rachford, S. Goeb and F. N. Castellano, J. Phys. Chem. A, 2009, 113, 5763–5768 CrossRef CAS PubMed.
- M. T. Colvin, E. M. Giacobbe, B. Cohen, T. Miura, A. M. Scott and M. R. Wasielewski, J. Phys. Chem. A, 2010, 114, 1741–1748 CrossRef CAS PubMed.
- E. M. Giacobbe, Q. Mi, M. T. Colvin, B. Cohen, C. Ramanan, A. M. Scott, S. Yeganeh, T. J. Marks, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2009, 131, 3700–3712 CrossRef CAS PubMed.
- X. Zhang, A. A. Sukhanov, E. Y. Yildiz, Y. E. Kandrashkin, J. Zhao, H. G. Yaglioglu and V. K. Voronkova, ChemPhysChem, 2021, 22, 55–68 CrossRef CAS PubMed.
- M. Mayländer, S. Chen, E. R. Lorenzo, M. R. Wasielewski and S. Richert, J. Am. Chem. Soc., 2021, 143, 7050–7058 CrossRef PubMed.
- O. Nolden, N. Fleck, E. R. Lorenzo, M. R. Wasielewski, O. Schiemann, P. Gilch and S. Richert, Chem.–Eur. J., 2021, 27, 2683–2691 CrossRef CAS PubMed.
- Y. Kandrashkin and A. van der Est, J. Chem. Phys., 2004, 120, 4790–4799 CrossRef CAS PubMed.
- V. Rozenshtein, A. Berg, E. Stavitski, H. Levanon, L. Franco and C. Corvaja, J. Phys. Chem. A, 2005, 109, 11144–11154 CrossRef CAS PubMed.
- A. Kawai and K. Shibuya, J. Photochem. Photobiol., C, 2006, 7, 89–103 CrossRef CAS.
- S. Yamauchi, Bull. Chem. Soc. Jpn., 2004, 77, 1255–1268 CrossRef CAS.
- M. Gouterman, in The Porphyrins, ed. D. Dolphin, Academic Press Inc., New York, 1978, Vol III Search PubMed.
- N. Mizuochi, Y. Ohba and S. Yamauchi, J. Phys. Chem. A, 1999, 103, 7749–7752 CrossRef CAS.
- F. Conti, C. Corvaja, A. Toffoletti, N. Mizuochi, Y. Ohba, S. Yamauchi and M. Maggini, J. Phys. Chem. A, 2000, 104, 4962–4967 CrossRef CAS.
- L. Franco, M. Mazzoni, C. Corvaja, V. P. Gubskaya, L. S. Berezhnaya and I. A. Nuretdinov, Mol. Phys., 2006, 104, 1543–1550 CrossRef CAS.
- Y. Teki, T. Toichi and S. Nakajima, Chem. –Eur. J., 2006, 12, 2329–2336 CrossRef CAS PubMed.
- S. Laimgruber, H. Schachenmayr, B. Schmidt, W. Zinth and P. Gilch, Appl. Phys. B, 2006, 85, 557–564 CrossRef CAS.
- S. Laimgruber, T. Schmierer, P. Gilch, K. Kiewisch and J. Neugebauer, Phys. Chem. Chem. Phys., 2008, 10, 3872–3882 RSC.
- S. Fröbel, L. Buschhaus, T. Villnow, O. Weingart and P. Gilch, Phys. Chem. Chem. Phys., 2015, 17, 376–386 RSC.
- A. Reiffers, C. Torres Ziegenbein, L. Schubert, J. Diekmann, K. A. Thom, R. Kühnemuth, A. Griesbeck, O. Weingart and P. Gilch, Phys. Chem. Chem. Phys., 2019, 21, 4839–4853 RSC.
- M. Lorenc, M. Ziolek, R. Naskrecki, J. Karolczak, J. Kubicki and A. Maciejewski, Appl. Phys. B, 2002, 74, 19–27 CrossRef CAS.
- S. Prathapan, S. I. Yang, J. Seth, M. A. Miller, D. F. Bocian, D. Holten and J. S. Lindsey, J. Phys. Chem. B, 2001, 105, 8237–8248 CrossRef CAS.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- J. B. Birks, D. J. Dyson and B. H. Flowers, Proc. R. Soc. London, Ser. A, 1963, 275, 135–148 CAS.
- J. Feng, Y. Zhang, C. Zhao, R. Li, W. Xu, X. Li and J. Jiang, Org. Biomol. Chem., 2011, 9, 8246–8252 RSC.
- J. Chateauneuf, J. Lusztyk and K. U. Ingold, J. Org. Chem., 1990, 55, 1061–1065 CrossRef CAS.
- A. J. Tilley, R. D. Pensack, T. S. Lee, B. Djukic, G. D. Scholes and D. S. Seferos, J. Phys. Chem. C, 2014, 118, 9996–10004 CrossRef CAS.
- Y. Wu, R. M. Young, M. Frasconi, S. T. Schneebeli, P. Spenst, D. M. Gardner, K. E. Brown, F. Würthner, J. F. Stoddart and M. R. Wasielewski, J. Am. Chem. Soc., 2015, 137, 13236–13239 CrossRef CAS PubMed.
- Z. Yu, Y. Wu, Q. Peng, C. Sun, J. Chen, J. Yao and H. Fu, Chem. –Eur. J., 2016, 22, 4717–4722 CrossRef CAS PubMed.
- C. Rehhagen, M. Stolte, S. Herbst, M. Hecht, S. Lochbrunner, F. Würther and F. Fennel, J. Phys. Chem. Lett., 2020, 11, 6612–6617 CrossRef CAS PubMed.
- C. Wohlfarth, in Landolt-Börnstein, New Series, ed. M. D. Lechner, Springer, Berlin, 2008 Search PubMed.
- W. E. Ford, H. Hiratsuka and P. V. Kamat, J. Phys. Chem., 1989, 93, 6692–6696 CrossRef CAS.
- D. Gosztola, M. P. Niemczyk, W. Svec, A. S. Lukas and M. R. Wasielewski, J. Phys. Chem. A, 2000, 104, 6545–6551 CrossRef CAS.
- T. Van der Boom, R. T. Hayes, Y. Zhao, P. J. Bushard, E. A. Weiss and M. R. Wasielewski, J. Am. Chem. Soc., 2002, 124, 9582–9590 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- A. Kubas, J. Chem. Theory Comput., 2021, 17, 2917–2927 CrossRef CAS PubMed.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef CAS PubMed.
- S. S. Skourtis, C. Liu, P. Antoniou, A. M. Virshup and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8115–8120 CrossRef CAS PubMed.
- S. Bai, P. Zhang, P. Antoniou, S. S. Skourtis and D. N. Beratan, Faraday Discuss., 2019, 216, 301–318 RSC.
- S. Richert, C. E. Tait and C. R. Timmel, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS PubMed.
- C. E. Swenberg, R. Van Metter and M. Ratner, Chem. Phys. Lett., 1972, 16, 482–485 CrossRef CAS.
- M. C. Thurnauer, J. J. Katz and J. R. Norris, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3270–3274 CrossRef CAS PubMed.
- D. E. Budil and M. C. Thurnauer, Biochem. Biophys. Acta, 1991, 1057, 1–41 CAS.
- Y. Teki, H. Tamekuni, J. Takeuchi and Y. Miura, Angew. Chem., Int. Ed., 2006, 45, 4666–4670 CrossRef CAS PubMed.
- Z. E. X. Dance, S. M. Mickley, T. M. Wilson, A. Butler Ricks, A. M. Scott, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef CAS PubMed.
- A. L. Buchachenko and V. L. Berdinsky, J. Phys. Chem., 1996, 100, 18292–18299 CrossRef CAS.
- A. L. Buchachenko and V. L. Berdinsky, Chem. Rev., 2002, 102, 603–612 CrossRef CAS PubMed.
- A. Bencini and D. Gatteschi, EPR of exchange coupled systems, Dover Publications, New York, 2012 Search PubMed.
- R. Carmieli, T. A. Zeidan, R. F. Kelley, Q. Mi, F. D. Lewis and M. R. Wasielewski, J. Phys. Chem. A, 2009, 113, 4691–4700 CrossRef CAS PubMed.
- Z. E. X. Dance, Q. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef CAS PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- L. Fábregas Ibáñez, G. Jeschke and S. Stoll, Magn. Reson., 2020, 1, 209–224 CrossRef PubMed.
- A. Weber, O. Schiemann, B. Bode and T. F. Prisner, J. Magn. Reson., 2002, 157, 277–285 CrossRef CAS PubMed.
- B. E. Bode, J. Plackmeyer, T. F. Prisner and O. Schiemann, J. Phys. Chem. A, 2008, 112, 5064–5073 CrossRef CAS PubMed.
- D. Margraf, P. Cekan, T. F. Prisner, S. T. Sigurdsson and O. Schiemann, Phys. Chem. Chem. Phys., 2009, 11, 6708–6714 RSC.
- S. Richert, J. Cremers, I. Kuprov, M. D. Peeks, H. L. Anderson and C. R. Timmel, Nat. Commun., 2017, 8, 14842 CrossRef CAS PubMed.
- A. V. Astashkin and A. Schweiger, Chem. Phys. Lett., 1990, 174, 595–602 CrossRef CAS.
- N. Mizuochi, Y. Ohba and S. Yamauchi, J. Phys. Chem. A, 1997, 101, 5966–5968 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, details on the optical characterization including Strickler-Berg analysis as well as excitation energy transfer and electron transfer calculations, additional fsTA data including global kinetic analysis, complementary EPR data and discussion, DFT calculations of the excited state energies and magnetic parameters. See https://doi.org/10.1039/d2sc01899c |
| This journal is © The Royal Society of Chemistry 2022 |