Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of surface chemistry on the mechanochemical decomposition of tricresyl phosphate†
Egheosa
Ogbomo
 *abc,
Fakhrul H.
Bhuiyan
*abc,
Fakhrul H.
Bhuiyan
 d,
Carlos Ayestarán
Latorre
abc,
Ashlie
Martini
d,
Carlos Ayestarán
Latorre
abc,
Ashlie
Martini
 d and
James P.
Ewen
d and
James P.
Ewen
 *abc
*abc
aDepartment of Mechanical Engineering, Imperial College London, South Kensington Campus, SW7 2AZ, London, UK. E-mail: e.ogbomo21@imperial.ac.uk; j.ewen@imperial.ac.uk
bInstitute of Molecular Science and Engineering, Imperial College London, South Kensington Campus, SW7 2AZ, London, UK
cThe Thomas Young Centre, Imperial College London, South Kensington Campus, SW7 2AZ, London, UK
dDepartment of Mechanical Engineering, University of California-Merced, 5200 N. Lake Road, Merced 95343, CA, USA
First published on 30th November 2023
Abstract
The growth of protective tribofilms from lubricant antiwear additives on rubbing surfaces is initiated by mechanochemically promoted dissociation reactions. These processes are not well understood at the molecular scale for many important additives, such as tricresyl phosphate (TCP). One aspect that needs further clarification is the extent to which the surface properties affect the mechanochemical decomposition. Here, we use nonequilibrium molecular dynamics (NEMD) simulations with a reactive force field (ReaxFF) to study the decomposition of TCP molecules confined and pressurised between sliding ferrous surfaces at a range of temperatures. We compare the decomposition of TCP on native iron, iron carbide, and iron oxide surfaces. We show that the decomposition rate of TCP molecules on all the surfaces increases exponentially with temperature and shear stress, implying that this is a stress-augmented thermally activated (SATA) process. The presence of base oil molecules in the NEMD simulations decreases the shear stress, which in turn reduces the rate constant for TCP decomposition. The decomposition is much faster on iron surfaces than iron carbide, and particularly iron oxide. The activation energy, activation volume, and pre-exponential factor from the Bell model are similar on iron and iron carbide surfaces, but significantly differ for iron oxide surfaces. These findings provide new insights into the mechanochemical decomposition of TCP and have important implications for the design of novel lubricant additives for use in high-temperature and high-pressure environments.
1 Introduction
Mechanochemistry describes a wide range of phenomena where mechanical force influences chemical reactivity.1 This includes reactions in ball mills, where energy is transferred from moving balls to the reactants during collisions of the balls with each other and the jar walls.2 Mechanochemical reactions can be performed without solvents or heating, which can provide considerable environmental benefits over conventional routes.3 The choice of ball and jar materials are known to affect reactivity for a range of processes, such as cocrystallisation4 and cycloaddition,5 emphasizing the important role of the solid material. In some cases, the milling balls themselves are the catalyst of the reaction, which is known as direct mechanocatalysis.6 Another example and particularly high-value application of mechanochemistry is lubricant additives that reduce wear in tribological contacts.7 The most popular antiwear additive for automotive lubricants, zinc dialkyldithiophosphate (ZDDP), forms protective tribofilms on rubbing surfaces through mechanochemical processes.8–10The tribofilm growth of ZDDP is strongly dependent on the nature of the rubbing surfaces.11 Surfaces with a high elastic modulus, such as tungsten carbide,9 require lower loads to form tribofilms than steel,10 due to higher contact stresses. In experiments using aluminium–silicon alloys, thicker ZDDP tribofilms form on the silicon phase than the aluminium matrix, which is also due to the higher elastic modulus and thus stress.12 As well as the mechanical properties of the rubbing surfaces, the surface energy can also affect ZDDP adsorption and tribofilm growth.13 ZDDP forms thicker tribofilms on surfaces to which it readily adsorbs, such as steel, silicon nitride, and tungsten carbide surfaces than those where minimal adsorption occurs, such as diamond-like carbon (DLC) and silicon carbide.14 Ion-implanting alloying elements into steel can affect ZDDP tribofilm growth, nickel promotes tribofilm formation, molybdenum and chromium slows growth, while vanadium and tungsten have no significant effect.15 ZDDP forms thicker tribofilms on aluminium–magnesium alloys than on either of the pure metals due to the stronger adsorption of the ZDDP molecules on the alloy.16 A recent study revealed how the interplay of mechanical and chemical factors determine the tribological behaviour of ZDDP on DLC, with hydrogen-free coatings of moderate elastic modulus being most wear-resistant, while still allowing ultralow friction.17 Surface chemistry can also affect other mechanochemical processes inside rubbing contacts. For example, the rate of α-pinene tribopolymerisation is higher on palladium, copper oxide, nickel oxide, and chromium oxide than gold, silicon oxide, aluminium oxide, and DLC surfaces.18 Moreover, the α-pinene tribopolymerisation rate is higher on bare silica surfaces than hydroxylated silica.19 These observations can be explained by the fact that mechanochemical processes are accelerated when the confined molecules chemisorb to one20 or both21 sliding surfaces, since the shear stress applied through the sliding surfaces results in more strain within the strongly adsorbed molecules.
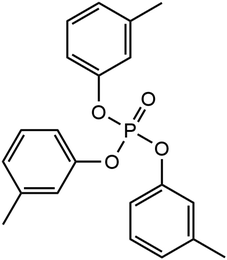
Phosphate esters lubricant additives have numerous industrial applications due to their stability, particularly in the presence of oxygen.22 Their versatility in structure including the ability to incorporate a variety of substituent groups has led to their application as lubricant additives to improve the antiwear, boundary lubrication, antioxidant, anti-corrosion, anti-foaming, and metal deactivation performance.23 Phosphate esters come in various forms, including aromatic, alkyl, thiophosphates, and metal-containing esters, and are readily accessible for commercial use.23 One of the most popular of these additives is tricresyl phosphate (TCP), which has been widely employed in aviation lubricants for gas turbine engines for several decades.24 The molecular structure of TCP is shown in Fig. 1. Like ZDDP, TCP is an effective antiwear additive for steel contacts.25,26 An additional benefit of TCP for aviation lubricants is that the tribofilms it forms on metal surfaces slow the degradation of synthetic neopentyl polyol ester base stocks.27
It was initially suggested that the ability of TCP to reduce wear on steel surfaces originated from polishing of the surfaces through the formation of iron phosphide.24 However, later studies have shown that the major component of the tribofilms formed from TCP on steel was iron phosphate, which acted as a protective layer, rather than polishing the surfaces.28–30 It has also been shown that either organic polyphosphates31 or iron polyphosphates32,33 are eventually formed from TCP inside tribological contacts, which are ultimately responsible for its antiwear performance on steel surfaces. At high temperatures, TCP molecules form relatively thick (60–100 nm) thermal films on steel surfaces;34 however, it forms thinner tribofilms (∼20 nm) on rubbing surfaces.26 This is much thinner that the ZDDP tribofilms that form on rubbing steel surfaces (∼100 nm).26
The thermal decomposition of TCP has been studied on several different substrates. Wheeler and Faut35 used X-ray photoelectron spectroscopy (XPS) to compare the adsorption and dissociation of TCP on gold and iron surfaces. On both substrates, adsorption saturated at about one monolayer, but adsorption was slower on gold than on iron.35 TCP underwent non-dissociative adsorption on gold and desorbed upon heating, with no TCP left on the surface at 473 K.35 On iron, no desorption occurred upon heating and additional interactions were observed between the substrate and the tolyl groups on the TCP molecule.35 TCP decomposed on iron between 423 K and 473 K with one of the tolyl groups being removed to form iron phosphate.35 The temperature range for decomposition is close to the temperature at which TCP significantly reduced the friction of rubbing steel surfaces in tribometer experiments.30 It has since been shown that the thermal decomposition of TCP on iron surfaces occurs mainly via P–O bond scission to form methylphenoxy intermediates.36 When TCP was heated to 800 K on iron, the methylphenoxy intermediates either desorbed as cresol via hydrogenation or decomposed further to generate tolyl intermediates.36 Some of these tolyl intermediates desorbed as toluene via hydrogenation, but the majority decomposed resulting in hydrogen and carbon monoxide desorption and carbon deposition onto the iron surface.36
The steel surfaces inside tribological contacts are chemically heterogeneous and are covered by multiple different iron oxides.37,38 From experiments conducted at high temperature (750 K), it was suggested that, due to acid–base reactions, TCP vapor preferentially reacts with iron in higher oxidation states, with reactivity increasing in the order: Fe < FeO < Fe3O4 < Fe2O3.32 However, more recent experiments suggested that reactivity towards TCP increases in the order Fe3O4 < Fe < Fe2O3.39 In both of these experimental studies, the iron surfaces will also form oxide layers that react with the TCP, rather than the native metal.39 In addition to surface oxides, metal carbides are another important component of bearing steels.40 A previous study of thermal decomposition found that TCP reactivity increases in the order: tungsten carbide < molybdenum carbide < chromium carbide < vanadium carbide.41
In recent years, experimental studies of TCP adsorption and decomposition have been complemented by molecular simulations. For example, Khajeh et al.43 used molecular dynamics (MD) simulations with a reactive force field (ReaxFF) to study the adsorption of TCP on hydroxylated amorphous Fe3O4. They found that, at lower temperatures (≤500 K), chemisorption occurred mostly via Fe–C bond formation through the tolyl groups. At higher temperatures (600–700 K), a significant amount of Fe–O and O–P bonding also occurred, indicating chemisorption through the central phosphate group. Ewen et al.44 compared the chemisorption and dissociation of TCP to trialkyl phosphates on Fe3O4(001) surfaces. In agreement with previous experiments,36,45 they found that the triaryl phosphate TCP was much less reactive compared to the trialkyl phosphates. The MD simulations also showed that, while the main decomposition mechanism for trialkyl phosphates was C–O bond dissociation, the only bonds that broke in TCP were P–O bonds.44 For the trialkyl phosphates, Ewen et al.44 also compared the adsorption and dissociation on Fe3O4(001) to hydroxylated amorphous Fe3O4 and α-Fe surfaces. They found that the reactivity of the trialkyl phosphates increased in the order: hydroxylated amorphous Fe3O4 < Fe3O4(001) < α-Fe. Ayestarán Latorre et al.46 studied the mechanochemical decomposition of trialkyl phosphates between sliding iron surfaces using non-equilibrium molecular dynamics (NEMD) simulations with ReaxFF. They found that secondary trialkyl phosphates were much more reactive than primary ones,46 in agreement with previous experiments on ZDDP.10 The influence of surface chemistry on the mechanochemical response of organophosphates is yet to be explored either experimentally or through NEMD simulations.
In this study, we use NEMD simulations with ReaxFF to compare the mechanochemical decomposition of TCP molecules confined between different ferrous surfaces over a range of temperatures and pressures. We observe significant differences in the mechanochemical reactivity of TCP on iron, iron oxide, and iron carbide surfaces. The variations in reactivity can be explained by differences in surface energy and stiffness, which can be accounted for in theoretical models for mechanochemistry.
2 Methodology
2.1 System setup
We used NEMD simulations47 to compare the mechanochemical reactivity of TCP on three ferrous surfaces, as shown in Fig. 2. This is a molecule composed of three cresyl (methylphenyl) groups linked to a phosphate group. TCP is produced from cresol, which naturally contains a mixture of isomers with the methyl group in the ortho-, meta- and para-positions. The ortho-isomers of TCP are known to be toxic and modern production methods have reduced the concentration of these to very low levels.48 Therefore, the TCPs used in current aviation lubricants generally contain mixtures of the meta-isomers and also some para-isomers.48 The para-isomers were shown to have poorer lubricating properties compared to mixtures of isomers.29 However, a recent study showed that the para-isomer is only slightly more reactive than the meta-isomer on ferrous surfaces.39 In this study, we chose to study pure tri-meta-cresyl phosphate for simplicity; its molecular structure is shown in Fig. 1.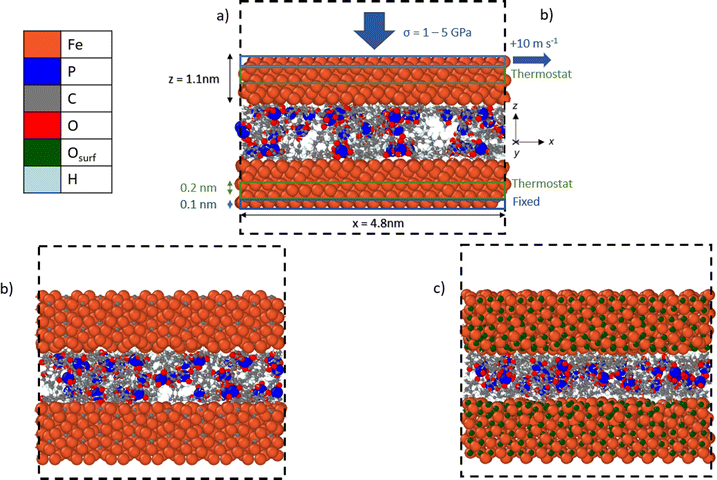 | ||
| Fig. 2 Side-view snapshots showing the model systems with TCP molecules confined between (a) α-Fe(110), (b) Fe3C(010), and (c) Fe3O4(001)-SCV surfaces. Systems shown after minimisation and equilibration, but before heating, compression, and shear. Black dashed line shows the simulation box. Rendered using OVITO.42 | ||
All the systems were constructed using the materials and processes simulations (MAPS) platform from Scienomics SARL. The three model surfaces were native iron, cementite, and magnetite. Symmetrical contacts were used with the same material for the upper and lower surface. Native iron surfaces were considered due to the possibility that they are exposed to the additive following removal of surface oxides in rubbing steel contacts.49 Cementite was chosen as a representative iron carbide surface because it was identified in previous thermal degradation experiments using TCP.50 Magnetite was selected since previous experiments have shown that it is the major oxide formed on the surface of bearing steel following tribometer experiments.37 We used an α-Fe(110) for the iron surface,51 Fe3C(010) as the cementite surface,52 and Fe3O4(001) with a subsurface cation vacancy (SCV) reconstruction as the magnetite surface53 due to their relatively low surface energies.
Periodic boundary conditions were applied in the x and y directions. Since the materials all had different lattice constants, it was not possible to create periodic surfaces with exactly the same dimensions. The α-Fe(110) surfaces had dimensions of x = 4.8, y = 4.8 and z = 1.1 nm. The Fe3C(010) surfaces had dimensions of x = 4.9, y = 4.7 and z = 1.05 nm. The Fe3O4(001) surfaces had dimensions of x = 5.0, y = 5.0 and z = 1.1 nm. At the start of the simulations, two of each type of surface were separated by a 3.0 nm in the z-direction. A fixed boundary condition is applied in the z-direction.
To replicate tribometer experiments under full-film EHL conditions,9,10,54 we ensured that no direct contact between the sliding ferrous surfaces occurred during the simulations. In most of the NEMD simulations, 48 TCP molecules were randomly inserted between the surfaces, leading to a fluid film thickness of approximately 1 nm. Experiments have shown that the molecular area of TCP is around 1.1 nm2 at the air–water interface.55 The molecular area of TCP on ferrous surfaces is likely to be similar as on the air–water interface, as shown for other surfactants.56 Thus, the chosen number of molecules is representative of the surface coverage expected for one TCP monolayer adsorbed on each of the two confining surfaces (24 molecules/∼25 nm2). Previous experiments have confirmed that monolayers of TCP adsorb on ferrous surfaces both from the vapour phase35,57 and also from toluene solution.28
While the main application of TCP is as an additive dissolved in a base oil for aviation lubricants,22 it can also be used as a lubricant as a pure substance in both the liquid phase30 and the vapour phase for high-temperature applications.58 Due to the significant additional computational expense of simulating non-reactive base oil molecules, these were excluded from the majority of our simulations. Although some reactive NEMD simulation studies of lubricant additive mechanochemistry have simulated the base oil molecules,59,60 the vast majority have not.21,46,61–63 Previous NEMD simulations of sulfur-based additives with ReaxFF have shown that there were only minor differences when unreactive base oils were included in the simulations.59 To assess the effect of including base oil molecules in our systems, we performed a subset of simulations that contained 48 TCP molecules randomly mixed with 48 diisodecyl adipate molecules (DIDA)34 between α-Fe(110) surfaces. This is the same molar ratio used in a previous NEMD simulations of additive-base oil systems.59 Although the concentration of TCP used in commercial formulations (1–5%)64 and tribometer experiments (≤10%)65 is typically much lower than 50%, this represents a reasonable compromise between computational efficiency and closeness to real-life applications.
2.2 Simulation details
All the simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) open-source software.66 The velocity Verlet67 integration scheme was used with a timestep of 0.25 fs.43 The simulations were conducted in three phases: energy minimisation, equilibration, and then simultaneous heating, compression, and shear. The energy minimisation phase was conducted using the conjugate gradient method. For all the systems and conditions investigated, equilibration was performed at an ambient temperature of 300 K for 0.1 ns. During the equilibration phase, the two ferrous surfaces were brought closer together by applying a low pressure of 10 MPa. The system was pressurised by applying a constant normal force (z-direction) equally distributed across the topmost layer of atoms (0.1 nm) in the upper surface, as shown in Fig. 2a. The lowermost layer of atoms (0.1 nm) in the bottom surface was kept fixed in the z-direction. The equilibration at 10 MPa ensured that a realistic liquid density of TCP (1.2 ± 0.1 g cm−3) was obtained prior to the heating, compression, and shear phase.Following the equilibration phase, the compression and shear phase of the simulations were run for 1 ns. Here, a constant sliding velocity of 10 m s−1 was applied to the outer layer of atoms in the upper surface in the x-direction, as shown in Fig. 2a. This is representative of the sliding velocities found in lubricated components inside gas turbine engines and tribometer experiments with TCP, which have been performed at sliding velocities as high as 10 m s−1.64 The pressure was increased to the target value of 1–5 GPa using the same method as during the equilibration. The temperatures were increased to 400–900 K using a Langevin thermostat with a damping parameter of 25 fs.68 The thermostat acted only in the y-direction and on the central layer of atoms (0.2 nm) in the upper and lower surfaces, as shown in Fig. 2a. This approach enabled a temperature gradient to develop in the centre of the TCP film and heat to be dissipated at the surfaces, as would occur experimentally.69 The thermostat was sufficiently efficient to ensure that the average system temperature was within 10 K of the target value at the chosen sliding velocity. The selected range of temperatures and pressures spans those expected in applications of TCP such as antiwear additives in gearboxes for gas turbine engines26 and as vapour-phase lubricants.58
The temperature, pressure, and sliding velocity were all increased simultaneously to capture their combined effects on the reaction rate. Some previous NEMD simulations of mechanochemical reactions with ReaxFF have isolated the effects of temperature, pressure, and sliding by using separate phases of the simulations.20,62,70 The number of additive molecules in the NEMD simulations is finite, so separating the simulations into different phases (thermalisation, pressurisation, and sliding) means that fewer molecules are available to react in any subsequent phases. Conversely, in experimental mechanochemistry studies,9,10,54 additive-containing lubricants are entrained between the sliding surfaces, continuously replenishing the number of additive molecules. Hence, in our NEMD simulations, we elected to increase the temperature, pressure, and sliding velocity to their target values concurrently.46
The combined C/H/O/Fe/P ReaxFF parameters43 have been successfully applied to study the thermal and mechanochemical decomposition of phosphate esters with different alkyl and aryl substituents on several ferrous surfaces.39,44,46 The ReaxFF parameters have also been validated against first principles calculations for the non-dissociative adsorption energy, C–O bond dissociation energy, and P–O bond dissociation energy for trialkyl phosphates on α-Fe(110).44 The ReaxFF parameters for Fe/O/H have been shown to accurately reproduce the experimental lattice constants for α-Fe (within 1%),77 Fe3C (within 0.5%),77 and Fe3O4 (within 3%).76 The ReaxFF parameters have also been shown to perform favourably compared to other many-body force fields in describing the mechanical properties of α-Fe.81 At 300 K, the experimental elastic modulus is 166 GPa for α-Fe,82 174 GPa for Fe3C,83 and 186 GPa for Fe3O4(100).84 With the ReaxFF parameters used here,43,76,77 the bulk elastic modulus at 300 K is 136 GPa for α-Fe,85 148 GPa for Fe3C,85 and 129 GPa for Fe3O4.86 Thus, at 300 K, the experimental bulk elastic modulus is underpredicted by 18% for α-Fe, 15% for Fe3C, and 31% for Fe3O4. Since previous density functional theory (DFT) calculations have highlighted the importance of contact stiffness to mechanochemical processes,87 we also calculated the elastic properties of thin single slabs of the three materials used in the NEMD simulations. For this calculation, the lowermost layer of atoms in each slab of material was fixed in the z-direction, while a constant normal force was applied the topmost layer of atoms to compress the system to 2 GPa. The temperature was varied between 300–900 K using the same thermostat as applied in the NEMD simulations. The corresponding elastic constant (C33) was calculated from the strain fluctuations at constant normal stress.88 The elastic constant results for the thin slabs are shown in the ESI† (Table S1). For the α-Fe(110) slabs, the elastic constant C33 decreases from 206 GPa at 300 K to 196 GPa at 900 K. The elastic constant C33 also decreases with increasing temperature for the Fe3C(010) (from 200 GPa to 181 GPa) and Fe3O4(001) (from 220 GPa to 196 GPa) slabs. The higher stiffness of thin solid slabs compared to bulk solids was also observed in previous MD simulations and was attributed to geometrical confinement.89 The decreasing stiffness with increasing temperature is also consistent with previous experiments.82
3 Results and discussion
3.1 Base oil effects on TCP decomposition
The primary application of TCP is as an antiwear additive for aviation lubricants where it is dissolved in a base oil.22 Thus, to ensure that not simulating the base oil molecules did not significantly affect the mechanochemical decomposition mechanism, we performed a subset of simulations containing 50% TCP and 50% DIDA molecules. Despite some bonding of DIDA molecules to the surfaces, negligible decomposition of the ester base oil occurs during the simulations (<2 molecules). Previous experiments have suggested that ester base oil decomposition may become significant when it is heated for several hours with a stainless steel coupon at temperatures above about 600 K.65 However, this process is much slower than TCP decomposition, which occurred experimentally at much lower temperatures.65 The mechanochemical decomposition mechanism of TCP is also unaffected by the presence of base oil molecules. This observation is consistent with previous NEMD simulations, which showed that the addition of dodecane base oil molecules did not affect the mechanochemical reaction pathway of sulfur-based lubricant additives on ferrous surfaces.59For a given normal stress, the shear stress is much lower for the 50% TCP, 50% DIDA system than the 100% TCP system, as shown in the ESI† (Fig. S1). This reduction in shear stress is expected to due the lubricating effect of the low-friction ester base oil.90 From previous mechanochemistry experiments of ZDDP tribofilm growth,9,10,91 it is anticipated that the lower shear stress will result in lower reactivity for the 50% TCP, 50% DIDA than the 100% TCP system.
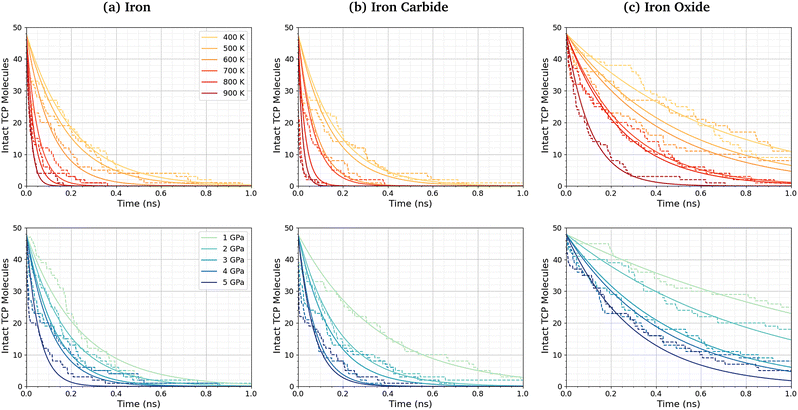
Fig. 3a shows the change in the number of intact TCP molecules for 100% TCP at 600 K and 1–5 GPa, while Fig. 3b shows the same for the 50% TCP, 50% DIDA system. The TCP molecules are counted as dissociated, i.e., no longer intact, if any bond other than a C–H is broken. The number of TCP molecules decreases faster for the pure TCP system than the 50% TCP, 50% DIDA system. For both systems, there is an exponential decay of the number of intact TCP molecules with time, which is indicative of a first-order reaction.92 For first-order reactions, the reaction rate, r = k[C], where k is the rate constant and [C] is the concentration of reactant. Previous NEMD simulations showed that the mechanochemical decomposition of trialkyl phosphate decomposition between α-Fe(110) surfaces also followed first-order kinetics.46 In mechanochemistry experiments with ZDDP, the rate of tribofilm growth followed either zero-order or fractional-order kinetics.8,10,54 The observation of zero-order kinetics indicates that the rate-determining step for tribofilm growth involves surface-adsorbed molecules,10 which masks the underlying first-order kinetics.93 In experiments, the surface-adsorbed additive molecules are continually replenished from the base oil solution and the bulk concentration does not significantly decrease.10 On the other hand, there is a finite number of additive molecules in the NEMD simulations, which means that the decomposition rate inevitably decreases with time as fewer molecules become available to react.46
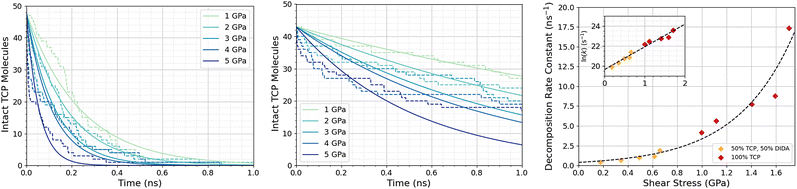 | ||
| Fig. 3 Change in the number of intact TCP molecules with time at 600 K and 1–5 GPa for (a) 100% TCP system (b) 50% TCP, 50% DIDA system. The dashed lines show the simulation data and the solid lines are exponential decay fits used to calculate the first-order rate constants, k. (c) Change in k for TCP decomposition with shear stress, τ. The data with and without DIDA can be fit using eqn (1) with a single activation volume (13.6 ± 2.6 Å3). Inset shows the same data versus ln(k). | ||
Fig. 3c shows the change in the decomposition rate constants, k, with shear stress for the 100% TCP and 50% TCP, 50% DIDA systems. The k values were determined from the exponential decay fits shown in Fig. 3a and b and the shear stress values were taken from Fig. S1 (ESI†). For all the systems and conditions shown in Fig. 3, k increases exponentially with shear stress, suggesting that TCP decomposition is a stress-augmented thermally activated (SATA) processes.94 The Bell model95 can be used to describe the kinetics of SATA processes:
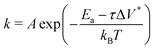 | (1) |
3.2 Surface chemistry effects on shear stress
We compared the change in the shear stress with normal stress for the iron, iron carbide, and iron oxide systems, as shown in Fig. 4. The steady-state shear stress was block averaged over the final 0.5 ns of the NEMD simulations. At all the studied temperature and normal stress conditions, the shear stress is lower for the systems with TCP molecules sheared between iron oxide surfaces than iron and iron carbide surfaces. For all three surfaces, the shear stress increases linearly with normal stress with a finite intercept, as predicted by the extended Amontons–Coulomb law: τ = μσ + τ0, where τ is the shear stress, μ is the friction coefficient, τ0 is the Derjaguin offset, and σ is the normal stress.97 The friction coefficient and Derjaguin offset for the different systems and temperatures are shown in the ESI† (Tables S2 and S3). The friction coefficient, given by the gradient of the linear fits in Fig. 4, is similar for all three surfaces. The Derjaguin offset, given by the intercept of the linear fit, is similar for iron and iron carbide surfaces, but is around 50% lower for iron oxide. This is likely due to the higher surface energy and adhesion of TCP molecules on iron and iron carbide compared to iron oxide.13 Previous DFT calculations suggested that the surface energy of α-Fe(110) (2.3 J m−2)51 and Fe3C(010) (2.2 J m−2)52 is much larger than Fe3O4(001) (1.0 J m−2).98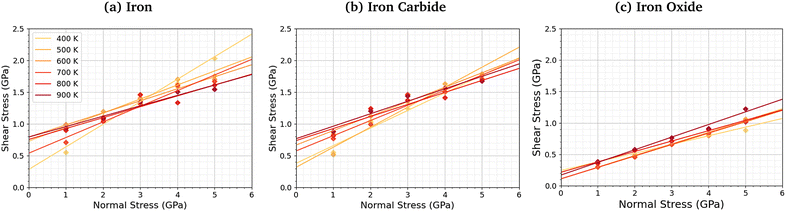 | ||
| Fig. 4 Variation in shear stress with changes in normal stress for (a) α-Fe(110), (b) Fe3C(010), and (c) Fe3O4 (001) surfaces. | ||
For the iron and iron carbide systems, the friction coefficient decreases with increasing temperature (Table S2, ESI†); in contrast, the Derjaguin offset increases with increasing temperature (Table S3, ESI†). As the temperature increases, the amount of TCP decomposition will also increase,44 which affects the temperature-dependence of the friction coefficient and Derjaguin offset. For the iron oxide surfaces, the temperature has a negligible effect on the friction coefficient and Derjaguin offset, which is probably due to the much lower reactivity of TCP on this surface.44 The addition of base oil molecules as well as TCP molecules between the iron surfaces leads to a large reduction in the Derjaguin offset (τ0 = 0.79 GPa to τ0 = 0.20 GPa), but a negligible change in the friction coefficient (μ = 0.18 to μ = 0.17), as shown in Fig. S1 (ESI†). This observation is in agreement with previous NEMD simulations of iron surfaces lubricated by monolayers formed from polar lubricant additive molecules.99 Consequently, if lubricant molecules were added to the iron carbide and iron carbide systems, the shear stress conditions would probably be similar for all the surfaces.
3.3 Surface chemistry effects on TCP dissociation
Fig. 5 shows the change in the number of intact TCP molecules with time for α-Fe(110), Fe3C(010), and Fe3O4(001) surfaces at constant normal stress (4 GPa) and varied temperature (400–900 K), and constant temperature (600 K) and varied normal stress (1–5 GPa). Results for other conditions are shown in the ESI† (Fig. S2). The exponential decay curves are used to calculate the TCP decomposition rate constant, k, for each temperature and stress condition. Ayestarán Latorre et al.46 investigated the mechanochemical decomposition of trialkyl phosphates between 300–500 K and 1–4 GPa for α-Fe(110) surfaces. Comparing the current results to this previous study, it is clear that triaryl phosphates such as TCP have much lower decomposition rate constants than trialkyl phosphates under the same conditions. This observation agrees with previous experimental36,45 and simulation44 studies of the thermal decomposition of phosphate esters on ferrous surfaces.The TCP decomposition rate constants, k, vary significantly depending on the surface chemistry, with the fastest reactions being observed for the α-Fe(110) systems, followed by Fe3C(010), and finally Fe3O4(100). This may be due to the differences in surface energies of the three ferrous surfaces, as discussed in the previous section.51,52,98 Higher surface energies promote stronger molecular adsorption100 and thus faster TCP decomposition. Indeed, DFT calculations have shown that adsorption is a crucial step the decomposition of TCP on iron surfaces.101
Previous high-temperature (750 K) thermal decomposition experiments suggested that TCP preferentially reacted with iron oxides that were in a higher oxidation state, i.e. Fe < FeO < Fe3O4 < Fe2O3.32 This contrasts with first principles NEMD simulations of other lubricant additives, such as molybdenum dithiocarbamates, where native iron surfaces were found to be much more reactive than oxidised surfaces.63 We observe much higher mechanochemical reactivity on the iron surface compared to the iron oxide surface, which is in agreement with the simulations,63 but not the experiments.32 This is probably because the iron used surfaces in the experiments32 were also covered by an oxide layer rather than the native iron surfaces used in the simulations.39
No direct Fe–P bonds formed between the surfaces and TCP molecules in any of the NEMD simulations, but a large number of new Fe–O bonds form. This observation indicates that iron phosphate, rather than iron phosphide, is formed on the ferrous surfaces, which is consistent with observations in previous experimental studies.28–30 Previous MD simulations investigating the thermal decomposition of TCP on hydroxylated amorphous Fe3O4 have shown that the initial step involved Fe–C bonding.43 Indeed, DFT investigations have shown that benzene chemisorbs on iron oxide surfaces due to strong interactions between iron cations and the aromatic π-electrons.102 To investigate this further, we quantified the change in the number of Fe–C bonds formed at different pressures and temperatures. The Fe–C bonds present in the Fe3C(010) surfaces before exposure to TCP are not included in the analysis. Fig. 6 shows the variation in the number of Fe–C bonds with time for the simulated TCP systems at 600 K between 1–5 GPa for α-Fe(110), Fe3C(010), and Fe3O4(100). The number of Fe–C bonds at a given time increases as Fe3O4(100) < Fe3C(010) < α-Fe(110), which is the same order observed for the rate constants of TCP decomposition on the three surfaces. We also see a clear trend of an increase in the number of Fe–C bonds, and therefore chemisorption of TCP, with an increase in pressure for all three surfaces. The increased bonding of the TCP carbon atoms on α-Fe(110) compared to Fe3C(010) and Fe3O4(100) can be visualised in the number density profiles shown in the ESI† (Fig. S3). The carbon peaks from the TCP molecules show increased overlap with the iron peaks for α-Fe(110) compared to the other surfaces.
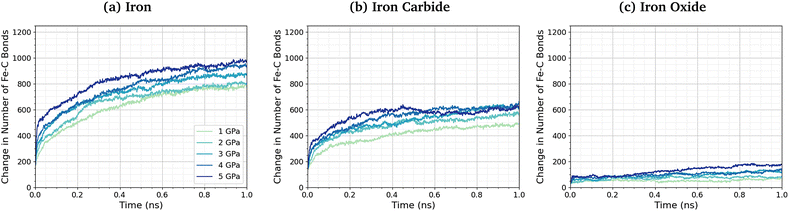 | ||
| Fig. 6 Change in the number of Fe–C bonds with simulation time at 600 K between 1–5 GPa for (a) α-Fe(110), (b) Fe3C(010), and (c) Fe3O4(100). | ||
Fig. 7 shows the relationship between the number of Fe–C bonds formed and the TCP decomposition rate constant. There is a logarithmic increase in the TCP decomposition rate constant with the number of Fe–C bonds formed for all three surfaces. This implies that increased chemisorption of the molecules leads to faster dissociation.13 Indeed, previous experiments have shown that ZDDP forms thicker tribofilms on surfaces to which it more strongly adsorbs.14
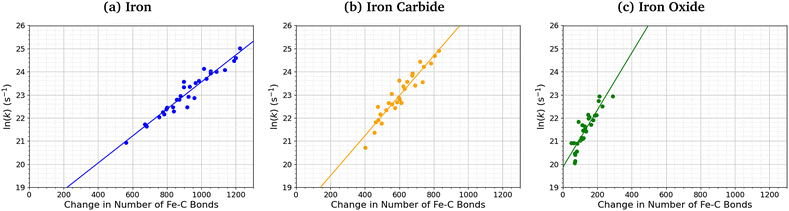 | ||
| Fig. 7 Variation in ln(k) for TCP decomposition with the change in the number of Fe–C bonds from 0–1 ns for (a) α-Fe(110), (b) Fe3C(010), and (c) Fe3O4(100). | ||
3.4 TCP decomposition mechanisms
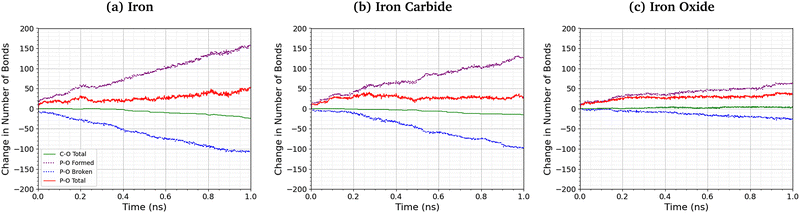
Fig. 8 shows the change in the total number of C–O and P–O bonds with sliding time for an intermediate temperature (500 K) and pressure (3 GPa). For the Fe3O4 (001) surfaces, bonds formed with surface oxygen atoms are included in the analysis. The red lines represent the total change in the number of bonds P–O bonds compared to the initial TCP molecules, the blue lines show the contribution from P–O bonds in TCP that are broken, and purple lines show new bonds that are formed. A negligible number of new C–O bonds form in the simulations and the total change is shown by the solid green lines. For all the surfaces, P–O cleavage precedes C–O cleavage and, by the end of the simulations, approximately five times as many P–O bonds were broken than C–O bonds, suggesting that P–O cleavage is the dominant decomposition mechanism. These observation are consistent with previous MD simulations39,44 and experiments36 of the thermal decomposition of TCP. Conversely, in previous NEMD simulations of trialkyl phosphates confined between α-Fe(110) surfaces, the C–O bonds broke first and approximately twice as many C–O bonds were broken than P–O bonds.46 The decomposition mechanism is therefore affected by the much stronger C–O bonds in triaryl phosphates compared to those in trialkyl phosphates. Moreover, unlike triaryl phosphates, some alkyl intermediates formed by C–O cleavage in trialkyl phosphates, such as butyl chains, can readily undergo β-hydride elimination reactions on ferrous surfaces to produce gaseous olefins.36 In Fig. 8, the number of C–O and P–O bonds broken for the α-Fe(110) and Fe3C(010) surfaces is similar, but fewer bonds are broken for the Fe3O4(001) surfaces.More P–O bonds are formed than are broken in the TCP molecules, leading to an overall increase in the number of P–O bonds, as shown by the solid red lines in Fig. 8. This is due to the formation of P–O–P linkages between the phosphorus atoms, resulting in polyphosphate chain growth.32,33 This process occurs mainly through nucleophilic substitution reactions, whereby P–O–R bonds in TCP (where R is a cresyl group) are replaced by P–O–P bonds.46
The total increase in the number of P–O bonds at the end of the 1 ns simulation is similar (40–50 bonds) for the α-Fe(110), Fe3C(010), and Fe3O4(001) surfaces. This is because both the P–O cleavage (blue dotted lines) and P–O formation (purple dotted lines) reactions are accelerated by the more reactive surfaces (α-Fe(110)), as shown by the steeper lines in Fig. 8. The total number of P–O bonds at the end of the simulation is also not sensitive to the temperature and pressure, as shown in the ESI† (Fig. S4).46
For the Fe3O4(001) surface, nucleophilic attack from the surface oxygen atoms could increase the rate of P–O dissociation in the TCP molecules.44 The variation in the number of P–Osurf bonds formed between phosphorus atoms in the TCP molecules and oxygen atoms in the Fe3O4(001) surface is shown in the ESI† (Fig. S5). At low temperature and pressure, the number of P–Osurf bonds formed (Fig. S4, ESI†) is much less than the total number of P–O bonds formed (Fig. 8), suggesting that this process plays a negligible role in the nucleophilic substitution reactions. However, at high temperature and pressure, the number of P–Osurf bonds increases, such that it they represent a significant proportion (>10%) of the total P–O bonds formed. Overall, surface oxygen atoms do not seem to promote the decomposition of TCP on ferrous surfaces, as was suggested from previous experiments.32
3.5 Surface chemistry effects on polyphosphate growth
Fig. 9 shows the number of phosphate-containing oligomers, toluene, and cresol molecules formed from TCP at 500 K and 3 GPa on the three surfaces. On iron and iron carbide, the primary product of TCP decomposition is cresol, formed directly from P–O bond cleavage. Some toluene is also formed on these surfaces via C–O cleavage, but this occurs only after the formation of cresol. The number of oligomers formed is similar for all three surfaces. On iron oxide, phosphate-containing oligomers are the major product rather than cresol, due to the reduced rate of P–O cleavage reactions (Fig. 8).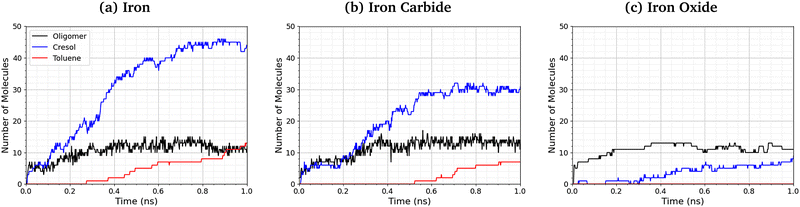 | ||
| Fig. 9 Comparison of oligomer, toluene, and cresol quantities at 500 K and 3 GPa for the (a) α-Fe(110), (b) Fe3C(010), and (c) Fe3O4(001) systems. | ||
The length of the polyphosphate chains in tribofilms is important to their antiwear performance.103Fig. 10 shows the change in the number of polyphosphate chains (dimers, trimers, tetramers, and ≥ pentamers) with sliding time for the three studied systems. In all cases, the total number of polyphosphate fragments increases at short times before asymptoting towards a steady-state value of ∼10. For Fe3C(010) and Fe3O4(001), the majority of TCP molecules form dimers, but longer chains, up to octomers, form in some cases. In general, longer polyphosphate chains are formed on the α-Fe(110) surfaces than Fe3C(010) and particularly Fe3O4(001) surfaces. For α-Fe(110), a similar number of dimers and trimers form, with some of the chains growing up to octamers. The relatively short polyphosphate chains formed in our NEMD simulations are consistent with the average chain length of approximately 2.5 monomers found in tribometer experiments with ZDDP.103 Much longer chains (up to 40 linked monomers) were formed in previous NEMD simulations with ReaxFF of phosphoric acid confined between sliding silica surfaces at very high temperature (1400 K).104 The longer chains formed in these previous simulations is probably due to the higher reactivity of phosphoric acid compared to TCP and the lack of iron atoms to catalyse the depolymerisation (P–O dissociation) reactions.
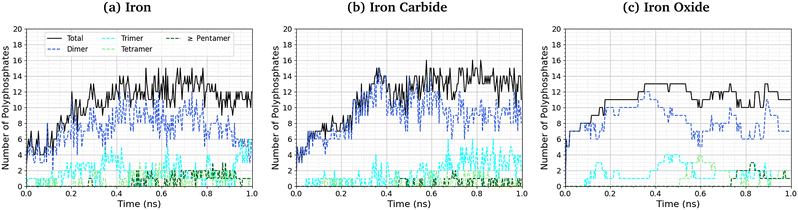 | ||
| Fig. 10 Change in the number of polyphosphate chains with sliding time at 500 K and 3 GPa for (a) α-Fe(110), (b) Fe3C(010) and (c) Fe3O4(100) systems. | ||
The difference in the polyphosphate chain length between the three surfaces is much more subtle than the change in TCP decomposition rates. This is probably because iron atoms or ions, which are most readily available in α-Fe(110), accelerate the depolymerisation of the polyphosphate chains by P–O bond cleavage.103 Similarly, the polyphosphate chain length does not vary significantly over the wide range of temperatures and pressures studied in the NEMD simulations, as shown in the ESI† (Fig. S6). This is because both the polymerisation (P–O formation) and depolymerisation (P–O dissociation) reactions are accelerated by a similar amount due to increased temperature and shear stress, as shown in the ESI† (Fig. S4).
3.6 Rate analysis
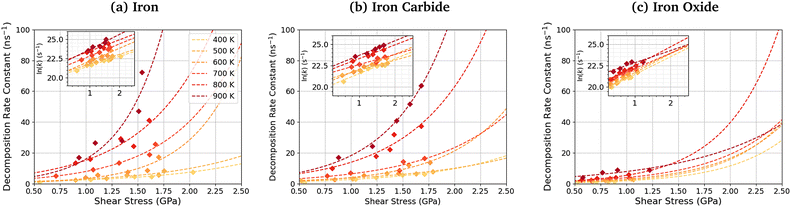
Fig. 11 shows the dependence of the TCP decomposition rate constant on shear stress for iron, iron carbide, and iron oxide surfaces. The Bell model95 (eqn (1)) accurately describes the rate of TCP decomposition with temperature and shear stress on the three surfaces, as shown in the ESI† (Fig. S7). The activation volume, ΔV*, is calculated from the 2D fits of the rate versus shear stress data to eqn (1) shown in the insets of Fig. 11. With this 2D fitting method, ΔV* is found to increase monotonically with temperature from 4.9 ± 1.7 Å3 at 400 K to 17.5 ± 8.4 Å3 at 900 K for TCP between the α-Fe(110) surfaces. In all cases, the activation volume is positive, which suggests that the rate determining step involves bond cleavage.96 This observation is consistent with previous experiments of tribofilm growth from antiwear additives.91 For the Fe3C(010) surfaces, ΔV* also increases with temperature from 6.6 ± 3.7 Å3 400 K to 15.3 ± 2.4 Å3 at 900 K, while for the Fe3O4(100) surfaces, ΔV* increases from 8.3 ± 4.5 Å3 at 400 K to 12.8 ± 6.6 Å3 at 900 K. The calculated ΔV* values are all consistent with the dimensions of single bonds. The molecular volume of TCP is approximately 500 Å3, meaning that the activation volumes for TCP on the three surfaces range between 1 and 4% of the molecular volume. This percentage range is consistent with previous NEMD simulations using trialkyl phosphates (4%),46 while experiments using ZDDPs with different alkyl substituent showed somewhat larger percentages (7–17%).54Based on the 2D fits to eqn (1) shown in Fig. 11, the activation volume is highly temperature-dependant, but there are no clear differences between the three surfaces due to the relatively large uncertainties. Previous experimental studies of mechanochemical tribofilm growth have treated the activation volume as a temperature-independent reaction constant; however, these studies considered a much smaller temperature range than the present study.8–10,54,91 In our recent NEMD study of trialkyl phophate mechanochemical decomposition, we also observed that the activation volume increased with increasing temperature.46 This was partially explained through a reduction in the elastic modulus of the α-Fe(110) slabs.46 A recent DFT study suggested that the contribution of the elastic deformation of the surrounding bulk to the activation volume of mechanochemical reactions can be significant and, in some cases, dominant.87 The elastic modulus of all three surfaces decreases with increasing temperature (Table S1, ESI†). Since the activation volume is inversely proportional to the contact stiffness,87 it is expected that higher temperatures will lead to lower activation energies, as observed in Fig. 11 and Table S4 (ESI†). However, the increase in the activation volume (up to 350%) is much larger than the decrease in the stiffness of the surfaces (up to 10%) between 400–900 K. Thus, other factors, such as a decrease in stiffness of the confined TCP molecules and its decomposition products, must also contribute to the increased activation volume at higher temperature.
The activation energy, Ea, is calculated from the slope of the 2D fits of eqn (1) to the rate versus inverse temperature data shown in the ESI† (Fig. S8). For TCP decomposition between the α-Fe(110) surfaces, Ea increases with pressure from 20.6 ± 5.5 kJ mol−1 at 1 GPa to 24.0 ± 6.5 kJ mol−1 at 5 GPa. For the Fe3C(010) surfaces, Ea also increases from 19.7 ± 6.1 kJ mol−1 at 1 GPa to 24.3 ± 7.5 kJ mol−1 at 5 GPa. For the Fe3O4(100) surfaces, Ea again increases from 10.2 ± 7.2 kJ mol−1 at 1 GPa to 19.5 ± 3.63 kJ mol−1 at 5 GPa. A previous experimental study suggested that the thermal activation energy for TCP decomposition on stainless steel is approximately 60 kJ mol−1.45 Thus, the activation energy values are considerably underpredicted in our simulations compared to experiments,45 which is probably due to the chromium-rich oxide layer formed on the surface of stainless steel in experiments.105 Chromium oxide is known to be much less reactive towards TCP than iron oxide,33,34,57 as was used in our NEMD simulations. Thus, the chromium oxide surface formed on stainless steel is expected to reduce the activation energy by a smaller amount than the iron oxides formed on conventional bearing steel.37,38 From in situ tribometer experiments, the activation energy for TCP decomposition on an iron substrate was estimated as 6.3 kJ mol−1,106 which is somewhat lower than our simulation results. This can be explained through the fact that the effect of shear stress on reducing the activation energy, as shown in eqn (1), was not considered in their calculations. As a result, the activation energy they calculated will be under-predicted.
The pre-exponential factor, A, is calculated from the intercept of the fits of eqn (1) to the rate versus inverse temperature data shown in the ESI† (Fig. S8). This is often expressed as A = Zρ, where Z is the frequency or collision factor, and ρ is the steric factor. The steric factor represents the fraction of successful collisions and is usually less than unity.107 For TCP molecules between the α-Fe(110) surfaces, ln(A) increases with pressure from 25.4 ± 3.2 at 1 GPa and to 28.1 ± 3.86 at 5 GPa. For the Fe3C(010) surfaces, ln(A) increases from 25.4 ± 3.6 at 1 GPa to 27.8 ± 4.7 at 5 GPa, while it increases from 22.6 ± 4.5 to 25.6 ± 2.1 for the Fe3O4(100) surfaces. The low-pressure values are in very good agreement with previous estimates of the pre-exponential factor for the thermal decomposition of TCP on stainless steel at atmospheric pressure, ln(A) = 22.7.45
Fig. 12 shows the variation of ln(A) with Ea from the 2D fits to the rate versus temperature data. The concurrent increase in Ea with ln(A), which is known as the kinetic compensation effect, is often observed in heterogeneously catalysed processes.93 Previous studies using ReaxFF to study the mechanochemical behaviours of trialkyl phosphates have also observed such an effect.46 The presence of a compensation effect suggests that the changes in these parameters may have a mathematical rather than physical origin and does not necessarily indicate any changes to the reaction pathway.108
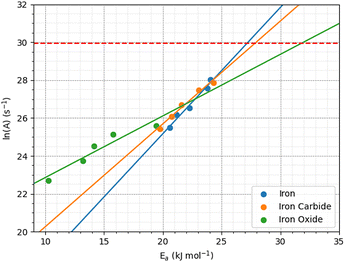 | ||
| Fig. 12 Kinetic compensation effect between the activation energy and pre-exponential factor for iron, iron carbide, and iron oxide. | ||
Experimental pre-exponential factors for surface reactions typically vary from 1010–1016 s−1.109 Some previous mechanochemistry studies8 have used a constant pre-exponential factor of 1013 s−1 to determine the activation energy. If a constant pre-exponential factor of 1013 s−1 (ln(A) = 30) is used for all three surfaces (horizontal red dashed line in Fig. 12), the activation energies of TCP decomposition for the three surfaces from the 2D fits increase in the order α-Fe(110) ∼ Fe3C(010) < Fe3O4(001). Thus, the more reactive surfaces towards TCP give lower activation energies, which is consistent with previous experiments of α-pinene tribopolymerisation.18
3.7 3D shear stress–temperature-rate constant fits
To investigate the combined influence of temperature and stress on reactivity, the decomposition rate data was also plotted as a 3D surface and fitted to eqn (1). This approach provided significantly reduced uncertainties in the activation volume, activation energy, and pre-exponential factor compared to 2D fits in our previous NEMD study of trialkyl phosphate mechanochemistry.46 The 3D fits for α-Fe(110), Fe3C(010) and Fe3O4(100) are presented in Fig. 13(a–c), respectively. To avoid biasing the 3D fits towards the higher decomposition rate constants, fits ln(k), rather than k were employed, as shown in the ESI† (Fig. S12).46 Using the 3D surfaces, we calculated ΔV*, Ea, and A values across the entire range of temperatures and pressures studied, as shown in Table 1. Unlike the 2D plots, the 3D fitting method does not capture the changes in the Bell model parameters with temperature and pressure. However, compared to the 2D fits, the 3D fits led to reduced uncertainties in all three parameters in eqn (1),46 as shown in the ESI† (Fig. S7, S10 and S11).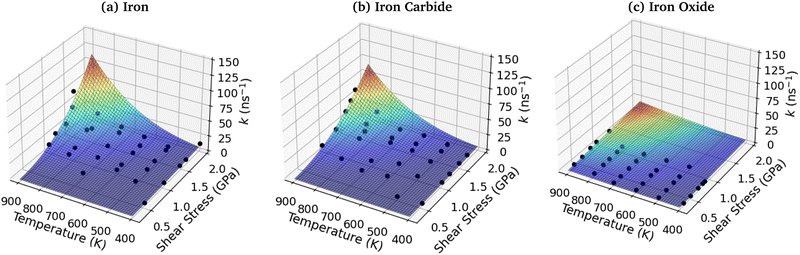 | ||
| Fig. 13 3D fits of TCP decomposition rate as a function of temperature and shear stress for (a) α-Fe(110), (b) Fe3C(010) and (c) Fe3O4(100) surfaces. | ||
| Surface | E a (kJ mol−1) | ln(A) (s−1) | ΔV* (Å3) |
|---|---|---|---|
| α-Fe(110) | 21.3 ± 2.8 | 27.0 ± 2.0 | 12.3 ± 3.3 |
| Fe3C(010) | 22.1 ± 2.6 | 26.2 ± 1.7 | 10.2 ± 2.6 |
| Fe3O4(100) | 11.2 ± 1.7 | 24.3 ± 1.8 | 8.1 ± 4.4 |
The 3D fits suggest that the activation energy increases in the order: Fe3O4(100) < Fe3C(010) ∼ α-Fe(110), which is opposite to that expected from the relative reactivity of the surfaces. The smaller energy barrier for the less reactive oxide surfaces may be due to the availability of oxygen atoms to promote P–O dissociation through nucleophilic substitution reactions at the phosphorus atoms. On the other hand, the pre-exponential factor is also much smaller for the iron oxide surface, suggesting that the fraction of successful collisions is also much lower. This may be due to the decreased availability of iron atoms at the surface, which are essential to promoting the P–O dissociation reactions.
The ΔV* values increase in the order: Fe3O4(100) < Fe3C(010) < α-Fe(110), suggesting that the more reactive surfaces lead to an increased shear stress dependence of the reactivity. The larger activation volume for α-Fe(110) than Fe3C(010) and particularly Fe3O4(100) could be because the more reactive surfaces anchor the TCP molecules, leading to more efficient transmission of shear stress applied through the surfaces to strain within the molecules. Similar suggestions have been made from previous NEMD simulations in other systems, which have shown accelerated mechanochemical reaction when molecules are anchored to one20 or both21 sliding surfaces. Our observation of higher ΔV* values on more reactive surfaces contrasts with previous experiments α-pinene tribopolymerisation, which showed that surfaces that promoted α-pinene chemisorption (e.g. copper oxide) gave smaller activation volumes than the ones only capable of physisorption (e.g. silicon oxide).18 This discrepancy may be because the experiments studied bond-forming mechanochemical reactions, rather than bond-breaking as in the current simulations. The reaction yield was higher on the more reactive surfaces, implying that the accelerated reactivity for the more reactive surfaces seen in the experiments was mostly due to a reduction in activation energy (although this was not quantified).18
Another factor contributing to the difference in activation volumes between the three surfaces could be the contact stiffness.46,87 In our NEMD simulations, at a given temperature, the stiffness of the three surfaces is quite similar (within 10%), as shown in the ESI† (Table S1). At most temperatures, the contact stiffness increases in the order Fe3C(010) < α-Fe(110) < Fe3O4(100). Since the activation volume is expected to be inversely proportional to the contact stiffness,87 the increased stiffness of the Fe3O4(100) surface may also contribute to its smaller activation volume compared to the other two surfaces. However, we expect that the differences in contact stiffness play a secondary role compared to the molecular adsorption strength in determining the variation in activation volume between the three surfaces.
4 Conclusions
We have studied the mechanochemical decomposition of TCP molecules confined between atomically-smooth iron, iron carbide, and iron oxide surfaces using NEMD simulations with ReaxFF. The iron surfaces are more effective in promoting TCP decomposition compared to iron carbide and particularly iron oxide surfaces, which correlates with the increase in Fe–C bonding between the molecules and the surface, as well as the surface energy. Once the molecules are adsorbed, decomposition of TCP proceeds through P–O bond dissociation for all of the surfaces to form cresol molecules. In some cases, a subsequent C–O bond dissociation within the cresol molecule leads to the formation of toluene.The rate of TCP decomposition increases exponentially with temperature and shear stress, indicating that this is a SATA process. We show that the presence of DIDA base oil molecules does not affect the decomposition mechanism, but reduces the shear stress and thus the TCP decomposition rate. The change in the TCP decomposition rate constants with shear stress for the systems with and without DIDA can be described with a single fit to the Bell model using the same activation volume. This observation justifies the use of base oil-free NEMD simulations for the subsequent wide parameter study.
As well as TCP decomposition, we also investigate the early stages of polyphosphate growth. Despite the fact that P–O bond formation is accelerated on the more reactive surfaces (iron), the rate of P–O bond cleavage is also increased by a similar amount, meaning that the total number of P–O bonds is comparable between the three surfaces. The polyphosphate chain length is also similar between the surfaces, with a skew in the distribution to higher chain lengths (up to octomers) for the more reactive iron surfaces.
3D fits to the Bell model lead to activation energies and pre-exponential factors both increasing in the order: Fe3O4(100) < Fe3C(010) ∼ α-Fe(110). This implies that, although the energy barrier is smaller for the less reactive oxide surfaces, the fraction of successful collisions is also much lower. This trend may be due to the decreased availability of iron atoms on the surface, which are essential to promoting the decomposition reactions. The activation energies and pre-exponential factors calculated from the NEMD simulations are within the experimental range reported for iron and stainless steel (chromium oxide) surfaces. The activation volume from the 3D fits increases in the order: Fe3O4(100) < Fe3C(010) < α-Fe(110), which suggests that higher surface energy causes the TCP molecules to be anchored to the surface, leading to more efficient transmission of mechanical energy. An additional contribution to the larger activation energy for α-Fe(110) surfaces could be the lower contact stiffness.
We have shown that surface chemistry plays a central role in the mechanochemical decomposition of an industrially-important additive for aviation lubricants. The differences between the three ferrous surfaces can be rationalised through parameters from the Bell model. Future NEMD simulations could consider the impact of heterogeneous, rough surfaces, such as steel on mechanochemical reactions. On the other hand, experiments could consider using more chemically controllable surfaces, such as specific iron oxides grown on top of atomically-smooth silicon wafers, for optimal comparison with molecular simulations of mechanochemistry within nanoscale contacts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. O. thanks the Engineering and Physical Sciences Research Council (EPSRC) for PhD funding through their Doctoral Training Partnership (DTP) scheme (EP/T51780X/1). J. P. E. acknowledges the support of the Royal Academy of Engineering through their Research Fellowships scheme. J. P. E. and C. A. L. thank Shell and the EPSRC for funding via the InFUSE Prosperity Partnership (EP/V038044/1). A. M. and F. H. B. acknowledge support from the National Science Foundation (NSF) grant CMMI-2038499. The authors acknowledge the use of Imperial College London Research Computing Service (https://doi.org/10.14469/hpc/2232) and the UK Materials and Molecular Modelling Hub, which is partially funded by the EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1). We thank Daniele Dini for useful discussions.References
- R. T. O'Neill and R. Boulatov, Nat. Rev. Chem., 2021, 5, 148–167 CrossRef PubMed.
- E. Colacino, M. Carta, G. Pia, A. Porcheddu, P. C. Ricci and F. Delogu, ACS Omega, 2018, 3, 9196–9209 CrossRef CAS PubMed.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- A. A. Michalchuk, I. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2019, 21, 2174–2179 RSC.
- R. A. Haley, A. R. Zellner, J. A. Krause, H. Guan and J. Mack, ACS Sustainable Chem. Eng., 2016, 4, 2464–2469 CrossRef CAS.
- S. Hwang, S. Gratz and L. Borchardt, Chem. Commun., 2022, 58, 1661–1671 RSC.
- A. Boscoboinik, D. Olson, H. Adams, N. Hopper and W. T. Tysoe, Chem. Commun., 2020, 56, 7730–7733 RSC.
- N. N. Gosvami, J. A. Bares, F. Mangolini, A. R. Konicek, D. G. Yablon and R. W. Carpick, Science, 2015, 348, 102–106 CrossRef CAS PubMed.
- J. Zhang and H. Spikes, Tribol. Lett., 2016, 63, 24 CrossRef.
- J. Zhang, J. P. Ewen, M. Ueda, J. S. Wong and H. A. Spikes, ACS Appl. Mater. Interfaces, 2020, 12, 6662–6676 CrossRef CAS PubMed.
- A. Neville, A. Morina, T. Haque and M. Voong, Tribol. Int., 2007, 40, 1680–1695 CrossRef CAS.
- P. Mittal, Y. Maithani, J. P. Singh and N. N. Gosvami, Tribol. Int., 2020, 151, 106419 CrossRef CAS.
- C. McFadden, C. Soto and N. D. Spencer, Tribol. Int., 1997, 30, 881–888 CrossRef CAS.
- M. Ueda, A. Kadiric and H. Spikes, Tribol. Online, 2020, 15, 318–331 CrossRef.
- M. Ueda, A. Kadiric and H. Spikes, Tribol. Lett., 2021, 69, 62 CrossRef CAS.
- S. Peeters, A. Barlini, J. Jain, N. N. Gosvami and M. C. Righi, Appl. Surf. Sci., 2022, 600, 153947 CrossRef CAS.
- V. R. S. Ruiz, T. Kuwahara, J. Galipaud, K. Masenelli-Varlot, M. B. Hassine, C. Heau, M. Stoll, L. Mayrhofer, G. Moras, J. M. Martin, M. Moseler and M.-I. De Barros Bouchet, Nat. Commun., 2021, 12, 4550 CrossRef PubMed.
- X. He and S. H. Kim, Langmuir, 2018, 34, 2432–2440 CrossRef CAS PubMed.
- A. Khajeh, X. He, J. Yeon, S. H. Kim and A. Martini, Langmuir, 2018, 34, 5971–5977 CrossRef CAS PubMed.
- J. Yeon, X. He, A. Martini and S. H. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 3142–3148 CrossRef CAS PubMed.
- T. Kuwahara, P. A. Romero, S. Makowski, V. Weihnacht, G. Moras and M. Moseler, Nat. Commun., 2019, 10, 151 CrossRef PubMed.
- B. Guan, B. A. Pochopien and D. S. Wright, Lubr. Sci., 2016, 28, 257–265 CrossRef CAS.
- D. W. Johnson and J. E. Hils, Lubricants, 2013, 1, 132–148 CrossRef.
- O. Beeck, J. Givens and E. Williams, Proc. R. Soc. London, Ser. A, 1940, 177, 103–118 CAS.
- D. H. Han and M. Masuko, Tribol. Trans., 1999, 42, 902–906 CrossRef CAS.
- J. Airey, J. Simpson, M. Spencer, R. W. Greenwood and M. J. Simmons, Proc. Inst. Mech. Eng., Part J, 2023, 237, 1548–1567 CrossRef CAS.
- R. L. Jones, H. Ravner and R. L. Cottington, ASLE Trans., 1970, 13, 1–10 CrossRef CAS.
- F. Barcroft and S. Daniel, J. Basic Eng., 1965, 87, 761–767 CrossRef CAS.
- D. Godfrey, ASLE Trans., 1965, 8, 1–11 CrossRef CAS.
- O. D. Faut and D. R. Wheeler, ASLE Trans., 1983, 26, 344–350 CrossRef CAS.
- A. H. J. M. Gauthier, H. Montes and J. M. Georges, ASLE Trans., 1982, 25, 445–455 CrossRef CAS.
- C. Saba and N. Förster, Tribol. Lett., 2002, 12, 135–146 CrossRef CAS.
- D. W. Johnson, S. Morrow, N. H. Förster and C. S. Saba, Chem. Mater., 2002, 14, 3767–3775 CrossRef CAS.
- B. Acharya, T. Pardue, K. Avva and J. Krim, Tribol. Int., 2018, 126, 106–115 CrossRef CAS.
- D. R. Wheeler and O. D. Faut, Appl. Surf. Sci., 1984, 18, 106–122 CrossRef CAS.
- D. Sung and A. Gellman, Tribol. Int., 2002, 35, 579–590 CrossRef CAS.
- R. D. Evans, K. L. More, C. V. Darragh and H. P. Nixon, Tribol. Trans., 2004, 47, 430–439 CrossRef CAS.
- R. D. Evans, K. L. More, C. V. Darragh and H. P. Nixon, Tribol. Trans., 2005, 48, 299–307 CrossRef CAS.
- A. Khajeh, F. H. Bhuiyan, J.-E. Mogonye, R. A. Pesce-Rodriguez, S. Berkebile and A. Martini, J. Phys. Chem. C, 2021, 125, 5076–5087 CrossRef CAS.
- H. K. D. H. Bhadeshia, Prog. Mater. Sci., 2012, 57, 268–435 CrossRef CAS.
- D. W. Johnson, J. E. Hils and N. Förster, Tribol. Lett., 2011, 42, 223–232 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- A. Khajeh, X. Hu, K. Mohammadtabar, Y. K. Shin, A. C. Van Duin, S. Berkebile and A. Martini, J. Phys. Chem. C, 2019, 123, 12886–12893 CrossRef CAS.
- J. P. Ewen, C. A. Latorre, C. Gattinoni, A. Khajeh, J. D. Moore, J. E. Remias, A. Martini and D. Dini, J. Phys. Chem. C, 2020, 124, 9852–9865 CrossRef CAS.
- J. F. Makki and E. E. Graham, Tribol. Trans., 1990, 33, 595–603 CrossRef CAS.
- C. Ayestarán Latorre, J. E. Remias, J. D. Moore, H. A. Spikes, D. Dini and J. P. Ewen, Commun. Chem., 2021, 4, 178 CrossRef PubMed.
- J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386 CrossRef CAS.
- C. Winder and J. C. Balouet, Environ. Res., 2002, 89, 146–164 CrossRef CAS PubMed.
- R. Lu, K. Kobayashi, H. Nanao and S. Mori, Tribol. Lett., 2009, 33, 1–8 CrossRef CAS.
- E. E. Klaus, J. Phillips, S. C. Lin, N. L. Wu and J. L. Duda, Tribol. Trans., 1990, 33, 25–32 CrossRef CAS.
- P. Blonski and A. Kiejna, Surf. Sci., 2007, 601, 123–133 CrossRef CAS.
- W. C. Chiou and E. A. Carter, Surf. Sci., 2003, 530, 88–100 CrossRef.
- R. Bliem, E. McDermott, P. Ferstl, M. Setvin, O. Gamba, J. Pavelec, M. A. Schneider, M. Schmid, U. Diebold, P. Blaha, L. Hammer and G. S. Parkinson, Science, 2014, 346, 1215–1218 CrossRef CAS PubMed.
- J. Zhang, J. P. Ewen and H. A. Spikes, Mol. Syst. Des. Eng., 2022, 7, 1045–1055 RSC.
- G. L. Clark and J. V. Robinson, J. Am. Chem. Soc., 1940, 62, 1948–1951 CrossRef CAS.
- S. Ramachandran, B. L. Tsai, M. Blanco, H. Chen, Y. Tang and W. A. Goddard, Langmuir, 1996, 12, 6419–6428 CrossRef CAS.
- M. Abdelmaksoud, J. W. Bender and J. Krim, Tribol. Lett., 2002, 13, 179–186 CrossRef CAS.
- E. E. Graham and E. E. Klaus, ASLE Trans., 1986, 29, 229–234 CrossRef CAS.
- K. Mohammadtabar, S. J. Eder, N. Dörr and A. Martini, Tribol. Int., 2022, 176, 107922 CrossRef CAS.
- S. Hayashi, N. Uemura, M. Uranagase and S. Ogata, J. Comput. Chem., 2023, 44, 766–776 CrossRef CAS PubMed.
- S. Loehlé and M. Righi, Lubricants, 2018, 6, 31 CrossRef.
- K. Mohammadtabar, S. J. Eder, N. Dörr and A. Martini, J. Phys. Chem. C, 2019, 123, 19688–19692 CrossRef CAS.
- S. Peeters, C. Charrin, I. Duron, S. Loehlé, B. Thiebaut and M. C. Righi, Mater. Today Chem., 2021, 21, 100487 CrossRef CAS.
- L. Wang and R. J. Wood, Tribol. Int., 2007, 40, 1655–1666 CrossRef CAS.
- D. W. Johnson, M. Bachus and J. E. Hils, Lubricants, 2013, 1, 48–60 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- T. Schneider and E. Stoll, Phys. Rev. B: Solid State, 1978, 17, 1302–1322 CrossRef CAS.
- X. Yong and L. T. Zhang, J. Chem. Phys., 2013, 138, 084503 CrossRef PubMed.
- F. H. Bhuiyan, S. H. Kim and A. Martini, Appl. Surf. Sci., 2022, 591, 153209 CrossRef CAS.
- M. Koyama, J. Hayakawa, T. Onodera, K. Ito, H. Tsuboi, A. Endou, M. Kubo, C. A. D. Carpio and A. Miyamoto, J. Phys. Chem. B, 2006, 110, 17507–17511 CrossRef CAS PubMed.
- S. J. Plimpton and A. P. Thompson, MRS Bull., 2012, 37, 513–521 CrossRef CAS.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik and H. M. Aktulga, et al. , npj Comput. Mater., 2016, 2, 1–14 CrossRef.
- A. Martini, S. J. Eder and N. Dörr, Lubricants, 2020, 8, 44 CrossRef.
- M. Aryanpour, A. C. van Duin and J. D. Kubicki, J. Phys. Chem. A, 2010, 114, 6298–6307 CrossRef CAS PubMed.
- C. Zou, A. C. Van Duin and D. C. Sorescu, Top. Catal., 2012, 55, 391–401 CrossRef CAS.
- C. Verlackt, E. Neyts, T. Jacob, D. Fantauzzi, M. Golkaram, Y. K. Shin, A. Van Duin and A. Bogaerts, New J. Phys., 2015, 17, 103005 CrossRef.
- K. Chenoweth, A. C. V. Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- A. K. Rappe and W. A. Goddard III, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS.
- L. S. Morrissey, S. M. Handrigan, S. Subedi and S. Nakhla, Mol. Simul., 2019, 45, 501–508 CrossRef CAS.
- J. J. Adams, D. Agosta, R. Leisure and H. Ledbetter, J. Appl. Phys., 2006, 100, 113530 CrossRef.
- J. Li, H. K. Mao, Y. Fei, E. Gregoryanz, M. Eremets and C. S. Zha, Phys. Chem. Miner., 2002, 29, 166–169 CrossRef CAS.
- H. J. Reichmann and S. D. Jacobsen, Am. Mineral., 2004, 89, 1061–1066 CrossRef CAS.
- M. M. Islam, C. Zou, A. C. V. Duin and S. Raman, Phys. Chem. Chem. Phys., 2015, 18, 761–771 RSC.
- T. D. Ta, H. M. Le, A. K. Tieu, H. Zhu, H. T. T. Ta, N. V. Tran, S. Wan and A. C. T. van Duin, ACS Appl. Nano Mater., 2020, 3, 2687–2704 CrossRef CAS.
- Z. Li and I. Szlufarska, Phys. Rev. Lett., 2021, 126, 076001 CrossRef CAS PubMed.
- G. Clavier, N. Desbiens, E. Bourasseau, V. Lachet, N. Brusselle-Dupend and B. Rousseau, Mol. Simul., 2017, 43, 1413–1422 CrossRef CAS.
- K. Sebeck, C. Shao and J. Kieffer, ACS Appl. Mater. Interfaces, 2016, 8, 16885–16896 CrossRef CAS PubMed.
- J. Zhang, A. Tan and H. Spikes, Tribol. Lett., 2017, 65, 13 CrossRef.
- L. Fang, S. Korres, W. A. Lamberti, M. N. Webster and R. W. Carpick, Faraday Discuss., 2023, 241, 394–412 RSC.
- X. Chen, K. Kawai, H. Zhang, K. Fukuzawa, N. Koga, S. Itoh and N. Azuma, J. Phys. Chem. C, 2020, 124, 22496–22505 CrossRef CAS.
- E. Roduner, Chem. Soc. Rev., 2014, 43, 8226–8239 RSC.
- H. Spikes, Friction, 2018, 6, 1–31 CrossRef.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- B. Chen, R. Hoffmann and R. Cammi, Angew. Chem., Int. Ed., 2017, 56, 11126–11142 CrossRef CAS PubMed.
- J. P. Gao, W. D. Luedtke, D. Gourdon, M. Ruths, J. N. Israelachvili and U. Landman, J. Phys. Chem. B, 2004, 108, 3410–3425 CrossRef CAS.
- X. Yu, C. F. Huo, Y. W. Li, J. Wang and H. Jiao, Surf. Sci., 2012, 606, 872–879 CrossRef CAS.
- S. J. Eder, A. Vernes and G. Betz, Langmuir, 2013, 29, 13760–13772 CrossRef CAS PubMed.
- S. S. Tafreshi, A. Roldan, N. Y. Dzade and N. H. De Leeuw, Surf. Sci., 2014, 622, 1–8 CrossRef CAS.
- E. Osei-Agyemang, S. Berkebile and A. Martini, Tribol. Lett., 2018, 66, 1–22 CrossRef CAS.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, Minerals, 2014, 4, 89–115 CrossRef.
- R. Heuberger, A. Rossi and N. D. Spencer, Tribol. Lett., 2007, 25, 185–196 CrossRef CAS.
- D. C. Yue, T. B. Ma, Y. Z. Hu, J. Yeon, A. C. V. Duin, H. Wang and J. Luo, J. Phys. Chem. C, 2013, 117, 25604–25614 CrossRef CAS.
- C. A. Olsson and D. Landolt, Electrochim. Acta, 2003, 48, 1093–1104 CrossRef CAS.
- K. Sasaki, N. Inayoshi and K. Tashiro, Wear, 2010, 268, 911–916 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- P. J. Barrie, Phys. Chem. Chem. Phys., 2012, 14, 318–326 RSC.
- H. Lynggaard, A. Andreasen, C. Stegelmann and P. Stoltze, Prog. Surf. Sci., 2004, 77, 71–137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05320b |
| This journal is © the Owner Societies 2024 |