Automated standard dilution analysis
Willis B.
Jones
 a,
George L.
Donati
a,
George L.
Donati
 a,
Clifton P.
Calloway
Jr.
b and
Bradley T.
Jones
*a
a,
Clifton P.
Calloway
Jr.
b and
Bradley T.
Jones
*a
aDepartment of Chemistry, Wake Forest University, Winston-Salem, NC 27109, USA. E-mail: jonesbt@wfu.edu
bDepartment of Chemistry, Physics and Geology, Winthrop University, Rock Hill, SC 29733, USA
First published on 25th November 2019
Abstract
Standard dilution analysis (SDA) is a recently described calibration method that combines internal standardization and standard additions to improve accuracy and precision. By combining these two traditional methods, SDA offers corrections for sample matrix effects while also minimizing signal fluctuations due to changes in the excitation source and the sampling process. In its most basic form, SDA is performed by introducing a constant amount of sample into an instrument while varying the amount of standard solution added to the sample. The procedure is simple to perform by hand, but automation of the process is challenging because the dilution of the standard solution by a blank occurs on-line while the measurement is taking place. The experiments presented here are aimed at improving the automation of the SDA process. Inductively coupled plasma optical emission spectrometry (ICP OES) is used as a model for SDA applications, although the calibration method is applicable to any technique that accepts samples as a liquid flow. The end goal of automation is for successive samples to be analyzed quickly by using an automatic sampler to switch from sample to sample, as it is the case in routine analytical methods. The required dilution of the standard by a blank mixture is achieved through the use of a two-channel pinch valve, with dilution occurring by diffusion as the solution is pulled from the valve toward the plasma by a second channel in the instrument's peristaltic pump. The proposed automated SDA method is effective, with analyte recoveries within a few percent of 100 for the elements evaluated (i.e. Al, Cd, Co, Cr, Cu, Fe, Ni and Pb) and nine different sample matrices. The method also provides promising results when analyzing real-world samples. The limits of detection obtained with the automated SDA method are similar to those typically found for external standard calibration and ICP OES, falling within the single-digit μg L−1 range.
Introduction
Accurate calibration is the ultimate goal of most analytical techniques, as it allows for determination of the concentration of analytes in real-world samples. At its core, calibration involves the preparation of a series of standard solutions containing analytes of known, increasing concentration, which allows for the calculation of the unknown analyte concentration in a sample. The simplest of the traditional calibration methods, external standard calibration (EC), is performed by direct comparison of a sample to a series of calibration solutions. It assumes that the sample matrix does not affect the analytical signal to a significant degree when compared to an identical concentration of analyte prepared in pure solvent, which usually is an inaccurate assumption.1 More advanced calibration methods have been designed to correct for problems that arise in simple EC. The standard additions (SA) method introduces an identical amount of sample solution into each of the calibration standards. The SA method is cumbersome and time consuming, especially if multiple samples are being analyzed, but it is effective at correcting for matrix effects, as the sample matrix is present in each calibration standard in equal parts.2,3 The internal standard (IS) method is put into practice if the analytical signal is affected by changes in the sampling process or the excitation source. An extra species, called the internal standard, is added to all calibration and sample solutions. For an ideal IS species, changes in the sample position, volume, or analyte atomization and excitation processes affect the analyte as well as the internal standard, thus these external changes are corrected.4 In addition to these traditional calibration methods, other correction strategies such as extrapolation to infinite dilution,5 multi-energy calibration,6 and multi-flow calibration7 have also been proposed in order to correct for matrix effects.Standard dilution analysis
Standard Dilution Analysis (SDA) is a recently described calibration strategy that combines the traditional SA and IS methods.8 It is simple to perform, and requires only two solutions for a full calibration. The first solution consists of 50% sample and 50% standard. The standard contains both the analytes and an internal standard. The second solution consists of 50% sample and 50% blank. SDA is performed as the second solution is poured into the first, resulting in an on-line dilution of the standard while the amount of sample is kept constant. SDA calculations are also simple, as described in detail below. This new calibration method has been successfully applied to multiple analytical techniques, including flame atomic emission spectrometry (FAES),9 flame atomic absorption spectrometry (FAAS),10 microwave-induced plasma optical emission spectrometry (MIP OES),11,12 inductively coupled plasma OES (ICP OES),8,13–15 ICP mass spectrometry (ICP-MS),16 Raman spectroscopy,17 and visible absorption spectrometry.8In practice, SDA offers significantly improved accuracies and precisions when compared to traditional EC and IS methods, while offering slight improvements over SA.8,13 Two reviews are referenced that incorporate SDA into summaries of other commonly used calibration techniques in atomic spectrometry.18,19 The most significant benefit that SDA provides over traditional SA is its improved sample throughput due to a simpler sample preparation procedure. In SDA, a full calibration is performed with only two solutions. On the other hand, an important challenge for implementing SDA in routine analysis is associated with its automation. In its earliest iterations, SDA was performed manually, by pouring the blank-containing solution into the standard-containing solution. Recent advances in the method have been aimed at the automation of solution mixing, namely the use of a three-port mixing chamber directly coupled to the sample introduction system of an ICP OES.13 This setup allowed for SDA to be performed in its entirety using only the commercial instrument's own automatic sampler to dilute the standard-containing solution with the blank. However, it involved an elongated rinsing step to completely wash out residual sample from the mixing chamber before proceeding to the next cycle. In another work, a multi-channel nebulizer was used to perform SDA inside the spray chamber of an ICP OES instrument. However, automation was also limited in this case, as the instrument's automatic sampler was not used and the sample had to be fed manually into the system.15
The method presented here uses a new version of SDA solution preparation in order to speed up the automation process. These experiments use ICP OES as an application model for the calibration strategy. However, it is essential to reiterate that SDA is not limited to ICP OES, and it may be applied to any technique capable of accepting liquid samples and simultaneously monitoring multiple analytical signals. As mentioned previously, SDA requires a constant amount of sample to be introduced into the analytical system, while the amount of standard is varied through dilution with a blank. To simplify the automation of the method, the two calibration solutions are introduced into the ICP using two separate channels on the instrument's peristaltic pump. One channel is connected to the instrument's automatic sampler, which moves between individual samples as would be the case in any typical analysis. The second channel introduces the standard and blank solutions in an alternating fashion. Consistently alternating between standard and blank solutions eliminates the need for an elongated cleaning step beyond the typical rinse time adopted between samples. This is possible because the dilution occurs in a separate channel from the sample introduction itself.
SDA theory
The calculations used in SDA have changed since their original derivation,13 and the newest, simplest iteration is described here. Again, SDA functions on the premise that there is a constant amount of sample present in an analytical system, while the ratio of standard to blank is varied. Thus, the measured analyte signal has contributions from both the sample itself and the calibration standard, as described by eqn (1), where S is the signal, A is the analyte, and std and sam correspond to the standard and sample, respectively.| StotalA = SstdA + SsamA | (1) |
To simplify the math, a constant K is defined in eqn (2) as the ratio of analyte signal in the standard solution alone to internal standard signal, where I represents the internal standard. This definition of K allows for eqn (1) to be rewritten as shown in eqn (3).
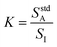 | (2) |
| StotalA = KSI + SsamA | (3) |
Eqn (3) is the equation for a line when the analyte signal is plotted against the internal standard signal, with a slope of K and a y-intercept that is equal to the analyte signal that arises from the sample alone. Now consider the ratio of this intercept and slope, as shown in eqn (4).
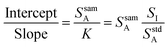 | (4) |
In general, a measured signal is equal to the concentration of analyte, C, multiplied by the calibration sensitivity, m. Substituting this in to eqn (4), the concentration of the analyte in the sample is now present in the calculation, as shown in eqn (5).
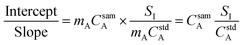 | (5) |
This equation can be rearranged to allow for direct calculation of the analyte concentration in the sample, as shown in eqn (6).
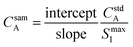 | (6) |
When the analyte in the standard is undiluted, the internal standard must also be undiluted, thus the internal standard signal is at its maximum. The maximum internal standard signal can be estimated by first introducing the standard into the experimental system and allowing the signal to stabilize before dilution by the blank,8 or it can be calculated by introducing a second internal standard into the blank solution, providing an inverse relationship between the two internal standards. The internal standard present with the analytes in the standard solution is referred to as the primary internal standard, while the internal standard present in the blank is referred to as the secondary internal standard. The two internal standards are plotted against each other, and the maximum internal standard signal is defined as the y-intercept of this second plot. The use of a secondary internal standard improves sample throughput, as the maximum primary internal standard signal is calculated from the same points in time that provide the full calibration.13
Note that the final calculation presented in eqn (6) assumes that the sample solution and the standard plus blank solution mix are present in the analytical system in equal parts. The addition of a simple dilution factor to eqn (6) corrects for an experiment in which the sample to standard plus blank ratio is not one to one.
Experimental
Solution preparation
Standard and blank solutions were prepared using distilled-deionized water (DDI) and trace-metal grade nitric acid. A multi-element stock solution containing Al, Cd, Co, Cr, Cu, Fe, Ni and Pb as analytes was prepared using 1000 mg L−1 single-element standards. This solution was prepared in such a way that the selected analyte lines provided intensities on the same order of magnitude. Scandium and Y were used as internal standards, also prepared from 1000 mg L−1 single-element standards. The stock solution was diluted in 1% v/v HNO3, and contained final concentrations of 1.36 mg L−1 Al and Cu, 2.27 mg L−1 Cr, 4.54 mg L−1 Cd, Co, Fe and Ni, and 13.6 mg L−1 Pb as analytes, with 0.5 mg L−1 Y as an internal standard. The blank solution, prepared in 1% v/v HNO3, contained 0.5 mg L−1 Sc as the second internal standard and 100 mg L−1 Li to help balance the ionic strength of the two solutions.Nine different sample matrices were spiked with the stock solution to have the same added analyte concentration as the diluted standard, in order to determine how well the automated SDA process corrected for matrix effects. The examined matrices included DDI, tap water, 50% v/v ACS grade nitric acid, 40% v/v ethanol, a soft drink, a zero-sugar soft drink, a red wine, 50% v/v mouthwash, and 1% m/v Ca.
Several reference materials were analyzed in order to evaluate the accuracy of the automated SDA method. A water pollution standard (VHG Labs, Manchester, NH, USA) was diluted in 1% v/v HNO3 before performing SDA. A standard reference material of Oyster Tissue (NIST 1566B) from the National Institute of Standards and Technology (NIST, Gaithersburg, MD, USA) and two standards of metals in hydrocarbon oil (300 and 900 μg g−1, Agilent Technologies, Wilmington, DE, USA) were subjected to microwave-assisted digestion before analysis. The digestion program used with an Ethos Up system (Milestone, Sorisole, Italy) consisted of a 15 min ramp to 200 °C, a 15 min hold at 200 °C, and a 10 min cooling step. Aliquots of 1.5 mL trace-metal grade HNO3, 6.5 mL DDI and 2 mL 30% v/v H2O2 were used in the digestion process.
A second stock solution was prepared for the analysis of the reference materials and for determination of the method's limits of detection (LODs). A multi-element standard containing all of the 8 analytes and Sc as an internal standard at 100 mg L−1 (Teledyne Leeman Labs, Hudson, NH, USA) was diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 in DDI with added 1% v/v HNO3. A second blank was prepared in 1% v/v HNO3, with 0.5 mg L−1 Y as an internal standard and 100 mg L−1 Li to help balance the ionic strength of the two solutions.
100 in DDI with added 1% v/v HNO3. A second blank was prepared in 1% v/v HNO3, with 0.5 mg L−1 Y as an internal standard and 100 mg L−1 Li to help balance the ionic strength of the two solutions.
The analyte and internal standard emission lines used here are provided in Table 1. Emission intensities of each analyte and internal standard were monitored at two different wavelengths, but only results from one line are presented here. The use of different emission lines for a given analyte changes the calculations to a minimal extent, and the use of multiple internal standard emission lines is even more inconsequential. Unless otherwise noted, all results discussed here use the measured intensity of the lines provided in Table 1.
| Element | Species | Wavelength (nm) |
|---|---|---|
| Al | I | 396.152 |
| Cd | I | 228.802 |
| Co | II | 237.863 |
| Cr | II | 267.716 |
| Cu | I | 324.754 |
| Fe | II | 259.940 |
| Ni | I | 341.476 |
| Pb | I | 405.781 |
| Sc | II | 361.383 |
| Y | II | 371.029 |
Automation of SDA
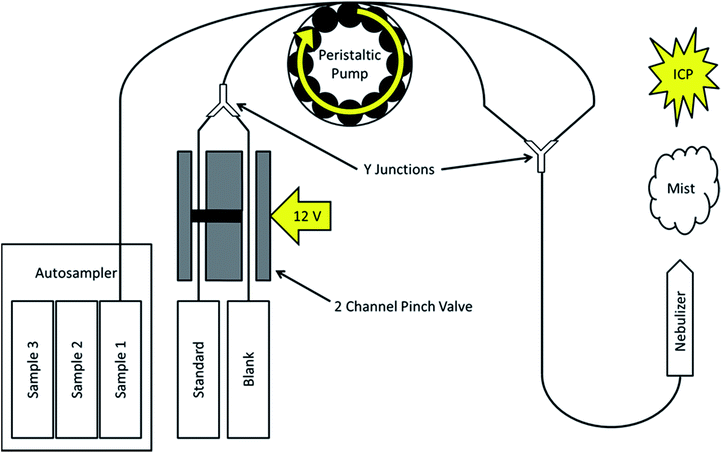
The instrument used to evaluate the automated SDA method was an Agilent 5110 ICP OES (Agilent Technologies, Santa Clara, CA, USA). However, as previously discussed, it is applicable to any system that accepts samples as a liquid flow, and is thus not limited to ICP OES. Fig. 1 provides a basic schematic of how the SDA process has been automated in this experimental setup. Solutions are introduced into the ICP through the use of the standard peristaltic pump and nebulizer on the instrument.The novelty of the automation technique presented here lies in how the sample and standard plus blank solutions are introduced into the plasma simultaneously, with the standard being diluted from a maximum to blank level in an alternating fashion. Sample solutions are placed in an automatic sampler and drawn up through the tubing by the peristaltic pump. A second channel on the peristaltic pump creates the standard plus blank mixture through the use of a two channel pinch valve (Cole-Parmer, Vernon Hills, IL, USA). Tubing from one channel in the valve draws the prepared standard solution, while the second channel draws from the prepared blank solution. One channel of the valve is open by default. When 12 V are applied to the valve, the first channel closes and the second one opens. A digital timer outlet (NEARPOW, TX, USA) is used to switch a low cost, simple 12 V DC power supply (120 VAC to 12 VDC) adapter, from off to on, and vice versa, every 60 s. This results in an alternating flow of pure standard or blank solution once per minute. The two channels are joined together into a single piece of tubing by a plastic Y junction. The pinch valve allows for the standard and blank solutions to be interchanged without the introduction of air bubbles into the tubing. As the liquid flow remains constant, the standard solution is diluted by the blank solution on-line inside of the tubing as it travels from the valve through the peristaltic pump. The sample and the standard plus blank flows are joined together on the back end of the peristaltic pump by a second Y junction before introduction into the nebulizer and into the plasma.
All instrumental parameters used in the present work are provided in Table 2. All of the ICP OES operating parameters were kept at their default values. As the pinch valve setup provided dilution of the standard plus blank mixture independent of the ICP OES′ automatic sampler, the uptake delay and stabilization time relate to the introduction of the sample itself into the plasma. These parameters were also kept at their default values. Only minimal changes were required to the software in order to run automated SDA. The pump speed was kept constant during the rinse step instead of speeding it up in order to preserve the nature of the standard plus blank dilution. The read time and number of replicates are the two most important parameters when SDA is performed. The read time was kept short (to the software minimum of 1 s) to provide the highest possible time resolution of the signal change provided by the dilution of the standard by the blank, and vice versa. The number of replicates was kept high (to the software maximum of 100) to provide additional points in the SDA calibration curve (as each point in time provides one point on the curve).
| Instrumental parameter | Operating condition |
|---|---|
| Plasma | |
| RF applied power | 1.20 kW |
| Viewing mode | Axial |
| Nebulizer gas flow rate | 0.7 L min−1 |
| Plasma gas flow rate | 12.0 L min−1 |
| Auxillary gas flow rate | 1.0 L min−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| General | |
| Pump speed | 12 rpm |
| Uptake delay | 90 s |
| Stabilization time | 30 s |
| Rinse time | 30 s |
| Replicates | 100 |
| Read time | 1 s |
Results and discussion
Basic examples
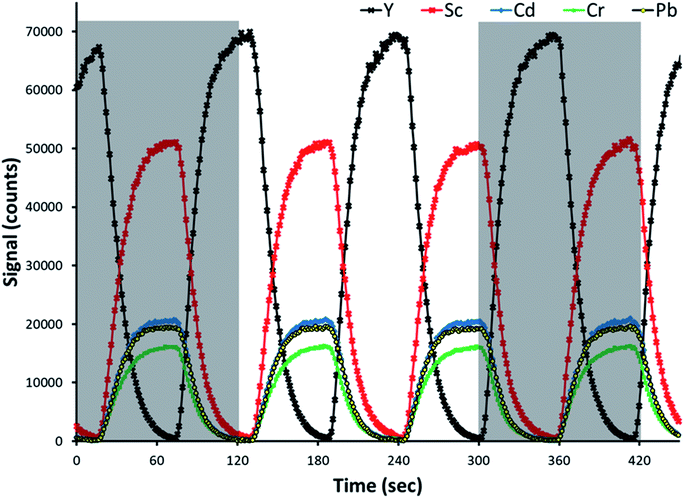
Representative time-resolved intensity traces for three analytes and both internal standards are provided in Fig. 2. An additional standard solution was prepared for the sake of making this representative plot. The analytes and primary internal standard, Sc in this example, are present in the standard solution, and thus signal intensities increase for all of them following the same profile, at the same time. The secondary internal standard, Y in this example, is present in the blank solution as a means of calculating the undiluted signal of the primary internal standard. Its signal intensity increased at the same time as the analytes and primary internal standard decreased. Note that in the representative traces provided in Fig. 2, as well as investigations of reference standards and determination of limits of detection, Sc served as the primary internal standard while Y was the secondary internal standard present in the blank. The primary and secondary internal standards are reversed for the other further discussed examples.As the valve was switching channels every 60 s, the signal intensity traces switch from increasing to decreasing every 60 s. Although the channels in the pinch valve operate in an on/off logic fashion, the intensities changed rapidly over a time of approximately 30 s before stabilizing instead of changing immediately. This means that the dilution of the standard by the blank happened by diffusion as the solution travels from the valve through the peristaltic pump and into the plasma. That explains why one observes a ramp rather than a jump in the signal profiles, as shown in Fig. 2. The gray boxes in Fig. 2 show representative times for which a single automated SDA run is performed (100 time points), with the rinse, sample uptake, and stabilization times accounting for the gap in between. A 100-point collection consisted of a full cycle of signal change from minimum to maximum and back to minimum again, but not necessarily beginning and ending with a maximum or minimum.
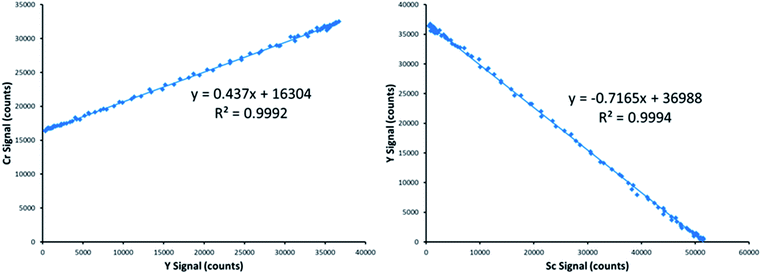
Fig. 3 provides an example of the plots needed to perform SDA calculations. The sample was DDI spiked with 2.27 mg L−1 Cr, which is the same concentration of Cr present in the prepared standard. Recall that Y is present in the standard solution as an internal standard, with Sc in the blank solution as the secondary internal standard. The Cr versus Y signal plot has a y-intercept of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304 and a slope of 0.437. The Y vs. Sc signal plot has a y-intercept of 36
304 and a slope of 0.437. The Y vs. Sc signal plot has a y-intercept of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988. Eqn (7) provides an example SDA calculation using the data shown in Fig. 3, which return a result of a 2.29 mg L−1 Cr, only a + 0.9% error from the true spike value of 2.27 mg L−1.
988. Eqn (7) provides an example SDA calculation using the data shown in Fig. 3, which return a result of a 2.29 mg L−1 Cr, only a + 0.9% error from the true spike value of 2.27 mg L−1.
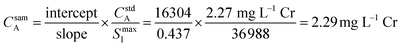 | (7) |
Robustness of automated SDA
Fig. 4 displays SDA plots obtained for Cr spiked into 9 sample matrices. This analyte was not detected in any of the unspiked samples. The topmost trend in Fig. 4 (black diamonds) corresponds to spiked DDI, which was the cleanest matrix chosen. Note that the other 8 matrices all suppressed both the analyte and internal standard signals, at least to a slight degree, as evidenced by the lowering of both the y-intercept and maximum internal standard signal. This makes it simple to envision that an external calibration method with standards prepared in DDI would provide inaccurate results, as most of the examined sample matrices suppress the analytical signal.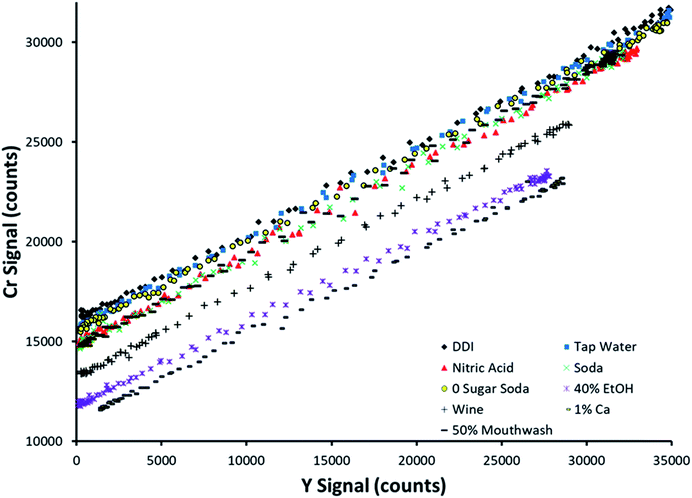 | ||
| Fig. 4 SDA plots obtained for Cr spiked into 9 different matrices. The topmost curve (black diamonds) corresponds to spiked deionized water. | ||
Note that the slope of the line was preserved between sample matrices. This is predicted by the theory, as the slope is defined as the signal ratio of the analyte present in the standard alone to the internal standard. If this ratio was not preserved between samples, the internal standard reacts differently to sample matrices than the analyte, making it a poor choice of internal standard (in a traditional sense) when examining multiple sample types. However, SDA would still work if the lines have different slopes, as the sample matrix for a given sample is preserved between the standard and blank solutions for an individual sample run.
Full investigations comparing SDA to traditional calibration methods have been performed and published previously.8,13 The focus of this research was simplifying the automation of SDA, and thus a comparison with a traditional calibration method was not performed. Nevertheless, previous results can be summarized as follows:8,13 SDA provides improved accuracy and precision when compared to a simple external standard calibration or internal standard method, while providing similar or slightly improved results compared to the traditional standard additions method. The major benefit provided by SDA over standard additions is the simplified solution preparation, and thus improved sample throughput.
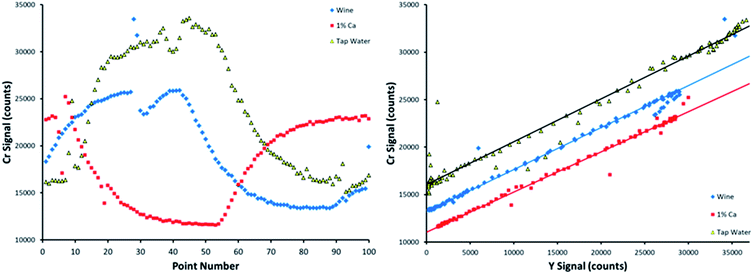
Each of the 9 matrices was initially run in triplicate. One additional measurement was taken for the tap water, soda, and wine matrices, resulting in a total number of 30 measurements for each element. This additional measurement was to assess the effect of small bubbles passing through the peristaltic pump tubing, as shown in Fig. 5.
Traditional ICP OES methods involve averaging emission signals over extended lengths of time in order to improve signal precision. However, this is not possible in the case of automated SDA, as the signals need to be collected as quickly as possible in order to achieve a wide range of signal coverage. If too long of a time period is averaged, the dilution of the standard by the blank is lost in the averaging, resulting in no signal change over time. Collecting data points quickly provides many points on individual calibration curves. Although short measurement times are more subject to noise than longer integrations, the additional points collected in a single calibration averages the noise out in the end.
When a bubble comes through the pump tubing, discontinuities appear in the time resolved signals, as shown by the Cr emission intensities on the left-hand side of Fig. 5. The dominant, slowly increasing and decreasing signals are created by the dilution of the standard by the blank, and vice versa, that allow SDA to function. The sharp deviations in signal that occur over two or three data points were caused by bubbles. SDA plots of these data sets, bubbles included, are provided on the right-hand side of Fig. 5. The linear fits depict all 100 data points, including the bubble points that fall far away from the line. The sheer number of points in the calibration curve allows for the method to correct for a bubble or two passing through the sample introduction line over the course of the measurement.
Recall that the sample matrices were spiked with 2.27 mg L−1 Cr. When including all 100 data points, the data sets shown in Fig. 5 return a calculated spiked Cr concentration of 2.31, 2.07, and 2.32 mg L−1 in the wine, 1% m/v Ca, and tap water matrices, respectively. When removing the points caused by bubbles, these calculated concentrations are basically unchanged in wine and 1% m/v Ca, and only slightly changed in tap water, returning values of 2.30, 2.06, and 2.20 mg L−1, respectively, showing that this method is capable of handling bubbles passing through the pump tubing, even when collecting data points quickly.
Limits of detection
Limits of detection (LODs) were calculated as three times the standard deviation of the concentration found for each element in 10 successive replicates of unspiked DDI. The standard used for LOD determinations was the previously discussed 100 mg L−1 multi-element standard containing all 8 analytes and Sc as an internal standard. This solution was diluted down to both 10 and 1 mg L−1 concentrations, and LODs were calculated using both dilutions. The values calculated for each element are provided in Table 3.| Element | LOD (mg L−1) | |
|---|---|---|
| 1 mg L−1 standard | 10 mg L−1 standard | |
| Al | 0.006 | 0.05 |
| Cd | 0.005 | 0.03 |
| Co | 0.005 | 0.04 |
| Cr | 0.002 | 0.04 |
| Cu | 0.003 | 0.05 |
| Fe | 0.006 | 0.05 |
| Ni | 0.008 | 0.05 |
| Pb | 0.1 | 0.06 |
The LODs are largely similar for each element, with lead being the lone exception. When using a 1 mg L−1 standard, the LOD for each element (except lead) is on the order of single digit parts per billion. When using a 10 mg L−1 standard the LODs increase similarly, up an order of magnitude, to tens of parts per billion. The LOD for lead is on the order of 100 μg L−1 for both standard concentrations. These are typical LODs for ICP OES when using traditional calibration methods. The LODs differ when using different concentration standards because a full calibration is collected every time SDA is performed.
When performing a calibration by SDA, using a higher concentration standard results in more uncertainty in values near zero. If the standard concentration is the only parameter that is changed between two SDA calibrations, the total number of points in the changing signal profile is unchanged. Thus using lower concentrations improves estimates of the noise level as the detection limit is approached, as there are more points in the calibration at low standard concentrations because the maximum standard concentration is lower. As a full calibration is required in order to return a blank signal using SDA, using a lower concentration standard provides slightly lower LODs.
Spiked sample matrices
Before comparing the results obtained across the spiked sample matrices, each matrix was run in triplicate without the spike to determine the amount of analytes inherently present in each matrix. Most of the analytes returned concentrations near or below their LODs in every matrix. The exceptions were approximately 100 μg L−1 Cu in tap water, 120 μg L−1 Cu in soda, and 700 μg L−1 Al, 200 μg L−1 Cu, and 2 mg L−1 Fe in wine. The average blank concentrations for each element in every examined sample matrix were subtracted from their corresponding spiked matrix results before calculating recovery values.Table 4 displays the average percent recovery calculated for each analyte element across the 9 sample matrices. The automated SDA method accurately corrects for matrix effects regardless of the analyte selected, returning a recovery of near 100% for each element. Table 5 displays the same data in a different way, showing the average percent recovery calculated for each sample matrix across the 8 spiked analytes. Again, SDA is able to provide accurate results across a wide range of matrix types. Even a 1% m/v Ca solution, which is a particularly difficult matrix, returns an accurate average recovery of 92%. The repeatability of the automated SDA method was examined by running spiked DDI, 1% m/v Ca, and 50% v/v mouthwash matrices in 10 successive replicates. The results are shown in Table 6. As expected from the previous results, both DDI and 50% v/v mouthwash return concentrations within a few percent of the spiked value. The 1% m/v Ca matrix again returns results that are below the spiked value, but still accurate especially considering the difficulty of the matrix itself. Regarding the precision of the automated SDA technique, the RSDs were on the order of 3% irrespective of the matrix examined. It is important to note that accuracy and precision need to be combined in order to provide better estimates of uncertainty between different measurement techniques.20 As the goal of this work was to simplify the automation of SDA as a calibration technique, a full comparison of SDA to other traditional calibration methods was not performed, but has been previously reported. SDA has been shown to offer similar results to traditional standard additions methods, while improving upon simple external calibration or internal standardization methods.8,13
| Element | Recovery (%) | n |
|---|---|---|
| Al | 98 ± 3 | 30 |
| Cd | 99 ± 3 | 30 |
| Co | 98 ± 3 | 30 |
| Cr | 100 ± 3 | 30 |
| Cu | 99 ± 7 | 30 |
| Fe | 100 ± 3 | 30 |
| Ni | 97 ± 3 | 30 |
| Pb | 96 ± 3 | 30 |
| Matrix | Recovery (%) | n |
|---|---|---|
| DDI | 100 ± 2 | 24 |
| Tap water | 102 ± 6 | 32 |
| 50% v/v nitric acid | 98 ± 2 | 24 |
| 40% v/v ethanol | 99 ± 3 | 24 |
| Soda | 99 ± 1 | 32 |
| 0 sugar soda | 98 ± 4 | 24 |
| Wine | 100 ± 3 | 32 |
| 1% m/v Ca | 92 ± 2 | 24 |
| 50% v/v mouthwash | 99 ± 2 | 24 |
| Element | Spike | DDI matrix | 1% Ca m/v matrix | 50% v/v mouthwash matrix | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mg L−1 | Avg | StDev | RSD (%) | Accuracy (%) | Avg | StDev | RSD (%) | Accuracy (%) | Avg | StDev | RSD (%) | Accuracy (%) | |
| Al | 1.36 | 1.34 | 0.04 | 2.7 | −1.4 | 1.42 | 0.09 | 6.3 | 4.6 | 1.44 | 0.05 | 3.6 | 5.9 |
| Cd | 4.54 | 4.5 | 0.1 | 2.5 | −1.4 | 4.2 | 0.1 | 3.0 | −8.4 | 4.5 | 0.1 | 3.2 | 0.06 |
| Co | 4.54 | 4.5 | 0.1 | 2.6 | −1.9 | 4.1 | 0.1 | 3.2 | −9.5 | 4.4 | 0.2 | 3.7 | −2.1 |
| Cr | 2.27 | 2.27 | 0.06 | 2.7 | −0.1 | 2.09 | 0.08 | 3.7 | −7.8 | 2.27 | 0.09 | 3.9 | −0.04 |
| Cu | 1.36 | 1.34 | 0.03 | 2.5 | −1.9 | 1.25 | 0.03 | 2.7 | −8.3 | 1.34 | 0.05 | 3.4 | −1.3 |
| Fe | 4.54 | 4.5 | 0.1 | 2.6 | 0.2 | 4.2 | 0.2 | 3.8 | −7.5 | 4.5 | 0.2 | 3.7 | 0.07 |
| Ni | 4.54 | 4.4 | 0.1 | 2.4 | −2.6 | 4.0 | 0.1 | 2.9 | −11.6 | 4.5 | 0.2 | 3.4 | −1.9 |
| Pb | 13.6 | 13.0 | 0.3 | 2.4 | −4.9 | 12.1 | 0.3 | 2.6 | −10.9 | 13.2 | 0.5 | 3.7 | −3.3 |
Reference standards
Several reference materials were analyzed to reemphasize the applicability of automated SDA to real-world samples. Sample digestions and the samples themselves were described in the solution preparation section. A summary of the obtained results is provided in Table 7. Blanks in the table correspond to elements that were not certified in concentration. The concentrations reported are those obtained directly from the SDA calculations, not accounting for dilution or digestion, to allow for comparison to LODs.| Element | Water pollution standarda | Oyster tissueb | 300 μg g−1 metals in oilc | 900 μg g−1 metals in oilc | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Concentration (mg L−1) | Recovery (%) | n | Concentration (mg L−1) | Recovery (%) | n | Concentration (mg L−1) | Recovery (%) | n | Concentration (mg L−1) | Recovery (%) | n | |
| a VHG Labs, Manchester, NH, USA. b NIST, Gaithersburg, ND, USA. c Agilent Technologies, Wilmington, DE, USA. | ||||||||||||
| Al | 4.53 | 91 ± 8 | 6 | 0.38 | 93 ± 3 | 3 | 0.40 | 110 ± 6 | 6 | 1.10 | 103 ± 3 | 6 |
| Cd | 0.27 | 110 ± 2 | 6 | 0.34 | 94 ± 2 | 6 | 0.99 | 93 ± 2 | 6 | |||
| Co | 0.97 | 98 ± 3 | 6 | |||||||||
| Cr | 1.01 | 102 ± 3 | 6 | 0.25 | 67 ± 1 | 6 | 0.84 | 79 ± 2 | 6 | |||
| Cu | 1.12 | 113 ± 3 | 6 | 0.16 | 107 ± 4 | 3 | 0.34 | 93 ± 2 | 6 | 1.00 | 94 ± 3 | 6 |
| Fe | 0.96 | 97 ± 5 | 6 | 0.41 | 95.3 ± 0.8 | 3 | 0.32 | 88 ± 2 | 6 | 0.90 | 85 ± 3 | 6 |
| Ni | 1.17 | 118 ± 4 | 6 | 0.37 | 102 ± 2 | 6 | 1.13 | 106 ± 3 | 6 | |||
| Pb | 1.08 | 109 ± 4 | 6 | 0.32 | 89 ± 4 | 6 | 1.04 | 97 ± 5 | 6 | |||
Overall the results obtained using automated SDA for real samples were accurate, with average recoveries largely falling between 90 and 110%. The lone exception is Cr in the hydrocarbon oil samples, which provided recoveries significantly below 90%. However, the results for the EC method applied to the same sample were worse than those obtained by SDA, which suggests not a problem with the SDA method in the determination of Cr, but more likely a problem during the sample preparation.
The results obtained for Al in the water pollution standard and oil standards used a secondary emission line at 167.019 nm. This was necessary due to an interfering emission that was observed in the sample causing a falsely high recovery value.
Conclusions
Standard dilution analysis has proven to be a robust, simple to perform, accurate, and precise calibration method as it has been developed over the past several years. Combining two traditional calibration methods, SDA offers corrections for sample matrix effects using standard additions while also offering corrections for changes in the excitation source and sampling process through the use of an internal standard. SDA provides results that are superior (or at worst comparable) to simple external standard calibration and internal standardization methods, while providing slightly improved results when compared to traditional standard additions alone.8,13Experiments presented here were aimed at improving the automation of the SDA process, allowing for successive samples to be analyzed quickly by simply using an automatic sampler to switch from sample to sample, as is the case in most routine analytical methods. The automation of the dilution of the standard plus blank mixture was achieved through the use of a two-channel pinch valve, with the dilution occurring by diffusion as the solution is pulled from the valve to the plasma by a second channel in the instrument's peristaltic pump. The proposed automated SDA method proved to be effective over various sample matrices, and also provided promising results when analyzing real-world samples.
Conflicts of interest
The authors declare that there are no conflicts of interest associated with this manuscript.Acknowledgements
The authors would like to thank the Graduate School of Arts and Sciences and Department of Chemistry at Wake Forest University for supporting this study.References
- L. Cuadros-Rodríguez, L. Gámiz-Gracia, E. M. Almansa-López and J. M. Bosque-Sendra, Calibration in chemical measurement processes: II. A methodological approach, Trends Anal. Chem., 2001, 20, 620–636 CrossRef.
- M. Bader, A systematic approach to standard addition methods in instrumental analysis, J. Chem. Educ., 1980, 57, 703–706 CrossRef CAS.
- D. Harvey, External standards of standard addition? Selecting and validating a method of standardization, J. Chem. Educ., 2002, 79, 613–615 CrossRef CAS.
- W. B. Barnett, V. A. Fassel and R. N. Kniseley, Theoretical principles of internal standardization in analytical emission spectroscopy, Spectrochim. Acta, Part B, 1968, 23, 643–664 CrossRef CAS.
- M. Thompson and M. H. Ramsey, Extrapolation to infinite dilution: a method for overcoming matrix effects, J. Anal. At. Spectrom., 1990, 5(8), 701–704 RSC.
- A. Virgilio, D. A. Gonçalves, T. McSweeney, J. A. Gomes Neto, J. A. Nóbrega and G. L. Donati, Multi-energy calibration applied to atomic spectrometry, Anal. Chim. Acta, 2017, 982, 31–36 CrossRef CAS PubMed.
- C. B. Williams, B. T. Jones and G. L. Donati, Multi-flow calibration applied to microwave-induced plasma optical emission spectrometry, J. Anal. At. Spectrom., 2019, 34(6), 1191–1197 RSC.
- W. B. Jones, G. L. Donati, C. P. Calloway and B. T. Jones, Standard dilution analysis, Anal. Chem., 2015, 87, 2321–2327 CrossRef CAS PubMed.
- F. M. Fortunato, M. A. Bechlin, J. A. Gomes Neto, A. Virgilio, G. L. Donati and B. T. Jones, Standard dilution analysis in flow system: sodium determination by flame atomic emission spectrometry, Microchem. J., 2016, 124, 662–667 CrossRef CAS.
- F. M. Fortunato, M. A. Bechlin, J. A. Gomes Neto, G. L. Donati and B. T. Jones, Internal standard addition calibration: determination of calcium and magnesium by atomic absorption spectrometry, Microchem. J., 2015, 122, 63–69 CrossRef CAS.
- D. A. Goncalves, T. McSweeney, M. C. Santos, B. T. Jones and G. L. Donati, Standard dilution analysis of beverages by microwave-induced plasma optical emission spectrometry, Anal. Chim. Acta, 2016, 909, 24–29 CrossRef CAS PubMed.
- A. G. Althoff, C. B. Williams, T. McSweeney, D. A. Goncalves and G. L. Donati, Microwave-induced plasma optical emission spectrometry (MIP OES) and standard dilution analysis to determine trace elements in pharmaceutical samples, Appl. Spectrosc., 2017, 71(12), 2692–2698 CrossRef CAS PubMed.
- J. T. Sloop, H. J. B. Bonilla, T. Harville, B. T. Jones and G. L. Donati, Automated matrix-matching calibration using standard dilution analysis with two internal standards and a simple three-port mixing chamber, Talanta, 2019, 205, 120160 CrossRef CAS PubMed.
- A. Virgilio, D. Schiavo, J. A. Nobrega and G. L. Donati, Evaluation of standard dilution analysis (SDA) of beverages and foodstuffs by ICP OES, J. Anal. At. Spectrom., 2016, 31(6), 1216–1222 RSC.
- M. García, M. A. Aguirre Pastor and A. Canals, New multinebulizer for spectrochemical analysis: wear metals determinatino in used lubricating oils by on-line standard dilution analysis (SDA) using inductively coupled plasma optical emission spectrometry (ICP OES), J. Anal. At. Spectrom., 2019 10.1039/c9ja00255c.
- A. Virgilio, D. Schiavo, L. M. Costa, J. A. Nobrega, B. T. Jones and G. L. Donati, Inductively coupled plasma mass spectrometry and standard dilution analysis applied to concentrated acids, Talanta, 2016, 161, 826–829 CrossRef CAS PubMed.
- F. M. Fortunato, A. L. Vieira, J. A. Gomes Neto, G. L. Donati and B. T. Jones, Expanding the potentialities of standard dilution analysis: determination of ethanol in gasoline by Raman spectroscopy, Microchem. J., 2017, 133, 76–80 CrossRef CAS.
- G. L. Donati and R. S. Amais, Fundamentals and new approaches to calibration in atomic spectrometry, J. Anal. At. Spectrom., 2019, 34, 2353–2369 RSC.
- J. A. Carter, A. I. Barros, J. A. Nobrega and G. L. Donati, Traditional calibration methods in atomic spectrometry and new calibration strategies for inductively coupled plasma mass spectrometry, Front. Chem., 2018, 6, 504 CrossRef CAS PubMed.
- M. Schappert, D. Montoya, S. Aragon, M. Rearick, N. Xu and K. J. Mathew, Combining accuracy and precision of traceable standards to estimate uncertainties in trace element content measurements, J. Radioanal. Nucl. Chem., 2018, 318, 323–330 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |