Open Access Article
Open Access ArticleGraphene–Si CMOS oscillators†
Carlo
Gilardi
a,
Paolo
Pedrinazzi
 a,
Kishan Ashokbhai
Patel
a,
Luca
Anzi
a,
Kishan Ashokbhai
Patel
a,
Luca
Anzi
 a,
Birong
Luo
b,
Timothy J.
Booth
a,
Birong
Luo
b,
Timothy J.
Booth
 b,
Peter
Bøggild
b,
Peter
Bøggild
 b and
Roman
Sordan
b and
Roman
Sordan
 *a
*a
aL-NESS, Department of Physics, Politecnico di Milano, Via Anzani 42, 22100 Como, Italy. E-mail: Roman.Sordan@polimi.it; Tel: +39 031 332 7622
bCNG, DTU Nanotech, Department of Micro- and Nanotechnology, Technical University of Denmark, Ørsted Plads, Building 345C, 2800 Lyngby, Denmark
First published on 11th February 2019
Abstract
Graphene field-effect transistors (GFETs) offer a possibility of exploiting unique physical properties of graphene in realizing novel electronic circuits. However, graphene circuits often lack the voltage swing and switchability of Si complementary metal–oxide-semiconductor (CMOS) circuits, which are the main building block of modern electronics. Here we introduce graphene in Si CMOS circuits to exploit favorable electronic properties of both technologies and realize a new class of simple oscillators using only a GFET, Si CMOS D latch, and timing RC circuit. The operation of the two types of realized oscillators is based on the ambipolarity of graphene, i.e., the symmetry of the transfer curve of GFETs around the Dirac point. The ambipolarity of graphene also allowed to turn the oscillators into pulse-width modulators (with a duty cycle ratio ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) and voltage-controlled oscillators (with a frequency ratio ∼1
4) and voltage-controlled oscillators (with a frequency ratio ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) without any circuit modifications. The oscillation frequency was in the range from 4 kHz to 4 MHz and limited only by the external circuit connections, rather than components themselves. The demonstrated graphene–Si CMOS hybrid circuits pave the way to the more widespread adoption of graphene in electronics.
8) without any circuit modifications. The oscillation frequency was in the range from 4 kHz to 4 MHz and limited only by the external circuit connections, rather than components themselves. The demonstrated graphene–Si CMOS hybrid circuits pave the way to the more widespread adoption of graphene in electronics.
1 Introduction
The development of graphene electronic circuits is mostly guided by the state-of-the-art circuit design of Si transistor technology. Such circuits try to exploit very large mobility1 and saturation velocity2 of charge carriers in graphene to match the performance of the corresponding Si circuits. However, this approach has not yielded satisfactory results so far because graphene does not have a bandgap3–5 and therefore graphene field-effect transistors (GFETs) exhibit insufficient drain current saturation6,7 and cannot be turned off. For instance, graphene ring oscillators8 can indeed match the speed of the Si CMOS ring oscillators but only at the expense of considerable static power dissipation, which is unacceptable in highly-integrated digital circuits.9 If graphene were to find applications in electronics, its unique properties, such as flexibility,10 transparency,11 and ambipolarity,3 should be exploited to achieve either novel functionality or the same functionality with fewer transistors, rather than to mimic Si circuits. One of the truly unique electronic properties of graphene not exhibited by conventional semiconductors is ambipolarity. The ambipolarity of graphene has been used in the past to realize very simple logic gates12 and frequency multipliers.13 However, the logic gates suffered from large power dissipation and the mixers from large conversion loss, rendering both types of circuits unusable in realistic applications.Here we demonstrate a novel class of graphene–Si CMOS circuits that exploit the ambipolarity of graphene to simplify the circuit and provide additional functionality. To illustrate the concept, we experimentally demonstrate two types of simple oscillators comprising just a GFET, a Si CMOS D latch, and a timing RC circuit. The D latch provides switching and large voltage swing for controlling the GFET, while the RC circuit is used to set the oscillation frequency (fosc). The highest obtained oscillation frequency was fosc = 4.2 MHz, limited only by the connections between the used discrete components. The ambipolarity of graphene allows realization of pulse-width modulators (PWMs) and voltage-controlled oscillators (VCOs) from the same oscillators, i.e., without any circuit modifications. Oscillating signals with a duty cycle in the range from 20% to 80% and maximum-to-minimum frequency ratio of 7.7 were obtained in this way. The concept of exploiting favorable electronic properties of GFETs and Si CMOS is general and can be realized with any ambipolar material, although graphene is preferable for high-speed operation.
2 Results
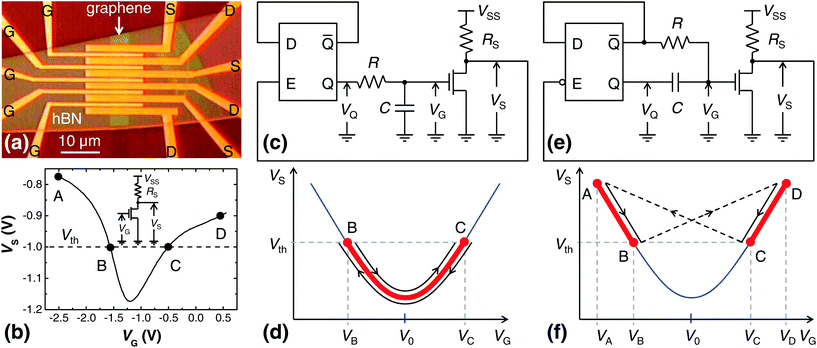
Top-gated GFETs were fabricated from graphene grown by chemical vapor deposition14,15 (CVD) and then transferred to SiO2/Si substrates on which hBN16 was previously exfoliated (Fig. 1(a)). The ambipolarity of graphene is reflected in the transfer curves of GFETs in which the same channel resistance (Rch) is obtained at two different gate voltages (VG). These gate voltages are symmetrically distributed around the Dirac point (VG = V0) at which Rch(VG) reaches the maximum Rch(V0), as illustrated in ESI Fig. S1.† When a GFET is connected to a power supply (VSS) via a series resistor (RS), as shown in Fig. 1(b), the output voltage of such a simple graphene circuit is VS = VSS/(1 + RS/Rch).12 Therefore, the output voltage VS has a maximum at the Dirac point for a positive supply (VSS > 0) and minimum for a negative supply (VSS < 0), as shown in Fig. S1.† Throughout this work, a negative supply was used (VSS = −2 V) because it allowed to obtain more symmetric digital signals, as discussed in the Experimental section. The measured static voltage transfer characteristic of such graphene circuit is shown in Fig. 1(b).To simplify the oscillator circuit, the supply VSS of the graphene circuit was also used for the latch, hence the Si CMOS logic threshold was Vth ≈ VSS/2 = −1 V. Therefore, VSS = −2 V defined the low logic level (Boolean 0), while ground (0 V) defined the high logic level (Boolean 1). The output voltage VS of the graphene circuit was used to gate the Si CMOS logic, in this case a D latch. To be able to efficiently control, i.e., change the state of the latch, the output voltage VS had to symmetrically swing around the threshold Vth, as shown in Fig. 1(b). This was adjusted with the series resistor RS, which had to be below Rch(V0) to ensure VS(V0) < Vth. Under these conditions, the graphene circuit was able to trigger the latch in two operating points, denoted by B and C in Fig. 1(b), in which VS = Vth.
Two types of oscillators were realized: parabolic (Fig. 1(c)) and bow tie (Fig. 1(e)), depending whether the Dirac point was a part of the oscillation cycle or not. In the first case, the operating point of the GFET oscillates between the points B and C moving through the Dirac point, as depicted in Fig. 1(d). In the case of the bow tie oscillator, the operating point oscillates outside of the operating range of the parabolic oscillator, i.e., between the points A and B and between the points D and C in Fig. 1(f). In both cases, the D latch was operated in the toggle mode, i.e., the latch changed its state whenever it was enabled, which was realized by connecting the complementary output (![[Q with combining macron]](https://www.rsc.org/images/entities/char_0051_0304.gif) ) of the latch to its data input (D). The latch in the parabolic oscillator was enabled for VS > Vth and in the bow tie for VS < Vth. The basic principle of operation of a D latch is briefly described in Fig. S2.†
) of the latch to its data input (D). The latch in the parabolic oscillator was enabled for VS > Vth and in the bow tie for VS < Vth. The basic principle of operation of a D latch is briefly described in Fig. S2.†
In the parabolic oscillator, shown in Fig. 1(c), the high level at the output of the latch (VQ = 0 V, i.e., Q = 1) charges the capacitor C through the resistor R, i.e., the gate voltage VG (equal to the capacitor voltage) increases. As VG increases, the output voltage VS of the GFET first decreases (for VB < VG < V0) and then increases (for V0 < VG < VC), as shown in Fig. 1(d). When VG reaches VC (the voltage in the operating point C), the output voltage of the graphene circuit reaches the threshold voltage Vth enabling the latch. This changes the state of the latch, i.e., the output switches to the low state (VQ = VSS = −2 V, i.e., Q = 0) and the capacitor starts discharging through the same resistor. As VG decreases, VS decreases below the threshold Vth disabling the latch. With the further decrease of VG, VS first decreases (for V0 < VG < VC) and then increases (for VB < VG < V0), finally reaching the threshold voltage Vth in the operating point B. This enables the latch again, which switches to the high state (Q = 1) and starts charging the capacitor. As VS decreases, the latch disables and the entire cycle repeats again. In this way, the present relaxation oscillator keeps oscillating between the operating points B and C.
In the bow tie oscillator, shown in Fig. 1(e), when the latch is in the low state (VQ = VSS = −2 V, i.e., Q = 0), the high state at the complementary output (![[Q with combining macron]](https://www.rsc.org/images/entities/char_0051_0304.gif) = 1) charges the capacitor C through the resistor R, and the gate voltage increases to VB, as shown in Fig. 1(f). As VG increases, the output voltage VS of the graphene circuit decreases and when it reaches the threshold Vth in the operating point B, the latch is enabled and switches to the high state (VQ = 0 V, i.e., Q = 1). The sudden increase of VQ by |VSS| is transferred to the gate voltage VG because the capacitor voltage is a continuous function of time. As a consequence, the oscillator switches to the operating point D in which VD = VB + |VSS|. This disables the latch and the low state at the complementary output (
= 1) charges the capacitor C through the resistor R, and the gate voltage increases to VB, as shown in Fig. 1(f). As VG increases, the output voltage VS of the graphene circuit decreases and when it reaches the threshold Vth in the operating point B, the latch is enabled and switches to the high state (VQ = 0 V, i.e., Q = 1). The sudden increase of VQ by |VSS| is transferred to the gate voltage VG because the capacitor voltage is a continuous function of time. As a consequence, the oscillator switches to the operating point D in which VD = VB + |VSS|. This disables the latch and the low state at the complementary output (![[Q with combining macron]](https://www.rsc.org/images/entities/char_0051_0304.gif) = 0) starts discharging the capacitor and therefore decreasing VG. Consequently, VS decreases from VD to VC, enabling the latch at the operating point C in which VS = Vth. The latch switches to the low state again, instantly decreasing VG by |VSS|. The oscillator therefore switches to the operating point A in which VA = VC − |VSS| initiating the same cycle again.
= 0) starts discharging the capacitor and therefore decreasing VG. Consequently, VS decreases from VD to VC, enabling the latch at the operating point C in which VS = Vth. The latch switches to the low state again, instantly decreasing VG by |VSS|. The oscillator therefore switches to the operating point A in which VA = VC − |VSS| initiating the same cycle again.
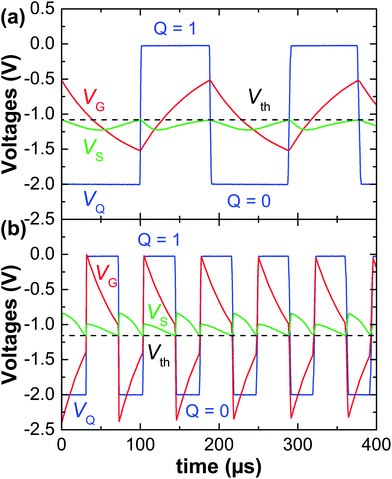
The measured signals in the oscillators are shown in Fig. 2, in which they were tuned to audio frequencies (fosc < 20 kHz) for clarity. The highest measured oscillation frequency was fosc = 4.2 MHz (Fig. S3†), limited by the off-chip connections between the graphene and Si CMOS chips. This limitation could be overcome by integrating both technologies in a single chip.17,18 The oscillation frequency was set by the timing RC circuit, i.e., by the charging and discharging times of the capacitor. In the parabolic oscillator, the durations of the high state (Q = 1) and low state (Q = 0) are t1 = RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(VB/VC) and t0 = RC
ln(VB/VC) and t0 = RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((VC − VSS)/(VB − VSS)), respectively, which can easily be obtained from the transient response of a simple RC circuit.19 In the bow tie oscillator, they are t1 = RC
ln((VC − VSS)/(VB − VSS)), respectively, which can easily be obtained from the transient response of a simple RC circuit.19 In the bow tie oscillator, they are t1 = RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((VB − 2VSS)/(VC − VSS)) and t0 = RC
ln((VB − 2VSS)/(VC − VSS)) and t0 = RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((VC + VSS)/VB). This gives for the oscillation frequency fosc = 1/T ∝ 1/(RC), where T = t1 + t0 is the period.
ln((VC + VSS)/VB). This gives for the oscillation frequency fosc = 1/T ∝ 1/(RC), where T = t1 + t0 is the period.
The gate voltage levels VB and VC, at which VS = Vth, mainly influence the duty cycle (D = t1/T) of the signals. The advantage of the oscillators is that the symmetric signals (D = 50%) are obtained for VSS = VB + VC, regardless of the asymmetry of the transfer curve of the GFET around the Dirac point (Fig. 1(b)). In this case, the output voltage VS of the GFET has the fundamental frequency of 2fosc, i.e., the oscillators are capable of generating the signals at frequencies fosc and 2fosc at the same time. The asymmetry of the transfer curve of the GFET only causes the asymmetry of VS in Fig. 2, which is observable due to the large signal operation of the circuit.
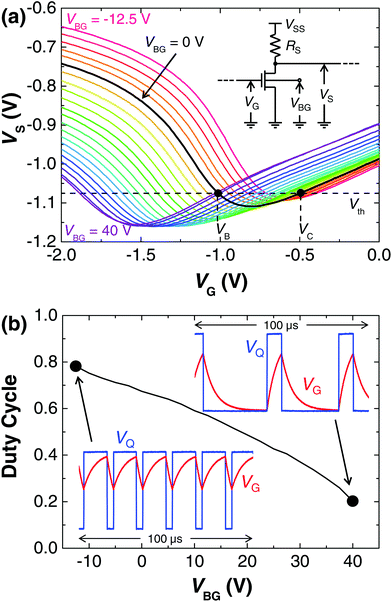
The gate voltage levels VB and VC and therefore the duty cycle D can be controlled by the GFET back-gate voltage, thus turning the oscillators into the PWMs without any circuit modifications. PWMs are typically used to digitally control the power supplies in electronic circuits.20Fig. 3(a) shows the static voltage transfer characteristic VS(VG) at different back-gate voltages (VBG). As the back-gate voltage is increased, a smaller top-gate voltage was required to reach the same carrier density in the channel, i.e., the transfer characteristic was shifted towards smaller voltages, as shown in Fig. 3(a). This decreased both VB and VC as VBG increased (Fig. S4†). In the parabolic oscillator, this increased t0 (Fig. S4†) and therefore decreased the duty cycle, as shown in Fig. 3(b). The measured duty cycle changed from 20% to 78% in one of the parabolic oscillators. In the bow tie oscillator, the duty cycle increased with VBG, as the capacitor was charged in the low state (Fig. S4†) rather than in the high state as with the parabolic oscillator.
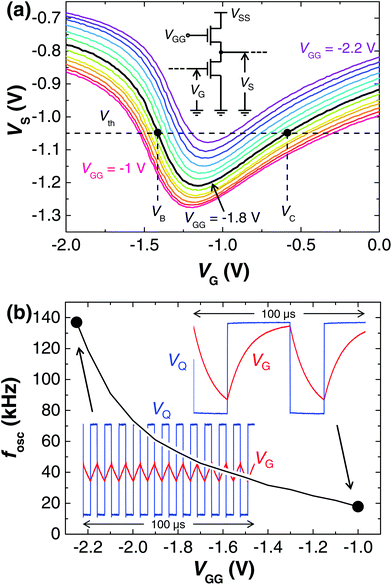
The graphene chip was fully integrated, i.e., the fixed load resistor RS was integrated with the GFET as the channel of another GFET with a floating gate (Fig. 1(a)). However, the channel resistance RS could also be changed by connecting this gate to a voltage source VGG, as shown in Fig. 4(a). The increase of VGG decreased RS and therefore shifted the static voltage transfer characteristic VS(VG) to smaller output voltages VS, as shown in the same figure. This decreased VB and increased VC (Fig. S5†) and therefore increased both t1 and t0 in the parabolic oscillators, decreasing their oscillation frequency fosc. In this way, the gate voltage VGG was used to control fosc realizing the functionality of a VCO, one of the most used electronic circuits in communications systems.21 By increasing VGG, the measured oscillation frequency decreased from 137 to 18 kHz in one of the parabolic oscillators, as shown in Fig. 4(b). In contrast, the increase of VGG decreased t1 and t0 (Fig. S5†) and therefore increased the oscillation frequency in the bow tie oscillators.
3 Discussion
For the same circuit components, the oscillation frequency of the bow tie oscillator is higher than that of the parabolic oscillator because the operating point of the bow tie oscillator stays only on one side of the Dirac point during each half period. Assuming a duty cycle of 50% in both oscillators, i.e., VSS = VB + VC, the bow tie oscillator oscillates at twice the frequency of the parabolic oscillator if VB = 0.742VSS and VC = 0.258VSS. The disadvantage of the bow tie oscillator is that its gate voltage can overshoot the supply voltage rails at the signal edges, e.g., |VG| > |VSS| at the falling edge of Q in Fig. 2(b). This could be dangerous for other components in the circuit, primarily the GFET which has the gate voltage breakdown of ∼2.9 V. In a bow tie PWM, the largest overshoots are at the two extremes of the duty cycle.The present oscillators can be fabricated on a large scale because they do not require exfoliated hBN or a global back gate. The exfoliated hBN was used only because of the large doping of the GFETs on SiO2 in the used batch. Similarly, the global backgate was used in PWMs only for demonstration; in realistic devices this can easily be replaced by a local back gate so that each PWM is individually gated. Control voltages in PWMs and VCOs are typically obtained from the output of other circuits rather than separate power supplies. For example, a VCO is driven by a phase detector in a phase-locked loop (PLL).21
The demonstrated principle of operation is general, i.e., the other ambipolar materials, e.g., amorphous Si,22 Si nanowires23 or semiconducting carbon nanotubes,24 could also be used. Although their ambipolarity has been exploited in applications25,26 similar to that of graphene,12 they have not been combined with Si CMOS logic so far. In contrast to other ambipolar materials, graphene has much larger carrier mobility1 and saturation velocity2 allowing much faster operation. The symmetric band structure of graphene27 (i.e., almost identical electron and hole mobilities) also leads to symmetric digital signals, which cannot easily be obtained in materials with different electron and hole mobilities.
In terms of the component count, the present oscillators are similar to the simplest Si field-effect transistor (FET) oscillators, because they were made of only 5 components. However, it should be noted that a gated D latch28 is usually made of 10 FETs, resulting in 14 components in the oscillator. The commercial discrete D latches usually comprise more than 10 FETs because they also provide three-state outputs (which were not used here). For comparison, the simplest conventional astable multivibrators with vertical signal edges19 have only 2 FETs, but also 10 other components, bringing the total component count to 12. The simplest Si CMOS ring oscillators29 have 6 FETs but their oscillation frequency is determined by internal gate delays8,9 rather than a timing RC circuit. Finally, the simplest Schmitt trigger inverter oscillators30 have 8 components. Despite similar component count, the present oscillators provide additional functionalities of the PWMs and VCOs. Compared to graphene ring oscillators,8,9 which have a limited output voltage swing, the output voltage swing in the present oscillators is determined by the Si CMOS part of the circuit providing rail-to-rail operation.
Although the oscillators use a GFET which cannot be turned off, the static power dissipation is not a critical factor because the relaxation oscillators do not spend any time in the idle state and dissipate the dynamic power continuously. This could also be understood from the ratio between the static power dissipation of the graphene circuit Ps ∼ VSS2/(2Rs) and dynamic (switching) power dissipation Pd ∼ foscCVSS2/2 of the timing RC circuit. Here it was assumed for simplicity that the voltage on the capacitor oscillates between 0.25VSS and 0.75VSS (as in Fig. 2(a)) and that the power dissipation of the D latch is negligible. The ratio Ps/Pd ∼ R/Rs, because fosc ∼ 1/(RC), meaning that for large fosc (i.e., R < Rs), Ps < Pd. For example, R/Rs ∼ 50 in the low-frequency oscillators shown in Fig. 2, but R/Rs ∼ 0.25 in the high-frequency oscillator shown in Fig. S3.†
The realized oscillators could be used to provide high-frequency reference required for the signal up/down conversion in high frequency transmitters/receivers. The D latch is not expected to limit the bandwidth of the fully integrated oscillators because high-speed Si CMOS technology is capable of operating at very high serial data rates (up to 120 Gb s−1).31
The realized oscillators could also be used to generate clock signals for digital data processing which requires the exact clock duty cycle of 50%. In microprocessors, this is typically achieved by running a VCO (inside the PLL) at twice the clock frequency and then dividing the frequency by two.32,33 However, such realizations significantly increase the dynamic power dissipation and are not practical at very high frequencies. Our oscillators offer an alternative solution because both PWM (duty cycle tuning) and VCO (frequency tuning) are integrated in the same circuit.
The integration of graphene with Si CMOS technology should be considered in the context of 3D monolithic integrated circuits (ICs). Such ICs cannot be easily made in Si CMOS technology due to high temperatures required for the fabrication of each Si CMOS layer in a 3D stack. This problem can be overcome by stacking other transistor technologies, which do not require high-temperature fabrication, on top of Si CMOS.34 Alternative transistor technologies also allow realization of additional functionalities which cannot be obtained with Si CMOS alone.34,35 Graphene is a good candidate for the integration with Si CMOS in 3D monolithic ICs because it can be transferred to a target substrate at room temperature.
4 Conclusions
We exploited the symmetry of the transfer characteristics of GFETs to realize a new class of very simple electronic relaxation oscillators comprising a GFET, Si CMOS latch, and RC timing circuit. The difference between the two types of the realized oscillators was in the movement of the operating point, oscillating through the Dirac point in the first type and jumping over the Dirac point in the second type. The simplicity of the oscillators and additional PWM and VCO functionalities, obtained without any circuit modifications, stemmed from the ambipolarity of graphene. The switching and large voltage swing of generated waveforms were provided by Si CMOS logic. The introduction of graphene in Si CMOS logic may prove to be a feasible approach in simplifying it and providing additional functionality while at the same time overcoming barriers to entry of graphene in electronics.5 Experimental
hBN was exfoliated on highly p-doped (>1019 cm−3) Si substrates with a 300 nm thick top layer of SiO2. The back of the Si substrates was metallized and used as a global back-gate, if needed. Monocrystalline monolayer graphene was grown by CVD on Cu from the CH4 precursor and then transferred (by a wet process) to the same substrates on which hBN was previously exfoliated. The GFETs were patterned by electron-beam (e-beam) lithography using poly(methyl methacrylate) resist. The GFET channels (the channel width W = 5 μm) were defined by etching graphene in O2 plasma both in parts of the substrates covered and uncovered by hBN flakes. This allowed fabrication of a large number of GFETs on hBN (the only selection criteria were the lateral size >5 μm and thickness <50 nm of the hBN flakes) and control GFETs on SiO2 in the same chips.The rest of the fabrication process was the same in both cases. Top-gates were patterned first by e-beam lithography followed by e-beam evaporation of 100 nm of Al. Al oxidized after a few days in air ambient creating a thin (∼4 nm) native layer of AlOx on all surfaces of Al, including the interface with graphene.36–40 This formed an AlOx/Al gate stack with a top-gate oxide capacitance8,40Cox = 1.37 μF cm−2. Source and drain Au contacts (100 nm) were finally fabricated by e-beam lithography and e-beam evaporation. The gate length was L = 1 μm, source-to-drain distance LSD = 1.2 μm (i.e., the access length from both sides of the gate was 100 nm), and length of the source and drain contacts was 2 μm.
The oscillators worked both with a positive and negative power supply. However, we found that a negative supply allowed more symmetric digital signals at |VSS| ∼ 2 V, i.e., the signals with a duty cycle closer to 50%. This is because the unbiased GFETs on hBN had the Dirac voltage V0 ≈ −0.5 V, which changed to ≈V0 + VSS/4 when VSS was applied (because Rch ≈ RS at the Dirac point). The signal symmetry requires VH − VC = VB − VL, i.e., that the Dirac voltage is approximately half way between the voltage rails. This means V0 + VSS/4 ≈ VSS/2, i.e., VSS ≈ 4V0, which is the reason the supply VSS = −2 V was used. The series resistance RS was realized as either an external discrete resistor or another GFET with a floating gate. The output voltage swing of the graphene circuit depends on RS, e.g., the highest swing in the parabolic oscillator is obtained for 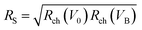 .
.
The GFETs were made on hBN substrate because the lower |V0| allowed the use of lower supply voltages |VSS|, as described above. We also found that GFETs on hBN had much better long-term stability than GFETs on SiO2. The same GFETs on hBN were repeatedly measured in the oscillators for months without any apparent degradation of their electrical properties.
The Si CMOS part of the oscillator circuit (including the timing RC circuit) was built on a breadboard (in low-frequency oscillators) or printed circuit board (in high-frequency oscillators) and connected to the GFET via a FormFactor probe station. The Si CMOS gated D latch was 74HC375AP or 74AC573P. The dc characteristics were measured by Keithley 2611A source measure units, while the waveforms were measured by Keysight Infiniium DSO9404A oscilloscope and Keysight N2795A and 1158A active probes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the EU H2020 Graphene Flagship Core 2 Grant No. 785219.References
- A. S. Mayorov, R. V. Gorbachev, S. V. Morozov, L. Britnell, R. Jalil, L. A. Ponomarenko, P. Blake, K. S. Novoselov, K. Watanabe, T. Taniguchi and A. K. Geim, Nano Lett., 2011, 11, 2396–2399 CrossRef CAS PubMed.
- V. E. Dorgan, M.-H. Bae and E. Pop, Appl. Phys. Lett., 2010, 97, 082112 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805 CrossRef PubMed.
- B. N. Szafranek, G. Fiori, D. Schall, D. Neumaier and H. Kurz, Nano Lett., 2012, 12, 1324–1328 CrossRef CAS PubMed.
- E. Guerriero, P. Pedrinazzi, A. Mansouri, O. Habibpour, M. Winters, N. Rorsman, A. Behnam, E. A. Carrion, A. Pesquera, A. Centeno, A. Zurutuza, E. Pop, H. Zirath and R. Sordan, Sci. Rep., 2017, 7, 2419 CrossRef PubMed.
- E. Guerriero, L. Polloni, M. Bianchi, A. Behnam, E. Carrion, L. G. Rizzi, E. Pop and R. Sordan, ACS Nano, 2013, 7, 5588–5594 CrossRef CAS.
- M. Bianchi, E. Guerriero, M. Fiocco, R. Alberti, L. Polloni, A. Behnam, E. A. Carrion, E. Pop and R. Sordan, Nanoscale, 2015, 7, 8076–8083 RSC.
- T. Carey, S. Cacovich, G. Divitini, J. Ren, A. Mansouri, J. M. Kim, C. Wang, C. Ducati, R. Sordan and F. Torrisi, Nat. Commun., 2017, 8, 1202 CrossRef PubMed.
- P. Blake, E. W. Hill, A. H. Castro Neto, K. S. Novoselov, D. Jiang, R. Yang, T. J. Booth and A. K. Geim, Appl. Phys. Lett., 2007, 91, 063124 CrossRef.
- R. Sordan, F. Traversi and V. Russo, Appl. Phys. Lett., 2009, 94, 073305 CrossRef.
- H. Wang, D. Nezich, J. Kong and T. Palacios, IEEE Electron Device Lett., 2009, 30, 547–549 CAS.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314 CrossRef CAS PubMed.
- J. D. Wood, S. W. Schmucker, A. S. Lyons, E. Pop and J. W. Lyding, Nano Lett., 2011, 11, 4547–4554 CrossRef CAS.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed.
- M. C. Lemme, T. J. Echtermeyer, M. Baus and H. Kurz, IEEE Electron Device Lett., 2007, 28, 282–284 CAS.
- S. K. Hong, C. S. Kim, W. S. Hwang and B. J. Cho, ACS Nano, 2016, 10, 7142–7146 CrossRef CAS PubMed.
- J. Millman and H. Taub, Pulse, Digital, and Switching Waveforms, McGraw-Hill, Kogakusha, 1965 Search PubMed.
- D. G. Holmes and T. A. Lipo, Pulse Width Modulation for Power Converters: Principles and Practice, Wiley-IEEE Press, Hoboken, 2003 Search PubMed.
- S. Voinigescu, High-Frequency Integrated Circuits, Cambridge University Press, Cambridge, 2013 Search PubMed.
- H. Pfleiderer and W. Kusian, Solid-State Electron., 1986, 29, 317–319 CrossRef CAS.
- S.-M. Koo, M. D. Edelstein, Q. Li, C. A. Richter and E. M. Vogel, Nanotechnology, 2005, 16, 1482 CrossRef CAS.
- R. Martel, V. Derycke, C. Lavoie, J. Appenzeller, K. K. Chan, J. Tersoff and P. Avouris, Phys. Rev. Lett., 2001, 87, 256805 CrossRef CAS PubMed.
- R. Sordan, K. Balasubramanian, M. Burghard and K. Kern, Appl. Phys. Lett., 2006, 88, 053119 CrossRef.
- D. Sacchetto, Y. Leblebici and G. D. Micheli, IEEE Electron Device Lett., 2012, 33, 143–145 CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- R. C. Jaeger and T. N. Blalock, Microelectronic Circuit Design, McGraw-Hill, New York, 2011 Search PubMed.
- B. Razavi, Design of Analog CMOS Integrated Circuits, McGraw-Hill, Boston, 2001 Search PubMed.
- R. J. Baker, CMOS Circuit Design, Layout, and Simulation, Wiley-IEEE Press, Hoboken, 2010 Search PubMed.
- K. K. Tokgoz, S. Maki, J. Pang, N. Nagashima, I. Abdo, S. Kawai, T. Fujimura, Y. Kawano, T. Suzuki, T. Iwai, K. Okada and A. Matsuzawa, 2018 IEEE Int. Solid - State Circuits Conf. - (ISSCC), 2018, pp. 168–170.
- I. A. Young, J. K. Greason and K. L. Wong, IEEE J. Solid-State Circuits, 1992, 27, 1599–1607 Search PubMed.
- S. Tam, S. Rusu, U. N. Desai, R. Kim, J. Zhang and I. Young, IEEE J. Solid-State Circuits, 2000, 35, 1545–1552 Search PubMed.
- M. M. Shulaker, G. Hills, R. S. Park, R. T. Howe, K. Saraswat, H. S. P. Wong and S. Mitra, Nature, 2017, 547, 74–78 CrossRef CAS PubMed.
- T. Palacios, Nat. Nanotechnol., 2011, 6, 464–465 CrossRef CAS PubMed.
- H. Miyazaki, S. Li, A. Kanda and K. Tsukagoshi, Semicond. Sci. Technol., 2010, 25, 034008 CrossRef.
- E. Guerriero, L. Polloni, L. G. Rizzi, M. Bianchi, G. Mondello and R. Sordan, Small, 2012, 8, 357–361 CrossRef CAS.
- C.-C. Lu, Y.-C. Lin, C.-H. Yeh, J.-C. Huang and P.-W. Chiu, ACS Nano, 2012, 6, 4469–4474 CrossRef CAS PubMed.
- C.-H. Yeh, Y.-W. Lain, Y.-C. Chiu, C.-H. Liao, D. R. Moyano, S. S. H. Hsu and P.-W. Chiu, ACS Nano, 2014, 8, 7663–7670 CrossRef CAS PubMed.
- C. D. English, K. K. Smithe, R. Xu and E. Pop, Int. El. Devices Meet., San Francisco, CA, USA, 2016, pp. 5.6.1–5.6.4.
Footnote |
| † Electronic supplementary information (ESI) available: Discussions on the shape of the static voltage transfer characteristic of the graphene circuit used in the oscillators, the highest frequency waveforms measured in a parabolic oscillator, and calculated PWM and VCO characteristics of the oscillators. See DOI: 10.1039/C8NR07862A |
| This journal is © The Royal Society of Chemistry 2019 |