 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anharmonic excited state frequencies of para-difluorobenzene, toluene and catechol using analytic RI-CC2 second derivatives†
David P.
Tew
 *a,
Christof
Hättig
*a,
Christof
Hättig
 b and
Nora K.
Graf
b
b and
Nora K.
Graf
b
aMax Planck Institute for Solid State Research, 70569 Stuttgart, Germany. E-mail: d.tew@fkf.mpg.de
bQuantum Chemistry Group, Ruhr-Universität Bochum, 44780 Bochum, Germany. E-mail: christof.haettig@rub.de
First published on 7th January 2019
Abstract
Analytic second nuclear derivatives for excited electronic state energies have been implemented for the resolution-of-the-identity accelerated CC2, CIS(D∞) and ADC(2) models. Our efficient implementation with ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) memory demands enables the treatment of medium sized molecules with large basis sets and high numerical precision and thereby paves the way for semi-numerical evaluation of the higher-order derivatives required for anharmonic corrections to excited state vibrational frequencies. We compare CC2 harmonic and anharmonic excited state frequencies with experimental values for para-difluorobenzene, toluene and catechol. Basis set problems occur for out-of-plane bending vibrations due to intramolecular basis set superposition error. For non-planar molecules and in plane modes of planar molecules, the agreement between theory and experiment is better than 30 cm−1 on average and we reassign a number of experimental bands on the basis of the ab initio predictions.
2) memory demands enables the treatment of medium sized molecules with large basis sets and high numerical precision and thereby paves the way for semi-numerical evaluation of the higher-order derivatives required for anharmonic corrections to excited state vibrational frequencies. We compare CC2 harmonic and anharmonic excited state frequencies with experimental values for para-difluorobenzene, toluene and catechol. Basis set problems occur for out-of-plane bending vibrations due to intramolecular basis set superposition error. For non-planar molecules and in plane modes of planar molecules, the agreement between theory and experiment is better than 30 cm−1 on average and we reassign a number of experimental bands on the basis of the ab initio predictions.
1 Introduction
The characterisation of molecules in excited electronic states remains a challenge, both for experimental and theoretical chemistry. Electronic excitation is often accompanied by significant structural change and complex intramolecular vibrational energy redistribution processes,1–3 resulting in rich spectra that are sometimes difficult to interpret. Better theoretical treatments of electronic excited states are key to understanding photochemical phenomena and ultimately to harnessing photochemistry as a route to controlling molecular bond fission processes.4–7Coupled cluster methods are among the most accurate ab initio electronic structure methods.8 Coupled cluster methods for excited state properties have been developed extensively by Stanton and Gauss in the framework of equation of motion coupled cluster (EOM-CC) theory.9–11 Benchmark studies,12–15 found that EOM-CCSD ground and excited state harmonic frequencies agree with values derived from experiment with a root mean squared deviation (RMSD) of 20–30 cm−1.
CC2 was designed16 as approximation to CCSD with an ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 5) scaling of the computational costs with system size
5) scaling of the computational costs with system size ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) instead of
instead of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 6). CC2 conserves the order in the fluctuation potential through which single excitation dominated transitions are described correctly in CCSD theory. In the original implementations with exact four-index electron repulsion integrals the high prefactor of the computational costs and the high memory demands for transforming and storing the two-electron integrals severely limited system and basis set sizes for which calculations could be performed on commonly available computer hardware. This bottleneck is removed by combining CC2 with the resolution of the identity (RI) approximation for the two electron integrals.17,18 The RI approximation accelerates the calculations by one to two orders of magnitude, depending on the basis set, reduces memory demands to
6). CC2 conserves the order in the fluctuation potential through which single excitation dominated transitions are described correctly in CCSD theory. In the original implementations with exact four-index electron repulsion integrals the high prefactor of the computational costs and the high memory demands for transforming and storing the two-electron integrals severely limited system and basis set sizes for which calculations could be performed on commonly available computer hardware. This bottleneck is removed by combining CC2 with the resolution of the identity (RI) approximation for the two electron integrals.17,18 The RI approximation accelerates the calculations by one to two orders of magnitude, depending on the basis set, reduces memory demands to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) and reduces disc storage demands to
2) and reduces disc storage demands to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 3). These computational savings make it possible to study large molecules such as chlorophylls,19 which previously could only be studied with CIS or TDDFT.
3). These computational savings make it possible to study large molecules such as chlorophylls,19 which previously could only be studied with CIS or TDDFT.
The same technique can be used to accelerate other second-order methods for excited states, e.g. configuration interaction singles with a perturbative doubles correction,20 CIS(D), and its iterative variant21 CIS(D∞), and the algebraic diagrammatic construction through second-order,22 ADC(2), with similarly pivotal efficiency savings. Compared to the non-iterative perturbative CIS(D) approximation, the iterative methods CIS(D∞), ADC(2), and CC2 have the advantage that they provide a consistent description of excited state potential energy surfaces (PES), even in the region of avoided crossings, and can thus be used more straightforwardly for searching and characterizing stationary points on the excited state PES.
Implementations of analytic excited state gradients of these approximate second order methods have been reported in ref. 23 and 24, where it is demonstrated that memory demands for first derivatives scale at most as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) when using the RI approximation. Recently, second-order electronic response properties for ground and excited states and ground state nuclear Hessians as analytic second derivatives of the energy have been implemented.25–27 To preserve both the high computational efficiency and the low storage demands for second derivatives the RI approximation is combined with a numerical Laplace transformation of orbital energy denominators28 for the contribution of double excitation amplitudes to first derivatives of the density matrices.
2) when using the RI approximation. Recently, second-order electronic response properties for ground and excited states and ground state nuclear Hessians as analytic second derivatives of the energy have been implemented.25–27 To preserve both the high computational efficiency and the low storage demands for second derivatives the RI approximation is combined with a numerical Laplace transformation of orbital energy denominators28 for the contribution of double excitation amplitudes to first derivatives of the density matrices.
In the current work, we extend the theory and implementation to analytic geometrical second derivatives for CC2, CIS(D∞) and ADC(2) excited state energies. Analytic second derivatives are particularly important for obtaining the high numerical accuracy required to calculate semi-numerical third and fourth derivatives for polyatomic molecules. Only recently has a similar route has been pursued for TDDFT.29,30 With the implementation of analytic Hessians for CC2 and ADC(2) it becomes possible to compute anharmonic vibrational spectra of polyatomic molecules with a correlated ab initio wavefunction method. We demonstrate the applicability of our implementation by computing harmonic and anharmonic excited state frequencies for medium sized molecules, which we compare to experimentally observed band centres.
2 Theory
2.1 Excited state Hessian for RI-CC2
The theory and implementation of orbital-relaxed electric second-order response properties for excited states at the RI-CC2 level has been presented in ref. 26. In the current work we focus on the additional theory required for geometric second derivatives. We use identical notation to that of ref. 26 and 27 and, rather than repeat them here, refer the reader to that work for the full definition of all of the terms and intermediates.In coupled cluster theory, properties of an excited state f can be obtained as derivatives of the excited state quasienergy Lagrangian26
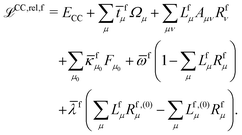 | (1) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) fμ, and the excitation energies
fμ, and the excitation energies 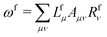 . The fourth term is the orbital-rotation constraint, which imposes vanishing Fock matrix elements Fpq for the relevant orbital pairs pq ∈ μ0. The last and second last terms determine the phase and normalisation of the left and right eigenvectors of the Jacobi matrix A, by coupling them to the eigenvectors Lf,(0) and Rf,(0) of the unperturbed limit.26
. The fourth term is the orbital-rotation constraint, which imposes vanishing Fock matrix elements Fpq for the relevant orbital pairs pq ∈ μ0. The last and second last terms determine the phase and normalisation of the left and right eigenvectors of the Jacobi matrix A, by coupling them to the eigenvectors Lf,(0) and Rf,(0) of the unperturbed limit.26
The hessian of the excited state is obtained by differentiating the Lagrangian twice with respect to the nuclear positions. The result can be obtained in the same way as for excited state polarisabilities, presented in ref. 26:
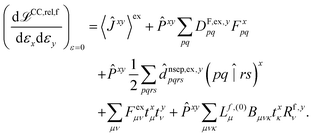 | (2) |
The only difference to polarizabilities are that for derivatives with respect to nuclear coordinates the AO basis and consequently all AO one- and two-electron integrals depend on the perturbation. This also gives rise to additional contributions to the derivatives of the MO coefficients related to the changes in the AO overlap. We write the first derivative of the molecular orbital (MO) coefficients with respect to nuclear displacements as
| Cx = C0Ux | (3) |
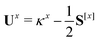 | (4) |
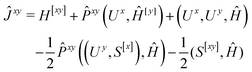 | (5) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) memory demands will be described below.
2) memory demands will be described below.
The last two terms in eqn (2) depend only indirectly on the derivatives of the one- and two-electron integrals, through the derivatives of the cluster amplitudes, txμ, and right eigenvectors, Rf,yν. These are evaluated as described in ref. 26 for electronic derivatives, with the difference that now the first derivatives of the AO two-electron integrals have to be included in the calculation of the amplitude and eigenvector derivatives. Detailed expressions for the derivatives of the cluster amplitudes are given in ref. 27 and the changes to the expressions for the derivatives of the eigenvectors are obtained in an analogous way.
The second and third terms in eqn (2) combine (via the densities) first derivatives of the amplitudes tyν and eigenvectors Rf,yν for a coordinate y with first derivatives of the MO Fock matrix Fxpq and two-electron integrals (pq![[| with combining circumflex]](https://www.rsc.org/images/entities/char_007c_0302.gif) rs)x for a coordinate x. Here, as for all two-electron integrals in the correlation treatment, we employ the RI approximation
rs)x for a coordinate x. Here, as for all two-electron integrals in the correlation treatment, we employ the RI approximation
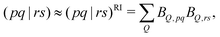 | (6) |
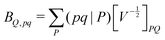 composed of two-index VPQ = (P|Q) and three-index (pq|P) electron repulsion integrals. The indices P and Q denote functions from an auxiliary basis set. For an efficient evaluation we rewrite the two-particle term as:
composed of two-index VPQ = (P|Q) and three-index (pq|P) electron repulsion integrals. The indices P and Q denote functions from an auxiliary basis set. For an efficient evaluation we rewrite the two-particle term as: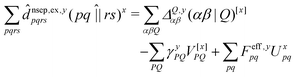 | (7) |
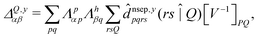 | (8) |
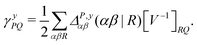 | (9) |
![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) nsep,ypqrs. Full working expressions for the effective Fock matrix and for the two- and three-index densities are provided in the ESI.†
nsep,ypqrs. Full working expressions for the effective Fock matrix and for the two- and three-index densities are provided in the ESI.†
The one-electron densities DF,ex,y require contractions of the doubles parts of the left eigenvectors and the derivatives of the right eigenvectors of the form 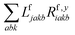 and
and 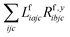 . For undifferentiated eigenvectors and amplitudes the RI approximation is sufficient to implement these contractions efficiently with only
. For undifferentiated eigenvectors and amplitudes the RI approximation is sufficient to implement these contractions efficiently with only ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) memory demands and without storing doubles vectors as four-index quantities on disc. For differentiated eigenvectors, however, this is not the case. There are additional terms that are not simply dressed two-electron integrals, but come from contractions of the undifferentiated eigenvectors with derivatives of the Fock matrix:
2) memory demands and without storing doubles vectors as four-index quantities on disc. For differentiated eigenvectors, however, this is not the case. There are additional terms that are not simply dressed two-electron integrals, but come from contractions of the undifferentiated eigenvectors with derivatives of the Fock matrix:
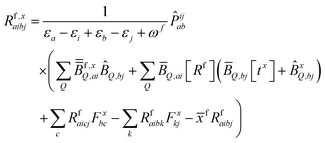 | (10) |
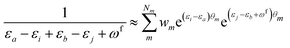 | (11) |
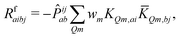 | (12) |
KQm,ai = ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) Q,aie(εi−εa)θm, Q,aie(εi−εa)θm, | (13) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) Qm,ai = Qm,ai = ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) Q,ai[Rf]e(εi−εa+ωf)θm, Q,ai[Rf]e(εi−εa+ωf)θm, | (14) |
We now turn to the evaluation of the expectation value Ĵxy of the second order Hamiltonian for an excited state. The contributions to Ĵxy are grouped into three terms. The first term contains the second derivatives of the AO integrals for the Hamiltonian. It is evaluated in the same manner in the AO basis as the respective contribution from H[x] to the gradient described in ref. 23:
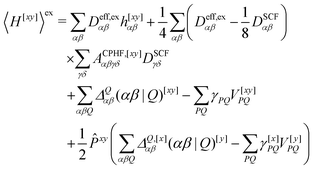 | (15) |
All other contributions to 〈Ĵxy〉ex are rewritten as contractions of effective Fock matrices with derivatives of the overlap matrices and Ux. This is done to avoid the evaluations of two-electron integrals in the MO basis and with this any ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 5) scaling steps that depend on two perturbations.
5) scaling steps that depend on two perturbations.
The second and third contribution to Ĵxy are combined by introducing a modified first-order Hamiltonian,27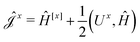 , to:
, to:
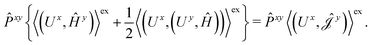 | (16) |
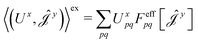 | (17) |
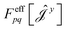 have been given in ref. 26 and 27. The last two contributions to Ĵxy are combined by introducing the second derivative of the overlap matrix Sxy = S[xy] +
have been given in ref. 26 and 27. The last two contributions to Ĵxy are combined by introducing the second derivative of the overlap matrix Sxy = S[xy] + ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) xy(Uy,S[x]) to
xy(Uy,S[x]) to(S[xy],Ĥ) + ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) xy((Uy,S[x]),Ĥ) = (Sxy,Ĥ) xy((Uy,S[x]),Ĥ) = (Sxy,Ĥ) | (18) |
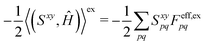 | (19) |
The above formulas have been implemented in the development version of the ricc2 program of the TURBOMOLE package.33 All contributions are evaluated using integral-direct algorithms in the AO basis with ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2) memory demands and strictly avoiding any operations that scale as
2) memory demands and strictly avoiding any operations that scale as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 5) with the basis set size and at the same time quadratically with the number of perturbations, so that the computation of the full Hessian still scales only as
5) with the basis set size and at the same time quadratically with the number of perturbations, so that the computation of the full Hessian still scales only as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 6) with the system size. The time-determining steps are the solution of the linear equations for the first derivatives of the amplitudes and eigenvectors and the calculation of the first-order density matrices that have to be done for each perturbation.
6) with the system size. The time-determining steps are the solution of the linear equations for the first derivatives of the amplitudes and eigenvectors and the calculation of the first-order density matrices that have to be done for each perturbation.
The implementation of the excited state hessians and the excited state polarizabilities enables also the calculation of the derivatives of the (excited state) dipole moment as mixed derivatives by differentiating once with respect to the strength of an electric field and once with respect to the nuclear coordinates.
2.2 CIS(D∞) and ADC(2)
With only few modifications the implementation is easily adapted to CIS(D∞) and ADC(2).21,22 In both methods the coupled cluster ground state amplitudes are replaced by the amplitudes from first-order Møller–Plesset perturbation theory (MPPT). We assume that the Brillouin condition is fulfilled and thus the singles ground state amplitudes t(0) and their derivatives tx vanish in first order MPPT, as do the singles Lagrange multipliers![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) f,(0). Discarding all contributions from these singles parameters turns the CC2 code into a CIS(D∞) code. As a side effect, the equations for the derivatives of the cluster amplitudes can be inverted directly, in the canonical implementation, bypassing the iterative solution procedure.
f,(0). Discarding all contributions from these singles parameters turns the CC2 code into a CIS(D∞) code. As a side effect, the equations for the derivatives of the cluster amplitudes can be inverted directly, in the canonical implementation, bypassing the iterative solution procedure.
The implementation for ADC(2) is closely related to the implementation CIS(D∞). Here the secular matrix is symmetrised:22,24
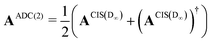 | (20) |
2.3 Thresholds and numerical accuracy
The numerical accuracy of the excited state Hessians, and also the computational costs, depend mainly on two thresholds: TLap and TLRE. TLap controls the numerical Laplace transformation such that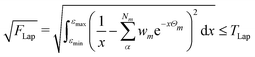 | (21) |
We investigated the dependence of the results on the thresholds for a test set composed of the lowest excited states of glyoxal, methanethial, propinal, benzene and naphthalene at their equilibrium structures, the lowest two excited states of water and formaldehyde at the ground and the excited state equilibrium structure, and the third excited state of formaldehyde and the lowest two excited states of thiophene again at their equilibrium structures. For all 16 cases we computed the Hessian for the cc-pVDZ and the aug-cc-pVDZ basis sets with different values for both thresholds, TLap and TLRE, and evaluated the deviations in the elements of the Hessian from a reference calculation with very tight thresholds. For the aug-cc-pVDZ result the mean absolute deviations of the Hessian elements follow roughly the relation
| ΔMADHess,CC2 ≤ 5TLap + 10TLRE | (22) |
In this work we used a tight threshold for the response equations TLRE = 10−10 and 11 grid points for the numerical Laplace integration, which corresponds to TLap between 2 × 10−5 and 2 × 10−10. These tight values were required because the third and fourth derivatives for VPT2 theory are obtained by numerical differentiation of the hessian. We kept the number of Laplace points the same for all hessians used in a finite difference formula to prevent any numerical noise from changes of the grid points.
2.4 Calculation of anharmonic corrections and frequencies
The analytical implementation of the hessians enables a semi-numerical evaluation of third and fourth derivatives of the energy, which are sufficiently accurate to be used as cubic and quartic force constants for the calculation of anharmonic frequencies. The third and fourth derivatives are calculated by central finite differences of hessians. Since only semi-diagonal quartic derivatives are required for VPT2 theory, the total number of hessians required is Nacc·(3N − 6) + 1, where Nacc is either two or four. Nacc = 4 is required when four- and five-point formulas are used for cubic and quartic derivatives to reduce the error to![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (δ4) in the displacement δ.34
(δ4) in the displacement δ.34
We did not use the normal coordinates ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) m of the equilibrium structure for the displacement vectors since they are normalized in the mass weighted coordinate system, which leads to unbalanced step sizes. Instead, we used rescaled coordinates
m of the equilibrium structure for the displacement vectors since they are normalized in the mass weighted coordinate system, which leads to unbalanced step sizes. Instead, we used rescaled coordinates
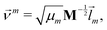 | (23) |
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) m denotes the mth eigenvector of the mass weighted hessian M−1/2FM−1/2 and M is the diagonal matrix of the atomic masses, and
m denotes the mth eigenvector of the mass weighted hessian M−1/2FM−1/2 and M is the diagonal matrix of the atomic masses, and 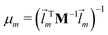 is the reduced mass of the normal mode m.
is the reduced mass of the normal mode m.
The anharmonic force constants are used for the calculation of anharmonic frequencies, by setting up the vibrational Hamiltonian as:35
| Hvib = H0vib + H1vib + H2vib | (24) |
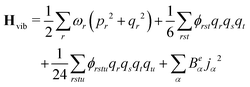 | (25) |
The anharmonic frequencies are calculated using second order vibrational perturbation theory (VPT2), as it is implemented in the program DYNAMOL.36 Therein, the VPT2 equations and treatment of resonance effects follow the formulation described in the paper of Amos et al.37
3 Results
We have used our new efficient CC2 excited state hessian implementation to construct harmonic and quartic force fields of toluene, para-difluorobenzene and catechol in their first excited electronic state, from which we obtain the band centres of vibrational transitions using VPT2. These medium sized molecules have been studied experimentally and we compare the computed and experimental wavenumbers, assessing the accuracy of the CC2 predictions and correcting assignments where appropriate. The nomenclature of the normal modes is adopted from the systematic studies of the Wright group for substituted benzenes,38–40 which provides a more unique assignment than the Mulliken41 or Wilson42 nomenclature. For modes localised on the substituents, the common spectroscopic notation for stretches (ν), bends (δ) and torsions (τ) is used. Outputs from all of our VPT2 calculations are provided in the ESI.† These contain a full list of fundamentals, overtones, combination bands, all Fermi and Darling–Dennyson resonances, and all effective Hamiltonians for the polyads used to treat these resonances variationally.3.1 para-Difluorobenzene
The molecule para-difluorobenzene has been the focus of a considerable number of spectroscopic explorations to determine its ground and excited state structure and dynamics43–48 including the intramolecular vibrational redistribution pathways in the excited state, which are mediated by rotational coupling and through Fermi resonance.49,50 Here we examine the fundamental vibrational transitions of para-difluorobenzene in its first excited state 11B2u using CC2 theory.Spectroscopic studies reveal that para-difluorobenzene exhibits D2h symmetry in both its ground and first excited state,45 and the CC2/cc-pVTZ optimised geometries indeed retain D2h symmetry. The optimised structures are listed in the ESI.† The computed 0–0 transition is 4.67 eV, which is close to the experimentally determined energy of 4.57 eV.46
Table 1 reports harmonic and anharmonic wavenumbers for the fundamental vibrational transitions of para-difluorobenzene in its first excited state, computed using CC2/cc-pVTZ and CC2/cc-pVQZ levels of theory using the optimised CC2/cc-pVTZ excited state geometry. The harmonic wavenumbers computed using the cc-pV5Z basis set are also listed. Using the normal mode vectors, each transition has been assigned using the Di labeling convention of ref. 39 for para-di-substituted benzenes. For ease of reference, the irreducible representation, Mulliken labeling and ground state experimental wavenumbers have also been included.
| p D i | Sym. | Exp. | Harm. | VPT2 | Exp. | ||||
|---|---|---|---|---|---|---|---|---|---|
| S0 | TZ | QZ | 5Z | TZ | QZ | S1 | S1 | ||
| 20 | 30(b3u) | 158 | 120 | 121 | 126 | 120 | 121 | 12047 | 120 |
| 14 | 8(au) | 422 | 148 | 147 | 161 | 169 | 168 | 17547 | 175 |
| 19 | 17(b2g) | 374 | 271 | 276 | 280 | 307 | 305 | 27447 | 274 |
| 30 | 22(b2u) | 348 | 352 | 353 | 352 | 349 | 350 | 35247 | 352 |
| 29 | 27(b3g) | 446 | 388 | 388 | 392 | 380 | 381 | 40347 | 403 |
| 13 | 9(b1g) | 800 | 404 | 406 | 411 | 453 | 476 | 58846 | * |
| 11 | 6(ag) | 450 | 411 | 412 | 423 | 407 | 408 | 41047 | 410 |
| 18 | 29(b3u) | 505 | 472 | 471 | 473 | 466 | 466 | 43847 | 438 |
| 12 | 7(au) | 945 | 486 | 490 | 503 | 612 | 676 | 58347 | * |
| 17 | 16(b2g) | 692 | 527 | 546 | 539 | 651 | 647 | 52847 | * |
| 28 | 26(b3g) | 635 | 558 | 558 | 558 | 541 | 542 | 55847 | 558 |
| 15 | 15(b2g) | 838 | 610 | 616 | 623 | 700 | 658 | 67047 | 670 |
| 16 | 28(b3u) | 928 | 614 | 621 | 624 | 636 | 813 | 61947 | * |
| 10 | 14(b1u) | 740 | 716 | 716 | 713 | 702 | 703 | 66646 | 666 |
| 9 | 5(ag) | 859 | 824 | 825 | 819 | 812 | 811 | 81847 | 818 |
| 8 | 13(b1u) | 1014 | 960 | 962 | 961 | 949 | 951 | 93747 | 937 |
| 27 | 21(b2u) | 1085 | 1025 | 1025 | 1022 | 1014 | 1006 | 110048 | |
| 7 | 4(ag) | 1140 | 1119 | 1117 | 1116 | 1100 | 1102 | 111646 | 1116 |
| 6 | 12(b1u) | 1228 | 1228 | 1222 | 1218 | 1203 | 1195 | 101546 | |
| 26 | 25(b3g) | 1285 | 1254 | 1257 | 1256 | 1241 | 1244 | 93346 | |
| 5 | 3(ag) | 1257 | 1273 | 1265 | 1260 | 1241 | 1234 | 125147 | 1251 |
| 25 | 20(b2u) | 1306 | 1317 | 1319 | 1315 | 1297 | 1298 | 159148 | |
| 4 | 11(b1u) | 1514 | 1449 | 1444 | 1439 | 1412 | 1408 | 133546 | 1335 |
| 23 | 24(b3g) | 1595 | 1510 | 1509 | 1497 | 1475 | 1475 | 151648 | 1516 |
| 3 | 2(ag) | 1615 | 1557 | 1552 | 1540 | 1507 | 1503 | ||
| 24 | 19(b2u) | 1437 | 1680 | 1677 | 1664 | 1635 | 1632 | 1591 | |
| 22 | 23(b3g) | 3085 | 3253 | 3252 | 3246 | 3118 | 3116 | ||
| 2 | 10(b1u) | 3073 | 3257 | 3255 | 3249 | 3118 | 3116 | ||
| 21 | 18(b2u) | 3091 | 3267 | 3265 | 3258 | 3107 | 3103 | ||
| 1 | 1(ag) | 3088 | 3271 | 3268 | 3261 | 3125 | 3123 | ||
Examining the basis set convergence of the harmonic frequencies, we find that while the in plane modes converge rapidly with the basis set, the out of plane modes (au, b1g, b2g and b3u) converge slowly, with deviations of more than 10 cm−1 between cc-pVTZ and cc-pV5Z values for the low frequency vibrations. As highlighted by Martin, Taylor and Lee for benzene and acetylene,51,52 modes that break planarity suffer from basis set inconsistency errors that artificially lower the frequency and overestimate anharmonic terms in the quartic force field.
This artificial enhancement of the anharmonic couplings to out-of-plane vibrations complicates ab initio assignment the experimental bands. These difficulties notwithstanding, our calculations confirm the majority of the assignments of the 24 fundamental bands observed experimentally. The rightmost two columns of Table 1 list the previous assignment as collated in ref. 47 and our own ab initio assignment, respectively.
The fundamentals D6 and D27 were tentatively assigned to a b1u band at 1015 cm−1 and a b2u band at 1100 cm−1, respectively, in gas phase two-photon spectroscopy measurements.48 These assignments can be confidently discarded on the basis of our calculations and it is likely that these bands do not correspond to fundamental transitions. Similarly, Knight and Kable's tentative assignment of the b3g band at 933 to the D26 fundamental can also be discarded. There is a somewhat larger than expected discrepancy between the predicted and observed D4 fundamental, which we cannot explain. Finally, we make a reassignment of the b2u band at 1591 cm−1 to D24. The problems encountered with the low frequency out of plane modes prevent meaningful comment of the assignments of modes D12, D13, D16 and D17, which is indicated by an asterix in the table. For the in plane modes, the overall agreement between anharmonic CC2/cc-pVQZ and experimentally observed transitions is very good, with an RMSD of 26 cm−1.
3.2 Toluene
The excited state vibrational frequencies of toluene have been studied using dispersed fluorescence spectroscopy,53 UV-IR double resonance spectroscopy,54 one-colour resonance-enhanced multiphoton ionization and two-colour zero kinetic energy spectroscopy.55,56 21 of the 39 fundaments have been assigned, as have the methyl group internal rotor bands, five further overtone bands and several combination bands in the range 200–1500 cm−1.The CC2/cc-pVTZ optimised structures have Cs symmetry in both the ground and first (1B2) excited states. In the ground state the carbon atoms fall in a plane, one hydrogen of the methyl group orientated perpendicular to the plane. In the excited state, the methyl group moves slightly out of plane and has a dihedral angle of 4 degrees with the benzene ring. The 0–0 transition energy for the first excited state is at 4.65 eV,53 which is closely reproduced by CC2/cc-pVTZ theory, which yields 4.86 eV.
Table 2 summarises the calculated and experimental frequencies of toluene in its first excited state. We list harmonic frequencies in cc-pVTZ, cc-pVQZ and cc-pV5Z basis sets, computed at the optimised cc-pVTZ structure, and VPT2 anharmonic frequencies using the cc-pVTZ basis set. The normal mode vectors were analysed and classified using the Mi nomenclature of Gardner and Wright38 for the ring modes, and given pseudo C2v symmetry labels, where the methyl group is treated as a single pseudo-atom.
| M i | Sym. | Harm. | VPT2 | Exp. | ||
|---|---|---|---|---|---|---|
| TZ | QZ | 5Z | TZ | S1 | ||
| τ | 86 | 118 | 122 | 28 | ||
| 20 | b 1 | 141 | 148 | 151 | 140 | 145 |
| 14 | a 2 | 234 | 238 | 238 | 236 | 226 |
| 19 | b 1 | 319 | 325 | 325 | 331 | 314 |
| 30 | b 2 | 323 | 328 | 329 | 325 | 331 |
| 18 | b 1 | 432 | 441 | 445 | 460 | |
| 11 | a 1 | 449 | 450 | 451 | 442 | 457 |
| 29 | b 2 | 524 | 524 | 526 | 512 | 532 |
| 13 | a 2 | 539 | 544 | 560 | 563 | |
| 17 | b 1 | 556 | 560 | 566 | 552 | |
| 16 | b 1 | 639 | 651 | 669 | 734 | 697 |
| 12 | a 2 | 658 | 667 | 686 | 736 | |
| 15 | b 1 | 717 | 733 | 747 | 839 | |
| 10 | a 1 | 751 | 749 | 749 | 737 | 753 |
| 28 | b 2 | 932 | 932 | 932 | 915 | |
| 8 | a 1 | 943 | 939 | 938 | 928 | 934 |
| 9 | a 1 | 969 | 969 | 972 | 957 | 966 |
| δ as − | 1003 | 1003 | 1002 | 972 | ||
| δ as − | 1048 | 1047 | 1047 | 1024 | 1021 | |
| 27 | b 2 | 1157 | 1155 | 1156 | 1137 | |
| 7 | a 1 | 1162 | 1160 | 1160 | 1143 | |
| 6 | a 1 | 1220 | 1214 | 1214 | 1196 | 1193 |
| 26 | b 2 | 1302 | 1304 | 1305 | 1281 | |
| 24 | b 2 | 1386 | 1385 | 1386 | 1364 | |
| δ s + | 1393 | 1394 | 1395 | 1358 | ||
| 5 | a 1 | 1426 | 1423 | 1424 | 1394 | |
| δ as + | 1474 | 1472 | 1472 | 1432 | ||
| δ as + | 1485 | 1484 | 1483 | 1443 | ||
| 23 | b 2 | 1534 | 1526 | 1524 | 1482 | |
| 4 | a 1 | 1557 | 1547 | 1545 | 1505 | |
| 25 | b 2 | 1685 | 1668 | 1661 | 1635 | |
| ν s | 3024 | 3015 | 3013 | 2921 | 2893 | |
| ν as | 3098 | 3091 | 3088 | 2956 | 2956 | |
| ν as | 3142 | 3135 | 3133 | 3013 | 2988 | |
| 22 | b 2 | 3209 | 3203 | 3202 | 3076 | 3048 |
| 3 | a 1 | 3209 | 3204 | 3203 | 3077 | 3063 |
| 2 | a 1 | 3218 | 3212 | 3210 | 3079 | 3077 |
| 21 | b 2 | 3231 | 3224 | 3222 | 3087 | 3087 |
| 1 | a 1 | 3240 | 3233 | 3231 | 3098 | 3097 |
| Overtones | ||||||
| 20 | a 1 | 281 | 296 | 302 | 281 | 290 |
| 14 | a 1 | 469 | 476 | 476 | 471 | 452 |
| 19 | a 1 | 638 | 650 | 650 | 666 | 629 |
| 8 | a 1 | 1885 | 1878 | 1876 | 1854 | 1868 |
| 9 | a 1 | 1939 | 1939 | 1945 | 1914 | 1929 |
| Combination bands | ||||||
| 14 + 20 | b 2 | 375 | 386 | 389 | 374 | 371 |
| 19 + 20 | a 1 | 460 | 473 | 476 | 473 | 462 |
| 14 + 19 | b 2 | 553 | 563 | 563 | 566 | 539 |
| 18 + 19 | a 1 | 751 | 766 | 770 | 796 | 734 |
| 29 + 30 | a 1 | 847 | 852 | 855 | 837 | 864 |
| 11 + 29 | b 2 | 973 | 974 | 977 | 956 | 988 |
| 12 + 14 | a 1 | 892 | 905 | 924 | 975 | 916 |
| 10 + 29 | b 2 | 1275 | 1273 | 1275 | 1248 | 1263 |
| 8 + 11 | a 1 | 1392 | 1389 | 1389 | 1370 | 1390 |
| 8 + 29 | b 2 | 1467 | 1463 | 1464 | 1439 | 1463 |
| 9 + 11 | a 1 | 1418 | 1419 | 1423 | 1399 | 1426 |
| 9 + 29 | b 2 | 1493 | 1493 | 1498 | 1468 | 1494 |
| 8 + 9 | a 1 | 1912 | 1908 | 1910 | 1885 | 1900 |
| 6 + 29 | b 2 | 1743 | 1738 | 1740 | 1706 | 1727 |
| 23 + 25 | a 1 | 3219 | 3194 | 3185 | 3121 | 3101 |
| 4 + 25 | b 2 | 3241 | 3215 | 3206 | 3140 | |
Concerning the basis set convergence of the harmonic wavenumbers, we find a similar pattern as for para-difluorobenzene. The in plane modes are converged to within 10 cm−1 with the cc-pVTZ basis, which is well below the intrinsic error bar of 30 cm−1 commonly ascribed to CC2 theory (for ground state frequencies) due to missing higher order correlation effects. As for para-difluorobenzene, the out-of-plane modes display a much slower basis set convergence, with differences of more than 30 cm−1 between cc-pVTZ and cc-pV5Z values for the torsion and for modes M12, M15 and M16.
Overall, the CC2/cc-pVTZ anharmonic frequencies agree very well with the experimental band centres for the fundamental transitions. The only outlier is mode M16, which appears to have artificially enhanced positive anharmonic corrections due to the basis set incompleteness errors. By the same token, we expect the predicted fundamentals for modes M12 and M15 to also lie above the experimental bands, should they be measured in the future. The methyl internal rotation is not expected to be well described through VPT2 theory and requires a more advanced vibrational treatment using a potential energy surface that exhibits the three equivalent minima, see ref. 57–59 for examples of such theories. The experimental assignment of the five aromatic C–H stretching frequencies M1, M2, M3, M21 and M22, is complicated by the presence of Fermi resonances, which have not yet been untangled. Our calculations predict that M21 is in resonance with M4M25 and that both M1 and M2 are in resonance with M23M25. The computed M4M25 and M23M25 combination bands are listed in Table 2 and lie at higher frequency than the principle C–H stretches. Since we lack predicted intensities or experimental band shape information, we pragmatically assign the experimental bands in order of increasing frequency, which results in excellent agreement between computed and experimental values.
In Table 2 we also list selected overtones and combination bands for comparison with those determined experimentally, collected from ref. 53, 54 and 56. The overtone and combination bands agree with experiment to within the error bar expected from the agreement found for the fundamentals. Some Fermi resonances observed in the spectra are not reproduced by our VPT2 calculations. Specifically, we do not find a resonance between M11 and M19M20 and we find no indication that mode M6 is in resonance with other states. Others, however, are identified by our calculations. The resonance between M10 and M18M19 is found in both theory and experiment, but our calculations predict the fundamental M10 to be lower in energy than M18M19, which if reliable would interchanging Garderner et al.'s assignment of the resonant pair, which has M18M19 lower in energy than M10. Our calculations also verify the resonance between M10M29 and M18M19M29.
Overall, the RMSD between observed and predicted band centres using VPT2 theory with a CC2/cc-pVTZ force field is 16 cm−1 for the fundamental transitions in the excited electronic state.
3.3 Catechol
Catechol (l,2-dihydroxybenzene) is biochemically important since the catecholamines adrenaline, noradrenaline, and dopamine are active in neurotransmission. It has been the subject of extensive spectroscopic studies, many of which have focused on the structure and dynamics of the low energy rotamers formed through changing the relative orientations of the hydroxyl groups, and the resulting differing levels of intra- and intermolecular hydrogen bonding.60 The vibrational frequencies of the excited state have been probed using resonant two-photon ionization, fluorescence emission techniques, and molecular-beam hole-burning experiments.61,62Catechol is planar in the lowest energy isomer of the ground electronic state and the hydroxyl groups form an intermolecular hydrogen bond, but the structure of the excited state is assumed to be slightly distorted out of plane.62 Our structural investigations, using CC2/cc-pVTZ theory to optimise geometries of the ground and excited states, confirm that the ground state is planar with an intermolecular hydrogen bond. We find that the excited state retains the intermolecular hydrogen bond, but is significantly distorted from planarity, puckering at the carbons with the hydroxyl groups. The optimised structures are reported in the ESI.† CC2/cc-pVTZ predicts the 0–0 transition at 4.53 eV which is in line with the experimentally determined 0–0 excitation energy of 4.42 eV.62
The calculated and experimental frequencies of the ground and excited states are compiled in Table 3. Only 16 fundamentals of the excited state have been reported. The previous assignment was predicated on the assumption that the selection rules and band shapes for the planar S0 state can be transferred to guide assignment of the S1 state.62,63 Our calculations indicate that this assumption was flawed and we report a completely fresh assignment for the observed S1 vibrational bands. We therefore present frequencies also for the ground state, comparing our purely ab initio assignment procedure to the more comprehensive experimental assignments available for this state.64–67 We use the oDi labeling for ortho-di-substituted benzene rings of ref. 40 and, following the convention of earlier works,64 use ν1, δ1, τ1 to refer to the motions of the hydrogen donating OH group, and ν2, δ2, τ2 to refer to the motions of the hydrogen accepting OH group.
| o D i | C 2v | S0 | S1 | ||||
|---|---|---|---|---|---|---|---|
| Harm. | VPT2 | Exp. | Harm. | VPT2 | Exp. | ||
| 30 | a 2 | 178 | 220 | 199 | 148 | 145 | |
| τ 2 | a 2 | 209 | 254 | 475 | 425 | 461 | |
| 29 | b 1 | 293 | 295 | 299 | 130 | 127 | 113 |
| 21 | a 1 | 303 | 300 | 320 | 295 | 293 | 299 |
| τ 1 | b 1 | 432 | 433 | 585 | 576 | 607 | |
| 20 | b 2 | 438 | 434 | 449 | 399 | 390 | 395 |
| 28 | b 1 | 456 | 454 | 456 | 369 | 348 | 317 |
| 19 | b 2 | 552 | 545 | 542 | 517 | 486 | 472 |
| 27 | a 2 | 561 | 590 | 582 | 342 | 347 | |
| 18 | a 1 | 578 | 569 | 564 | 544 | 495 | 488 |
| 26 | a 2 | 674 | 802 | 721 | 444 | 420 | |
| 25 | b 1 | 743 | 744 | 741 | 495 | 508 | 502 |
| 17 | a 1 | 772 | 760 | 768 | 732 | 714 | 735 |
| 24 | a 2 | 820 | 846 | 851 | 595 | 560 | 588 |
| 16 | b 2 | 854 | 840 | 859 | 829 | 812 | 840 |
| 23 | b 1 | 897 | 924 | 916 | 761 | 732 | 746 |
| 22 | a 2 | 930 | 988 | 963 | 837 | 836 | 863 |
| 15 | a 1 | 1043 | 1028 | 1030 | 968 | 950 | 950 |
| 14 | b 2 | 1098 | 1079 | 1092 | 1044 | 1028 | 1061 |
| 13/δ2 | a 1 | 1163 | 1143 | 1151 | 1149 | 1122 | |
| 13/δ2 | a 1 | 1168 | 1150 | 1151 | 1166 | 1159 | |
| 12 | b 2 | 1210 | 1190 | 1195 | 1122 | 1104 | |
| 11 | b 2 | 1268 | 1240 | 1251 | 1254 | 1220 | |
| 10 | a 1 | 1309 | 1278 | 1263 | 1286 | 1252 | |
| δ 1 | b 2 | 1367 | 1338 | 1365 | 1343 | 1312 | |
| 9 | a 1 | 1458 | 1419 | 1324 | 1402 | 1368 | |
| 8 | b 2 | 1494 | 1455 | 1479 | 1450 | 1415 | |
| 7 | a 1 | 1540 | 1502 | 1504 | 1635 | 1581 | |
| 6 | b 2 | 1646 | 1601 | 1607 | 1511 | 1466 | |
| 5 | a 1 | 1651 | 1609 | 1616 | 1566 | 1517 | |
| 4 | b 2 | 3186 | 3048 | 3051 | 3177 | 3046 | |
| 3 | a 1 | 3211 | 3092 | 3051 | 3250 | 3102 | |
| 2 | b 2 | 3224 | 3101 | 3060 | 3190 | 3065 | |
| 1 | a 1 | 3235 | 3105 | 3081 | 3204 | 3065 | |
| ν 1 | b 1 | 3750 | 3553 | 3605 | 3612 | 3390 | |
| ν 2 | a 1 | 3813 | 3626 | 3663 | 3542 | 3252 | |
The procedure adopted for assigning the vibrational modes of the S0 state was as follows: first the normal modes were analysed and categorised according to the oDi nomenclature, resulting in approximate C2v symmetry labels a1, b2, b1, a2 with corresponding type A, B, C line shapes for the IR active bands a1, b2, b1, respectively; these were then assigned in frequency order in effective C2v symmetry blocks to the bands observed by Wilson for vapour phase catechol;64 the only exception to this are the four α(CH) bending modes, where the a1 and b2 labels are swapped compared to Wilson's and where recent work casts doubt on the original assignment.40 Where additional or more precise measurements are available, Wilson's band centres are replaced or supplemented by the modern values and the Raman active a2 modes are assigned in frequency order using measurements from solid state catechol; the bands assigned to the OH bending (δ), stretching (ν) and torsional (τ) modes are identified from examination of the normal mode coordinates.
The overall agreement with experiment and CC2/cc-pVTZ theory is excellent, with an RMSD of 29 cm−1. The difficulties associated with out-of-plane vibrations are much less pronounced here and there is only one outlier of this type, the ring puckering mode D26. The only other significant outlier is mode D9, which is the mode distorting from a aromatic ring to three localised double bonds.
Turning now to the S1 state, comparison with experiment is problematic. Only 16 frequencies have been assigned and the assignment appears flawed. A vibronic progression with a spacing of 113 cm−1 was observed in resonant two-photon ionisation spectra of catechol and was assigned to OH torsional overtones.62 Our calculations do not predict low frequency torsional modes, but in fact predict a significant redshift of the torsional frequencies upon electronic excitation. The more tetrahedral arrangement at the oxygen centres in the excited state structure leads to a stronger intermolecular hydrogen bond, higher torsional frequencies and lower OH stretching frequencies. Instead, our calculations suggest assigning the progression of 113 cm−1 to the low frequency D29 ring bend. Note that the selection rules based on spatial symmetry do not rigorously apply since the excited state structure is significantly distorted out of plane. Having discounted the presence of low-frequency torsional modes, many of the spectral features observed in the experimental works must be reassigned. Proceeding to match computed and experimental values, accounting for band shape information where available, we report a fresh ab initio assignment in Table 3. The RMSD between VPT2 fundamentals using a CC2/cc-pVTZ force field and the observed bands with our fresh assignment is 22 cm−1.
4 Conclusion
Excited state hessians have been implemented for CC2, with a focus on keeping the scaling of the main memory demands to at most![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) 2). This has been realized by exploiting the RI approximation for the two electron integrals and by choosing a Laplace decomposition of orbital energy denominators in the calculation of the first-order density matrices. The implementation is an extension of that for excited state polarizabilities and was extended straightforwardly to excited state hessians for the CIS(D∞) and ADC(2) methods. The code is parallelized with OpenMP and MPI to make use of modern computer hardware. The analytic implementation enables the semi-numerical calculation of third and fourth derivatives for anharmonic corrections.
2). This has been realized by exploiting the RI approximation for the two electron integrals and by choosing a Laplace decomposition of orbital energy denominators in the calculation of the first-order density matrices. The implementation is an extension of that for excited state polarizabilities and was extended straightforwardly to excited state hessians for the CIS(D∞) and ADC(2) methods. The code is parallelized with OpenMP and MPI to make use of modern computer hardware. The analytic implementation enables the semi-numerical calculation of third and fourth derivatives for anharmonic corrections.
We applied VPT2 theory based on CC2 quartic force fields to para-difluorobenzene, toluene and catechol and compared the computed frequencies to experimentally observed vibrational bands of the first excited states. In contrast to previous benchmark studies, we find that the accuracy of CC2 frequencies for excited electronic states is comparable to MP2 or CC2 frequencies for the ground electronic state, with typical average deviations between theory and experiment of less than 30 cm−1 for fundamental transitions when using a cc-pVTZ basis. However, we find that out-of-plane modes carry a much larger uncertainty due to internal basis set superposition errors, which leads to a strong basis set dependence of the force field terms, and unphysically large anharmonic corrections to typically underestimated harmonic frequencies.
In addition to assessing the accuracy of CC2 theory, our calculations have revealed some anomalies in the assignment of some of the experimentally observed bands. Our calculations discount some of the more tentative assignments in the spectrum of para-difluorobenzene. More significantly, our calculations indicate that the assignment of the lowest frequency features in the vibrational bands of catechol to OH torsions is incorrect, and that these lie much higher in energy due to the stronger hydrogen bond in the distorted S1 excited state than in the planar S0 state. Instead, we assign these features to ring modes, which become symmetry allowed transitions due to the low symmetry of the relaxed excited state structure. Due to this re-interpretation of the experimental bands it was necessary to perform a completely fresh assignment, and our new assignment can be considered a pure ab initio assignment.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Open Access funding provided by the Max Planck Society.References
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef PubMed.
- T. N. V. Karsili, A. M. Wenge, B. Marchetti and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2014, 16, 588–598 RSC.
- A. G. Sage, T. A. A. Oliver, G. A. King, D. Murdock, J. N. Harvey and M. N. R. Ashfold, J. Chem. Phys., 2013, 138, 164318 CrossRef PubMed.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093 RSC.
- T. N. V. Karsili, A. M. Wenge, D. Murdock, S. J. Harris, J. N. Harvey, R. N. Dixon and M. N. R. Ashfold, Chem. Sci., 2013, 4, 2434–2446 RSC.
- T. A. A. Oliver, G. A. King, D. P. Tew, R. N. Dixon and M. N. R. Ashfold, J. Phys. Chem. A, 2012, 116, 12444–12459 CrossRef CAS PubMed.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238 RSC.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1995, 103, 8931–8943 CrossRef CAS.
- J. F. Stanton and J. Gauss, Theor. Chim. Acta, 1995, 91, 267–289 CAS.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1996, 104, 9859–9869 CrossRef CAS.
- O. Christiansen, J. F. Stanton and J. Gauss, J. Chem. Phys., 1998, 108, 3987–4001 CrossRef CAS.
- K. W. Sattelmeyer, J. F. Stanton, J. Olsen and J. Gauss, Chem. Phys. Lett., 2001, 347, 499–504 CrossRef CAS.
- H. Larsen, J. Olsen, P. Jørgensen and O. Christiansen, J. Chem. Phys., 2000, 113, 6677–6686 CrossRef CAS.
- M. Musiał, K. Kowalska and R. J. Bartlett, THEOCHEM, 2006, 768, 103–109 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- O. Vahtras, J. Almlöf and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- T. S. Balaban, P. Braun, C. Hättig, A. Hellweg, J. Kern, W. Saenger and A. Zouni, Biochim. Biophys. Acta, Bioenerg., 2009, 1787, 1254–1265 CrossRef CAS PubMed.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, Chem. Phys. Lett., 1994, 219, 21–29 CrossRef CAS.
- M. Head-Gordon, M. Oumi and D. Maurice, Mol. Phys., 1999, 96, 593–602 CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- D. H. Friese, N. O. C. Winter, P. Balzerowski, R. Schwan and C. Hättig, J. Chem. Phys., 2012, 136, 174106 CrossRef PubMed.
- N. K. Graf, D. H. Friese, N. O. C. Winter and C. Hättig, J. Chem. Phys., 2015, 143, 244108 CrossRef PubMed.
- D. H. Friese, C. Hättig and J. Koßmann, J. Chem. Theory Comput., 2013, 9, 1469–1480 CrossRef CAS PubMed.
- J. Almlöf, Chem. Phys. Lett., 1991, 181, 319–320 CrossRef.
- F. Egidi, D. B. Williams-Young, A. Baiardi, J. Bloino, G. Scalmani, M. J. Frisch, X. Li and V. Barone, J. Chem. Theory Comput., 2017, 13, 2789–2803 CrossRef CAS PubMed.
- J. Liu and W. Liang, J. Chem. Phys., 2011, 135, 184111 CrossRef PubMed.
- T. U. Helgaker, in Geometrical Derivatives of Energy Surfaces and Molecular Properties, ed. P. Jørgensen and J. Simons, Reidel, Dordrecht, Netherlands, 1986, p. 1 Search PubMed.
- T. Helgaker and P. Jørgensen, Adv. Quantum Chem., 1988, 19, 183–245 CrossRef CAS.
- TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- B. Fornberg, Math. Comput., 1988, 51, 699–706 CrossRef.
- I. M. Mills, in Molecular Spectroscopy: Modern Research, ed. K. Narahari Rao and C. Weldon Mathews, Academic Press, Inc., New York and London, 1972, p. 115 Search PubMed.
- W. Mizukami and D. P. Tew, J. Chem. Phys., 2013, 139, 194108 CrossRef PubMed.
- R. D. Amos, N. C. Handy, W. H. Green, D. Jayatilaka, A. Willetts and P. Palmieri, J. Chem. Phys., 1991, 95, 8323–8336 CrossRef CAS.
- A. M. Gardner and T. G. Wright, J. Chem. Phys., 2011, 135, 114305 CrossRef PubMed.
- A. Andrejeva, A. M. Gardner, W. D. Tuttle and T. G. Wright, J. Mol. Spectrosc., 2016, 321, 28–49 CrossRef CAS.
- W. D. Tuttle, A. M. Gardner, A. Andrejeva, D. J. Kemp, J. C. Wakefield and T. G. Wright, J. Mol. Spectrosc., 2018, 344, 46–60 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1997–2011 CrossRef.
- E. B. Wilson, Phys. Rev., 1934, 45, 706–714 CrossRef CAS.
- T. Den, H.-M. Frey, P. M. Felker and S. Leutwyler, J. Chem. Phys., 2015, 143, 144306 CrossRef PubMed.
- R. Zimmerman and T. Dunn, J. Mol. Spectrosc., 1985, 110, 312–325 CrossRef CAS.
- T. Cvitaš and J. Hollas, Mol. Phys., 1970, 18, 793–800 CrossRef.
- A. E. W. Knight and S. H. Kable, J. Chem. Phys., 1988, 89, 7139–7160 CrossRef CAS.
- H. J. Elston, E. R. Davidson, F. G. Todd and C. S. Parmenter, J. Phys. Chem., 1993, 97, 5506–5518 CrossRef CAS.
- M. Robey and E. Schlag, Chem. Phys., 1978, 30, 9–17 CrossRef CAS.
- K. L. Reid, T. A. Field, M. Towrie and P. Matousek, J. Chem. Phys., 1999, 111, 1438–1445 CrossRef CAS.
- J. Long, C. Qin, Y. Liu, S. Zhang and B. Zhang, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 063409 CrossRef.
- J. M. Martin, P. R. Taylor and T. J. Lee, Chem. Phys. Lett., 1997, 275, 414–422 CrossRef CAS.
- J. M. L. Martin, T. J. Lee and P. R. Taylor, J. Chem. Phys., 1998, 108, 676–691 CrossRef CAS.
- C. G. Hickman, J. R. Gascooke and W. D. Lawrance, J. Chem. Phys., 1996, 104, 4887–4901 CrossRef CAS.
- C. Minejima, T. Ebata and N. Mikami, Phys. Chem. Chem. Phys., 2002, 4, 1537–1541 RSC.
- A. M. Gardner, A. M. Green, V. M. Tamé-Reyes, V. H. K. Wilton and T. G. Wright, J. Chem. Phys., 2013, 138, 134303 CrossRef PubMed.
- A. M. Gardner, A. M. Green, V. M. Tamé-Reyes, K. L. Reid, J. A. Davies, V. H. K. Parkes and T. G. Wright, J. Chem. Phys., 2014, 140, 114308 CrossRef.
- D. P. Tew, N. C. Handy and S. Carter, Phys. Chem. Chem. Phys., 2001, 3, 1958–1964 RSC.
- D. P. Tew, N. C. Handy and S. Carter, Mol. Phys., 2004, 102, 2217–2226 CrossRef CAS.
- D. P. Tew and W. Mizukami, J. Phys. Chem. A, 2016, 120, 9815–9828 CrossRef CAS PubMed.
- T. Dunn, R. Tembreull and D. Lubman, Chem. Phys. Lett., 1985, 121, 453–457 CrossRef CAS.
- M. Gerhards, W. Perl, S. Schumm, U. Henrichs, C. Jacoby and K. Kleinermanns, J. Chem. Phys., 1996, 104, 9362–9375 CrossRef CAS.
- T. Bürgi and S. Leutwyler, J. Chem. Phys., 1994, 101, 8418–8429 CrossRef.
- F. Ramírez and J. L. Navarrete, Vib. Spectrosc., 1993, 4, 321–334 CrossRef.
- H. W. Wilson, Spectrochim. Acta, Part A, 1974, 30, 2141 CrossRef.
- S. J. Greaves and W. P. Griffith, Spectrochim. Acta, Part A, 1991, 47, 133–140 CrossRef.
- T. Y. Koh, S. J. Greaves and W. P. Griffith, Spectrochim. Acta, Part A, 1994, 50, 857–873 CrossRef.
- H. G. Kjaergaard, D. L. Howard, D. P. Schofield, T. W. Robinson, S.-I. Ishiuchi and M. Fujii, J. Phys. Chem. A, 2002, 106, 258–266 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp06952b |
| This journal is © the Owner Societies 2019 |
