Open Access Article
Open Access ArticlePhotoinduced electron-driven proton transfer from water to an N-heterocyclic chromophore: nonadiabatic dynamics studies for pyridine–water clusters
Xiaojuan
Pang
abc,
Chenwei
Jiang
 ab,
Weiwei
Xie
ab,
Weiwei
Xie
 *cd and
Wolfgang
Domcke
*cd and
Wolfgang
Domcke
 *c
*c
aKey Laboratory for Quantum Information and Quantum Optoelectronic Devices, Shaanxi, China
bDepartment of Applied Physics, Xi’an Jiaotong University, Xi’an 710049, China
cDepartment of Chemistry, Technical University of Munich, D-85747 Garching, Germany. E-mail: domcke@ch.tum.de
dInstitute of Physical Chemistry, Karlsruhe Institute of Technology, Karlsruhe, Germany. E-mail: weiwei.xie@kit.edu
First published on 11th January 2019
Abstract
It has been found in recent molecular beam experiments that pyridine molecules photoexcited at 255 nm can abstract hydrogen atoms from hydrogen-bonded water molecules in pyridine–water clusters, resulting in pyridinyl-hydroxyl radical pairs. The reaction could only be detected for clusters containing at least four water molecules. To provide insight into the mechanisms of this reaction, we performed ab initio excited-state trajectory surface-hopping dynamics simulations for two pyridine–water complexes, containing one and four water molecules, respectively, using the second-order algebraic-diagrammatic-construction (ADC(2)) electronic-structure method. A computationally efficient surface-hopping algorithm based on the Landau–Zener formula has been used to evaluate the transition probability between electronic states. The formation of the pyridinyl radical via an electron-driven proton transfer (EDPT) process from water to pyridine is confirmed by the simulations. The analysis of the competing excited-state reaction mechanisms up to 500 fs reveals that adiabatic relaxation to local minima of the S1(nπ*) potential-energy surface is the dominant channel in both clusters, followed by internal conversion to the electronic ground state via so-called ring-puckering conical intersections. The efficiency of the latter contribution is weakly dependent of the size of the clusters. The EDPT reaction occurs on the fastest time scales (faster than 200 fs) with a branching ratio of several percent. It is found to be four times more efficient in the pyridine–(H2O)4 cluster than in the pyridine–H2O cluster, which is qualitatively consistent with the experimental observations. A detailed understanding of the photoinduced reaction mechanisms in complexes of N-heterocyclic chromophores with water molecules is of relevance for future systematic knowledge-based developments of optimized materials for photocatalytic water splitting with sunlight.
1. Introduction
Photoinduced electron-driven proton-transfer (EDPT) reactions,1 a subset of so-called proton-coupled electron-transfer (PCET) reactions,2 are of great importance in the photochemistry of hydrogen-bonded complexes, being relevant for the function of various sunscreens,3,4 the photostability of nucleobases,5,6 and for artificial photosynthesis.7–11 The most extensively studied EDPT reactions are excited-state chromophore-to-solvent hydrogen-transfer reactions, in which a hydrogen atom is transferred from a photoexcited chromophore to solvent molecules, such as ammonia or water.12–17 Extensive experimental and theoretical investigations have shown that these reactions can take place in clusters consisting of several water molecules and an acidic aromatic chromophore, such as phenol,14,17 adenine18 or imidazole.19,20 It was found that the number of solvent molecules in micro-solvated systems can have a significant influence on the rate constant of the EDPT reaction.19–21Alternatively, an H-atom can be transferred from a solvent molecule to a photoexcited chromophore. While limited experimental evidence exists for such photoreactions, extensive computational studies have shown that heterocyclic aromatic chromophores, such as pyridine,22,23 triazine,24 heptazine25 or adenine,18 can upon photoexcitation abstract a hydrogen atom from a water molecule by a low-barrier H-atom transfer reaction, resulting in the formation of a reduced chromophore and a hydroxyl radical. By the absorption of a second photon, the H-atom can be photodetached from the reduced chromophore. Thereby the chromophore is recovered and the water molecule is split with two photons into a hydrogen atom and a hydroxyl radical. Recently, this biphotonic homolytic water-splitting reaction was discovered in a molecular beam experiment for photoexcited hydrogen-bonded pyridine–water clusters by Jouvet and coworkers.26 In this experiment, the formation of the pyridinyl neutral radical was detected in pyridine–water clusters upon 255 nm irradiation, which confirms that pyridine (Py) can serve as a photocatalyst for the splitting of water molecules by UV light. An interesting observation made in this experiment was that at least four water molecules were necessary for the photoinduced water-splitting reaction to be detectable.26 To find an explanation for this observation, we recently explored the photoinduced EDPT reaction from water to pyridine in Py–(H2O)n (n = 1–4) clusters.27 It was found that for Py–(H2O)n clusters with n = 1–3, the hydrogen bond between pyridine and the nearest water molecule is significantly weakened in the S1 excited state of nπ* character, which is unfavorable for the EDPT reaction. In the Py–(H2O)4 cluster, on the other hand, the S1 excited state is of ππ* character and the hydrogen bond with the nearest water molecule is strengthened. Moreover, determination of the reaction barriers showed that the Py–(H2O)4 cluster has the lowest barrier for the EDPT reaction among these clusters.
While these static excited-state electronic-structure calculations provide a plausible explanation why at least four water molecules are necessary for the EDPT reaction in pyridine–water complexes, zero-point energy and finite-temperature effects as well as dynamical phenomena, which are not taken into account in these static calculations, may be important in the EDPT reaction. In the present study, ab initio on-the-fly nonadiabatic dynamics simulations have been performed to further unveil the underlying mechanisms of the EDPT reaction in pyridine–water clusters. The relatively small pyridine–water clusters serve herein as model systems which allow relatively inexpensive explorations of these phenomena with first-principles methods. These studies are intended to pave the way for simulations of the photochemistry of larger chromophores, such as heptazine (tri-s-triazine)25,28 or trianisole-heptazine29 in aqueous environments. These chromophores are potential photocatalysts for water splitting with visible light.29,30
2. Computational methods
The ground-state equilibrium geometries of Py–(H2O)n (n = 1 and 4) complexes were optimized with second-order Møller–Plesset perturbation theory (MP2)31 with the cc-pVDZ basis set. For the Py–(H2O)4 complex, there exist numerous equilibrium structures with comparable energies. We selected a low-energy structure for this cluster such that the hydrogen bonds among the water molecules are optimally saturated. The excited-state calculations were performed with the second-order algebraic-diagrammatic-construction (ADC(2)) method32,33 using the cc-pVDZ basis set. The TURBOMOLE program package34 was used for the electronic-structure calculations.The absorption spectra of the pyridine–water complexes were simulated using the nuclear ensemble method proposed by Barbatti and coworkers.35 A set of 2000 initial conditions were generated from the harmonic-oscillator thermal Wigner distribution at room temperature. Vertical excitation energies and oscillator strengths of the five lowest-lying excited states were computed for each initial geometry. The lines were broadened by a Lorentzian function with a width of 0.05 eV and summed up to provide the spectrum.
The nonadiabatic dynamics was simulated with a trajectory surface-hopping (TSH) method which is based on the Landau–Zener (LZ) formula.36–38 In this method, the transition probability between adiabatic electronic states for a given classical trajectory is determined from the local shape of the adiabatic potential energies near surface crossings. This is possible because the electronic mixing angle (and therefore the nonadiabatic electronic coupling element) in the vicinity of a two-state avoided crossing is uniquely determined by the shape of the adiabatic potential-energy functions. The explicit construction of diabatic potential-energy surfaces is therefore not required in this method nor is the time-dependent electronic wave function computed. Therefore, the “lack-of-decoherence” problem, which arises in the widely used fewest-switches surface-hopping (FSSH) method of Tully39 does not apply to these calculations. The LZ-based surface-hopping (LZSH) method is computationally more efficient than the fewest-switches algorithm, since the computation of derivative couplings, which are sharply peaked at conical intersections, is avoided.
Briefly, the absolute value of the energy gap ΔVajk between the energy of the current adiabatic electronic state j and another adiabatic electronic state k is monitored at each time step of the trajectory. If a local minimum of the energy gap is attained, the hopping probability is evaluated according to the adiabatic formulation of the Landau–Zener formula36–38
 | (1) |
As in the fewest-switches algorithm,39 a pseudorandom number uniformly generated from (0,1) is compared with Pj→kLZ to determine whether the trajectory hops to state k or continues in the current state j.
The accuracy of the LZSH method has been critically examined in comparison with the FSSH method and with exact nonadiabatic quantum dynamics calculations for a few benchmark model systems. These calculations showed that the LZSH method provides a qualitatively correct description for few-state few-mode models of the excited-state nonadiabatic dynamics of the ammonia cation,37 phenol38 and pyrazine.40 The ab initio direct-dynamics implementation of the LZSH method has recently been applied to the investigation of the radiationless decay dynamics of the S2(ππ*) excited state of pyrazine.40
In the simulations, Newton's equations for the nuclear motion were integrated with a time step of 0.5 fs using the velocity-Verlet algorithm. The trajectories were propagated up to 500 fs. Since the ADC(2) excitation energies are determined by the diagonalization of a Hermitian matrix,32 the adiabatic energies exhibit proper behavior in the vicinity of conical intersections between excited states and hopping probabilities between excited states can be evaluated according to eqn (1). This is not the case for S1–S0 conical intersections, since the single-reference character of the electronic ground-state wave function necessarily breaks down in the vicinity of S1–S0 conical intersections. Therefore, the propagation of a trajectory was terminated when the energy gap between the S1 surface and the S0 surface dropped below 0.2 eV. These events were counted as radiationless decay to the electronic ground state. Possible back reactions from the S0 surface to the S1 surface and possible H-atom back-transfer reactions on the S0 surface are therefore neglected.
3. Results and discussion
3.1. Absorption spectrum
The ground-state equilibrium geometries of the Py–H2O and Py–(H2O)4 clusters are shown in Fig. 1(a) and (b), respectively. The pyridine–water hydrogen-bond length (RNH) of the Py–(H2O)4 cluster is 0.23 Å shorter than the hydrogen-bond length of the Py–H2O cluster, which indicates that the strength of the hydrogen bond is substantially increased in the larger cluster.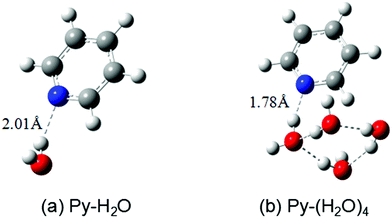 | ||
| Fig. 1 Ground-state equilibrium geometries of the pyridine–(H2O) cluster (a) and the pyridine–(H2O)4 cluster (b) calculated with the MP2/cc-pVDZ method. | ||
A comparison of the computed absorption spectra of the Py–H2O and Py–(H2O)4 clusters with the experimental spectrum of pyridine in aqueous solution41,42 is shown in Fig. 2. For the sake of comparison, the maxima of the spectra are normalized to unity. The peak of the absorption band of the Py–(H2O)4 cluster is red-shifted by 0.12 eV with respect to the peak of the spectrum of the Py–H2O cluster. This is due to a redshift of the bright 1ππ* state of Py with increasing number of water molecules. While the 1nπ* state of pyridine is optically dark, it can borrow intensity from the bright 1ππ* state in the Py–H2O cluster, since the 1ππ* and 1nπ* state are nearly degenerate in this cluster.22,27 As the number of water molecules increases from one to four, the stabilization of the n orbital by the surrounding water molecules leads to a further increase of the excitation energy of the 1nπ* state, which removes the near-degeneracy of the 1ππ* and 1nπ* states and results in a lower oscillator strength of the 1nπ* state. The ADC(2) method predicts the band maximum of the Py–(H2O)4 cluster at 5.06 eV, which is blue-shifted by 0.2 eV with respect to the band maximum of the experimental spectrum.41
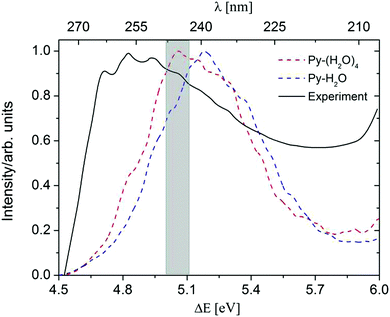 | ||
| Fig. 2 Absorption spectra of the Py–H2O cluster (blue) and the Py–(H2O)4 cluster (red), simulated at the ADC(2)/cc-pVDZ level. The black line is the experimental spectrum of pyridine in aqueous solution.38 The initial conditions for excited-state dynamics simulations of both clusters are sampled from an energy window of 5.06 ± 0.05 eV (marked in grey). | ||
3.2. Nonadiabatic dynamics simulations
The initial conditions for excited-state dynamics simulations of the Py–H2O and Py–(H2O)4 clusters were sampled from an energy window of 5.06 ± 0.05 eV to mimic the gas-phase experiment in which the laser frequency was chosen near the peak of the absorption spectrum of pyridine.26 A stochastic algorithm, using the oscillator strength as the criterion for the transition probability was used, which results in 144 and 65 trajectories started in the S1 and S2 states, respectively, of the Py–H2O cluster. In the Py–(H2O)4 cluster, 180 and 58 trajectories are initiated in the S1 and S2 states, respectively. The calculated time-dependent population probabilities of the ground state (with zero initial population) and the three lowest excited adiabatic electronic states of the Py–H2O and Py–(H2O)4 clusters are shown in Fig. 3. Overall, the electronic population dynamics of the two clusters is similar. The S2 state population exhibits a few weak recurrences and then decays to a low value within 100 fs. The population of the S1 state attains a maximum of 0.95 at 50 fs and then decays with a long decay constant of 4.3 ps (2.5 ps) for the Py–H2O (Py–(H2O)4) cluster. The population of the S3 state (a higher 1nπ* state of pyridine) rises to a maximum value of 0.1 (0.05) within the first 10 fs for the Py–(H2O)4 (Py–H2O) cluster and then quickly decays to zero. The ground-state population increases monotonously with the same time constant as the S1 decay. The computed excited-state lifetime of the Py–(H2O)4 cluster is (presumably fortuitously) almost identical with the experimental result of 2.2 ps for pyridine in aqueous solution.41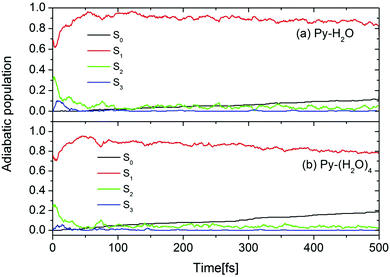 | ||
| Fig. 3 Population probabilities of the electronic ground state and three lowest adiabatic excited electronic states for the Py–H2O (a) and Py–(H2O)4 (b) clusters. | ||
The trajectories were analyzed with respect to the reaction mechanism they represent. The fractions of trajectories corresponding to the different radiationless deactivation mechanisms for the Py–H2O and Py–(H2O)4 clusters are shown in Fig. 4(a) and (b), respectively. At the end of the simulations, relaxation to local minima of the S1(nπ*) surface of pyridine is the dominant channel for both clusters (88.9% and 81.9%, respectively). Most of these trajectories show a migration of the water molecules towards one of faces the pyridine ring, while the hydrogen bond between the N-atom of pyridine and the nearest water molecule weakens or breaks. 10.1% and 13.9% of trajectories return to the ground state through conical intersections of the ring-puckering type for the Py–H2O and Py–(H2O)4 clusters, respectively. S1–S0 conical intersections of pyridine have been located and discussed in ref. 43 and 44. They result from the lowering of the energy of the diabatic 1ππ* state and the increase of the energy of the S0 state of pyridine upon out-of-plane distortion of the nitrogen atom. These ring-puckering conical intersections are well known for benzene45,46 as well as for N-heterocycles, for example pyrazine,46 or pyrimidine bases, such as uracil or thymine.47 Increasing the number of water molecules seems to have a moderate effect on the efficiency of the ring-puckering internal conversion pathway.
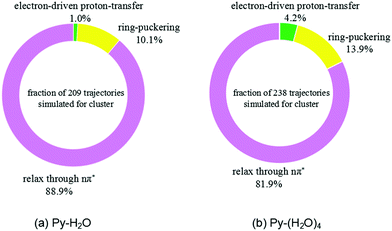 | ||
| Fig. 4 Branching ratios of different excited-state deactivation channels for the Py–H2O cluster (a) and the Py–(H2O)4 cluster (b) within the first 500 fs after excitation. | ||
For the Py–(H2O)4 cluster, about 4.2% of the trajectories of the simulations up to 500 fs reach a conical intersection with ground state via the EDPT photorelaxation pathway, which is about four times more than found for the Py–H2O cluster. The EDPT pathway is thus not the dominant pathway for the radiationless deactivation of photoexcited pyridine–water clusters. It should be kept in mind, however, that the branching ratio for the EDPT process is systematically underestimated by the present simulations due to the omission of proton tunneling in the classical trajectory calculations.
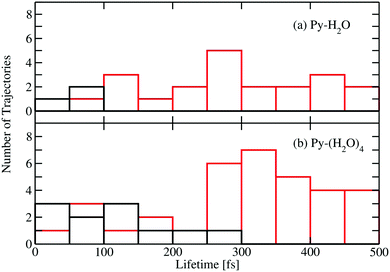
Fig. 5 shows a histogram of the excited-state lifetimes, defined as the time when the trajectory hits an S1/S0 conical intersection. The numbers of trajectories returning to the ground state by the EDPT and ring-puckering channels are represented by the black and red histograms, respectively. Most EDPT events occur within the first 200 femtoseconds, while most of the ring-puckering events take place after 300 fs. All EDPT events in the Py–H2O cluster occur within the first 100 fs, while in the Py–(H2O)4 cluster some EDPT events take place after 200 fs. The surrounding water molecules in the Py–(H2O)4 cluster stabilize the hydrogen bond of the central water molecule with pyridine, which reduces the probability of dissociation of the pyridine–water hydrogen bond.
This interpretation is confirmed by Fig. 6, which shows the time evolutions of the N–H hydrogen-bond distance for all trajectories of both clusters. During the first 100 femtoseconds, the N–H bond distance is seen to increase significantly faster for the Py–H2O cluster than for the Py–(H2O)4 cluster. For both clusters, the pyridine–water hydrogen bond for most trajectories either weakens or breaks within 100 fs. The trajectories undergoing the EDPT reaction in the Py–(H2O)4 cluster roam around conical intersection seams for several vibrational periods of the mobile H-atom before they cross to the electronic ground state (indicated by trajectories with RNH < 1.5 Å in Fig. 6(b)). Similar N–H vibrational oscillations are not observed in the Py–H2O cluster (Fig. 6(a)).
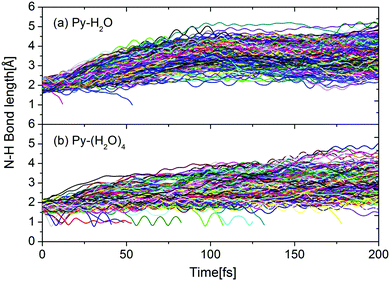 | ||
| Fig. 6 Time evolution of the N–H hydrogen-bond distance between pyridine and water for the Py–H2O cluster (a) and the Py–(H2O)4 cluster (b). | ||
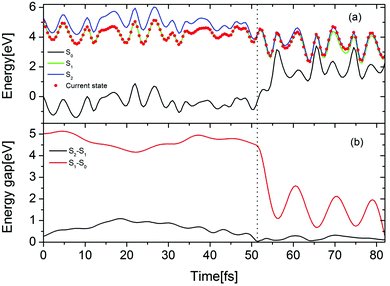
The time-dependent potential energies of the ground state and two lowest excited states are shown in Fig. 7(a) for a typical trajectory undergoing the EDPT reaction in the Py–(H2O)4 cluster. At t = 0, the trajectory is started in the adiabatic S1 state which is the locally-excited 1ππ* state in the Franck–Condon region. At 52.5 fs, the energy gap between the S1 and the S2 states reaches a local minimum and a hopping takes place from the S1 to the S2 state. The evolution in the S2 state leads to a pronounced destabilization of the electronic ground state. The time evolutions of the S2–S1 and S1–S0 energy gaps are displayed in Fig. 7(b). After about 30 fs propagation in the quasi-degenerate S1 and S2 states, the trajectory hits a conical intersection with the ground state. In this region, the S2–S1 as well as S1–S0 energy gaps are small (0.11 eV for S2–S1 and 0.29 eV for S1–S0), which implies that this conical intersection may be a three-state conical intersection.
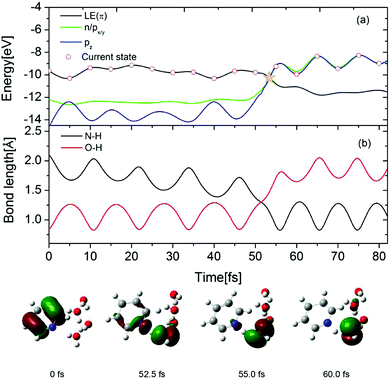
To gain further insight into the EDPT process in the Py–(H2O)4 cluster, the time-dependent energies of the occupied frontier Hartree–Fock orbitals are shown in Fig. 8(a) for a selected trajectory which was initiated in the S1(ππ*) state. The dot marks the orbital which carries the hole in the excited electronic state. In the lower part of the figure, snapshots of the hole-carrying orbital are shown at specific times. The photoexcitation of pyridine to the 1ππ* state generates a hole in the π orbital of pyridine and the hole amplitude is localized on the pyridine ring (0 fs). The energy of the π orbital of pyridine crosses the energies of the accidentally nearly degenerate n (on pyridine) and pz (on the hydrogen-bonded water molecule) orbitals at 52.5 fs. The trajectory hopping from the S1 state to the nearly degenerate S2 state is accompanied by a hole transfer from the π orbital to the n orbital. The amplitude of the latter is distributed almost equally among the pyridine ring and the hydrogen-bonded water molecule (see Fig. 8, 52.5 fs). As time proceeds, the amplitude becomes fully localized on the px/y orbital of the water molecule (see Fig. 8, 55.0 fs). Beyond 55 fs, the hole remains localized on the water molecule and oscillates between the px/y and pz orbitals (see Fig. 8, 60.0 fs). Once the hole is localized on the water molecule, the proton involved in the hydrogen bond with the N-atom of pyridine is driven away for the oxygen atom of water and attaches to the N-atom of the negatively charged pyridine, which completes the EDPT reaction. The time evolution of the N–H and O–H distances is shown in Fig. 8(b). For the initial 50 fs, the N–H distance decreases gradually with periodic oscillations with a period of 10 fs. The O–H bond length is equal to the N–H hydrogen-bond length at 52.5 fs. As time proceeds, the O–H bond breaks and a covalent N–H bond is formed. It can be seen that the formation of the covalent N–H bond is nearly coincident with the hole transfer from the π orbital to the n orbital shown in Fig. 8(a).
4. Conclusions
In the present work, we performed the first excited-state nonadiabatic dynamics simulations for photoexcited pyridine–water clusters, using a recently developed surface-hopping method based on the Landau–Zener formula at PES crossings and the ADC(2) electronic-structure model. To obtain insight into the dependence of the dynamics on the size of the clusters, the reaction dynamics of two clusters, containing one and four water molecules, respectively, was considered. Recent benchmarking studies have shown that this surface-hopping method can provide qualitatively correct descriptions of the nonadiabatic excited-state dynamics.40 A limitation of the simulations at the present stage is the neglect of proton tunneling effects, which may lead to a systematic underestimation of the branching ratio of the EDPT reaction.The dynamics simulations for the two selected Py–water clusters show that relaxation to local minima of the S1(nπ*) PES is the dominant reaction channel. On the S1 surface, a rearrangement of the clusters takes place by an extension of the hydrogen bond with the N-atom of Py and the formation of hydrogen bonds with the π-system of the aromatic ring. Internal conversion to the electronic ground state via S1–S0 conical intersections of the ring-puckering type is found with a branching ratio of about 10%, which does not strongly depend on the size of the clusters. The EDPT process, that is, H-atom transfer from the N-hydrogen-bonded water molecule to the N-atom of pyridine, is the fastest process with a low branching ratio (1%) for the Py–H2O cluster. This branching ratio increases to about 4% in the Py–(H2O)4 cluster. The increased efficiency of the EDPT reaction in the Py–(H2O)4 cluster is qualitatively consistent with the observation that clusters with at least four water molecules are necessary for the experimental detection of the excited-state H-atom transfer reaction.26 The relatively efficient excited-state deactivation of Py via ring-puckering conical intersection is a loss process which is undesirable for photocatalytic water splitting. Out-of-plane deformations in ππ* excited states are suppressed, however, in fused aromatic ring systems, such as, for example, heptazine. Heptazine-based polymeric materials, such as graphitic carbon nitride,48 indeed show excellent photostability.
The mechanism of the EDPT reaction mechanism has been visualized in the Hartree–Fock orbital picture. Photoexcitation of an electron from the π orbital to the π* orbital in the pyridine chromophore in Py–water complexes initially creates an exciton (electron–hole pair). When the OH distance of the N-hydrogen-bonded water molecule extends (that is, the NH distance decreases) during the dynamics, the energy of the π orbital decreases, while the energies of the n orbital of pyridine and the p orbitals of the water molecule increase. When two (or more) of the these orbitals become degenerate, a hole transfer from pyridine to the nearest water molecule takes place, resulting in a negatively charged pyridine ring and a positively charged water molecule. This charge separation provides the driving force for the proton transfer from the water molecule to the pyridine ring, resulting in the pyridinyl-hydroxyl biradical.
The first ab initio study of the dynamics of hydrogen abstraction from a water molecule by a photoexcited organic chromophore was performed for the cluster of adenine with a single water molecule by Došlić and coworkers.49 In the present study, the first ab initio excited-state dynamics simulations have been performed for pyridine–water clusters which reveal the effect of an increasing number of water molecules on the photoinduced water-splitting reaction. In future extensions of the present work, the effects of proton tunneling should be quantified. It should also be interesting to perform simulations for photoexcited aromatic chromophores in a liquid water environment at finite temperature with ab initio (DFT) molecular dynamics simulations or QM/MM simulation methods.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
X. P. acknowledges support by the China Scholarship Council (CSC). W. X. acknowledges support by a postdoctoral research fellowship of the Alexander von Humboldt-Foundation and by a research grant of the Deutsche Forschungsgemeinschaft for W. D.References
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2007, 111, 11725 CrossRef CAS PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016 CrossRef CAS PubMed.
- J. E. A. Otterstedt, J. Chem. Phys., 1973, 58, 5716 CrossRef CAS.
- L. A. Baker, B. Marchetti, T. N. V. Karsili, V. G. Stavros and M. N. R. Ashfold, Chem. Soc. Rev., 2017, 46, 3770 RSC.
- A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2004, 6, 2763 RSC.
- J. Hemminger, G. Crabtree and M. Kastner, Basic Energy Sciences Advisory Committee, US Department of Energy, 2008 Search PubMed.
- M. Pagliaro, A. G. Konstandopoulos, R. Ciriminna and G. Palmisano, Energy Environ. Sci., 2010, 3, 279 RSC.
- G. F. Moore and G. W. Brudvig, Annu. Rev. Condens. Matter Phys., 2011, 2, 303 CrossRef CAS.
- D. Gust, T. A. Moore and A. L. Moore, Faraday Discuss., 2012, 155, 9 RSC.
- M. D. Kärkäs, O. Verho, E. V. Johnston and B. Åkermark, Chem. Rev., 2014, 114, 11863 CrossRef PubMed.
- O. David, C. Dedonder-Lardeux and C. Jouvet, Int. Rev. Phys. Chem., 2002, 21, 499 Search PubMed.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093 RSC.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 2000, 321, 479 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 2000, 329, 130 CrossRef CAS.
- W. Domcke and A. L. Sobolewski, Science, 2003, 302, 1693 CrossRef CAS PubMed.
- X. Wu, T. N. V. Karsili and W. Domcke, ChemPhysChem, 2016, 17, 1298 CrossRef CAS PubMed.
- R. Szabla, R. W. Góra, M. Janicki and J. Šponer, Faraday Discuss., 2016, 195, 237 RSC.
- R. Szabla, J. Šponer and R. W. Góra, J. Phys. Chem. Lett., 2015, 6, 1467 CrossRef CAS PubMed.
- R. Szabla, J. E. Šponer, J. Šponer, A. L. Sobolewski and R. W. Góra, Phys. Chem. Chem. Phys., 2014, 16, 17617 RSC.
- X. Liu, A. L. Sobolewski, R. Borrelli and W. Domcke, Phys. Chem. Chem. Phys., 2013, 15, 5957 RSC.
- X. Liu, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 7788 CrossRef CAS PubMed.
- J. Ehrmaier, M. J. Janicki, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2018, 20, 14420 RSC.
- J. Ehrmaier, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754 CrossRef CAS PubMed.
- N. Esteves- López, S. Coussan, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2016, 18, 25637 RSC.
- X. Pang, J. Ehrmaier, X. Wu, C. Jiang, W. Xie, A. L. Sobolewski and W. Domcke, Chem. Phys., 2018, 515, 550 CrossRef CAS.
- J. Ehrmaier, W. Domcke and D. Opalka, J. Phys. Chem. Lett., 2018, 9, 4695 CrossRef CAS PubMed.
- E. J. Rabe, K. L. Corp, A. L. Sobolewski, W. Domcke and C. W. Schlenker, J. Phys. Chem. Lett., 2018, 9, 6257 CrossRef CAS PubMed.
- W. Domcke, J. Ehrmaier and A. L. Sobolewski, ChemPhotoChem, 2019, 3, 10 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395 CrossRef CAS.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37 CrossRef.
- TURBOMOLE, v. 6.6, 2014; a development of the University of Karlsruhe and Forschungszentrum Karlsruhe 1989–2007; TURBOMOLE GmbH since 2007.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26 CAS.
- A. K. Belyaev and O. V. Lebedev, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 014701 CrossRef.
- A. K. Belyaev, W. Domcke, C. Lasser and G. Triglia, J. Chem. Phys., 2015, 142, 104307 CrossRef PubMed.
- W. Xie and W. Domcke, J. Chem. Phys., 2017, 147, 184114 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- W. Xie, M. Sapunar, M. Sala, N. Došlić and W. Domcke, J. Chem. Phys., in revision Search PubMed.
- H. H. Perkampus, UV-Vis Atlas of Organic Compounds, VCH, 1992 Search PubMed.
- M. Chachisvilis and A. H. Zewail, J. Phys. Chem. A, 1999, 103, 7408 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 1991, 180, 381 CrossRef CAS.
- P. C. Varras, P. S. Gritzapis and K. C. Fylaktakidou, Mol. Phys., 2018, 116, 154 CrossRef CAS.
- I. J. Palmer, I. N. Ragazos, F. Bernardi, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1993, 115, 673 CrossRef CAS.
- A. L. Sobolewski, C. Woywod and W. Domcke, J. Chem. Phys., 1993, 98, 5627 CrossRef CAS.
- R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540 CrossRef CAS PubMed.
- Y. Wang, X. Wang and M. Antonietti, Angew. Chem., Int. Ed., 2012, 51, 68 CrossRef CAS PubMed.
- S. Chaiwongwattana, M. Sapunar, A. Ponzi, P. Decleva and N. Došlić, J. Phys. Chem. A, 2015, 119, 10637 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2019 |