Quantitation of the Fe spatial distribution in biological tissue by online double isotope dilution analysis with LA-ICP-MS: a strategy for estimating measurement uncertainty†
David N.
Douglas
a,
Jennifer
O'Reilly
a,
Ciaran
O'Connor
b,
Barry L.
Sharp
c and
Heidi
Goenaga-Infante
*a
aInorganic Analysis, Science and Innovation, LGC Group, Queens Road, Teddington, Middlesex TW11 0LY, UK. E-mail: Heidi.Goenaga-Infante@lgcgroup.com
bESI New Wave Research Division, Bozeman, Montana 59715, USA
cChemistry Department, School of Science, Loughborough University, Epinal Way, Loughborough, LE11 3TU, UK
First published on 3rd November 2015
Abstract
A novel strategy is reported for the quantitative analysis of the Fe spatial distribution in biological tissue using laser ablation with ICP-MS and on-line double isotope dilution analysis (LA-ICP-IDMS). The proposed on-line IDMS method involves post-ablation introduction of an isotopically enriched 57Fe spike solution using a total consumption nebuliser. To investigate the potential applicability of the developed method to biological tissue with varying Fe concentrations (akin to those observed in bio-imaging), the effect of sample-to-calibration standard blend ratio on the accuracy of the Fe data was investigated over a range of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 to 1
0.2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. To achieve this, homogenised sheep brain tissue doped with Fe (251 μg g−1) was used as the model sample. Recoveries of 80–109% of the expected Fe concentration in the model tissue sample (as determined by ID-ICP-MS of the tissue digest) were obtained over a sample-to-standard ratio range of 1
10. To achieve this, homogenised sheep brain tissue doped with Fe (251 μg g−1) was used as the model sample. Recoveries of 80–109% of the expected Fe concentration in the model tissue sample (as determined by ID-ICP-MS of the tissue digest) were obtained over a sample-to-standard ratio range of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. A systematic estimation of measurement uncertainty for LA-ICP-IDMS was undertaken and for the first time the mass flow rate of the material was determined via single-IDMS. An overall combined expanded uncertainty (k = 2) of 15–27% was achieved for ratio matching of 1
5. A systematic estimation of measurement uncertainty for LA-ICP-IDMS was undertaken and for the first time the mass flow rate of the material was determined via single-IDMS. An overall combined expanded uncertainty (k = 2) of 15–27% was achieved for ratio matching of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. The factors with greatest contribution to the overall uncertainty were the mass of spike, the measured ratio of the standard blend and the mass of calibrant. External calibration with internal standardisation was performed on the same model sample for the purpose of comparison. The measurement uncertainty associated with this calibration approach was for the first time estimated for LA bio-imaging by taking into account the contributions from the signal intensity variance, the errors from least squares regression and concentration of the standards. For external calibration the overall relative expanded uncertainty was approximately 50% (k = 2), with the uncertainty in the linear least squares regression (R2 of 0.9833) and the signal variation being the main contributing factors. The results for Fe in the model sample agreed well with those determined via LA-ICP-IDMS. For the first time, the potential of a LA-ICP-MS isotope dilution calibration strategy to validate higher throughput calibration methodologies (e.g. matrix-matched external calibration with internal standardisation), as would be required for routine medical applications, has been demonstrated.
5. The factors with greatest contribution to the overall uncertainty were the mass of spike, the measured ratio of the standard blend and the mass of calibrant. External calibration with internal standardisation was performed on the same model sample for the purpose of comparison. The measurement uncertainty associated with this calibration approach was for the first time estimated for LA bio-imaging by taking into account the contributions from the signal intensity variance, the errors from least squares regression and concentration of the standards. For external calibration the overall relative expanded uncertainty was approximately 50% (k = 2), with the uncertainty in the linear least squares regression (R2 of 0.9833) and the signal variation being the main contributing factors. The results for Fe in the model sample agreed well with those determined via LA-ICP-IDMS. For the first time, the potential of a LA-ICP-MS isotope dilution calibration strategy to validate higher throughput calibration methodologies (e.g. matrix-matched external calibration with internal standardisation), as would be required for routine medical applications, has been demonstrated.
Introduction
Significant laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) bio-imaging research has focused on the role of transition metals1,2 and their potential link with neurodegenerative diseases. For example, the association of Fe with Alzheimer's disease3–5 (AD), Cu with Wilson's disease6 and Al with Parkinson's disease.7 Whilst LA-ICP-MS offers good sensitivity and spatial-resolution, traceable quantitative information is difficult to obtain due to a lack of suitable certified reference materials8,9 or SI traceable/reference calibration strategies. As such, much of the published information regarding elemental spatial distribution is based on qualitative images10 and relative differences therein. Thus with the potential utilisation of LA-ICP-MS in underpinning clinical diagnosis techniques, and to help inform on absolute elemental concentrations for disease model development,11 a traceable reference method is required that provides a comprehensive estimate of the measurement uncertainty for analyte spatial distribution. This can then be used to validate existing higher throughput calibration strategies.External calibration is a relatively high throughput strategy often adopted to obtain quantitative information, and for bio-imaging a number of in-house prepared standards have been reported: powdered pellets,12 sol–gel matrix,13 doped bovine serum or whole blood,14etc. However, significant deviation of the standard matrix composition from that of the sample can result in poor accuracy of the quantitative data. Differences in tissue density or matrix composition result in different mass flow rates and changing plasma conditions. For tissue imaging, matrix-matched materials, e.g. spiked homogenised tissue, have been suggested as a more appropriate standard for external calibration.15–17 However, due to the varied nature of tissues, homogenised standards are of an approximate match and cannot exactly replicate the different structures and densities encountered when imaging sample sections. Thus an internal standard (I.S.) is required to correct for variation in sample mass flow rate caused by changes in tissue density and thickness, and to correct for any deviation of calibration standard–sample matching. Instrumental drift, particle transport and particle processing in the ICP can also be corrected, but requires careful selection of a suitable I.S., ideally occurring in the same particle fraction as the analyte. Alternatively, embedding tissue sections in a polymer and doping the blank resin with analytes has been suggested as a means of creating matrix matching calibrants.18 However, investigation of potential changes in analyte distribution via the embedding process has not been reported so far.
For homogenised tissues an I.S. can be spiked directly into the material and thoroughly mixed. However for imaging of real samples, where structural features must be preserved, this approach cannot be adopted. Several methods to address the difficulty in applying an I.S. whilst retaining tissue structure have been reported.19–22 However, these methods describe production of a uniform layer containing the I.S. external to the tissue section, and although useful in correcting for instrumental drift, they cannot compensate for variation of mass flow. To address this problem, methodology that introduces the I.S. into both sample and standard, without affecting the original composition of the sample has been recently reported.23
Isotope dilution mass spectrometry (IDMS), is often the quantitative method of choice to achieve high accuracy with very low uncertainty.24,25 IDMS is advantageous in that it uses the ideal I.S. for the analyte, an isotopic variant of itself, to correct for instrumental signal drift, matrix effects or losses of analyte. It is most effective when the enriched isotope spike is mixed with the sample at the earliest point in the preparation procedure, which for homogenised materials is relatively simple, allowing for gravimetric determination of sample and spike mass. For imaging, the I.S. must be distributed such that it reflects changes in material density and thickness whilst also achieving equilibration with the sample. Alternatively, online addition of a solution to the laser aerosol, pre- or post-sample ablation can be utilised to add an isotopically enriched solution to the laser aerosol and facilitate IDMS calibration.26–29
Fernández et al.27 reported the use of online double-IDMS with LA-ICP-MS for the direct quantitative analysis of solid certified reference materials (silicate glasses and powdered samples). Double IDMS is advantageous in that it negates the need to accurately determine the isotopically enriched spike concentration. In order to apply double-IDMS Fernández et al. assumed the mass flow rate of sample and standard were equal and as such the respective mass components cancelled in the IDMS equation. However, the method was demonstrated to achieve poor accuracy when the sample and standard matrices were different e.g. different opacities between glass matrices, thus highlighting the need for more accurate matching to ensure similar mass flow rates. By removing the mass component of the double-IDMS equation, the mass variation, knowledge of which is required for a comprehensive estimation of measurement uncertainty, is unaccounted for.
Here we present a systematic approach for estimating the measurement uncertainty associated with spatial Fe quantitation by online-addition double-IDMS, in a biological tissue. This has been conducted within a range of concentrations relevant to medical research with pre-clinical AD models. The Fe concentrations of matrix-matched standards and the model sample (homogenised sheep brain tissue doped with 251 μg g−1 of Fe), both prepared in-house, were determined by double-IDMS of tissue digests. The spatial homogeneity of Fe distribution was investigated both in the standards and the synthetic sample by LA-ICP-MS. For the first time, a strategy based on single IDMS was implemented to determine the mass flow rate, and thus for a given integration period, the mass of ablated tissue. Investigation of the spatial mass variation within and between the in-house prepared matrix-matched tissues and accurate determination of the online-spike mass flow rate were used to provide a more robust and detailed estimation of the measurement uncertainty. The feasibility of an online double-IDMS LA-ICP-MS measurement strategy was investigated to validate an external calibration approach previously developed by O'Reilly et al.23 using homogenised sheep brain standards doped with Fe. A detailed estimation of measurement uncertainty for external calibration by least-squares regression was also performed.
Experimental
Materials and reagents
An elemental stock solution of Fe (Ultra Scientific, LGC Standards, Middlesex, UK) was used to prepare matrix-matched calibration blends for the IDMS and external calibration approaches. Methanol (Promochem, LGC Standards, Middlesex, UK) was used for the immersion of calibration standards into a solution containing 250 ng g−1 Rh (Ultra Scientific, LGC Standards, Middlesex, UK) for internal standardisation correction purposes. High purity deionised water (18.2 MΩ cm) from an ELGA purelab Milli-Q flex system (ELGA, Veolia Water, Marlow, UK) was used throughout. Nitric acid (5% v/v, Romil, Cambridge, UK) was used as diluent for the spike solution. 57Fe spike (95.10%, AEA, Oxfordshire, UK) was used to prepare the isotopically enriched spike solution for LA-ICP-IDMS. Calibration standards and the model sample were prepared from sheep brain, obtained from a local Halal butchers in the Hounslow area.Instrumentation
A double-focusing sector field ICP-MS (Element 2, Thermo Fisher Scientific, Bremen, DE) operated in time resolved analysis (TRA) mode was used for LA analysis throughout. All measurements were performed in medium mass resolution (m/Δm = 4000) to eliminate polyatomic ion interferences at m/z 56 and 57. Typical operating parameters are given in Table 1. A NWR213 laser ablation system (ESI, New Wave Research Division, Huntingdon, UK) equipped with a two-volume cell was configured to perform parallel line scanning of tissue sections. Operating conditions for laser ablation to ensure complete removal of standard/sample are summarised in Table 1, and were the same for all experimental investigations detailed below. Optimisation of carrier gas flow, makeup gas flow (nebuliser gas flow in the case of online addition of spike solution), plasma power, and torch position were carried out daily using NIST SRM 612 glass, (National Institute of Standards and Technology, NIST, Gaithersburg, US) with a certified value of 51 ± 2 μg g−1 Fe, to achieve maximum sensitivity whilst minimising oxide formation.| Laser ablation system (ESI NWR213) | |
|---|---|
| Repetition rate | 20 Hz |
| Laser energy | 0.037 mJ, equating to 7.62 J cm−2 |
| Spot size/sampling mode | 30 μm/single line scan |
| Stage translation rate | 121 μm s−1 |
| Carrier gas flow | 0.8 L min−1 He |
| ICP-MS (Thermo Fisher Scientific Element2) | |
|---|---|
| Plasma RF power | 1450 W |
| Nebuliser (wet plasma) | Agilent CapLC total consumption |
| Sampler/skimmer cones | Ni/Ni |
| Cooling gas flow | 15 L min−1 Ar |
| Auxiliary gas flow | 1 L min−1 Ar |
| Nebuliser/make-up gas flow | 0.975 L min−1 Ar |
| Isotopes monitored | 56Fe, 57Fe, 103Rh |
| Detector mode | Dual range |
| Dwell time | 150 ms |
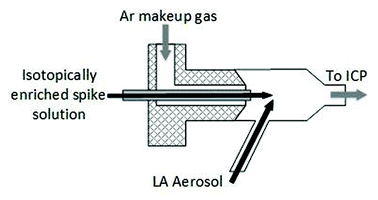
Different sample introduction configurations were employed for wet plasma (IDMS experiments) and dry plasma (spatial homogeneity studies and matrix matched external calibration experiments). For LA-ICP-IDMS (wet plasma), online addition of a 57Fe isotopically enriched spike solution (59.9 ng g−1 Fe) was achieved using a total consumption nebulizer and a small quartz spray chamber (CapLC, Agilent capillary LC interface kit G3680A). The solution was aspirated via the CapLC interface (coupled to the base of the ICP torch), to which the dry LA aerosol from the laser cell was added to the sidearm of the spray chamber via Tygon® tubing (1 m × 1/8′′ I.D.), within which the LA and solution aerosols mixed at a ca. 45° angle, as shown in Fig. 1. A fixed solution flow rate of 8 μl min−1, selected for optimal signal stability, was applied from a 5 ml PTFE Luer Lok valve syringe (Crawford Scientific, Lanarkshire, UK), driven by a syringe infusion pump (KdS Scientific, Massachusetts, US). The resulting wet plasma has been shown to be more robust than dry plasma and mitigates against detrimental effects of sample loading.30,31
For matrix matched external calibration and spatial homogeneity studies (dry plasma) coupling of the LA and ICP-MS instruments was achieved using Tygon® tubing (1 m × 1/8′′ I.D.) between the ablation cell and the ICP-MS torch, with an argon make-up gas added to the laser aerosol via a y-piece directly after the cell.
Procedures
Preparation of matrix-matched calibration standards and model sample
Tissue sections doped with Fe were prepared as described by Hare et al.15 Whole sheep brain was first washed with D.I. water and then blended using a handheld TissueRuptor homogeniser (Qiagen, West Sussex, UK) to create a bulk homogenous material. The tissue was sampled into histology moulds and a constant mass of 2% (v/v) HNO3 solution (<6% mass of tissue), containing a range of Fe concentrations, was added to each tissue to yield a concentration range within the solids of ca. 0–2000 μg g−1 Fe; being representative of the range observed previously in mouse brain tissue sections.23 A blank tissue section was prepared by adding deionised water only. The calibration standards were re-homogenised to ensure complete uniformity of the stock standard in the tissue matrix. Each ‘doped’ aliquot was then set/frozen at −80 °C before being cryosliced at −20 °C into 30 μm thick sections (Leica Cryostat CM1850, Milton Keynes, UK), mounted onto glass microscope slides (Thermo Fisher Scientific, Loughborough, UK) and air-dried at room temperature ready for analysis. A model sample tissue was prepared in the same manner, to yield a Fe concentration of 251 μg g−1, representative of the average Fe concentration previously observed.Determination of total Fe tissue concentration by digestion and double-IDMS
Total Fe determination of the prepared slide-mounted homogenised sheep brain standards and model samples was carried out by IDMS using the ‘approximate’ double matched method (sample and primary standard spiked with an enriched 57Fe source, to give an optimal 56Fe/57Fe ratio close to 1). Tissue material was removed from the slides using a glass scraper. Approximately 8–10 mg of each replicate material, weighed on a 5-figure balance, was taken and spiked with 57Fe prior to digestion (SK-10 high pressure PTFE vessels with μ-inserts in a Milestone Ethos microwave system), using 1 ml of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) mixed HNO3/H2O2 acid digest.
1 (v/v) mixed HNO3/H2O2 acid digest.
Triplicate analyses (3 tissue sections per digest) for standards and model sample were carried out by closed vessel microwave digestion to determine the Fe concentrations. The primary calibration standard was prepared using SRM 3126a, an Fe standard solution, (NIST, Gaithersburg, US) at a certified Fe concentration of 10.001 ± 0.023 μg g−1. Digested samples and the calibration blend were diluted with Milli-Q water to approximately 20 ng g−1 immediately prior to analysis to yield similar signal intensities; thus approximately matching. Total Fe determination was carried out using an Agilent 7700x ICP-MS, operated in hydrogen mode, using the conditions summarised in Table S1 of the ESI.†
Spatial homogeneity of Fe across prepared tissue sections
Spatial homogeneity of the prepared standards was investigated for tissue sections in the X and Y axis by monitoring 56Fe using LA-ICP-MS; two sections per standard, sectioned 0.5 mm apart. The sampling pattern employed, shown in Fig. 2, was used to cover the maximum representable area with the minimum number of lines. In brief, eight lines were traversed in both the X and Y axis to create nine quadrants, such as to cover the entire tissue with equal spacing between ablation paths. Within three of the quadrants (diagonally aligned), labelled A, B and C in Fig. 2, a further 8 ablation lines were traversed. In total 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 pixels were generated, 5456 in the X-axis and 5392 the Y-axis (X-axis was sampled first and as such there were 64 less points in the Y-axis due to transect crossing).
848 pixels were generated, 5456 in the X-axis and 5392 the Y-axis (X-axis was sampled first and as such there were 64 less points in the Y-axis due to transect crossing).
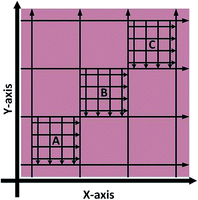 | ||
| Fig. 2 LA-ICP-MS sampling strategy to investigate Fe X–Y homogeneity within doped homogenised sheep brain tissue (not to scale). | ||
Homogeneity of the doped tissue in the Z-axis was investigated through comparison of the individual digests for each standard described above. Sub-samples (digest replicates) were selected so as to provide information on tissue sections at 0.5 mm sectioned intervals, such that in triplicate a 1.0 mm range was covered. This provided an indication of bulk Fe homogeneity in the Z-axis across the tissue volume used.
LA-ICP-IDMS with online-addition of isotopic spike
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 μm in length. As the total Fe concentration for the model sample was known via double IDMS of the tissue digests, the sample mass flow rate was also investigated. An average mass flow rate was calculated from ablation of 5 parallel lines, each 12
815 μm in length. As the total Fe concentration for the model sample was known via double IDMS of the tissue digests, the sample mass flow rate was also investigated. An average mass flow rate was calculated from ablation of 5 parallel lines, each 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 μm in length, for 7 replicates.
815 μm in length, for 7 replicates.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 up to 1
0.2 up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 were investigated. Signal matching of the spike was performed against the model sample homogenised sheep brain containing 251 μg g−1 Fe, ensuring consistency for sample–standard ratio comparison. A ratio of ca. 1 was achieved for the raw 56Fe and 57Fe signal intensities.
10 were investigated. Signal matching of the spike was performed against the model sample homogenised sheep brain containing 251 μg g−1 Fe, ensuring consistency for sample–standard ratio comparison. A ratio of ca. 1 was achieved for the raw 56Fe and 57Fe signal intensities.
The total concentration of Fe within the model sample determined by LA-ICP-IDMS was calculated from the mean of 5 ablation lines, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 μm in length. Each sample ablation line was bracketed by the ablation of a respective standard line, equal in length so as to achieve the same integration period (total 6 ablation lines for each standard bracket/matching).
815 μm in length. Each sample ablation line was bracketed by the ablation of a respective standard line, equal in length so as to achieve the same integration period (total 6 ablation lines for each standard bracket/matching).
Comparison of total Fe concentration by LA-ICP-IDMS and matrix-matched external calibration
The inclusion of an I.S. in both the model sample and standards has been described in detail previously by O'Reilly et al.23 In brief: the prepared matrix-matched standards and model sample were immersed in a methanolic solution containing 250 ng g−1 Rh I.S. standard, were ablated under dry plasma conditions, and an average I.S. corrected Fe response calculated for each standard from 5 line scans, each 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 μm in length. Responses were plotted against respective total Fe (determined from double IDMS characterisation outlined earlier) and least squares regression employed to generate a calibration curve.
815 μm in length. Responses were plotted against respective total Fe (determined from double IDMS characterisation outlined earlier) and least squares regression employed to generate a calibration curve.
LA calibration strategies and associated uncertainty
When the mass flow rates (g s−1) of the sample and primary standard are equivalent, the related mass terms cancel. By adding an isotopically enriched spike online to the ablated aerosol, the mass of spike can be assumed constant and the related terms also cancel, see simplified eqn (2). Although approximate terms can be cancelled, to create a full uncertainty budget their associated variation must be investigated, as discussed below.
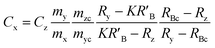 | (1) |
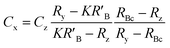 | (2) |
A mass bias correction factor, K, can also be included and is defined by the ratio of the true calibration blend, RBc, to that of the measured calibration blend ratio, R′Bc, see eqn (3). RBc, the true ratio, can be calculated from knowledge of the concentration of spike in the calibration blend, Cyc; the sum of the spike isotope amount ratio, ∑Ry; and the sum of the primary standard isotope amount ratio, ∑Rz, see eqn (4). However, the mass of spike and the mass of the standard terms must also be known. Below we present a method to determine the mass of the sample by means of single-IDMS using knowledge of the concentration of the analyte and mass flow rate of the online-addition of spike solution.
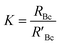 | (3) |
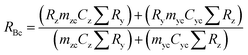 | (4) |
Contribution to the overall uncertainty arising from the natural isotope ratio and sum of ratios, Rz and ∑Rz respectively, can be calculated from the isotope abundance uncertainty provided by IUPAC. The uncertainty contribution from the spike isotope ratio and sum of isotope ratios, Ry and ∑Ry respectively, can be determined from the isotopic abundance uncertainty detailed within the spike certification. The uncertainty of the spike concentration, Cy, can be estimated gravimetrically, whilst that from the calibration standard concentration, Cz, can be estimated via double IDMS calibration of the tissue digests.
Mass terms were determined experimentally in order to estimate the associated uncertainty and thus their contribution to the overall final measurement error.
The concentration of an element can be determined using single IDMS, as shown in eqn (5). If the concentration is known and well characterised, such as with a primary standard or calibration standard determined via IDMS, then the equation can be rearranged to calculate the mass of the material, see eqn (6). In this rearrangement the spike mass (my, g) is substituted for the spike mass flow rate (Ṁy, g s−1), so as to calculate a mass flow rate of the standard (Ṁz). This can then be applied to determine the total mass (mz) for a given ablation line; multiplying by the total integration time.
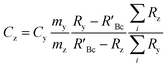 | (5) |
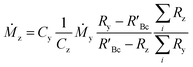 | (6) |
Least squares regression was performed for each line scan per standard (n = 5) rather than an average of the tissue in generating a response curve; accounting for spatial Fe differences (variance in y). Following EURACHEM/CITAC guidelines, for unweighted calibration data, where the observed variation in y, var(yobs), is based on p measurements, with S the residual standard deviation and b1 the gradient, eqn (7) was applied:
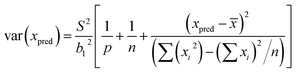 | (7) |
For the determination of error uncertainty associated with the prepared standards, eqn (8) was employed. Where n is the number of xi values used to create the calibration curve and u(xi) the standard uncertainty associated with the concentration of each standard used in the calibration, x.
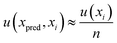 | (8) |
Standard uncertainties for calibration data, concentration values of standards and the sample signal were combined to yield the final measurement uncertainty estimation.
Results and discussion
Total tissue Fe concentration and spatial distribution
The mean Fe concentration (n = 3) and expanded uncertainty (k = 2) of the standards and model sample, determined by double IDMS of tissue digests, are given in Table 2. The ratio of Fe concentration in the standard to that in the sample (Cz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cx) is also given. As discussed below, due to the inhomogeneity of real samples this was used to investigate the effect of calibration to sample blend ratio matching on the accuracy and uncertainty of the Fe results. This information is invaluable for future imaging work with real tissue samples.
Cx) is also given. As discussed below, due to the inhomogeneity of real samples this was used to investigate the effect of calibration to sample blend ratio matching on the accuracy and uncertainty of the Fe results. This information is invaluable for future imaging work with real tissue samples.
| Tissue | Fe (μg g−1) | U (k = 2) | % RU (k = 2) |
C
z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cx Cx |
|---|---|---|---|---|
| a U, the expanded standard uncertainty; % RU, percent relative standard uncertainty. | ||||
| Std 1 | 48.1 | 2.6 | 5.5 | 0.2 |
| Std 2 | 142 | 7.0 | 4.9 | 0.6 |
| Std 3 | 250 | 4.8 | 1.9 | 1.0 |
| Std 4 | 520 | 72 | 14 | 2.1 |
| Std 5 | 721 | 25 | 3.4 | 2.9 |
| Std 6 | 1449 | 53 | 3.7 | 5.8 |
| Std 7 | 2505 | 71 | 2.8 | 10 |
| Sample | 251 | 6.4 | 2.6 | — |
Relative uncertainties for the measurement of single digest solutions ranged from 0.75 to 1.2% (k = 2). No significant variation between tissue replicates (indicative of distribution in the Z-axis) was observed.
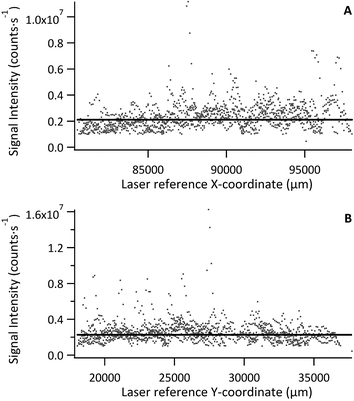
Signal intensity relative to laser recorded X or Y position was used to visualise homogeneity in either direction, with each data point representing a pixel 30 μm × 30 μm, as shown in Fig. 3 for a tissue section of Std 2 (142 μg g−1 Fe). No significant trends or variations in response were observed for standard or model sample tissues, with the majority of data points falling close to the mean. However, a few exceptions (3–4 out of ca. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points), where Fe signal intensity reached 3–4 times that of the mean, were observed. These were restricted to single data points and it must be noted that this was a quick inspection of the Fe distribution. As internal standardisation and wet plasma conditions were not applied; pixels depicting Fe signal intensity much greater than the mean must be treated with caution as they most likely result from variation in tissue thickness and subsequently the mass flow rate, or from liberation of particulate trapped within the transport conduit. Signal representing wash-in and washout of the material from the ablation cell were not included in the data processing.
000 data points), where Fe signal intensity reached 3–4 times that of the mean, were observed. These were restricted to single data points and it must be noted that this was a quick inspection of the Fe distribution. As internal standardisation and wet plasma conditions were not applied; pixels depicting Fe signal intensity much greater than the mean must be treated with caution as they most likely result from variation in tissue thickness and subsequently the mass flow rate, or from liberation of particulate trapped within the transport conduit. Signal representing wash-in and washout of the material from the ablation cell were not included in the data processing.
The mean Fe signal intensity and standard deviation was calculated from each ablation path to estimate variation in either X or Y as % RSD. The resulting data is summarised in Table 3. The average variation across all standards and sample in X and Y was 16% and 16% RSD, respectively. Some large variations were observed, namely for Std 5 in the Y-axis and Std 7 in the X-axis. These sections were smaller than the others and as such less tissue area was sampled. However, overall the Fe distribution was fairly homogenous. It is expected that internal standardisation would lower the observed variation through data correction where only partial sample was ablated, also by excluding data where no sample was present, accounting for mass flow rate variation and signal drift.
| Tissue | % RSD in X | % RSD in Y |
|---|---|---|
| Std 1 | 9.5 | 6.5 |
| Std 2 | 13 | 17 |
| Std 3 | 17 | 10 |
| Std 4 | 11 | 13 |
| Std 5 | 19 | 21 |
| Std 6 | 12 | 9.0 |
| Std 7 | 25 | 13 |
| Model sample | 19 | 19 |
LA-ICP-IDMS
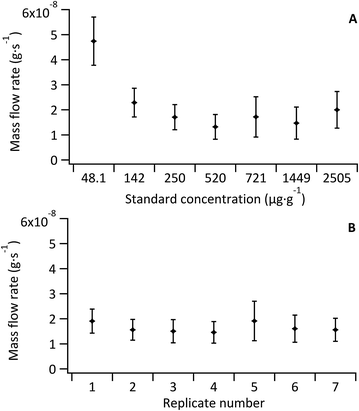
As the Fe concentration in the model sample was also well known via double-IDMS of the tissue digest, the mean mass flow rate of the sample (n = 5) was investigated for each standard-bracketing experiment discussed below (see Fig. 4B). Mass flow rates of the sample replicates (mean 1.5 × 10−8 ± 5.2 × 10−9 g s−1) were in agreement with each other and with that of the standards (mean, excluding the blank, of 1.8 × 10−8 ± 6.2 × 10−9 g s−1). No variation or trend was observed given that data for sample mass flow rate determination was collected over two consecutive days.
The sample mass flow rate with the largest uncertainty was observed for replicate 5, which coincided with the largest uncertainty observed for a standard mass flow rate (Std 5; 721 μg g−1 Fe); a result of an increase in the 57Fe signal variance from decreased stability of the total consumption nebuliser. Overall the largest uncertainty contribution for all standards and sample replicates came from the noise of the measured 56Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57Fe ratio. The uncertainty associated to the measured ratios accounted for 50% of the overall uncertainty in the un-doped tissue and ranged from 70% to 80% in the Fe-doped standards. Other contributions to the uncertainty included the Fe concentration in the spike and in the tissue (determined via double-IDMS of tissue digests).
57Fe ratio. The uncertainty associated to the measured ratios accounted for 50% of the overall uncertainty in the un-doped tissue and ranged from 70% to 80% in the Fe-doped standards. Other contributions to the uncertainty included the Fe concentration in the spike and in the tissue (determined via double-IDMS of tissue digests).
Investigation of sample–standard matching ratio for LA-ICP-IDMS
The lowest uncertainty for double–IDMS can be achieved by exact matching of the standard and sample isotope ratios, as discussed by Hearn et al.34 This is impractical for imaging of real samples, which are heterogeneous and where regions of interest contain elevated analyte concentrations, ‘hot-spots’. Thus approximate matching of the sample–standard ratio was investigated. To establish a working range, concentration ratios between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 and 1
0.2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 were investigated and the effects of moving away from the optimal 1
10 were investigated and the effects of moving away from the optimal 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio on the uncertainty and accuracy were examined.
1 ratio on the uncertainty and accuracy were examined.
The concentrations of Fe in the model tissue sample as determined by LA-ICP-MS with on-line double-IDMS are shown in Table 4. Sample to standard matching ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 up to 1
1 up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.8 showed fairly good recoveries from the expected Fe concentrations (determined by tissue digestion and ICP-IDMS) considering the estimated measurement uncertainties. Poor recovery was found for the other investigated ratios (farthest from the 1
5.8 showed fairly good recoveries from the expected Fe concentrations (determined by tissue digestion and ICP-IDMS) considering the estimated measurement uncertainties. Poor recovery was found for the other investigated ratios (farthest from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio).
1 ratio).
C
z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cx Cx |
Fe (μg g−1) | U (k = 2) | % RU (k = 2) | % recovery |
|---|---|---|---|---|
| 0.2 | 103 | 15 | 15 | 41 |
| 0.6 | 171 | 28 | 17 | 68 |
| 1.0 | 217 | 41 | 19 | 86 |
| 2.1 | 274 | 68 | 25 | 109 |
| 2.9 | 200 | 55 | 27 | 80 |
| 5.8 | 272 | 68 | 25 | 108 |
| 10 | 197 | 44 | 22 | 78 |
For 56Fe, the standard to sample mean ratio was plotted against the Fe concentration ratio. The obtained graph is represented in Fig. 5. Linearity was good for a concentration-ratio range of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.8 (R2 = 0.9978), but much poorer (R2 = 0.9762) when the bottom 2 and top standards were included. For matching sample and standard blends, the 56Fez
5.8 (R2 = 0.9978), but much poorer (R2 = 0.9762) when the bottom 2 and top standards were included. For matching sample and standard blends, the 56Fez![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56Fex ratio should equal the concentration ratio Cz
56Fex ratio should equal the concentration ratio Cz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cx, such that 56Fez
Cx, such that 56Fez![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56Fex/Cz
56Fex/Cz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cx equals 1. Deviations from this value are thus indicative of differences between the blends and are most likely due to subtle variations in density or particle size distributions between the model sample and standard.
Cx equals 1. Deviations from this value are thus indicative of differences between the blends and are most likely due to subtle variations in density or particle size distributions between the model sample and standard.
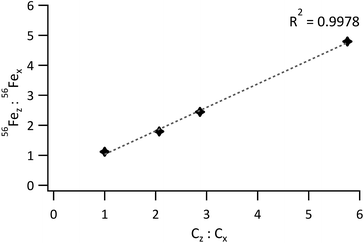 | ||
| Fig. 5 Ratio of the 56Fe signal from the standard to the 56Fe signal from the sample vs. the ratio of the Fe concentration in the standard to the Fe concentration in the sample. | ||
Expanded uncertainties (k = 2) ranged from 15% to 27% for sample to calibration Fe ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.8. The main contributing factors to the overall uncertainties were the mass of standard (assumed equal to the sample), the mass of spike and the measured ratio of the standard blend, see Table 5. Uncertainties from LA-ICP-IDMS were less than half of those determined by matrix-matched external calibration, as detailed below. The limit of detection (LOD, 3σ criterion) for Fe using a 30 μm spot was calculated according to that described by Longerich et al.,35 where here na and nb both equalled 5 and sensitivity was calculated from linear regression of ratio response for sample-to-calibration Fe ratios of 1
5.8. The main contributing factors to the overall uncertainties were the mass of standard (assumed equal to the sample), the mass of spike and the measured ratio of the standard blend, see Table 5. Uncertainties from LA-ICP-IDMS were less than half of those determined by matrix-matched external calibration, as detailed below. The limit of detection (LOD, 3σ criterion) for Fe using a 30 μm spot was calculated according to that described by Longerich et al.,35 where here na and nb both equalled 5 and sensitivity was calculated from linear regression of ratio response for sample-to-calibration Fe ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.8. The LOD and LOQ were found to be 17 μg g−1 and 57 μg g−1 (for 56Fe), respectively. Lower limits could be achieved by increasing the tissue thickness, increasing the spot diameter or reducing the contribution of the isotopically enriched spike to the 56Fe signal intensity.
5.8. The LOD and LOQ were found to be 17 μg g−1 and 57 μg g−1 (for 56Fe), respectively. Lower limits could be achieved by increasing the tissue thickness, increasing the spot diameter or reducing the contribution of the isotopically enriched spike to the 56Fe signal intensity.
| Component | Relative contribution (%) | |
|---|---|---|
| M zc | Mass of calibration standard | 65.6 |
| M yc | Mass of spike used in calibration blend | 29.6 |
| R′Bc | Measured isotope ratio of standard blend | 4.70 |
| All other components | <0.1 |
Matrix-matched external calibration with 103Rh internal standardisation
As outlined in the Procedure section, linear regression was used to generate a response curve of the I.S. corrected 56Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103Rh ratio; using the range of standards employed in the LA-double-IDMS matching ratio investigation. The I.S. corrected intensity from the model sample was calibrated against this response curve, (R2 = 0.9833). Linearity for the response curve was good as Rh at a fixed concentration, homogenously distributed, compensated for any variability in mass flow rate. It must be noted that the mass flow rates of standards calculated by single IDMS, shown in Fig. 4 above, were determined prior to immersion in a methanolic solution. As well as being an effective means of delivering an I.S., immersion in methanol also dehydrates the tissue sections.36 Experimental observation showed that after immersion, complete consumption of the material by laser ablation was achieved at lower fluence. However this variable was held constant across all experiments for consistency. Any variation in the local water content could result in a large variability in local tissue density remaining and result in a mass flow rate difference, however Rh internal standardisation accounts for this.
103Rh ratio; using the range of standards employed in the LA-double-IDMS matching ratio investigation. The I.S. corrected intensity from the model sample was calibrated against this response curve, (R2 = 0.9833). Linearity for the response curve was good as Rh at a fixed concentration, homogenously distributed, compensated for any variability in mass flow rate. It must be noted that the mass flow rates of standards calculated by single IDMS, shown in Fig. 4 above, were determined prior to immersion in a methanolic solution. As well as being an effective means of delivering an I.S., immersion in methanol also dehydrates the tissue sections.36 Experimental observation showed that after immersion, complete consumption of the material by laser ablation was achieved at lower fluence. However this variable was held constant across all experiments for consistency. Any variation in the local water content could result in a large variability in local tissue density remaining and result in a mass flow rate difference, however Rh internal standardisation accounts for this.
Table 6 summarises the model tissue sample Fe concentration and corresponding measurement uncertainty, as determined via external calibration, the LOD for this procedure has been reported by O'Reilly et al.23 As can be seen, this Fe concentration is in good agreement with that determined by LA-double-IDMS and with that determined by ICP-IDMS after tissue digestion. However, when taking into account errors arising from the linearity of the least squares regression, the noise of the sample signal and the uncertainty of standard concentrations, the final expanded uncertainty (k = 2) was found to be 46%. This final uncertainty was ca. 3 times larger than the signal % RSD, often incorrectly quoted as the measurement uncertainty. The main contributing factors, shown in Table 7, were the error arising from the response curve determined by least squares regression (estimated using eqn (7)) and the 56Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103Rh isotope ratio variance. A small contribution from the concentration error of Std 4 was also observed.
103Rh isotope ratio variance. A small contribution from the concentration error of Std 4 was also observed.
| Fe (μg g−1) | U (k = 2) | % RU (k = 2) | % RSD signal | % recovery | |
|---|---|---|---|---|---|
| Rh corrected | 248 | 110 | 46 | 15 | 99.1 |
| Component | Relative contributions (%) Rh corrected |
|---|---|
| Regression | 52.7 |
| Signal | 46.9 |
| Std 1 | <0.1 |
| Std 2 | <0.1 |
| Std 3 | <0.1 |
| Std 4 | 0.3 |
| Std 5 | <0.1 |
| Std 6 | <0.1 |
| Std 7 | <0.1 |
Errors arising from least squares regression are often not considered when quoting an associated uncertainty for matrix-matched external calibration where the final uncertainty is only a function of the variance in the observed sample signal. For linear regression where R2 = 1, an offset is not observed and the associated standard concentration errors are negligible, this approximation is then acceptable; but where deviation of any of these components does occur, they must be considered for final uncertainty estimation.
Conclusions
A novel, systematic approach, to calculate the uncertainty associated with Fe spatial distribution determined by LA-ICP-MS with online double IDMS has been demonstrated using a model tissue sample (251 μg g−1 Fe, homogenised sheep brain). The sample-to-calibration standard blend ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 up to 1
1 up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 provided the best accuracy, thus demonstrating the potential of the developed calibration strategy for tissue with a native non-homogeneous elemental distribution. The relative expanded uncertainty (k = 2) was found to be independent of the concentration level within the sample-to-calibration standard blend ratios investigated. It was found to range from 15 to 27% for blend ratio matching of 1
5 provided the best accuracy, thus demonstrating the potential of the developed calibration strategy for tissue with a native non-homogeneous elemental distribution. The relative expanded uncertainty (k = 2) was found to be independent of the concentration level within the sample-to-calibration standard blend ratios investigated. It was found to range from 15 to 27% for blend ratio matching of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. Such uncertainty levels are less than half of that found by external calibration.
5. Such uncertainty levels are less than half of that found by external calibration.
Offline determination of the online-added spike mass flow rate and the well-defined tissue Fe concentrations in the samples and standards, (as determined by double-IDMS) facilitated the development of a novel strategy to determine material mass flow rate (Ṁ) using single-IDMS. The largest contributions to calculating the mass flow rate standard uncertainty were from the noise of the measured 56Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57Fe ratio and from that of the spike concentration, 52% and 45% respectively. Comparison of the sample and standard mass flow rate was used as an indication of suitable matrix-matching, and apart from the un-doped calibration standard, no significant differences between standard and sample tissues were observed.
57Fe ratio and from that of the spike concentration, 52% and 45% respectively. Comparison of the sample and standard mass flow rate was used as an indication of suitable matrix-matching, and apart from the un-doped calibration standard, no significant differences between standard and sample tissues were observed.
Investigation of mass flow rate components and their variance allowed a comprehensive estimate of the measurement uncertainty budget, where the mass of the calibration standard and the mass of spike showed the largest contributions, 65.6% and 29.6% respectively. The measured isotope ratio of the calibration blend contribution to the overall uncertainty was approximately 4.7%.
A relative expanded uncertainty of 46% for external calibration using the same calibration standards and model sample as used for LA-double-IDMS; was achieved, following EURACHEM/CITAC guidelines.30
A model sample, containing a well characterised homogenously distributed analyte at a concentration relevant to medical research with pre-clinical AD models, was employed here to systematically study the LA-ICP-IDMS strategy and its related uncertainty. Future work will study the feasibility of the developed strategy for quantitative imaging of real biological samples on a pixel-by-pixel basis, targeting “hot spot” regions of Fe that have been identified by external calibration strategies or complementary techniques such as XRF. Focus will be on the improvement of the efficiency of online mixing of spike and sample37 and the investigation of the suitability of different materials as matrix matching calibration standards. This will be achieved by determining their respective mass flow rates in comparison to real sample tissues.
Acknowledgements
The authors would like to acknowledge the UK National Measurement and Regulatory Office for funding this work within the Chemical and Biological Metrology project CB/2012/IS12; and Innovate UK (formerly the Technology Strategy Board, TSB) for funding the associated knowledge transfer partnership (KTP 8979).References
- J. S. Becker, M. Zoriy, B. Wu, A. Matusch and J. S. Becker, J. Anal. At. Spectrom., 2008, 23, 1275–1280 RSC.
- C. Giesen, T. Mairinger, L. Khoury, L. Waentig, N. Jakubowski and U. Panne, Anal. Chem., 2011, 83, 8177–8183 CrossRef CAS PubMed.
- J. S. Becker, M. Zoriy, A. Matusch, B. Wu, D. Salber, C. Palm and J. S. Becker, Mass Spectrom. Rev., 2010, 29, 156–175 CAS.
- R. W. Hutchinson, A. G. Cox, C. W. McLeod, P. S. Marshall, A. Harper, E. L. Dawson and D. R. Howlett, Anal. Biochem., 2005, 346, 225–233 CrossRef CAS PubMed.
- D. J. Lehmann, M. Worwood, R. Ellis, V. L. J. Wimhurst, A. T. Merryweather-Clarke, D. R. Warden, A. D. Smith and K. J. H. Robson, J. Med. Genet., 2006, 43, e52 CrossRef CAS PubMed.
- G. Loudianos and J. D. Gitlin, Semin. Liver Dis., 2000, 20, 353–364 CrossRef CAS PubMed.
- C. Exley, Coord. Chem. Rev., 2012, 256, 2142–2146 CrossRef CAS.
- B. Jackson, S. Harper, L. Smith and J. Flinn, Anal. Bioanal. Chem., 2006, 384, 951–957 CrossRef CAS PubMed.
- N. Miliszkiewicz, S. Walas and A. Tobiasz, J. Anal. At. Spectrom., 2015, 30, 327–338 RSC.
- D. S. Urgast, J. H. Beattie and J. Feldmann, Curr. Opin. Clin. Nutr. Metab. Care, 2014, 17, 431–439 CrossRef CAS PubMed.
- J. F. Collingwood and M. R. Davidson, Front. Pharmacol., 2014, 5, 191 Search PubMed.
- M. Pakieła, M. Wojciechowski, B. Wagner and E. Bulska, J. Anal. At. Spectrom., 2011, 26, 1539–1543 RSC.
- A. J. Fitzpatrick, T. Kurtis Kyser, D. Chipley and D. Beauchemin, J. Anal. At. Spectrom., 2008, 23, 244–248 RSC.
- J. A. T. Pugh, A. G. Cox, C. W. McLeod, J. Bunch, B. Whitby, B. Gordon, T. Kalber and E. White, J. Anal. At. Spectrom., 2011, 26, 1667–1673 RSC.
- D. J. Hare, J. Lear, D. Bishop, A. Beavis and P. A. Doble, Anal. Methods, 2013, 5, 1915–1921 RSC.
- D. Hare, C. Austin and P. Doble, Analyst, 2012, 137, 1527–1537 RSC.
- K. Jurowski, M. Szewczyk, W. Piekoszewski, M. Herman, B. Szewczyk, G. Nowak, S. Walas, N. Miliszkiewicz, A. Tobiasz and J. Dobrowolska-Iwanek, J. Anal. At. Spectrom., 2014, 29, 1425–1431 RSC.
- O. Reifschneider, C. A. Wehe, I. Raj, J. Ehmcke, G. Ciarimboli, M. Sperling and U. Karst, Metallomics, 2013, 5, 1440–1447 RSC.
- M. Bonta, H. Lohninger, M. Marchetti-Deschmann and A. Limbeck, Analyst, 2014, 139, 1521–1531 RSC.
- I. Konz, B. Fernández, R. Pereiro, H. Gonzáalez, L. Álvarez, M. Coca-Prados and A. Sanz-Medel, Anal. Bioanal. Chem., 2013, 405, 3091–3096 CrossRef CAS PubMed.
- C. Austin, F. Fryer, J. Lear, D. Bishop, D. Hare, T. Rawling, L. Kirkup, A. McDonagh and P. Doble, J. Anal. At. Spectrom., 2011, 26, 1494–1501 RSC.
- C. Austin, D. Hare, T. Rawling, A. M. McDonagh and P. Doble, J. Anal. At. Spectrom., 2010, 25, 722–725 RSC.
- J. O'Reilly, D. Douglas, J. Braybrook, P. W. So, E. Vergucht, J. Garrevoet, B. Vekemans, L. Vincze and H. Goenaga-Infante, J. Anal. At. Spectrom., 2014, 29, 1378–1384 RSC.
- P. De Bievre and H. S. Peiser, Fresenius. J. Anal. Chem., 1997, 359, 523–525 CrossRef CAS.
- Guidelines for achieving high accuracy in isotope dilution mass spectrometry (IDMS), ed. M. Sargent, C. Harrington and R. Harte, RSC Analytical Methods Committee, January 2002 Search PubMed.
- F. Claverie, J. Malherbe, N. Bier, J. L. Molloy and S. E. Long, Anal. Bioanal. Chem., 2013, 405, 2289–2299 CrossRef CAS PubMed.
- B. Fernández, P. Rodríguez-González, J. I. G. Alonso, J. Malherbe, S. García-Fonseca, R. Pereiro and A. Sanz-Medel, Anal. Chim. Acta, 2014, 851, 64–71 CrossRef PubMed.
- C. Pickhardt, A. V. Izmer, M. V. Zoriy, D. Schaumlöffel and J. S. Becker, Int. J. Mass Spectrom., 2006, 248, 136–141 CrossRef CAS.
- C. K. Yang, P.-H. Chi, Y.-C. Lin, Y.-C. Sun and M.-H. Yang, Talanta, 2010, 80, 1222–1227 CrossRef CAS PubMed.
- C. O'Connor, B. L. Sharp and P. Evans, J. Anal. At. Spectrom., 2006, 21, 556–565 RSC.
- L. Flamigni, J. Koch and D. Günther, J. Anal. At. Spectrom., 2014, 29, 280–286 RSC.
- F. Claverie, J. Malherbe, N. Bier, J. L. Molloy and S. E. Long, Anal. Chem., 2013, 85, 3584–3591 CrossRef CAS PubMed.
- Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, ed. S. L. R. Ellison and A. Williams, 3rd edn, 2012, Search PubMedavailable from www.eurachem.org.
- R. Hearn, P. Evans and M. Sargent, J. Anal. At. Spectrom., 2005, 20, 1019–1023 RSC.
- H. P. Longerich, S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 1996, 11, 899–904 RSC.
- M. A. Brown, R. B. Reed and R. W. Henry, J. Int. Soc. Plastination, 2002, 17, 28–33 Search PubMed.
- L. Feng and J. Wang, J. Anal. At. Spectrom., 2014, 29, 2183–2189 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ja00351b |
| This journal is © The Royal Society of Chemistry 2016 |