Accuracy of laser-ablation (LA)-MC-ICPMS Sr isotope analysis of (bio)apatite – a problem reassessed†
Wolfgang
Müller
*a and
Robert
Anczkiewicz
b
aDepartment of Earth Sciences, Royal Holloway University of London, Egham, UK. E-mail: wolfgang.muller@rhul.ac.uk
bInstitute of Geological Sciences, Polish Academy of Sciences, Krakow, Poland
First published on 28th October 2015
Abstract
Apatite is a key mineral whose Sr-isotope record has a wide range of applications including palaeofluid flow studies from inorganic apatite, and past faunal/human mobility or palaeoecology using bioapatite. The incremental growth of mammalian enamel bioapatite potentially allows extraction of Sr isotopic compositions at sub-annual time-resolution using laser-ablation plasma mass spectrometry (LA-MC-ICPMS). However, existing apatite LA-MC-ICPMS Sr-isotope data have yielded mixed results. Here we assess the achievable accuracy/precision of (bio)apatite LA-MC-ICPMS Sr-isotope analysis and evaluate sources of inaccuracy. Using robust plasma conditions (ThO+/Th+ < 0.2%), we obtain long-term (4 year) accurate and precise Sr-isotope data for modern shark teeth for both radiogenic 87Sr/86Sr (0.709171 ± 0.000053, 2 SD), and naturally invariant 84Sr/86Sr (0.056500 ± 0.000040, 2 SD). Based on our accurate 84Sr/86Sr-results also for low-Sr enamel, we deduce that interferences are successfully corrected (Kr) or negligible (Ca-argide/dimer), leaving 87Rb and 40Ca31P16O isobaric interferences as key potential sources for 87Sr/86Sr inaccuracy. Our (pseudo)high-resolution mass scans using a virtually Rb–Sr-free, concentrated Ca–P-solution simulating apatite LA analysis show no evidence for 40Ca31P16O at the required intensities to explain previously observed 87Sr/86Sr offsets. Rather, using the same Ca–P solution with varying Rb + Sr isotope standard additions, we accurately constrain the mass bias-corrected 85Rb/87Rb-ratio, and using apatite glasses assess the extent of Rb/Sr elemental fractionation during laser-ablation. Finally, we present concordant LA-MC-ICPMS and microsampled-TIMS 87Sr/86Sr results for low-Sr tooth enamel with highly variable inter & intra-87Sr/86Sr ratios and comparatively high Rb/Sr-ratios. This archaeological example also illustrates well the problem of defining equivalent sample volumes that allow unequivocal comparison between LA and TIMS data.
1 Introduction
The (Rb-)Sr system is particularly well-suited for in situ isotopic analysis. This is due to (1) the occurrence of large natural Sr-isotopic variations resulting from the strongly contrasting geochemical behaviour of Rb and Sr coupled with the radioactive decay of 87Rb to 87Sr, (2) the high Sr yet concomitantly low Rb concentrations found in a variety of materials due to the geochemical resemblance of Sr with major element Ca, and (3) the ubiquitous occurrence of Sr-rich minerals (e.g. feldspars, apatite, clinopyroxene), rocks (carbonates, phosphates) or biological materials (e.g. otoliths, teeth).In situ analysis at high-spatial resolution is essential in order to extract the time-series information at high resolution stored in continuously growing samples like otoliths, dental enamel or speleothems and/or to retrieve isotopic information with textural control (e.g. in zoned plagioclase). Besides the much improved spatial resolution compared to conventional microsampling,1,2in situ analysis is also faster than thermal ionization mass spectrometry (TIMS) or solution multi-collector inductively-coupled-plasma mass spectrometry (MC-ICPMS), but at the expense of not being able to chemically remove isobaric interferences off-line via ion-exchange chemistry.
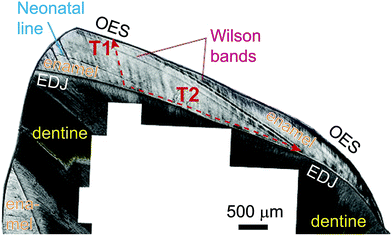
The potential of in situ Sr isotope analysis using laser-ablation-MC-ICPMS (LA-MC-ICPMS) with precision comparable to TIMS was realized early in the development of MC-ICPMS.3 Consequently, LA-MC-ICPMS Sr-isotope analyses applied to carbonates or feldspars have gradually become standard methodological repertoire,4–7 despite the occasionally reported accuracy problems.8,9 On the other hand, LA-MC-ICPMS Sr isotope investigations of inorganically or biologically formed Ca-phosphates (apatite) have often resulted in inaccurate data, attributed to the existence of an interference on m/z = 87 from 40Ca31P16O,10–12 even though some successful applications also have been reported, albeit with somewhat reduced precision/accuracy.13,14 Apatite is not only a key inorganic mineral recording, for example, palaeo-fluid flow processes,15 but it is especially also the key biomineral in vertebrate skeletons. The Sr-isotopic composition particularly of tooth enamel has arguably become the key methodology in palaeoecology and archaeology to trace past faunal or human mobility.16,17 Owing to the incremental two-stage mineralization18,19 of tooth enamel over several years, for example in humans of ∼15 years, spatially-resolved Sr-isotopic data of enamel have the potential to reveal sub-seasonal mobility patterns, especially if combined with counted chronologies from enamel histology20 (Fig. 1).
Here we report the results of systematic investigations aimed at evaluating the various sources of inaccuracy of LA-MC-ICPMS 87Sr/86Sr ratio analysis of (bio)apatite, focusing on radiogenic variability rather than natural stable Sr-isotope variations. Besides reporting accurate values of the naturally invariant 84Sr/86Sr ratio (if normalized to constant 88Sr/86Sr (ref. 21)), we focus on the presence of 40Ca31P16O signals via detailed mass scans at various mass resolutions, because at m/z = 87, molecular interferences such as 40Ca31P16O are resolvable from either 87Sr or 87Rb at medium or high mass resolution. We also assess the crucial 87Rb correction, the accuracy of which for (bio)apatite is paramount in view of the often elevated 85Rb/86Sr ratios (∼5 × 10−2 to 10−4). Finally, we show not only long-term (∼4 year) external standard reproducibilities of Sr-isotope ratios by LA-MC-ICPMS, but importantly also results of comparative microsampling-TIMS vs. LA-MC-ICPMS analyses of the same archaeological human teeth to evaluate accuracy of the latter.
2 Materials and methods
All Sr isotopic data – both in solution and laser-ablation mode – were obtained in dry-plasma mode using a ThermoFisher Neptune MC-ICPMS at the Institute of Geological Sciences, Krakow Research Centre of the Polish Academy of Sciences. The MC-ICPMS is either coupled with an Aridus II desolvating nebulizer (Cetac) or a RESOlution M-50 excimer (193 nm) laser-ablation system (Resonetics, now Australian Scientific Instruments (ASI); Table 1). The latter features a two-volume Laurin LA cell which ensures signal uniformity as well as rapid washout anywhere in the cell.22 Eight of the nine Neptune Faraday (FAR) cups equipped with 1011 Ω resistors were used for static analysis; L4 could not be utilized due to its limited mobility caused by the attached block of four ion counters (Table 2). Faraday cups L2 and H2 were placed at half mass positions (nominal m/z = 83.5 and 86.5) using both Er–Yb doped Rb–Sr solutions and LA of Durango apatite to monitor the presence of REE2+ since diagenetically-modified bioapatite may contain appreciable REE concentrations.23 Cup efficiencies were set to unity, and gain of amplifiers measured at least once daily. Mass scan experiments utilized either the axial FAR detector or the axial secondary electron multiplier (SEM) detector. All Neptune LA data were obtained in low mass resolution (ΔM/M = 400), whereas some solution experiments, especially regarding mass scans, were conducted at (pseudo)medium and (pseudo)high mass resolution (ΔM/M = 4000, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively). Peak centering was done at the start of an analysis and was found to be extremely stable. In order to accurately correct for Kr isobars (typical 84Kr-signals ∼0.3–0.45 mV; ∼1–1.5% of 84Sr) and all other baseline signals, extended (2 × 90 s) on-peak background measurements were used. In order to have an isotopic match for the on-peak baseline measurement, a quick (1–2 min) ‘pre-ablation’ of the material to be analyzed preceded the baseline measurements following signal washout. Data were collected in cycles each comprising four or eight 1.05 s integrations. Peak intensities were corrected online for baseline contributions, exported and all further data reduction was done offline. Exponential mass bias correction using constant 88Sr/86Sr (ref. 21) was applied following offline peak-stripping using custom data reduction in EXCEL. Doubly-charged Er and Yb signals were monitored but found to be negligible for both standards and samples analyzed herein because modern and well-preserved fossil/archaeological teeth are characterized by [REE] in the (sub-)ppb concentration range.23
000, respectively). Peak centering was done at the start of an analysis and was found to be extremely stable. In order to accurately correct for Kr isobars (typical 84Kr-signals ∼0.3–0.45 mV; ∼1–1.5% of 84Sr) and all other baseline signals, extended (2 × 90 s) on-peak background measurements were used. In order to have an isotopic match for the on-peak baseline measurement, a quick (1–2 min) ‘pre-ablation’ of the material to be analyzed preceded the baseline measurements following signal washout. Data were collected in cycles each comprising four or eight 1.05 s integrations. Peak intensities were corrected online for baseline contributions, exported and all further data reduction was done offline. Exponential mass bias correction using constant 88Sr/86Sr (ref. 21) was applied following offline peak-stripping using custom data reduction in EXCEL. Doubly-charged Er and Yb signals were monitored but found to be negligible for both standards and samples analyzed herein because modern and well-preserved fossil/archaeological teeth are characterized by [REE] in the (sub-)ppb concentration range.23
| MC-ICPMS: Neptune | |
|---|---|
| RF power | Soln.: 1250–1350 W; LA: 1150–1250 W |
| Sampler, skimmer cones | Normal, not Xcone |
| Carrier, sweep gas flow (Ar); diatomic gas flow (N2) | Aridus II: PFA nebulizer, 50 μl min−1 uptake, ∼0.89 l min−1 carrier gas, ∼3.5 l min−1 sweep gas, ∼10 ml min−1 N2 (all optimized daily) |
| LA: ∼520 ml min−1 (optimized daily), ∼6.5 ml min−1 N2 (optimized daily) | |
| Coolant gas flow | 15 l min−1 |
| Auxilliary gas flow | 0.9 l min−1 |
| ThO+/Th+ (248/232) | Solution: <0.1% (typically 0.06%); LA: <0.2% |
| 232Th/238U | Solution & LA: >0.93 |
| Er2+/Er+; Yb2+/Yb+ | 0.7; 0.4% |
| Integration time | 8 or 4 × 1.04 s |
| Laser-ablation system RESOlution M-50 | |
|---|---|
| Energy density (fluence) on target | 8 J cm−2 |
| LA cell | Laurin two-volume M-50 cell |
| He gas flow | 900 ml min−1 |
| Laser repetition rate | 5–30 Hz |
| Laser spot size | 60–110 μm |
| Ablation mode | Path ablation, X–Y stage speed 0.3–0.5 mm min−1 |
| Transport tubing | Nylon |
| Signal smoothing | Squid included |
| Faraday cup | L3 | L2 | L1 | C | H1 | H2 | H3 | H4 |
|---|---|---|---|---|---|---|---|---|
| Element/isotope (m/z) | 82 | 83.5 | 84 | 85 | 86 | 86.5 | 87 | 88 |
| Sr | 84 (∼0.56%) | 86 (∼9.9%) | 87 (∼7.0%) | 88 (∼82.6%) | ||||
| Rb | 85 (72.2%) | 87 (27.8%) | ||||||
| Kr | 82 (11.6%) | 84 (57.0%) | 86 (17.3%) | |||||
| xx Ca40Ar, xxCa40Ca, (40Ca: 96.941%, 40Ar: 99.60%) | 42CaAr, 42CaCa (0.647%) | 44CaAr, 44CaCa (2.086%) | 46CaAr, 46CaCa (0.004%) | 48CaAr, 48CaCa (0.187%) | ||||
| REE2+ | 164Dy (28.18%), 164Er (1.61%) | 167Er (22.93%) | 168Er (26.78%), 168Yb (0.13%) | 170Er (14.93%), 170Yb (3.04%) | 172Yb (21.83%) | 173Yb (16.13%) | 174Yb (31.83%), 174Hf (0.16%) | 176Yb (12.76%), 176Hf (5.26%), 176Lu (2.59%) |
| CaPO | 40Ca31P16O (16O: 99.76%) | 40Ca31P17O (17O: 0.038%) |
Additional contextual LA-ICPMS trace element concentration data were obtained at Royal Holloway University of London (RHUL) using the RESOlution M-50 prototype LA system featuring a Laurin two-volume LA cell coupled to an Agilent 7500ce quadrupole-ICPMS.22
Emphasis of both solution and LA-MC-ICPMS analyses was on ‘robust’ plasma conditions characterized by very low ThO+/Th+-ratios (<0.2%; unless deliberately detuned, see below) and 232Th/238U-ratios > 0.93 (solutions with equal Th–U concentrations or SRM612), which were achieved by attention to carrier gas flow, RF power and aided by using a dry plasma with N2-addition24,25 (Table 1). We note that ThO+ represents the maximum metal oxide-production owing to its highest metal–oxygen bond strength,26–30 and that other common oxide-production monitoring ratios (e.g. UO+/U+ (ref. 31) and CeO+/Ce+) are ∼2.5–3.5× lower. With the exception of the alkali-metals, this is valid not only for neutrals but also for metal-cations because the corresponding metal–O or metal-cation–O bond strengths differ by no more than ±10–20%.26,27,30 Er2+ and Yb2+ production rates were 0.7 and 0.4%, respectively. Overall, conditions were kept as similar as possible between the two modi so as to allow comparability of the corresponding results. X-geometry skimmer cones were not used due potentially elevated oxide production that is offset only with minimal (<10%) sensitivity gain.32
2A Solution MC-ICPMS analysis
Solution analysis was designed such that it simulated LA analysis of apatite as closely as possible, especially regarding the presence of Ca and P ions to obtain equivalent mass bias data for the correction of LA analyses. Based on the Sr sensitivity of ∼140 V ppm−1 for above tuning conditions, 50 ppb Sr yield ∼7 V Srtotal (5.8 V 88Sr), which also constitutes a Sr-signal for suitably precise LA-MC-ICPMS isotope analysis (ideally >1.5 V 88Sr). Considering bioapatite stoichiometry characterized by both Ca/P-ratios of ∼2.15 and Sr/Ca ratios between 3 × 10−4 to 3 × 10−3 (equivalent to [Sr] 100–1000 ppm), we prepared a 50–22 ppm Ca–P solution from 1000 ppm single element ICP/AAS standard solutions. Residual Rb and Sr impurities were removed from this Ca–P solution via two-stage ion exchange chemistry using cation resin AG50W-X8 (BioRad) and SrSpec resin33 (Eichrom). This Ca–P-solution was used for all mass scan experiments as well as the experiments to assess the prevailing 85Rb/87Rb-ratio for accurate Rb-correction via variable SRM987/SRM984 (Sr/Rb) additions (see below). Detailed conditions such as integration time, detector type, mass resolution of the mass scans are given where applicable.2B Laser-ablation-MC-ICPMS analysis
Using an energy density on the sample surface of ∼8 J cm−2, laser-ablation took place in a He atmosphere (∼900 ml min−1 flowrate through LA cell), with Ar and N2 (∼520, ∼6.5 ml min−1, respectively; all optimized daily) being admixed downstream of the ablation cell before the squid signal smoothing device22 (Table 1). All LA data acquisition took place in continuous path ablation mode. Depending on analyte Sr concentration and the desired spatial resolution, laser spot and repetition rate were selected and ranged between 60–110 μm and 5–30 Hz, respectively, with target 88Sr signals in LA mode ranging between ∼2–8 V.Tuning for maximum sensitivity and signal stability as well as best peak shape while maintaining above mentioned robust plasma characteristics was performed in path ablation mode using SRM616 glass (41.7 ppm Sr34), which yielded 0.8–1.8 mV ppm−1 88Sr using a 60 μm spot, 5 Hz repetition rate and 1 mm min−1 stage speed, depending on cones and prior usage. SRM616 with its low Rb/Sr ratio (0.0025) was chosen so as to avoid unnecessary Rb build-up on cones, crucial in view of maintaining accurate on-peak baselines. Using the higher concentrated NIST-glasses (SRM612, 610) can lead to increasing Rb-signals due to ‘cone-erosion’; the latter, however, were used briefly to assess 232Th/238U and ThO+/Th+-ratios. Matrix-matched Ca–P–(Si) STDP glasses35 were used to evaluate elemental Rb/Sr fractionation.
The main in-house Sr-isotope standard used is the isotopically-homogenous (Sr) enameloid of modern shark teeth captured off-shore W-Australia and S-Africa, respectively, with [Sr] of ∼2500 μg g−1. These record the modern open-marine 87Sr/86Sr ratio of 0.709175;36 whale teeth were evaluated but not utilized further because of their too thin enamel.
2C Comparative TIMS analysis
Thick sections (∼200 μm) were prepared from tooth halves of medieval humans from the small Pb–Ag mining community of Sulzburg (Black Forest, SW Germany)37,38 and used for comparative Sr-isotope LA-MC-ICPMS and microsampling-TIMS (msp) analyses. Microsampling of enamel fragments (∼160–720 μg) using a microscope-mounted drill followed by conventional TIMS analysis2,33 provides comparative data to LA-MC-ICPMS results. The former followed previously published methodology2,33 with the exception that analyses utilized a VG354 TIMS in multi-dynamic mode at RHUL.39 Sr total procedure blanks were 47.4 ± 14.6 pg (1 SD, n = 4) and no blank correction was necessary in view of sample Sr contents. Corresponding analyses of SRM987 (≥30 ng) yielded 87Sr/86Sr 0.710253 ± 0.000018 (2 SD; n = 10).3 Results and discussion
All results are listed in Tables S1–S3 (ESI†) and displayed in Fig. 2–6.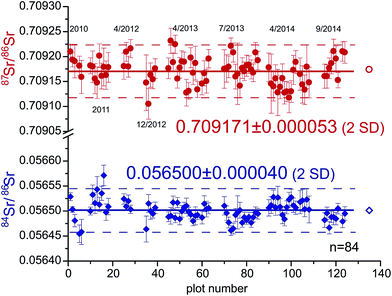 | ||
| Fig. 2 Long-term Sr-isotope ratios of two modern shark in-house reference samples analyzed by LA-MC-ICPMS interchangeably over four years (Aug. 2010–Sep. 2014; n = 84 of 88). Both 87Sr/86Sr and 84Sr/86Sr ratios yield good long-term reproducibility and resultant averages demonstrate remarkable accuracy as they agree well with modern marine 87Sr/86Sr (0.709175 ± 0.000019) and natural 84Sr/86Sr ratios (0.056492 ± 0.0000016)28,31 (open symbols on right hand side). | ||
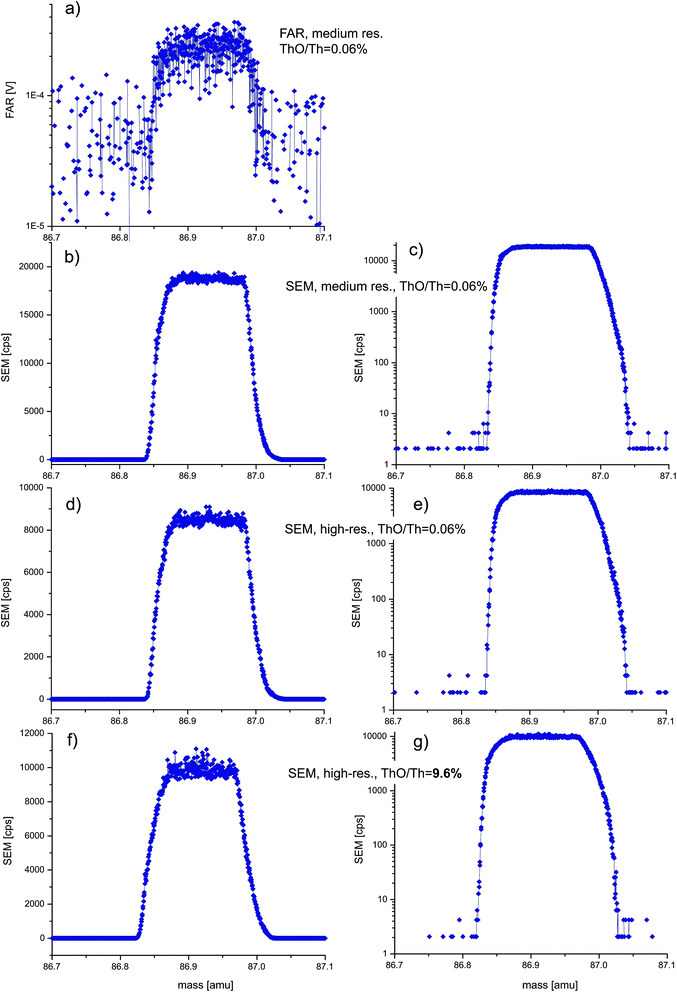 | ||
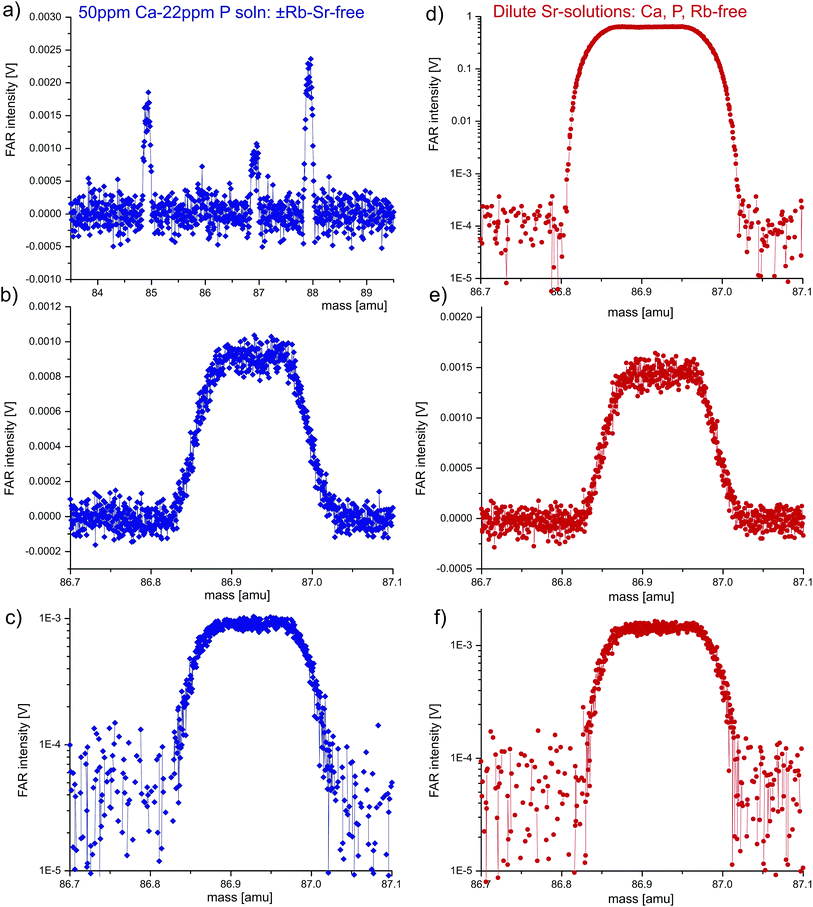
| Fig. 4 Mass scan experiments using a ±Rb–Sr-free, concentrated Ca–P solution at (pseudo)medium (a–c) and (pseudo)high mass-resolution (d–g) to evaluate the presence of molecular interference 40Ca31P16O at m/z = 87. In view of the small residual signals, Faraday (a) or SEM collectors (b–g) were used. ‘Robust’ plasma conditions (ThO/Th = 0.06%, a–e) vs. deliberately detuned, high oxide plasma conditions (ThO/Th = 9.6%, f, g) reveal neither differences in peak-shape, nor, crucially, any minor peaks offset towards slightly higher mass that would indicate molecular interferences. This suggests that 40Ca31P16O does not occur at the required intensities to explain offsets in LA-MC-ICPMS 87Sr/86Sr ratios of apatite11,12 (see text; steps: 800, integration time/step: SEM 0.52 s, FAR 1.04 s). | ||
3A LA-MC-ICPMS Sr isotope data of marine Ca-phosphates
The long-term (Aug. 2010–Sep. 2014) LA-MC-ICPMS reproducibility of both 87Sr/86Sr and 84Sr/86Sr ratios of two modern shark enameloid specimens serving as in-house reference samples analyzed interchangeably over four years are shown in Fig. 2 and Table S1 (ESI†). The resultant 87Sr/86Sr and 84Sr/86Sr ratios are 0.709171 ± 0.000053 (2SD; 0.075‰) and 0.056500 ± 0.000040 (2 SD; 0.71‰), respectively (n = 84 of 88). These values agree well with the modern marine 87Sr/86Sr (0.709175 ± 0.000019 (ref. 36)) and the natural 84Sr/86Sr ratios (0.056492 ± 0.0000016 (ref. 39)). There is no significant trend discernible in either of the two Sr-isotope ratios over the four-year measurement period. Corresponding SRM987 solution data obtained in dry-plasma mode on the same MC-ICPMS during the same time period are 0.710249 ± 0.000014 (2SD) and 0.056494 ± 0.000037 (2 SD; n = 48) for 87Sr/86Sr and 84Sr/86Sr, respectively. Our external LA-MC-ICPMS reproducibilities (2SD) of ±0.000053 (87Sr/86Sr) and ±0.000040 (84Sr/86Sr) are 3.80× and 1.07× larger than the respective solution values, which is interpreted to stem from residual biases from spectral interferences such as 87Rb and 84,86Kr. The strongly Kr-interference-affected 84Sr/86Sr-ratio has a comparable precision thus indicating that both solution and LA analyses may be similarly limited by the ability of correcting for 84,86Kr that affects both sample introduction modi equally via the Ar plasma gas. On the other hand, the 87Sr/86Sr values are almost fourfold less reproducible relative to solution data. We interpret this to reflect that on-peak baselines for the very small 85Rb signals in shark teeth in tandem with slightly varying residual on-peak Rb-memories from e.g. cones may have contributed to the degraded reproducibility (see below). Alternatively, the slightly worse LA vs. solution reproducibility of the 84Sr/86Sr ratio (0.05‰) may also partially help explain the difference (∼0.04‰) between the best reported LA 87Sr/86Sr-isotope ratio reproducibilities (0.000024; 0.035‰ (ref. 4)) and the one observed here (0.000053; 0.075‰).Our LA-MC-ICPMS data of marine bioapatite are remarkably accurate not only for the 87Sr/86Sr but especially also the 84Sr/86Sr ratio. The latter is a particularly sensitive indicator for the presence of spectral interferences because 84Sr is the least abundant Sr isotope (0.56% abundance), yet interfered not only by the most abundant Kr isotope (84Kr = 57.0%) but potentially also the largest Ca-dimer (44Ca40Ca) and Ca-argide (44Ca40Ar; 44Ca = 2.086%). In addition, the denominator-isotope 86Sr is interfered by the second most abundant Kr-isotope (86Kr = 17.3% and a small Ca-argide/dimer interference, 46Ca = 0.004%). The fact that we routinely obtain accurate 84Sr/86Sr data suggests that not only the extended on-peak baselines adequately correct for invariably present 84,86Kr (84Kr ∼ 1–1.5% of 84Sr) but also that no resolvable molecular Ca-dimer/argides are present. The latter is further confirmed because m/z = 82 (chiefly 42Ca40Ar, 42Ca40Ca) typically shows background-corrected intensities not resolvable from 0 μV (see below for equally accurate 84Sr/86Sr ratios of lower-[Sr] human enamel). Other studies, notably with different MC-ICPMS instrumentation, report the presence of significant Ca–Ca/Ar signals4,7,8 affecting especially the 84Sr/86Sr ratio, whereas others report no such effects.40,41 We surmise that both different plasma sources of MC-ICPMS instruments and especially attention to plasma tuning contribute to this difference, and deduce from our results that the Kr, Ca-dimers/argides (and REE2+) spectral interferences have successfully been corrected herein.
3B Presence of 40Ca31P16O at m/z = 87
While the very similar atomic masses of 87Rb and 87Sr (86.9092 and 86.9089 amu, respectively) make mass spectrometric resolution other than via reaction-chemistry42 essentially impossible, the presence of the potentially interfering Ca–P–O compound can be evaluated because its molecular mass is 0.0224 amu larger than the nuclide masses (86.931 vs. 86.909 amu) and it may form composite peaks akin to e.g. Fe-isotope analysis.43 Owing to the required mass resolution of ≥3900 (R = ΔM/M), we utilized both (pseudo)medium as well as (pseudo)high mass resolution to assess the presence of this interference. Because no homogenous low-Sr apatite is available for lengthy mass scans in LA mode, we mimicked laser-ablation of apatite using a nearly Rb–Sr-free, concentrated Ca–P solution (50 + 22 ppm, respectively) in dry-plasma mode (see above). The major element concentration was chosen so as to emulate a bioapatite LA analysis with [Sr] of 100 ppm (Sr/Ca = 3 × 10−4, equivalent to ∼2 V 88Sr).Using the central Faraday detector, comparative mass scans at low mass resolution of both the Ca–P solution and clean Sr-solutions are shown in Fig. 3. Based on both residual 85Rb and 88Sr peaks (1.5, 2.0 mV), the contribution of both 87Rb and 87Sr to m/z = 87 can be evaluated, which leaves <0.04 mV non-87(Rb + Sr) at m/z = 87. This strongly contrasts with the suggestion that 0.3–1% of m/z = 87 are Ca–P–O-related,11 implying that for LA apatite analysis yielding 2 V 88Sr (170 mV 87Sr), Ca–P–O should be ∼0.5–1.7 mV (>10–45× of what is seen here). Apart from observing identical (residual) m/z = 87 peaks for both the Ca–P and the clean Sr solutions (Fig. 3c–f) and quantifying the Rb + Sr contributions, low mass resolution is not sufficient to assess the potential presence of 40Ca31P16O.
At medium and high mass resolving power (Fig. 4) the residual m/z = 87 signals using the Ca–P solution are very small (<0.2 mV) and thus not only FAR but also SEM mass scans are shown. Neither the Faraday nor SEM scans show any evidence for a secondary (molecular) peak offset towards higher mass, even though the MC-ICPMS was also deliberately detuned towards high oxide production (ThO+/Th+ ∼ 9.6% vs. typically 0.06%; Fig. 4(f and g)vs.(a–e)). Yet even at these unusual plasma conditions, the mass scans are not noticeably different. We note that the SEM scans are not as symmetric as the equivalent FAR scans but crucially show no difference despite >150× varying oxide-levels. Slight peak asymmetry using the SEM is not untypical in our experience also with other elements, but most importantly m/z = 87 at (pseudo)high-mass resolution shows a flat peak plateau. We therefore deduce that 40Ca31P16O does not occur at the intensities high enough to explain the 87Sr/86Sr offsets observed in some cases of LA-MC-ICPMS analysis of apatite.11,12 Both Ca and P (and indeed Ca+ and P+ cations) are characterized by significantly lower oxygen affinity compared to Th (or Th+),26–28,30 and their oxide production can be approximated from the logarithmic relationship between metal-oxide/metal-ion ratio to M–O bond strength.29 Plotting our measured log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Th+, U+ and Ce+ oxide production relative to the respective bond strengths (bond dissociation energies) facilitates an approximate extrapolation to both Ca+ and P+, whose oxide productions become ∼0.0007 and ∼0.004%, respectively. It is unclear how likely a more complex triatomic CaPO molecule would form, but it may well form even less likely than Ca–O, in which case the ∼0.0007% value would represent an upper limit, supporting our observation of essentially negligible 40Ca31P16O at m/z = 87.
Th+, U+ and Ce+ oxide production relative to the respective bond strengths (bond dissociation energies) facilitates an approximate extrapolation to both Ca+ and P+, whose oxide productions become ∼0.0007 and ∼0.004%, respectively. It is unclear how likely a more complex triatomic CaPO molecule would form, but it may well form even less likely than Ca–O, in which case the ∼0.0007% value would represent an upper limit, supporting our observation of essentially negligible 40Ca31P16O at m/z = 87.
3C Accuracy of 87Rb correction
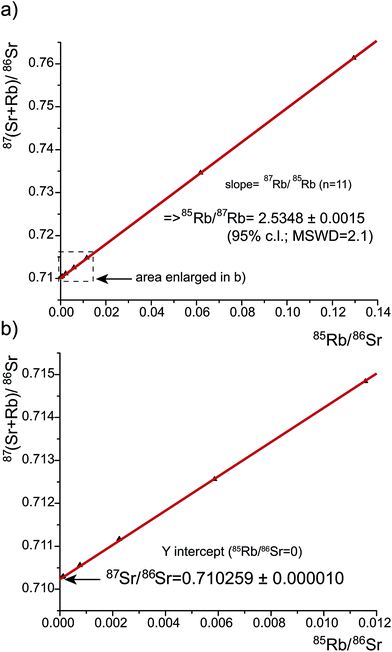
Apart from the potential of direct online Rb–Sr separation by ETV44 or reaction cell chemistry,42 the necessary isobaric correction of 87Rb on 87Sr for LA-MC-ICPMS analyses is performed by monitoring isobaric-interference-free 85Rb and applying an appropriate 85Rb/87Rb-ratio. In contrast to most carbonates with low 85Rb/86Sr ratios4 (∼10−4), bioapatite often has elevated 85Rb/86Sr ratios between ∼5 × 10−2 and 10−4 (see below). A 85Rb/86Sr ratio of 0.0026 results in a 87Rb/86Sr correction of ∼0.001 on 87Sr/86Sr, whose accuracy however depends on the effective 85Rb/87Rb and Rb/Sr ratios during analysis.Using our essentially Rb–Sr-free concentrated Ca–P solution as apatite matrix (see above), we prepared aliquots with varying 85Rb/86Sr ratios from 9.1 × 10−5 to 1.3 × 10−1 by adding varying amounts of SRM984 (Rb) and SRM987 (Sr) while maintaining few tens of ppb [Sr] (Table S2 (ESI†)). Plotting the Sr-mass-bias-corrected but 87Rb-uncorrected 87(Sr + Rb)/86Sr-ratio vs. the measured 85Rb/86Sr ratio yields the effective 87Rb/85Rb-ratio as slope and the SRM987 87Sr/86Sr-ratio as y-intercept of the regression line. The resultant regression line is highly linear across the considerable range of Rb/Sr-ratios, yielding a slope, converted into 85Rb/87Rb, of 2.5348 ± 0.0015 (95% c.l., MSWD = 2.1, n = 11 (MSWD – mean square weighted deviation)) and a y-intercept (0.710259 ± 0.000010), the latter in line with Rb-free SRM987 values (Fig. 5). These values remain indistinguishable within uncertainties if the highest two 85Rb/86Sr ratios are excluded (85Rb/87Rb = 2.5265 ± 0.0172 (95% c.l., MSWD = 2.0, n = 9)). As expected from ICP mass bias, the 2.5348 value is lower than the accepted natural 85Rb/87Rb-ratio (2.59265;45 −2.24%) and interpreted to represent the 85Rb/87Rb ratio necessary for an accurate Rb-mass-bias correction in the presence of large Ca–P ion beams such as during LA-MC-ICPMS analysis of apatite.
We note that there are considerable differences on how to correct for the inevitable isobaric 87Rb amongst the various Sr-isotope LA-MC-ICPMS studies. Some suggest strongly mass bias affected 85Rb/87Rb values of ∼2.468,6,46 others utilize natural-Rb (85Rb/87Rb = 2.59265) and assume Sr-mass bias to be applicable,31,41 others use 85Rb/87Rbused > 85Rb/87Rbnatural (2.5970)13 and in some cases relatively little detail is provided.12,47 While this is less important for lowest-Rb/Sr minerals (e.g. carbonates), we want to highlight current inconsistencies whose impact may be particularly important for elevated Rb/Sr-material such as bioapatite (see below).
The extent of elemental fractionation during LA-MC-ICPMS analysis of apatite was assessed using matrix-matched Ca–P–(Si) STDP-glasses.35 It was found that the ‘true’/measured value for Rb/Sr-ratios for the three different STDP-compositions is 1.155 ± 0.023 (1 SD), which is unsurprising given the strong difference in volatility between Rb and Sr,48 affecting the elements differently during condensation from the laser-induced-plasma.49 Hence we utilize above factor during correction for 87Rb interference and thus also report more accurate sample Rb/Sr (85Rb/86Sr) ratios based on LA-MC-ICPMS (Tables S1 and S3 (ESI†)).
3D Application
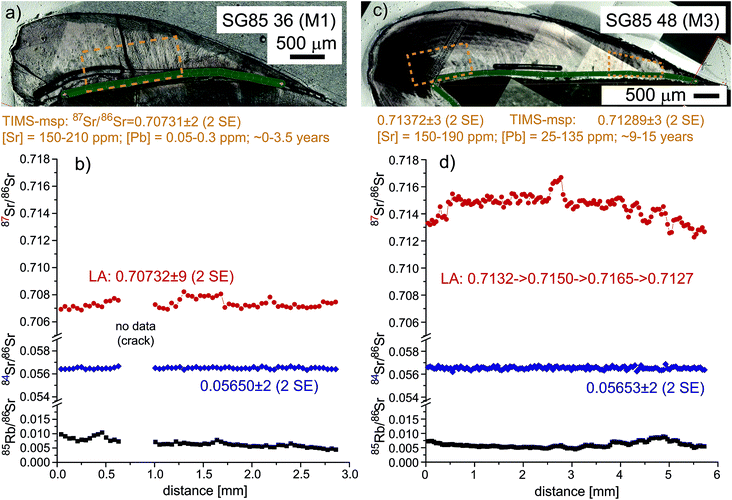
From the medieval Pb–Ag mining village of Sulzburg (Black Forest, SW Germany, 12th century AD37,38), well-preserved earliest and late mineralizing molars (M1 and M3) from the same individual were chosen to evaluate the accuracy of LA-MC-ICPMS Sr-isotope results in bioapatite with [Sr] of 150–200 ppm and moderately elevated Rb/Sr ratios typical of mammalian dental enamel. Individual SG85 (adult, female?) was selected because of the strongly contrasting in vivo Pb concentrations revealed by LA-ICPMS50 in the M1 and M3 enamel, recording Pb-exposure during earliest childhood (∼0–3.5 years) and adolescence (∼9–15 years),51 respectively. Tooth enamel grows sequentially and does not remineralize after formation, thus preserving time-series information of changing environmental parameters. The inter- and intra-tooth enamel Pb concentrations of SG85 range between 0.05–0.3 ppm (nearly Pb-unpolluted; M1) and 25–135 ppm (heavily Pb-exposed; M3), respectively, and thus exceed three orders of magnitude for the same individual (a detailed presentation and discussion of the trace element data is beyond the scope of this paper and mentioned here for contextual purposes only). This potentially indicated residential change thus warranting inter & intra-tooth 87Sr/86Sr analysis as key mobility proxy, all facilitated by the variable geology at the Rhine graben/Black Forest boundary near Sulzburg. Corresponding comparative microsampling-TIMS and LA-MC-ICPMS analyses are found in Table S3 (ESI†) and Fig. 6 (it should be noted that this example is shown here for methodological purposes rather than fully discussing all application-specific implications).In line with the contrasting Pb-concentrations in SG85, strongly different inter & intra-tooth-87Sr/86Sr ratios are recorded for the early and late mineralizing teeth. The 1st molar (SG85-36) has a low 87Sr/86Sr ratio of 0.70731 ± 0.00003 (2 SE; TIMS msp, ∼720 μg), which compares well with the average from the rather uniform LA-MC-ICPMS profile analyzed in growth direction along the enamel-dentine-junction (EDJ; 0.70732 ± 0.00009; 2 SE). The corresponding 84Sr/86Sr ratio is 0.05650 ± 0.00002 (2 SE) and agrees well with the naturally invariant 84Sr/86Sr ratio;39 the 85Rb/86Sr ratio decreases slightly from ∼0.009 to 0.005.
Two fragments from near occlusal and cervical end of the 3rd molar (SG85-48, M3, wisdom tooth; no data available for the middle fragment) analyzed by TIMS-msp reveal much more radiogenic 87Sr/86Sr ratios of 0.71372 ± 0.00003 and 0.71289 ± 0.00003 (2 SE; 350 + 160 μg), respectively. In this case, the comparative LA-MC-ICPMS profile analyzed in growth direction is highly variable and reveals more fine detail. The initial 0.6 mm show 87Sr/86Sr values between 0.7132–0.7135, followed by a rapid rise to 0.7150 ± 0.0001 (∼2 mm), a further 0.35 mm wide peak (0.7165), before 87Sr/86Sr again decreases via a series of 3–4 ‘wiggles’ to 0.7127. Overall the 87Sr/86Sr data are in line with the TIMS msp data but this sample illustrates well the problem of defining equivalent volumes that allow unequivocal comparison between TIMS and LA data. Because of the observed intra-enamel variability combined with the complex enamel mineralization process along and across the EDJ (Fig. 1), uncertainties remain which parts to integrate across to obtain the best TIMS-msp value relative the narrow LA track. Despite considerable 87Sr/86Sr variability, the corresponding 84Sr/86Sr profile is flat throughout recording 0.05653 ± 0.00002, while the 85Rb/86Sr ratio varies considerably (0.0073–0.0047–0.0087–0.0055). Despite necessitating a substantial 87Rb-correction on 87Sr/86Sr, overall the 87Sr/86Sr ratio agreement between LA-MC-ICPMS and TIMS-msp for virtually homogenous M1 is excellent (within error) and for variable M3 highly satisfactory (see above); both also record accurate and spatially-invariant 84Sr/86Sr ratios.
The local 87Sr/86Sr range for Sulzburg can be approximated from both water and diagnetically-altered high-[Sr] bone samples, which are 0.7138 ± 0.0009 and 0.7148 ± 0.0009 (2 SD), respectively.52 These imply that the lowest-[Pb] childhood Sr-isotopic composition of SG85 (M1) is incompatible with that of mining village, strongly suggesting that individual SG85 was born elsewhere. In contrast, the adolescence 87Sr/86Sr-range recorded in the M3 agrees with Sulzburg values, implying that SG85 migrated there sometime between ∼4 and ∼9 years of age and became exposed to high-levels of Pb. The fairly unradiogenic M1 composition suggests carbonate-dominated soils as childhood home, and given the low value of 0.7073 it furthermore hints at Jurassic bedrock compositions.36,53
4 Conclusions
On the basis of our laser-ablation and solution experiments and given the rapidly growing significance of spatially resolved Sr-isotope analyses of apatite for a range of applications, we conclude as follows:(1) Our shark-teeth Sr-isotope data obtained by LA-MC-ICPMS over a four-year period demonstrate accurate radiogenic 87Sr/86Sr and naturally-invariant 84Sr/86Sr-ratios, without any significant long-term trend. Not only high-[Sr] shark teeth, but also low-[Sr] human tooth enamel samples record accurate 84Sr/86Sr-ratios, showing that Ca-argide/dimers are negligible and Kr corrections valid.
(2) The external precision for 84Sr/86Sr in both solution and laser-ablation mode are essentially similar (±0.7‰; 2 SD), yet 87Sr/86Sr in laser-mode is about four times less reproducible (±0.075‰, 2 SD). While this is still satisfactory for many applications in view of the large natural 87Sr/86Sr variations, we attribute this deterioration mainly to slightly fluctuating on-peak 85Rb baselines not uncommon for volatile Rb, which may occur despite best efforts to introduce minimal Rb during instrument setup. This becomes significant mainly when dealing with low(est)-Rb/Sr samples such as shark teeth, silicate minerals or carbonates; for the latter we obtain broadly similar long-term precision during carbonate LA-MC-ICPMS Sr-isotope analysis.54
(3) We advocate the routine reporting of the non-radiogenic, invariant 84Sr/86Sr ratio (if ‘traditionally’ 88Sr/86Sr-normalized) for all samples and standards analyzed by LA-MC-ICPMS, which facilitates routine accuracy assessment of obtained data, akin to e.g. Hf-isotopes.32 Given the significant potential from unaccounted spectral interferences for inaccurate LA-MC-ICPMS Sr-isotope data, this opportunity should not be omitted and Sr-data without accurate 84Sr/86Sr ratios could be considered unreliable.
(4) Even though REE concentrations in modern or well-preserved fossil/archaeological bioapatite are exceedingly low (lowest-ppb range), doubly-charged REE (mainly Er, Yb) should be monitored at nominal half-mass(es), as any deviation from baseline values constitutes a simple yet powerful way to monitor the level of alteration in fossil samples.
(5) We find no evidence for significant polyatomic interferences, neither Ca-argides/dimers (cf. accurate 84Sr/86Sr ratios), nor any significant 40Ca31P16O at m/z = 87. The presence of the latter is testable via mass scan experiments at (pseudo)high mass resolution, but no evidence of a minor peak (shoulder) at slightly higher mass was found using either FAR or SEM, even when plasma conditions were deliberately detuned to simulate very high ThO+/Th+-ratios. This is in line with the lower metal-(cation)-oxide bond strengths of Ca+–O and P+–O (and likely even more so for triatomic CaPO) that are known to be correlated with metal-oxide production rates.29
(6) In view of the moderately elevated 85Rb/86Sr-ratios often typical of (bio)apatite, we focus on the accuracy of the 87Rb correction. We constrain both the effective 85Rb/87Rb-ratio in the presence of major Ca–P ions, as well as the extent of elemental Rb/Sr fractionation during laser-ablation, using matrix-matched phosphate glasses. The latter does not appear to have been sufficiently explored in previous LA-MC-ICPMS Sr-isotope analysis of (bio)apatite but is significant (∼15%), and in line with the strong volatility difference between Rb and Sr. Similar to the routine reporting of 84Sr/86Sr ratios, we propose that LA-MC-ICPMS Sr-isotope data routinely include corresponding85Rb/86Sr-ratios.
(7) We showcase our LA-MC-ICPMS Sr methodology via a case study of human teeth from a medieval German mining site, characterized by fairly elevated 85Rb/86Sr ∼0.005–0.009. One early and one late mineralizing molar of the same individual record highly variable intra/inter-enamel 87Sr/86Sr ratio profiles, while maintaining accurate invariant 84Sr/86Sr. We finally validate the accuracy of the LA 87Sr/86Sr ratios via comparative TIMS-microsampling Sr-isotope data. However, there is a limit in the usefulness of any LA vs. TIMS data comparison, owing to the complex enamel mineralization process with differently condensed time-series across and along enamel. It is evident that in case of highly variable intra-tooth 87Sr/86Sr ratios, it is difficult to define equivalent sample volumes, which in our view needs to be acknowledged when assessing the reliability of such comparisons.
The outlined methodology allows reliable, simple and fast spatially-resolved Sr isotope analysis, applicable to high-time resolution studies in palaeoecology, archaeology/anthropology or any (geological) sciences, whose potential overall has insufficiently been explored so far.
Acknowledgements
We are indebted to Ashley Norris and Jarosław Wilczyński for their help with the modern shark teeth provision. We thank Jakub Bazarnik for his help with the chemical purification of the Ca–P solution. We are grateful to Stephan Klemme and Andy Carter for providing the STDP glasses and Durango apatite, respectively. Kurt Alt, Julia Bastin, David Evans and Mark Rauschkolb are thanked for help with various aspects of the Sulzburg work, as is Matthew Thirlwall for some assistance with TIMS analysis at RHUL. Special thanks are due to Luca Bondioli for the photograph in Fig. 1 and many discussions on enamel mineralization and histology. Funding from an internal IGS PAS grant (to RA) and EU FP7-REGPOT-2011-1 (‘ATLAB’) is most gratefully acknowledged. Thanks to Detlef Günther and Frank Vanhaecke for the invitation to contribute to JAAS 30th anniversary volume. The comments of two anonymous reviewers helped to clarify our arguments and are gratefully acknowledged.References
- B. L. A. Charlier, C. Ginibre, D. Morgan, G. M. Nowell, D. G. Pearson, J. P. Davidson and C. J. Ottley, Chem. Geol., 2006, 232, 114–133 CrossRef CAS.
- W. Müller, D. Aerden and A. N. Halliday, Science, 2000, 288, 2195–2198 CrossRef.
- J. N. Christensen, A. N. Halliday, D. C. Lee and C. M. Hall, Earth Planet. Sci. Lett., 1995, 136, 79–85 CrossRef CAS.
- S. Burla, F. Oberli, U. Heimhofer, U. Wiechert and H. Weissert, Terra Nova, 2009, 21, 401–409 CrossRef CAS.
- F. C. Ramos, J. A. Wolff and D. L. Tollstrup, Geology, 2005, 33, 457–460 CrossRef.
- M. McCulloch, M. Cappo, J. Aumend and W. Müller, Mar. Freshwater Res., 2005, 56, 637–644 Search PubMed.
- J. Woodhead, S. Swearer, J. Hergt and R. Maas, J. Anal. At. Spectrom., 2005, 20, 22–27 RSC.
- T. Waight, J. Baker and D. Peate, Int. J. Mass Spectrom., 2002, 221, 229–244 CrossRef CAS.
- P. Z. Vroon, B. van der Wagt, J. M. Koornneef and G. R. Davies, Anal. Bioanal. Chem., 2008, 390, 465–476 CrossRef CAS PubMed.
- M. Bizzarro, A. Simonetti, R. K. Stevenson and S. Kurszlaukis, Geochim. Cosmochim. Acta, 2003, 67, 289–302 CrossRef CAS.
- M. S. A. Horstwood, J. A. Evans and J. Montgomery, Geochim. Cosmochim. Acta, 2008, 72, 5659–5674 CrossRef CAS.
- A. Simonetti, M. R. Buzon and R. A. Creaser, Archaeometry, 2008, 50, 371–385 CrossRef CAS.
- S. R. Copeland, M. Sponheimer, P. J. le Roux, V. Grimes, J. A. Lee-Thorp, D. J. de Ruiter and M. P. Richards, Rapid Commun. Mass Spectrom., 2008, 22, 3187–3194 CrossRef CAS PubMed.
- V. Balter, P. Telouk, B. Reynard, J. Braga, F. Thackeray and F. Albarede, Geochim. Cosmochim. Acta, 2008, 72, 3980–3990 CrossRef CAS.
- D. E. Harlov, Elements, 2015, 11, 171–176 CrossRef CAS.
- R. A. Bentley, J. Archaeol. Meth. Theor., 2006, 13, 135–187 CrossRef.
- W. Müller, H. Fricke, A. N. Halliday, M. T. McCulloch and J. A. Wartho, Science, 2003, 302, 862–866 CrossRef PubMed.
- L. Bondioli, P. F. Rossi and W. Müller, Geochim. Cosmochim. Acta, 2009, 73, A136 Search PubMed.
- J. Montgomery, J. A. Evans and M. S. A. Horstwood, Environ. Archaeol., 2010, 15, 32–42 CrossRef.
- C. FitzGerald, S. Saunders, L. Bondioli and R. Macchiarelli, Am. J. Phys. Anthropol., 2006, 130, 179–189 CrossRef PubMed.
- R. H. Steiger and E. Jäger, Earth Planet. Sci. Lett., 1977, 36, 359–362 CrossRef CAS.
- W. Müller, M. Shelley, P. Miller and S. Broude, J. Anal. At. Spectrom., 2009, 24, 209–214 RSC.
- E. A. Hinz and M. J. Kohn, Geochim. Cosmochim. Acta, 2010, 74, 3213–3231 CrossRef CAS.
- F. Vanhaecke, C. Vandecasteele, H. Vanhoe and R. Dams, Microchim. Acta, 1992, 108, 41–51 CrossRef CAS.
- S. F. Durrant, Fresenius' J. Anal. Chem., 1994, 349, 768–771 CrossRef CAS.
- H. H. Cornehl, R. Wesendrup, M. Diefenbach and H. Schwarz, Chem.–Eur. J., 1997, 3, 1083–1090 CrossRef CAS.
- D. K. Bohme, Ion Chemistry Laboratory - Thermodynamics and Physical Properties Database, 2015, http://www.chem.yorku.ca/profs/bohme/research/tpp__MAIN.html, (accessed September 2015) Search PubMed.
- Y.-R. Luo and J. A. Kerr, in CRC handbook of chemistry and physics, ed. D. R. Lide, CRC press, 2005, vol. 86, pp. 9-54–9-63 Search PubMed.
- A. J. R. Kent and C. A. Ungerer, J. Anal. At. Spectrom., 2005, 20, 1256–1262 RSC.
- D. Schröder, H. Schwarz and S. Shaik, in Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, ed. B. Meunier, Springer, Berlin Heidelberg, 2000, vol. 97, ch. 4, pp. 91–123 Search PubMed.
- J. Lewis, C. D. Coath and A. W. G. Pike, Chem. Geol., 2014, 390, 173–181 CrossRef CAS.
- T. M. Harrison, J. Blichert-Toft, W. Müller, F. Albarede, P. Holden and S. J. Mojzsis, Science, 2005, 310, 1947–1950 CrossRef CAS PubMed.
- W. Müller, N. S. Mancktelow and M. Meier, Earth Planet. Sci. Lett., 2000, 180, 385–397 CrossRef.
- K. P. Jochum, U. Weis, B. Stoll, D. Kuzmin, Q. C. Yang, I. Raczek, D. E. Jacob, A. Stracke, K. Birbaum, D. A. Frick, D. Gunther and J. Enzweiler, Geostand. Geoanal. Res., 2011, 35, 397–429 CrossRef CAS.
- S. Klemme, S. Prowatke, C. Munker, C. W. Magee, Y. Lahaye, T. Zack, S. A. Kasemann, E. J. A. Cabato and B. Kaeser, Geostand. Geoanal. Res., 2008, 32, 39–54 CrossRef CAS.
- J. M. McArthur, R. J. Howarth and T. R. Bailey, J. Geol., 2001, 109, 155–170 CrossRef CAS.
- K. W. Alt, B. Lohrke, R. Brenn, W. Müller, M. Rauschkolb and H. Steuer, Die mittelalterliche Bergbaubevölkerung des 12. Jahrhunderts von Sulzburg, Kr. Breisgau-Hochschwarzwald. Anthropologische und archäometrische Studien, VML Verlag Leidorf, 2008 Search PubMed.
- K. W. Alt, C. P. Adler, C. H. Buitrago-Tellez and B. Lohrke, Int. J. Osteoarchaeol., 2002, 12, 442–448 CrossRef.
- M. F. Thirlwall, Chem. Geol., 1991, 94, 85–104 CrossRef CAS.
- F. C. Ramos, J. A. Wolff and D. L. Tollstrup, Chem. Geol., 2004, 211, 135–158 CrossRef CAS.
- Y.-H. Yang, F.-Y. Wu, J.-H. Yang, D. M. Chew, L.-W. Xie, Z.-Y. Chu, Y.-B. Zhang and C. Huang, Chem. Geol., 2014, 385, 35–55 CrossRef CAS.
- L. J. Moens, F. F. Vanhaecke, D. R. Bandura, V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 2001, 16, 991–994 RSC.
- S. Weyer and J. Schwieters, Int. J. Mass Spectrom., 2003, 226, 355–368 CrossRef CAS.
- R. Brogioli, B. Hattendorf, J. Koch, H. Wiltsche, L. Flamigni and D. Günther, Anal. Bioanal. Chem., 2011, 399, 2201–2209 CrossRef CAS PubMed.
- E. Catanzaro, T. Murphy, E. Garner and W. Shields, J. Res. Natl. Bur. Stand., Sect. A, 1969, 73, 511–516 CrossRef CAS.
- J. I. Kimura, T. Takahashi and Q. Chang, J. Anal. At. Spectrom., 2013, 28, 945–957 RSC.
- V. Balter, J. Braga, P. Telouk and J. F. Thackeray, Nature, 2012, 489, 558–560 CrossRef CAS PubMed.
- K. Lodders, Astrophys. J., 2003, 591, 1220 CrossRef CAS.
- S. M. Eggins, L. P. J. Kinsley and J. M. G. Shelley, Appl. Surf. Sci., 1998, 129, 278–286 CrossRef.
- W. Müller, unpublished data.
- S. J. Alqahtani, M. Hector and H. Liversidge, Am. J. Phys. Anthropol., 2010, 142, 481–490 CrossRef CAS PubMed.
- M. Wormuth, MSc (Diplom) thesis, Georg-August-Universität Göttingen, 2000.
- R. A. Bentley and C. Knipper, Archaeometry, 2005, 47, 629–644 CrossRef CAS.
- W. Müller and R. Anczkiewicz, unpublished data.
- K. J. R. Rosman and P. D. P. Taylor, J. Anal. At. Spectrom., 1998, 13, 45N–55N Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ja00311c |
| This journal is © The Royal Society of Chemistry 2016 |