Integrated 3D modeling unravels the measures to mitigate nickel migration in solid oxide fuel/electrolysis cells†
Zhenjun
Jiao
*a,
Yunpeng
Su‡
 a,
Wenyue
Yang
a,
Jianli
Zhou
a,
Jin
Zhang
a,
Wenyue
Yang
a,
Jianli
Zhou
a,
Jin
Zhang
 a,
Xiaofeng
Tong
cb,
Yijing
Shang
a,
Xiaofeng
Tong
cb,
Yijing
Shang
 b and
Ming
Chen
b and
Ming
Chen
 *b
*b
aSchool of Science, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, China. E-mail: jiaozhenjun@hit.edu.cn
bDepartment of Energy Conversion and Storage, Technical University of Denmark, 2800, Kgs. Lyngby, Denmark. E-mail: minc@dtu.dk
cInstitute of Energy Power Innovation, North China Electric Power University, Beijing 102206, China
First published on 21st November 2023
Abstract
Numerical modeling plays an important role in understanding the multi-physics coupling in solid oxide fuel/electrolysis cells (SOFCs/SOECs) operated at elevated temperatures. During long-term operation of SOFCs and SOECs, cell durability is limited by nickel (Ni) morphological changes and migration. To reveal the mechanisms behind these phenomena, a unified numerical model utilizing the phase-field (PF) method is integrated with a finite element (FE) multi-physics coupled heterogeneous single-cell model to quantitatively investigate the microstructure evolution of hydrogen electrodes operated in different modes. Based on the 3D microstructures of single-cell components reconstructed using the focused ion beam-scanning electron microscopy (FIB-SEM) technique, the performances of different cells and the corresponding microstructure evolutions caused by Ni coarsening and migration can be simulated under an identical framework in the FC and EC modes, taking into account the complex multi-physics coupling effects. It is shown that, in addition to conventional interfacial energies, the Ni migration driven by the electrochemical potential gradient induced by current also plays an important role in the microstructure evolution. The integrated model is also applied to the simulation of the microstructure evolution of the Ni–YSZ hydrogen electrode infiltrated with GDC nanoparticles to interpret their positive effect on the improvement of the electrode durability.
1. Introduction
Solid oxide fuel/electrolysis cells (SOFCs/SOECs) have attracted tremendous interest due to their promising potential for reversible conversion of chemical and electrical energy.1 However, the limited long-term durability of these cells remains a major challenge for their commercialization.2,3 Currently, Ni-yttria-stabilized zirconia cermets (Ni–YSZ) are utilized in most SOFCs/SOECs as composite hydrogen electrode materials. Although these Ni–YSZ electrodes exhibit excellent activity in both FC and EC modes, their stability properties differ significantly and show considerable degradation during continuous operation at high current densities.4–7 In our previous work,8 the initial performance and degradation of an SOFC operated over 7000 hours were analyzed, which clearly showed the phenomenon of ionic current concentrating at electrolyte, caused by Ni coarsening and accumulation toward electrolyte, which dominated the degradation of the cell. The work of Sun et al.9 compared the initial and final performances of a SOEC after long-term operation over 4000 hours, and the results demonstrated that the degradation of the cell was dominated by the microstructural changes of the Ni–YSZ electrode based on post-mortem analysis.Redistribution of Ni, including coarsening and migration of Ni, has been recognized as a major contributor to degradation by impacting the ionic and electrical conductivities and active triple-phase-boundaries (TPBs) in the hydrogen electrode, which causes the performance degradation of the cells.10–13 It is well known that Ni coarsening occurs during operation in FC and EC modes and under open circuit voltage (OCV) conditions.14–16 There are few studies dealing with the investigation of Ni migration in the FC mode. Menzler et al. reported the phenomenon of Ni migration toward the electrolyte in an SOFC after more than 10 years of operation.17 In contrast, Ni migration away from the electrolyte was frequently observed during EC operation under strong polarization, but not under OCV conditions.13,18 Recently, we investigated the morphological changes occurring on patterned Ni film electrodes during operation in FC and EC modes.19–21 We attempted to explain the phenomena by establishing a correlation between the wettability of Ni on YSZ and the degree of adsorbed oxygen on the Ni surface. This indicates a strong correlation between the degradation behavior and the overpotential experienced. Recently, some efforts have been made to elucidate the mechanism underlying Ni migration, but it remains elusive. For example, Mogensen et al.18 proposed that Ni migrates in the form of Ni(OH)x species. However, we recently observed Ni migration during the EC operation of CO2, suggesting that the Ni(OH)x species may not be the main contributor to Ni migration.14 Cheng et al.22 proposed a theory based on a hypothesis, that the dynamic redox of Ni, combined with the coarsening and gas transport processes, could be related to Ni migration. However, the 1D steady-state model proposed showed limitations, mainly regarding the lack of the description of the microstructure of the electrode and the consideration of the transient effect of charge transport. So far, it is clear that the migration of Ni, either toward or away from the electrolyte, appears to be governed by a combination of complex mechanisms during long-term operation in a particular mode. Experiments have shown that Ni migration at relatively high current densities depends on the electrochemical process, while no migration is expected at low current densities.18 These phenomena were explained by the assumption that migration is driven by the contact angle gradient of Ni on YSZ, which correlates with the electric potential gradient and/or the oxygen partial pressure gradient.
Given the time-consuming and costly nature of durability testing, as well as the potential for observational error in ex situ experiments, numerical studies have become increasingly important in investigating the mechanisms of Ni redistribution. In recent years, various numerical methods such as the lattice Boltzmann method (LBM) and the finite element method (FEM) have been used in the study of multi-physics coupling for SOCs.8,23–28 In addition to these approaches, the phase-field method (PFM) has been shown to be a powerful simulation tool for predicting the microstructural evolution of hydrogen electrodes. Wang et al. employed29 a combination of the LBM and PFM to simulate the effects of Ni depletion on cell performance during EC operation. Their results showed that Ni depletion exacerbated the coarsening of Ni and lengthened the ion transport pathway, leading to an increase in activation overpotential. Lei et al.30,31 employed the PF method to simulate Ni migration and found that neither the Ni(OH)x species nor the contact angle gradient of Ni on YSZ, which can be affected by gas partial pressure alone, can serve as sufficient driving forces for Ni migration. Rorato et al.32 combined an electrochemical model with the PF model to simulate Ni migration in both FC and EC modes. Their model considered that the contact angle gradient of Ni on YSZ was influenced not only by the gas partial pressure, but also by the presence of oxygen vacancies at the Ni–YSZ interface related to the overpotential of the hydrogen electrode. Nevertheless, no clear explanation or accurate numerical modeling was proposed to reproduce the phenomena of Ni migration in different modes considering the complex effects of multi-physics coupling, which made it difficult to provide theoretical guidance for improving cell performance and stability. At the current stage, most studies analyzed Ni migration qualitatively, while achieving real-time coupling between electrochemical and thermodynamic models remains a major challenge in a quantitative simulation. Therefore, limited progress has been made in the microstructural optimization of the hydrogen electrode to prolong its performance stability and durability without accurate theoretical guidance.
Based on previous studies, we present a unified numerical modeling framework for simulating Ni migration in hydrogen electrodes in both FC and EC modes in this work. Taking into account the complex real-time multi-physics coupling effects between electrochemical and thermodynamic models, for the first time we achieved real-time integrated modeling of the hydrogen electrode microstructure evolution during operation. Integrated modeling involving the FEM and PFM is performed based on real 3D microstructures reconstructed using the focused ion beam-scanning electron microscopy (FIB-SEM) dual-beam technique,20,33 with the goal of providing a fundamental understanding of the underlying mechanisms of Ni migration during operation in different modes. Based on the integrated modeling framework proposed, the infiltration of nano-sized GDC particles in the hydrogen electrode to improve SOEC durability by inhibiting Ni migration was analyzed and quantitatively interpreted based on simulations.
2. Experimental
2.1. Electrochemical performance test
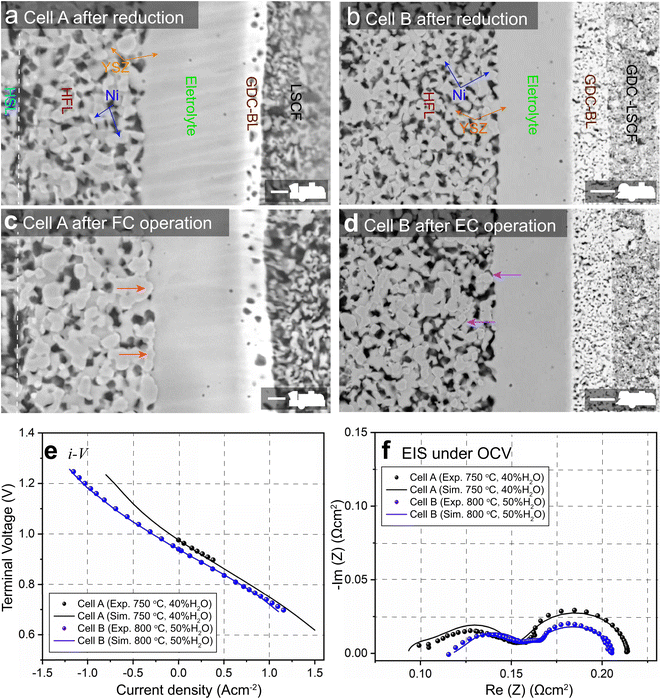
SOCs built with a Ni–YSZ hydrogen electrode as the support structure have the advantage of low ohmic resistance due to electrolyte thickness, which allows lower operating temperature and higher performance. 8YSZ (8 mol% yttria-doped zirconia) and 3YSZ are conventionally utilized in the functional layer (FL) and the supporting layer (SL) of the hydrogen electrode, respectively, due to their high ionic conductivity and mechanical strength. In this work, two types of hydrogen electrode-supported SOCs were tested during long-term operation in either FC or EC mode. The first type is a commercial SOC composed of a Ni-3YSZ hydrogen electrode support layer (HSL), a Ni-8YSZ hydrogen electrode functional layer (HFL), an 8YSZ electrolyte, a gadolinium-doped ceria (GDC) barrier layer (BL), and a lanthanum strontium cobalt ferrite (LSCF) oxygen electrode. The second type is a self-manufactured SOC composed of a Ni-3YSZ HSL, a Ni-8YSZ HFL, an 8YSZ electrolyte, a GDC-BL, and a GDC-LSCF composite oxygen electrode. The two types of SOCs were denoted as cells A and B in this work. To investigate the influences of operation modes on Ni migration in Ni–YSZ hydrogen electrodes, samples of cells A and B were taken before and after long-term operation in FC and EC modes, respectively. Cell A was sampled after operation from the center of a short stack operated at a current density of 0.3 A cm−2 in H2 humidified with 6% H2O as the fuel and air as the oxidant at 1023 K for 7000 hours. For cell B, the sample was taken after operation from a single-cell test with a current density of −1 A cm−2 in H2 humidified with 50% H2O at 1073 K for 1000 hours.2.2. FIB-SEM technique
The SEM images of the cross-sections of cells A and B before and after long-term operation are shown in Fig. 1(a)–(d) and compared. The phenomena of Ni accumulation toward the electrolyte with an enhanced Ni–YSZ interface in FC mode and the opposite Ni migration away from the electrolyte in EC mode are clearly observed. Coarsening of Ni can also be observed in both the HSL and HFL after operation in both modes. To facilitate subsequent numerical simulations, the initial microstructures of cells A and B before operation were reconstructed using the FIB-SEM (Carl Zeiss, Crossbeam 350) dual-beam technique. The samples were infiltrated with low viscosity epoxy resin in a low pressure atmosphere to facilitate the segmentation of different phases. The cured samples were polished using an Ar-ion beam cross-section polisher (JEOL Ltd, SM-09010), and the series of FIB-SEM images were filtered and aligned using ImageJ software. The microstructures were then reconstructed in 3D by stacking the segmented image sequence. Based on the 3D reconstructions, adaptive tetragonal meshes were generated in MATLAB and imported into COMSOL for FE simulations; details of the 3D reconstruction can be found in ref. 8.3. Results and discussion
3.1. Scheme
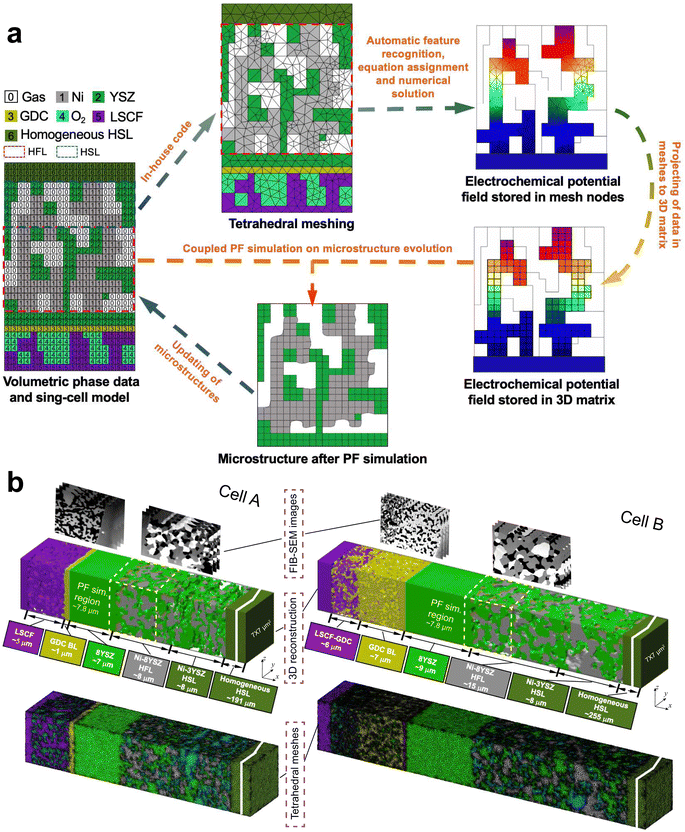
The scheme of integrated modeling in this work is shown in Fig. 2(a). The microstructures of cells A and B were first reconstructed in 3D with a voxel length of l0 = 39.1 nm. To simulate the evolution of the Ni–YSZ hydrogen electrode microstructure under complex coupling effects among conductions, electrochemical reactions, and mass transfer processes, a multi-physics coupled FE model was integrated with a PF model via the 3D microstructure reconstruction on a full-cell scale. In-house codes were developed for integrated simulation with automatic feature recognition, equation assignment, and subsequent numerical solution, linking MATLAB and COMSOL softwares. Adaptive tetrahedral meshes were generated in MATLAB and then imported into COMSOL. The FE modeling was first performed to predict the experimental electrochemical performances of a cell on the full-cell scale to validate the model in the appropriate mode. The 3D multi-physics field data generated in the FE simulation, such as gas concentrations and electrochemical potential distributions in solid phases, were then extracted and imported into the subsequent PF model by projecting them onto the corresponding OP matrices using the k-nearest neighbor algorithm. The full-cell reconstruction with the hydrogen electrode after evolution predicted utilizing the PFM was converted to adaptive tetrahedral meshes to update the microstructure for the FE simulation. The cyclic process was repeated to complete the integrated numerical simulation. Details of the FE and PF models are described in the ESI.†3.2. FE simulations
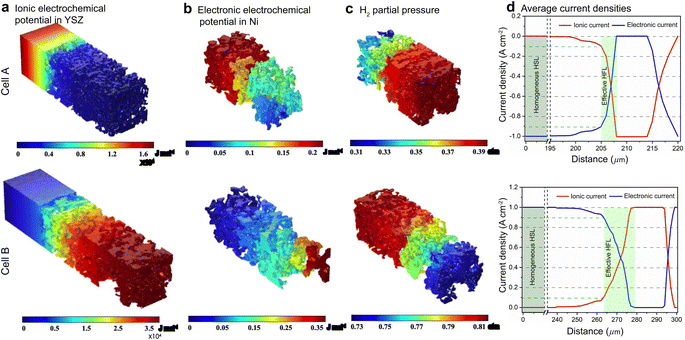
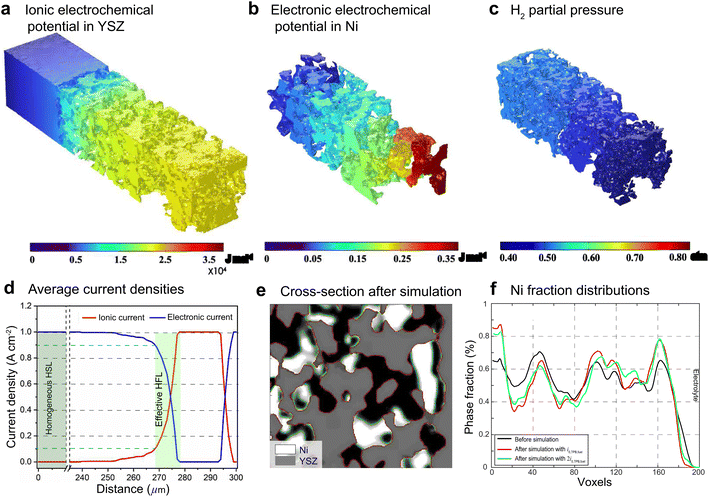
For FE modeling, further details of parameters and empirical formulae can be referred to in our previous work in ref. 8. In this work, the performances of cell A operated in FC mode and cell B operated in EC mode were simulated under the unique framework based on the 3D reconstructions of the full cell. To validate the modeling of FE, the initial performances in terms of the current density–voltage relationship (i–V) and electrochemical impedance spectroscopy (EIS) were simulated using the environmental parameters presented in the experimental section for both cells. The corresponding simulation results of i–V and EIS were compared with the experimental data, as shown in Fig. 1(e) and (f). It is clearly seen that the actual experimental data can be well reproduced in the simulations.To facilitate PF simulations of microstructure evolution in hydrogen electrodes during long-term operation, further simulations were performed using cells A and B under different conditions in FC and EC modes, respectively. The simulation of cell A was performed at a current density of 1 A cm−2 in H2 humidified with 40% H2O as the fuel at 1023 K to approximate the conditions in the central part of the stack tested in the experiment. For cell B, the simulation was performed at a current density of −1 A cm−2 in H2 humidified with 50% H2O as the fuel at 1073 K, as in the single-cell experiment. The corresponding 3D distributions of the ionic electrochemical potential in YSZ, the electronic potential in Ni, the specified H2 partial pressure in pores, and the ionic and electronic current densities averaged over the cross-section along the x-axis are shown in Fig. 3. The effective thickness of the HFL in both cells was defined as the thickness of the HFL from the electrolyte in which 90% of the total electrochemical electronic current is generated. It is clearly seen that the effective thickness of the HFL in cell A is much thinner than that in cell B, which can be attributed to a much larger TPB density. The corresponding 3D multi-physics field data were then extracted from the adaptive tetrahedral mesh nodes and projected onto the corresponding OP matrices utilized as multi-physical conditions in the PF modeling to update the microstructure of the hydrogen electrode.
3.3. PF simulations
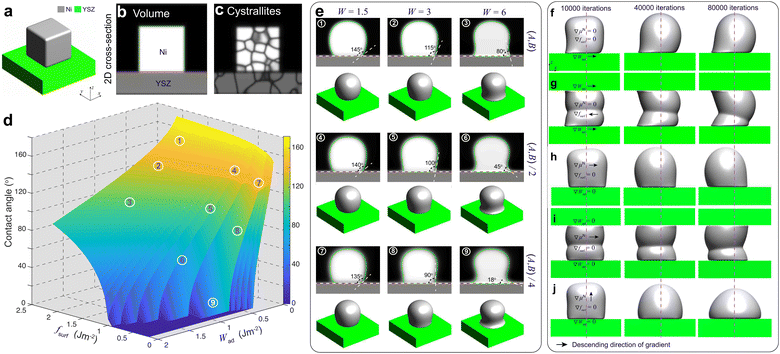
For PF modeling, the phenomenological parameters in eqn (8) in the ESI† were calibrated by performing PF simulations on a simplified system of a polycrystalline Ni block bonded to a YSZ substrate, as shown in Fig. 4(a)–(c). The Ni–YSZ system was assumed to be exposed to a uniform gas environment. In the subsequent simulations, the effect of electromigration of Ni caused by electronic current was neglected to calibrate the coefficients by fitting the simulation results to the theoretical values of the contact angle θ.In our previous work, θ of Ni bonded on a YSZ surface in a certain gas environment was correlated with the change in Ni surface tension, which can be modified by oxygen adsorption.19 It was demonstrated that the change in θ at TPBs can be attributed to the variation of H2O partial pressure, assuming a constant work of adhesion at the Ni–YSZ interface. Based on the approximation of the Ni surface tension using the surface energy fsurf, the work of adhesion Wad was correlated with θ and fsurf as
Wad = fsurf(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). θ). | (1) |
The surface energy of Ni fsurf can be calculated as
fsurf = fpsurf − Γ0RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 + KaaO), ln(1 + KaaO), | (2) |
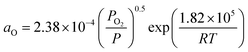 . Patm is the atmospheric pressure and PO2 is the partial pressure of oxygen, which can be equilibrated by the partial pressure of humidity PH2O as follows:
. Patm is the atmospheric pressure and PO2 is the partial pressure of oxygen, which can be equilibrated by the partial pressure of humidity PH2O as follows: 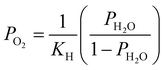 , where KH is the equilibrium constant at a conventional SOC operating temperature of T. Details of the parameters can be referred to in ref. 19. Based on the FE simulation results, the local Ni surface energy can thus be calculated using the PH2O from the adjacent gas atmosphere.
, where KH is the equilibrium constant at a conventional SOC operating temperature of T. Details of the parameters can be referred to in ref. 19. Based on the FE simulation results, the local Ni surface energy can thus be calculated using the PH2O from the adjacent gas atmosphere.
The work of adhesion Wad at the Ni–YSZ interface can be predicted by using the Boltzmann expression as34
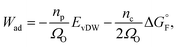 | (3) |
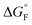 is the standard molar Gibbs free energy of the formation of NiO at T, which is calculated using an empirical formula as
is the standard molar Gibbs free energy of the formation of NiO at T, which is calculated using an empirical formula as 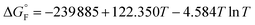 .35EVDW is the energy of the Ni–O-Van der Waals pair interaction, which is defined as36
.35EVDW is the energy of the Ni–O-Van der Waals pair interaction, which is defined as36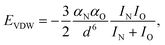 | (4) |
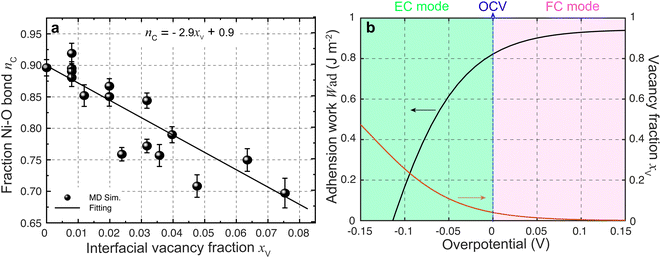 | ||
| Fig. 5 (a) Ionic Ni–O bond fraction against the YSZ surface vacancy fraction. (b) Work of adhesion against overpotential predicted using eqn (3). | ||
According to the work of Hendriks et al.,37 the vacancy concentration on the YSZ surface increases with increasing overpotential and reached a temperature-dependent maximum. The behavior can be understood under the assumption that only a fraction of the oxygen sub-lattice is available for oxygen vacancy distribution, which can be affected by the overpotential at a specific temperature and composition. Thus, the oxygen vacancy fractions in YSZ at Ni–YSZ interfaces during operation in FC or EC mode may be affected by the local overpotential. With variations in the overpotential, the oxygen vacancy fraction in a near-surface YSZ layer can be predicted as
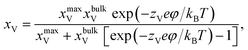 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/kBT), where E and C0 are constants at a given temperature T.37 Based on eqn (3) and (5), Wad at the Ni–YSZ interface can thus be correlated with the local overpotential during operation in any mode, as shown in Fig. 5(b). It is seen that Wad can be largely decreased with decreasing overpotential. Conversely, increasing overpotential leads to a limited increase in Wad. Based on the FE simulation results, the local overpotential can thus be used to calculate Wad at the Ni–YSZ interface.
exp(−E/kBT), where E and C0 are constants at a given temperature T.37 Based on eqn (3) and (5), Wad at the Ni–YSZ interface can thus be correlated with the local overpotential during operation in any mode, as shown in Fig. 5(b). It is seen that Wad can be largely decreased with decreasing overpotential. Conversely, increasing overpotential leads to a limited increase in Wad. Based on the FE simulation results, the local overpotential can thus be used to calculate Wad at the Ni–YSZ interface.
Different from our previous work,19 the influences of fsurf and Wad were considered simultaneously in PF simulations. According to eqn (1), the theoretical contact angle is correlated with fsurf and Wad, as shown in Fig. 4(d). The phenomenological parameters W, A and B were tuned to reproduce the theoretical values of the contact angle. The variation in fsurf was controlled by multiplying A and B by a common factor of fsurf/f0surf, where f0surf is the reference surface energy.19 A tuning function of W = −9.35Wad + 4.69 was extrapolated to control the variation in Wad by setting a reference contact angle under OCV conditions to 115°,14 and another contact angle under high polarization φ = 0.1 V to 18°, as shown in Fig. S0 in the ESI.†21 After substituting the given parameters for the environmental conditions into eqn (2)–(5), the relevant phenomenological parameters reflecting the changes in fsurf and Wad can be obtained for the PF simulations. The PF simulation results of the morphological changes in Ni and the corresponding θ with different combinations of W, A and B are shown in Fig. 4(e). Each simulation was terminated after 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations to ensure that the Ni morphology reached an equilibrium state. The initial crystallographic orientations of both Ni and YSZ were generated from random initial OPs.20 It can be clearly seen that theoretical θ, as shown in Fig. 4(d), can be reproduced using different combinations of the phenomenological parameters.
000 iterations to ensure that the Ni morphology reached an equilibrium state. The initial crystallographic orientations of both Ni and YSZ were generated from random initial OPs.20 It can be clearly seen that theoretical θ, as shown in Fig. 4(d), can be reproduced using different combinations of the phenomenological parameters.
The observations in our previous work indicated that current plays a major role in driving Ni migration, while the contribution of the gas diffusion pathway is minor.14 The Ni–YSZ contact angle gradient caused by the current could play an important role in driving the Ni surface diffusion in different gas environments. To verify the influence of the contact angle gradient along the Ni–YSZ interface, the simplified PF simulations were rerun by introducing continuous gradients for both fsurf and Wad along the x-axis by using ∇W = −0.01/voxel and ∇(fsurf/f0surf) = 0.01/voxel, while W = 4 and (fsurf/f0surf) = 0.75 were set at the center indicated by the dashed line, as shown in Fig. 4(f) and (g). It can be seen that a gradient in the Ni–YSZ contact angle led to Ni redistribution with limited local migration before the contact angles reached the equilibrium state. The gradients in both fsurf and Wad cannot cause continuous Ni migration with different constraints from the YSZ surfaces.
Our previous work20 reported the in situ observations of the continuous spreading of Ni at TPBs in Ni-film electrodes under high anodic polarization using a high-resolution 3D laser scanning confocal microscope. It is clearly seen that the current PF model cannot reproduce the phenomenon of continuous Ni spreading without considering another driving force acting on the Ni phase. After introducing an electrochemical potential gradient on Ni by setting 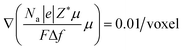 along different axes, without considering the gradients of fsurf and Wad, the PF simulations were performed with different combinations of boundary conditions, as shown in Fig. 4(h) and (i).38,39 It can be clearly seen that a continuous translation of the entire Ni along the YSZ surface can be simulated with deformation. When an electrochemical potential gradient is applied along the z-axis on Ni in the simulation, a continuous accumulation of Ni at the YSZ surface can be simulated, as shown in Fig. 4(j). The results show that the continuous migration of Ni under the complex multi-physics coupled influences in both FC and EC modes cannot be reproduced in simulations considering only gradients in fsurf and Wad. After a limited range of the redistribution of Ni at the TPBs, the migration stops when the contact angles reach the equilibrium state. Thus, the electrochemical potential gradient induced by the current in the Ni phase is the key factor determining the continuous Ni migration in opposite directions in FC and EC modes in hydrogen electrodes.
along different axes, without considering the gradients of fsurf and Wad, the PF simulations were performed with different combinations of boundary conditions, as shown in Fig. 4(h) and (i).38,39 It can be clearly seen that a continuous translation of the entire Ni along the YSZ surface can be simulated with deformation. When an electrochemical potential gradient is applied along the z-axis on Ni in the simulation, a continuous accumulation of Ni at the YSZ surface can be simulated, as shown in Fig. 4(j). The results show that the continuous migration of Ni under the complex multi-physics coupled influences in both FC and EC modes cannot be reproduced in simulations considering only gradients in fsurf and Wad. After a limited range of the redistribution of Ni at the TPBs, the migration stops when the contact angles reach the equilibrium state. Thus, the electrochemical potential gradient induced by the current in the Ni phase is the key factor determining the continuous Ni migration in opposite directions in FC and EC modes in hydrogen electrodes.
To simulate the microstructure evolutions of the hydrogen electrodes in HFLs for cells A and B, the data of the multi-physics fields, as shown in Fig. 3, were first extracted from the nodes of the adaptive tetrahedral meshes and projected onto the corresponding OP matrices. The OP matrices were then used as multi-physical conditions in subsequent PF simulations to control the relevant phenomenological parameters as mentioned above. The PF simulations were then performed based on the reconstruction regions of cells A and B, as indicated in Fig. 2, to update the microstructures. Theoretically, the multi-physical conditions need to be updated after each iteration in a PF simulation, whereas in this work, the update was performed only after every 2000 iterations in the PF simulation to save computational resources given the time-consuming and costly nature of the integrated simulation. Within the limits of our current computational power, the simulation of cell A was terminated after 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, while the simulation of cell B was terminated after 32
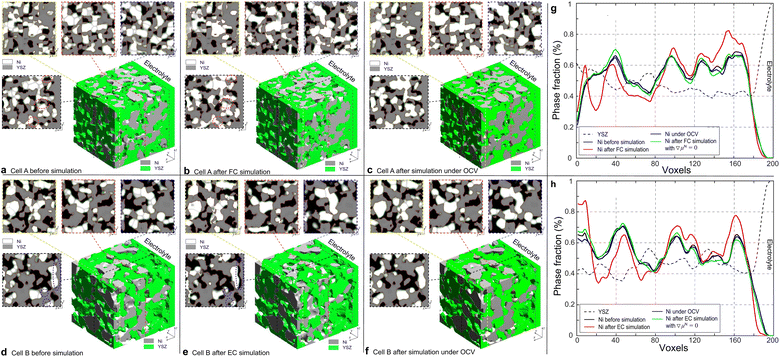
000 iterations, while the simulation of cell B was terminated after 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations according to the different temperatures to achieve the convergence of the simulations. With the same dimensionless time, the simulations of the microstructure evolutions were also performed under OCV conditions for cells A and B for comparison. The 3D microstructure and the corresponding 2D cross-sectional images of the HFLs in cells A and B before and after the PF simulations in different modes are shown in Fig. 6. It can be clearly seen that the microstructures of both cases under OCV conditions retained most of their original microstructure morphologies. During the simulations, only obvious crystal grain growth and coarsening of Ni are observed, which together change the morphology of the microstructures to a very limited extent under the constraints of the YSZ network. In the simulation of cell A operated in FC mode, significant Ni migration toward the electrolyte could be observed after simulation, as shown in Fig. 6(b). In contrast, Ni migration away from the electrolyte can be observed after the simulation of cell B in EC mode, as shown in Fig. 6(e). In both cases, the extent of Ni migration was much higher at a location closer to the electrolyte, which can be attributed to the larger gradients in current density, as shown in Fig. 3(d). No obvious Ni migration phenomena are observed in the region far from the electrolyte, as shown in the cross-sectional images.
000 iterations according to the different temperatures to achieve the convergence of the simulations. With the same dimensionless time, the simulations of the microstructure evolutions were also performed under OCV conditions for cells A and B for comparison. The 3D microstructure and the corresponding 2D cross-sectional images of the HFLs in cells A and B before and after the PF simulations in different modes are shown in Fig. 6. It can be clearly seen that the microstructures of both cases under OCV conditions retained most of their original microstructure morphologies. During the simulations, only obvious crystal grain growth and coarsening of Ni are observed, which together change the morphology of the microstructures to a very limited extent under the constraints of the YSZ network. In the simulation of cell A operated in FC mode, significant Ni migration toward the electrolyte could be observed after simulation, as shown in Fig. 6(b). In contrast, Ni migration away from the electrolyte can be observed after the simulation of cell B in EC mode, as shown in Fig. 6(e). In both cases, the extent of Ni migration was much higher at a location closer to the electrolyte, which can be attributed to the larger gradients in current density, as shown in Fig. 3(d). No obvious Ni migration phenomena are observed in the region far from the electrolyte, as shown in the cross-sectional images.
To investigate Ni migration quantitatively, specific cross-section-averaged Ni fraction distributions along the x-axis were calculated as 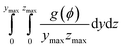 and plotted after the simulations for cells A and B, as shown in Fig. 6(g) and (h). Compared to the reference Ni fraction distributions before the simulations, it is clear that Ni migrates toward the electrolyte when simulating FC mode for cell A, while Ni migrates away from the electrolyte when simulating EC mode for cell B. Under OCV conditions, both cells show almost no redistribution of Ni after the simulations, compared to the initial microstructure. For comparison, two other simulations were performed without considering the gradients of the electrochemical potential in Ni for cells A and B. Similar to the cases under OCV conditions, almost no migration of Ni can be observed after the simulations, which again proves that the electromigration driving force caused by the gradient of electrochemical potential in Ni plays an important role. It is thus known that the change in the contact angle leads to only limited local redistribution of Ni. The experimental observations in the FC and EC modes, as shown in Fig. 1(b) and (d), were well reproduced in the integrated simulations performed under the unique framework, taking into account the dynamic influences of the multi-physics coupling effect.
and plotted after the simulations for cells A and B, as shown in Fig. 6(g) and (h). Compared to the reference Ni fraction distributions before the simulations, it is clear that Ni migrates toward the electrolyte when simulating FC mode for cell A, while Ni migrates away from the electrolyte when simulating EC mode for cell B. Under OCV conditions, both cells show almost no redistribution of Ni after the simulations, compared to the initial microstructure. For comparison, two other simulations were performed without considering the gradients of the electrochemical potential in Ni for cells A and B. Similar to the cases under OCV conditions, almost no migration of Ni can be observed after the simulations, which again proves that the electromigration driving force caused by the gradient of electrochemical potential in Ni plays an important role. It is thus known that the change in the contact angle leads to only limited local redistribution of Ni. The experimental observations in the FC and EC modes, as shown in Fig. 1(b) and (d), were well reproduced in the integrated simulations performed under the unique framework, taking into account the dynamic influences of the multi-physics coupling effect.
3.4. Case study of the integrated modeling
Ovtar et al.6 reported that infiltration of nano-sized GDC particles into the conventional Ni–YSZ hydrogen electrode drastically reduced the degradation rate of SOEC performance at high current density. Unlike the bare Ni–YSZ electrode, no contact loss was observed at the Ni–YSZ interface during long-term operation. The lower degradation rate of the hydrogen electrode infiltrated with GDC nanoparticles was attributed to the enlarged active sites compared to those of the conventional TPBs, which can increase the steam splitting rate and reduce the local overpotential. According to the integrated modeling proposed in this work, a smaller local overpotential leads to a drastic increase in Wad, as shown in Fig. 5(b), which leads to an enhancement of the Ni–YSZ interface and inhibits Ni migration. At the same time, the Ni surface energy can be reduced by increasing the local concentration of humidity and decreasing the thickness of the active HFL. To quantify the subsequent comprehensive effect caused by the change in overpotential, another simulation was performed on cell B in EC mode, where the exchange current density i0,TPB,fuel was doubled in eqn (5).The simulation was performed for cell B under identical conditions as those described in the previous case shown in Fig. 3. The corresponding 3D distributions of the ionic electrochemical potential in YSZ, the electronic potential in Ni, the specified H2 partial pressure in the pore, and the ionic and electronic current densities averaged over the cross-section along the x-axis are shown in Fig. 7(a)–(c). Compared to Fig. 3, it is clearly seen that the effective thickness of the HFL has decreased from about 15 μm to about 10 μm, following the obvious decrease in the local H2 partial pressure, which can strongly reduce the surface energy of Ni and thus the local contact angle. The much lower ionic electrochemical potential in YSZ confirmed the prediction of the smaller local overpotential. Therefore, it is reasonable to predict a lower migration rate of Ni with the increase in Wad, as shown in Fig. 7(d).
The subsequent PF simulation was performed based on the condition matrices extracted from the 3D FE simulation results as described previously. Considering the constraining effect of the infiltrated GDC nanoparticles on the Ni surface, the mobility function of the Ni phase was modified by setting 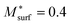 in the PF simulation without importing the actual GDC nanoparticle morphology into the 3D reconstruction. The 2D cross-sectional images of the HFLs in cell B after the PF simulation are shown in Fig. 7(e). Compared with the initial microstructure shown in Fig. 6(d), it is clear that similar phenomena of obvious crystal grain growth and coarsening of Ni are observed, while Ni migration from the electrolyte was suppressed to some extent by the stronger bonding at the Ni–YSZ interface. The distributions of the Ni fraction along the x-axis after the simulations with the original i0,TPB,fuel and 2i0,TPB,fuel, as shown in Fig. 7(f), reflect the extent to which Ni migration is inhibited. The inhibition of Ni migration can also be attributed to the thickness of the effective HFL, which was narrowed by about 30%, as shown in Fig. 7(d), which limits the electromigration driving force within a thinner region of the HFL. It is expected that the phenomenon may become more evident after prolonged operation. Thus, the simulation results theoretically explain the positive effect caused by the infiltration of GDC nanoparticles into the Ni–YSZ hydrogen electrode at high current density.6
in the PF simulation without importing the actual GDC nanoparticle morphology into the 3D reconstruction. The 2D cross-sectional images of the HFLs in cell B after the PF simulation are shown in Fig. 7(e). Compared with the initial microstructure shown in Fig. 6(d), it is clear that similar phenomena of obvious crystal grain growth and coarsening of Ni are observed, while Ni migration from the electrolyte was suppressed to some extent by the stronger bonding at the Ni–YSZ interface. The distributions of the Ni fraction along the x-axis after the simulations with the original i0,TPB,fuel and 2i0,TPB,fuel, as shown in Fig. 7(f), reflect the extent to which Ni migration is inhibited. The inhibition of Ni migration can also be attributed to the thickness of the effective HFL, which was narrowed by about 30%, as shown in Fig. 7(d), which limits the electromigration driving force within a thinner region of the HFL. It is expected that the phenomenon may become more evident after prolonged operation. Thus, the simulation results theoretically explain the positive effect caused by the infiltration of GDC nanoparticles into the Ni–YSZ hydrogen electrode at high current density.6
Due to limited computational resources, current simulations of microstructural evolution have been limited to finite time and spatial scales. In future research, larger scale computations over multiple scales and long-term operation can be achieved by improving the relevant algorithms. In addition to the study of Ni migration in hydrogen electrodes, the integrated modeling proposed can also be flexible and open to study the degradation mechanisms of the electrolyte and air electrode for SOCs. The current multi-physics coupled full cell model can be further developed for a specific combination of different microstructures to study the comprehensive degradation of SOC life cycle performance in different modes, which could provide an opportunity for revolutionary microstructure investigation and optimization for fuel cells, batteries and other relevant fields.
4. Conclusions
SOCs are clean, efficient, and reversible energy conversion solutions that have great potential for a wide range of applications. To fully realize this potential, issues related to improving the durability and lifetime of these systems need to be addressed. In this work, we investigated the phenomena of Ni migration in the hydrogen electrodes of SOCs during operation in the FC and EC modes. An integrated model was developed based on the real 3D microstructures reconstructed at the single-cell scale using the FIB-SEM dual-beam technique. The model linked the FE multi-physics coupled heterogeneous single-cell model with the PF simulations of microstructure evolution by projecting the multi-physical field data from tetragonal meshes onto OP matrices to simulate the morphological changes in Ni, taking into account the complex multi-physics coupling effects. The FE model was verified by the experimental measurements in the FC and EC modes under an identical framework. The PF simulation results of the morphological changes in the HFLs of different hydrogen electrodes show that, in addition to conventional coarsening and interfacial energies, Ni migration driven by the electrochemical potential gradient induced by the current plays an important role in Ni migration during operation in the FC and EC modes. The integrated model was also applied in predicting the positive effect of the infiltration of GDC nanoparticles into the Ni–YSZ hydrogen electrode on improving the durability during operation in EC mode. The simulation results agreed well with the experimental observations, demonstrating the potential of the integrated model in improving the durability of SOCs.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors acknowledge the funding provided by the Guangdong Basic and Applied Basic Research Foundation, China (2023A1515011003), the Shenzhen Science and Technology Innovation Commission (JCYJ20210324120404013), the Shenzhen Science and Technology Program, China (GJHZ20210705141401004), the Talent Recruitment Project of Guandong Province (2019QN01G098) and the National Natural Science Foundation of China (No. 11932005; 52102244).References
- A. Hauch, R. Kungas, P. Blennow, A. B. Hansen, J. B. Hansen, B. V. Mathiesen and M. B. Mogensen, Recent advances in solid oxide cell technology for electrolysis, Science, 2020, 370(6513), 1–8 CrossRef.
- J. T. S. Irvine, D. Neagu, M. C. Verbraeken, C. Chatzichristodoulou, C. Graves and M. B. Mogensen, Evolution of the electrochemical interface in high-temperature fuel cells and electrolysers, Nat. Energy, 2016, 1, 15014 CrossRef CAS.
- C. Graves, S. D. Ebbesen, S. H. Jensen, S. B. Simonsen and M. B. Mogensen, Eliminating degradation in solid oxide electrochemical cells by reversible operation, Nat. Mater., 2015, 14, 239–244 CrossRef CAS.
- S. D. Ebbesen, S. H. Jensen, A. Hauch and M. B. Mogensen, High temperature electrolysis in alkaline cells, solid proton conducting cells, and solid oxide cells, Chem. Rev., 2014, 114, 10697–10734 CrossRef CAS.
- M. B. Mogensen, M. Chen, H. L. Frandsen, C. Graves, J. B. Hansen, K. V. Hansen, A. Hauch, T. Jacobsen, S. H. Jensen, T. L. Skafte and X. Sun, Reversible solid-oxide cells for clean and sustainable energy, Clean Energy, 2019, 3, 175–201 CrossRef.
- S. Ovtar, X. Tong, J. J. Bentzen, K. T. S. Thyden, S. B. Simonsen and M. Chen, Boosting the performance and durability of Ni/YSZ cathode for hydrogen production at high current densities via decoration with nano-sized electrocatalysts, Nanoscale, 2019, 11, 4394–4406 RSC.
- X. Tong, S. Ovtar, K. Brodersen, P. V. Hendriksen and M. Chen, A 4 × 4 cm2 nanoengineered solid oxide electrolysis cell for efficient and durable hydrogen production, ACS Appl. Mater. Interfaces, 2019, 11, 25996–26004 CrossRef CAS.
- Y. Su, Z. Zhong and Z. Jiao, A novel multi-physics coupled heterogeneous single-cell numerical model for solid oxide fuel cell based on 3D microstructure reconstructions, Energy Environ. Sci., 2022, 15(6), 2410–2424 RSC.
- X. Sun, P. V. Hendriksen, M. B. Mogensen and M. Chen, Degradation in solid oxide electrolysis cells during long term testing, Fuel Cells, 2023, 19(6), 740–747 CrossRef.
- M. Chen, Y. L. Liu, J. J. Bentzen, W. Zhang, X. Sun, A. Hauch, Y. Tao, J. R. Bowen and P. V. Hendriksen, Microstructural degradation of Ni/YSZ electrodes in solid oxide electrolysis cells under high current, J. Electrochem. Soc., 2013, 160, F883–F891 CrossRef CAS.
- A. Hauch, K. Brodersen, M. Chen and M. B. Mogensen, Ni/YSZ electrodes structures optimized for increased electrolysis performance and durability, Solid State Ionics, 2016, 293, 27–36 CrossRef CAS.
- M. P. Hoerlein, M. Riegraf, R. Costa, G. Schiller and K. A. Friedrich, A parameter study of solid oxide electrolysis cell degradation: microstructural changes of the fuel electrode, Electrochim. Acta, 2018, 276, 162–175 CrossRef CAS.
- M. B. Mogensen, A. Hauch, X. Sun, M. Chen, Y. Tao, S. D. Ebbesen, K. V. Hansen and P. V. Hendriksen, Relation between Ni particle shape change and Ni migration in Ni–YSZ electrodes–a hypothesis, Fuel Cells, 2017, 434–441 CrossRef CAS.
- Y. Shang, A. L. Smitshuysen, Y. Miao, Y. Liu, X. Tong, P. S. Jorgensen, L. Rorato, J. Laurencin and M. Chen, 3D microstructural characterization of Ni/yttria stabilized zirconia electrodes in long-term CO2 electrolysis, J. Mater. Chem. A, 2023, 12245–12257 RSC.
- D. Kennouche, Y. c. K. Chen-Wiegart, J. S. Cronin, J. Wang and S. A. Barnett, Three-dimensional microstructural evolution of Ni-yttria-stabilized zirconia solid oxide fuel cell anodes at elevated temperatures, J. Electrochem. Soc., 2013, 160(9), F1293–F1304 CrossRef CAS.
- E. Lay-Grindler, J. Laurencin, J. Villanova, P. Cloetens, P. Bleuet, A. Mansuy, J. Mougin and G. Delette, Degradation study by 3D reconstruction of a nickel–yttria stabilized zirconia cathode after high temperature steam electrolysis operation, J. Power Sources, 2014, 269, 927–936 CrossRef CAS.
- N. H. Menzler, D. Sebold, Y. J. Sohn and S. Zischke, Post-test characterization of a solid oxide fuel cell after more than 10 years of stack testing, J. Power Sources, 2020, 478, 228770 CrossRef CAS.
- M. B. Mogensen, M. Chen, H. L. Frandsen, C. Graves, A. Hauch, P. V. Hendriksen, T. Jacobsen, S. H. Jensen, T. L. Skafte and X. Sun, Ni migration in solid oxide cell electrodes: review and revised hypothesis, Fuel Cells, 2021, 415–429 CrossRef CAS.
- Z. Jiao and N. Shikazono, Study on the effects of polarization on local morphological change of nickel at active three-phase-boundary using patterned nickel-film electrode in solid oxide fuel cell anode, Acta Mater., 2017, 135, 124–131 CrossRef CAS.
- Z. Jiao and N. Shikazono, In operando optical study of active three phase boundary of nickel-yttria stabilized zirconia solid-oxide fuel cell anode under polarization, J. Power Sources, 2018, 396, 119–123 CrossRef CAS.
- Z. Jiao, E. P. Busso and N. Shikazono, Influence of polarization on the morphological changes of nickel in fuel electrodes of solid oxide cells, J. Electrochem. Soc., 2020, 167, 024516 CrossRef CAS.
- T.-L. Cheng, Y. Lei, Y. Chen, Y. Fan, H. Abernathy, X. Song and Y.-H. Wen, Oxidation of nickel in solid oxide cells during electrochemical operation: experimental evidence, theoretical analysis, and an alternative hypothesis on the nickel migration, J. Power Sources, 2023, 569, 232991 CrossRef CAS.
- A. He, J. Gong and N. Shikazono, Three dimensional electrochemical simulation of solid oxide fuel cell cathode based on microstructure reconstructed by marching cubes method, J. Power Sources, 2018, 385, 91–99 CrossRef CAS.
- K. Matsuzaki, N. Shikazono and N. Kasagi, Three-dimensional numerical analysis of mixed ionic and electronic conducting cathode reconstructed by focused ion beam scanning electron microscope, J. Power Sources, 2011, 196, 3073–3082 CrossRef CAS.
- T. Carraro, J. Joos, B. Ruger, A. Weber and E. Ivers-Tiffee, 3D finite element model for reconstructed mixed-conducting cathodes: I. Performance quantification, Electrochim. Acta, 2012, 77, 315–323 CrossRef CAS.
- J. Joos, T. Carraro, A. Weber and E. Ivers-Tiffee, Reconstruction of porous electrodes by FIB/SEM for detailed microstructure modeling, J. Power Sources, 2011, 196, 7302–7307 CrossRef CAS.
- Q. Li, D. Chai, L. Wang, X. Zhang and G. Li, Fine three-dimensional simulation of the heterogeneous anode of a solid oxide fuel cell with direct internal reforming, Chem. Eng. Sci., 2021, 242, 116747 CrossRef CAS.
- M. E. Lynch, D. Ding, W. M. Harris, J. J. Lombardo, G. J. Nelson and W. K. S. Chiu, Flexible multiphysics simulation of porous electrodes conformal to 3D reconstructed microstructures, Nano Energy, 2013, 2, 105–115 CrossRef CAS.
- Y. Wang, C. Wu, B. Zu, M. Han, Q. Du, M. Ni and K. Jiao, Ni migration of Ni-YSZ electrode in solid oxide electrolysis cell: an integrated model study, J. Power Sources, 2021, 516, 230660 CrossRef CAS.
- Y. Lei, T.-L. Cheng, H. Abernathy, W. Epting, T. Kalapos, G. Hackett and Y. Wen, Phase field simulation of anode microstructure evolution of solid oxide fuel cell through Ni(OH)2 diffusion, J. Power Sources, 2021, 482, 228971 CrossRef CAS.
- Y. Lei, Y.-L. Lee, W. K. Epting, J. H. Mason, T.-L. Cheng, H. Abernathy, G. Hackett and Y.-H. Wen, Modeling Ni redistribution in the hydrogen electrode of solid oxide cells through Ni(OH)2 diffusion and Ni-YSZ wettability change, J. Power Sources, 2022, 545, 231924 CrossRef CAS.
- L. Rorato, Y. Shang, S. Yang, M. Hubert, K. Couturier, L. Zhang, J. Vulliet, M. Chen and J. Laurencin, Understanding the Ni Migration in Solid Oxide Cell: A Coupled Experimental and Modeling Approach, J. Electrochem. Soc., 2023, 170, 034504 CrossRef CAS.
- Z. Jiao and N. Shikazono, Simulation of nickel morphological and crystal structures evolution in solid oxide fuel cell anode using phase field method, J. Electrochem. Soc., 2014, 161(5), F577–F582 CrossRef CAS.
- J. M. Howe, Bonding, structure, and properties of metal/ceramic interfaces: part 1 chemical bonding, chemical reaction, and interfacial structure, Int. Mater. Rev., 1993, 38(5), 233–256 CrossRef CAS.
- H. Comert and J. N. Pratt, The standard molar Gibbs free energy of formation of NiO from high-temperature e.m.f. measurements, J. Chem. Thermodyn., 1984, 16(12), 1145–1148 CrossRef CAS.
- D. Chatain, L. Coudurier and N. Eustathopoulos, Wetting and interfacial bonding in ionocovalent oxide-liquid metal systems, Rev. Phys. Appl., 1988, 23(6), 1055–1064 CrossRef CAS.
- M. G. H. M. Hendriks, H. J. M. Bouwmeester, J. E. ten Elshof and H. Verweij, The defect structure of the double layer in yttria-stabilised zirconia, Solid State Ionics, 2002, 154, 467–472 CrossRef.
- W. Q. Wang and Z. Suo, A simulation of electromigration-induced transgranular slits, J. Appl. Phys., 1996, 79(5), 2394–2403 CrossRef CAS.
- S. B. Liang, C. B. Ke, M. Y. Tan, M. B. Zhou and X. P. Zhang, Phase field simulation of the microstructural evolution and electromigration-induced phase segregation in line-type Cu/Sn-Bi/Cu solder interconnects, in 17th International Conference on Electronic Packaging Technology, 2016, pp. 836–840 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06563d |
| ‡ Co-first authors of the article. |
| This journal is © The Royal Society of Chemistry 2024 |